发动机进气系统噪声是汽车噪声的重要组成部分之一，它对于车辆通过噪声和车内乘客的乘坐舒适性有很大影响. 通常为了降低进气噪声，在进气系统中设计有波长管、赫姆霍兹谐振腔等消声元件. 目前，有许多汽车厂商逐渐将编织管应用到进气系统中^[1]，以提升进气系统的NVH水平.

常用的编织管由高强度尼龙线编织而成，覆盖有棉织物、树脂涂层. 编织管具有良好的韧性和灵活性，相较于其他声学元件更有利于舱内布置，通常应用于接近进气口的引气管部位^[2]. 编织管能够在宽频范围内对进气噪声起到衰减作用^[3]，对于高频成分的衰减有利于降低声音的尖锐度，从而提高车内声品质^[4]，但编织管的使用会导致流动阻力的增加^[5]. 编织管的降噪原理复杂，目前国内外对编织管声学性能的研究较少. Park等^{[1, 6]}提出编织管声阻抗的测量方法，对传递损失进行预测. Dokumaci^[7]考虑平均流影响下编织管内、外声场的耦合，将传递损失的理论预测值与实验值进行对比.

编织管的管壁类似于滤芯这类多孔介质，声波在管内传播时，会进入管壁的孔隙内，引起孔隙内空气及材料纤维的振动；由于摩擦及黏滞阻力的作用，声能得到了有效耗散^[8]. 计算机仿真计算方法是研究进气系统声学性能的重要手段^[9]，有限元法用于进气系统消声元件声学性能的预测，准确性得到了验证，能够考虑多孔介质的影响^[10-11].

本文对编织管进行有限元建模，采用Johnson-Champoux-Allard等效流体模型，研究多孔介质材料中的5个特性参数对编织管声学性能的影响. 通过仿真与试验相结合的方法，提取编织管管壁的最佳参数组合，计算传递损失；通过台架试验对实际工作状态下编织管的声学性能进行评估，与编织管静态声学试验结果进行对比，验证编织管的实际应用价值.

1 理论背景 1.1 Johnson-Champoux-Allard (JCA)模型

JCA模型^[12]用于描述多孔吸声材料，应用十分广泛. JCA模型将刚性骨架的空气饱和多孔材料看作等效流体，计算等效密度及等效体积模量，表达式如下：

$\rho = {\alpha _\infty }{\rho _0}\left[ {1 + \frac{{\sigma \phi }}{{{\rm j}{\rho _0}\omega {\alpha _\infty }}}{{\left( {1 + \frac{{4{\rm j}\alpha _\infty ^2\eta {\rho _0}\omega }}{{{\sigma ^2}{\varLambda ^2}{\phi ^2}}}} \right)}^{\frac{1}{2}}}}\right],\quad\quad\quad\quad $

(1)

$K\!\! =\! \!\frac{{\gamma {p_0}}}{{\gamma - \left( {\gamma - 1} \right){{\left[ {1 + \displaystyle\frac{{\sigma '\phi }}{{{\rm j}{N_{{\rm{pr}}}}\omega {\rho _0}{\alpha _\infty }}}{{\left( {1 + \frac{{4{\rm j}\alpha _\infty ^2\eta {\rho _0}\omega {N_{{\rm{pr}}}}}}{{{{\sigma '}^2}{{\varLambda '}^2}{\phi ^2}}}} \right)}^{\frac{1}{2}}}} \right]}^{ - 1}}}}.$

(2)

式中： ${\alpha _\infty }$ 为形状因子， ${\rho _0}$ 为空气密度， $\sigma $ 为流阻率， $\phi $ 为孔隙率， $\omega $ 为角频率， $\eta $ 为空气黏滞系数， $\varLambda $ 为黏性特征长度， $\gamma $ 为绝热常数， ${p_0}$ 为空气压强， ${N_{{\rm{pr}}}}$ 为普朗特数， $\varLambda '$ 为热特征长度. 由此可知，使用JCA模型计算多孔材料的声学性能，需要确定流阻率、孔隙率、形状因子、黏性特征长度及热特征长度这5个特性参数.

流阻率是多孔吸声材料的一个重要参数，它反映了多孔材料对气流的阻碍作用，表达式^[13]为

$\sigma = \frac{{\Delta p}}{{vh}}.$

(3)

式中： $\Delta p$ 为多孔材料两侧的压力差， $v$ 为气体在多孔材料内的平均流速， $h$ 为材料厚度.

孔隙率定义为多孔材料孔隙内气体所占体积与材料总体积的比值，表达式为

$\phi = \frac{{{V_{\rm{a}}}}}{{{V_{\rm{T}}}}}.$

(4)

式中： ${V_{\rm{a}}}$ 为材料孔隙内气体所占体积， ${V_{\rm{T}}}$ 为多孔材料总体积.

形状因子称为曲折度^{[12, 14]}，它从微观上对多孔材料内部的弯曲程度作了描述，表达式为

${\alpha _\infty } = \frac{1}{{{{\cos }^2}\theta }}.$

(5)

式中： $\theta $ 为孔轴线与声传播方向的夹角.

在JCA模型中引入2个特征长度，即 $\varLambda $ 和 $\varLambda '$ ^[12]. 黏性特征长度由多孔介质骨架的几何结构决定，热特征长度基于孔隙的具体形状，并且表征了几何因素对等效体积模量的影响. 两者不完全独立，热特征长度约为黏性特征长度的两倍^[15]，表达式分别如下：

$\varLambda = \frac{{2\int\limits_{{V_{\rm{a}}}} {{{\left| {v(r)} \right|}^2}{\rm d}{V_{\rm{a}}}} }}{{\int\limits_S {{{\left| {v\left( {{r_s}} \right)} \right|}^2}{\rm d}S} }},$

(6)

$\varLambda ' = \frac{{2\int\limits_{{V_{\rm{a}}}} {{\rm d}{V_{\rm{a}}}} }}{{\int\limits_S {{\rm d}S} }}.$

(7)

式中： $v\left( r \right)$ 为气体在孔隙内的流速， ${V_{\rm{a}}}$ 为孔隙内体积， $v\left( {{r_s}} \right)$ 为气体在孔隙内壁表面的流速， $S$ 为孔隙内壁表面积.

1.2 传递损失(transmission loss, TL)

TL^[16]是消声元件入射声功率级与透射声功率级之差，它是对消声元件本身声学特性的反映，只与消声元件本身有关，不包括声源及管道末端声学特性的影响，因此适用于评估系统的声学性能，表达式为

${\rm{TL}} = {L_{{W_{\rm{i}}}}} - {L_{{W_{\rm{t}}}}} = 10{\rm{ lg}}\frac{{{W_{\rm{i}}}}}{{{W_{\rm{t}}}}}.$

(8)

式中： ${L_{{W_{\rm{i}}}}}$ 为入射声功率级， ${L_{{W_{\rm{t}}}}}$ 为透射声功率级， ${W_{\rm{i}}}$ 为入射声功率， ${W_{\rm{t}}}$ 为透射声功率.

2 声学模型 2.1 有限元模型的建立

研究的编织管引气管如图1所示.

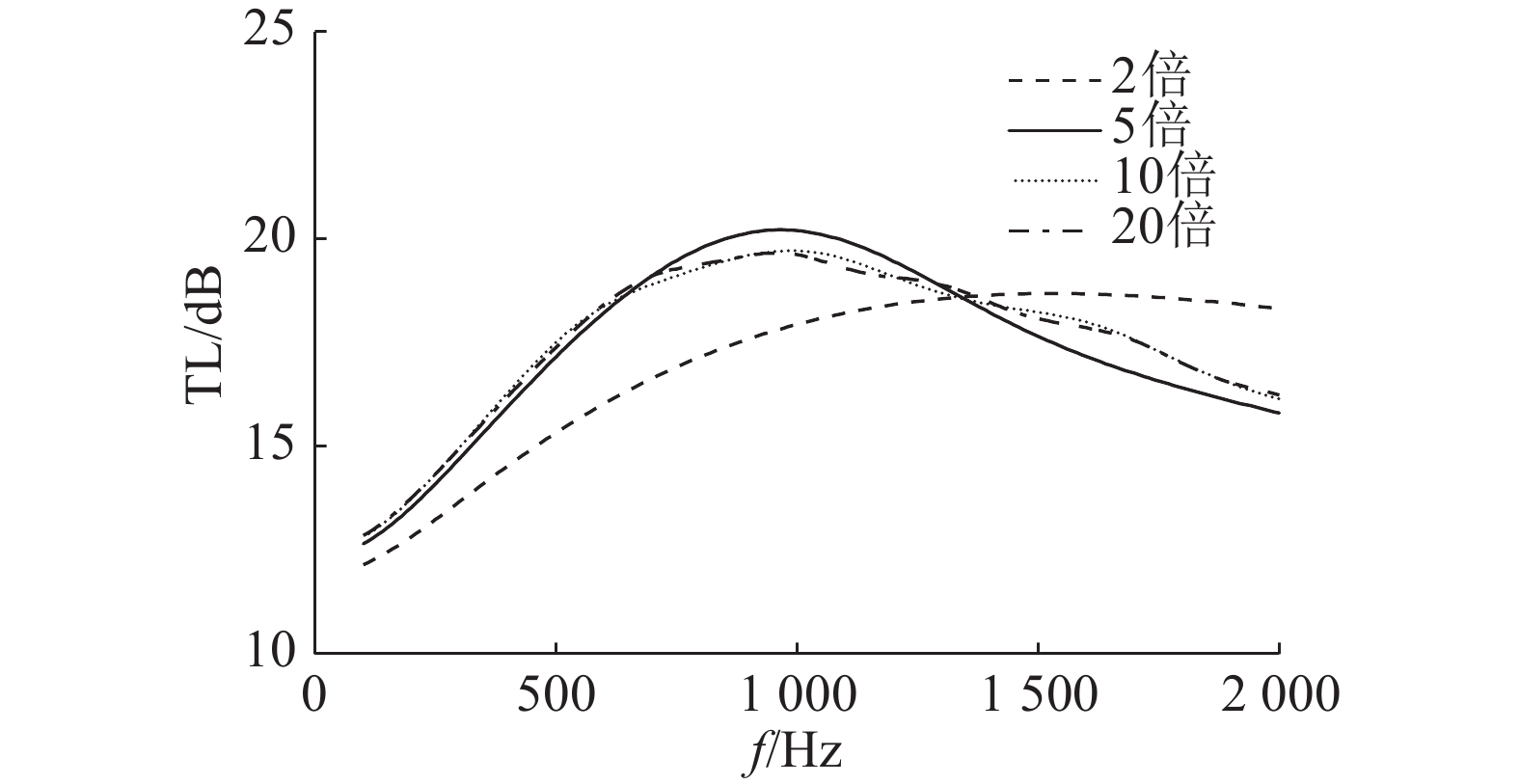
对编织管建立声学有限元模型，编织段管长145 mm，内径约为49.36 mm，壁厚约为2.70 mm. 整个模型分为3个部分：管内声腔、环状编织管管壁段及管外声腔. 由于管壁外侧直接与大气接触，管壁本身作为多孔材料，声音会透过管壁发生少量透射. 为了准确地模拟声音在管内的传播，需要在管壁外侧建立大气模拟区域. 在研究过程中，分别选取编织管外径的2倍、5倍、10倍、20倍尺寸圆柱形区域用于模拟实际的大气边界，TL计算结果如图2所示. 根据计算与修正发现，当大气模拟区域达到10倍编织管外径时，再增大该区域，结果基本保持不变，满足网格无关性. 对于该编织管，取大气半径为300 mm，能够保证计算结果的准确性. 在Hypermesh中对模型进行四面体网格划分，网格模型如图3所示.

2.2 各参数对声学性能的影响

为了获取编织管管壁的材料特性参数，首先需要研究JCA模型中各参数对声学性能的影响. 编织管的骨架可以视为刚性骨架，仅需要分析 $\sigma $ 、 $\phi $ 、 ${\alpha _\infty }$ 、 $\varLambda $ 及 $\varLambda '$ .

采用控制变量法，首先研究流阻率对TL的影响. 通常多孔材料的流阻率为10³~10⁶ Pa·s/m^2[15]，为了保证参数合理，须保证流阻率在该区间内，参数设置如表1所示.

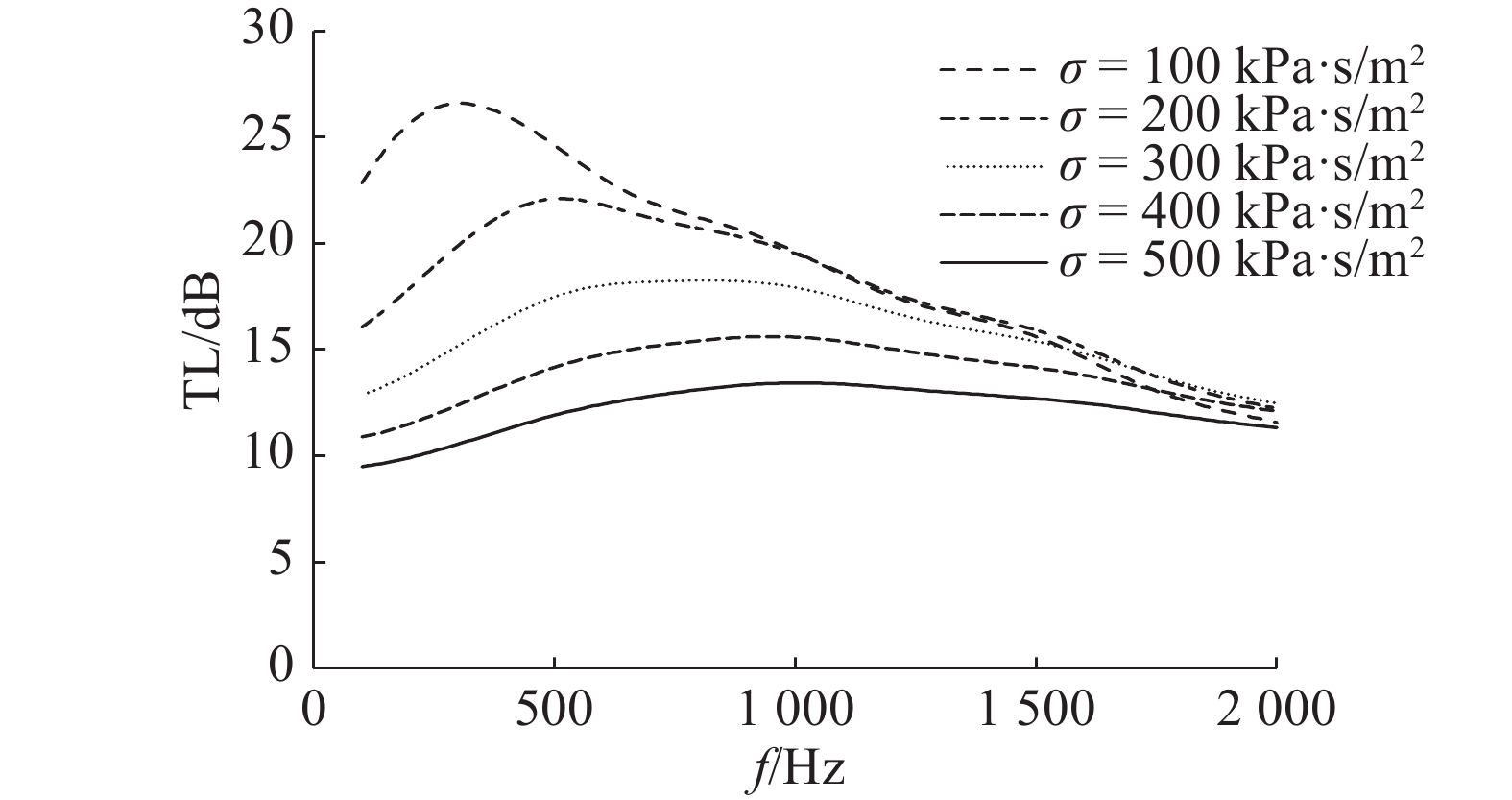
TL受流阻率的影响规律如图4所示. 随着流阻率的增大，TL总体显著下降，曲线趋于平滑. 低频部分下降明显，TL峰值逐渐减小，并且向高频方向移动. 高频部分TL的变化较小. 总体而言，流阻率对于TL尤其是低频范围的影响显著.

由于编织管包含骨架及织物成分，并且壁面通过编织而成，孔隙率比滤芯式多孔材料低得多. 参考金属纤维材料及织物的孔隙率^[17-18]，确定编织管的孔隙率为0.3~0.5. 对孔隙率进行研究，参数设置如表2所示.

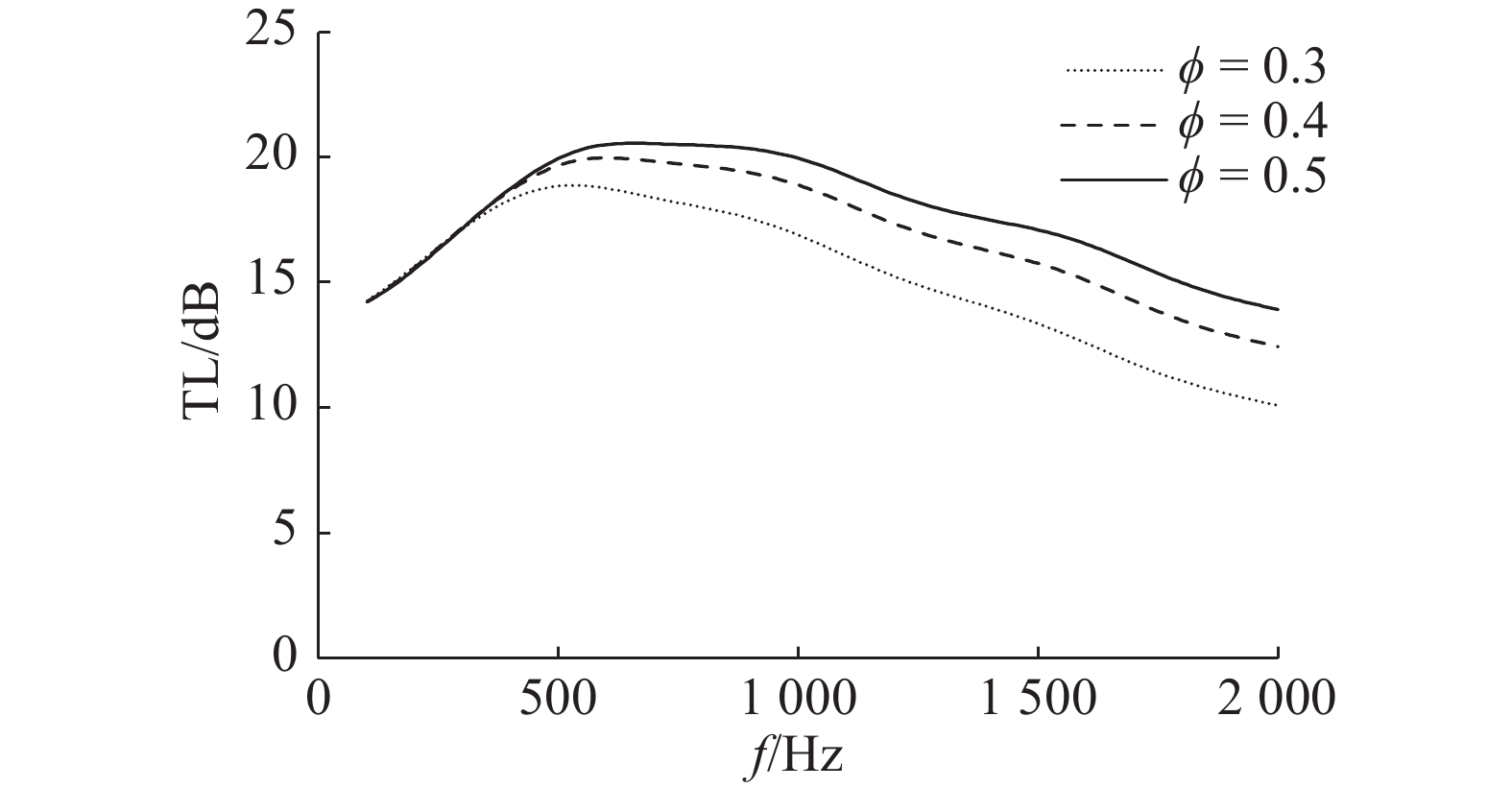
TL受孔隙率的影响规律如图5所示，随着孔隙率的增大，TL总体增加. 在500 Hz以下的低频范围内，TL基本不受孔隙率的影响；在500 Hz以上较高的频率范围内，随着孔隙率的增大，TL明显增大. 这说明孔隙率的改变主要影响了编织管对于高频成分的吸收作用.

由于编织管壁面材料内部存在复杂的弯曲变形结构，需要通过形状因子来进行修正，通常形状因子为1~3^[15]，参数设置如表3所示.

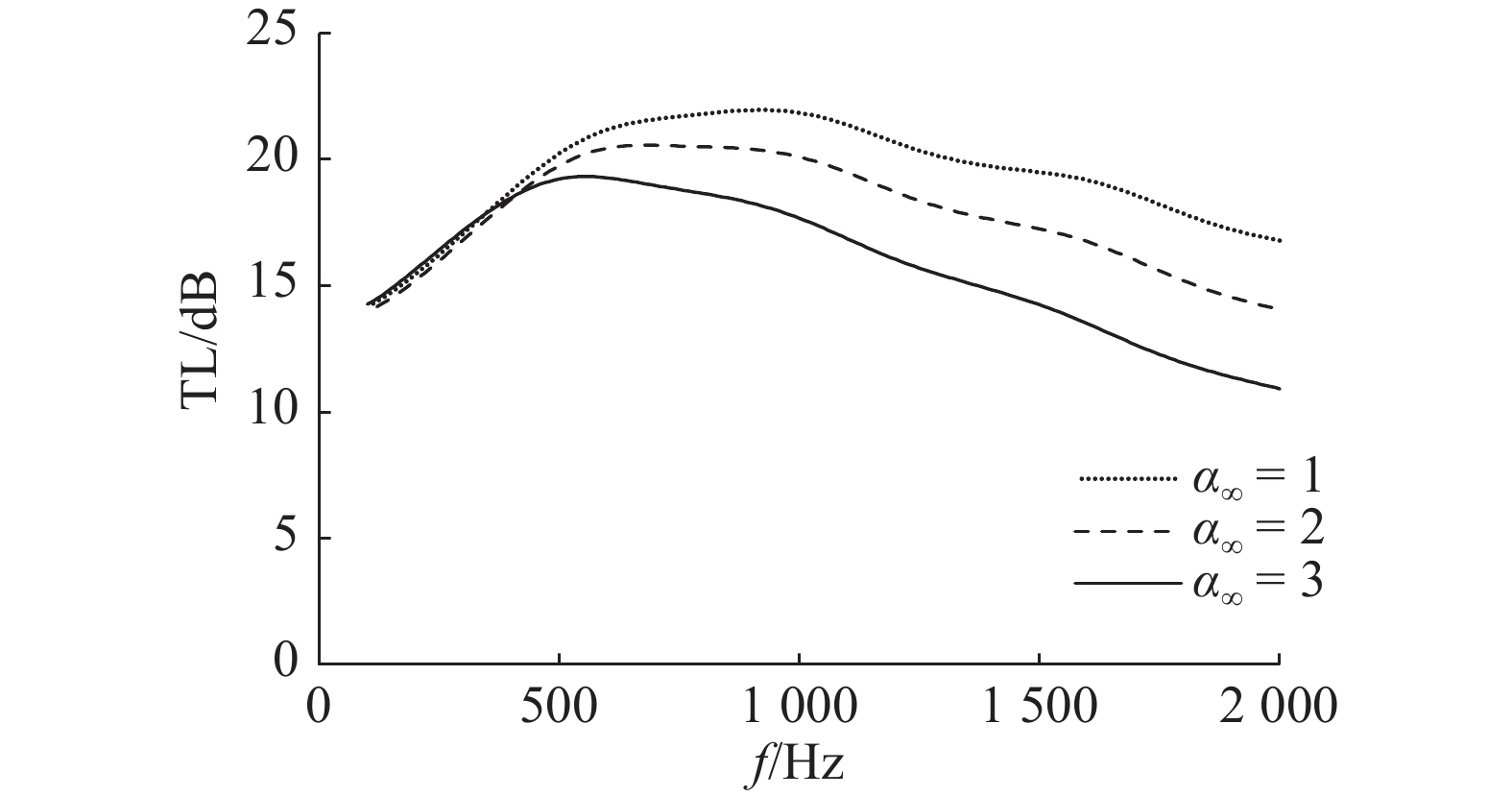
TL受形状因子的影响规律如图6所示，随着形状因子的增大，TL总体下降. 在500 Hz以下的低频范围内，形状因子改变，TL基本不变. 500 Hz以上的频率范围内，TL随形状因子的增大而明显降低.

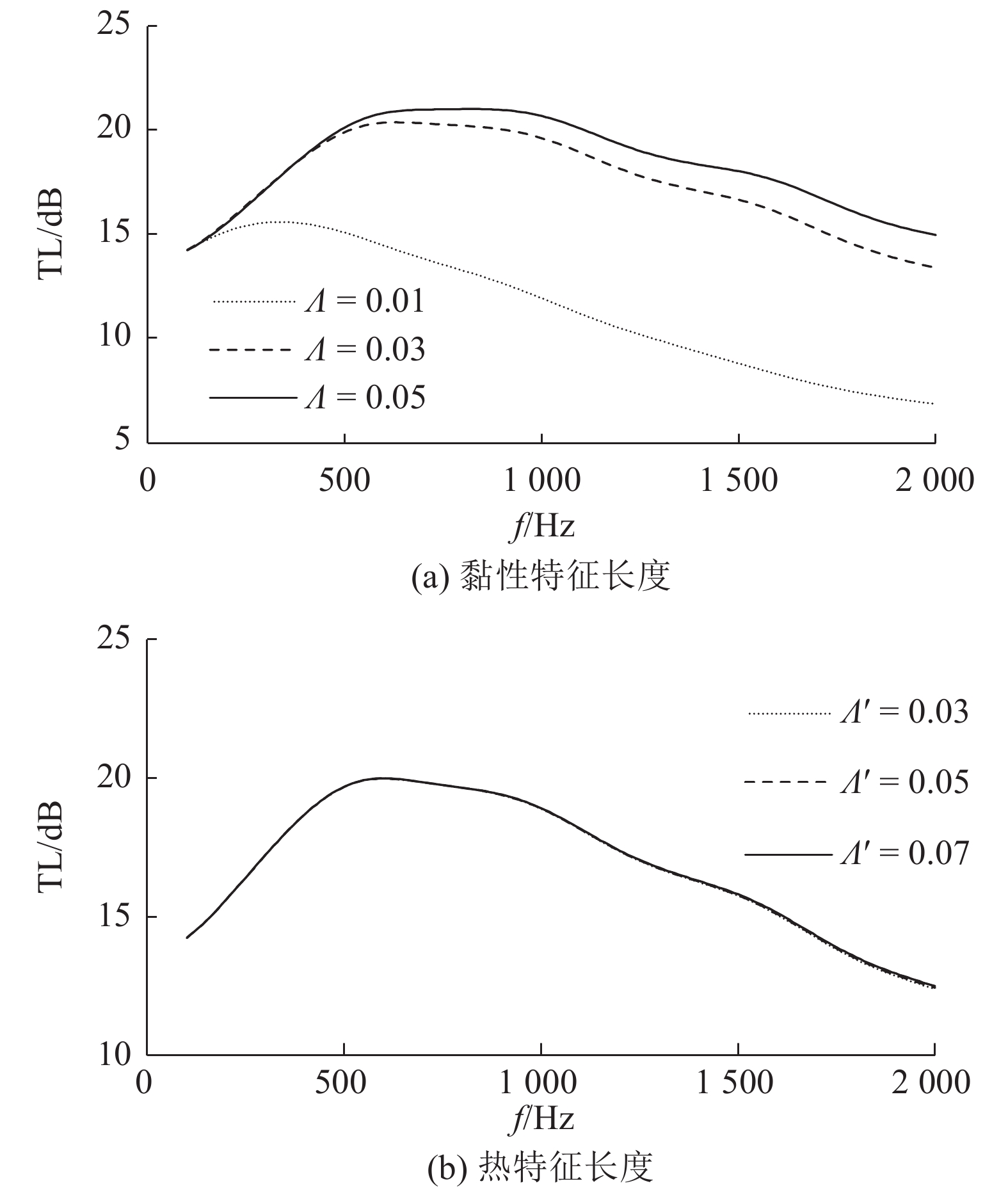
黏性特征长度及热特征长度用来表征多孔介质的孔径大小. 为了分别探究2种特征长度的影响，首先固定热特征长度为0.05 mm，改变黏性特征长度，参数如表4所示. 然后固定黏性特征长度为0.025 mm，改变热特征长度，参数如表5所示.

2个参数的影响规律结果分别如图7(a)、(b)所示. 可知，黏性特征长度增加，TL整体增大，但低频部分保持不变. 这是由于孔隙间的连通性更好，声音被有效吸收，尤其对于高频成分的吸收效果显著. 固定黏性特征长度，仅改变热特征长度，对于TL几乎无影响.

3 静态声学性能

由于编织管的结构特性复杂，并且实际状态下编织和包裹状态存在不均匀性，需要利用仿真与试验相结合的方法^[11]来获取编织管管壁的特性参数组合.

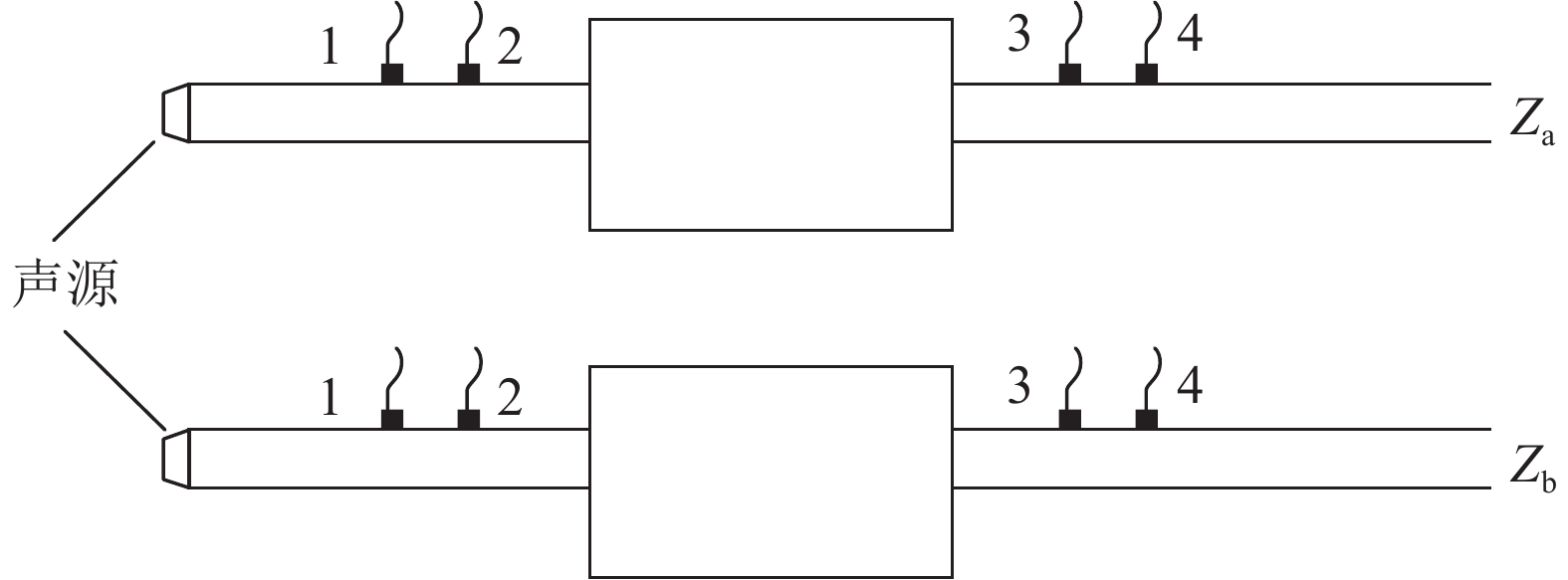
3.1 TL测量试验

TL在实际测量中难以保证管道末端达到全消音，因而对于TL的测量采用两负载法^[19]. 两负载法主要基于传递矩阵法，测量原理如图8所示. 麦克风1、2置于声学元件入射侧，麦克风3、4置于声学元件透射侧，声学元件位于麦克风2、3之间，建立各麦克风之间的传递矩阵. 通过改变末端负载进行两次测量，计算消声元件的四极参数并得到TL. 计算的TL表达式为

${\rm{TL}} = 20{\rm{ }}\lg \left\{ {\frac{1}{2}\left| {{A_{23}} + \frac{{{B_{23}}}}{{\rho c}} + \rho c {C_{23}} + {D_{23}}} \right|} \right\} + 10{\rm{ }}\lg \left( {\frac{{{S_{\rm{i}}}}}{{{S_{\rm{o}}}}}} \right).$

(9)

式中： ${A_{{\rm{23}}}}$ 、 ${B_{23}}$ 、 ${C_{23}}$ 、 ${D_{{\rm{23}}}}$ 为声学元件的四极参数， ${S_{\rm{i}}}$ 、 ${S_{\rm{o}}}$ 分别为入口、出口处的横截面积.

编织管TL的测量试验在半消声室内开展，测试现场如图9所示.

对编织管段进行测量，上游通过一根PVC管将白噪声声源引至编织管声学入口，下游由一根PVC管引出. 上、下游分别放置一对麦克风，保证麦克风顶面与管内壁面平齐. 两对麦克风之间的距离分别为40和20 mm，由于最高分析频率设为2 000 Hz，麦克风间距满足ASTM Standard E1050-12^[20]的规定，即麦克风间距与最高分析频率须满足如下关系：

$l \ll \frac{{{c_0}}}{{2{f_{\rm{m}}}}}.$

(10)

3.2 试验与仿真结果

通过2.2节中各参数对TL影响的探究，经过反复调试，最终确定编织管壁面的5个特性参数，参数组合如表6所示.

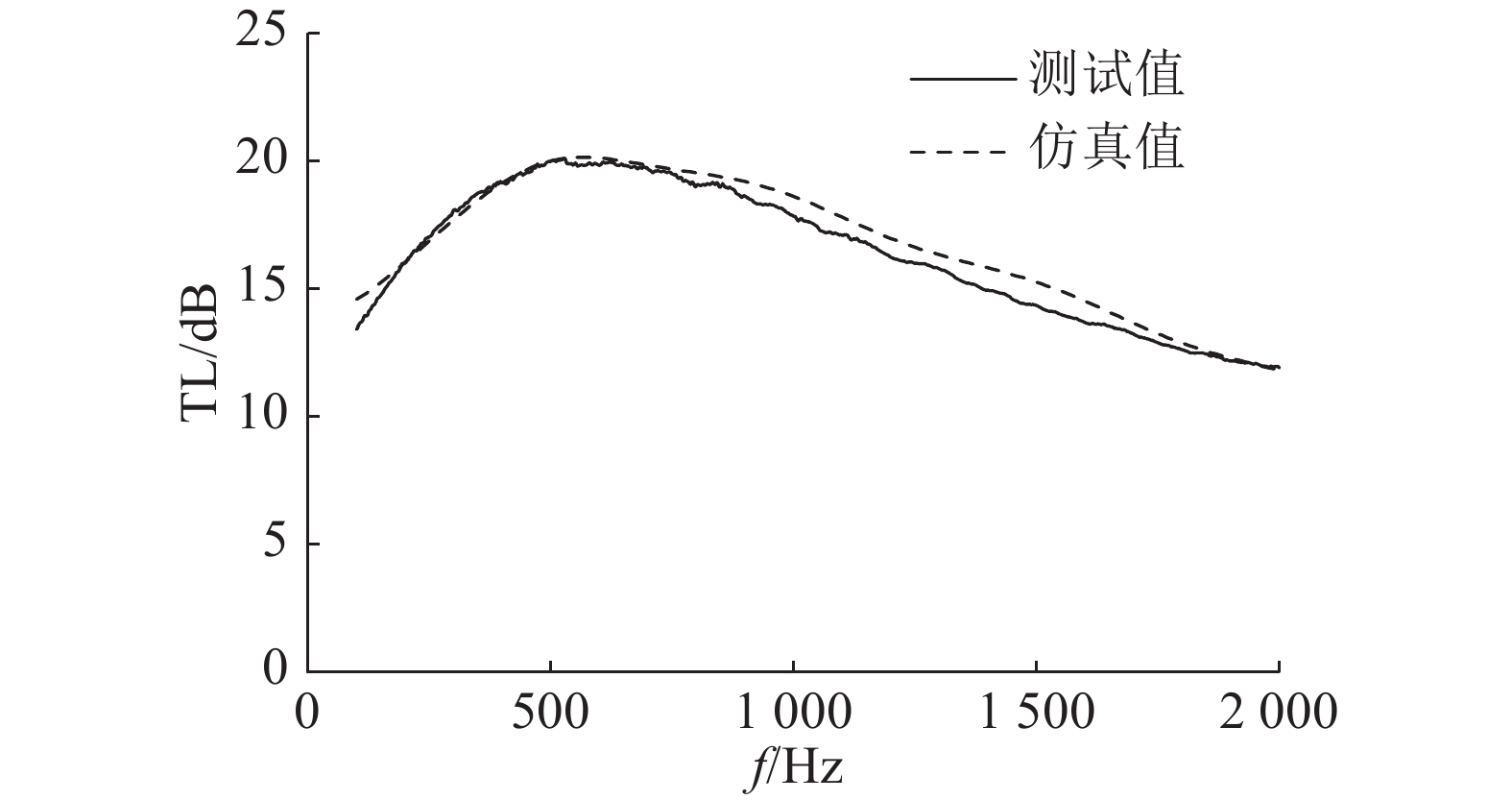
在LMS Virtual.lab中计算编织管的TL时，在入口端施加单位振动速度边界条件，出口端及模拟大气区域外侧定义为无反射边界条件. 仿真计算结果与试验测量结果如图10所示. 可知，计算结果与测试结果基本吻合，仅在部分频率范围内存在少许误差，误差基本不超过1 dB. 这可能是由于在测试过程中编织管部分区域在两端直管连接作用下受力发生了些微变形，导致管壁编织状态变得不均匀，从而对测试结果产生了一定影响. 由TL的测试结果可知，该编织管的平均TL约为16.4 dB，在580 Hz左右存在一个20 dB的消声峰值，之后TL随着频率的升高而降低. 总体而言，编织管在小于2 000 Hz的频率下整体消声性能较强，对于1 000 Hz以下频率的消声作用优于1 000 Hz以上的高频.

4 发动机台架试验

在发动机工作过程中，编织管引气管内有气流流动，气体的流动对编织管的壁面声阻抗会产生一定的影响^[7]. 需要通过发动机台架试验研究，对比编织管静态声学性能，验证评估实际工作状态下编织管的声学性能.

4.1 瞬态加速工况

台架试验在半消声室中开展，测量2.0T涡轮增压发动机在全负荷加速工况下分别安装塑料直管及编织管时的噪声值. 为了减小发动机及测功机等其他背景噪声对进气口测点的影响，用直管将进气噪声引出，并在进气系统与发动机之间采用吸音材料设置一道屏蔽墙. 进气口测点位于距离进气口10 cm且与进气气流轴线成45°处，试验布置如图11所示.

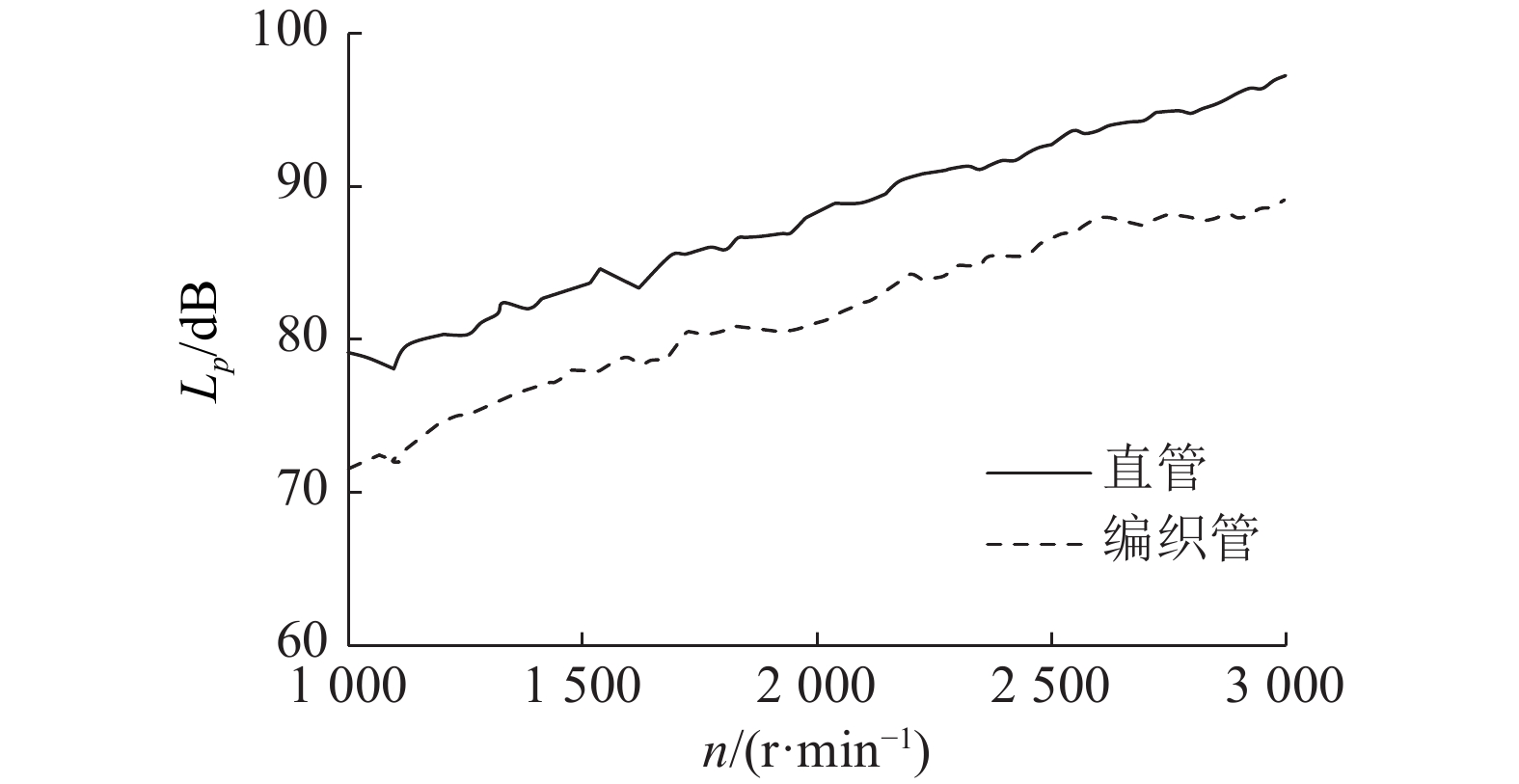
测量屏蔽墙后噪声值发现，200 Hz以上的背景噪声得到有效衰减，能够满足工程测量的需要. 结合TL测试结果的分析，确定关注频段下限为200 Hz，因此在提取噪声总值时不考虑200 Hz以下的低频成分，结果如图12所示. 本文声压级采用A计权后的数值. 图中，n为转速，L_p为声压级.

由进气口声压级测试结果可以看出，安装编织管后全转速范围内的进气口噪声得到了显著衰减，平均约下降了6.3 dB.

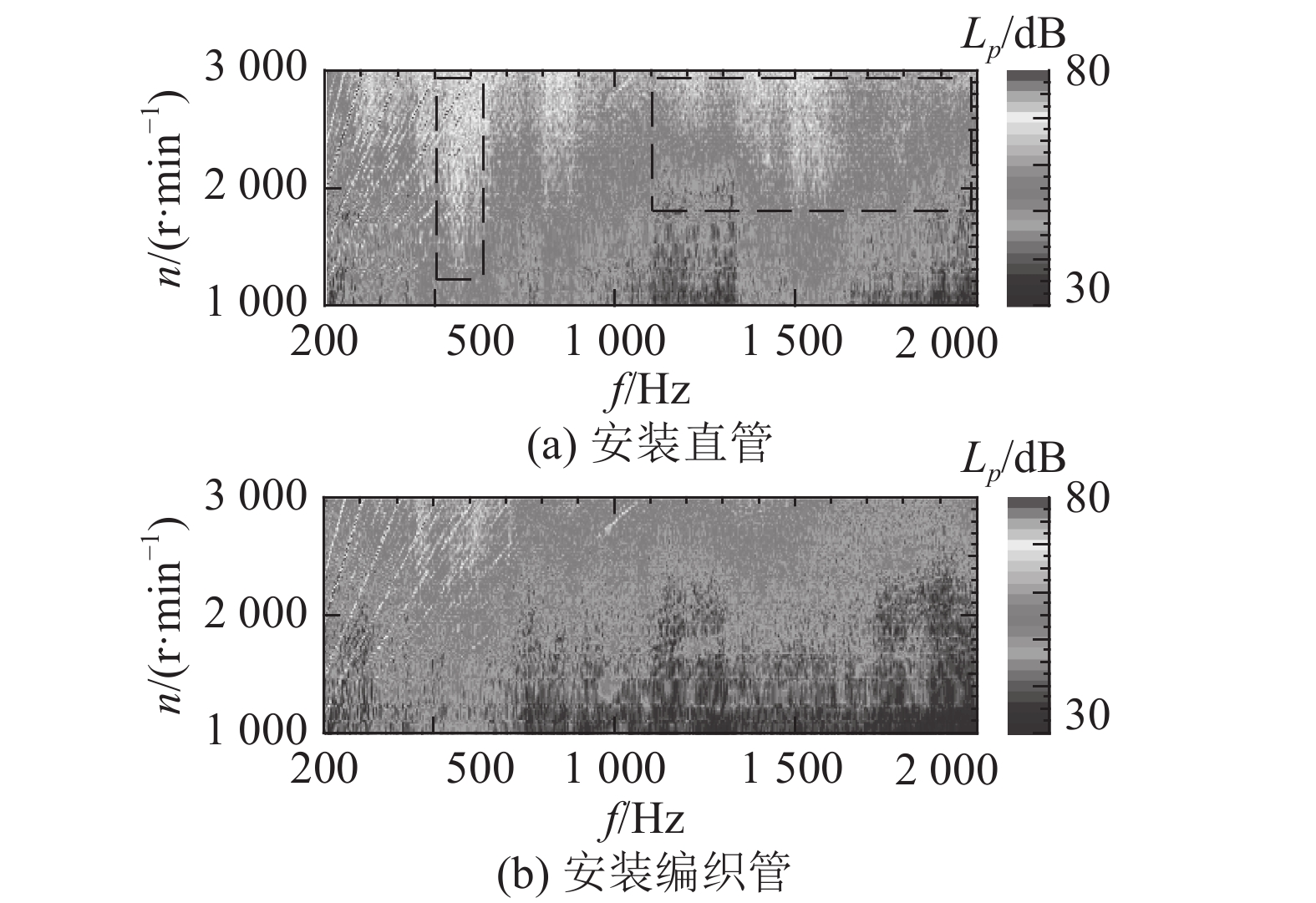
如图13所示为分别安装直管和编织管引气管测得的进气口声压时频图. 在安装直管的状态下，进气口560 Hz附近的噪声能量较高，编织管的使用对于该频率下的噪声衰减作用十分显著. 在发动机的实际工作状态下，进气系统内部存在气流与管壁间的摩擦，随着转速的升高，进气流速增大，进气口1 350~2 000 Hz高频下的气流噪声成分明显增大. 在安装编织管后，噪声能量明显削弱，并且管壁的多孔结构有效衰减了高频噪声能量. 编织管在实际使用中对降低进气口噪声起到了明显的作用.

4.2 稳态工况

为了分析编织管声学性能的频域特性，选取1 000、2 000、3 000 r/min几个稳态工况开展噪声频谱分析，如图14所示. 在各稳态工况下，编织管在宽频范围内对噪声的衰减作用明显，尤其在450~1 000 Hz较低的频率下，SPL最高降低约15 dB，这与静态TL试验结果基本吻合. 结合图13分析可知，1 300 Hz以上的高频下主要为气流噪声成分，编织管作为多孔介质材料，能够有效地衰减声波高频成分，因此各稳态工况下进气口噪声1 300 Hz以上频段成分均得到了显著的降低.

5 结　论

（1）建立编织管声学有限元模型，通过建立管壁外部模拟大气区域来模拟声音的实际传播情况，并确定该区域至少为10倍编织管外径.

（2）基于Johnson-Champoux-Allard模型研究进气系统编织管的声学性能. 结果表明：流阻率对TL的影响最显著，并且主要影响了低频部分，流阻率越高，TL越小；孔隙率、形状因子以及黏性特征长度的改变主要影响了管壁对高频成分的吸收作用，且孔隙率越大，形状因子越小，黏性特征长度越大，则TL随之增大；仅改变热特征长度对于声学性能几乎无影响.

（3）通过静态声学试验的测量，结合仿真方法，提取了编织管管壁的5个特性参数. 由编织管的TL曲线可知，编织管的整体消声性能较强，且对于1 000 Hz以下低频噪声的消声作用优于1 000 Hz以上的高频噪声.

（4）通过发动机台架试验，验证了编织管引气管显著的消声作用. 与静态TL试验进行对比发现，在实际工作状态下，编织管不仅对1 000 Hz以下的低频噪声衰减效果显著，对进气系统中气流产生的高频噪声也有明显的衰减作用. 总体而言，编织管的应用对于降低进气口噪声的效果显著.