目前,在我国使用静电除尘器的燃煤电厂占90%以上[1-3]. 面对日益严格的环境保护标准,电除尘器的除尘效率日益受到重视. 电场内部气流分布是影响电除尘器众多因素中极重要的因素之一,一般是通过多孔板和导流板进行调整,实现气流均布与阻力之间的平衡需要优化多孔板阻力特性.
国内对多孔板的研究相对较少,主要集中在节流及空化特性上. 国际上的研究只局限于使用常温单相流介质(空气或水)的模拟或实验,很少有人模拟除尘器高温环境,研究多孔板阻力系数的影响因素. 赵天怡等[4]使用水介质,研究厚度为2 mm,开孔率为0.04~0.16的多孔板的节流特性,结果发现等效直径比最影响多孔板的节流特性. 田红等[5]通过数值模拟,研究多孔板用于液氮时开孔形式、孔板厚度、开孔大小及等效直径比对压损系数的影响情况. Choi等[6]利用数值计算的方法,确定多孔板不均匀开孔的方案,总结出针对速度不均匀的来流,确定开孔率的公式. Gan等[7]研究薄多孔板在一定范围雷诺数下的压损,通过模拟得到压损系数的计算式. Weber等[8]以水为介质,研究筛水多孔板压损系数与开孔率、厚度、孔口雷诺数的影响关系. Guo等[9]通过计算流体动力学(CFD)模拟研究雷诺数、开孔率、孔径、板厚度、表面粗糙度以及板的倾斜角对多孔板压降及流动状态的影响. 张颉等[10]使用近流线数值模拟方法,模拟两层多孔气流分布板的气固两相流动特性,模拟结果与现场试验结果吻合较好. Bayazit等[11]以空气为工作介质,研究在层流和湍流状态下多孔板压降与雷诺数和孔板厚度的关系,发现孔板厚度是最大的影响因素. Malavasi等[12-14]研究开孔数为3~50、相对厚度为0.2~1.44、开孔率为0.04~0.52的多孔板的阻力特性,总结出相关因素的影响情况. Zhao等[15]采用水作为介质,研究2 mm厚、开孔数为3~13、开孔率为0.04~0.2的多孔板的节流特性,提出计算压降的经验公式. 赵锴等[16]研究中高开孔率,多孔数多孔板的阻力特性,对试验结果进行拟合,得到阻力系数公式,但仅限于单相流常温介质. 多孔板应用十分广泛,在水污染处理、制冷制热装置、气流均布等领域均有应用,研究多孔板在实际环境条件下的阻力特性有利于多孔板在多个工业领域中发挥作用. 本文研究与实际烟温相似环境中高开孔率、多孔数多孔板的阻力特性,包括雷诺数、孔板开孔率、孔板相对厚度及温度对阻力特性的影响.
1 试验方法 1.1 关键参数定义多孔板阻力系数ζ是表征多孔板阻力特性的重要参数. 影响ζ的因素很多,主要包括开孔率β、雷诺数Rep、相对厚度t/d、开孔数n、粉尘质量流量G.
1)开孔率β:多孔板开孔面积与管道截面总面积的比值. 定义为
| $\beta = \frac{{{A_{\rm h}}}}{{{A_{\rm p}}}}.$ | (1) |
式中:Ah为多孔板开孔面积,Ap为管道截面总面积.
2)相对厚度t/d:多孔板厚度t与开孔孔径d的比值.
3)开孔数n:多孔板开孔的个数.
4)雷诺数Rep:用管内流体的雷诺数来描述横管内的流动情况. 定义为
| $R{e_{\rm{p}}} = \frac{{vD}}{\upsilon }.$ | (2) |
式中:v为流体的流速,D为管道直径,ʋ为流体的运动黏度.
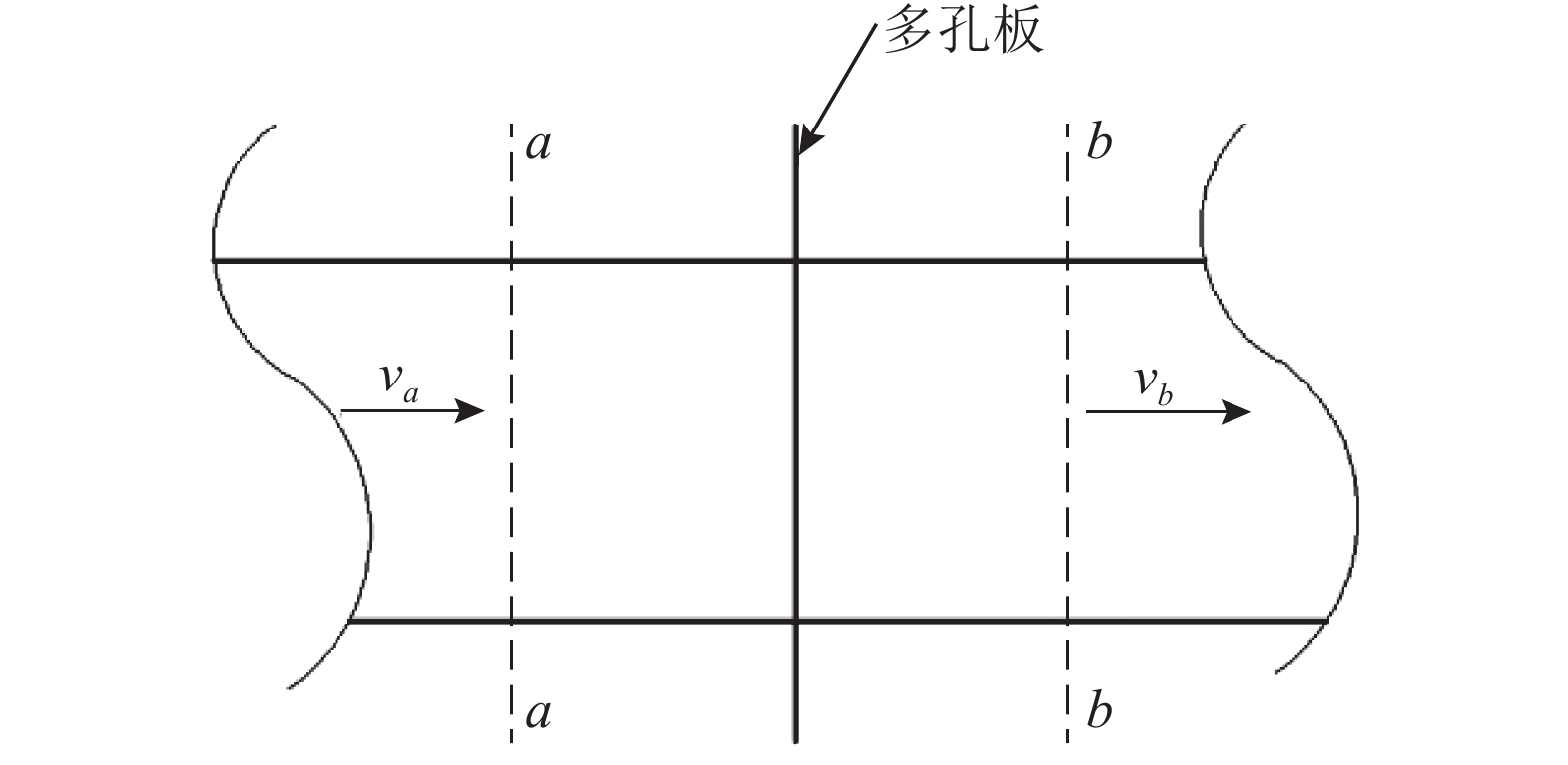
1.2 试验原理该次试验的流动介质为空气或粉尘与空气的混合两相流,如图1所示为试验原理说明图. 取管道上游截面a,管道下游截面b. 根据伯努利方程,可得
| $\begin{split} \rho g{z_a} +& {p_a} + \frac{{{\alpha _a}\rho v_a^2}}{2} = \rho g{z_b} + {p_b} + \frac{{{\alpha _b}\rho v_b^2}}{2} + \\ & \zeta \frac{{\rho v_a^2}}{2} + {\lambda _a}\frac{{{L_a}\rho v_a^2}}{{2{D_a}}} + {\lambda _2}\frac{{{L_b}\rho v_a^2}}{{2{D_b}}}. \end{split} $ | (3) |
式中:za、zb为截面a与截面b的高度,pa、pb为截面a和截面b的压强,va、vb为截面a和截面b上的平均速度,αa、αb为截面a和截面b的动能修正系数,λa、λb为截面a和截面b至管道入口处沿程阻力系数,Da、Db为截面a和截面b的管道直径,La、Lb为截面a和截面b至多孔板的距离,ρ为空气密度,g为重力加速度.
|
图 1 流体流过多孔板示意图 Fig. 1 Air flow through perforated plates |
在该次试验中水平放置试验段,za=zb,αa=αb=1,沿程阻力较小,可以忽略,多孔板上、下游管道直径相等,Da=Db,va=vb. 式(3)简化为
| ${p_{\rm{a}}} - {p_b} = \Delta p = \zeta \frac{{\rho {v^2}}}{2}.$ | (4) |
式中:ζ为多孔板局部阻力系数,
| $\zeta = \frac{{2\Delta p}}{{\rho {v^2}}};$ | (5) |
Δp为上、下游测压孔压差;v为管道内流速.
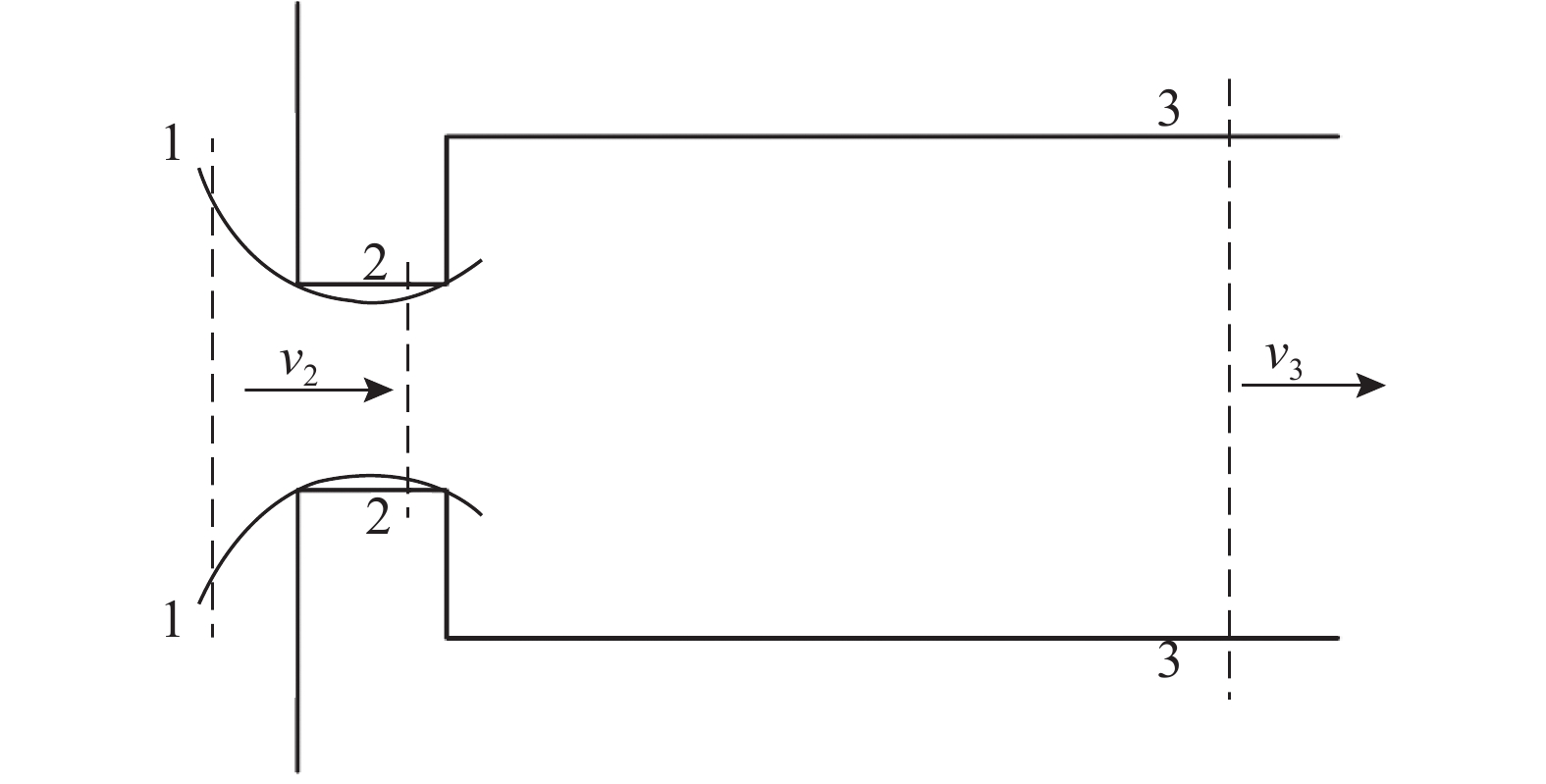
流体穿过多孔板可以看作多股小射流穿过一个个小孔,因此利用理论分析单孔阻力系数表达式. 如图2所示为流体流过薄单孔板的说明图. 流体流过小孔时不完全贴壁,流体流动截面先减小后增大. 取上游截面1、射流最小截面2、下游截面3.
|
图 2 流体流过薄单孔板 Fig. 2 Air flow through thin single orifice plate |
忽略沿程阻力,根据伯努利方程,可得
| ${z_2} + \frac{{{p_2}}}{{\rho {{g}}}} + \frac{{v_2^2}}{{2{{g}}}} = {z_3} + \frac{{{p_3}}}{{\rho g}} + \frac{{v_3^2}}{{2g}}{\rm{ + }}{h_{\rm j}}.$ | (6) |
式中:z2、z3为截面2和截面3的位置高度,p2、p3为截面2和截面3的压强,v2、v3为截面2和截面3上的平均速度,hj为单孔局部阻力造成的能量损失.
忽略体积力,列动量方程为
| ${p_2} {A_2} - {p_3} {A_3} = \rho (v_3^2 {A_3} - v_2^2 {A_2}).$ | (7) |
式中:A1、A2、A3分别为截面1、截面2及截面3的面积.
列连续性方程为
| ${v_{\rm H}}{A_{\rm H}}{\rm{ = }}{v_3} {A_3}{\rm{ = }}{v_2} {A_2}.$ | (8) |
式中:AH为单孔的截面积,vH为单孔内平均流速.
联立式(6)~(8),可得单孔阻力系数表达式:
| ${\zeta _{\rm{s}}} = \frac{{{p_1} - {p_3}}}{{2\rho {v^2}}} = {\left(\frac{{{A_3}}}{{{A_{\rm H}}}} \times \frac{1}{\alpha } - 1\right)^2},$ | (9) |
| ${\zeta _{\rm{s}}} = {\left(\frac{1}{\beta } \times \frac{1}{\alpha } - 1\right)^2}.$ | (10) |
式中:ζs为单孔板局部阻力系数;p1为截面1的压强;α为孔的收缩系数,α=Ac/AH,与孔的流动状态和形状有关.
1.3 多孔板介绍试验采用的多孔板材料为钢板,开孔率为0.30~0.68,厚度为2.5 mm,开孔直径为5、8、12、16 mm. 管道截面为直径为80 mm的圆,多孔板开孔区域为直径为100 mm的圆,可以保证管道中流体介质完全流过多孔板开孔区域. 开孔数为20~272,如图3所示,具体参数如表1所示.

|
图 3 多孔板实物图 Fig. 3 Schematic of perforated plates |
| 表 1 多孔板参数 Table 1 Parameters of perforated plates |
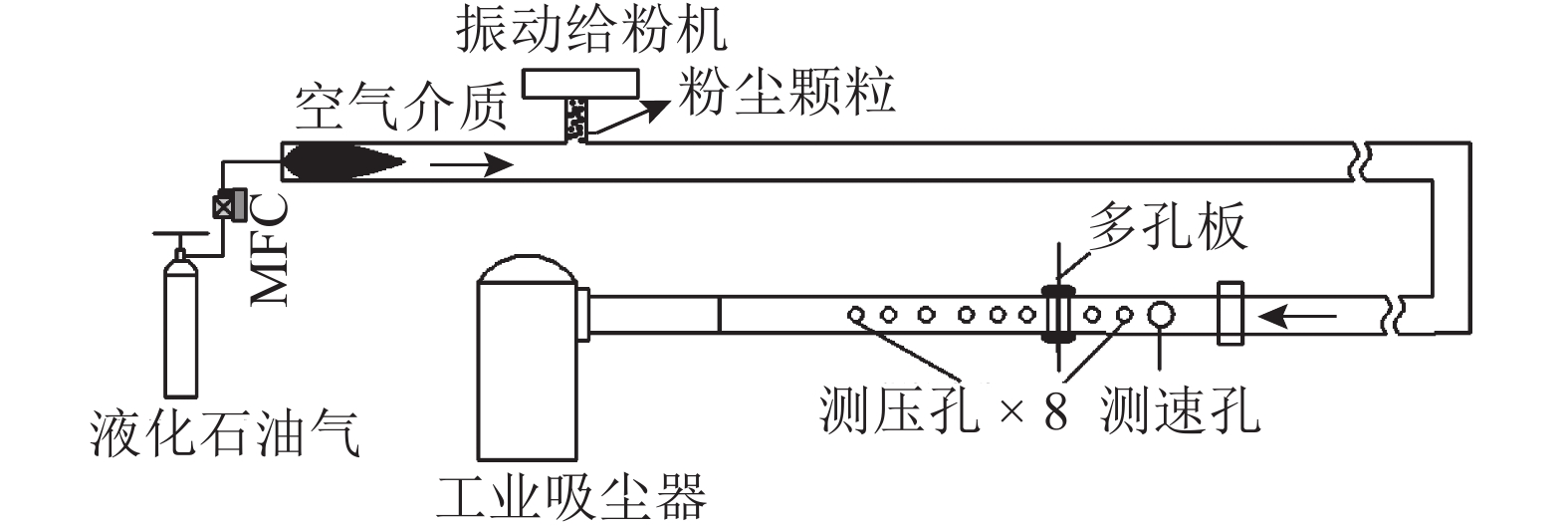
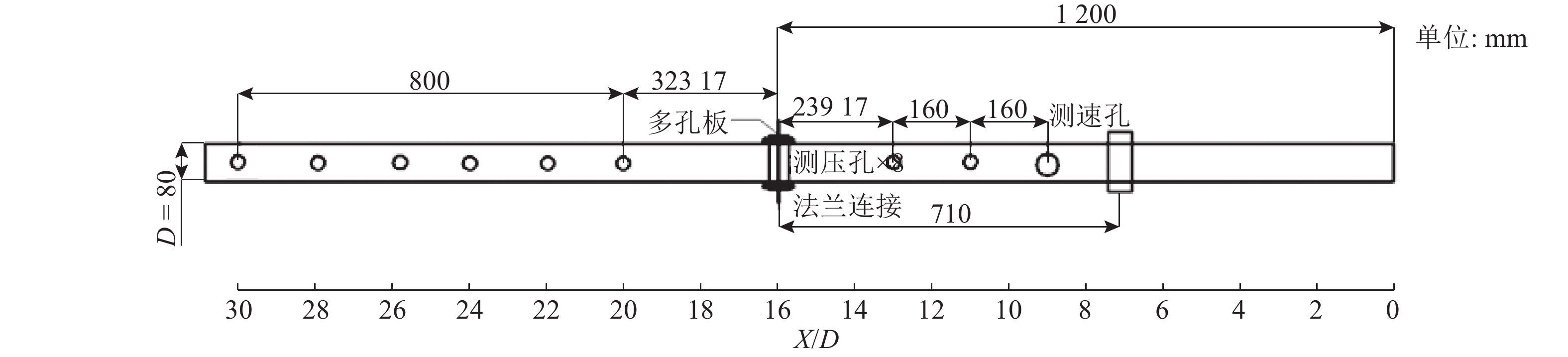
所用的多孔板压降试验台如图4所示. 采用燃烧液化石油气的方式对流体介质加热,由2台工业吸尘器引风. 在试验段中,多孔板放置在管道中间,由法兰固定连接. 管道截面为直径为80 mm的圆形,多孔板前管道段长1.200 m,板后管段长1.123 m,共2.323 m. 测速孔布置在多孔板前管段,距多孔板距离为0.559 m. 测压孔共8个,分别在多孔板前管段布置2个,多孔板后管段布置6个. 如图5所示为详细位置分布图. 图中,X为距离进气入口位置的长度,D为管道直径.
|
图 4 多孔板阻力特性试验系统图 Fig. 4 Schematic diagram of perforated plate resistance characteristics experiment |
|
图 5 测压孔位置分布 Fig. 5 Distribution of pressure measurement holes |
通过试验,对单相不同温度下的多孔板阻力特性进行实验分析.
1)开孔率及雷诺数对阻力系数的影响. 选取不同开孔率的多孔板1~9(β=0.30、0.35、0.40、0.45、0.50、0.55、0.60、0.65、0.68),通过调节吸尘器功率及阀门改变管内流速,用热线风速仪测量管内流速,开展常温单相流介质下开孔率及雷诺数对阻力特性的影响试验.
2)相对厚度对阻力系数的影响. 选取开孔率为0.5,厚度为2.5 mm,孔径分别为5、8、12、16 mm的多孔板(板5、10、11、12)开展试验. 4块多孔板的相对厚度分别为0.5、0.31、0.21、0.16.
3)气体温度对阻力系数的影响. 选取不同开孔率的多孔板1~9分别进行实验,气体温度为10~140 °C.
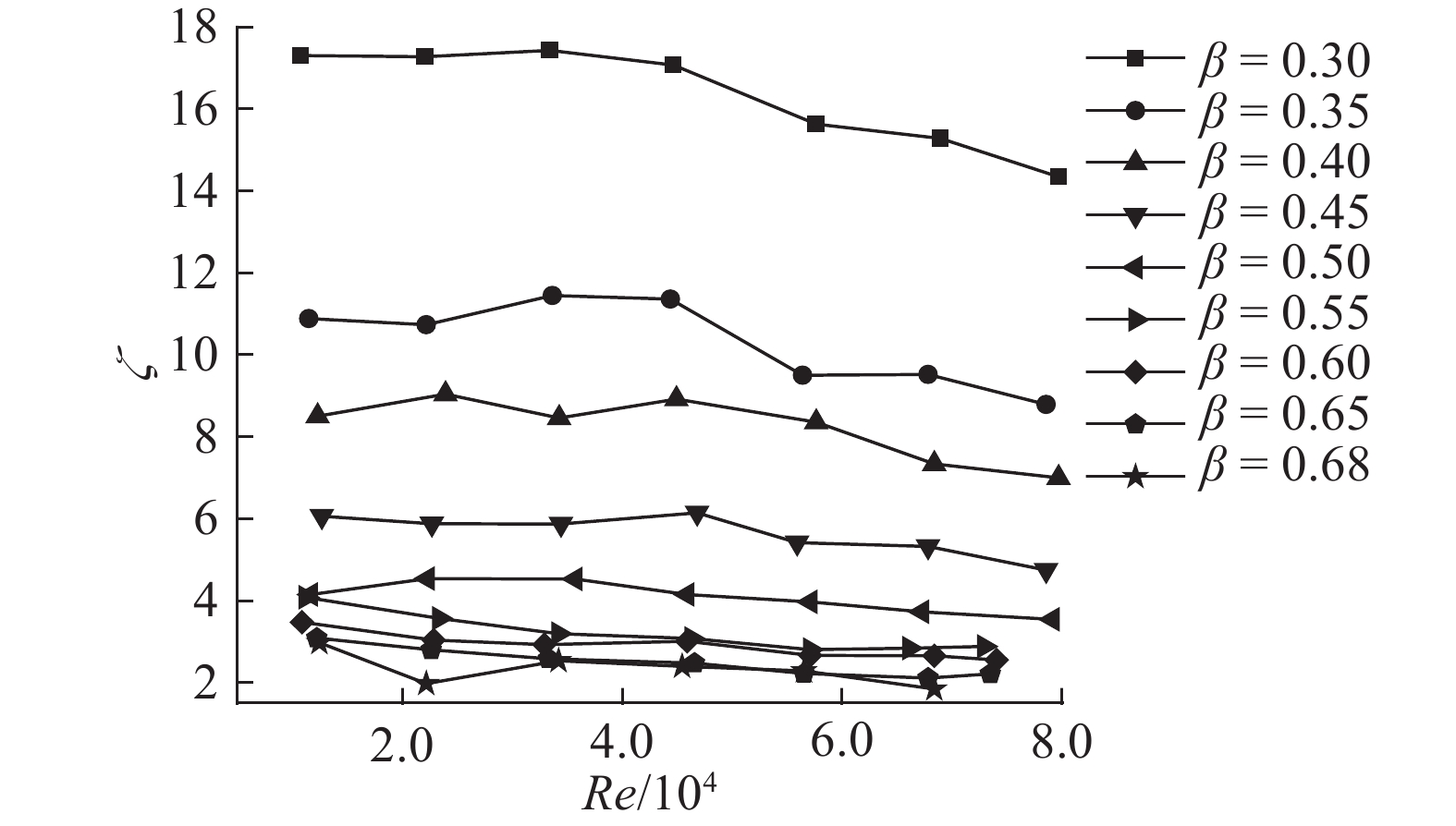
2 试验结果及讨论 2.1 雷诺数对多孔板阻力系数的影响如图6所示为当d=5 mm,θ=10 °C时,多孔板1~9阻力系数随雷诺数的变化情况. 当多孔板开孔率较小(β=0.35、0.40、0.45)时,阻力系数随着雷诺数的增大先缓慢增加,后快速下降,趋势较明显. 当开孔率增大时,变化趋势明显减小,说明当开孔率较大时,雷诺数对阻力系数的影响较小. 这一规律与赵锴等[16]研究的高开孔率多孔板的结果类似. 当空气流体通过多孔板时,可以认为是多股射流穿过多孔板的小孔. 射流与周围空气形成速度不同的间断面. 当雷诺数较小时,射流的核心动量较小,间断面会更容易失去稳定而形成涡旋,使得多孔板的阻力系统较大;随着雷诺数的增大,涡旋较难形成,阻力系数下降.
|
图 6 多孔板阻力系数随雷诺数的变化(d=5 mm, θ=10 °C) Fig. 6 Change of resistance coefficient varying with Reynolds number (d=5 mm, θ=10 °C) |
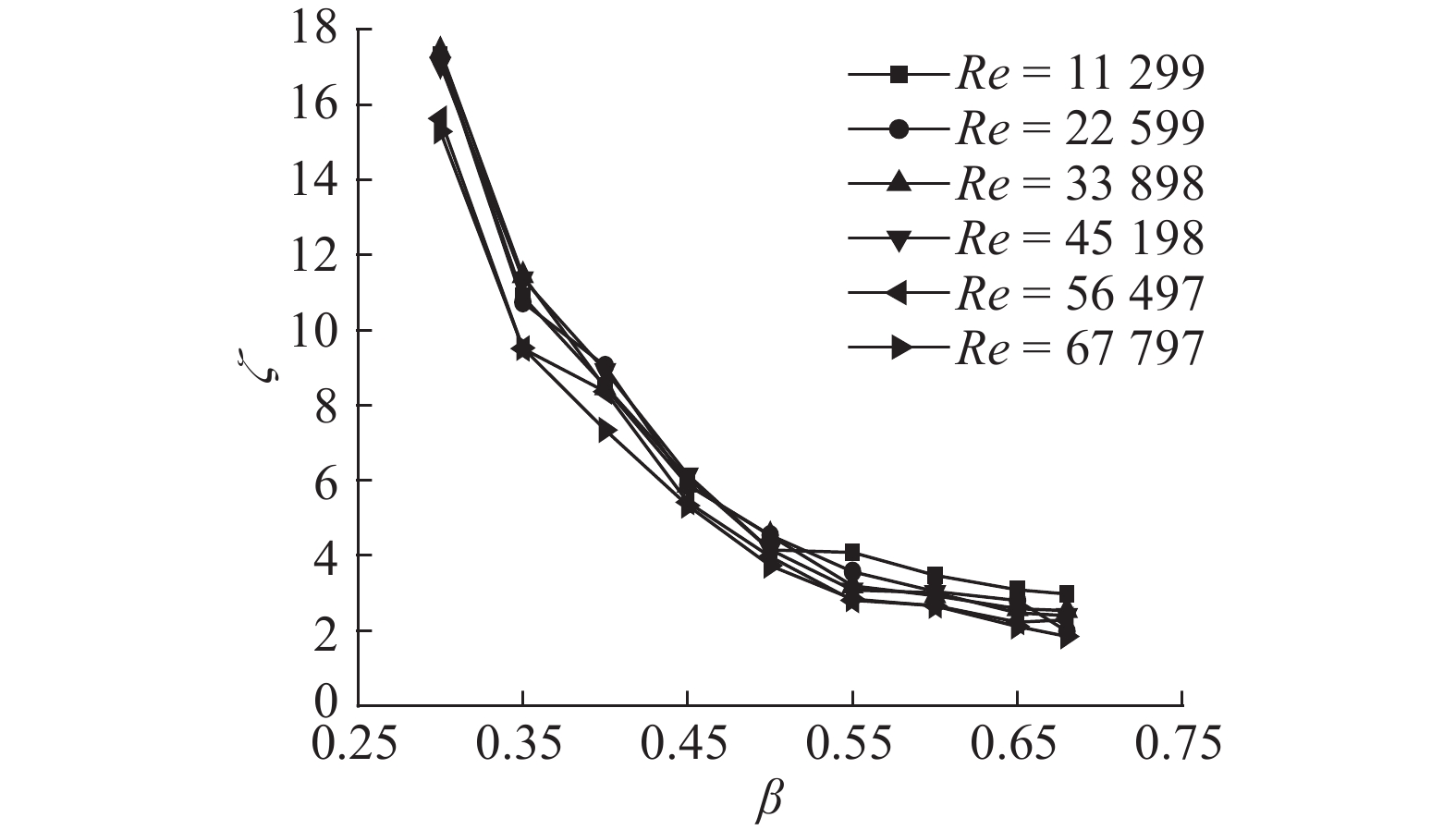
如图7所示为在d=5 mm,θ=10 ℃,不同雷诺数条件下多孔板阻力系数随开孔率的变化情况. 可以看出,在不同的雷诺数条件下,阻力系数随着开孔率的变化趋势一致,阻力系数均随着开孔率的增加而下降,且随着开孔率的增加,下降趋势逐渐变缓. 在相同的雷诺数下,随着开孔率的逐渐减小,管道中流体介质回流区与主流区之间,流体质点与质点之间产生越发剧烈的摩擦、碰撞,流体介质中越来越多的微团分离,然后与主流汇合. 在该过程中,能量消耗逐渐增加,压损增大,所以最终的阻力系数随着开孔率的减小而增大.
|
图 7 多孔板阻力系数随开孔率的变化(d=5 mm, θ=10 °C) Fig. 7 Change of resistance coefficient varying with porosity (d=5 mm, θ=10 °C) |
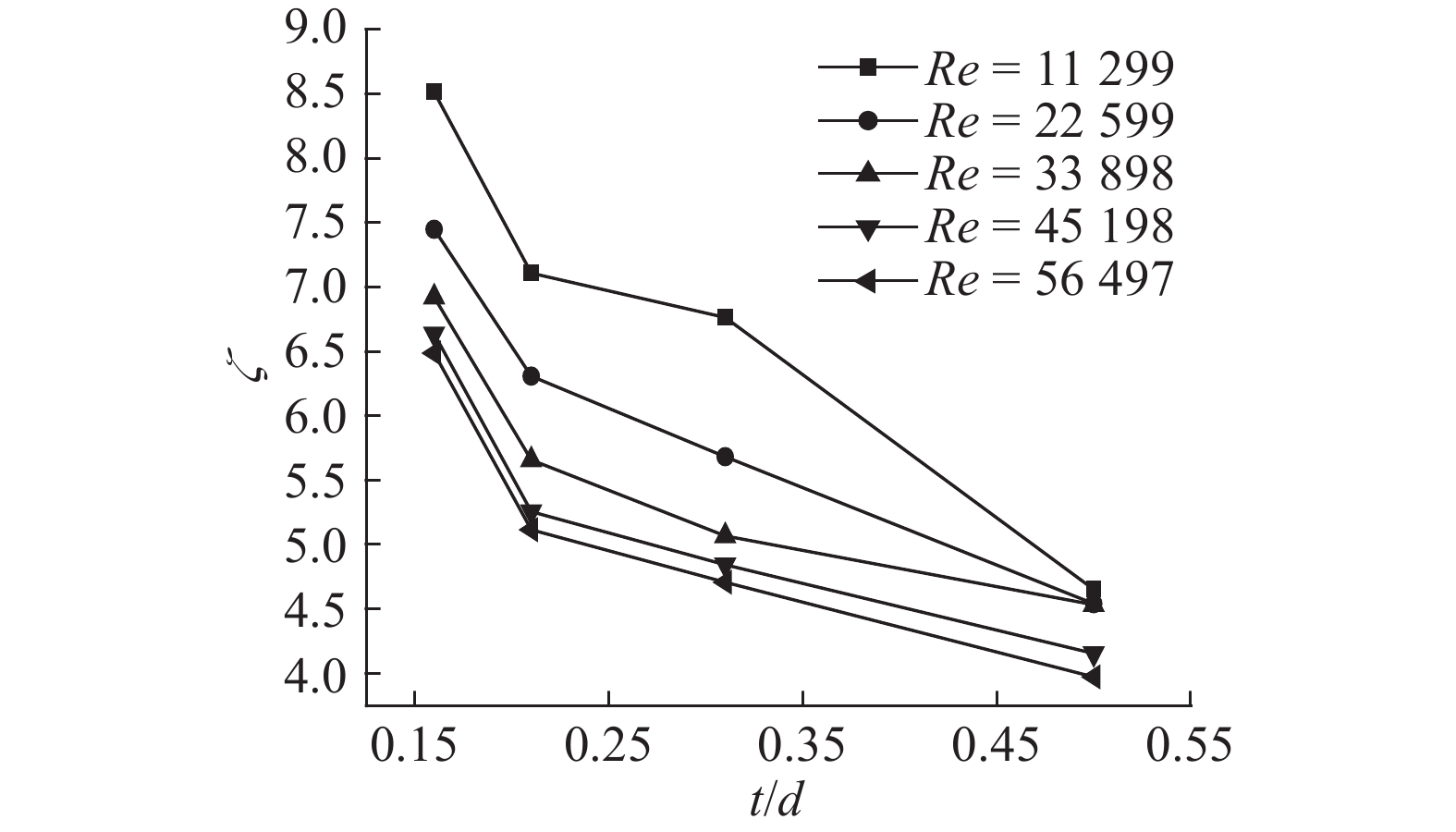
如图8所示为阻力系数随相对厚度(t/d=0.5、0.31、0.21、0.16)的变化情况. 可以看出,随着相对厚度的增加,阻力系数先快速降低;当t/d>0.21时,阻力系数开始缓慢下降. Miller[17]在过去的试验中得到了相似的结论. 随着相对厚度和多孔板的开孔数增加,多孔板多孔之间、孔与管道壁面之间的回流区减小,流体质点与质点之间的摩擦损失减小,导致多孔板压降减小,阻力系数降低.
|
图 8 多孔板阻力系数随相对厚度的变化(β=0.50,θ=10 °C) Fig. 8 Change of resistance coefficient varying with relative thickness (β=0.50, θ=10 °C) |
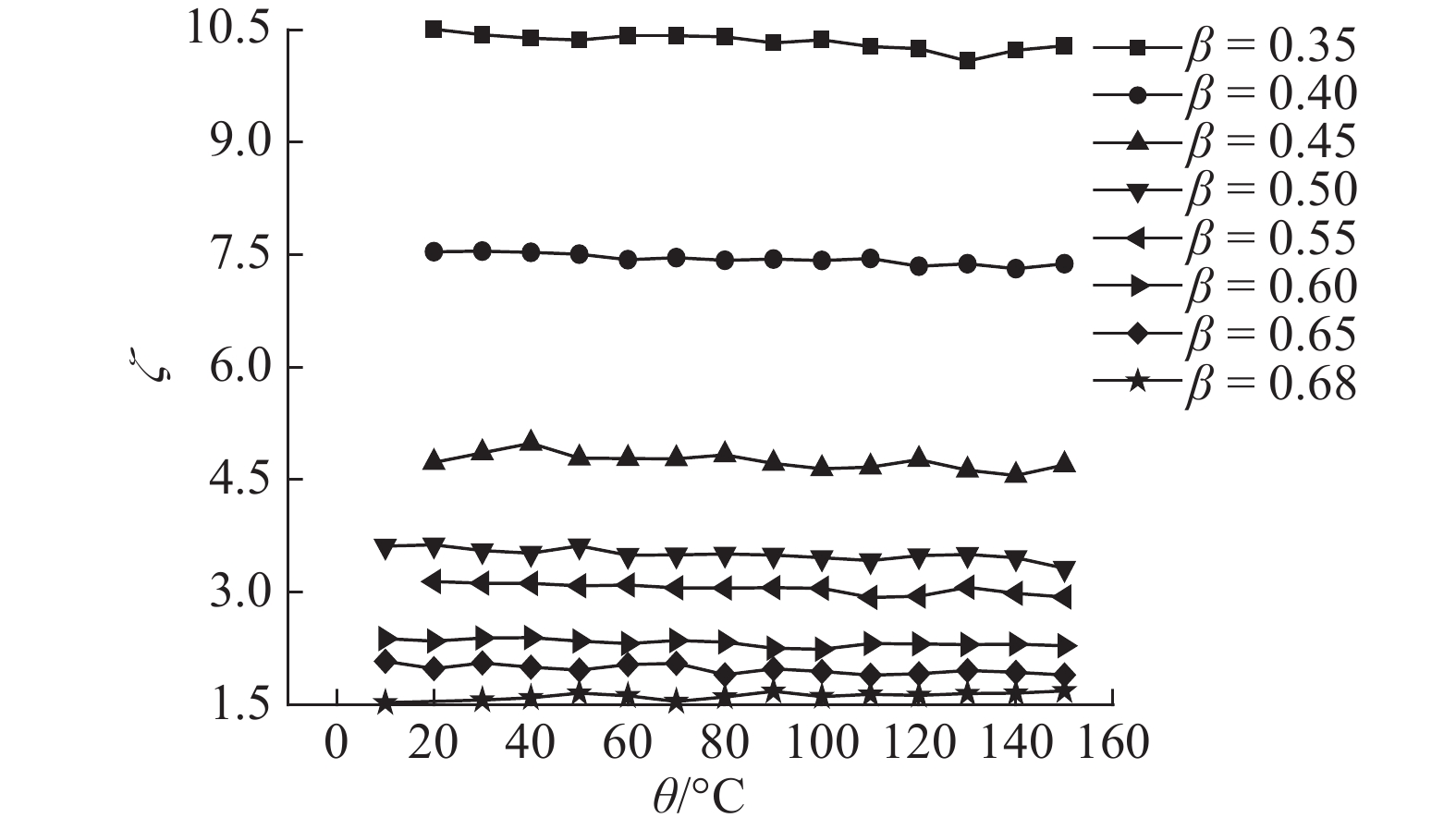
图9给出当孔径均为5 mm时,不同开孔率多孔板1~9阻力系数随气体温度的变化情况. 可以看出,不同多孔板的阻力系数均受气体温度的影响很小.
|
图 9 多孔板阻力系数随温度的变化 (d=5 mm) Fig. 9 Change of resistance coefficient varying with temperature (d=5 mm) |
(1)多孔板压降随着雷诺数的增大而增大,当雷诺数增大时,不同开孔率多孔板的压降差距逐渐增大;当开孔率较大时,雷诺数对阻力系数的影响较弱. 总体来讲,多孔板阻力系数受雷诺数的影响较小.
(2)多孔板阻力系数随着开孔率的增加而下降,随着开孔率的增加,下降趋势逐渐变缓.
(3)随着多孔板的相对厚度增大,阻力系数先快速降低,t/d=0.21后开始缓慢降低.
(4)气体温度对多孔板的阻力系数基本无影响.
| [1] |
VIJAPUR S H. Design optimization and experimental study of a wet laminar electrostatic precipitator for enhancing collection efficiency of aerosols [D]. Ohio: Ohio University, 2008. http://www3.aiche.org/proceedings/Abstract.aspx?PaperID=100639
|
| [2] |
熊贵龙, 李水清, 陈晟, 等. 增强 PM2.5 脱除的新型电除尘技术的发展[J]. 中国电机工程学报, 2015, 35(9): 2217-2223. XIONG Gui-long, LI Shui-qing, CHEN Sheng, et al. Development of advanced electrostatic precipitation technologies for reducing PM2.5 emissions from coal-fired power plants[J]. Proceedings of the CSEE, 2015, 35(9): 2217-2223. |
| [3] |
CHAKINALA A G, GOGATE P R, BURGESS A E, et al. Treatment of industrial wastewater effluents using hydrodynamic cavitation and the advanced Fenton process[J]. Ultrasonicssonochemistry, 2008, 15(1): 49-54. |
| [4] |
赵天怡, 张吉礼. 多孔孔板节流特性主效应因素试验[J]. 哈尔滨工业大学学报, 2007, 39(12): 1878-1881. ZHAO Tian-yi, ZHANG Ji-li. Experimental study on main factor affecting throttling characteristic for multi-hole orifice[J]. Journal of Harbin Institute of Technology, 2007, 39(12): 1878-1881. DOI:10.3321/j.issn:0367-6234.2007.12.007 |
| [5] |
田红, 高旭, 汤珂, 等. 结构参数对多孔板低温流量计性能影响分析[J]. 低温工程, 2015(06): 43-48. TIAN Hong, GAO Xu, TANG Ke, et al. Influence of geometric parameters on performance of a cryogenic fluid flow meter with perforated plate[J]. Cryogenics, 2015(06): 43-48. DOI:10.3969/j.issn.1000-6516.2015.06.009 |
| [6] |
CHOI M K, LIM Y B, LEE H W, et al. Flow uniformizing distribution panel design based on a non-uniform porosity distribution[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 130(130): 41-47. |
| [7] |
GAN G, RIFFAT S B. Pressure loss characteristics of orifice and perforated plates[J]. Experimental Thermal and Fluid Science, 1997, 14(2): 160-165. DOI:10.1016/S0894-1777(96)00041-6 |
| [8] |
WEBER L J, CHERIAN M P, ALLEN M E, et al. Headloss characteristics for perforated plates and flat bar screens [R]. Iowa City, IA: Iowa Institute of Hydraulic Engineering, 2000.
|
| [9] |
GUO B Y, HOU Q F, YU A B, et al. Numerical modelling of the gas flow through perforated plates[J]. Chemical Engineering Research and Design, 2013, 91(3): 403-408. DOI:10.1016/j.cherd.2012.10.004 |
| [10] |
张颉, 张泽, 胡永锋. 高浓度电除尘器入口封头气固两相流动的近流线数值模拟[J]. 化工学报, 2004, 55(9): 1448-1454. ZHANG Jie, ZHANG Ze, HU Yong-feng. Close-to-streamline numerical simulation of gas-solid flow in high concentration ESP gas inlet hood[J]. Journal of Chemical Industry and Engineering, 2004, 55(9): 1448-1454. DOI:10.3321/j.issn:0438-1157.2004.09.014 |
| [11] |
BAYAZIT Y, SPARROW E M, JOSEPH D D. Perforated plates for fluid management: plate geometry effects and flow regimes[J]. International Journal of Thermal Sciences, 2014, 85(85): 104-111. |
| [12] |
MALAVASI S, MACCHI S, MEREGHETTI E. Cavitation and dissipation efficiency of multihole orifices [Z]. Institute of Thermomechanics Academy of Sciences of the Czech Republic, Prague, 2008: 581–586.
|
| [13] |
MALAVASI S, MESSA G V, MACCHI S. The pressure loss coefficient through sharp-edged perforated plates [Z]. Attidel XXXII Convegno Nazionale di Idraulica e Costruzioni Idrauliche, Dipt. of IIAA University of Palermo, 2010: 193.
|
| [14] |
MALAVASI S, MESSA G, FRATINO U, et al. On the pressure losses through perforated plates[J]. Flow measurement and Instrumentation, 2012(28): 57-66. |
| [15] |
ZHAO T, ZHANG J, MA L. A general structural design methodology for multi-hole orifices and its experimental application[J]. Journal of Mechanical Science and Technology, 2011, 25(9): 2237-2246. DOI:10.1007/s12206-011-0706-3 |
| [16] |
周昊, 赵锴, 郭无双, 等. 中高开孔率电除尘器多孔板的阻力特性试验研究[J]. 中国电机工程学报, 2016, 37(9): 2629-2637. ZHOU Hao, ZHAO Kai, GUO Wu-shuang, et al. Research on resistance characteristics of electrostatic precipitator’s perforated plates with medium and high porosity[J]. Proceedings of the CSEE, 2016, 37(9): 2629-2637. |
| [17] |
MILLER D S. Internal flow system [M]. Cranfield: BHRA, 1990: 366–369.
|


