镧改性锆钛酸铅PLZT陶瓷自1970年问世起,由于存在的反常光生伏打效应和光致形变效应,而被研究人员广泛关注. PLZT陶瓷既属于铁电材料和热释电材料,也属于压电材料. 经过极化处理的PLZT陶瓷在受到365 nm的紫外光照射时,在电极两端会产生kV级的光生电压,基于逆压电效应和热弹性效应产生光致形变,可以用作光激励驱动器.
在过去的几十年里,诸多学者针对PLZT陶瓷的理论与工程应用开展一系列研究. Fridkin[1]提出沿极化方向的PLZT陶瓷的RC电学模型;Poosanaas等[2]研究不同组分下PLZT陶瓷的光生伏特现象;2000年,Poosanaas提出光学的二次非线性是导致反常光生伏特效应的重要原因.
PLZT陶瓷具有非接触式的激励作用,在微驱动方面,国内外研究人员提出许多具有应用前景的装置. Uchino等[3]基于PLZT陶瓷双晶片的光致形变特点,设计光继电器和微行走机构;Ichiki等[4]基于PLZT的光伏效应,设计光电机. 李琼等[5]设计光控伺服系统,对该系统进行特性研究,指出提高PLZT响应速度是PLZT陶瓷广泛应用工程的关键.
Tzou等[6]提出将PLZT陶瓷层合于薄壳结构表面,利用PLZT的光致形变来实现振动控制;Tong等[7]将0-3极化的PLZT陶瓷应用于光电层合梁的主动控制,通过优化作动器的布局来实现良好的模态控制;王新杰[8]研究不同尺寸的作动器的驱动能力;Zheng[9]对0-1极化的PLZT陶瓷进行多物理场耦合建模,开展有限元数值仿真.
在对PLZT陶瓷的驱动特性研究和应用研究中发现,光致形变的响应速度迟滞于光生电压现象的存在,极大地制约了PLZT陶瓷工程应用. 黄家瀚等[10-11]建立多场耦合下的PLZT本构方程,提出光生热的存在是导致迟滞效应的主要原因. 为了提高响应速度,姜晶等[12]提出将PLZT与压电作动器直接相连的光控压电驱动方式,提高了驱动器的响应速度,避免了PLZT陶瓷存在单向驱动的问题,但是姜晶等[12]主要分析光控压电驱动器输出电压的影响因素,对层合悬臂梁的挠度输出特性没有进行相应的理论与实验分析.
本文在阐述0-1极化的PLZT/PVDF复合驱动原理的基础上,研究PVDF压电作动器的尺寸参数与层合悬臂梁输出挠度之间的关系,为实现光电/压电复合驱动的效能优化奠定一定的理论基础. 本文所提及的PLZT陶瓷均为0-1极化.
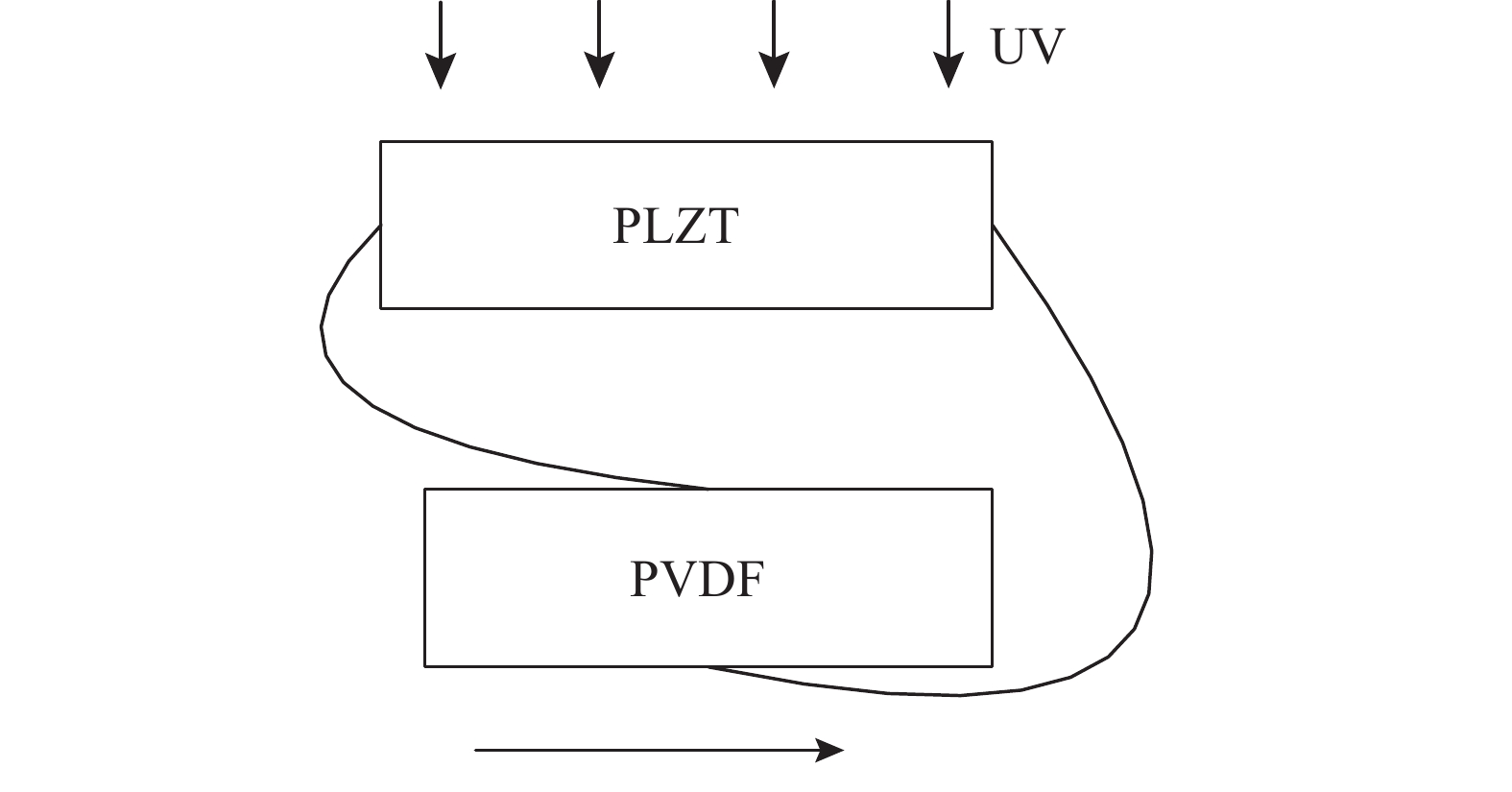
1 PLZT/PVDF层合柔性悬臂梁数学模型 1.1 PLZT/PVDF复合驱动器的数学模型基于0-1极化的PLZT/PVDF的光电/压电复合驱动原理如图1所示.
|
图 1 光电压电复合驱动原理示意图 Fig. 1 Photoelectric/piezoelectric compound driving principle |
PLZT陶瓷电极两端分别用银导线与压电作动器PVDF上、下表面的电极相连接. 在PLZT受到波长为365 nm的紫外光激励以后,PLZT陶瓷内部光生载流子作定向移动,产生光电流,为压电作动器PVDF供给能量. 当UV紫外光低于400 mW/cm2时,光焦热对PLZT陶瓷的影响可以忽略. 由于压电元件通常被等效为一个电容和电阻元件的并联,单片PLZT连接PVDF的等效电路图如图2所示.

|
图 2 PLZT/PVDF等效电路图 Fig. 2 PLZT/PVDF equivalent circuit diagram |
根据图2,建立PLZT/PVDF复合驱动器驱动电压的数学模型[12]:
| ${V_{_{\rm{d}}}} = {I_{\rm{P}}}R\left[ {1 - {{\rm exp}\left({ - \frac{t}{\tau }}\right)}} \right].$ | (1) |
式中:Vd为压电作动器PVDF两侧的驱动电压;IP为PLZT陶瓷光生电流;t为时间;τ为时间常数,
| $\tau = RC.$ | (2) |
其中,R为总电阻,
| $R = \frac{{{R_{\rm{P}}}{R_{\rm{f}}}}}{{{R_{\rm{P}}} + {R_{\rm{f}}}}} ,$ | (3) |
RP为PLZT 陶瓷光生电阻,Rf为PVDF电阻;
C为总电容,
| $C = {C_{\rm{P}}} + {C_{\rm{f}}},$ | (4) |
CP为PLZT陶瓷光生电容,Cf为PVDF电容.
1.2 层合悬臂梁的光电/压电复合驱动数学模型柔性悬臂梁结构的位移放大作用在微型机电系统设计中被广泛采用. 构建PLZT/PVDF层合悬臂梁的光电/压电数学模型.
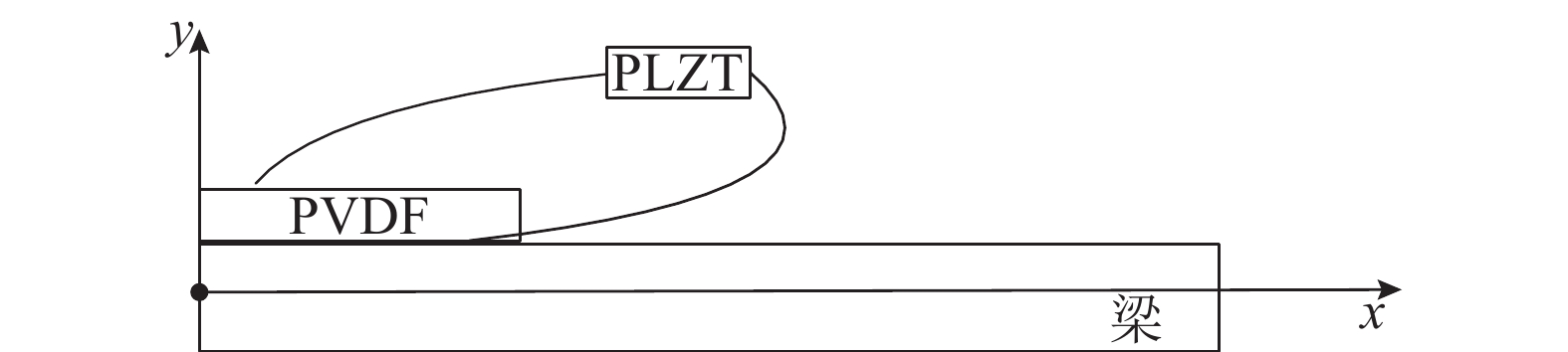
当PLZT陶瓷受365 nm紫外光激励后,产生的驱动电压来驱动PVDF薄膜片作动器;PVDF利用绝缘黏结剂粘贴在悬臂梁紧靠固定端处,用上、下导线引出电极与PLZT两端相连,如图3所示. PVDF受到驱动电压作用后,会产生驱动力,在绝缘黏结剂的传递作用下,作用于悬臂梁,悬臂梁绕z轴发生弯曲变形.
|
图 3 PLZT/PVDF复合驱动悬臂梁示意图 Fig. 3 PLZT/PVDF composite driven cantilever beam |
设悬臂梁长度为L,宽度为W,厚度为H,PVDF长度为Lf,宽度为Wf,厚度为Hf. PVDF在受到驱动电压作用后,会发生沿着x方向的形变εf,则PVDF产生的力为
| $F = {H_{\rm{f}}}{W_{\rm{f}}}{E_{\rm{f}}}{\varepsilon _{\rm{f}}}\left[ {u(x) - u(x - {L_{\rm{f}}})} \right].$ | (5) |
式中:u(x)为阶跃函数[13]. 该力绕着y轴产生的驱动力矩为
| $\begin{split}M = &\displaystyle\frac{{H + {H_{\rm{f}}}}}{2}F=\\ &\displaystyle\frac{{H + {H_{\rm{f}}}}}{2}{H_{\rm{f}}}{W_{\rm{f}}}{E_{\rm{f}}}{\varepsilon _{\rm{f}}}\left[ {u(x) - u(x - {L_{\rm{f}}})} \right].\end{split}$ | (6) |
式中:Ef为PVDF的弹性模量.
悬臂梁弯曲挠度微分方程为
| $\frac{M}{{EI}} = \frac{{{\partial ^2}w}}{{\partial {x^2}}}.$ | (7) |
式中:E为悬臂梁的弹性模量,I为悬臂梁的惯性截面矩,w为悬臂梁的挠度.
当x=0时,w和转角∂w/∂x都为零. 结合该边界条件,联立式(6)、(7),可得
| $\begin{split}w = & \displaystyle\frac{{M{L_{\rm{f}}}}}{{EI}}\left(L - \frac{{{L_{\rm{f}}}}}{2}\right)=\\ & \displaystyle\frac{{{E_{\rm{f}}}{W_{\rm{f}}}}}{{2EI}}\left(H_{\rm{f}}^2 + H{H_{\rm{f}}}\right){\varepsilon _{\rm{f}}}\left(L{L_{\rm{f}}} - 0.5L_{\rm{f}}^2\right).\end{split}$ | (8) |
根据压电效应可知,
| ${\varepsilon _{\rm{f}}} = {d_{31}}\frac{{{V_{\rm{d}}}}}{{{H_{\rm{f}}}}}.$ | (9) |
式中:d31为PVDF的压电常数,Vd为施加在PVDF薄膜片两端的电压.
对于PLZT/PVDF驱动的悬臂梁系统而言,联立式(6)、(8)和(9),可得悬臂梁自由端端部的挠度方程:
| $\begin{aligned}w(t) = \frac{{{d_{31}}{I_{\rm{P}}}R{E_{\rm{f}}}{W_{\rm{f}}}}}{{2EI}}({H_{\rm{f}}} + H)\left(L{L_{\rm{f}}} - 0.5L_{\rm{f}}^2\right)\left[1 - {{\rm exp}\left({ - \frac{t}{\tau }}\right)}\right].\end{aligned}$ | (10) |
由PVDF的尺寸参数,计算可得
| $R = \frac{{{R_{\rm{P}}}\rho {H_{\rm{f}}}}}{{{R_{\rm{P}}}{L_{\rm{f}}}{W_{\rm{f}}} + \rho {H_{\rm{f}}}}}.$ | (11) |
式中:ρ为PVDF的体积电阻率.
悬臂梁的挠度方程为
| $\begin{split}w(t) =& \displaystyle\frac{{{d_{31}}{I_{\rm{P}}}{E_{\rm{f}}}{W_{\rm{f}}}}}{{2EI}}\displaystyle\frac{{{R_{\rm{P}}}\rho {H_{\rm{f}}}}}{{{R_{\rm{P}}}{L_{\rm{f}}}{W_{\rm{f}}} + \rho {H_{\rm{f}}}}} \times \\&\left(H + {H_{\rm{f}}})(L{L_{\rm{f}}} - 0.5{L_{\rm{f}}}^2\right)\left(1 - {{\rm exp}\left({ - \frac{t}{\tau }}\right)}\right).\end{split}$ | (12) |
将式(12)简写为
| $w(t) = {W_{\rm S}}\left(1 - {{\rm exp}\left({ - \frac{t}{\tau }}\right)}\right).$ | (13) |
式中:WS为悬臂梁挠度的幅值,
| $\begin{split}{W_{\rm{S}}} =& \displaystyle\frac{{{d_{31}}{I_{\rm P}}{E_{\rm{f}}}{W_{\rm{f}}}}}{{2EI}}\displaystyle\frac{{{R_{\rm{P}}} \rho {H_{\rm{f}}}}}{{{R_{\rm P}}{L_{\rm{f}}}{W_{\rm{f}}} + \rho {H_{\rm{f}}}}} \times \\&{\kern 1pt} ({H_{\rm{f}}} + H)\left(L{L_{\rm{f}}} - 0.5{L_{\rm{f}}}^2\right).\end{split}$ | (14) |
从式(14)可以看出,对于特定的悬臂梁结构,PLZT/PVDF的悬臂梁挠度幅值与PLZT陶瓷的光生电流、光生电阻、PVDF的材料特性参数、PVDF尺寸参数有关. 当PLZT陶瓷尺寸参数与光照强度确定时,PLZT陶瓷的光生电流与光生电阻随之确定. PLZT/PVDF的悬臂梁挠度输出特性(即驱动特性)仅与PVDF的材料特性及尺寸参数有关,即当Hf为常数时,式(14)可以改写为
| ${W_{\rm{S}}} = \frac{{A{I_{\rm{P}}}{R_{\rm{P}}}\rho {H_{\rm{f}}}(H + {H_{\rm{f}}})}}{{\rho {H_{\rm{f}}} + {W_{\rm{f}}}{L_{\rm{f}}}{R_{\rm{P}}}}}\left(L{L_{\rm f}} - 0.5L_{\rm f}^2\right).$ | (15) |
当Lf为常数时,式(14)可以改写为
| ${W_{\rm{S}}} = \frac{{A{I_{\rm{P}}}{R_{\rm{P}}}\rho (L{L_{\rm{f}}} - 0.5L_{\rm{f}}^2)}}{{\rho {H_{\rm{f}}} + {W_{\rm{f}}}{L_{\rm{f}}}{R_{\rm{P}}}}}{H_{\rm f}}\left(H + {H_{\rm f}}\right).$ | (16) |
式中:
PLZT陶瓷的尺寸参数为15 mm(LP)×5 mm(WP)×1 mm(HP);悬臂梁选用PMMA材料,尺寸参数为140 mm(L)×5 mm(W)×1 mm(H),弹性模量为3 GPa. PVDF物理特性参数如表1所示.
| 表 1 PVDF物理特性参数 Table 1 physical characteristic parameters of PVDF |
针对PVDF薄膜的长度和厚度,对WS的影响进行实验研究,搭建的实验平台如图4所示.

|
图 4 PLZT/PVDF层合柔性悬臂梁驱动特性实验装置图 Fig. 4 Experimental setup for driving characteristics of PLZT/PVDF laminated flexible cantilever beam |
当LED-UV面光源产生的365 nm的紫外光,照射在PLZT陶瓷表面上时,PVDF层合悬臂梁在光生电压的驱动下产生挠度变形,利用STIL色散位移计测量悬臂梁自由端的挠度,PC接收位移计采集得到的位移信号. PLZT尺寸为15 mm(LP)×5 mm(MP)×1 mm(HP),沿长度方向极化.
在该实验中,光照强度均为200 mW/cm2,对应的PLZT陶瓷饱和电压经测量为950 V,即式(15)、(16)中IPRP=950 V. 光照时间均为180 s,利用位移计可以采集得到不同长度PVDF薄膜层合悬臂梁的挠度曲线.
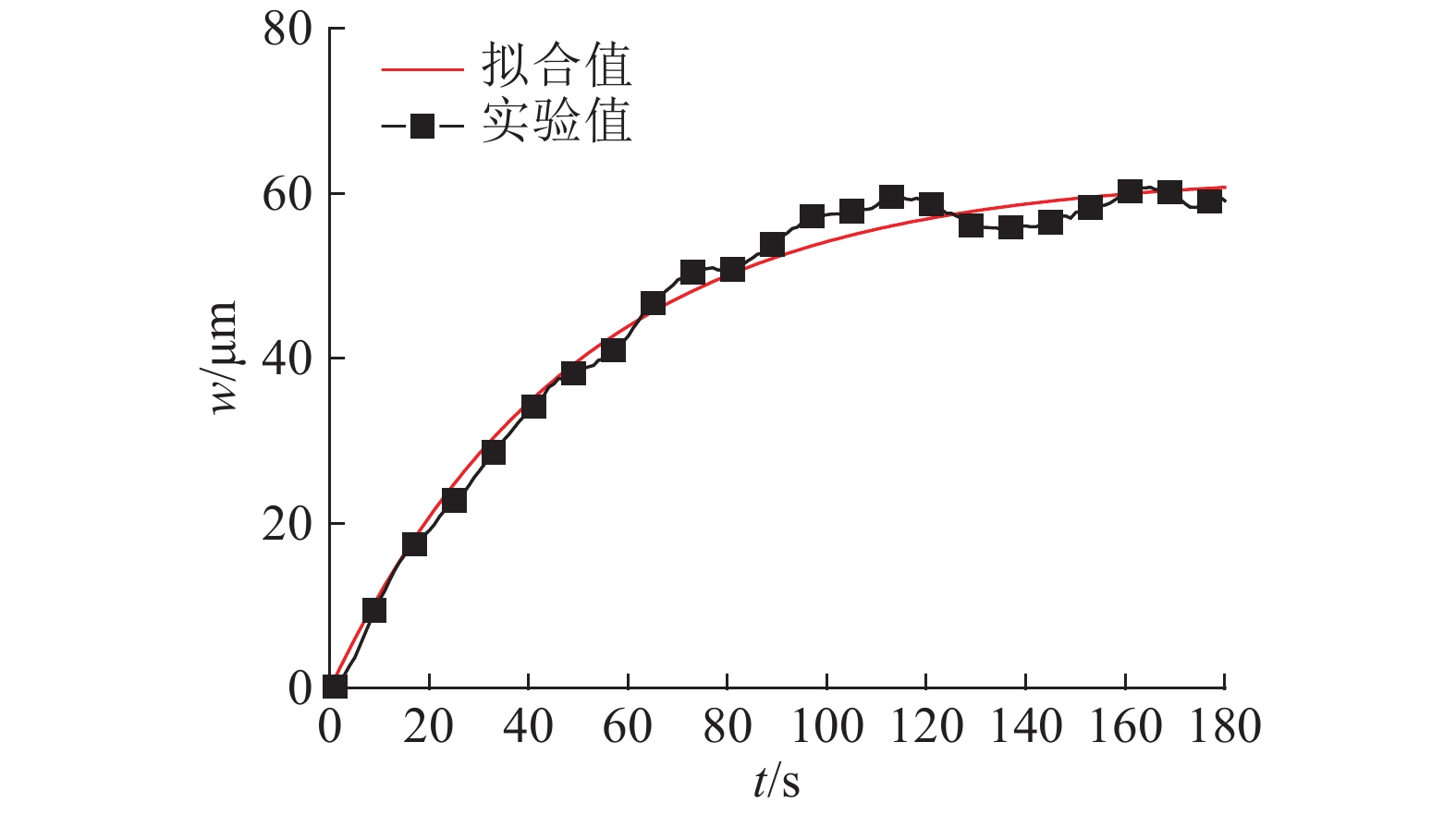
如图5所示为当Lf=80 mm时悬臂梁的挠度实验曲线图. 利用1stOPT数学拟合软件,根据式(13)拟合可得,此时挠度幅值拟合值WSFit为62.35 μm.
|
图 5 Lf=80 mm时悬臂梁的挠度实验曲线与拟合曲线 Fig. 5 Experiment curve and fitting curve of cantilever beam when Lf=80 mm |
分析式(15)可知,利用该悬臂梁挠度反求PLZT陶瓷的光生电阻为
| ${R_{\rm{P}}} = \frac{{A{I_{\rm{P}}}{R_{\rm{P}}}(H + {H_{\rm{f}}}){H_{\rm{f}}}\left(L{L_{\rm{f}}} - 0.5{L_{\rm{f}}}^2\right) - {W_{\rm{S}}}\rho {H_{\rm{f}}}}}{{{W_{\rm{S}}}{L_{\rm{f}}}{W_{\rm{f}}}}}.$ | (17) |
将Lf=80 mm时通过拟合方法获得的WSFit代入式(17),得到200 mW/cm2光强下PLZT陶瓷的RP=1.19×1013 Ω.
由于PLZT陶瓷在恒定光强下,RP保持不变,当PVDF薄膜厚度确定时,将RP代入式(15),可得WS受Lf的影响规律. 如图6所示为当Hf=50 μm时PLZT/PVDF层合悬臂梁WS随Lf的理论曲线. 可以看出,WS随着Lf先增加后减小,当Lf约为40 mm时,WS最大.

|
图 6 Hf=50 μm时悬臂梁挠度幅值随PVDF长度变化的曲线 Fig. 6 Deflection magnitude of cantilever beam varies with length of PVDF when Hf=50 μm |
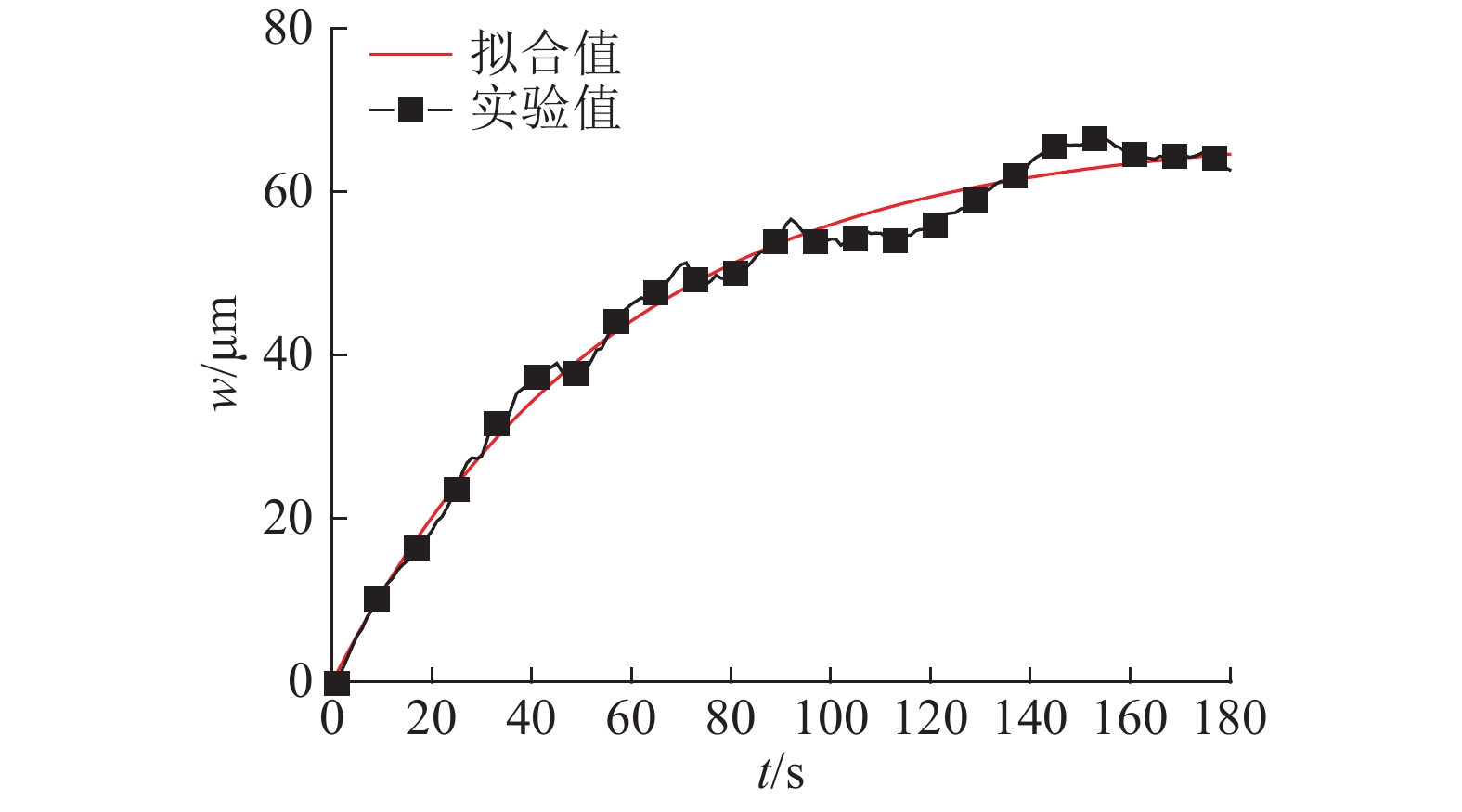
将Hf为50 μm,Lf分别为40和60 mm的PVDF薄膜层合到悬臂梁,得到悬臂梁挠度随时间变化的实验曲线,对该曲线进行拟合,如图7、8所示. 从图7、8可以分别得到WSFit为66.12、65.39 μm,依据式(15)可得对应的理论值WS;将WSFit和WS进行对比,如表2所示.

|
图 7 Lf=40 mm时悬臂梁的挠度实验曲线与拟合曲线 Fig. 7 Experiment curve and fitting curve of cantilever beam when Lf=40 mm |
|
图 8 Lf=60 mm时悬臂梁的挠度实验曲线与拟合曲线 Fig. 8 Experiment curve and fitting curve of cantilever beam when Lf=60 mm |
| 表 2 PVDF长度不同悬臂梁挠度幅值理论值与实验拟合值 Table 2 Theoretical deflection amplitude and fitting deflection amplitude with different length of PVDF |
从表2可以看出,Lf=40 mm时的WSFit大于Lf=60 mm时的WSFit,与图6所示的悬臂梁挠度幅值随PVDF长度变化的规律吻合. 通过实验拟合得到挠度幅值与理论值之间的误差Δ小于4%,误差原因如下:1)数学建模上忽略胶层[14]的客观存在,因此计算得到的理论挠度比实测挠度大一些;2)在参数识别过程中,通过数据拟合反求得到的PLZT陶瓷光生电阻与真实电阻存在偏差;3)当对悬臂梁自由端进行测量时,被测点不是理想的自由端端部,通过实验得到的挠度偏小.
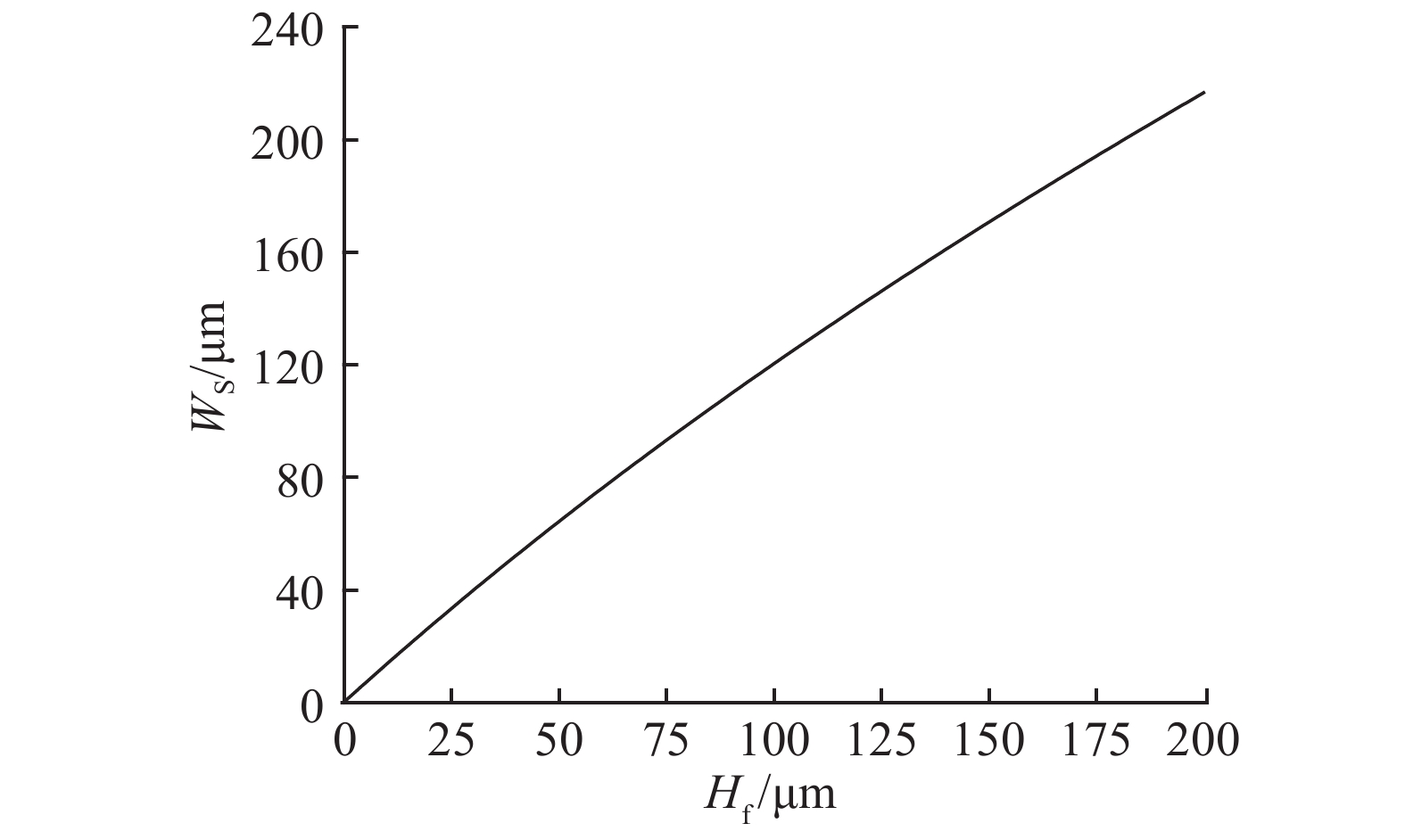
由式(16)可得WS受Hf的影响规律. 如图9所示为Lf=60 mm时WS随Hf的理论曲线. 可以看出,随着Hf不断增大,WS增大.
|
图 9 Lf=60 mm时悬臂梁挠度幅值随PVDF厚度变化的曲线 Fig. 9 Deflection magnitude of cantilever beam varies with thickness of PVDF when Lf=60 mm |
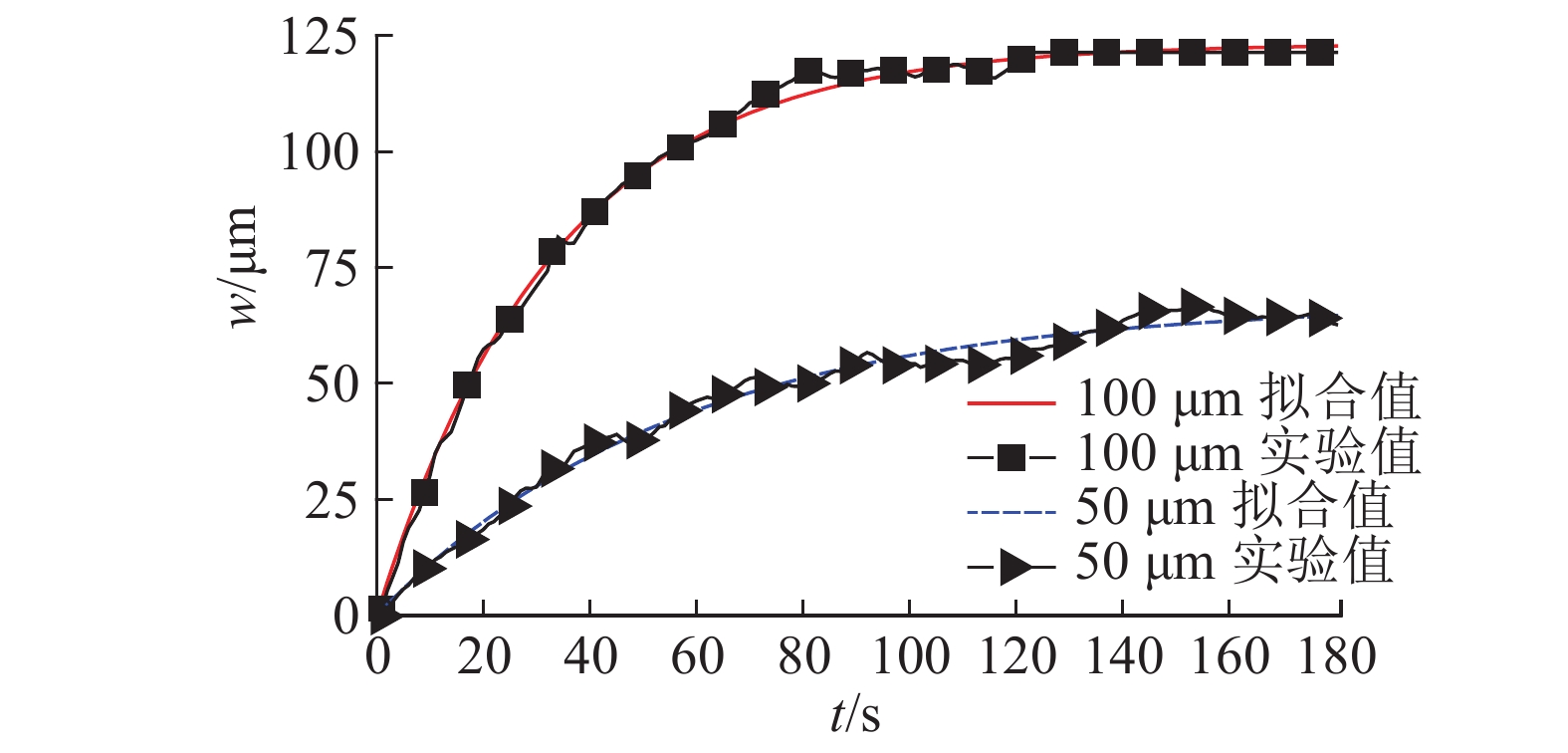
将长度为60 mm、厚度分别为50和100 μm的 PVDF薄膜层合到柔性悬臂梁表面,得到的挠度实验曲线及对应的拟合曲线如图10所示. 如表3所示为在50和100 μm厚度下理论幅值与拟合幅值的对比.
|
图 10 不同厚度PVDF薄膜层合悬臂梁的挠度曲线 Fig. 10 Deflection curves of cantilever beam laminated with PVDF films with different thickness |
| 表 3 PVDF厚度不同悬臂梁挠度幅值理论值与实验拟合值 Table 3 Theoretical deflection amplitude and fitting deflection amplitude with different thickness of PVDF |
从表3可以看出,Hf= 100 μm时的WSFit大于Hf=50 μm时的WSFit,如图9所示,WS随Hf变化的规律吻合.
3 结 论(1) 随着PVDF薄膜长度的增长,PLZT/PVDF层合柔性悬臂梁挠度幅值先增大后减小,该变化规律及PVDF长度的最优值取决于PLZT电学参数、PVDF厚度参数和悬臂梁的具体尺寸参数.
(2) 随着PVDF薄膜厚度的增大,PLZT/PVDF层合柔性悬臂梁的挠度幅值增大,光电/压电复合驱动能力增强.
| [1] |
FRIDKIN V M. Photoferroelectrics [M]. New York: Springer, 1979.
|
| [2] |
UCHINO K, POOSANAAS P, TONOOKA K. Photostrictive actuators[J]. Ferroelectrics, 2001, 264(1): 303-308. |
| [3] |
SADA T, INOUE M, UCHINO K. Photostriction in PLZT ceramics[J]. International Journal of High Technology Ceramics, 1988, 4(1): 91. |
| [4] |
ICHIKI M, MORIKAWA Y, MABUNE Y. Electrical properties of photovoltaic lead lanthanum zirconate titanate in an electrostatic-optical motor application[J]. Journal of the European Ceramic Society, 2004, 24(6): 1709-1714. DOI:10.1016/S0955-2219(03)00474-6 |
| [5] |
李琼, 王少萍, 梁磊. 光控伺服系统建立、建模与仿真[J]. 压电与声光, 2007, 29(2): 213-215. LI Qiong, WANG Shao-ping, LIANG Lei. The structure, modeling and simulation of optical drive servo system[J]. Piezoelectrics and Acoustooptics, 2007, 29(2): 213-215. DOI:10.3969/j.issn.1004-2474.2007.02.030 |
| [6] |
TZOU H S, CHOU C S. Nonlinear opto-electromechanics and photodeformation of optical actuators[J]. Smart Materials and Structures, 1996, 5(2): 230. DOI:10.1088/0964-1726/5/2/012 |
| [7] |
LUO Q, TONG L. Constitutive equations for 0-3 polarized actuators[J]. International Journal of Solids and Structures, 2009, 46(25): 4313-4321. |
| [8] |
王新杰. PLZT光致伸缩特性及光电层合回转薄壳的主动控制研究[D] 哈尔滨: 哈尔滨工业大学, 2011. WANG Xin-jie. Research on potostrictive characteristics of PLZT and active control of photostrictive laminated thin shells of revolution [D]. Harbin: Harbin Institute of Technology, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D264232 |
| [9] |
ZHENG S J. Finite element simulation of wireless structural vibration control with photostrictive actuators[J]. Scinence China Technological Sciences, 2012, 55(3): 245-249. |
| [10] |
黄家瀚, 王新杰, 王炅. PLZT陶瓷在多能场耦合下的光致伸缩效应[J]. 光学精密工程, 2015, 23(3): 760-768. HUANG Jia-han, WANG Xin-jie, WANG Jiong. Photostrictive effect of PLZT ceramic at coupling of multiple energy fields[J]. Optics and Precision Engineering, 2015, 23(3): 760-768. |
| [11] |
黄家瀚. 0-1极化的PLZT陶瓷光致特性及其光控驱动微镜的驱动基础研究[D]. 南京: 南京理工大学, 2016. HUANG Jia-han. Basic research on photo-induced characteristics of 0-1 polarized PLZT ceramic and driving of light-activated micromirror [D]. Nanjing: Nanjing University of Science and Technology, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3192730 |
| [12] |
姜晶, 李晓楠, 岳洪浩, 等. 光控压电混合驱动特性及影响因素的分析[J]. 机械工程学报, 2017, 53(1): 65-71. JIANG Jing, LI Xiao-nan, YUE Hong-hao, et al. The characteristic and influence factors analysis of non-contact hybrid photostrictive/piezoelectric actuation mechanism[J]. Journal of Mechanical Engineering, 2017, 53(1): 65-71. |
| [13] |
SHIH H R, WATKINS J, TZOU H S. Displacement control of a beam using photostrictive optical actuators[J]. Journal of Intelligent Material Systems and Structures, 2005, 16(4): 355-363. DOI:10.1177/1045389X05050101 |
| [14] |
牛一虹, 刘波, 韩雪峰, 等. 复合材料与金属接头胶接建模精度研究[J]. 计算机仿真, 2013, 30(4): 248-252. NIU Yi-hong, LIU Bo, HAN Xue-feng, et al. Study on modeling precision of composite and metal adhesive joints[J]. Computer Simulation, 2013, 30(4): 248-252. DOI:10.3969/j.issn.1006-9348.2013.04.056 |



