探地雷达（ground penetrating radar, GPR）通常利用高频电磁波在媒质电磁特性不连续处的反射达到近地表地球物理探测的目的^[1]，是一项快速无损且分辨率较高的方法. 与其他调查方法相比，GPR不仅在异常体平面展布信息上有较好反映，还可以提供更多深度上的信息，这是GPR在考古、环境调查和工程等应用中广受青睐的重要原因^[2]. 然而，GPR发射的脉冲信号在传播过程中会因高频成分的衰减而成为一个带宽有限的子波，这导致原始资料的分辨率受到限制. 为了解决这个问题，需要对信号作反褶积处理，以压缩子波、拓宽频带，完成纵向分辨率的提高.

在地震勘探领域，已经有很多关于反褶积的研究和应用^[3-4]. 随着GPR的广泛应用，越来越多的反褶积技术被尝试用于GPR数据处理. 首先是一些基于统计学子波的方法^[5-8]，在一些领域取得了较好的效果^[9-11]. 后来Xia等^[12-13]在做沉积研究时，认为这些方法依据的假设很难适用，提出了利用确定性子波作反褶积，并成功将其应用于碳酸盐地层研究上. 不过，Annan^[14]认为这些经典的地震反褶积方法在大量实际工作中还是鲜有好的应用效果，并指出部分原因在于子波高频成分在传播过程中的衰减，需要用反Q滤波等技术对此进行补偿^[15]，后来国内苏茂鑫等^[16-17]也针对补偿方法作了有益的尝试. 近年来，一些新的方法被陆续提出，包括基于贝叶斯估计子波的频率域反褶积^[18]、时变子波的反褶积^[19]等，国内也不乏相关的研究^[20-24]. 不过随着GPR应用的逐渐推广，反褶积技术的发展仍然赶不上分辨率的需求，例如薄层识别的问题变得越来越多^[25]. 值得注意的是，一些反褶积方法基于反射系数可由稀疏脉冲表示的假设，对分辨率有着明显的提升，不过对子波的处理则仍然采用估计的策略^{[18, 26-27]}.

GPR剖面常常包含各种成因复杂的噪声，而常规的反褶积方法对噪声比较敏感，这也是现在反褶积技术没有大规模推广应用到实际工作中的主要原因之一. 另外，传统的反褶积需要假设子波是最小相位以及反射系数序列是白噪声序列，这在GPR工作中经常是难以满足的. 如果不考虑这2种假设，为了提取地下复杂介质信息的主要特征，将地下地层的反射系数看作可由一系列稀疏分布的脉冲表示，则GPR信号可以理解为子波与一个综合反射系数序列褶积的结果，这个综合反射系数序列包括了稀疏分布的、代表地下地层的大反射系数和随机分布、由噪声引起的小反射系数. 稀疏脉冲反褶积就是基于该条件约束的一种反演策略^[28-32]，其对噪声的敏感度较小，通过迭代优化能够从信号中恢复主要反射系数的准确位置和大小，并且突破了分辨率的限制，极大提升了频带的宽度. 在地震勘探领域，稀疏脉冲反褶积已被广泛用于石油工业的波阻抗反演当中^[33]，对于子波的获取，主要是靠井震标定工作来完成. 关于GPR波阻抗反演的研究近年来也有所发展^[34-38]，但对于子波的处理方法尚无细致的研究. 不同于地震勘探中震源激发条件的差异化，GPR特定型号的主机和天线所激发的子波应该是比较稳定的. 虽然GPR的子波相比地震子波面临着更大的频率损失，但通过前文提到的补偿方法，仍然能够假设子波是稳定的、时不变的. 因此本文提出，通过类似Xia等^[12-13]的实验获取确定性子波，避免估计子波因噪声干扰等问题引起的误差；利用地震勘探中经典的约束和优化策略做稀疏脉冲反褶积，从含噪信号中提取高分辨率的有效信息，甚至突破GPR信号理论上最小分辨率的限制.

本文介绍GPR确定性子波的获取手段，以及稀疏脉冲反褶积的方法原理；通过对2个理论模型的分析，验证该方法在抗噪能力和薄层识别效果上与传统方法相比的优势；利用该方法对实际数据进行处理，得到高分辨率的结果，证明该方法的可行性.

1 确定性子波的获取

不同的GPR产品有着不同的仪器系统，因此需要对特定型号的主机以及所选天线作专门的试验和研究. 本文以PulseEKKO pro系统搭配50 M板状天线为例. 为了获取干净的GPR子波，并且减少能量衰减和频率损失，需要选择一个空旷的场地，避免来自周围环境或者人文噪声的干扰，将收发天线垂直于地面以固定间距互相正对底面（如图1所示），以便采集到空气中的直达波. 这种情况下，来自草地的反射相对于空气直达波来说非常弱，可以忽略^[12]. 天线之间的最佳间隔则需要经过试验来确定，对于PulseEKKO pro系统，则可以通过搜索模式来完成. 如果间隔较近，可能信号中会包含电磁波在天线之间周期性回荡而产生的交混回响，因此需要调试不同间距的效果. 选择好最优间距后，在实际采集时需要选择较多的叠加次数，从而使随机噪声的影响减少到最小. 具体的例子将在第4章进行介绍.

2 稀疏脉冲反褶积

根据褶积模型，GPR信号 ${{d}_t}$ 可以看作是一个有限带宽的静态子波 ${{{w}}_t}$ 与地下反射系数序列 ${{r}_t}$ 的褶积，又因为野外采集不可避免会遇到噪声 ${n_t}$ n_t，即有

${{{d}}_t} = {{{w}}_t}{\rm{*}}{{{r}}_t} + {{{n}}_t},\, t = 1,2, \cdots ,{N} .$

(1)

从式：可以看出，信号的频带受到了子波的影响. 为了从 ${{d}_t}$ 中恢复 ${{r}_t}$ ，可以通过已知子波或者统计学方法，设计一个相当于褶积作用反过程的滤波器并与GPR信号褶积. 最经典的反褶积方法是基于维纳滤波器的最小平方反褶积^[3]，滤波器的设计准则是使其实际输出与期望输出的误差平方和最小. 不过，该方法假设地震反射系数序列是白噪声序列，并且子波是最小相位的，从而在未知子波的条件下用记录的自相关和与期望输出的互相关，代替子波的自相关和与期望输出的互相关. 当期望输出为一个零延时或有一定延时脉冲时，该方法被称为脉冲反褶积. 实际情况中前面2个假设通常难以成立，另外GPR信号不可避免会包含未知的噪声，因此设计出滤波器的效果经常难以令人满意.

根据式(1)求取 ${{r}_t}$ 可以被认为是一个高度病态的反问题，需要采取正则化的方法来求解^[29]，下面介绍具体的过程. 首先假设反射系数序列是稀疏分布的，计算值和观测值的残差为

${{{e}}_t} = \mathop \sum \limits_i \,{{{w}}_{t - i}}{{{r}}_i} - {{{d}}_t},\,i = 1,2, \cdots ,{{N}}.$

(2)

反问题的目的就是找到符合条件的 ${{r}_t}$ ，使下面的目标函数最小：

${{J}} = {{{J}}_r} + {\rm{\mu }}{{{J}}_x}.$

(3)

该目标函数的第一项：

${{{J}}_r} = \mathop \sum \limits_t\, \frac{1}{2}{{{e}}_t}^2,$

对残差进行最小平方约束，保证所求结果与GPR信号符合；第二项为正则化项，对反射系数进行稀疏约束，能够保证求解结果稀疏，提升解的稳定性， ${{\mu }}$ 称作阻尼系数，需要选取适当的值进行稀疏控制. ${{{J}}_x}$ 的选取可以有不同的策略，本文采取L1范数正则化方法，即

${{{J}}_x} = \mathop \sum \limits_t \,\left| \,{{{{r}}_t}} \right|.$

(4)

为J达到最小，可由解决下式来完成：

$\frac{{\partial {{J}}}}{{\partial {{{r}}_i}}} = \mathop \sum \limits_t \,\left({{{e}}_t}{{{w}}_{t - i}}\right) + {\rm{\mu }}\mathop \sum \limits_i \,\frac{{\left| {{{{r}}_i}} \right|}}{{{{{r}}_i}}} = 0.$

(5)

根据上式可以推导出：

$\mathop \sum \limits_t \mathop \sum \limits_i\, \Big[\Big({{{w}}_{t - i}}{{{w}}_{t - i}} + {\rm{\mu }}\frac{1}{{\left| {{{{r}}_i}} \right|}}\Big){{{r}}_i}\Big] = \mathop \sum \limits_t\, \Big({{{w}}_{t - i}}{{{d}}_t}\Big).$

(6)

将上式转化成矩阵形式，有：

$\left( {{{R + Q}}} \right){{x = g}},\,{{Q}} = {\rm{diag}}\,\left( {{\rm{\mu }}\frac{1}{{\left| {{{{r}}_i}} \right|}}} \right).$

(7)

其中，diag表示将括号中的列向量转换成相应的对角矩阵； ${{x}}$ 即为反射系数序列 ${{r}_t}$ 的列向量. 根据式（7）求解 ${{x}}$ 的方法有很多，由于GPR数据的规模通常并不大，矩阵的求逆运算是可以接受的，本文采用迭代重复加权最小二乘法算法，以求取较高精度的解. 该方法的步骤具体如下：

1）根据已知子波和GPR信号计算矩阵 ${{R}}$ 和 ${{g}}$ ，选取适当的阻尼系数 ${\rm{\mu }}$ ，利用脉冲反褶积结果 ${{{x}}_s}$ 计算初始的矩阵：

${{{Q}}^{\left( 0 \right)}} = {\rm{diag}}\,\,\left( {{\rm{\mu }}\frac{1}{{\left| {{{{x}}_s}} \right|}}} \right).$

2）根据 ${{{Q}}^{\left( {{\rm{k}} - 1} \right)}}$ 计算 ${{{x}}^{\left( {\rm{k}} \right)}} = {\left( {{{R}} + {{{Q}}^{\left( {{\rm{k}} - 1} \right)}}} \right)^{ - 1}}{{g}}$ ，并迭代更新：

${{{Q}}^{\left( {\rm{k}} \right)}} = {\rm{diag}}\,\,\left( {{\rm{\mu }}\frac{1}{{\left| {{{{x}}^{\left( {\rm{k}} \right)}}} \right|}}} \right).$

其中，k为迭代的次数；

3）给出一个固定的次数，步骤2)的迭代次数达到该值后停止并输出结果 ${{x}}$ ; 也可以设置一个阈值，当步骤2)结果的目标函数小于该值时停止迭代.

3 数值试验

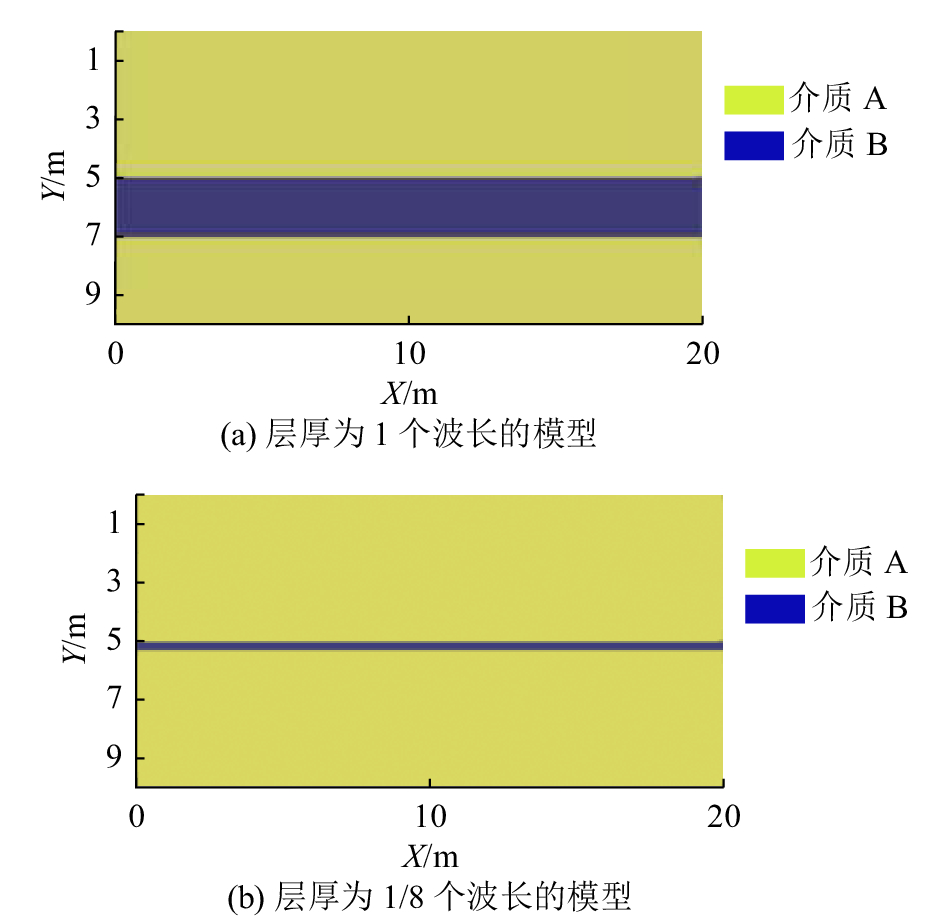
为了验证子波确定条件下的稀疏脉冲反褶积效果，设计2个简单的层状模型，如图2所示. 模型中共有A和B两种介质：背景介质A的相对介电常数为16，电导率为0.001 S/m，相对磁导率为1；目标水平层B的相对介电常数为9，电导率为0.001 S/m，相对磁导率为1. 考虑到GPR信号理论上垂直分辨率极限为1/4波长（这里即2 m），设置图2（a）中的介质B层厚为1个波长，图2（b）中的介质B层厚为1/8个波长. 正演模拟采用时间域有限差分的方法^[1]，设置激励源为50 MHz中心频率的雷克子波^[39]，采用2 m收发距以共偏移距方式采集.

图2（a）模型产生的数据经过增益和去直达波处理后（如图3（a）所示，其中A为信号振幅），对各道数据加上20%主频50 MHz的随机噪声（如图3（b）所示）. 考虑到各道信号的相似性，并且为了放大细节特征，下面主要分析剖面中抽取的第5道信号（如图3（c）所示）. 图3（d）显示了对该道作常规的脉冲反褶积处理后的结果，可以看出，由于噪声的影响，产生了很多没有意义的尖脉冲. 数据分辨率提升的同时，信噪比大大降低，数据解译工作变得更加困难. 即使对数据再作频域滤波处理（如图3（e）所示），也很难挽回信噪比的损失，并且真实反射系数位置附近的信号比较杂乱，已经很难推知真实的信息. 再对图3（c）数据基于已知的子波作稀疏脉冲反褶积（如图3（f）所示），得到的结果只有2个大小相近、方向相反的大脉冲和1个较小的脉冲. 2个大脉冲即真实的反射序列，而小脉冲则是由于噪声引起的误差，不过这仍在可以接受的范围内. 不难看出，在稀疏控制项的约束下，稀疏脉冲反褶积的结果对噪声不那么敏感，可以在噪声较为严重的情况下较为准确地找出最主要的反射系数.

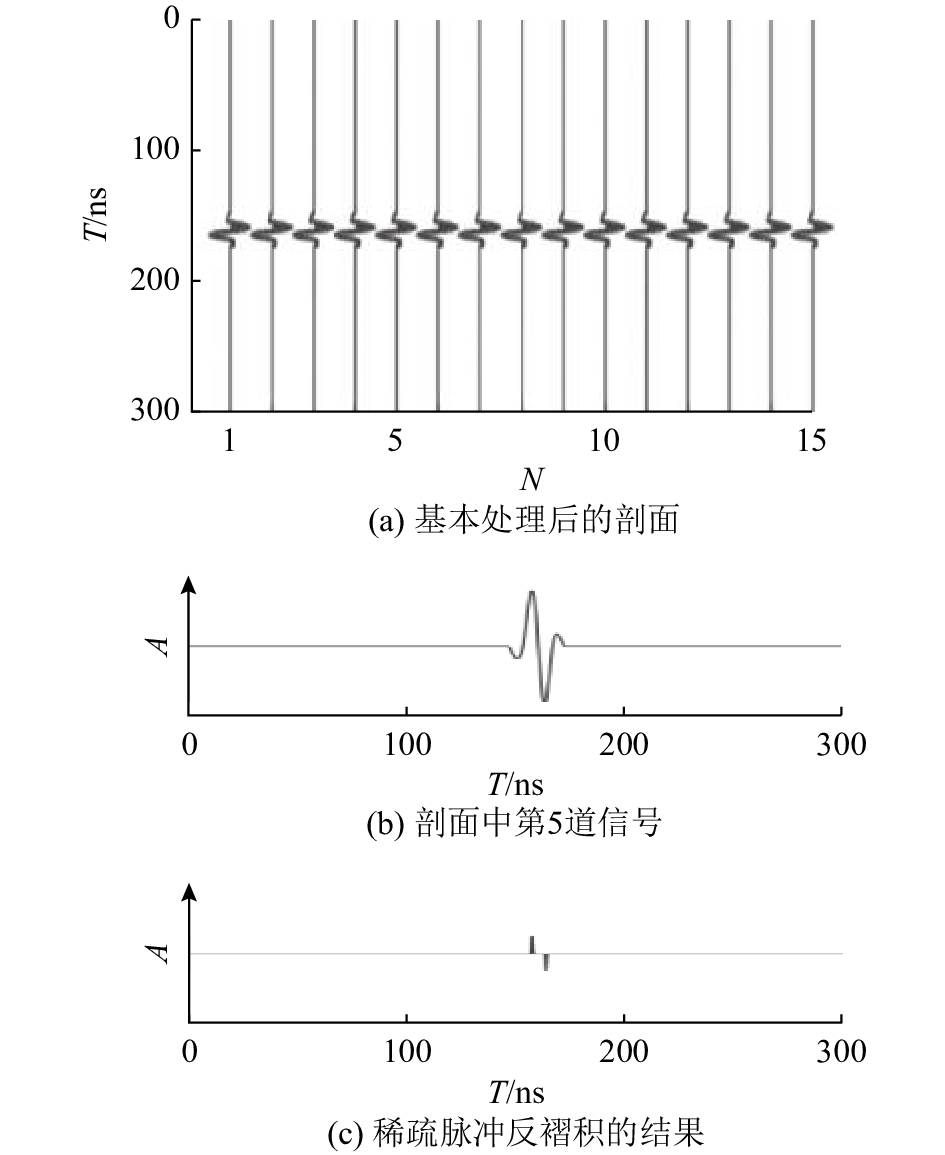
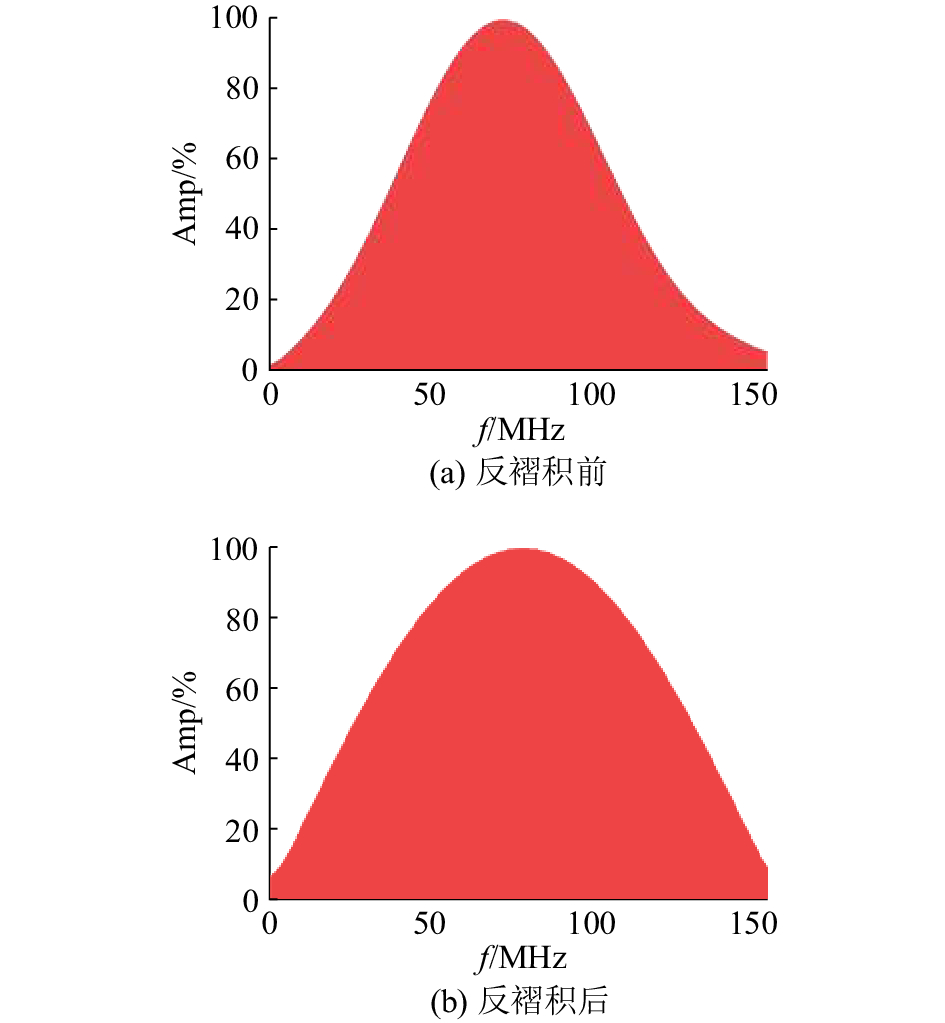
图2（b）模型产生的数据经过增益和去直达波处理后（如图4（a）所示），剖面仍然难以反映薄层的信息. 从剖面中抽取第5道信号（如图4（b）所示），可以发现由于层厚小于理论上的纵向分辨率的极限，来自水平层上 Anal 下界面的反射波发生了比较严重的干涉，传统的处理方法已经很难发挥作用. 对该道信号基于已知子波作稀疏脉冲反褶积处理，结果得到了分离得比较好的2个尖脉冲，可以很好地对薄层的上 Anal 下界面进行识别（如图4（c）所示）. 稀疏脉冲反褶积前后的谱振幅表明，处理后的信号在频带被拓宽的基础上，有效带宽上的能量也得到增强（如图5所示，Amp为信号的振幅比例）. 上面的分析说明，稀疏脉冲反褶积通过已知子波反演真实的反射系数，能够大大地提升数据的分辨率，甚至突破GPR信号理论上最小分辨率的限制.

4 实例分析

本研究的实例工作区域位于杭州市吴越国捍海塘某发掘地点（如图6所示）. 发掘工作表明，捍海塘主体为土塘，塘体之后有粗加工过的木材框架，以土、石为填充材料，结合竹篱、竹编等辅助材料形成整体，从而加固捍海塘^[40].

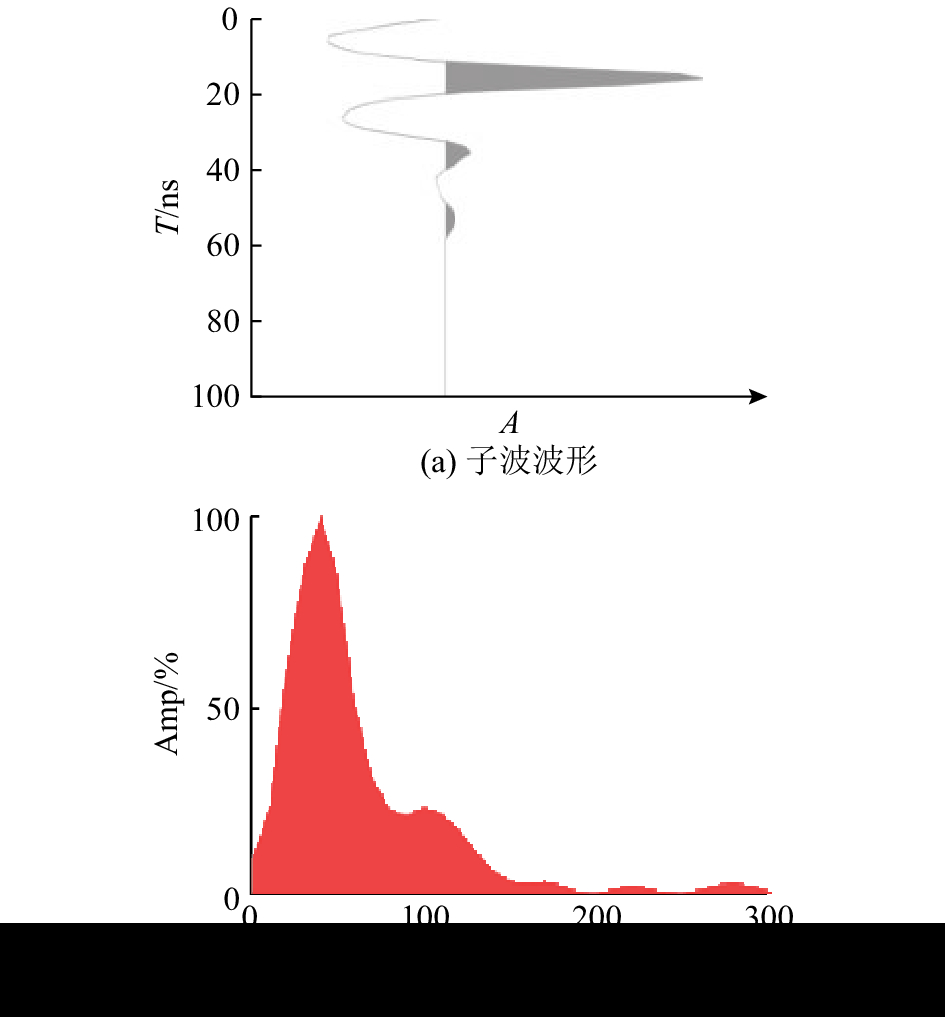
在工作区域布置一条测线，横切发掘后回填的捍海塘所在位置. 根据已知的捍海塘大致深度，选取50 MHz天线进行共偏移距测量. 在探测工作开始前，利用第1章所讲的方法试验1 、1.5 和2 m的天线间距，最终选择2 m间距采集了子波的信号. 应该注意的是，对原始子波的处理是有必要的，因为作稀疏脉冲反褶积之前信号需要作基本处理，子波处理要参考GPR信号的处理过程来进行. 这里对子波信号作零时校正、Dewow、预测反褶积和频域滤波处理. 信号中子波后面的噪声被压制但仍存在，为避免子波拖尾带来的误差，切除60 ns之后的非有效信息，得到最终的确定性子波（如图7所示），供后面稀疏脉冲反褶积所用.

采集到的原始剖面经过基本处理后（如图8（a）所示）已能较好地反映捍海塘石质结构的顶底界面，即21~26 m处位于约110 ns和170 ns的反射波组. 由于采用的是低频天线，信号的波长比较长，石质结构顶界面的细致位置还无法查明. 另外一些噪声，如剖面右部分的线性相干噪声^[41]，虽然被压制但仍旧明显，影响后面的解译工作. 通过上面获取到的确定性子波以及第2章所介绍的稀疏脉冲反褶积方法，对该剖面作子波确定性稀疏脉冲反褶积处理.

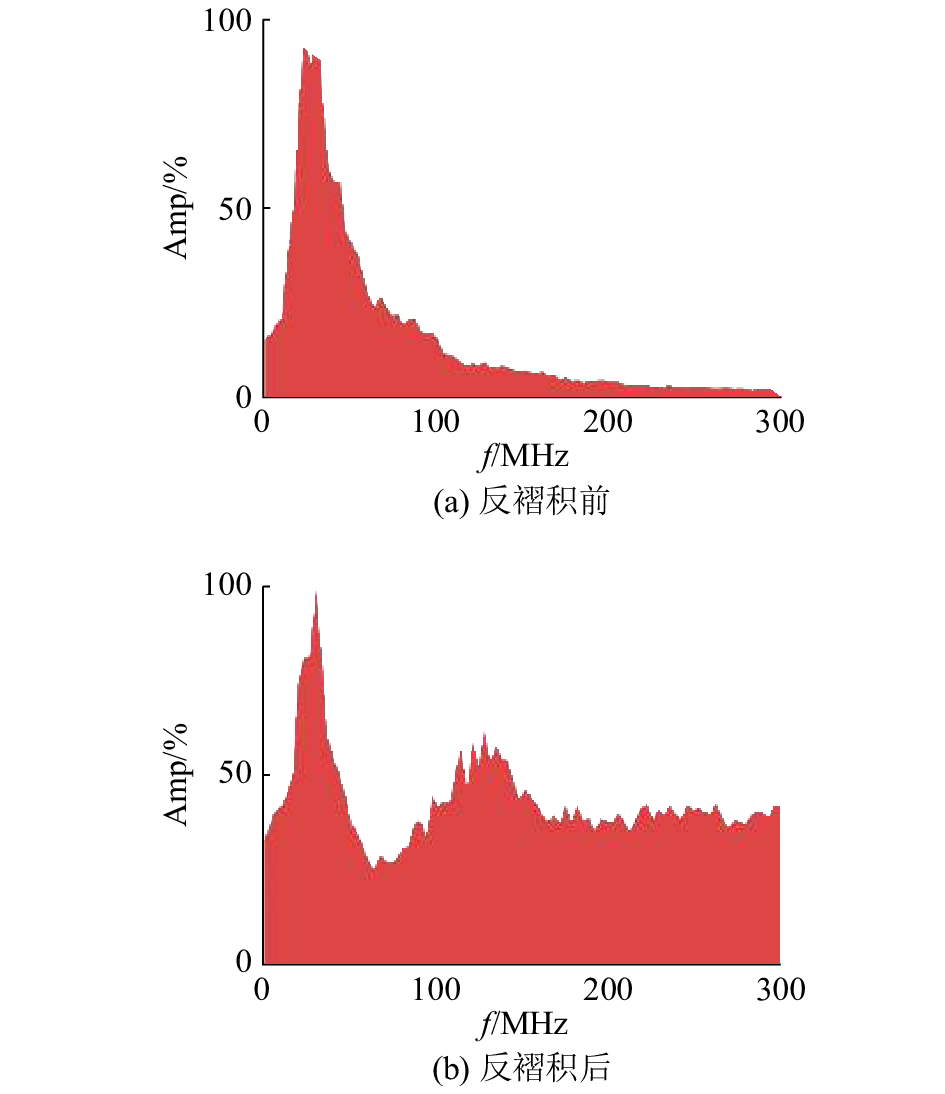
处理结果更为清晰地反映了捍海塘石质结构顶部界面的位置（如图8（b）所示），并且没有受到线性相干噪声的影响. 虽然一些微弱的有效信号受到了压制，但总体的成像效果更好. 观察处理前、后的振谱幅（如图9所示）可知，经过稀疏脉冲反褶积后的数据频带被明显拓宽，包含的信息较之前更为丰富. 综合上述分析，认为子波确定性稀疏脉冲反褶积针对该剖面的处理是十分有意义的.

5 结　论

(1)理论和实践表明，本文提出的探地雷达子波确定性稀疏脉冲反褶积技术在分辨率和信噪比上都能够有较好的效果. 采集到的确定性子波较为可信，以此对信号作稀疏脉冲反褶积处理，能够大大地提升数据的纵向分辨率；在稀疏控制项的约束下，反演得到的解比较稳定，对噪声敏感度低，可以在噪声较为严重的情况下较为准确地找出最主要的反射系数.

(2)本文作稀疏脉冲反褶积采取的策略是L1范数约束，迭代重复加权最小二乘算法求解优化问题. 反演方法的创新可以推动本研究的发展，因此可以尝试使用其他正则化方法约束，以及其他的最优化算法，或者与其他方法的数据联合反演^[42]，这里不再赘述.

(3)所提出的方法基于确定性子波，即假设子波是时不变的，这与补偿方法的研究密切相关. 另外基于时变子波对探地雷达信号作反褶积也是今后一个有意义的方向.

(4)稀疏脉冲反褶积虽然有一定的抗噪能力，但对于噪声问题过于严重的剖面还是很难奏效. 因此需要将稀疏脉冲反褶积和一些滤波方法有机地组合起来，方能发挥最佳效果.

(5)稀疏脉冲反褶积得到的反射系数如果质量较好，经过递推或道积分后可以得到电磁波波阻抗，进而推出介电常数、含水量等参数，这对于地球物理探测来说具有更大的意义.