近年来,越来越多的电力电子设备投入使用,一些通用的标准应运而生,如IEC/EN 61000-3-2对设备注入电网的谐波电流进行限制. 强制性的国际标准和严格的电能质量要求大大促进了功率因数校正技术的发展. 传统的功率因数校正变换器具有可靠性高、成本低、结构简单、共模干扰小的优点[1],但存在通态损耗大的缺点,尤其是在低输入电压的情况下. 在一个700 W的PFC变换器中,整流桥的损耗大概占据了总损耗的50%(除去EMI滤波器)[2].
为了提升PFC变换器的效率,很多无桥PFC变换器拓扑被提出来. 相对于传统的PFC变换器,无桥PFC变换器功率回路上的少一个二极管,从而提升了变换器的效率. 常见的无桥PFC变换器拓扑有双BOOST无桥变换器、图腾柱无桥变换器、背靠背无桥变换器、三电平无桥变化器和倍压无桥变换器. 其中图腾柱PFC变换器结构简单,同时具有低共模干扰的优点. 在每半个工频周期,慢速二极管桥臂能够将输入端电势分别钳位到输出电压和输出地[3]. 但是,功率MOSFET寄生二极管的反向恢复电流使得该变换器电流连续的情况下无法正常工作,即使采用宽禁带器件工作频率有所限制[4]. 当工作在电流临界模式时,图腾柱PFC变换器能够实现功率MOSFET的谷底导通(VS)或零电压开通(ZVS)以及二极管的零电流关断,从而减小功率MOSFET的开关损耗和二极管的反向恢复损耗.
其中文献[5]介绍了工作在DCM模式下的图腾柱PFC变换器. 利用无桥和交错并联技术的结合,提高了变换器的效率和功率密度,相比于传统交错并联Boost PFC,效率得到明显提升. 但是在相同情况下,DCM模式下的电感电流峰值明显大于临界导通模式(CRM);另外,DCM模式下电感电流降为0之后,电流还要继续谐振,增加了损耗. 因此相比于DCM模式,CRM模式更有优势.
相比于DCM模式,CRM模式下的电流纹波相对较小. 相比于CCM模式,由于CRM模式下可以实现开关管的零电压开通或者谷底导通,开关管反并二极管零电流关断,因此开关管损耗很小. 但是由于CRM模式下,电感电流每个开关周期都会降到0,电感电流峰值较大,电流纹波较大,需要较大的前级滤波器;另外由于该模式下变频工作,对于滤波器的设计也增加了难度.
由于诸多限制,CRM模式一般用于功率较小的工作情况下. 为了使其能够应用于更大功率的场合,就需要用到交错并联技术. 通过多相交错并联不仅可以提升功率等级,而且能够通过多相交错配合较小输入电流以及输出电流的纹波,减小前级滤波器的大小,对于提升功率密度很有意义. 但是传统交错并联技术在定频工况下实现. 变频工作交错并联的实现相比于定频工作相对复杂. 文献[6-8]曾提出几种方案,并且做出了理论和实验验证.
CRM模式下电路变频工作,必须检测电感电流过零点(zero current detection, ZCD)作为开关管的开通时刻. 其中Su等[9]提出了在续流主回路上添加一个采样电阻,通过检测该电阻上的电压来得到ZCD信号. 添加的电路简单有效,性价比极高. 但是这种电流检测方法不能用于交错并联工作的图腾柱无桥PFC,并且添加的采样电阻增加了导通损耗.
BIELA等[10]提出了一种三角波电流模式的控制方法,同时给出了一种通过辅助绕组进行电流过零检测(ZCD)的方案. 不会像添加采样电阻一样增加额外损耗,也能够适用于多相交错并联的情况. 但是在软启动阶段,输出电压达到输入电压峰值大小,此时电感续流时,此时电感电压为输出电压和输入电压的差值. 在输入电压峰值附近时,信号十分微弱无法达到后级比较器的阈值,导致电路无法正常工作.
本文提出了一种新的控制方法,不对电流过零点进行检测,通过对功率MOSFET漏源两端电压进行检测并且和设定阈值进行比较得到触发信号ZCD,控制图腾柱无桥PFC工作在CRM模式. 相比采样电阻和辅助绕组的方式,该控制方法不会引起额外的损耗,软启动阶段能够正常工作,且适用于多相交错并联的情况. 并且制作了一个两相交错并联的3.3 kW样机验证了可行性.
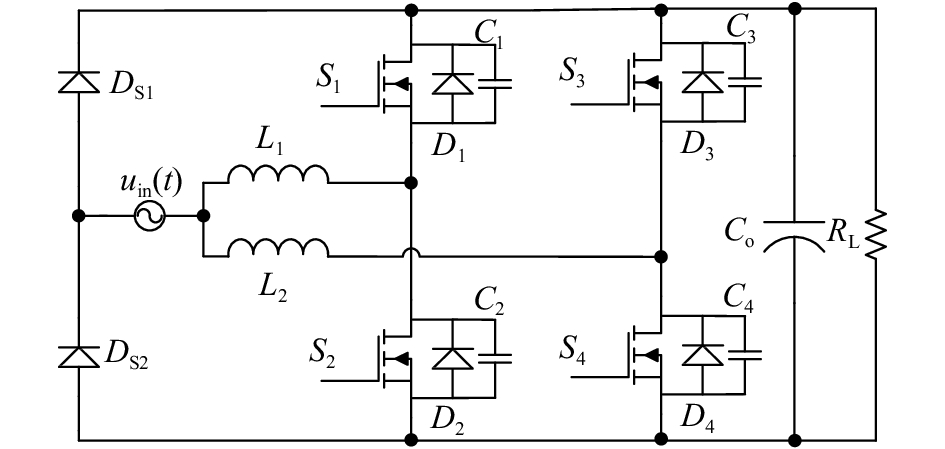
1 图腾柱无桥PFC工作原理如图1所示,uin(t)为输入电压,L1L2为输入电感,S1~S4为功率MOSFET,D1~D4分别为功率MOSFET的体二极管,C1~C4分别为功率MOSFET的结电容. DS1和DS2为低速二极管,Co为输出电容,RL为输出电阻. 2个桥臂有相同的控制信号,工作在180°相位差,两相交错并联. 由于图腾柱拓扑本身的对称性,交流输入电压正负半周的工作原理相同,只分析交流输入电压正半周时的情况. 为简化分析和讨论,假设L1=L2=L,输出电容足够大,输出电压为常数;在一个开关周期内,输入线电压保持不变。为简化分析和讨论,这里假设L1=L2=L,输出电容足够大,输出电压为常数;在一个开关周期内,输入线电压保持不变.
|
图 1 两相交错并联图腾柱无桥PFC原理图 Fig. 1 Schematic of two-phase imterleaved totem pole bridgeless PFC |
1)阶段1 [t0, t1],如图2(a)所示. t0时刻S2开通,S4此时仍导通,流过L1L2的电流线性上升:
| ${i_{{\mathop{L}\nolimits} x}}\left( t \right) = {I_{Lx}}\left( {{t_0}} \right) + \frac{{{u_{{\mathop{\rm in}\nolimits} }}\left( t \right)t}}{L};\;\;\;{x = 1{{,}}\;2}.$ | (1) |
式中:iLx(t)为L1L2的电感电流,ILx(t0)为电感电流t0时刻的值,uin(t)为输入电压.
2)阶段2:[t1, t2],如图2(b)所示. S4关断,电感电流iL2(t)开始给C4充电,给C3放电. 此时电感电流较大,充电过程短暂,电感电流可认为恒定,C2两端的电容电压可以表示为
| ${u_{{c_4}}}\left( t \right) = \frac{{{I_{{L_2}}}\left( {{t_1}} \right)t}}{{2{C_{\rm j}}}}.$ | (2) |
式中:Cj为S4的结电容,
当电容电压达到输出电压时,此阶段结束.
3)阶段3:[t2, t3],如图2(c)所示. D3导通,L2的电感电流线性下降
| ${i_{{L_2}}}\left( t \right) = {I_{{L_2}}}\left( {{t_2}} \right) + \frac{{\left[ {{{{u}}_{{\rm in}}}\left( t \right) - {U_{\rm o}}} \right]t}}{L}.$ | (3) |
L2的电感电流线性下降到零时此阶段结束.
4)阶段4:[t3, t4],如图2(d)所示. L2、C3、C4发生谐振,C4两端的电容电压可以表示为
| $\begin{split}{{{u}}_{{c_4}}}\left( t \right) =& {u_{{\rm in}}}\left( t \right) - \left[ {{u_{{\rm in}}}\left( t \right) - {U_{\rm o}}} \right]{\rm cos}\,\left({\omega _0}t\right) +\\ &{I_{{L_2}}}\left( {{t_3}} \right){Z_0}{\rm sin}\left({\omega _0}t\right).\end{split}$ | (4) |
通过式(4)可以直达,当uin(t)≥Uo/2,通过电感电容的自然谐振,
5)阶段5:[t4, t5],如图2(e)所示. D4导通,L2的电感电流线性上升:
| ${i_{{L_2}}}\left( t \right) = {I_{{L_2}}}\left( {{t_4}} \right) + \frac{{{{{u}}_{{\rm in}}}\left( t \right)t}}{L}.$ | (5) |
经过此阶段,S4再次开通时为零电压开通. 而另一桥臂的情况相同,不再赘述.

|
图 2 交流输入正半周等效电路以及主要工作波形 Fig. 2 Equivalent circuit and main working waveform at positive half cycle of AC input |
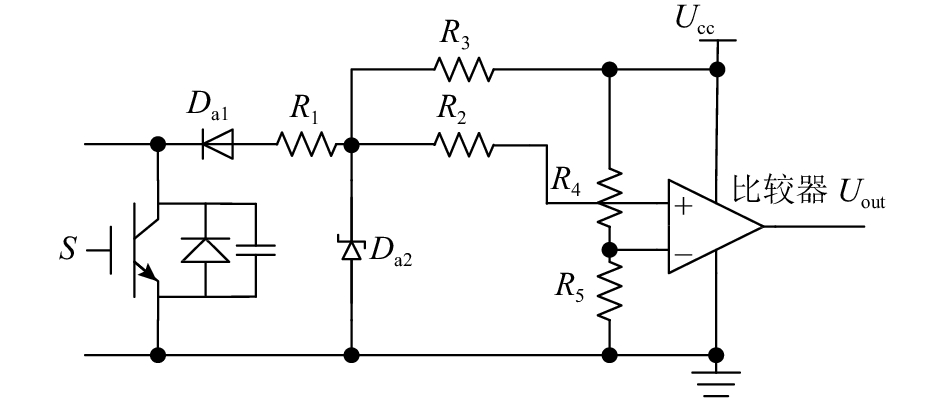
本文提出了一种新的提供临界连续模式下的过零检测信号的获取方式,即通过比较MOSFET漏源电压与阈值电压大小,具体检测电路如图3所示. 当漏源极电压大于供电电压UCC时,比较器的正相端大于负相端,比较器得到高电位. 而当漏源极电压小于供电电压UCC时,二极管Da1导通,比较器正相端电压拉低,比较器输出低电平. 这种检测方式能够精确的检测到开通瞬间MOSFET漏源两端电压与阈值电压的大小关系,保证电路的正常工作,还避免了MOSFET两端并联电阻,降低了检测电路的功耗.
|
图 3 MOSFET漏源两端电压与阈值电压比较电路 Fig. 3 Comparison circuit between drain-source voltage and threshold voltage |
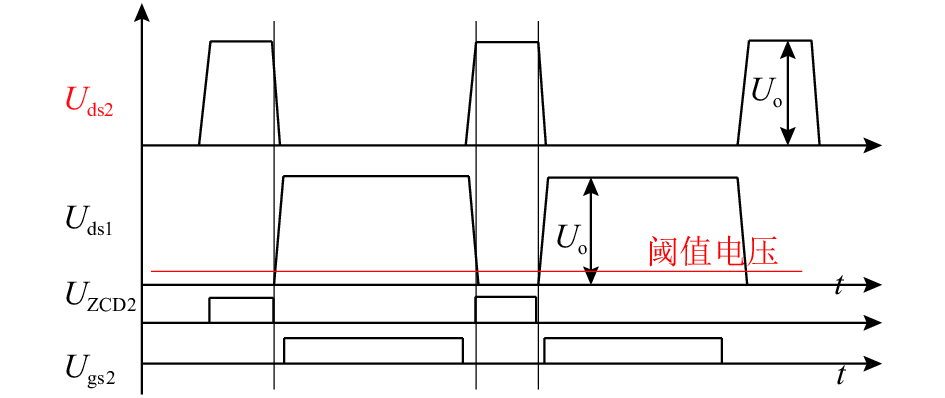
如图4所示,当Uds1从零上升到输出电压的过程中,漏源极电压检测电路的输出信号UZCD2从高电平变成低电平. 此下降沿之后,由于信号传输延迟一段时间,Uds2通过谐振下降,当下降到最小值或者0时,开通S2,实现零电压开通或者谷底导通.
|
图 4 漏源极电压检测与阈值比较控制方案 Fig. 4 Drain source voltage detection and threshold comparison control scheme |
通过本文提出的漏源极电压检测电路控制的实验波形如图5所示. 其中UZCD2就是用于控制S2开通时刻的过零检测信号,如图所示UZCD2能够准确反映出当前的S1漏源电压情况. 当Uds1高于阈值时,漏源极电压检测信号输出低电平;当Uds1低于阈值时,漏源极电压检测信号输出高电平,实现零电压开通(zero voltage switching,ZVS).

|
图 5 源漏极电压检测控制下的电路波形 Fig. 5 Measured waveforms controled by VDS signals |
理想条件下,临界连续模式下的功率因数矫正电路,保证每个开关周期开通时间相同,只要输入电压是正弦的,输入电流的平均值也是正弦的,从而使得功率因数接近1.
实际上在电感电流降为0之后,电感和MOSFET的寄生电容还会发生谐振,电感电流继续下降. 电感电流的平均值不是标准的正弦波形,产生电流畸变. 下面具体分析固定导通时间控制下的电流波形畸变情况.
临界连续Boost电感电流峰值为
| ${I_{{\rm pk}}}(t) = \frac{{{T_{{\rm on}}}{U_{\rm M}}|{\rm sin}\,(\omega t)|}}{L}.$ | (6) |
式中:Ipk(t)为Boost电感电流的峰值电流;UM为输入电压的峰值;Ton 为开关管的导通时间;ω为工频角频率.
电流下降的时间Toff为
| ${{{T}}_{{\rm{off}}}} = \frac{{{L_1}{I_{{\rm pk}}}(t)}}{{{U_{\rm o}} - {U_{\rm M}}|{\rm sin}\,(\omega t)|}}.$ | (7) |
根据之前的过程分析可知,电感电流降到0之后,电感电容发生谐振,电感电流继续下降,根据谐振原理得到反相电流峰值和谐振时间如下:
| ${I_{{\rm{neg}}}}(t) = ({U_{\rm o}} - {U_{\rm M}}|{\rm sin}\,(\omega t)|)\sqrt {\frac{{{C_j}}}{L}}{\text{,}}$ | (8) |
| ${t_{{\rm{neg}}}}(t) = \frac{{({U_{\rm o}} - {U_{\rm M}}|{\rm sin}\,(\omega t)|)}}{{{U_{\rm M}}|{\rm sin}\,(\omega t)|}}\sqrt {L{C_j}} .$ | (9) |
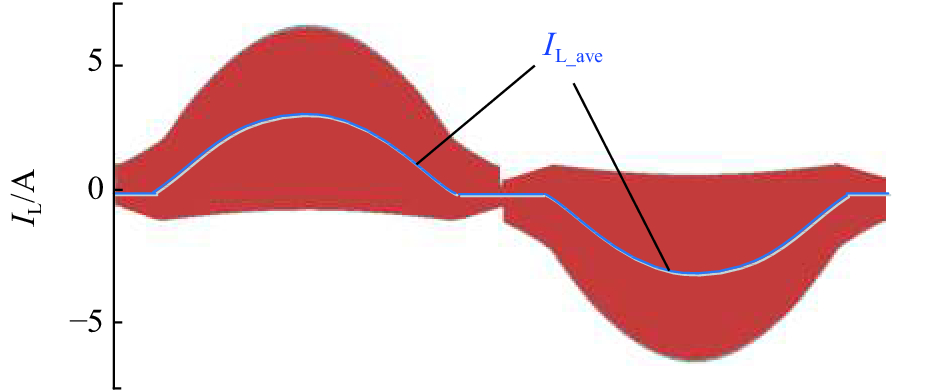
通过式(6)~(9)可以得到电感平均电流与开通时间的表达式IL_ave=f (Ton). 固定开通时间的控制方法得到的电感电流的仿真波形如图6所示. 电感电流均值在输入电压过零处存在明显的畸变,导致输入电流的THD较大.
|
图 6 固定开通时间电流畸变情况 Fig. 6 Current distortion at constant on-time |
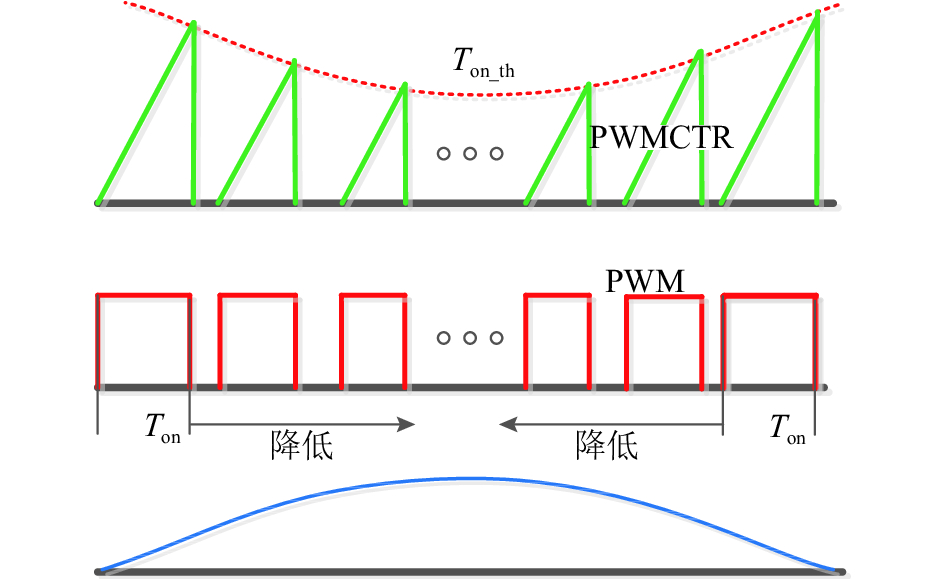
文献[11]针对电流过零畸变引起的THD偏高提出了变开通时间的做法. 本文以此为基础,设计了数字控制方案,在工频周期内调整Ton使得电感电流的平均值正比于锁相环正弦值,从而达到改善电流畸变的目的. 实际实现时,离线计算好相应开通时间,然后通过查表来更新当前的开通时间,控制更加方便,工频半周期变开通时间控制方案如图7所示. 实验在电网220 V交流输入,400 V直流输出,负载800 W的情况下,采用固定开通时间做法输入电流畸变严重,如图8(a)所示,THD达到14.58%;采用变开通时间算法后,如图8(b)所示,THD下降到4.11%.
|
图 7 工频半周期的变开通时间控制方案 Fig. 7 Variable on-time control at half cycle of AC input |

|
图 8 功率800 W时输入电压电流波形 Fig. 8 Input voltage and input current at 800 W |
为了验证本文的所有分析,设计了一款3.3 kW的样机,如图9所示. 具体参数以及器件选择如下表1所示,其中电感通过PQ35/35的铁氧体磁芯以及0.1 mm*100的利兹线绕制而成,磁芯结构采用中柱多段气隙结构,减小了由于漏感引起的额外损耗和EMI干扰[12-13]. 工作频率在50~200 KHz. 控制芯片采用TI公司的TMS320F28027,这是款主频为60 MHz的32位定点DSP,价格便宜,拥有灵活的ADC配置,方便的EPWM模块和丰富的中断,能够很好地支持此方案.
| 表 1 图腾柱PFC 3.3 KW样机参数列表 Table 1 Major parameters of 3.3 KW totem pole PFC prototype |

|
图 9 图腾柱PFC 3.3 kW样机 Fig. 9 Totem pole bridgless PFC 3.3 kW prototype |
临界连续模式下电感电流纹波较大,会造成很大的差模干扰. 实验采用两路交错并联的方法,抵消电流纹波. 具体实验结果如图10所示,电感电流纹波抵消明显.

|
图 10 两相交错并联的电感电流纹波消除情况 Fig. 10 Measured waveforms by two-phase interleaved and inductance current ripple elimination |
采用第2.1节所提出漏源极电压检测方案,电路能够很好地实现MOSFET零电压开通或谷底导通,降低了MOSFET的开关损耗. 实验测量了220 V/50 Hz输入,400 V直流输出的不同负载时候的效率,如图11所示,峰值效率将近99%. 另外本文通过采用2.2中介绍的变开通时间的做法改善了过零附近的电流畸变,使得输入电流的THD小于5%.

|
图 11 图腾柱 PFC 3.3 kW样机效率图 Fig. 11 Measured efficiency by totem pole PFC 3.3 kW prototype |
本文介绍了临界模式的图腾柱无桥PFC电路的电流拓扑和工作原理. 提出了一种新的一种新的图腾柱整流器临界连续的控制方法,通过检测MOSFET开通瞬间漏源两端电压与阈值电压的大小关系来控制电路的临界连续工作. 该方法有效的减小了变换器的开关损耗,提高了电路效率. 这种控制方法免去了对电感电流的检测,也可以扩展到交错并联的应用中去. 并且制作3.3 KW的样机,实测峰值效率为99.87%. 另外,通过变开通时间的算法以及两相交错并联的做法,改善了输入电流波形,使得输入电流THD达标. 本文所提方案能够明显提高整机效率,具有积极意义.
| [1] |
HUANG L, YAO W, LU Z. Interleaved totem-pole bridgeless PFC rectifier with ZVS and low input current ripple [C] // 2015 Energy Conversion Congress and Exposition. Montreal: IEEE, 2015: 166–171 http://ieeexplore.ieee.org/document/7309684/
|
| [2] |
KIM Y S, SUNG W Y, LEE B Y. Comparative performance analysis of high density and efficiency PFC topologies[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 2666-2679. DOI:10.1109/TPEL.2013.2275739 |
| [3] |
SU B, LU Z. An interleaved totem-pole boost bridgeless rectifier with reduced reverse-recovery problems for power factor correction[J]. IEEE Transactions on Power Electronics, 2010, 25(6): 1406-1415. DOI:10.1109/TPEL.2010.2040633 |
| [4] |
O'GRADY M, ZHU K, DODGE J, et al. Active switch impact on CCM totem-pole PFC efficiency [C] // 2017 International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy Mangement. Nuremberg: IEEE, 2017: 1-6. https://www.vde-verlag.de/proceedings-en/564424268.html
|
| [5] |
王议锋, 徐殿国, 徐博, 等. 图腾柱式无桥零纹波交错并联Boost功率因数校正器[J]. 电工技术学报, 2011, 26(9): 175-182. WANG Yi-feng, XU Dian-guo, XU Bo, et al. An interleaved totem-Pole bridgeless boost PFC rectifier with zero-ripple current filter[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 175-182. |
| [6] |
HUBER L, IRVING B T, JOVANOVIC M M. Open-loop control methods for interleaved DCM/CCM boundary boost PFC converters[J]. IEEE Transactions on Power Electronics, 2008, 23(4): 1649-1657. DOI:10.1109/TPEL.2008.924611 |
| [7] |
HUBER L, IRVING B T, JOVANOVIC M M. Open-loop control methods for interleaved DCM/CCM boundary boost PFC converters[J]. Power Electronics, IEEE Transactions on, 2008, 23(4): 1649-1657. DOI:10.1109/TPEL.2008.924611 |
| [8] |
HUBER L, IRVING B T, JOVANOVIC M M. Review and stability analysis of PLL-based interleaving control of DCM/CCM boundary boost PFC converters[J]. IEEE Transactions on Power Electronics, 2009, 24(8): 1992-1999. DOI:10.1109/TPEL.2009.2018560 |
| [9] |
SU B, ZHANG J, LU Z. Totem-pole boost bridgeless PFC rectifier with simple zero-current detection and full-Range ZVS operating at the boundary of DCM/CCM[J]. IEEE Transactions on Power Electronics, 2011, 26(2): 427-435. DOI:10.1109/TPEL.2010.2059046 |
| [10] |
BIELA J, HASSLER D, MINIBOCK J, et al. Optimal design of a 5kW/dm3 98.3% efficient TCM resonant transition single-phase PFC rectifier [C]// 2010 Inrenational Power Electronics Conference. Sapporo: IEEE, 2010: 1709-1716 https://www.researchgate.net/publication/224164781_Optimal_design_of_a_5kWdm3_983_efficient_TCM_resonant_transition_single-phase_PFC_rectifier
|
| [11] |
KIM J W, CHOI S M, KIM K T. Variable on-time control of the critical conduction mode boost power factor forrection converter to improve zero-crossing distortion [C]// 2005 International Conference on Power Electronics and Drives Systems. Kuala Lumpur: IEEE, 2005: 1542-1546 http://ieeexplore.ieee.org/document/1619933/
|
| [12] |
SUULLIVAN C R, BOUAYAD H, SONG Y. Inductor design for low loss with dual foil windings and quasi-distributed gap [C]// 2013 Energy Conversion Congress and Exposition. Danver: IEEE, 2013: 3693-3699 http://ieeexplore.ieee.org/document/6647188/
|
| [13] |
ACKERMANN B, LEWALTER A. Two-dimensional calculation of winding losses in planar magnetic components [C]// 2001 International Conference on Power Electronics and Drive Systems. Denpasar: IEEE, 2001: 674-679 http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&arnumber=975400&sortType%3Dasc_p_Sequence%26filter%3DAND%28p_IS_Number%3A21037%29%26rowsPerPage%3D75
|



