运行方式的优化选择是继电保护整定计算中的一个重要研究内容[1]. 随着电网的互联,以及新能源和分布式发电的增加,电网的拓扑结构越来越复杂,运行方式更加多样化,使得继电保护整定计算中运行方式的选择难度增加. 如何选择运行方式,从而高效地计算出最小和最大配合系数,使得相邻保护之间的定值配合更加合理,一直是继电保护整定计算领域所关注的重要技术问题之一.
在继电保护整定计算领域,有学者对配合系数的计算及运行方式的选择方法进行了研究[2-9]. 程小平等[4-5]就不同运行方式对配合系数影响的规律进行了研究和总结,对整定计算中的运行方式选择具有一定指导作用,然而这类经验规律主要适用于人工整定或者半自动整定. 随着计算机技术的发展,全自动的整定计算软件逐渐成熟[10-12]. 在利用计算机自动考虑运行方式选择的问题上,通常对所有可能的运行方式进行排列组合,这样计算量巨大,需要消耗较多的时间和硬件资源. 另一方面,这种基于枚举法的自动计算往往只有计算结果,缺乏推理性质的中间过程和步骤,这影响了自动计算的实用性[13]. 为了改进传统方法,在元件投停的选择方法上,张锋等[6]采用阻抗矩阵法挑选出电网中的重要线路参加运行方式的组合,提高了计算效率. 周志辉等[7]计算被保护元件与其他元件之间的耦合度,提出了选择耦合度较大的元件参与运行方式组合的方法. 在电源运行方式的选择方法上,曹国臣等[8]提出了电流分布系数的概念,其定义为电源电流与故障点短路电流的比值,描述了各电源对故障电流的影响程度;计算出各电源的电流分布系数后,设置某一门槛值,筛选出电流分布系数较大的电源并进行运行方式的组合. 李冰等[9]进一步提出了直接利用节点阻抗矩阵中的相关元素以及发电机支路阻抗来计算电流分布系数的方法. 但是,电流分布系数法存在着门槛值选择困难的问题.
为了提高整定计算的合理性与效率,本文提出一种基于电源贡献系数法的电源运行方式选择方法. 该方法利用节点阻抗矩阵中的相关元素,分别计算各电源对保护支路和助增支路的短路电流贡献系数,然后根据贡献系数的相角和幅值确定各电源在最小或最大配合系数的计算中所对应的大小方式。
1 配合系数计算中电源运行方式的选择问题配合系数反映了保护支路与配合支路的短路电流对定值配合的影响,是继电保护整定计算中的重要参数,也是整定计算的难点所在[4]. 配合系数在电流保护中通常称为分支系数[14],在距离保护中称为助增系数[15],两者在定义上为倒数关系. 根据整定计算所考虑序网分量的不同,又可分为正序网的配合系数和零序网的配合系数,由于零序网中通常不包含发电机,本文以正序网的助增系数为例,对配合系数计算中电源运行方式的选择方法进行分析和探讨.
助增系数的定义是流过配合支路的短路电流与流过保护支路的短路电流之比,常用KZ表示[16]. 对于如图1所示的网络,当对保护RA进行整定并考虑与保护RB的配合时,助增系数KZ=IB/IA. 在距离保护整定计算中,为了满足选择性,通常需要计算各种可能的运行方式下的最小助增系数;而为了校验灵敏性,则需要计算最大助增系数.

|
图 1 整定计算中配合系数的定义示意图 Fig. 1 Sketch map of coordination coefficient definition in relay setting calculation |
在图1网络中,若故障点和故障类型已确定,影响KZ大小的可变因素主要为2个方面[5]:一是支路BC和CD是否投运,即电网供电方式和设备检修安排;二是电源GA、GB、GC的阻抗,即电源运行方式对助增系数的影响,这是本文的研究重点.
电源的运行方式通常体现在其等值阻抗的变化上. 图1中的各个电源可能直接代表发电机组,也可能代表某个区域电网的等值. 一般由调度运行部门提供电源等值阻抗的上下限. 电源阻抗取最小时,该电源运行在最大方式下;电源阻抗取最大时,则该电源运行在最小方式下. 因此,在最小或最大助增系数的计算中,电源运行方式的选择就是确定网络中各个电源的等值阻抗是选择最大还是最小.
2 电源贡献系数计算方法 2.1 保护所在支路电源贡献系数的计算方法电源贡献系数的含义为各电源对所关注支路的短路电流的贡献度. 采用叠加原理对其进行计算.
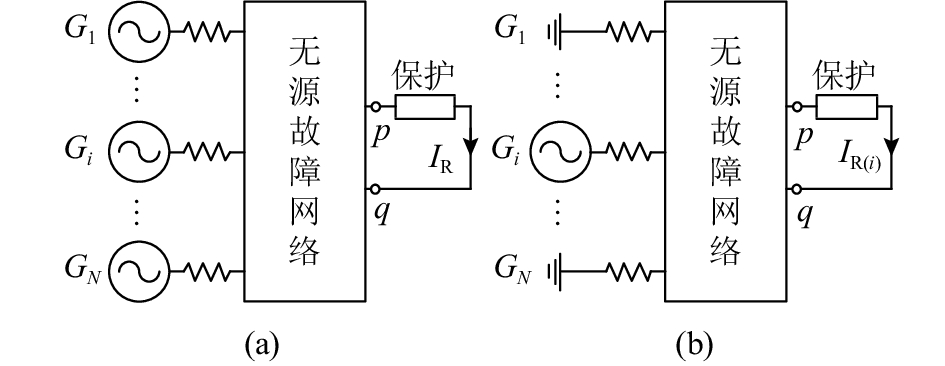
如图2所示,假设以保护所在支路pq作为关注支路. 图2(a)为将所有电源和保护所在支路从网络中单独提出后的等效示意图,其中,电源采用理想电压源串联等效阻抗的形式,IR表示流过保护所在支路的短路电流;图2(b)为仅电源Gi运行,其他电源接地时的等效示意图,IR(i)表示此情况下流过保护所在支路的短路电流. 由叠加原理可知,IR为(IR(1), …, IR(i), …, IR(N))之和,即所有电源单独贡献的短路电流的总和. 因此,定义某一电源对于保护所在支路的电源贡献系数:电网中仅有该电源运行时的保护支路电流与所有电源运行时的保护支路电流的比值:
| $ {C_{{\rm{R(}}i)}} = \frac{{{I_{{\rm{R}}\left( i \right)}}}}{{{I_{\rm{R}}}}} .$ | (1) |
式中:CR(i)表示电源Gi对于保护所在支路的电源贡献系数.
|
图 2 电源贡献系数示意图 Fig. 2 Sketch map of power source contribution coefficient |
根据上述定义进行计算,需要重复地进行电源支路参数修改和短路电流计算. 为提高效率,可利用网络的节点阻抗矩阵中的相关元素进行运算. 短路电流计算通常以节点导纳矩阵为基础进行求解,因而,首先可以利用三角分解法等从现有的节点导纳矩阵Y快速求出节点阻抗矩阵Z [17-18]. 需要注意的是,该节点阻抗矩阵中已经包含了故障点.
节点阻抗矩阵Z中的非对角元素Zij,即节点i和节点j之间的互阻抗,在数值上等于仅仅在节点i注入单位电流时,节点j的电压. 因此,假设在图2(b)中电源Gi处注入的电流为单位电流,可用下式计算此时流过保护所在支路的短路电流[19]:
| $ {I'_{{\rm{R}}\left( i \right)}} = \left( {{Z_{ip}} - {Z_{iq}}} \right){y_{\rm{R}}} .$ | (2) |
式中:
由于短路电流计算中电源电动势可以假定为1个标幺值,且相位一致[14],电源Gi的实际注入电流为1/ZGi,其中ZGi为电源Gi的阻抗. 因而,IR(i)可进一步用下式计算.
| $ {I_{{\rm{R}}\left( i \right)}} = \frac{{{{I'}_{{\rm{R}}\left( i \right)}}}}{{{Z_{{\rm{G}}i}}}}{\rm{ = }}\frac{{\left( {{Z_{ip}} - {Z_{iq}}} \right){y_{\rm{R}}}}}{{{Z_{{\rm{G}}i}}}} .$ | (3) |
所有N个电源运行时的保护支路电流IR即为
| $ {I_{\rm{R}}} = \sum\limits_{i = 1}^N \;\;{{I_{{\rm{R}}\left( i \right)}}} = \sum\limits_{i = 1}^N \;\;{\frac{{\left( {{Z_{ip}} - {Z_{iq}}} \right){y_{\rm{R}}}}}{{{Z_{{\rm{G}}i}}}}} .$ | (4) |
根据式(1)、(3)~(4)可得
| $ {C_{{\rm{R(}}i)}} = \frac{{{{\left( {{Z_{ip}} - {Z_{iq}}} \right)}/{{Z_{{\rm{G}}i}}}}}}{{\displaystyle\sum\limits_{i = 1}^N {\left[ {{{\left( {{Z_{ip}} - {Z_{iq}}} \right)}/{{Z_{{\rm{G}}i}}}}} \right]} }} .$ | (5) |
CR(i)的计算结果为复数,可以分为幅值和相角2个部分. 其相角
| $ \left. \begin{array}{l} -\; 90^\circ \leqslant {\text{∠}} {C_{{\rm{R(}}i)}} < 90^\circ ,\;\;{\text{方向为正}} ;\\{\text{∠}} {C_{{\rm{R(}}i)}} \geqslant 90^\circ \;{\text{或}}< -\; 90^\circ , \;\;{\text{方向为负}}.\end{array} \right\} $ | (6) |
幅值
由于助增系数的定义为配合支路与保护支路的短路电流之比,而配合支路的短路电流等于保护支路与助增支路的电流之和,可以进一步用下式表示助增系数:
| $ {K_{\rm{Z}}} = \frac{{{I_{\rm{F}}}}}{{{I_{\rm{R}}}}}{\rm{ = }}1 + \frac{{{I_{\rm{Z}}}}}{{{I_{\rm{R}}}}} .$ | (7) |
式中:IF表示流过故障支路(配合支路)的短路电流,IZ表示流过助增支路的短路电流. 由式(7)可知,保护支路和助增支路这两者的短路电流的大小关系决定了助增系数的大小. 上一节介绍了关于保护支路的电源贡献系数的计算方法,下面进一步介绍关于助增支路的电源贡献系数.
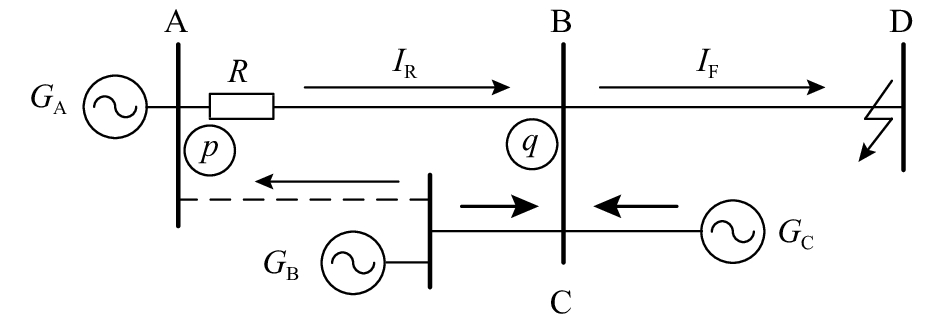
助增支路的电源贡献系数与前述关于保护支路的电源贡献系数类似,但由于助增支路可能不止一条(如图3中粗箭头所示,且图中仍然设保护支路的首端为p,末端为q),需要将各条助增支路的电流进行加和,作为一个整体:
|
图 3 助增支路电源贡献系数示意图 Fig. 3 Power source contribution coefficient of infeed branch |
| $ {C_{{\rm{Z(}}i)}} = {{{I_{{\rm{Z(}}i)}}}/{{I_{\rm{Z}}}}} = {{\sum\limits_{x \in {\rm{X}}} \;\;{{I_{qx{\rm{(}}i)}}} }\left/{\sum\limits_{x \in {\rm{X}}}\;\; {{I_{qx}}} }\right.} .$ | (8) |
式中:CZ(i)表示电源Gi对于助增支路的电源贡献系数;IZ(i)表示仅电源Gi运行时的助增支路电流;IZ表示所有电源运行时的助增支路电流;X为所有助增支路除节点q外的另一端节点所构成的集合;x为X中的元素,即某一条助增支路另一端的节点编号;Iqx(i)表示仅电源Gi运行时的流过节点q和x之间支路的电流;Iqx表示所有电源运行时的流过节点q和x之间支路的电流.
利用节点阻抗矩阵中的相关元素进行计算,则助增支路的电源贡献系数为
| ${C_{{{{\rm Z}(}}i)}} = \frac{{{{\left.\left[ {\displaystyle\sum\limits_{x \in {{X}}}^{} \;\;{\left( {{Z_{ix}} - {Z_{iq}}} \right){y_{qx}}} } \right]\right/}{{Z_{{{G_i}}}}}}}}{{\displaystyle\sum\limits_{i = 1}^N \;\;{\left\{ {{{\left.\left[ {\displaystyle\sum\limits_{x \in {{X}}}^{} \;\;{\left( {{Z_{ix}} - {Z_{iq}}} \right){y_{qx}}} } \right]\right/} {{Z_{{{G_i}}}}}}} \right\}} }} .$ | (9) |
式中:yqx为以节点q和x为两端的助增支路的导纳. 对于不存在助增支路的情况,考虑到方法和流程的一致性,本文中规定CZ(i)的取值为
同样地,可以利用式(6)的方法将CZ(i)也分为正、负2个方向,如下式所示:
| $ \left. \begin{array}{l} -\; 90^\circ \leqslant {\text{∠}} {C_{{\rm{Z(}}i)}} < 90^\circ , \;\;{\text{方向为正}};\\{\text{∠}} {C_{{\rm{Z(}}i)}} \geqslant 90^\circ\;{\text{或}} < -\; 90^\circ , \;\;{\text{方向为负}}.\end{array} \right\} $ | (10) |
若为正方向,则说明电源Gi有助于助增支路电流的增大;若为负方向,则倾向于使得助增支路电流减小. 其中,助增电流的方向规定为指向保护支路末端母线的方向. 若实际助增支路电流方向与规定方向相反,即“外汲”的情况,则式(10)中的结果取反.
3 基于电源贡献系数法的运行方式选择 3.1 基于电源贡献系数的电源运行方式选择方法在保护支路不存在环网的情况下,某电源Gi关于保护支路的电源贡献系数CR(i)和关于助增支路的电源贡献系数CZ(i)的方向性应为一正一负的关系. 例如,假设图3中的虚线线路不存在,根据电源贡献系数的定义,计算电源GA关于保护支路和助增支路的电源贡献系数时,电源GB和GC接地,因此GA在保护支路上贡献的短路电流与图中箭头方向一致,即CR(A)为正方向,而GA在助增支路上贡献的短路电流与图中箭头方向相反,即CZ(A)为负方向. 同样地,计算电源GB或GC的电源贡献系数时,其关于保护支路的电源贡献系数为负方向,关于助增支路的电源贡献系数为正方向. 因此,在保护支路不存在环网的情况下,某电源:1)有利于保护支路电流增大、不利于助增支路电流增大,则根据式(7),将使助增系数减小;2)不利于保护支路电流增大、有利于助增支路电流增大,则根据式(7),将使助增系数增大. 进而用上述方法将电源划分为使助增系数减小和使助增系数增大2个类别,分别用{G–}和{G+}表示:
| $\left. \begin{array}{l}{C_{{\rm{R}}(i)}}{\text{为正方向}}, {C_{{\rm{Z(}}i)}}{\text{为负方向}}, {{{G}}_i} \in \left\{ {{{G}} - } \right\};\\{C_{{\rm{R(}}i)}}{\text{为负方向}}, {C_{{\rm{Z(}}i)}}{\text{为正方向}}, {{{G}}_i} \in \left\{ {{{G}} + } \right\}。\end{array} \right\}$ | (11) |
在保护支路存在环网的情况下,如图3所示,电源GB关于保护支路和关于助增支路的电源贡献系数可能均为正方向,即同时有利于保护支路和助增支路电流的增大. 此时,需要进一步比较电源贡献系数的幅值大小来判断该电源对助增系数的影响. 根据式(7),若对保护支路电流增大的影响比对助增支路电流增大的影响更明显,则该电源倾向于使助增系数减小;反之,若对助增支路的影响更明显,则倾向于使助增系数增大. 因此,采用式(12)进行电源类别的划分. 若CR(i)和CZ(i)均为正方向,则
| $ \left. \begin{array}{l}\left| {{C_{{\rm{R(}}i)}}} \right|{\rm{ > }}\left| {{C_{{\rm{Z(}}i)}}} \right|, {{\rm{G}}_i} \in \left\{ {{\rm{G}} - } \right\};\\\left| {{C_{{\rm{R(}}i)}}} \right| \leqslant \left| {{C_{{\rm{Z(}}i)}}} \right|, {{\rm{G}}_i} \in \left\{ {{\rm{G}} + } \right\}.\end{array} \right\} $ | (12) |
对于CR(i)和CZ(i)均为负方向的情况,这意味着该电源将使得保护支路和助增支路的电流都减小. 由于保护支路和助增支路电流之和为故障支路电流,说明该电源的存在将使得故障电流减小,不符合电路规律,CR(i)和CZ(i)均为负方向的情况不存在.
根据式(11)和(12)划分出网络中所有电源的类别后,可依据如下规律选择电源运行方式:计算最小助增系数时,{G–}中的所有电源都设为大方式,{G+}中的所有电源都设为小方式;计算最大助增系数时,{G–}中的所有电源都设为小方式,{G+}中的所有电源都设为大方式.
3.2 最小、最大助增系数的计算流程利用本文方法计算最小或最大助增系数的流程如图4所示. 若将本文方法应用于正序网分支系数的计算,由于分支系数与助增系数在定义上为倒数关系,则电源运行方式的选择方法恰好与上文相反,即当计算最小分支系数时,{G–}中的所有电源都设为小方式,{G+}中的所有电源都设为大方式;当计算最大分支系数时,{G–}中的所有电源都设为大方式,{G+}中的所有电源都设为小方式.

|
图 4 电源贡献系数法流程图 Fig. 4 Flow chart of power source contribution coefficient method |
上述方法利用故障网络的节点导纳矩阵求取电源贡献系数,然后据此选择各电源的运行方式. 但是,其中所使用的节点导纳矩阵是在一个静态的故障网络的基础上求取的,而各电源设定大小方式后,其电源阻抗值相应改变,也会引起整个网络的节点导纳矩阵发生变化,可能会导致上述方法的电源运行方式选择结果不够准确. 因此,本文进一步采取迭代计算的方案进行改进,具体流程如下:
1)将网络中所有电源的运行方式设为基础方式(例如:各电源阻抗的基础值取为各自最大阻抗和最小阻抗的平均值),然后根据图4中的方法流程计算出最小或最大助增系数,以及相应的电源运行方式;
2)按照上一次的计算结果,对网络中所有电源进行大、小方式的设置,然后计算出新的最小或最大助增系数,以及新的电源运行方式;
3)比较最近2次的计算结果,若所有电源的运行方式安排是一致的(此时最小或最大助增系数也相同),或者达到迭代次数上限,则以最近一次计算作为最终结果;否则,回到2)继续迭代.
上述迭代计算方案能够提高本文方法的准确性,但也会增加一部分的计算量,本文将在下一节中结合算例进一步说明.
此外,需要说明的是,在助增系数的计算中通常需要同时考虑支路轮断和电源运行方式组合这2个方面. 因而,在实际应用中,可以先利用一些现有方法选择出若干条对助增系数影响较大的支路[3-7],然后轮流开断这些支路,逐一使用本文方法选择电源大、小方式,并计算助增系数,最后对以上计算结果进行比较,筛选出最终的最小或最大助增系数及对应的运行方式.
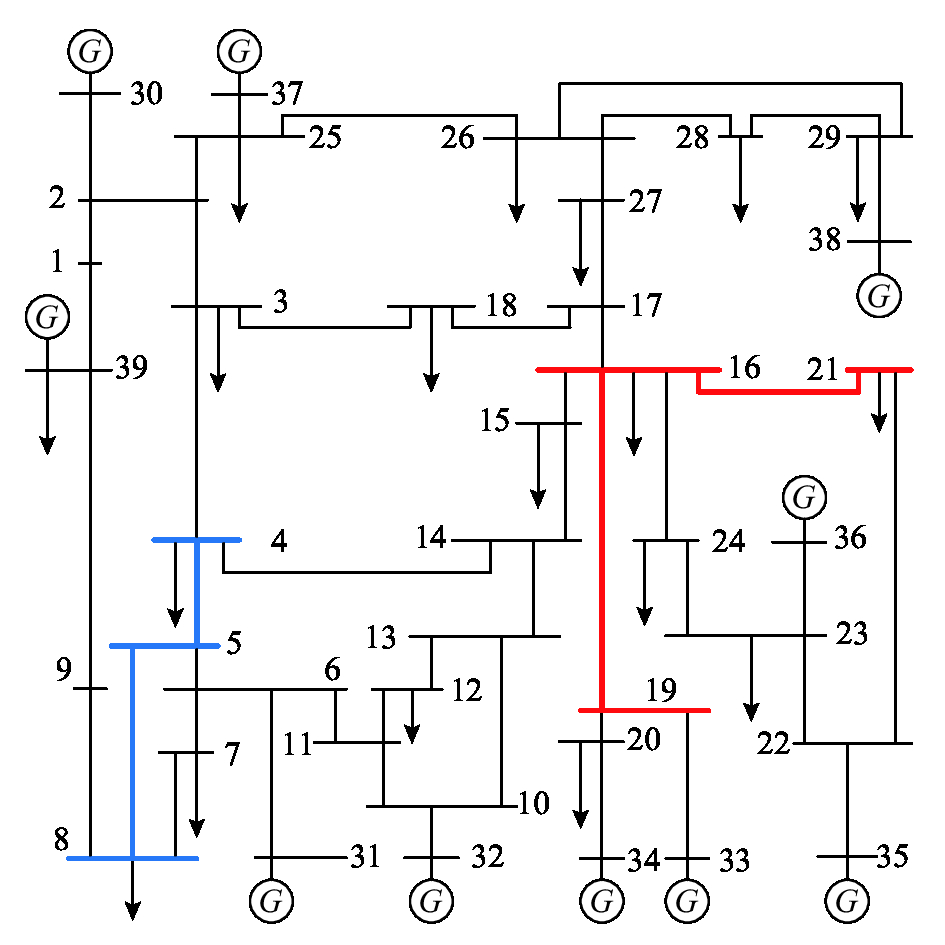
4 算例验证采用新英格兰10机39节点系统对本文方法进行验证,该系统的正序网络[20]如图5所示. 短路电流计算采用三角分解法求解节点电压方程. 整个计算过程采用Matlab (7.11.0)软件,运行在一台使用Windows 7操作系统的个人计算机上进行,处理器主频为2.60 GHz,内存为8 GB.
|
图 5 新英格兰10机39节点系统 Fig. 5 New England 10-unit 39-bus test system |
场景一:
以线路21-16,母线21侧的保护为例,考虑与下级线路16-19的保护配合,假设故障发生在下级线路末端,即母线19上. 当电源取大方式时,假设阻抗为原先阻抗值的0.8,当电源取小方式时,假设阻抗为原先阻抗值的1.2倍. 分别利用枚举法、电流分布系数法[8-9]、电源贡献系数法(不使用迭代,各电源以原先的阻抗值作为基础方式)计算最小和最大助增系数,结果如表1所示. 表中,Tcal为计算用时. 电流分布系数法中的α为门槛值,大于门槛值的电源将进行排列组合;小于门槛值的电源按原先的阻抗值设置,在表中未列出. 各电源采用其接入的母线序号作为编号. 为了进一步评估算法的计算用时,将所编写的Matlab程序连续运行100次,记录各方法在已知故障网络节点导纳矩阵的条件下,计算出最小和最大助增系数所耗费的时间,最后对计算用时取平均以减小误差. 虽然实际的计算用时会根据硬件、软件、编程方法的不同而变化,但本文算例中的时间统计基本可以反映出各方法计算效率的数量级关系.
| 表 1 电源贡献系数法、枚举法以及电流分布系数法的助增系数计算结果比较 Table 1 Comparison of coordination coefficient calculation results among power source contribution coefficient method, enumeration method and current distribution factor method |
由表1可知,枚举法对所有电源的运行方式进行排列组合,其计算出的最小和最大助增系数是精确的,然而计算用时长. 电流分布系数法在门槛值取值较小时,参与排列组合的电源较多,计算误差较小,但计算时间较长;而在门槛值取值较大时,参与排列组合的电源少,虽然计算时间减少,但计算误差较明显. 相比之下,电源贡献系数法的计算准确度和计算效率都优于电流分布系数法,并且不存在门槛值的选择问题.
上述算例中,{G–}中电源的贡献系数取关于保护支路的电源贡献系数幅值,{G+}中电源的贡献系数取关于助增支路的电源贡献系数幅值,各电源的贡献系数计算结果如表2所示. 在{G–}中,电源33、34的贡献系数接近于0,从图5中也可以看出,当故障发生在母线19上时,电源33、34与保护及配合支路分隔在两端,故电源33、34不会影响所关注的助增系数的计算,但由于本算例中采用一条阻抗很小的支路模拟金属性故障,电源33、34能够计算出一个非常小的数值. 然而,由于本文方法不需要排列组合,且电源33、34又几乎不影响所计算的助增系数,其存在不会影响计算效率和准确度.
| 表 2 电源贡献系数计算结果 Table 2 Calculation results of power source contribution coefficient |
然而,{G–}中的另外2个电源35、36,电源35的贡献作用相对更大,其主要原因之一是电源35相比电源36,离保护支路的首端母线21更近,离末端母线16更远,因而其对保护支路短路电流增大的作用更显著,即更有利于助增系数的减小. 在{G+}中,各电源的贡献系数都差不多,从图5中也可以看出,这些电源所贡献的电流都是作为助增电流汇入母线16,有利于助增系数的增大,且各电源距离母线16都较远,因而其作用相差不大. 从上述分析可见,电源贡献系数的计算结果基本与人工经验相符合.
场景二:
以线路8-5,母线8侧的保护为例,考虑与下级线路5-4的保护配合,假设故障发生在下级线路末端,即母线4上. 利用电源贡献系数法和枚举法计算最小和最大助增系数. 各电源以原先的阻抗值作为基础方式;第一次测试时,电源方式变化较小,取大方式时设为原先阻抗值的0.8倍,小方式时设为原先阻抗值的1.2倍(在表3中标记为“测试一”);第二次测试时,电源方式变化较大,大方式设为0.5倍,小方式设为1.5倍(在表3中标记为“测试二”). 在2次测试中分别考虑进行迭代和不进行迭代的方案. 计算结果如表3所示.
| 表 3 基于迭代的电源贡献系数法助增系数计算结果 Table 3 Coordination coefficient calculation results from iterative-based power source contribution coefficient method |
由表3可知,在该故障场景中,随着电源大、小方式阻抗倍率的增大,电源阻抗变化对网络参数的影响也有所增加,枚举法求解出的极端运行方式也产生了变化. 但电源贡献系数法不进行迭代时,由于仅在各电源的基础方式下进行计算,无法适应上述变化,在大小方式阻抗倍率较大的情况下,部分电源的运行方式选择不够准确,导致最小和最大助增系数的计算结果有略微的偏差. 而加入迭代后,这一问题得到改善,能进一步地寻找到极端运行方式,提高了方法的准确度. 同时,随着迭代次数增加,计算用时也会成比例增加,但由于电源贡献系数法本身的计算效率较高,计算用时的实际增加量相比枚举法仍然非常小.
场景三:
对图5网络中所有可能的保护支路-配合支路组合进行遍历(组合总数共158对),均假设故障发生在所关注保护的下级配合线路末端,计算助增系数. 电源取大方式时设为原先阻抗值的0.8倍,小方式时设为原先阻抗值的1.2倍. 使用迭代方案的电源贡献系数法、电流分布系数法和枚举法的计算结果如表4所示. 其中的误差统计,指的是以枚举法的计算结果为基准,统计其他方法结果的相对误差. 表中,Eave表示平均相对误差,Emax表示最大相对误差.
| 表 4 电源贡献系数法、电流分布系数法和枚举法的助增系数计算误差及计算用时对比 Table 4 Comparison of coordination coefficient calculation error and computing time among power source contribution coefficient method, current distribution factor and enumeration method method |
由表4可知,本文电源贡献系数法的最小和最大助增系数计算误差很小,在本算例网络中平均误差不超过1‱,最大误差不超过2‰,并且计算用时远小于传统枚举法. 与电流分布系数法相比,本文方法更加平衡,能够兼顾计算准确度与计算效率.
5 结 语本文提出了电源贡献系数的概念,以及基于保护支路和助增支路电源贡献系数的运行方式选择方法. 算例分析表明,该方法能够准确地给出各电源在最小或最大配合系数计算中所对应的大、小方式,避免了排列组合的枚举,可兼顾计算效率与准确度.
在实际电网的整定计算中,不仅需要计算正序配合系数,还需计算零序配合系数. 零序配合系数的计算与变压器接地方式有关,因此未来还需要进一步研究整定计算中变压器接地方式的选择方法.
| [1] |
贺家李. 电力系统继电保护原理(第四版)[M]. 北京: 中国电力出版社, 2010. http://www.bzfxw.com/soft/sort011/vlaveinfo/105218835.html
|
| [2] |
张健康, 粟小华. 超高压线路后备保护整定原则探讨[J]. 电力系统自动化, 2016, 40(8): 120-125. ZHANG Jian-kang, SU Xiao-hua. Discussion on setting calculation of backup protection for EHV transmission line[J]. Automation of Electric Power Systems, 2016, 40(8): 120-125. |
| [3] |
杨雄平, 段献忠, 石东源. 基于环网电气耦合指标的运行方式组合方法[J]. 电力系统自动化, 2005, 29(23): 64-68. YANG Xiong-ping, DUAN Xian-zhong, SHI Dong-yuan. Method for operation mode combination based on electric coupling of mesh network[J]. Automation of Electric Power Systems, 2005, 29(23): 64-68. DOI:10.3321/j.issn:1000-1026.2005.23.013 |
| [4] |
程小平. 配合系数与网络结构关系的研究[J]. 电力系统自动化, 2000(9): 52-55. CHENG Xiao-ping. Study on relation between network topology and cooperation coefficient[J]. Automation of Electric Power Systems, 2000(9): 52-55. DOI:10.3321/j.issn:1000-1026.2000.09.013 |
| [5] |
杨洋, 王慧芳, 时洪禹. 继电保护整定计算中运行方式的选择方法[J]. 继电器, 2006, 34(20): 1-4. YANG Yang, WANG Hui-fang, SHI Hong-yu. Setup and choice method for operating mode in protection setting calculation software[J]. Relay, 2006, 34(20): 1-4. |
| [6] |
张锋, 李银红, 段献忠. 电力系统继电保护整定计算中运行方式的组合问题[J]. 继电器, 2002, 30(7): 23-26. ZHANG Feng, LI Yin-hong, DUAN Xian-zhong. The research on problem of operation mode combination in relay coordination for electrical system[J]. Relay, 2002, 30(7): 23-26. |
| [7] |
周志辉, 周玲, 丁晓群, 等. 继电保护整定值计算中运行方式选择的新方法[J]. 电力设备, 2005, 6(2): 55-58. ZHOU Zhi-hui, ZHOU Ling, DING Xiao-qun, et al. New method of operation mode selection for relay protection in setting and calculation[J]. Electrical Equipment, 2005, 6(2): 55-58. |
| [8] |
曹国臣, 李娟, 张连斌. 继电保护运行整定中分支系数计算方法的研究[J]. 继电器, 1999, 27(2): 5-9. CAO Guo-chen, LI Juan, ZHANG Lian-bin. Study on method to calculate branch coefficient in relay setting and coordination[J]. Relay, 1999, 27(2): 5-9. |
| [9] |
李冰, 赵海鸣, 刘健, 等. 继电保护运行整定中计算分支系数的快速方法[J]. 继电器, 2004, 32(1): 21-27. LI Bing, ZHAO Hai-ming, LIU Jian, et al. Fast calculation on branch coefficient in protection relay setting and coordination[J]. Relay, 2004, 32(1): 21-27. |
| [10] |
段惠明, 何志勤, 李志宏, 等. 依托电网调控管理系统的省、地、县调保护一体化整定计算[J]. 电力系统自动化, 2014, 38(22): 118-122. DUAN Hui-ming, HE Zhi-qin, LI Zhi-hong, et al. Province-prefecture-county integrated relay protection setting calculation based on operation management system[J]. Automation of Electric Power Systems, 2014, 38(22): 118-122. DOI:10.7500/AEPS20140402004 |
| [11] |
杨洋, 吕飞鹏, 廖小君. 基于RUP" 4+1”视图建模及设计模式的整定计算软件设计[J]. 电力系统自动化, 2009, 33(2): 57-60. YANG Yang, LV Fei-peng, LIAO Xiao-jun. Relay coordination software development based on RUP 4+1 view modeling and design patterns[J]. Automation of Electric Power Systems, 2009, 33(2): 57-60. DOI:10.3321/j.issn:1000-1026.2009.02.013 |
| [12] |
王慧芳, 姚勇, 何奔腾, 等. 电网继电保护整定计算软件的实用性研究[J]. 电力系统自动化, 2004, 28(21): 85-88. WANG Hui-fang, YAO Yong, HE Ben-teng, et al. Practicality study of a protection setting calculation software[J]. Automation of Electric Power Systems, 2004, 28(21): 85-88. DOI:10.3321/j.issn:1000-1026.2004.21.019 |
| [13] |
王慧芳. 继电保护整定计算软件中的若干问题分析[J]. 继电器, 2006, 34(12): 14-19. WANG Hui-fang. Analysis on some problems about protection setting calculation software[J]. Relay, 2006, 34(12): 14-19. |
| [14] |
陈实, 邰能灵, 范春菊, 等. 考虑风力发电的配电网弱馈线路自适应电流保护[J]. 电工技术学报, 2017, 32(3): 65-73. CHEN Shi, DAI Neng-ling, FAN Chun-ju, et al. An adaptive current protection for weak-infeed distribution lines with wind generation[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 65-73. |
| [15] |
CHEN M, WANG H, SHEN S, et al. Research on a distance relay-based wide-area backup protection algorithm for transmission lines[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 97-105. DOI:10.1109/TPWRD.2016.2599198 |
| [16] |
DL/T 559-2007220 kV~750 kV电网继电保护装置运行整定规程[S]. 北京: 中国电力出版社, 2008. http://www.zbgb.org/20/StandardDetail342462.htm
|
| [17] |
王锡凡, 现代电力系统分析[M]. 北京: 科学出版社, 2003. https://wenku.baidu.com/view/517114c9b0717fd5360cdcf2.html
|
| [18] |
FAN S, DING H, KARIYAWASAM A, et al. Parallel electromagnetic transients simulation with shared memory architecture computers [J]. IEEE Transactions on Power Delivery, 2018, 33(1): 239-247. https://www.researchgate.net/publication/317557645_Parallel_Electromagnetic_Transients_Simulation_with_Shared_Memory_Architecture_Computers
|
| [19] |
CHEN Y, MEMBER S, DOMÍNGUEZ-GARCÍA A, et al. A sparse representation approach to online estimation of power system distribution factors[J]. IEEE Transactions on Power Systems, 2015, 30(4): 1727-1738. DOI:10.1109/TPWRS.2014.2356399 |
| [20] |
Power System Test Case Archive [Online]. University of Washington, Department of Electrical Engineering, 2013. https://www2.ee.washington.edu/research/pstca/index.html.
|



