链码是一种对离散边界的编码表示方法，其特点是利用一系列具有特定长度和方向的相连的直线段来表示区域的边界. 其基本思想是用编码来标识和存储离散边界上每一个网格与其相邻网格的方位关系. 链码结构属于压缩栅格数据结构的一种，可以有效地对线状地物或区域边界数据进行压缩，对于面积、长度、转折方向和凹凸度等运算十分方便. 因此，链码被广泛应用于计算机视觉^[1-2]、模式识别^[3-4]、数字图像处理^[5-6]以及地理信息系统^[7]等各个领域.

链码这一概念最早由Freeman^[8]于1961年提出，Freeman链码根据表达边界所采用的网格邻域不同，分为4方向和8方向链码2种，可分别由数字“0”~“3”和“0”~“7”表达，即 $ \displaystyle\sum ( {\rm{F4}} ) = \{ {0,1,2,3} \} $ ， $\displaystyle\sum {\left( {{\rm{F8}}} \right) = \left\{ {0,1,2,3,4,5,6,7} \right\}} $ .

1999年，Bribiesca等^[9]提出依次记录在区域边界外轮廓线上的网格顶点数，从而得到一种新的链码—顶点链(vertex chain code，VCC). 对于四边形网格，顶点链只需要“1”、“2”、“3”三个数字即可完成边界描述，分别对应边界网格的凸角转向、水平或垂直方向前进以及凹角转向. 类似地，VCC可表示为 $\displaystyle\sum {\left( {{\rm{VCC}}} \right) = \left\{ {1,2,3} \right\}} $ . 2005年，Sánchez等^[10-11]提出直角三方向链码(orthogonal three-direction chain code，3OT)，将3个相对变化的直角方向作为码值对边界进行表达. 3OT的码值有“0”，“1”，“2”三个，分别表示无方向变化、方向向前改变和向后回转，即 $\displaystyle\sum {\left( {{\rm{3OT}}} \right) = \left\{ {0,1,2} \right\}} $ . 2016年，Borut 等^[12]提出无符号曼哈顿链码(unsigned Manhattan chain code，UMCC). 该链码只使用“0”和“1”两个码值记录边界沿x轴和y轴方向的前进方向，并利用4组“00”开头的标识符分别表示2个方向上的单调性变化情况.

在以上列举的几种链码中，只有VCC可以表达三角形及六边形网格的边界，但其对三角形网格边界特殊情况的表达存在缺陷(具体分析见1.3节). 随着地球格网系统的发展，能够表达不同类型的网格边界的链码具有更广泛的适用性. 离散网格系统中对空间对象的编码、表达、存储、索引以及量测也需要更有效方便的链码. 针对这一目标，本文提出一种基于边界网格边数的新型链码—边链码(edge chain code，ECC)，ECC可以应用于目前常见的各类离散网格系统，并且具有更好的表达能力和更高的压缩率.

本文通过实例分别给出应用于四边形、六边形和三角形网格的边链码方法；列举分析边链码的特性；通过实验比较边链码和其他几种经典链码的表达效率与编码长度；给出研究结论.

边链码的核心思想是利用边界网格的独立边数来表达离散区域轮廓. 其中某个边界网格的独立边定义为该网格上不与其他相邻边界网格或内部网格共享的边，即位于形状外轮廓线上的边，以下用N_e表示. 首先以四边形网格为例，提出基于独立边数的链码方法.

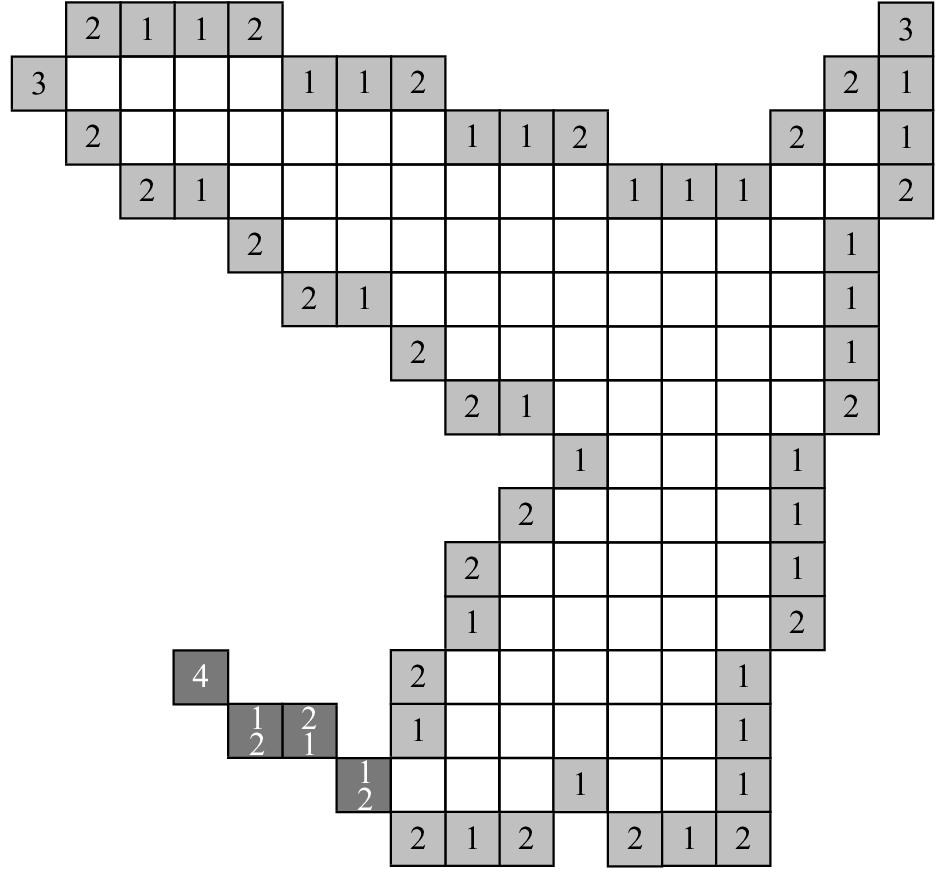
最常见的四边形网格是规则的正方形网格，除此之外，目前还有菱形网格，由于不同种类的四边形网格的空间关系和拓扑结构具有一致性，这里只使用正方形网格进行说明. 考虑较特殊的角相邻情况，四边形网格可能的独立边数为1~4. 以所示的形状为例，灰色网格为该形状的边界，其中的数字为对应边界网格上的独立边数. 注意左下角的特殊情况，边数为“4”的网格与相邻网格为角相邻关系，旁边3个深色网格在记录边界时先后经过2次，其独立边数也应分别计算.

图 1

图 1 形状边界及其独立边数 Fig. 1 Border of shape and independent edge numbers

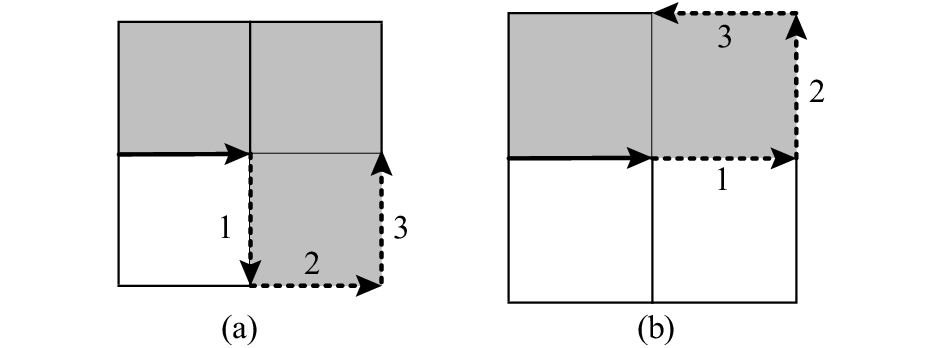
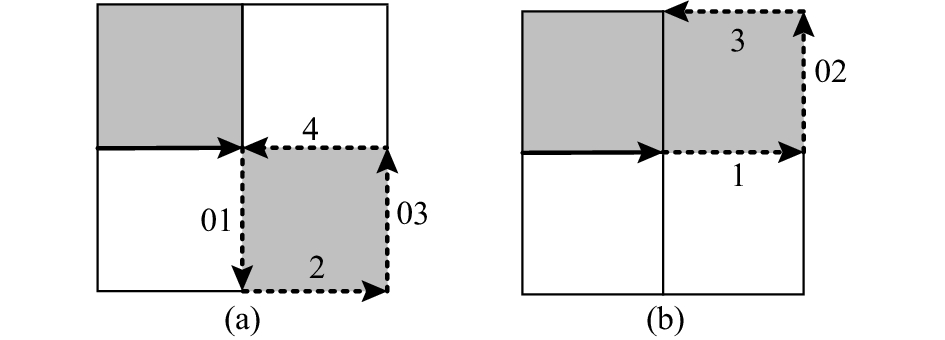
直接将独立边数序列作为链码进行边界表达具有歧义. 对于N_e = 1，2，3，当前的边界网格的轮廓前进方向可能有2种情况：1)平行；2)垂直于前一边界网格的轮廓方向，如图2所示. 其中灰色表示该网格为边界网格，白色表示形状外部网格，实线箭头位于上一边界网格最后一个独立边上，箭头方向即为该边界网格的轮廓前进方向，虚线箭头分别表示不同情况的独立边. 例如，图2（a）中N_e = 2以及图2（b）中N_e = 1，3时，当前边界网格的轮廓前进方向与前一网格平行(即相同或相反)，其他3种情况则为垂直. 因此，只要能对不同独立边数的这2种情况进行区分，即可唯一确定下一边界网格的位置. 基于这一思路，引入区分码“0”，并根据具体情况进行如下处理：1)如果边界网格轮廓方向垂直于前一边界网格，则将“0”插入N_e之前，并作为当前网格的码值；否则2)直接将N_e作为该网格的码值. 添加区分码后的边链码可由图3表示.

图 2

图 2 四边形边界网格可能的轮廓前进方向 Fig. 2 Possible contour move direction of rectangle border grids

图 3

图 3 增加区分码后的四边形网格边链码 Fig. 3 Rectangular edge chain code with distinguish code

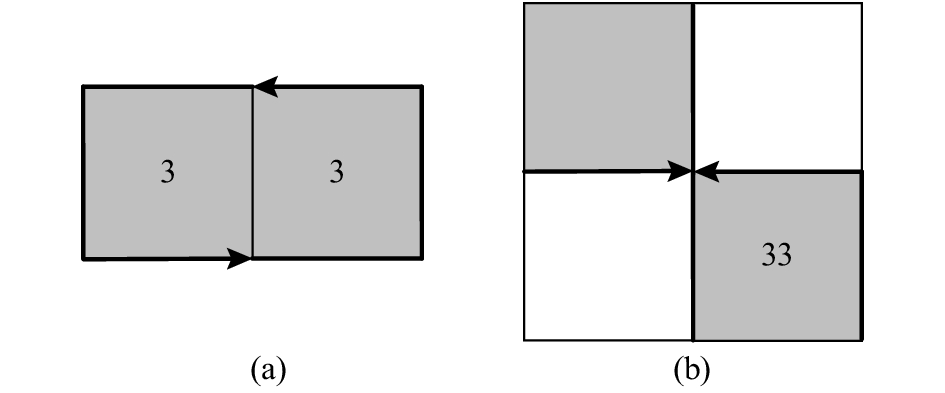
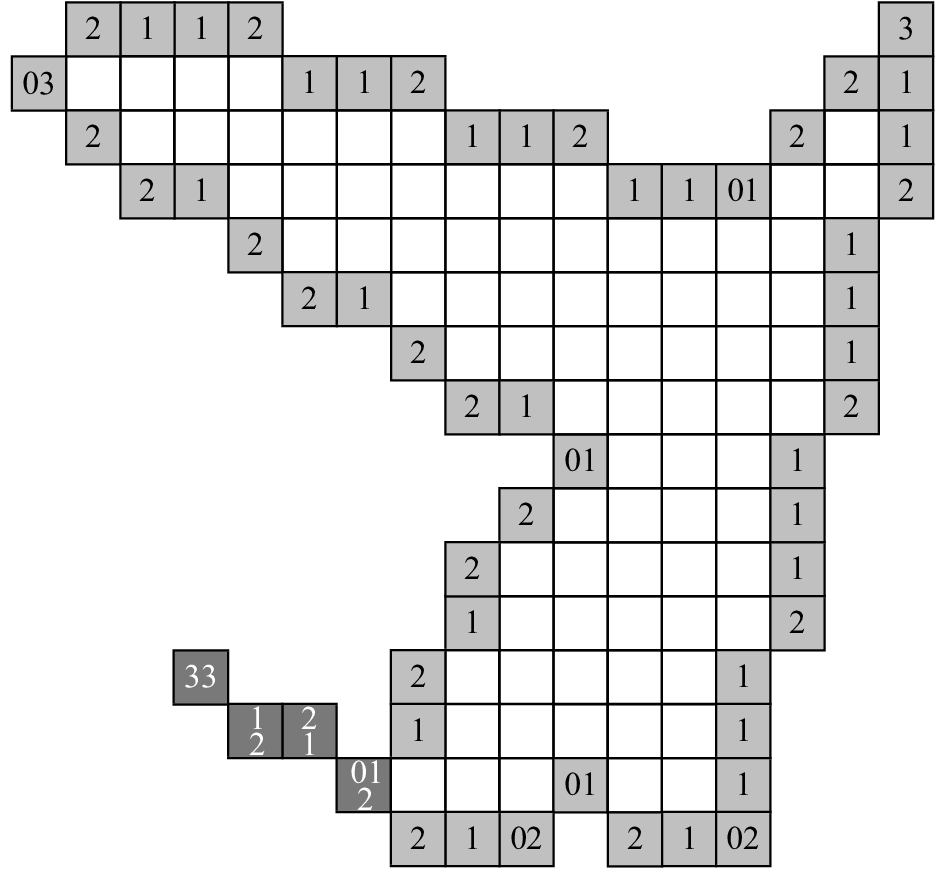
由于引入额外的区分码，此时的码值为“0”~“4”共计5个，每个码值需要3 bits存储空间. 而N_e=4在实际形状边界中出现机率极小，可考虑将其替换为其他不会出现的码值组合，以提高压缩率. 考虑到组合“33”表示仅由2个边界网格边相邻组成的闭合形状(如图4（a）所示)，因此可以将其作为N_e=4的码值，如图4（b）所示. 四边形的边链码可由 $\sum {\left( {{\rm{EC}}{{\rm{C}}_{\rm{rect}}}} \right) =} $ $\left\{ {0,1,2,3} \right\} $ 进行编码，其中每个边界网格由1~2个码值表达，每个码值占用2 bits存储空间. 图5展示了利用ECC_rect对图1中的形状边界进行编码的结果，其中边界轮廓按逆时针方向前进.

图 4

图 4 将四边形边链码的码值“4”替换为“33” Fig. 4 Replacing code “4” with “33” in rectangular edge chain code

图 5

图 5 四边形边链码编码结果 Fig. 5 Encoding results of rectangular edge chain code

对于由六边形网格表达的形状，边界网格只存在边相邻情况，而没有角相邻，其边界网格可能的独立边数为1~5，如图6所示.

图 6

图 6 六边形边界网格的独立边 Fig. 6 Independent edges of hexagonal border grids

与四边形网格不同的是，在确定六边形网格每个边界网格的独立边数后，下一边界网格的位置也唯一确定. 因此，只需要依次记录每个边界网格的独立边数即可完成对整个形状轮廓的表达.

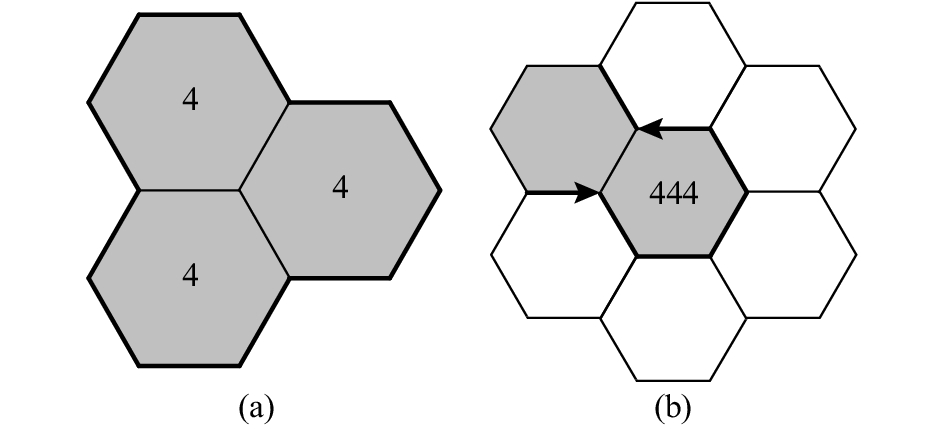
适用于六边形网格的边链码可由“1”~“5”五个码值表达，每个边界网格需占用3 bits. 类似地，由于码值“5”对应于边界上的突出点或线段的端点，出现频率较小，可考虑将其替换为其他不会出现的码值组合，以提高压缩率. 如组合“444”，按照六边形边链码的定义，只可能用于表达图7（a）这唯一一种情况，因此满足替换条件. 将码值“5”统一替换为组合“444”后，六边形网格的边链码可表达为 $\sum {\left( {{\rm{EC}}{{\rm{C}}_{\rm{hex}}}} \right) = \left\{ {1,2,3,4} \right\}} $ ，其中每个码值只需占用2 bits空间. 图8展示了六边形边链码的编码结果.

图 7

图 7 将六边形边链码的码值“5”替换为“444” Fig. 7 Replacing “5” with “444” in hexagonal edge chain code

图 8

图 8 六边形边链码编码结果 Fig. 8 Encoding results of hexagonal edge chain code

与四边形和六边形网格相比，三角形网格不仅单元方向不唯一，而且边相邻与顶点相邻网格共有12个，难以直接通过独立边数进行区分. 三角形边界网格的N_e可能取值包括1、2和3. 根据N_e不同，以下分2种情况进行讨论：

1) N_e = 1，2.

当独立边数为1或2时，分别对应4种不同的轮廓前进方向，如图9所示.通过观察可以发现，不同的轮廓前进方向可以通过相邻边界网格之间的内部网格数进行区分. 内部网格定义为与相邻边界网格共顶点的形状内非边界网格，即图9中的阴影部分，在此将内部网格数由I_n表示，由图9可知其取值范围为0~3. 由于三角形边界网格独立边数(N_e = 1，2)与内部网格数(I_n = 0，1，2，3)共存在8种组合，因此可将每种组合分别由一个码值表示，每个码值占用3 bits存储空间. 因此，可将图9表示的8种情况依次由“0”~“7”八个码值表示.

图 9

图 9 三角形边界网格的轮廓前进方向(Ne=1，2) Fig. 9 Contour move direction of triangular border grids (Ne=1，2)

2) N_e=3.

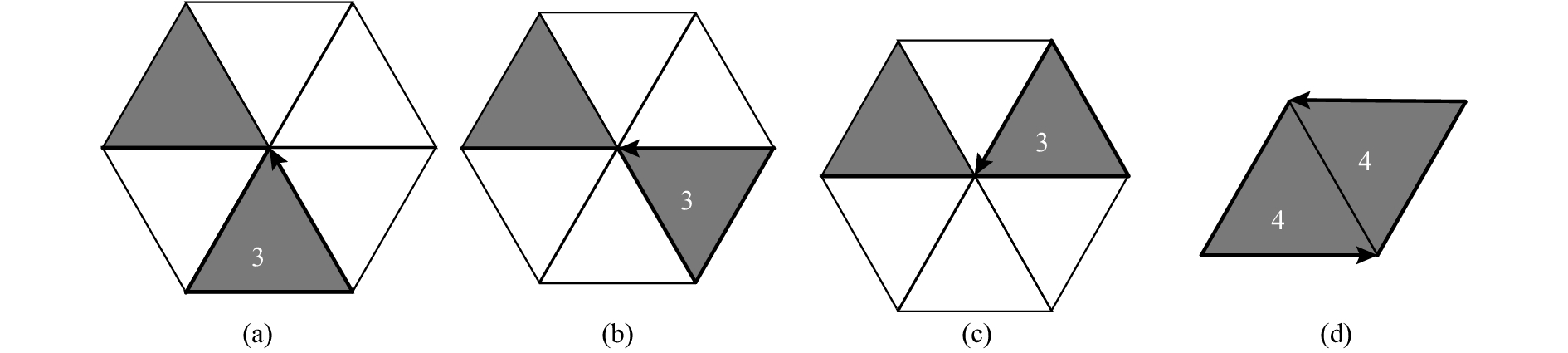
三角形网格独立边数为3时对应3种轮廓前进方向，如图10（a）~（c）所示. 如果将这3种出现频率较小的情况分别用新的码值表示，则一共存在11种可能，每个边界网格的边链码需要额外1 bit存储空间.

图 10

图 10 三角形边界网格的轮廓前进方向(Ne=3) Fig. 10 Contour move direction of triangular border grids (Ne=3)

借鉴四边形及六边形网格对特殊情况的处理思路，注意到码值组合“44”表示图10（d）中2个三角形网格的自闭合(码值“4”对应于图9（e）)，因此可将其作为E_n=3时的区分码，分别将图10（a）~（c）由“441”、“442”和“443”三个组合表达. 需要注意的是，这3种特殊情况在VCC中的编码均为“112”，无法进行区分.

基于以上讨论，最终确定三角形边链码可由 $\sum {\left( {{\rm{EC}}{{\rm{C}}_{\rm{tri}}}} \right) = \left\{ {0,1,2,3,4,5,6,7} \right\}} $ 编码，其中每个码值占3 bits存储空间. 下图展示了利用ECC_tri进行编码的结果.

本文提出的应用于3种网格类型的边链码具有若干相同的几何特性，包括归一化后链码与起始点选择无关、旋转不变性、翻转不变性、可检测形状边界上的直线段并能够方便地计算形状的周长等，具体分析如下.

1)与起始点的选择无关.

从任一边界网格出发，依次记录形状边界的边链码，通过循环排序选择具有最小整数的序列作为归一化结果. 这样就可以保证该形状边链码的唯一性. 如图12（a）所示，箭头所在位置为随机选择的边界网格起始点，得到的链码为“032010220222022103101”，经归一化后结果为“010220222022103101032”.

图 12

图 12 边链码特性示例 Fig. 12 Examples of edge chain code properties

从任一边界网格出发，依次记录形状边界的边链码，通过循环排序选择具有最小整数的序列作为归一化结果. 这样就可以保证该形状边链码的唯一性. 如图12（a）所示，箭头所在位置为随机选择的边界网格起始点，得到的链码为“032010220222022103101”，经归一化后结果为“010220222022103101032”.

2)旋转及翻转不变性.

根据以上3种网格的边链码的生成方法可知，六边形边链码仅与边界网格的独立边数有关，四边形边链码及三角形链码仅与独立边数及轮廓前进的相对方向有关. 而这两个因素均不受旋转或翻转操作影响.

根据以上三种网格的边链码的生成方法可知，六边形边链码仅与边界网格的独立边数有关，四边形边链码及三角形链码仅与独立边数及轮廓前进的相对方向有关. 而这两个因素均不受旋转或翻转操作影响.

将图 12（a）中的形状逆时针旋转 90°后的结果如图 12（b）所示，其边链码并无变化；图12（c）为将形状水平翻转后的结果，此时按顺时针方向记录其边链码，则得到的结果仍与之前相同.

3)直线段可检测.

通过观察图5、图8和图11三种网格下的形状边界及其边链码可发现，四边形网格的水平直线段和对角直线段分别由“11…1”和“22…2”组合表达，六边形网格边界直线段为“22…2”，三角形则包括“11…1”和“0202…02”两种. 通过识别边链码中的这些组合码值，便可将对应区域边界上的直线段检测出来.

图 11

图 11 三角形边链码编码结果 Fig. 11 Encoding results of triangular edge chain code

4)形状周长可计算.

由于边链码的核心思想是基于边界网格的独立边数进行形状边界表达，而形状的独立边数之和就是其基于曼哈顿距离计算的周长. 对于四边形和六边形网格，形状周长可直接由边链码各码值之和计算得到，即

对于三角形边链码，由于“0”~“3”表示N_e = 1，“4”~“7”表示N_e = 1，2的边界网格，因此其周长可表示为

其中，m表示码值小于4的边界网格数.

如何对编码的总码数和占用的存储空间进行压缩，一直是链码问题的一个重要研究方向^[13-15]. 从链码设计的角度来看，如果原始链码本身就具有较少的码数和较短的码长，则通过进一步的压缩编码可以得到更好的压缩效果.

为比较本文提出的边链码与之前典型链码的总码数和编码长度，选用12个不同的二值图形进行实验，如图13所示. 分别利用F8、VCC、3OT、UMCC和ECC五种方法对图13中的12个离散化为四边形网格的轮廓进行链码表达，并分别统计链码总码数和以bit为单位的链码总长度，结果如表1和2所示. 表中同时给出了由VCC和ECC对同一形状的六边形和三角形网格边界进行编码的结果.

图 13

图 13 用于链码实验的不同目标形状 Fig. 13 Different object shapes used in chain code experiments

表 1

表 1 采用不同方法得到的链码总码数 Table 1 Total code numbers by various chain codes 形状 四边形网格 六边形网格 三角形网格 F8 VCCrect 3OT UMCC ECCrect VCChex ECChex VCCtri ECCtri 骆驼 2 291 3 103 3 103 4 777 2 893 2 536 1 259 1 654 1 269 鹿 1 898 2 507 2 507 3 918 2 368 2 124 1 059 1 352 1 027 虎 1 724 2 269 2 269 3 550 2 058 1 962 978 1 257 935 狗 5 047 6 913 6 913 10 222 6 186 5 790 2 892 3 848 2 778 蝴蝶 3 234 4 743 4 743 6 556 4 110 3 828 1 907 2 516 1 863 鸟 3 252 4 795 4 795 6 666 4 037 3 742 1 865 2 497 1 954 螃蟹 6 845 9 669 9 669 14 124 8 540 7 683 3 840 5 129 3 981 树 5 843 8 003 8 003 13 125 7 496 6 265 3 107 4 241 3 289 飞机 2 361 3 071 3 071 4 860 3 021 2 579 1 288 1 714 1 300 笔 3 296 3 941 3 941 6 640 3 826 3 612 1 803 2 086 1 691 人物 3 065 3 955 3 955 6 376 3 576 3 417 1 703 2 100 1 662 地图 4 004 5 785 5 785 8 720 5 182 4 558 2 266 3 006 2 304 均值 4 443 6 025 6 025 9 449 5 515 4 931 2 456 3 174 2 489

表 1 采用不同方法得到的链码总码数 Table 1 Total code numbers by various chain codes

表 2

表 2 不同方法得到的链码总长度 Table 2 Total length of various chain codes 形状 四边形网格 六边形网格 三角形网格 F8 VCCrect 3OT UMCC ECCrect VCChex ECChex VCCtri ECCtri 骆驼 6 873 6 206 6 206 4 777 5 786 2 536 2 518 4 962 3 807 鹿 5 694 5 014 5 014 3 918 4 736 2 124 2 118 4 056 3 081 虎 5 172 4 538 4 538 3 550 4 116 1 962 1 956 3 771 2 805 狗 15 141 13 826 13 826 10 222 12 372 5 790 5 784 11 544 8 334 蝴蝶 9 702 9 486 9 486 6 556 8 220 3 828 3 814 7 548 5 589 鸟 9 756 9 590 9 590 6 666 8 074 3 742 3 730 7 491 5 862 螃蟹 20 535 19 338 19 338 14 124 17 080 7 683 7 680 15 387 11 943 树 17 529 16 006 16 006 13 125 14 992 6 265 6 214 12 723 9 867 飞机 7 083 6 142 6 142 4 860 6 042 2 579 2 576 5 142 3 900 笔 9 888 7 882 7 882 6 640 7 652 3 612 3 606 6 258 5 073 人物 9 195 7 910 7 910 6 376 7 152 3 417 3 406 6 300 4 986 地图 12 012 11 570 11 570 8 720 10 364 4 558 4 532 9 018 6 912 均值 13 329 12 051 12 051 9 449 11 030 4 931 4 913 9 523 7 466 压缩率 1 0.904 1 0.904 1 0.708 9 0.827 5 1 0.996 3 1 0.784 0

表 2 不同方法得到的链码总长度 Table 2 Total length of various chain codes

对于四边形网格，在以上5种链码方法中，F8每个码值唯一确定一个边界网格，整体所需要的码数最少，表达效率最高；而VCC和3OT记录每个顶点处的共顶点网格数或轮廓前进方向，因此两者的码数与长度均相同，且整体码数与边界的顶点数相同，约为边界网格数的1.35倍左右；UMCC的码数与编码长度相同，除区分码外，每个边界网格需要x和y两个方向的码值，因此码数最多，是边界网格数的2倍以上；ECC需要区分边界网格上的轮廓前进方向，因此平均码数也超过边界网格数，但与VCC、3OT和UMCC相比更少，是边界网格数的1.24倍左右，是除F8外最优结果.

另一方面，由于UMCC的每个码值只占1 bits空间，利用该链码编码得到的总长度最短：与F8相比，其压缩率平均可达70%；ECC、VCC和3OT三种链码的每个码值均需要2 bits空间，但ECC的链码总长度少于后2种链码，压缩率约为83%，这是由于ECC上的每个码值对应一个边界网格，一般情况下，其链码总长度即为边界网格数的2倍；而VCC和3OT的码值对应于边界网格上的顶点，其数量约为边界网格数的1.35倍左右，因此总的压缩率更低；由于F8上的每个码值占用3 bits空间，其链码长度最长.

对于六边形和三角形网格边界，目前能直接对其进行表达的链码只有VCC和ECC. 其中，六边形网格的VCC和ECC链码长度基本相同，但ECC对每个六边形边界网格只用1个码值进行表达，总体码数比前者少50%左右；由于三角形网格边界可能的顶点数有1~5个，VCC每个码值同样需要用3 bits进行表达，而应用于三角形网格边界的ECC码数和编码长度均只有VCC的78%左右，具有更好的压缩性能.

本文提出了一种基于独立边数的链码方法，通过计算每个边界网格的独立边数及增加区分码的方法，可方便得到适用于四边形、六边形和三角形等多种网格边界的边链码. 对于各类边界的特殊情况分别设计编码组合进行替换，不但克服了VCC的不足，而且有效减小了码值冗余. 边链码归一化后与起始点无关，旋转或翻转后保持不变，能够检测边界中的直线段，并快速计算形状周长. 实验结果表明，边链码在码数和编码长度方面均有一定优势，对3种网格边界的表达效率均优于VCC，对四边形和三角形网格的压缩率与VCC相比分别提高了10%和22%左右.