2. 中国建筑五局投资管理公司,湖南 长沙 410004
2. The investment Management Company of China Construction Fifth Engineering Division Co. Ltd, Changsha 410004, China
我国山区面积达国土面积的2/3,地质灾害频发,其中泥石流是仅次于滑坡的地质灾害,受泥石流灾害威胁的县城有70座[1]. 2010年舟曲特大泥石流造成1 400多人死亡,文家沟特大泥石流使6 000多人受灾[2],因此对村镇进行区域泥石流危险性进行评价已十分迫切. 目前,泥石流危险性评价方式主要是对单个泥石流沟的危险性进行评价,即勘察记录其沟谷条件、松散固体物质情况、历史发生频率等数据[2],然后对其危险性进行评价,这种方式的费用、时间花费均很大,且对区域泥石流的危险性进行评价时不适用. 基于地理信息系统(GIS)强大的空间数据管理及分析能力,将灾害点(单个泥石流沟)转向灾害面(区域泥石流)来进行其危险性评价和评价结果的可视化,是地质灾害评价研究的重点及难点之一.
基于GIS技术对区域泥石流危险性进行评价,关键之处在于:一是评价单元,即泥石流危险性评价的基础数据处理基本单元,目前评价单元大部分采用栅格单元、流域单元等[3];若以规则的栅格单元为基础单元,会导致沟谷与其地质、环境信息缺乏联系,评价结果与实际情况产生一定偏差[4];流域单元虽能保证沟谷与其地质、环境信息建立联系,但单个流域一般覆盖较大区域,如一个城镇可能只有几个流域单元,可能会导致其评价结果出现划分的危险等级少,或一个危险等级只包含一两个单元,这样评价结果并不合理[5]. 因此,合理的评价单元应能体现沟谷与流域面的综合特征,且能合理地划分研究区域. 二是区域泥石流危险性评价的指标体系及其获取,以往泥石流危险性评价指标达二三十个[6],而其中大部分指标难以获取,因此其评价指标不仅要能反映泥石流的沟谷特征,而且要能基于GIS来提取或计算其数据. 三是评价模型,区域泥石流危险性评价模型多采用层次分析法、模糊评判法等[7-8],但由于整个区域的评价指标的数据量较大,模糊评判法中隶属函数难以确定;层次分析中专家评判的主观性过大,导致评价结果精度不高. 因此若能将主、客观评价方法(如:神经网络法与层次分析法)相结合,采用神经网络模型来模拟专家思维,可提高评价模型的精度.
本文通过分析区域泥石流灾害的评价基础单元、评价指标体系、评价模型3个方面内容,以斜坡单元作为区域泥石流灾害的评价基础单元并研究斜坡单元划分方法;分析区域灾害评价指标的特点,提出适用于区域泥石流灾害危险性评价指标体系并提出指标数据提取方法;综合主客观评价模型的特点,提出运用径向基神经网络模型模拟专家思维的层次分析-径向基网络评价模型(即AHP-RBF评价模型). 将以上研究应用于湖北省神农架林区木鱼镇区域,采用已查明的泥石流灾害点的位置资料,验证评价结果的合理性.
1 斜坡单元划分方法及结果分析 1.1 斜坡单元划分山体地形是由一个个斜坡组成的,不管是滑坡、泥石流还是崩塌,一般是在斜坡上发生,因此在进行区域泥石流灾害评价时,将整个区域按地形斜坡轮廓划分成若干斜坡,再用斜坡去提取整个区的指标数据,就能较好体现泥石流发生的特定沟谷条件和流域面地貌的综合特征,且单元面积较小. 因此,为满足泥石流的综合特征,本文提出将斜坡单元作为区域泥石流危险评价的基本单元. 将泥石流灾害的信息划分至斜坡上,以斜坡代替泥石流灾害点进行计算. 实现单个泥石流都转向灾害面的区域灾害评价.
依据斜坡的自然特征,斜坡在沟谷两边,是沟谷集水区的一部分,用山谷线(山脊线)去划分集水域,将沟谷两边划分成斜坡,因此基于GIS平台划分斜坡单元关键的是山谷线和山脊线的提取[9].
斜坡单元受到栅格尺寸、填洼阈值与集水面积阈值计算3个方面的直接影响,使得划分的结果与实际坡型、坡面大小都出现较大差异,针对以上问题,提出斜坡单元自动划分的定量方法,划分原理及结果见文献[10].
1.2 划分结果及分析以湖北省神农架林区木鱼镇的5 m×5 m DEM为基础数据,基于ArcGIS软件平台进行斜坡单元划分,基于斜坡单元划分的关键值计算方法进行计算,确定最佳分辨率、填洼阈值和集水面积阈值,再根据斜坡划分原理将研究区域划分成多个坡面,经过人工合并、删除修整一些不合理的边坡后,得到的1 674个坡面,结果如图1所示.

|
图 1 木鱼镇斜坡单元划分结果 Fig. 1 Slope unit zoning results of Muyu town |
将斜坡单元划分结果与木鱼镇的山体地形正射影像图、木鱼镇已勘察的地质灾害点对比,经过分析发现,划分结果与地形的边坡轮廓大致相符,能较好地体现斜坡的特征以及大小,且每个灾害点大致都分布在一个斜坡单元上;同时将斜坡单元划分结果的边坡轮廓线与卫星遥感影像相叠加,将局部放大后如图1所示,可以看出划分结果与实际地形较为接近,说明斜坡单元划分结果较为合理,能够满足区域泥石流灾害的危险性评价要求.
2 区域泥石流危险性评价指标体系及其分级与赋值 2.1 区域泥石流危险性评价指标体系及其获取方法在进行泥石流危险性评价时,指标是必不可少的,而指标能在GIS平台上整体被提取是能够进行区域性评价的基础之一,因此指标选取时不仅要考虑地形地貌条件还要考虑其可获取性,如灾害历史规模、频率、植被种类等在整个区域无法获取或者获取难度太大. 区域泥石流危险性评价主要是对泥石流地形地质条件、沟谷环境进行评价,以评价孕育山区泥石流灾害的自然环境及预测爆发泥石流灾害的可能性,因此自然条件是泥石流评价的重要指标[11]. 降雨为诱发因素属于外在因素,而地形条件、地质条件因素等为内在因素,外在因素降雨具有实时动态变化的性质,文中着重于泥石流自然内在条件的评价而未考虑降雨,且降雨的数据在该区域往年记录的数据缺失,无法统计到如24 h降雨变化量、最大降雨量等数据. 年平均降雨量对于区域性的灾害评价影响较小,综上原因本文未考虑降雨因素. 地质条件中,地层岩性为关键因素,区内以砂岩、砾岩为主,松散固体物质主要来自于岸坡上的崩塌、滑坡,坡面风化的产物,沟床中的松散堆积物,道路、矿区和边坡工程中挖掘出的弃渣、弃方等. 这些物质可直接转化和补给于泥石流,增加泥石流的破坏性.
依据以上分析,在选取地形指标时应该反映以下3个方面:一是能反映泥石流灾害发生的流域沟谷环境特征,二是能够反映周边斜坡的地形地貌特征、地质条件,三是能够反映泥石流沟与斜坡相互作用的指标,因此选择具有代表性的8个影响因素作为影响因子:坡面面积、主沟长度、坡面相对最大高差、坡面平均坡度、坡面切割密度、主沟纵坡降、植被覆盖率、地层岩性,其提取方法如下。
1)斜坡主沟长度:基于GIS平台,提取沟谷矢量线性要素图层,裁去支沟后得到研究区域主沟图层,再以坡面单元统计出经过每个坡面的主沟长度.
2)斜坡坡面面积:在GIS中,矢量文件的属性表中,面要素文件有基本的面积大小信息,查阅属性信息,即可得到斜坡面积大小.
3)斜坡相对最大高差:对研究区斜坡单元划分结果的矢量图,以斜坡单元为掩膜,分别提取各坡面内DEM的最大值与最小值,其差值即为各个斜坡的相对最大高差.
4)斜坡主沟纵坡降:以经过斜坡主沟的矢量图为掩膜,分别计算坡面内主沟的最大与最小的高程差值,及斜坡内主沟的水平直线距离,两者比值即为斜坡主沟纵坡降.
5)斜坡切割密度:以斜坡主沟长度中每个斜坡沟谷长度除以坡面面积即可得到斜坡切割密度.
6)斜坡平均坡度:利用GIS中空间分析中表面分析一栏中坡度计算工具,即可计算得到栅格数据的坡度数据. 再以斜坡单元为掩膜,利用区域分析工具,统计每个坡面坡度平均值,即可得到坡面的平均坡度.
7)植被覆盖率:本文依据无人机航拍技术拍摄的正射影像图像,对其进行校正分析,提取木鱼镇植被覆盖阴影信息,并以斜坡单元为掩膜对遥感图像进行裁剪,然后对应到相应的斜坡单元进行分析,可得到斜坡单个斜坡植被覆盖率.
8)地层岩性:以当地水文地质局提供的当地地层岩性数据为基础,通过斜坡单元提取每个斜坡的地层岩性数据.
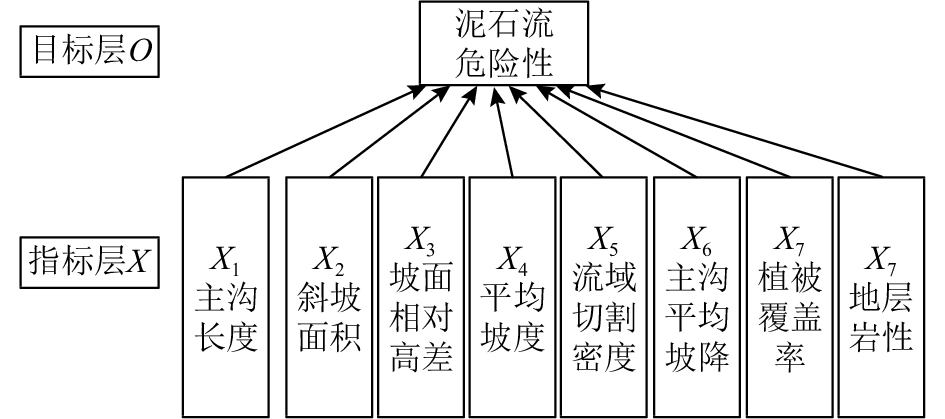
2.2 区域泥石流指标分级在运用AHP-RBF模型评价泥石流危险性时,因为各评价指标的取值变幅很大,所以需对评价指标进行等级划分和归一化处理,以保证评价的客观性和科学性. 评价指标等级一般用极度、高度、中度、轻度来定性描述. 以往研究中,指标评价分级呈现中间多两端少的规律,为平衡这种极端化分级,本文采用对称不等分分割法来划分评价指标的等级,将指标等级分为4个等级,并为评价指标等级赋值:极度为1,高度为0.7,中度为0.3,轻度为0,即评价指标根据其实际取值的相应等级取0、0.3、0.7或1. 本文结合以往研究[6]和泥石流灾害防治工程勘察规范(DZ/T0220-2006),得出了一个较合理的等级划分和赋值标准,评分细则分级如表1和2所示. 表1中X1、X2、X3、X4、X5、X6、X7分别表示主沟长度、斜坡面积、相对最大高差、平均坡度、斜坡切割密度、主沟平均坡降、植被覆盖率.
| 表 1 泥石流指标分级与赋值表 Table 1 Classification and assignment of debris flow index |
| 表 2 地层岩性分级 Table 2 Classification of formation lithology |
区域泥石流危险性评价指标多且相互之间联系密切,若仅利用层次分析法会导致评价结果主观性太强,在应用时分级标准难以把握,结果可信度不高;而单一使用客观方法——神经网络会导致评价结果变异性大,与实际情况偏差大,可靠度不高[12]. 在进行区域性泥石流灾害评价时,如果能对其进行人为干预,使计算机结合专家思维进行判断,有望提高评价的准确性. 本文将层次分析法与径向基神经网络相结合,改进径向基神经网络模型,使其适用于泥石流危险性评价方法,即AHP-RBF神经网络方法.
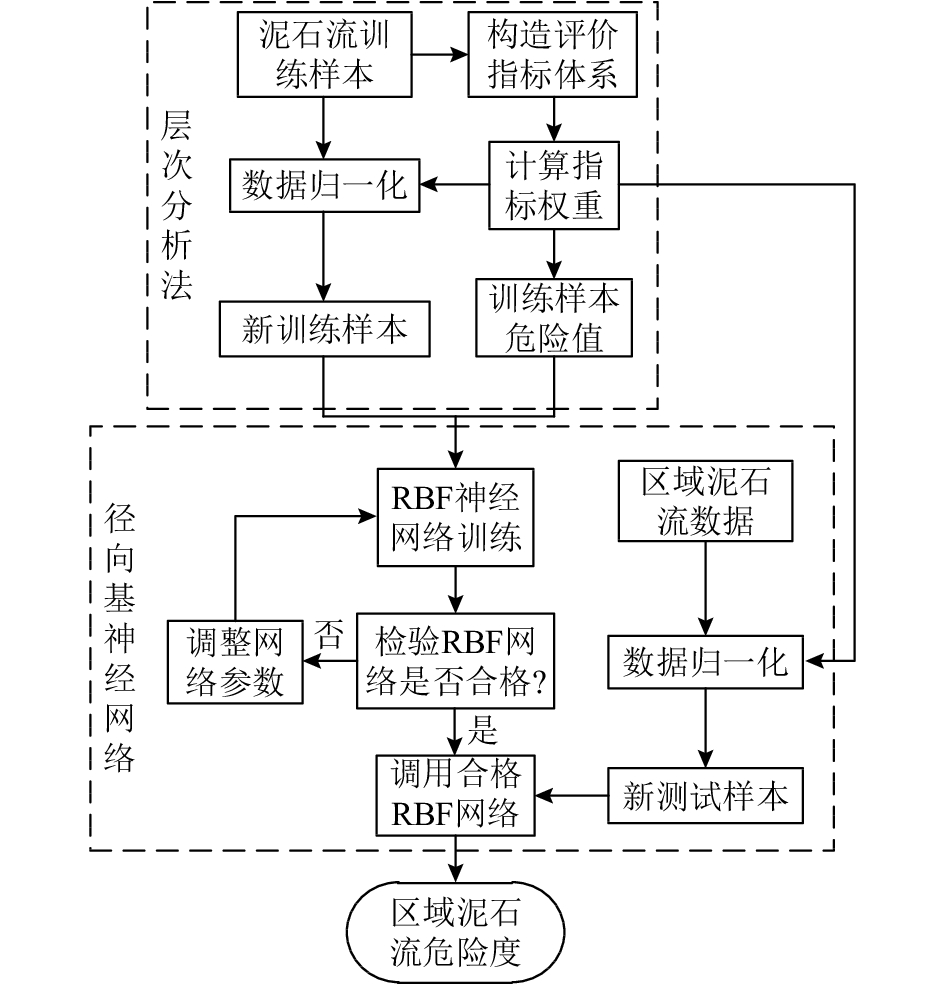
AHP-RBF泥石流危险性评价模型的关键在于利用AHP生成RBF神经网络新的训练样本数据和目标层(即输出层),即RBF神经网络的训练样本危险值由AHP模型计算得来,而其训练数据由样本数据归一化后乘以指标权重得到,其测试样本为区域坡面数据归一化后乘以指标权重得到. 权重是由专家评分确定,使得RBF神经网络也具备了专家的经验和知识,在后来对区域泥石流进行危险性评价时,RBF神经网络就能根据给予的输入样本来模拟专家思维,这样既避免了主观性太强所带来的误差,又提高了危险评价的科学性和准确性. 其评价流程见图2.
3.2 构建AHP-RBF模型构建AHP-RBF神经网络模型以上神经网络模型应用前需要进行训练,如图2所示,首先利用层次分析法(AHP)生成神经网络训练的输出层,以及依据计算得到的权重乘以归一化后的训练样本数据生成新的训练样本.
|
图 2 AHP-RBF泥石流危险性评价模型流程图 Fig. 2 AHP-RBF model flow chart of debris flow hazard assessment |
层次分析法建模可以分为4个步骤[13].
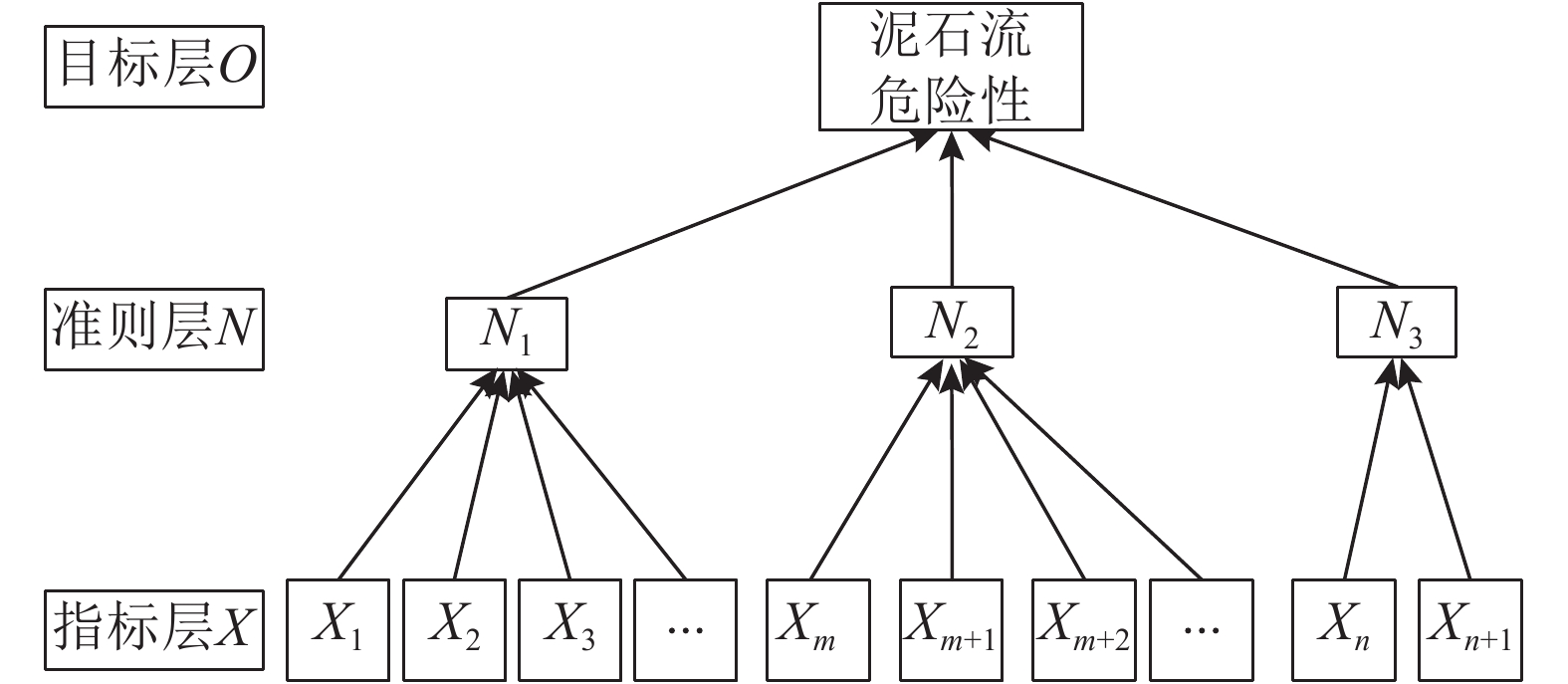
1)建立目标层、准则层、指标层,如图3所示.
|
图 3 AHP模型结构图 Fig. 3 Structure chart of AHP model |
2)建立判断矩阵.
建立判断矩阵,在层次分析中,某一个层次跟上一层次的因素进行对比较,得出判断矩阵. 假设N层与下一层B1,B2,···,Bn有联系通过上表即得到判断矩阵B.
| ${{B}} = \left[ {\begin{array}{*{20}{c}} {{b_{11}}}&{{b_{21}}}& \cdots &{{b_{n1}}} \\ {{b_{12}}}&{{b_{22}}}& \cdots &{{b_{n2}}} \\ \vdots & \vdots & {} & \vdots \\ {{b_{n1}}}&{{b_{n2}}}& \cdots &{{b_{nn}}} \end{array}} \right].$ | (3-1) |
3)计算最大特征值.
通常用计算方法得出矩阵的特征值及对应的特征向量,但由于判断矩阵大多是高阶矩阵,难以计算特征值及特征向量,因此先将判断矩阵每一列进行正规化处理.
| $\overline {{b_{ij}}} = {b_{ij}}\left/\displaystyle\sum\limits_{i = 1}^n \right.{{b_{ij}}} ;\; i,j = 1,2,3,\cdots,n.$ | (3-2) |
然后对正规化处理得到的矩阵按行相加.
| ${\overline W _i} = \sum\limits_{j = 1}^n {\overline {{b_{ij}}} }\;;\; i,j = 1,2,3,\cdots,n.$ | (3-3) |
在对上式所得向量正规化,这里得到向量W即为所求的特征向量.
| ${ W} = {{\overline {{W_i}} }}\left/{{\displaystyle\sum\limits_{i = 1}^n {\overline {{W_i}} } }}\right..$ | (3-4) |
最后计算判断矩阵的最大特征根λmax.
4)进行一致性检验.
| ${\rm CI} = \left( {{\lambda _{\max }} - n} \right)/\left( {n - 1} \right),$ | (3-5) |
| ${\rm CR} = {\rm CI}/{\rm RI}.$ | (3-6) |
式中:CI表示一致性指标,CR表示一致性检验参数,RI表示随机一致性指标:
| ${\rm RI} =\frac{ {{\rm{CI}}_1}+{{\rm{CI}}_2}+\cdots+{{\rm{CI}}_n}}n,$ |
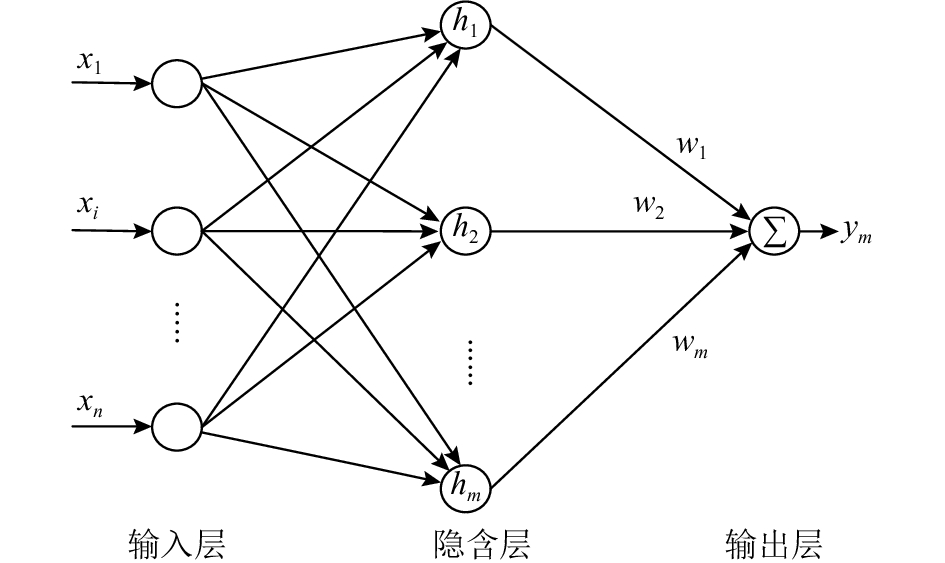
径向基函数(radial-basis function,RBF)神经网络属前馈式神经网络,自1985年Powell[14]首次提出RBF方法3年后,Broomhead等[15]将其应用到神经网络设计上,并建立了径向基神经网络,即RBF神经网络. RBF神经网络包括输入层、隐含层和输出层. 输入层将外部信息传递到内部网络;隐含层对输入信息进行非线性转换,通常可以有若干个隐层;输出层对信号线性转换后输出.
RBF网络的网络结构见图4,图中,输入向量(即输入层)为X,径向基向量(即隐含层)为H,隐含层到输出层的权向量为W,隐含层输出的线性加权和,即为RBF网络的输出层,见图4.
|
图 4 径向基函数(RBF)神经网络结构图 Fig. 4 Structure chart of radial-basis function (RBF) model |
径向基函数(RBF)是局部分布、关于中心点径向对称增强或衰减的非线性非负函数[16]. 其中逆多二次函数随着中心点距离增大而增大,多二次函数和高斯函数则相应减小. 高斯函数有着良好的局部特性,当有信号输入时,能在局部范围产生响应,随着输入变量x与RBF的中心不断靠近,函数的值也逐渐变大,最大为1;随着输入变量x与RBF的中心不断远离,函数的值也逐渐变小,直至为0.
这种局部逼近的特性在实际中应用比较广泛,本文采用高斯函数作为径向基函数:
| ${h_j} = \exp \, \left( - \frac{{{{\left\| {x{\rm{ - }}{c_j}} \right\|}^2}}}{{2b_j^2}}\right);\;j = 1,2,\cdots,m.$ | (3-7) |
式中:
(1)本文采用二级层次分析法,建立目标层、指标层,如图5所示.
|
图 5 泥石流危险性评价层次分析法结构模型 Fig. 5 AHP process model of debris flow hazard assessment |
(2)在建立判断矩阵 AHP计算过程中,为能够进行定量计算,常常需要形成有数值组成的判断矩阵,为此需要将对比判断根据一中规则进行判断定量化. 目前,常用的是1-9标度法,该方法使判断更加清晰,如图6所示.
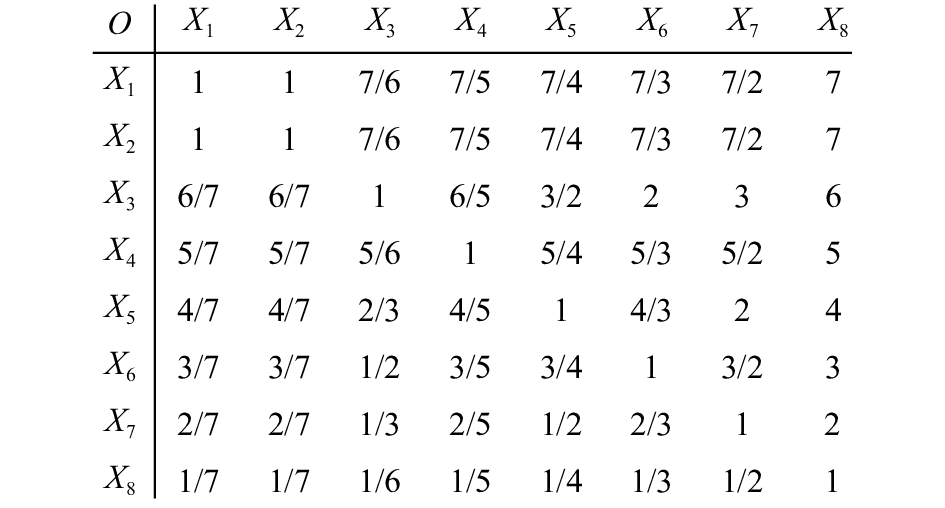
|
图 6 泥石流危险性评价指标判断矩阵 Fig. 6 Index judgment matrix of debris flow hazard assessment |
(3)计算最大特征值,对于矩阵的特征值,通常用计算方法得出矩阵的特征值和特征向量,文中向量W即为所求的特征向量. 最后计算矩阵的最大特征值为λmax=1,进行归一化处理得到各影响因子的权重为
W={0.200 0, 0.200 0, 0.171 4, 0.142 9, 0.114 3,0.085 7, 0.057 1, 0.028 6}
(4)进行一致性检验 CR=CI/RI,CR=0.050 2<0.1,表明矩阵中因子之间的比较在合理的范围之内. 判断矩阵的一致性可接受的范围是CR<0.1,为保持判断矩阵的一致性,当CR≥0.1时,就需要对其作适当修正.
通过查阅相关文献[6, 17-18],统计得到50条泥石流数据,作为本文评价模型的训练样本. 运用以上方法,基于GIS平台,分别提取木鱼镇区域泥石流评价各项指标,根据以上层次分析法(AHP)将指标数据按表1进行等级划分,再乘以指标权重,计算出RBF神经网络训练的目标层;将指标数据归一化处理后,作为RBF的训练数据,进行神经网络训练. RBF 网络的各个参数设置为:误差精度为 0.001,扩展因子为 1.554. 最终计算得出 N=0.009 0,即迭代次数为 25 次时,均方误差为0.009 0.
4 实际工程应用 4.1 研究区域概况木鱼镇位于湖北省神农架林区南部,是林区旅游重镇. 如图7所示,镇域面积为452.0 km2,木鱼镇属高山地貌区,地形起伏大,平均海拔在1 600 m,地势东南低西北高,地质环境条件复杂,属地质灾害高危险区. 木鱼镇是神农架林区重要的交通枢纽,县、乡道较多且河流分布广,对地质灾害发生影响较大.

|
图 7 木鱼镇地理位置图 Fig. 7 Location map of Muyu town |
木鱼镇镇域范围内地质灾害类型主要为滑坡、崩塌、不稳定边坡及泥石流. 随着社会经济和城镇建设的发展,近年来地质灾害发生的次数明显增多,灾害所造成的直接经济损失明显增加. 而泥石流作为地质灾害中爆发性最强、损失最严重地质灾害,已造成研究区域内上千万元的直接经济损失,造成上百人受灾,已严重威胁着人民的生命财产安全,制约经济可持续发展. 因此系统有效的进行区域性的泥石流灾害的评价,对防灾减灾、城镇规划提供参考,为保障人民生活生产具有重要意义.
4.2 区域评价指标提取将木鱼镇划分成多个斜坡,利用2.2评价因子指标值的提取的方法,提取研究区域的斜坡指标,数据提取后其结果如图8所示.
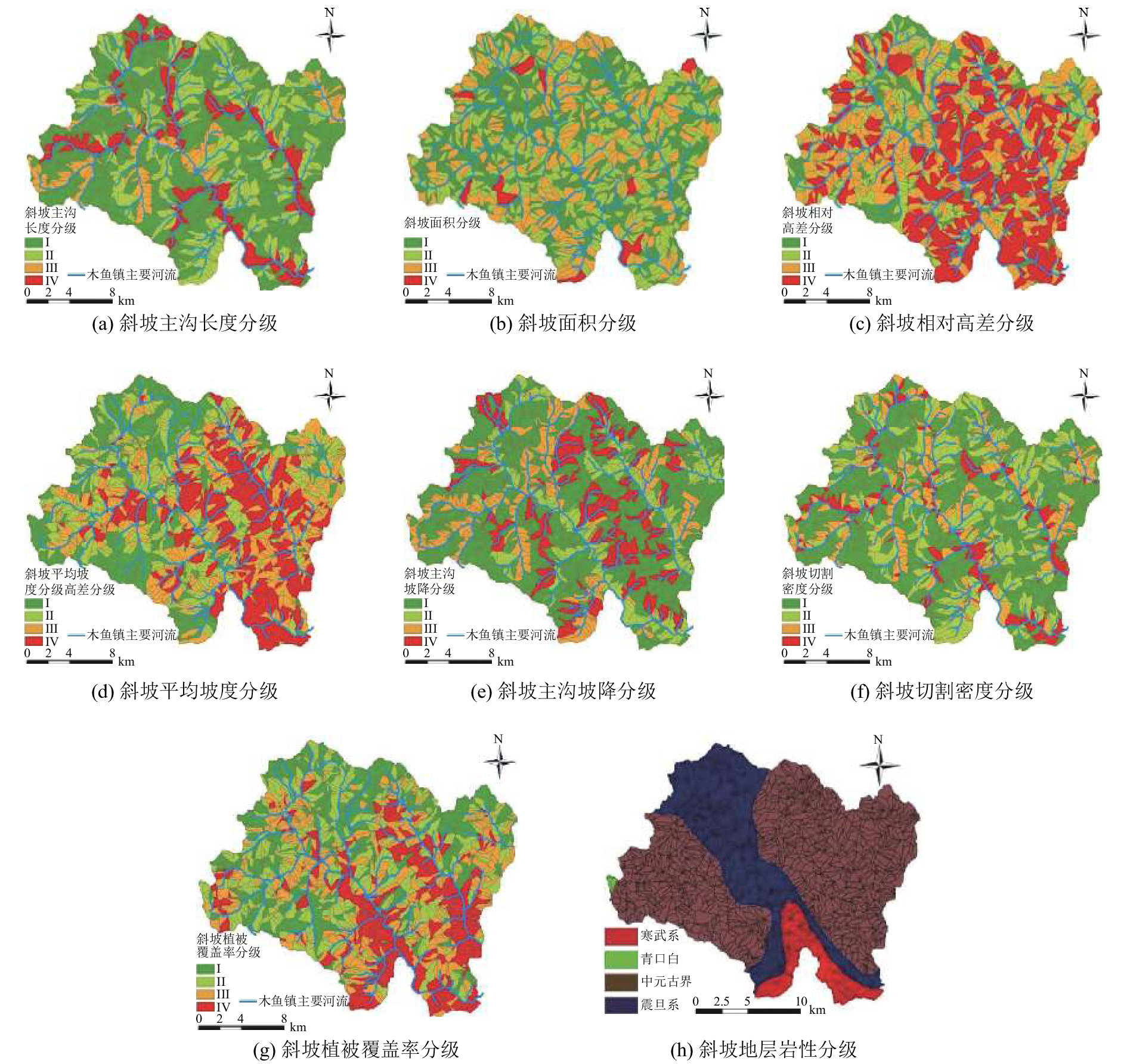
|
图 8 泥石流危险性评价指标分布及分级结果 Fig. 8 Distribution and classification results of index for debris flow hazard assessment |
将指标数据归一化后的结果,乘以各指标的权重,得到RBF神经网络新的预测数据,调用以上训练好的神经网络评价模型,进行区域的泥石流危险性评价. 评价结果采用GIS平台内置的常用的自然间断法进行等级划分,其分级指数如图9所示.
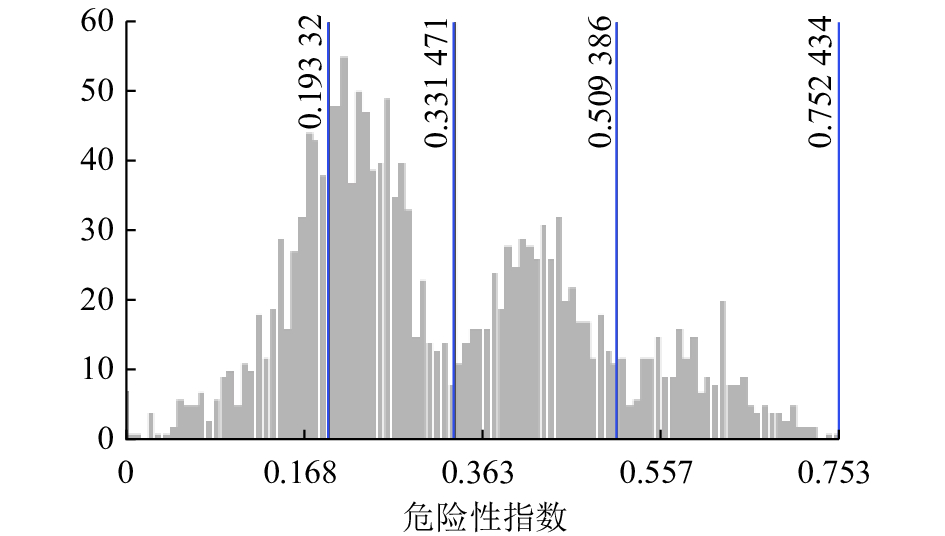
|
图 9 区域泥石流危险性评价结果等级划分数据 Fig. 9 Grade division data of regional debris flowhazard assessment |
将评价结果划分为4级,危险等级Ⅳ、Ⅲ、Ⅱ、Ⅰ,分别对应高度危险区、中度危险区、轻度危险区、无危险区. 区域泥石流灾害危险性等级划分采用自然间断法进行等级划分,其划分数据为如下:高危险性等级如下:(0.509~0.752),中度危险性等级为(0.331~0.509),轻度危险性等级为(0.192~0.331)、无危险性等级(0~0.193). 4个灾害等级由高到低,其中高度危险区、中度危险区、轻度危险区、无危险区面积分别为57.5、153.3、118.0、123.5 km2,分别占研究区总面积的12.7%、33.9%、26.1%、27.3%.
如图10所示为AHP-RBF评价结果,图中的高危险性等级在坡面主要是沿河流沟谷分布,泥石流危险性评价即泥石流沟的危险性评价,符合沟谷附近泥石流发生在可能性更高的规律. 且斜坡或附近斜坡上有已查明的滑坡、崩塌或泥石流灾害分布,滑坡及崩塌的发生,说明该坡面区域的地质条件较差,易产生大量的松散物源,可能为泥石流创造物源基础. 分析下图可知,在已查明的3处泥石流灾害中,都处于高危险区的坡面中,其他类型灾害大部分分布于高危险的斜坡上,表明评价结果可靠性.

|
图 10 木鱼镇泥石流灾害危险性评价结果 Fig. 10 Hazard assessment result of Muyu town regional debris flow |
(1)本文基于GIS技术提出了将斜坡单元作为区域泥石流的基础评价单元和斜坡单元的自动定量划分方法,并将湖北省神农架林区灾害防治示范区木鱼镇划分为1674个斜坡单元.
(2)依据研究区域的地形地貌特征结合对泥石流发生的影响及数据获取的难易程度,研究提出了区域泥石流危险性评价的指标体系(即斜坡面积、主沟长度、斜坡相对高差、平均坡度、斜坡切割密度、平均主沟坡降、植被覆盖率、地层岩性等8个指标),该指标体系可以通过GIS技术提取.
(3)提出了区域泥石流危险性评价的RBF神经网络改进模型(即APH-RBF神经网络评价模型),将专家评判经验结合到神经网络中,使神经网络模型模拟专家思维,提高了评价模型的精度.
(4)本文采用已查明的地质灾害点的位置信息与木鱼镇泥石流危险等级的评价结果进行分析对比,用以验证子本模型评价结果的合理性,对比结果表明该模型的评价结果可靠.
| [1] |
张杰坤. 泥石流研究综述[J]. 中国地质灾害与防治学报, 1994, 5(4): 18-8. ZHANG Jie-kun. Summary on debris flow research[J]. The Chinese Journal of Geological Hazard and Control, 1994, 5(4): 18-8. |
| [2] |
余斌, 杨永红, 苏永超, 等. 甘肃省舟曲8.7特大泥石流调查研究[J]. 工程地质学报, 2010, 18(4): 437-444. YU bin, YANG Yong-hong, SU Yong-chao, et al. Research on the giant debris flow hazards in Zhouqu county, Gansu province on August 7, 2010[J]. Journal of Engineering Geology, 2010, 18(4): 437-444. DOI:10.3969/j.issn.1004-9665.2010.04.001 |
| [3] |
GUZZETTI F, CARRARA A, CARDINALI M, et al. Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study, Central Italy[J]. Geomorphology, 1999, 31(1– 4): 181-216. |
| [4] |
杜国梁, 高金川, 胡新丽. 基于GIS和组合赋权的岷县板达沟泥石流危险性评价[J]. 自然灾害学报, 2014, 23(4): 235-24. DU Guo-liang, GAO Jin-chuan, HU Xin-li. Debris flow hazard assessment of banda gully in Minxian County based on GIS and combination weighting method[J]. Journal of Natural Disasters, 2014, 23(4): 235-24. |
| [5] |
王晓朋, 潘懋, 徐岳仁. 基于流域单元的泥石流区域危险性评价[J]. 山地学报, 2006, 24(2): 177-180. WANG Xiao-ming, PAN Mao, XU Yue-ren. Debris Flow Hazard Zonation Based on Cathment-unit[J]. Journal of Mountain Science, 2006, 24(2): 177-180. DOI:10.3969/j.issn.1008-2786.2006.02.009 |
| [6] |
刘希林, 唐川. 泥石流危险性评价[M]. 北京: 科学出版社, 1995: 5–19..
|
| [7] |
LIU H C, GU X Z. Hazard assessment of debris flow along highway based on extension AHP[J]. Chinese Journal of Geological Hazard & Control, 2010, 21(3): 61-66. |
| [8] |
沈简, 饶军, 傅旭东. 基于模糊综合评价法的泥石流风险评价[J]. 灾害学, 2016, 31(2): 171-175. SHEN Jian, RAO Jun, FU Xu-dong. Assessment on debris flow risk based on fuzzy comprehensive evaluation method[J]. Journal of Catastrophology, 2016, 31(2): 171-175. DOI:10.3969/j.issn.1000-811X.2016.02.033 |
| [9] |
谷天峰, 王家鼎, 付新平. 基于斜坡单元的区域斜坡稳定性评价方法[J]. 地理科学, 2013, 33(11): 1400-1405. GU Tian-feng, WANG Jia-ding, FU Xin-ping. Regional slope stability analysis method based on the slope unit[J]. Scientia Geographica Sinica, 2013, 33(11): 1400-1405. |
| [10] |
黄启乐, 陈伟, 唐绪波, 等. 区域地质灾害评价中斜坡单元划分方法研究[J]. 自然灾害学报, 2017(05): 157-164. HUANG Qi-le, CHEN Wei, TANG Xu-bo, et al. Study on the method of slope unit zoning in regional geo-hazards risk assessment[J]. Jounal of natual disaster, 2017(05): 157-164. |
| [11] |
王霖琳, 王明媚, 张建. 山东下港泥石流孕灾环境分析及危险度区划研究[J]. 山东农业大学学报: 自然科学版, 2005, 36(4): 524-528. WANG Lin-lin, WANG Ming-mei, ZHANG Jian. The pregnant environment analysis and risk assessment of debris flows for Xiagiang of Shandong[J]. Journal of Shandong Agricultural University: Engineering Science, 2005, 36(4): 524-528. |
| [12] |
LIU Y, GUO H C, ZOU R, et al. Neural network modeling for regional hazard assessment of debris flow in Lake Qionghai Watershed, China[J]. Environmental Geology, 2006, 49(7): 968-976. DOI:10.1007/s00254-005-0135-7 |
| [13] |
SAATY T L. What is the analytic hierarchy process? [M] // Mathematical Models for Decision Support. Berlin Heidelberg: Springer, 1988: 109–121. http://cn.bing.com/academic/profile?id=f15ed8aeabc8280f7d802fd2a575c20a&encoded=0&v=paper_preview&mkt=zh-cn
|
| [14] |
POWELL M J D. Radial basis functions for multivariable interpolation: a review[J]. Algorithms for Approximation, 1987, 143-167. |
| [15] |
BROOMHEAD D S, JONES R, MCWHIRTER J G, et al. Systolic array for nonlinear multidimensional interpolation using radial basis functions[J]. Electronics Letters, 1990, 26(1): 7-9. DOI:10.1049/el:19900005 |
| [16] |
OSANAI N, SHIMIZU T, KURAMOTO K, et al. Japanese early-warning for debris flows and slope failures using rainfall indices with Radial Basis Function Network[J]. Landslides, 2010, 7(3): 325-338. DOI:10.1007/s10346-010-0229-5 |
| [17] |
康志成, 崔鹏, 韦方强, 等. 中国科学院东川泥石流观测研究站观测实验资料集(1995-2000)[M]. 北京: 科学出版社, 2007: 208–224.
|
| [18] |
韩金华. 基于GIS的白龙江流域泥石流危险性评价研究[D]. 兰州: 兰州大学, 2010. HAN Jin-hua. Risk assessment of debris flow in Bai Longjiang basin based on GIS [D]. Lanzhou: Lanzhou University, 2010. |



