天地一体化网络作为国家重大基础设施，以独特位置、地域优势和特有的信息服务能力，带动着我国新兴产业的发展. 天地一体化网络由通信、导航、侦察、气象等各种功能的异构卫星网络、空间飞行器、深空网络以及地面网络基础设施组成，为国家安全、航空航天、环境监测、交通管理、教育医疗卫生、反恐、抗灾救险等领域提供战略信息服务. 在天地一体化网络中，卫星承担信息的获取、传输和分发功能，具有重要的作用. 随着科技的不断进步，许多国家全球性或全天候的应用使得卫星任务越来越复杂，功能单一、相互孤立的卫星网络架构已经不能满足用户对业务的实时性需求. 因此，随着卫星技术的发展，逐渐出现了分布式卫星技术和卫星星座技术. 分布式卫星技术是通过编队飞行使多颗小卫星形成一颗大的虚拟卫星，整个编队卫星群可以实现强大的功能. 与单颗卫星和卫星星座相比，编队飞行的卫星群的显著特点是星间相对位置较为静止，轨道周期相同，互相协同承担信号处理、通信、侦察、导航等任务. 由多颗小卫星编队飞行组成分布式卫星网络，协作完成航天任务，可以在功能和成本上超越甚至取代原有的单颗大卫星^[1].

现有的分布式卫星系统一般由空间卫星系统、跟踪遥测及指令系统、通信地球站系统、监控管理系统、地面数据处理系统5部分组成. 空间卫星系统要承担数据采集、通信和导航等功能；跟踪遥测及指令系统负责对卫星的轨道位置进行控制和跟踪测量；通信地球站系统是微波无线电站，用户通过通信地球站系统接入卫星线路进行通信；监控管理系统负责进行通信性能的监测和控制，对通信链路和卫星工作状态进行实时监测；地面数据处理系统负责海量数据的处理和分析过程^[2].

为了高效地存储和处理卫星传回地面站的数据，将云计算技术引入到地面应用系统，在地面站部署计算集群，构建数据处理的云平台^[3]，利用网络资源虚拟化技术构成资源池，存储和处理卫星转发来的数据，为用户提供集约化的计算服务. 然而，卫星采集的数据传回地面云计算数据中心进行计算、分析产生的通信开销大，时延高，无法有效支撑如抗灾救险、作战攻击等时延敏感型业务.

针对任务传输到云中心进行计算引起的高时延问题，思科于2012年提出雾计算^[4]. 雾计算技术在云计算层和终端用户之间，构建新的离终端用户更近的计算层^[5]，处理时延敏感类业务，大大降低了业务的处理时延，弥补了云计算的不足，引起学者们的广泛关注与研究. Gia等^[6]将雾计算应用于医疗物联网中，由雾计算层提供实时快速响应和在线数据分析，达到低时延数据处理和较低带宽占用的目的. Sarkar等^[7]对雾计算以及传统云计算架构的服务时延和能耗进行建模，在物联网（internet of things，IoT）场景下，从时延和能耗方面将云计算和雾计算架构进行对比分析. Truong等^[8]提出将雾计算引入到车辆自组织网络中提供时延敏感型和位置感知服务. 目前将雾计算应用于空间卫星的研究很少.

随着小型化编队卫星数量的增多和小型航天器计算能力的提高，小卫星编队组成的虚拟卫星拥有越来越强的计算能力，能够直接处理用户请求的计算任务. 在分布式卫星系统的云-分布式卫星-用户的系统架构中，分布式卫星编队与云计算中心相比更靠近用户. 提出利用分布式卫星雾进行计算的方法，将分布式卫星集群作为雾计算层，利用雾计算的优势解决卫星地面云计算中心处理数据存在的高时延问题，同时提高卫星网络的抗毁性. 分布式卫星编队承担雾计算层的功能，组成卫星雾网络. 卫星用户直接接入到卫星雾层，提交任务请求；卫星雾直接利用采集的数据进行计算、分析，减小卫星数据传回地面数据中心处理的传输时延. 同时，单颗卫星的计算能力较弱，并且单颗卫星一旦受到攻击或损坏将直接导致任务处理中断.为此提出卫星编队进行分布式计算处理任务，达到进一步减小处理时延、提高抗毁性的目的. 为了更加高效地处理业务，根据卫星的计算能力以及通信时延合理地划分任务；卫星处理任务增多导致卫星雾整体能耗增加，卫星工作寿命减短，因此如何规划任务分配，使得在能耗约束前提下任务处理时延最短，就成为重要问题.

Deng等^[9]将云雾系统划分为4个子系统，分别对子系统以及整个云雾系统的时延和能耗进行建模，并且在时延约束限制条件下研究负载分配问题，达到系统能耗约束下业务处理时延最小的目标. 但是，Deng等研究的时延和能耗的优化采用集中式的优化，没有详细分析负载在雾子系统内部以及云雾系统之间的分配方法.

考虑到卫星与地面站相距较远，卫星雾与地面站云联合优化将导致时延过高，因此利用地面站云辅助优化卫星雾的时延和能耗，提出分布式卫星云雾网络(distributed satellite cloud fog network, DSCFN)架构，并且提出时延与能耗均衡方案，在地面云计算中心利用改进的粒子群优化(modified article swarm optimization, MPSO) 算法均衡卫星雾网络的负载，达到在能耗约束下业务处理时延最小的目标.

1 分布式卫星云雾网络架构

为了解决卫星采集的数据传回地面数据中心进行计算、分析带来的高传输时延问题，同时提高卫星网络的抗毁性，提出分布式卫星云雾网络架构. 通过卫星编队与地面站统一的组网，有效进行全球网络覆盖，更加高效地提供通信、测绘、作战指挥等服务. 此外，直接在卫星上进行分布式计算数据，避免回传到地面站计算产生的较高的传输时延. 从计算和网络的角度将整个卫星系统视为由卫星雾层和云计算层构成的网络架构，如图1所示.

卫星雾层主要为空间卫星系统，由功能各异的多颗小卫星编队飞行组成，包括侦查、通信、遥感等多种卫星. 陆地用户、海洋用户、空中用户等所有卫星用户通过通信地球站系统直接接入到卫星雾网络，发送任务请求. 为了减小数据处理时延，时延敏感型业务传送至卫星后，卫星之间协同运作，进行分布式计算，并将计算结果直接反馈给卫星用户.

地面云计算层主要包括跟踪遥测及指令系统、监控管理系统和数据处理系统，包括高性能的服务器，多个服务器构建成云计算集群，通过卫星地面接收天线与卫星雾层相连. 云计算层一方面负责处理部分用户的业务请求，另一方面负责网络管理、卫星及卫星链路状态监控、控制卫星编队，辅助卫星编队飞行，以及卫星雾层的分布式计算负载均衡等维护业务.

为了提高效率并且保证系统的可靠性，云计算层充分利用监控管理分系统实时监测得到的卫星的工作状态及卫星间通信链路状态等数据. 依据实时状态数据，地面云中心根据卫星雾设备的计算能力和链路的通信时延提前制订分布式负载均衡方案. 当监测到卫星雾层的节点或节点间通信链路损坏导致卫星雾网络的拓扑结构发生变化时，云计算层立即基于MPSO算法利用可用卫星雾设备的计算能力以及链路的通信时延等参数重新规划新的拓扑结构下的分布式负载均衡方案. 当有新的任务请求时，卫星雾层直接根据规划好的分布式负载均衡方案进行任务分配和分布式协同计算，大大提高处理任务的实时性和系统的可靠性.

提出的新型网络架构和负载均衡方案建立在现有的分布式卫星系统之上，充分利用监控管理系统得到的卫星状态数据进行计算任务分配，不需要额外的设施建设.

2 DSCFN时延与能耗均衡方案 2.1 DSCFN架构理论模型

为了在卫星雾网络中合理地分配卫星计算资源，依据每颗小卫星的计算能力、通信时延、能耗约束等条件合理地划分任务，达到能耗约束下时延最小的目标，提出高效的时延与能耗均衡方案.

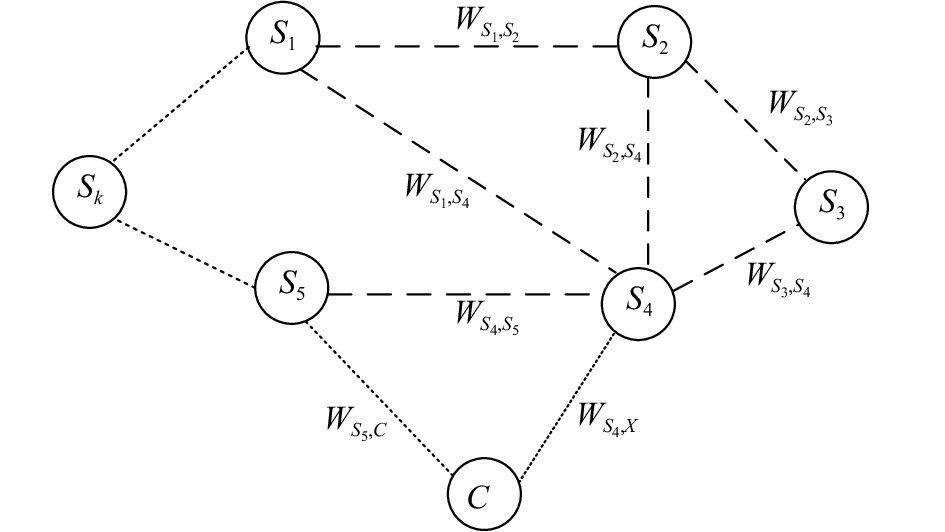
卫星系统的拓扑和链路状态动态变化，但是分布式卫星编队的拓扑相对稳定. 云计算中心对整个卫星集群进行全局性的信息获取和控制，不会给已经在执行计算任务的卫星节点分配新的计算任务. 另外，在监测到卫星状态变化后，计算能力强大的云计算层执行MPSO算法重新规划任务分配方案需要极短的时间. 所以，在云计算层任务规划和雾计算层任务执行的过程中，卫星系统的状态及拓扑不会产生变化. k颗小卫星编队飞行组成的DSCFN使用带权无向图G=(V, E)来描述，如图2所示. V = $ \left\{ {{S_1},{S_2}, \cdot \cdot \cdot ,{S_i}, \cdots ,{S_k},C} \right\}$ 为顶点集，顶点S_i为卫星雾中的小卫星，节点C为云计算层； ${{E}} =\left\{ {e_{{S_1},{S_2}}}, \cdots ,{e_{{S_i},\,{S_{\!\!j}}}}, \cdots ,{e_{{S_{k-1}}{S_k}}},{e_{{S_4},C}},{e_{{S_5},C}} \right\}$ 为边集，边 ${e_{{S_i},{S_{\!\!j}}}}$ 为卫星S_i和S_j之间的通信链路，边上的权重 ${W_{{S_i},{S_{\!\!j}}}}$ 为卫星{S_i, S_j}之间的通信时延.

在图2中，假设卫星S_i的计算能力为 $A_{S_i} $ . 终端用户每次直接提交请求到接入的卫星上，生成任务D. 由于单颗卫星的计算能力有限，C根据卫星雾设备的计算能力和链路的通信时延将任务D划分为若干子任务d_i，满足d_i = δ_iD，δ_i为比例系数；计算得出任务分配比例关系，发送给整个卫星雾网络. 卫星雾层处理任务D的总时间为

$t(\delta_i) = \max \,\, \left\{ \frac{{\delta_i D}}{{{A_{{{S}}i}}}} + W_{{{S}_i}{,{S}_{\!\!j}}} \right\}.$

(1)

式中：δ_iD/A_Si为卫星S_i处理子任务d_i的计算时间， ${W_{{{S}}i,{{S}}j}}$ 为任务传输过程中的通信时延.

${W_{{S_i},\,{S_{\!\!j}}}} = \frac{d_{{S_i},\,{S_{\!\!j}}}}{ \mu _{{S_i},\,{S_{\!\!j}}}} + \frac{l_{{S_i},\,{S_{\!\!j}}}}{\eta _{{S_i},\,{S_{\!\!j}}}}.$

(2)

式中： ${d_{{S_i},{S_{\!\!j}}}} $ / ${\mu_{{S_i},{S_{\!\!j}}} }$ 为卫星S_j向卫星S_i传输数据 $ {d_{{S_i},{S_{\!\!j}}}}$ 产生的传输时延， ${\mu_{{S_i},{S_{\!\!j}}} } $ 为{S_i ,S_j}通信链路的数据传输速率； $ {l_{{S_i},{S_{\!\!j}}}}$ / $ {\eta_{{S_i},{S_{\!\!j}}}} $ 为{S_i,S_j}通信链路的传播时延， $ {l_{{S_i},{S_{\!\!j}}}} $ 为信道长度， ${\eta_{{S_i},{S_{\!\!j}}}} $ 为电磁波在信道上的传播速度.

分布式计算总任务的处理时间等于所有子任务中最大的计算时延。为了在卫星雾整体耗能受限的条件下最大限度地降低处理时延，必须求一组最优的δ_i，使得目标函数t最小. 卫星雾的能耗约束下的时延建模如下：

$\left. \begin{array}{l}\min \,\,\left\{ {\max \,\,\left[ {\displaystyle\frac{{{\delta _i}D}}{{{A_{{{S}}i}}}} + \left( {\displaystyle\frac{{{\rm{ }}{d_{{{S}}_i,\,{{S}}_{\!\!j}}}}}{{{\mu _{{{S}}_i,\,{{S}}_{\!\!j}}}}} + \frac{{{\rm{ }}{l_{{{S}}_i,\,{{S}}_{\!\!j}}}}}{{{\eta _{{{S}}_i,\,{{S}}_{\!\!j}}}}}} \right)} \right]} \right\}{\mkern 1mu} ;\\{\rm{s}}.{\rm{t}}.\;\;{\rm{ }}{E_{{\rm{sys}}}} = \displaystyle\sum\limits_{{{S}}_i,\,{{S}}_{\!\!j} \in V} {{\theta _{{{S}}i,\,{{S}}j}}} {\rm{ }}{d_{{{S}}i,\,{{S}}j}} + \displaystyle\sum\limits_{i = 1}^k {{\theta _{{{S}}i}}{d_i}} \leqslant {\rm{ }}{E_{{\rm{max}}}},\\\displaystyle\sum\limits_{i = 1}^k {{\delta _i} = 1} ,\;\;\;{\kern 1pt} \;i,j = 1,2, \cdots ,k.\end{array} \right\}$

(3)

式中：θ_Si,Sj为传输单位比特数据的能耗；θ_Si为卫星S_i处理单位比特数据的能耗；E_sys为卫星雾系统的能耗；E_max为能耗阈值，即要求的能耗约束值.

由式（3）可知，k个卫星节点上分别处理的计算子任务可构成k维向量 ${{d}} = \mathop {\left[ {{d_1},{d_2}, \cdots ,{d_k}} \right]}\nolimits^{{{\rm T}}} $ . 由于计算任务D可能来自任意计算节点，假设来自节点S₁，由式(1)可知，在卫星雾层处理计算任务D的总时间为

$\begin{aligned} & t\left( {{d}} \right) = \max \\&\left\{ {\frac{{{d_1}}}{A_{S{\rm1}}} + \left(\frac{{\mathop d\nolimits_{{{{S_1},{S_1}}}} }}{{\mathop \mu \nolimits_{{{{S_1},{S_1}}}} }} + \frac{{\mathop l\nolimits_{{{{S_1},{S_1}}}} }}{{\mathop \eta \nolimits_{{{{S_1},{S_1}}}} }}\right), \cdots ,\frac{{{d_{{k}}}}}{A_{{{S}}k}} + \left(\frac{{\mathop d\nolimits_{{{{S_1},S}}_k} }}{\mathop \mu \nolimits_{{{{S_1},S}}_k} } + \frac{{\mathop l\nolimits_{{{{S_1},S}}_k} }}{{\mathop \eta \nolimits_{{\rm{{S_1},S}}_k} }}\right)} \right\}.\end{aligned}$

(4)

对卫星雾中每个计算节点上应处理的计算任务d_i的求解，即对任务向量d的求解，归结为优化问题：

$\left. \begin{array}{l}{{d}} = \mathop {\arg }\limits_{{{d}} \in {{I}}} \;\min \,\,\left\{ {t({{d}})} \right\};\\{\rm{s}}.{\rm{t}}.{\mkern 1mu} {\mkern 1mu} {\rm{ }}{E_{{\rm{sys}}}} = \displaystyle\sum\limits_{{{S}}_i,\,{{S}}_{\!\!j} \in V} {{\theta _{{{S}}_i,\,{{S}}_{\!\!j}}}} {\rm{ }}{d_{{{S}}_i,\,{{S}}_{\!\!j}}} + \displaystyle\sum\limits_{i = 1}^k {{\theta _{{{S}}_i,\,{{S}}_{\!\!j}}}} \leqslant {E_{{\rm{max}}}},\\{d_i} \geqslant 0,\;\;\displaystyle\sum\limits_{i = 1}^k {{d_i}} = D\;.\;\end{array} \right\}$

(5)

优化问题的搜索空间I为

${{I}}{{ \LARGE\triangleq }} \prod\limits_{i = 1}^k {\left[ {{d_{i\min }},{d_{i\max }}} \right]} = \prod\limits_{i = 1}^k {\left[ {0,D} \right]} .$

(6)

2.2 MPSO负载均衡算法

优化问题属于典型的NP-Hard问题，无法找到多项式时间的算法. 粒子群优化（PSO）算法^[10]具有全局搜索能力强、收敛速度快和编程容易实现的优点，在云计算层采用PSO算法求解优化问题，得到使卫星雾网络的时延和能耗折中的任务划分比例. 由于种群多样性的限制，PSO算法出现早熟收敛，因此本研究采用MPSO算法，将变异粒子逆向飞行^[11]引入到PSO算法中，避免迭代过程中陷入局部最优.

采用MPSO算法求解式(5)中的优化问题时，粒子群 $\{X_{i}^{r}\}_{i=1}^{n}$ 在搜索空间I内移动以寻找最优位置X，即d，n为粒子群的规模， $r \in \left\{ {0, \cdot \cdot \cdot ,{R_{\max }}} \right\}$ 为迭代次数，R_max为迭代次数的最大值. 第i个粒子的位置和速度为

$\mathop {{X}}\nolimits_i^r = [\mathop x\nolimits_{i1}^r \;,\mathop x\nolimits_{i2}^r \;, \cdot \cdot \cdot ,\mathop x\nolimits_{ik}^r],$

(7)

$\mathop {{v}}\nolimits_i^r = [\mathop v\nolimits_{i1}^r \mathop {,v}\nolimits_{i2}^r , \cdot \cdot \cdot ,\mathop v\nolimits_{ik}^r ].$

(8)

式中： $\mathop {{v}}\nolimits_i^r \in {{M}}$ ， ${{M}} \triangleq \prod\limits_{i = 1}^k {\left[ { - {v_{i\max }},{v_{i\max }}} \right]} $ ， ${v_{i\max }} = $ $\left( {{d_{i\max }} - {d_{i\min }}} \right)/2.$

式(5)为带约束的优化问题，定义适应度函数为^[12]

$f\left( {{X}} \right) = \left\{ {\begin{aligned} & {t\left( {{X}} \right),\quad \quad \quad \quad \quad \;\;\;\;\;\;\;\;\;\;\;\quad \quad\;\; {{X}} \in {{F}}} ;\\ & {t\left( {{X}} \right) + \alpha \sum\limits_{m = 1}^{k + 2} {{t_m}\left( {{X}} \right) + \varphi \left( {{{X}},r} \right),\;\;\;{{X}} \in {I - F}} .} \end{aligned}} \right.$

(9)

式中：F为搜索空间中的可行域，α为惩罚因子，t_m(X)为非可行粒子对第m约束的约束违背测度，φ(X, r)为在算法执行到r代对于非可行粒子的附加启发式值^[12]. t_m(X)和φ(X, r)分别为

${t_m}\left({X} \right) = \left\{ \begin{aligned}& \max \,\, \left( {0, - {X}\left( m \right)} \right),\;\;\; \;\;\;\;\;\;\; 1 \leqslant m \leqslant k; \\ & \max \,\, \{ 0,{\rm{ }}{E_{{\rm{sys}}}} - {\rm{ }}{E_{{\rm{max}}}}\}, \;\;\;\; m = k + 1;\\ & \left| {\sum\limits_{i = 1}^k { {X}\left( i \right) - D} } \right|,\;\;\; \;\;\; \;\;\;\;\;\;\;\;\; \;m = k + 2,\end{aligned} \right.$

(10)

$\varphi \left( {{{X}},r} \right) = \lambda \left( r \right) - \mathop {\min }\limits_{{{X}} \in {{I - F}}}\,\, \left\{ {t\left( {{X}} \right) + \alpha \sum\limits_{m = 1}^{k + 2} {{t_m}\left( {{X}} \right)} } \right\}.$

(11)

式中：X(m)为粒子第m维的位置，控制参数λ(r)跟踪记录了算法进化到第r代所获得的拥有最大适应度值的可行粒子，在迭代过程中确保所有可行粒子优于所有非可行粒子.

$\lambda (r) = \max \,\, \left\{ {\lambda \left( {r - 1} \right),\,\,\mathop {\max }\limits_{{{X}} \in {{F}}}\,\, \left\{ {t\left( {{X}} \right)} \right\}} \right\}.$

(12)

执行MPSO算法时，更新粒子i的速度和位置的迭代公式为^[13]

$ \mathop {{v}}\nolimits_i^{r + 1} = \omega \mathop {{v}}\nolimits_i^r + {\rm{rand}}(\;)\,{c_1}\left( {\mathop {{p}}\nolimits_i^r - \mathop {{X}}\nolimits_i^r } \right) + {\rm{rand}}(\;)\,{c_2}\left( {{{{g}}^r} - \mathop {{X}}\nolimits_i^r } \right),\!\!\! $

(13)

$\mathop {{X}}\nolimits_i^{r + 1} = \mathop {{X}}\nolimits_i^r + \mathop {{v}}\nolimits_i^{r + 1} .$

(14)

式中：ω为惯性权重；rand()为均匀分布于区间[0, 1]的随机数；c₁和c₂为2个加速因子，分别是粒子飞向局部和全局最好位置的速度权重； ${{P}}_i^r$ 为第r代粒子i在搜索空间中经历的最优位置，g^r为在第r代整个群体经历的最优位置. 惯性权重的更新公式为

$\mathop \omega \nolimits_{} = \mathop \omega \nolimits_{\min } - \frac{{\mathop \omega \nolimits_{\min } - \mathop \omega \nolimits_{\max } }}{{R_{\max} }} r.$

(15)

为了避免算法陷入局部最优，提高算法的全局收敛性能，在PSO算法搜索过程中引入变异粒子使粒子群保持一个相对较高的种群多样性. 在变异策略中，生成一个[0,n]的随机数q，作为变异粒子个数. 但是q不能太大，否则会使得算法迭代过程中所得到的粒子群的结构信息无法继承，影响到PSO算法通过粒子间信息交互求解的优势. 被选中的q个变异粒子的更新速度和位置为

$\mathop {{v}}\nolimits_i^{r + 1} = - \mathop {{v}}\nolimits_i^r ,$

(16)

$\mathop {{X}}\nolimits_i^{r + 1} = \mathop {{X}}\nolimits_i^r - \mathop {{v}}\nolimits_i^{r + 1} .$

(17)

MPSO算法求解卫星雾网络的最佳任务分配方式d的具体实现步骤如下.

1） 初始化. 设置粒子群规模n，粒子的最大速度为 ${v_{i\max }}$ ，控制参数为λ(0). 在搜索空间I内随机初始化粒子群位置和速度分别为 $\left\{ {\mathop {{X}}\nolimits_i^0 } \right\}_{i = 1}^n$ 和 $\left\{ {\mathop {{v}}\nolimits_i^0 = 0} \right\}_{i = 1}^n$ ；初始化每个粒子的最优经历位置及群体最优经历位置分别为

$\left\{ {\mathop {{p}}\nolimits_i^0 = \mathop {{X}}\nolimits_i^0 } \right\}_{i = 1}^n,{{{g}}^0} = \arg \mathop {\min }\limits_{\left\{ {\mathop {{X}}\nolimits_i^0 } \right\}_{i = 1}^n} t\left( {\mathop {{X}}\nolimits_i^0 } \right).$

2）根据式(15)计算粒子的惯性权重， $\mathop \omega \nolimits_{\min } = 0.4$ , $\mathop \omega \nolimits_{\max } = 0.9$ .

3）对于种群中的每个粒子，根据式(9)~(12)计算适应度值.

4） 将每个粒子的适应度值与最优适应度值进行比较，如果优于最优适应度值，将当前粒子位置作为p_i.

5） 将每个粒子的最优适应度值与群体最优适应度值进行比较，如果优于群体最优适应度值，将当前粒子位置作为g.

6） 根据式(13)和式(14)更新粒子的速度和位置. 根据搜索空间I和M，判断粒子的速度和位置是否超出边界值，如果超出使用边界值代替.

7）生成一个 [0, n]内的随机数q作为变异粒子个数，但生成的随机数不能太大，并且按照式(16)和(17)更新被选中的q个变异粒子的速度和位置.

8）当迭代次数达到最大值R_max时停止迭代，获得粒子的最优位置即最佳任务分配方式 ${{d}} = {{X}} = {{{g}}^{R_{\rm{max}}}}$ ，否则转到步骤2)继续执行.

3 仿真结果与分析

基于MPSO算法，分析卫星雾网络在不同能耗约束下的时延性能，并且比较DSCFN与当前普遍应用的分布式卫星云中心架构的时延性能. 同时，对比分析MPSO算法与加权轮转法(weighted round-robin, WRR)^[14]、最大最小算法(load balance max-min, LBMM)^[15]和 PSO算法^[10].

仿真平台为MATLAB，实验计算机CPU为Intel i5-3230M，内存为4 GB. 卫星雾网络由10个卫星节点编队组成，k = 10. 假设卫星S₁为接收请求的节点，并且S₁无法在用户可以接受的时间范围内完成任务D，按照划分比例将任务D发送给编队中的其他卫星节点进行计算. 简化部分不影响计算任务分配方案的参数指标，仿真中设置地面云计算中心给卫星雾节点S₁的任务请求分配的计算资源为10 GHz，云计算中心为卫星雾节点S₁预留的上、下行链路带宽均设置为20 Mb/s. 卫星雾节点S₁与终端用户之间的电磁波单向传播时延设置为t_p,S1 = 0.135 s，S₁与地面云计算中心间的电磁波的单向传播时延设置为t_C,S1 = 0.135 s，S₁与S_j之间的电磁波单向传播时延设置为t_1,j = 0.04 s. 卫星节点的计算能力、传输能耗、计算能耗以及卫星之间的通信上、下行链路带宽设置如表1所示.

在MPSO算法中，种群规模设置为n = 100，最大迭代次数为R_max = 1000，加速因子为c₁ = c₂ = 1.2，惩罚因子为α=10，控制参数为λ(0) = 10⁶.

3.1 能耗约束对任务处理时延的影响

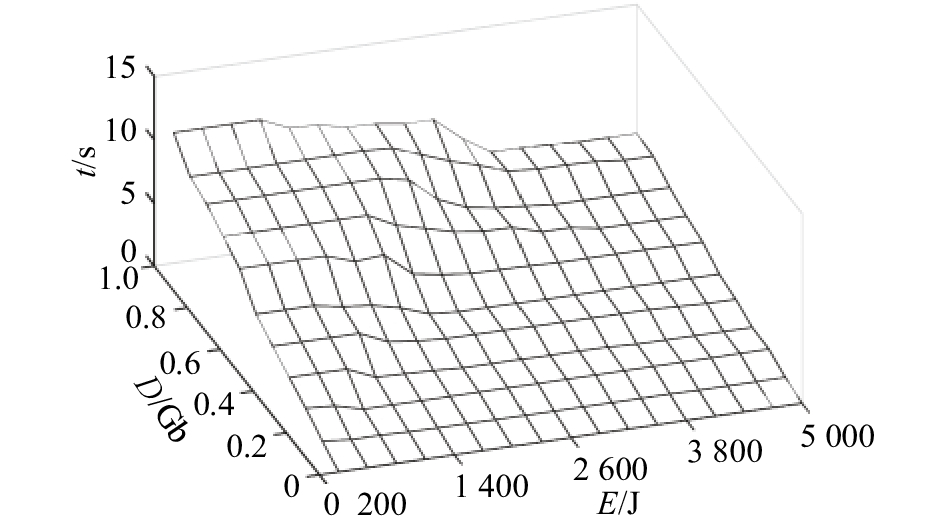
为了满足时延敏感型业务的需求，应该减小处理任务的时延，但时延减小会导致耗能加剧. 为了降低时延并且保障卫星编队整体的工作寿命，降低处理任务D时产生的能耗. 但是，能耗受限时，时延也会受到影响. 分析能耗约束条件下，卫星编队处理任务的时延性能. 当任务量D在0~1 Gb之间变化，能耗阈值E_max在200~5 000 J的范围内变化时，任务处理总时延的变化情况的仿真结果如图3所示.

图3的仿真结果表明，当DSCFN的能耗约束不变，例如能耗E_max=1 400 J时，时延随着任务量D的增大不断增加. 当任务量一定并且较小时，如D<0.2 Gb时，随着能耗E_max的变化，任务处理时延先稍微降低，然后在能耗 >500 J之后达到平衡稳定的状态保持不变. 处理0.2 Gb任务产生的能耗≤500 J，满足能耗约束，同时 E_max>500 J时，不同能耗约束条件下的时延几乎没有差异. 随着任务量的不断增加，时延达到平衡状态的能耗限制条件越来越大. 例如D =1 Gb，能耗阈值<3 800 J时，时延随着能耗E_max不断增加而降低. 能耗越小，限制越严格. 为了满足约束，卫星编队执行任务缓慢，需要耗费更长的时间来完成任务D. 然而，随着能耗阈值不断增大，能耗限制的影响越来越小，当E_max>3 800 J时，完成任务D所产生的能耗≤阈值，能耗对于任务处理时延几乎没有影响. 因此，卫星编队按照任务处理时延更小的任务划分比例执行任务，达到总时延最小的目标，并且达到稳定状态.

3.2 DSCFN与分布式卫星云中心网络(DSCN)架构的时延性能分析

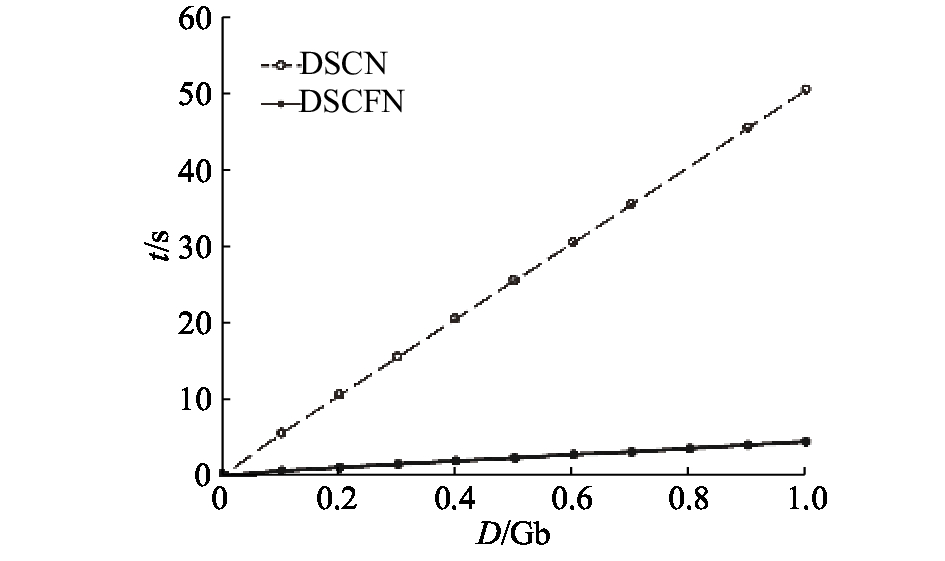
为了证明与DSCN架构相比，DSCFN可以有效地降低任务处理的时延，在无能耗约束下，任务量D在0~1 Gb范围变化时，对2种架构处理任务的时延性能进行仿真分析. 其中，云服务器整体的计算能力为10 GHz，上下行链路带宽分别为10 Mb/s和20 Mb/s. 图4表明，虽然地面站运用云计算技术处理数据，减小了计算时延t，但是卫星距离地面云中心较远，地面站与卫星之间的传输带宽受限，传输产生的能耗和时延较高，任务总的处理时延较DSCFN高出许多. 虽然卫星计算能力比云服务器弱，但是卫星雾层采用雾计算技术进行本地分布式计算，减小了传输时延，进一步降低了计算时延，有效地降低任务处理的总时延，满足时延敏感型业务的需求.

3.3 MPSO算法与几种经典负载均衡算法的时延性能比较

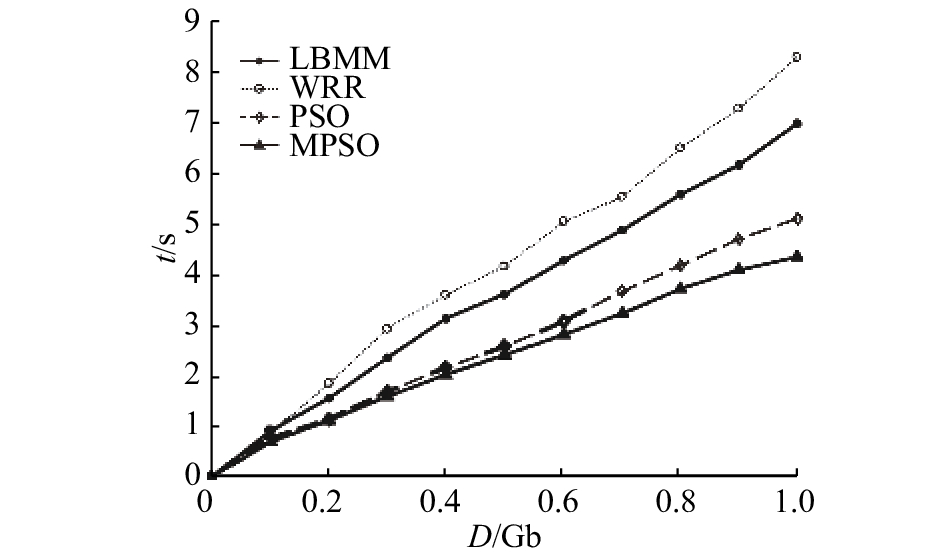
图5的结果表明，在DSCFN中，当任务量D<0.2 Gb时，随着任务量增大，4种算法的时延差别不明显. 但是，当任务量D>0.4 Gb时，MPSO算法的时延明显低于其他3种算法. 例如，当任务量为1 Gb时，MPSO、PSO、WRR和LBMM的时延分别为4.4、5.1、7和8.3 s，MPSO算法的时延相比于其他3种算法分别降低了13.7%、37.1%、46.9%. 这是因为与MPSO算法相比，PSO算法容易陷入局部最优，LBMM和WRR算法无法将通信时延与计算能力一起考虑进行联合优化. 应用MPSO算法得出的任务划分比例优于其他3种经典的负载均衡算法，可以达到有效降低任务处理时延的目标.

3.4 MPSO算法的可实施性和可扩展性分析

优化问题属于典型的NP-Hard问题，无法找到多项式时间的算法解决这类问题，在实际工程应用中，不需要理论最优解，只需要符合工程需求的相对最优解即可. MPSO算法效果较好，但是PSO算法属于集群智能算法，时间复杂度与算法执行次数和问题规模成正比. 随着问题维数的增大，分布式卫星编队内的卫星数量越来越多，PSO算法的迭代时间随之增长. 在实际工程应用中，为了适应高维度问题带来的计算复杂度的增长，采用并行和分布式的方式执行该算法. Tu等^[16]利用单机多线程的方法同步执行PSO算法降低了算法的迭代时间. Mussi等^[17]提出了利用图形处理器（graphic processing unit, GPU）加速PSO算法的执行过程. Waintraub等^[18]采用集群分布式计算的方法来降低PSO算法的运行时间，应用于解决核能工程的问题取得不错的性能. 因此，在地面云计算中心执行MPSO算法时，可以使用分布式计算和并行计算，充分利用多节点的集群处理能力和单机的并行执行能力来提高算法的效率以及解决高维数的问题.

4 结　语

针对分布式卫星云中心架构处理任务时时效性较差的问题，本文提出了分布式卫星云雾网络架构，解决了将数据传回地面站进行处理、分析而引起的高传输时延问题，节省了网络带宽，增强了用户体验. 针对卫星的能耗增加直接影响卫星的工作寿命的问题，本文研究了能耗约束条件下卫星编队的任务处理时延优化. 仿真结果表明，在合理的能耗限制条件下，卫星编队按照地面云中心执行MPSO算法得出的任务划分比例进行本地分布式计算，可以有效地降低任务处理时延，满足时延敏感型业务的需求.

除了卫星编队外，卫星星座技术也在蓬勃发展. 卫星星座技术可以实现全球通信能力的连续覆盖和空间通信的可视化，对于提高国防防御能力和满足日益发展的通信业务需要有重要的战略意义. 由于卫星星座的网络节点在各种轨道上运行，使得网络拓扑结构呈现周期性变化，如何针对卫星星座组网特殊性进行分布式计算将是下一步的研究方向.