2. 安全生产智能监控北京市重点实验室,北京 100876
2. Beijing Key Laboratory of Work Safety Intelligent Monitoring, Beijing 100876, China
物联网(internet of things,IoT)连接了现实事物与互联网信息世界[1],无线传感器等节点设备为物联网提供海量的数据信息,已经应用在军事[2]、环境监测[3-4]等领域中. 最新研究表明,可移动的汇聚节点(mobile sink)能够有效提升基于无线传感器网络(wireless sensor networks,WSNs)的物联网性能表现[5-6]. 但是,移动汇聚节点可能受到环境影响,不具备完全移动性,被称为移动性受限的汇聚节点. Smeets等[7]研究基于固定铁轨的无线传感器网络数据采集问题. Huang等[8-9]研究基于汽车的信息监控问题. 在偏远山区、河流,以及智能电网巡检等应用中,汇聚节点只能根据环境构造,沿着固定的路径移动并汇集数据. 在这类场景中,网络拓扑受到移动汇聚节点的路径影响,具有明显的分层结构. 能够与移动汇聚节点单跳通信的节点为静态汇聚节点(static sink). 在分层网络结构下,传统的数据采集策略不能高效地汇集网络数据并保证全网节点的能量有效性,因为集中的数据中继导致静态汇聚节点消耗大量能量,造成能源快速衰竭.
Zhang等[10]研究预定轨迹的数据采集策略,通过分簇将网络中节点进行分组,通过启发式算法求得近似最优的移动汇聚节点访问顺序,降低网络整体的能耗水平,并且满足数据采集延迟. 在可以规划汇聚节点移动轨迹的场景中具有启发意义. 徐新黎等[11]在移动汇聚节点移动性受限的应用场景中,为了提高网络寿命,使用无线充电的方式对静态汇聚节点进行能量补给. 采用的方法能有效提高静态汇聚节点的工作时长,在一定程度上优化数据采集的总量. 随着网络工作时间的累积,大量没有得到能量补给的数据节点正常死亡,不能稳定地保证数据采集的性能. 彭舰等[12]考虑简单的运动轨迹场景,认为移动汇聚节点按照圆形路径进行运动,数据节点随机分布在周围,提出有效的数据传输算法以及队列管理策略来提升网络的性能,改善了在运动模型下的传输延迟特性,但是没有考虑到实际应用场景以及网络层次结构所带来的影响. Gao等[13-14]提出最大数据量最短路径(max amount shortest path,MASP)策略. MASP直接使用经典的最短路径树(shortest path tree,SPT)协议进行路由建立与数据包传递. MASP在提升网络能量有效性时没有考虑静态汇聚节点以及具有相同位置特性的数据节点的能量均衡性问题,SPT中数据传递仅仅将第1个收到路由发现包的节点作为数据包中继的网关节点,导致部分节点的负载过重并且快速死亡,降低了网络的可靠性和健壮性. Sharma等[15]研究预定移动汇聚节点轨迹受到限制的应用场景. 基于分簇的方式,提出实时动态的数据融合策略来定制簇内成员节点的数据上报过程,在一定程度上降低了网络的能耗,但是没有对整体网络拓扑特性进行考虑,无法对此类具有能耗分层特性的网络进行优化.
针对汇聚节点移动性受限场景的已有研究中,网络的分层特性很少被纳入考虑. 在具有分层网络特性的物联网应用中,研究路径受限的可移动汇聚节点对网络性能的影响. 基于图论的基本概念与思想,提出高效平衡的数据采集策略,能够在移动汇聚节点路径受限的物联网应用场景中,均衡静态汇聚节点的能耗水平,降低全网数据节点的整体能量消耗,全面提升网络的能量有效性,同时保证网络具有较高的数据采集性能.
1 系统模型与分析 1.1 系统描述区域A中随机部署n个静态的数据节点(data node)Nd,所有节点的初始能量为Einit. 移动汇聚节点Sm的运动轨迹Pm为A的轴对称线,在后续讨论中只研究A单侧的情况. Sm沿着Pm的两端以vm作匀速往返运动. 包括Sm节点在内的所有节点的最大通信距离为r,每个节点都具有足够的存储空间来存放路由信息以及缓存数据. 节点能够在部署完成时获取并保存自己的位置信息[16]. 节点是静止的,仅在部署完成时获取位置信息,能耗忽略不计.
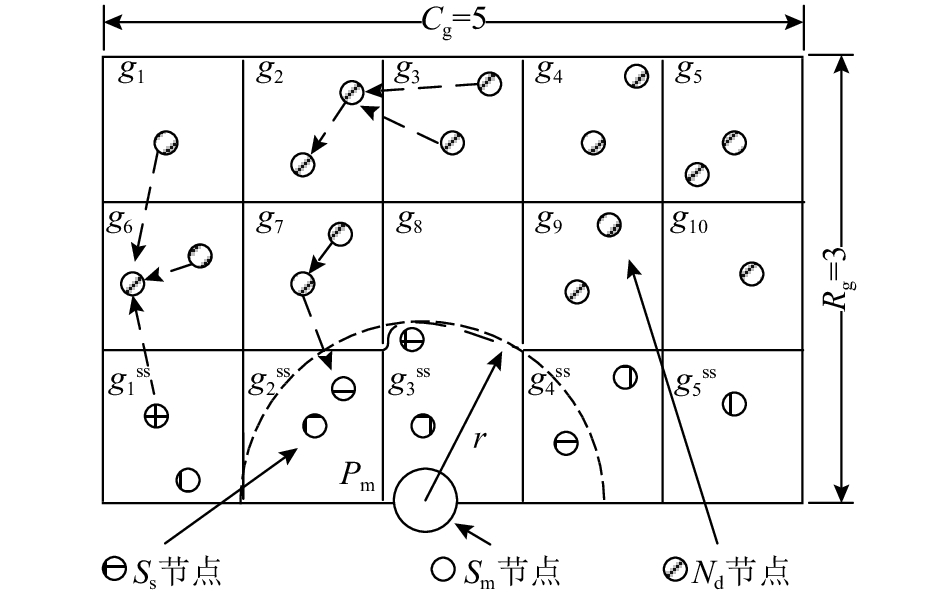
在Pm附近能与Sm进行单跳通信的Nd同时成为静态汇聚节点Ss,Ss的总个数为nss. 每个Nd节点以p bits/s生成数据,并且按照数据上报周期tint,通过多跳通信的方式将信息传输到某个可以到达的Ss节点,当Sm经过该Ss节点时,收集缓存的所有数据信息. 由于所有节点为随机部署,全体节点之间具有不完备的连通性. Nd节点与Ss节点之间的匹配关系决定了数据包上报的路径以及参与数据包中继的Nd节点. 对于Nd节点而言,选择不同的Ss节点作为数据包的目标节点,影响Ss节点的能量消耗均衡性,不同的数据包中继跳数影响全网消耗的总能量. 对于整个网络的数据采集性能和能量有效性而言,Nd节点与Ss节点的匹配选择的合理性是至关重要的. 系统模型如图1所示.
|
图 1 系统模型与图形划分描述 Fig. 1 System model and graphic description |
图论(graph theory)可以用于无线传感器网络的问题分析[17, 19]. 为了适应Sm受限移动性所带来的分层网络特性,将A均匀划分成Rg行×Cg列,共ng个同等大小的方格,如图1所示,并用gi表示任一方格,gi中包含ni个节点,
| ${n^{{\rm{ss}}}} = \sum\limits_{i = 1}^{{n^{\rm{ssg}}}} {n_i^{{\rm\;\, {ss}}}} = \sum\limits_{i = 1}^{{n^{\rm{ssg}}}} {\left| {g_i^{{\rm\;\, {ss}}}} \right|} .$ | (1) |
式中:nssg为Ss节点方格的总数. 其余节点方格称为Nd节点方格.
为了保证任意gi中的任意2个节点可以正常通信,在划分方格时,将所有方格的边长都设置为
经过图形划分,具有相同位置属性的节点被划分进同一个方格,与所有Ss的节点具有相近的路由属性. 将这些相同方格中的节点看成整体,并将Nd与Ss的匹配问题转换成gi与giss的匹配问题. gi,kdng为与giss匹配的第k个Nd节点方格,
| $n_i^{{\rm\;\, {dn}}} = \sum\limits_{k = 1}^{n_i^{{\rm\;\, {dng}}}} {\left| {g_{i,k}^{{\rm\;\, {dng}}}} \right|} .$ | (2) |
根据图论的基本概念,顶点V和边E的集合构成图G,且有
在大多数应用场景中,考虑数据节点中2个主要功能模块的能量消耗,即无线通信与数据处理. 对于数据发送节点,假定在单位时间1 s内,节点发送数据消耗的能量为
| ${E^{{\rm{node}}}} \approx e\left( {{q^{{\rm{tx}}}} + {q^{{\rm{rx}}}}} \right).$ | (3) |
式中:e为接收或发送每个数据包所消耗的能量,
每一个Nd节点方格都会有并且选择一个Ss节点方格作为内部Nd节点共同的数据发送目标. 根据式(2)和(3)可知,对于任一个Ss节点方格giss,内部所有Ss节点在数据周期tint中整体所消耗的能量为
| $E_i^{{\rm\;\, {ssg}}} = e\left( {2n_i^{{\rm \;\, {dn}}} + n_i^{{\rm\;\, {ss}}}} \right);\;i \in \left[ {1,\;{n^{{\rm {ssg}}}}} \right].$ | (4) |
为了表现Ss节点的能量均衡性,通过式(4)计算所有Ss节点的能耗方差值
| $D\left( {{E^{{\rm{ss}}}}} \right) \approx \frac{1}{{{n^{{\rm{ss}}}}}}\sum\limits_{i = 1}^{{n^{{\rm{ssg}}}}} {{{\left( {\frac{{E_i^{{\rm\;\, {ssg}}}}}{{n_i^{{\rm\;\, {ss}}}}} - \overline {{E^{{\rm{ss}}}}} } \right)}^2} \cdot n_i^{{\rm\;\, {ss}}}} .$ | (5) |
式中:
对于任一数据节点而言,一个数据周期内发送的数据包数量为
| $q_i^{{\rm\;\, {tx}}} = q_i^{{\rm\;\, {rx}}} + 1.$ | (6) |
由于全网数据包总数与路由总跳数直接相关,通过式(3)和(6)可以求得全网所有节点的总体能耗:
| ${E^{{\rm{total}}}} \approx e\sum\limits_{i = 1}^{{n^{\rm{g}}}} {\sum\limits_{k = 1}^{{n_i}} {\left( {2{h_{i,k}} + 1} \right)} } .$ | (7) |
式中:
全网能耗最优化问题的目标为在满足Ss节点能耗均衡的约束下,获得全网能耗Etotal的最小值:
| $\min \; \left( {{E^{{\rm{total}}}}} \right).$ | (8) |
满足约束条件:
| $\min \; \left( {D\left( {{E^{{\rm{ss}}}}} \right)} \right).$ | (9) |
在理想情况下,一个数据周期内的所有数据都能够被发送到与其匹配的Ss节点方格,Ss节点的能耗均衡性只与每个Ss节点承匹配的Nd节点数量有关. 通过式(2)可以将约束条件(9)变形为
| $\min \; \left[ {\frac{1}{{{n^{{\rm{ss}}}}}}\sum\limits_{i = 1}^{{n^{{\rm{ssg}}}}} {{{\left( {\frac{{n_i^{{\rm\;\, {dn}}}}}{{n_i^{{\rm\;\, {ss}}}}} - \overline {{n^{{\rm{dn}}}}} } \right)}^2} n_i^{{\rm\;\, {ss}}}} } \right].$ | (10) |
式中:
Sm路径受限的物联网应用中的能量优化目标即求得一种方格之间的匹配方式,使得每个Ss节点所承载的Nd节点数量均衡,同时使得全网数据上报路径跳数和最小. 将问题定义为分层能量优化(hierarchical optimization of energy efficiency,HOEE)问题.
为了直接准确地描述方格之间的匹配关系,使用二进制矩阵

|
图 2 方格匹配与相应的描述矩阵 Fig. 2 Grid match pattern and corresponding description matrixes |
mij为M矩阵的元素,下标i为Nd节点方格的序号,j为Ss节点方格的序号.
| $\sum\limits_{j = 1}^{{C_{\rm{g}}}} {{m_{ij}} = 1;\quad i \in \left[ {1, \;\left( {{R_{\rm{g}}} - 1} \right) {C_{\rm{g}}}} \right]} .$ | (11) |
式(11)表明每个Nd节点方格有且只选一个Ss节点方格作为目标.
hij为H矩阵的元素,值为第i个Nd节点方格中的全部Nd节点到第j个Ss节点方格的跳数和. 行向量V按序号顺序记录每个Nd节点方格中的节点总数. 具体部署场景下描述矩阵的生成结果如图2所示.
使用矩阵解决HOEE问题. 通过式(12)计算每个Ss节点方格所承载的Nd节点数量nidn,使用式(13)求得的行向量
| $n_i^{{\rm\;\, {dn}}} = \sum\limits_{j = 1}^{\left( {{R_{\rm{g}}} - 1} \right) {C_{\rm{g}}}} {{v_{1j}} {m_{ji}}} ,$ | (12) |
| ${{W}}_{1 \times {C_{\rm{g}}}} = {{V}}_{1 \times \left( {{R_{\rm{g}}} - 1} \right) {C_{\rm{g}}}} {{M}}_{\left( {{R_{\rm{g}}} - 1} \right) {C_{\rm{g}}} \times {C_{\rm{g}}}}.$ | (13) |
通过式(12)和(13),将约束条件(10)变形为
| $\min \; \left[ {\frac{1}{{{C_{\rm{g}}}}}{{\sum\limits_{i = 1}^{{C_{\rm{g}}}} {\left( {{w_{1i}} - \overline w } \right)^2}}}} \right].$ | (14) |
式中:
将目标函数(8)中的无关常数略去,通过矩阵M的元素将其变形为
| $\min \; \left[ {\sum\limits_{i = 1}^{\left( {{R_{\rm{g}}} - 1} \right) {C_{\rm{g}}}} {\sum\limits_{j = 1}^{{C_{\rm{g}}}} {{m_{ij}} {h_{ij}}} } } \right].$ | (15) |
通过目标函数(15)和约束条件(11)和(14)求解HOEE问题.
3.2 提出的算法HOEE是带有组合优化的NP难(non-deterministic polynomial hard)问题[23],采用遗传算法来寻找HOEE问题的最优解.
3.2.1 编码与种群初始化使用二进制描述矩阵M作为种群个体染色体基因信息,目标函数(15)表现个体的适应度:
| $f = \sum\limits_{i = 1}^{\left( {{R_{\rm{g}}} - 1} \right) {C_{\rm{g}}}} {\sum\limits_{j = 1}^{{C_{\rm{g}}}} {{m_{ij}} {h_{ij}}} } .$ | (16) |
使用约束条件(14)表现个体的不适应度:
| ${\rm{uf}} = \frac{1}{{{C_{\rm{g}}}}}{\sum\limits_{i = 1}^{{C_{\rm{g}}}} {\left( {{w_{1i}} - \overline w } \right)} ^2}.$ | (17) |
初始种群包含nga个不同的个体,生成遵循约束条件(11)和下述规则,每个Nd节点方格在选择Ss节点方格进行匹配时,只会在可以到达的目标中随机选取,避免出现不可行解,加快算法收敛.
3.2.2 选择算法图论的描述方法简化了HOEE问题的计算复杂度,采用简单的父代选择算法,选择种群中适应度第2和第3小的2个个体进行交叉运算. 既可以保护种群最优的个体,又可以保证进化出来的子代个体的基因较优.
3.2.3 交叉与变异在HOEE问题中,将基因矩阵M的每一行看作一个基因片段. 父代个体在交叉时,只对相对位置的基因片段进行交换操作,避免产生不可行的子代解. p1、p2和c分别为父代1、父代2和产生的子代.
交叉算法基于父代的适应度f来完成. 计算2个父代个体的适应度f (p1)和f (p2),求出两者的比值. 在p1中随机定位
| $n_{_1}^{{\rm\; \,{cs}}} + n_{_2}^{{\rm\; \,{cs}}} = \left( {{R_{\rm{g}}} - 1} \right) {C_{\rm{g}}},$ | (18) |
| $\frac{{n_{_1}^{{\rm \; \,{cs}}}}}{{n_{_2}^{{\rm \; \,{cs}}}}} \approx \frac{{f({p_2})}}{{f\left( {{p_1}} \right)}}.$ | (19) |
两者关系由前面计算出的适应度f (p1)和f (p2)的比值得出. 适应度较低的父代个体将传递更多的基因信息给子代.
3.2.4 种群更新算法交叉变异操作完成后,新的个体产生,需要考虑是否需要更新种群.
将子代个体c的基因与种群中具有相同适应值和不适应值的个体进行逐位比对,判断产生的子代是否与已有个体完全相同,如果已经有完全相同的个体,抛弃c.
如果子代c得以保留,使用c的不适应度与种群中不适应度最大的个体plu进行比较. 当c的不适应度较小时,使用c取代plu;当c的不适应度与plu相等时,比较c与plu的适应度,如果c的适应度更优,用c取代plu,否则抛弃c;当c的不适应度较大时,抛弃c.
为了准确地判断算法收敛并结束迭代,在遗传算法中加入用于评估当前种群基因稳定性的阈值istable,当前种群在最近的istable次迭代后没有进行过更新,当前种群已经达到稳定,结束算法迭代. 合适的istable值可以减少遗传算法的计算时间,同时保证得到最优解的可行性.
4 基于图形划分的数据传递协议Sm节点具有充足的计算和存储能力,因此采用集中式算法. 每一个Nd节点中都维护了一个特殊路由表,用于记录其数据包可以到达的Ss方格的最短路径信息. 如果经过不同管道节点到达同一个Ss方格的路径具有相同的跳数,那么该路由表将记录所有的路由信息,以实现动态网关路由,降低管道节点的中继负荷. 基于图形划分的数据传递协议如下.
协议中每个接收到数据包Data_Pkt的节点都在自己的路由信息中查询目标Ss节点方格的序号. 如果该接收节点已经在该方格中,表明该数据包已经达到与其源节点匹配的Ss方格,接收节点简单处理并且缓存数据. 否则接收节点为Nd节点,在数据处理后继续中继该数据包. 协议中current_pipe_node通过动态轮询机制,使得当前节点在选择网关时避免连续使用同一个管道节点,实现管道节点的能耗均衡.
5 实验仿真通过实验验证HOEE数据采集策略的高效性. 在NS-3(Network Simulator-3)[24]中进行仿真实验,实验参数如表1所示.
将HOEE与SPT、MASP策略进行对比,后两者均被应用于固定轨迹的Sm节点数据采集应用场景中. 使用随机匹配RANDOM策略作为对比算法.
| 表 1 实验参数设置 Table 1 Values of experiment parameters |
根据以下几个指标对提出的数据采集策略进行有效性验证:网络寿命在应用场景中被定义为第一个Ss节点死亡的时间,或者是动态数据采集率低于一定阈值的时间;全网能耗水平(network energy efficiency,NEE)用于衡量整个网络在运作时对能量的消耗情况,单位为Joules/s;Ss节点负载均衡水平(static sink load equilibrium,SSLE)用于表示Ss节点的数据负载均衡水平,直接影响网络寿命和数据采集效率;节点死亡数用于记录在网络寿命终结时,能源已经枯竭的节点数量,表示数据采集策略对网络鲁棒性的影响.
5.1 HOEE对网络寿命的影响在随机部署分层系统中,节点的能耗水平受到节点所在拓扑位置的影响. 随机部署会导致部分Nd节点过早地枯竭. 采用第一个死亡节点的寿命作为网络寿命的方式不能准确评估具有移动性受限汇聚节点的物联网网络寿命.
系统模型表现出分层特性,作为层次结构中最底层的Ss节点的能量消耗水平与在网络中的重要性会远高于其他Nd节点. 将第一个能量耗尽的Ss节点的网络寿命作为网络寿命,则新的问题是在Ss节点死亡之前,大量Nd节点可能因为极端部署的情况枯竭,并且阻碍上报汇集数据,降低动态数据采集率,以及Ss节点的负荷,造成网络寿命大幅延长的假象. 设置较高的动态数据采集率的阈值补充定义网络寿命,阈值设置为90%,保证较高的网络数据采集性能.
|
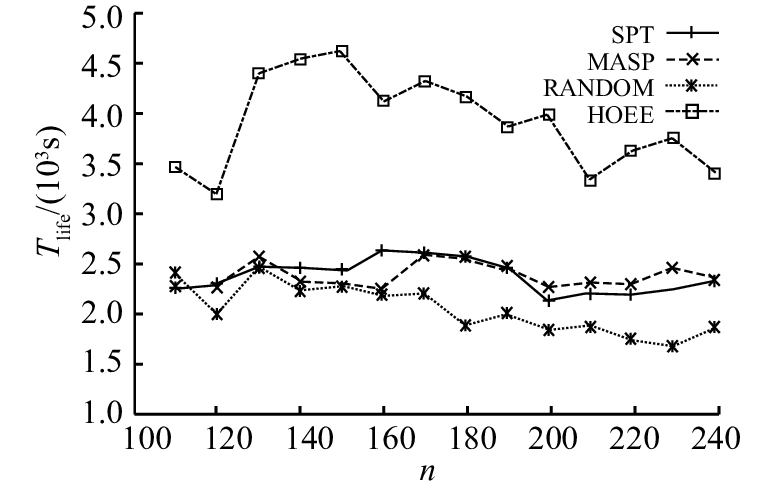
图 3 SPT、MASP、RANDOM和HOEE策略下网络寿命仿真结果对比 Fig. 3 Comparison of simulation results of network lifetime with SPT, MASP, RANDOM and HOEE schemes |
图3所示结果表明,HOEE网络寿命指标表现出明显的优越性,网络可以在较高的动态数据采集率下持续工作更长的时间. HOEE策略对Ss节点的能耗均衡起到了预期的优化作用. 图3中Tlife表示网络寿命.
5.2 HOEE对Ss节点能量有效性的影响为了衡量Ss节点的能量有效性,采用SSLE指标来表示所有Ss节点的能量均衡性. 如果匹配结果导致较高的SSLE,认定Ss节点在整体上具有较差的能量均衡性,导致网络寿命下降,因为个别Ss节点会因为数据业务量的分配不均导致过多地发送与接收数据包,加速Ss节点的能量消耗.
|
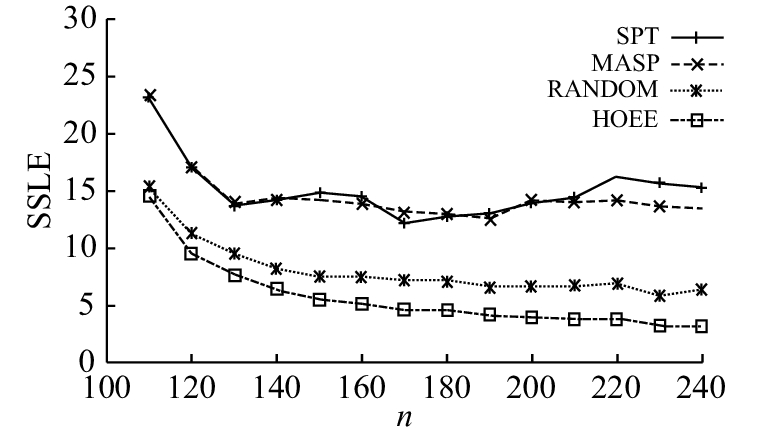
图 4 SPT、MASP、RANDOM和HOEE策略下静态汇聚节点负载均衡水平仿真结果对比 Fig. 4 Comparison of simulation results of static sink load equilibrium with SPT, MASP, RANDOM and HOEE schemes |
将Ss节点所承载的Nd节点数量的方差作为SSLE进行比较. 图4表明HOEE得益于启发式算法的近似最优匹配结果,Ss节点的负载得以均衡,延长工作时长,提高网络寿命,并且保证数据采集效率.
5.3 HOEE对全网能耗水平的影响全网能耗水平NEE代表整个网络在单位时间(1 s)内所消耗的能量(Joules),反映方格匹配算法的合理性与有效性. 如果匹配算法为Nd节点选择的目标方格不合理,导致大量不合理的数据包中继,NEE相应提高,网络数据采集效率受到负面影响,如RANDOM匹配策略.
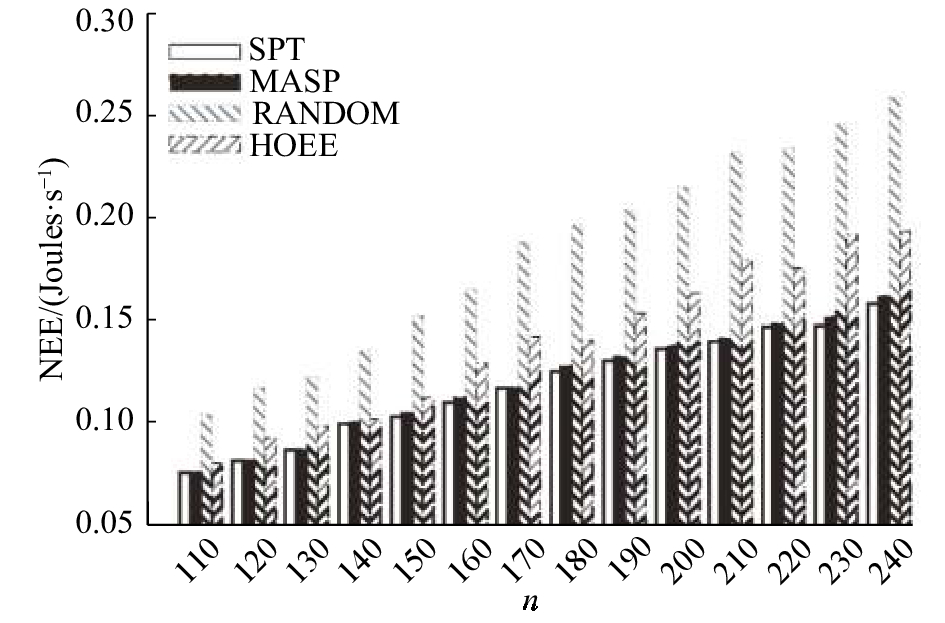
图5所示的结果表明,HOEE可以在提高网络寿命,保证数据采集效率和Ss节点负载均衡的前提下,达到与MASP和SPT接近的NEE水平,远优于RANDOM策略. HOEE虽然略微提高了全网数据包中继的次数,但是能够保证在其他重要指标上的优越性.
|
图 5 SPT、MASP、RANDOM和HOEE策略下全网能耗水平仿真结果对比 Fig. 5 Comparison of simulation results of NEE with SPT, MASP, RANDOM and HOEE schemes |
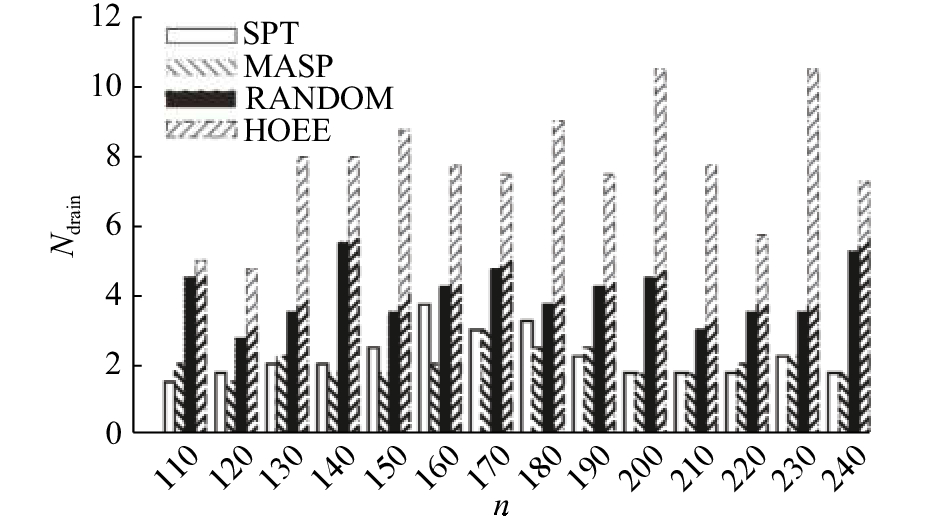
图6所示结果表明,在网络寿命终结时,HOEE可以容忍相对较高的Nd节点死亡数量,用Ndrain表示. 根据网络寿命的定义,HOEE使得网络的动态数据采集效率高于设置的阈值90%. 由于MASP和SPT没有对Ss节点能耗均衡性进行优化和重点考虑,Ss节点过早地死亡.
|
图 6 SPT、MASP、RANDOM和HOEE策略下节点枯竭数量仿真结果对比 Fig. 6 Comparison of simulation results of drained node amount with SPT, MASP, RANDOM and HOEE schemes |
由于RANDOM策略产生大量不合理和冗余的数据包中继,导致Nd节点大规模死亡,严重降低数据采集的效率和总量. HOEE增强了网络的鲁棒性,并且将数据采集效率维持在阈值90%以上.
6 结 语在物联网应用中,利用具有受限移动性的汇聚节点可以有效地提高数据信息的采集效率. 但是,随着应用场景的复杂化,网络能量有效性的提高和数据采集效率的保证问题依然具有挑战性. 移动性受限汇聚节点影响到网络拓扑结构,随机部署使得拓扑结构变得更加复杂. 基于图论的基本思想提出了分层优化能量有效性的数据采集策略,解决分层拓扑系统模型下的静态汇聚节点Ss的能量有效性问题.
利用图形划分方法对监控区域进行重新描述,降低系统的复杂性,为后续节点匹配算法提供模型基础. 针对系统模型的分层特性,利用启发式算法得到近似最优的节点方格匹配结果,使得Ss节点之间的负载差异最小化. 基于图形划分操作识别相邻方格之间的管道节点,基于管道节点建立方格之间动态的数据包中继协议,使得网络中同层高负载的Nd节点的能耗得以均衡化,避免个别管道节点因为不均衡的数据包中继数量而快速枯竭. 在NS-3仿真平台对提出的算法和通信协议进行验证,实验结果证明HOEE策略能够有效地提升网络寿命,提升网络的可用性,同时兼顾数据信息的采集效率. 在分层系统模型下,HOEE使得不同层面的节点能耗得以均衡化,全网的能耗水平得以降低,数据采集效率维持在较高可用水平.
研究中还发现,即使在HOEE策略下,网络寿命终结时,大量低负荷节点的剩余能量还很高,说明节点的能量没有得到合理的利用. 为此,将在今后的研究中设计高效的无线信息与能量同传方法,将低负荷节点的冗余能量合理转移到高负荷节点处,最大化利用现有能量资源,延长网络寿命,提高节点能效.
| [1] |
CHANG C, LOKE S W, DONG H, et al. An energy-efficient inter-organizational wireless sensor data collection framework [C] // Proceedings of 2015 IEEE International Conference on Web Services. New York: IEEE, 2015: 639-646 http://dro.deakin.edu.au/view/DU:30103537
|
| [2] |
BUTUN I, MORGERA S, SANKAR R. A survey of intrusion detection systems in wireless sensor networks[J]. IEEE Communications Surveys and Tutorials, 2014, 16(1): 266-282. DOI:10.1109/SURV.2013.050113.00191 |
| [3] |
SONG W, HUANG R, XU M, et al. Design and deployment of sensor network for real-time high-fidelity volcano monitoring[J]. IEEE Transactions on Parallel and Distributed Systems, 2010, 21(11): 1658-1674. |
| [4] |
LEE H C, CHO C Y, KING C T, et al. Design and implementation of non-autonomous mobile wireless sensor for debris flow monitoring [C]// Proceedings of 6th International Conference on Mobile Adhoc and Sensor Systems. Macau: IEEE, 2009: 1062-1064 https://www.computer.org/csdl/proceedings/mass/2009/5114/00/05337008-abs.html
|
| [5] |
GU Y, REN F J, JI Y S, et al. The evolution of sink mobility management in wireless sensor networks: a survey[J]. IEEE Communications Surveys and Tutorials, 2016, 18(1): 507-524. |
| [6] |
RESTUCCIA F, DAS S K. Lifetime optimization with QoS of sensor networks with uncontrollable mobile sinks[C] // Proceedings of 16th International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMaM). Boston: IEEE, 2015: 1-9 http://doi.ieeecomputersociety.org/10.1109/WoWMoM.2015.7158130
|
| [7] |
SMEETS H, SHIH C Y, ZUNIGA M, et al. Trainsense: A novel infrastructure to support mobility in wireless sensor networks [C] // Proceedings of European Conference on Wireless Sensor Networks. Ghent: Springer, 2013: 18-33 http://link.springer.com/content/pdf/10.1007/978-3-642-36672-7_2.pdf
|
| [8] |
HUANG H L, SAVKIN A V. Optimal path planning for vehicle collecting data in a wireless sensor network[C] // Proceedings of 35th Chinese Control Conference(CCC). Chengdu: IEEE, 2016: 8460-8463 https://www.researchgate.net/publication/308077603_Optimal_Path_Planning_for_a_Vehicle_Collecting_Data_in_a_Wireless_Sensor_Network
|
| [9] |
HULL B, BYCHKOVSKY V, ZHANG Y, et al. Cartel: a distributed mobile sensor computing system [C] // Proceedings of 4th International Conference on Embedded Networked Sensor Systems. Boulder: ACM, 2006: 125-138 http://dl.acm.org/citation.cfm?id=1182821
|
| [10] |
ZHANG Y Q, ZHOU Z B, ZHAO D, et al. Graph-based mechanism for scheduling mobile sensors in time-sensitive WSNs applications[J]. IEEE Access, 2017, 5: 1559-1569. |
| [11] |
徐新黎, 皇甫晓洁, 王万, 等. 基于无线充电的Sink轨迹固定WSN路由算法[J]. 仪器仪表学报, 2016, 37(3): 570-578. XU Xin-li, HUANGFU Xiao-jie, WANG Wan, et al. Wireless charging routing algorithm in WSN with a path-fixed sink[J]. Chinese Journal of Scientific Instrument, 2016, 37(3): 570-578. DOI:10.3969/j.issn.0254-3087.2016.03.013 |
| [12] |
彭舰, 徐飚, 孙彦清, 等. 基于Sink轨迹固定的异构延迟容忍网络数据传输机制[J]. 北京邮电大学学报, 2014, 37(3): 53-57. PENG Jian, XU Biao, SUN Yan-qing, et al. Data transmission algorithm based on path-fixed sink inheterogeneous delay tolerant mobile sensor networks[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(3): 53-57. |
| [13] |
GAO S, ZHANG H K, DAS S K. Efficient data collection in wireless sensor networks with path-constrained mobile sinks[J]. IEEE Transactions on Mobile Computing, 2011, 10(4): 592-608. |
| [14] |
GALLEGOS A, NOGUCHI T, IZUMI T, et al. Simulation study of maximum amount shortest path routing in wireless sensor networks using NS-3 [C] // Proceedings of 2016 Eighth International Conference on Ubiquitous and Future Networks (ICUFN). Vienna: IEEE, 2016: 5-8 http://ieeexplore.ieee.org/document/7537016/
|
| [15] |
SHARMA U, RAMA KRISHNA C, SHARMA T P. An efficient mobile data collector based data aggregation scheme for wireless sensor networks [C] // Proceedings of 2015 IEEE International Conference on Computational Intelligence and Communication Technology. Delhi: IEEE, 2015: 292-298
|
| [16] |
HAN G J, A J F, ZHANG C F, et al. A survey on mobile anchor node assisted localization in wireless sensor networks[J]. IEEE Communications Surveys and Tutorials, 2016, 18(3): 2220-2243. |
| [17] |
ZHOU Z, DU C, SHU L, et al. An energy balanced heuristic for mobile sink scheduling in hybrid WSNs[J]. IEEE Transactions on Industrial Informatics, 2016, 12(1): 28-40. DOI:10.1109/TII.2015.2489160 |
| [18] |
NAKE N B, CHATUR P N. An energy efficient grid based routing in mobile sink based wireless sensor networks[C] // Proceedings of 2nd International Conference on Science Technology Engineering and Management. Dubai: IEEE, 2016: 1-5 http://ieeexplore.ieee.org/document/7560872/
|
| [19] |
LIU Q, ZHANG K, SHEN J, et al. Glrm: an improved grid-based load-balanced routing method for WSN with single controlled mobile sink [C] // Proceedings of 2016 18th International Conference on Advanced Communication Technology (ICACT). Paris: IEEE, 2016: 34-38 http://ieeexplore.ieee.org/document/7423264/
|
| [20] |
YUN Y S, XIA Y, BEHDANI B, et al. Distributed algorithm for lifetime maximization in a delay-tolerant wireless sensor network with a mobile sink[J]. IEEE Transactions on Mobile Computing, 2013, 12(10): 1920-1930. |
| [21] |
HASAN M Z, AI-RIZZO H, GUNAY M. Lifetime maximization by partitioning approach in wireless sensor networks[J]. Eurasip Journal on Wireless Communications and Networking, 2017:15. |
| [22] |
CHEN H, LI Y, REBELATTO J L, et al. Harvest-then-cooperate: wireless-powered cooperative communications[J]. IEEE Transactions on Signal Processing, 2015, 63(7): 1700-1711. DOI:10.1109/TSP.2015.2396009 |
| [23] |
ONCAN T. A survey of the generalized assignment problem and its applications[J]. Information Systems and Operational Research, 2007, 45(3): 123-142. |
| [24] |
LACAGE M, CARNEIRO G. Network Simulator-3 [CP/OL]. [2017-11-20] . https://www.nsnam.org
|



