2. 工业与信息化部第五研究所, 广东 广州 510000;
3. 中国科学院 长春光学精密机械与物理研究所, 吉林 长春 130033
2. China Electronic Product Reliability and Environmental Testing Research Institute, Guangzhou 510000, China;
3. Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China
多旋翼无人飞行器已广泛应用于军事和民用领域中, 全球各地飞行器的安全事故随之剧增, 带来了重大的经济损失, 甚至是地面人员伤亡.对于无人飞行器的容错控制技术研究, 成为提高飞行器的安全性和可靠性的迫切任务[1-3].
容错控制技术已在航空航天的控制领域中得到了广泛的应用[4-8].该技术不仅可以有效地补偿故障对飞行器安全性和稳定性的影响, 而且能够使得飞行器控制系统保持良好的控制品质.通常, 飞行器的容错控制系统包括故障检测与隔离和控制自重构两个环节.针对多旋翼飞行器的相关研究工作, 大多集中在故障条件下的控制自重构问题[9-12];对于飞行器执行单元的故障检测与隔离, 特别是故障进行分类的检测与隔离和控制自重构的研究较少.故障的检测与隔离是构建飞行器容错控制系统的重要环节.故障检测与隔离环节能够快速检测到故障的发生, 确定故障发生的位置并将其隔离.目前, 针对故障检测与隔离问题的相关研究, 主要采用基于观测器的设计方法, 取得了较好的实际效果[13-17].
本文针对Hex-Rotor无人飞行器执行单元的故障检测和自重构问题, 在建立故障条件下执行单元的升力模型的基础上, 将执行单元的故障分为失效性故障和增益性故障两大类.基于扩展Kalman滤波算法, 设计出一组故障观测器, 实现各个执行单元故障的快速、准确检测, 确定故障的发生位置与类型.此外, 在故障检测与隔离之后, 设计基于多故障分类的自重构控制算法, 可以利用故障观测器的输出信号, 对不同故障进行相应的自重构, 保证飞行的安全性和可靠性.
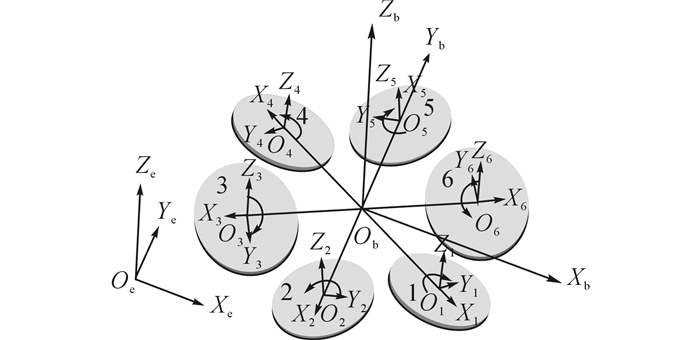
1 Hex-Rotor无人飞行器简介Hex-Rotor无人飞行器是在不显著增加重量的前提下, 对常规平面多旋翼无人飞行器的结构进行改进的一种多旋翼无人飞行器[18].这种结构配置在提高飞行器续航能力及带载能力的同时, 更能够增强飞行器控制偏航通道的力矩.Hex-Rotor无人飞行器的结构原理如图 1所示.
|
图 1 Hex-Rotor无人飞行器结构原理图 Fig. 1 Structure schematic of Hex-Rotor UAV |
从图 1可以看出, Hex-Rotor无人飞行器具有对称性.6个等长碳纤维连杆处于同一平面上, 均匀分布于飞行器中心点周围, 连杆末端垂直安装6组执行单元.机体坐标系ObXbYbZb的原点Ob位于飞行器的质心上, 该坐标系满足右手直角坐标系.惯性坐标系OeXeYeZe选择“北西天”坐标系, 原点Oe与飞行器起飞位置时机体坐标系的原点Ob重合.飞行器每个旋翼电机的转动轴均与ObZb成10°的倾角, 且相邻两个旋翼电机的转动轴的指向相反.关于原点Ob成中心对称关系的旋翼位于同一个平面上.
Hex-Rotor无人飞行器的原型机如图 2所示.

|
图 2 Hex-Rotor无人飞行器原型机 Fig. 2 Prototype of Hex-Rotor UAV |
原型机的物理参数如表 1所示.
| 表 1 Hex-Rotor原型机物理参数 Table 1 Physical parameters of prototype |
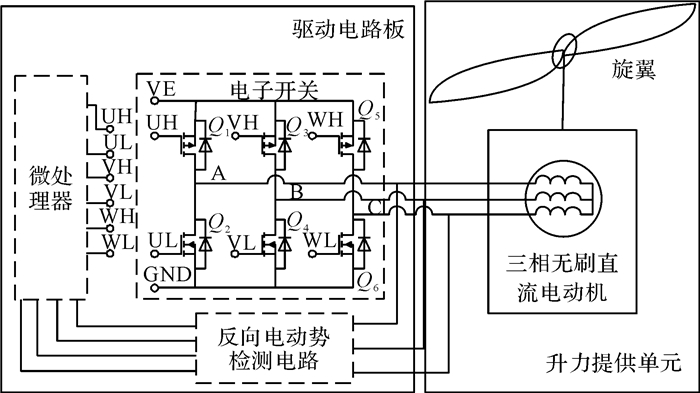
Hex-Rotor无人飞行器的执行单元不同于传统意义上的电动执行器, 由升力提供单元(旋翼+电机)与驱动电路板组成.执行单元的结构如图 3所示.
|
图 3 执行单元的结构图 Fig. 3 Block diagram of execution unit |
在飞行器的实际飞行中, 执行单元的工作负荷大, 由大负荷工作产生较高的工作温度, 加速了电子器件的老化;由高速旋转的旋翼电机引起的振动, 使得机械连接结构极易受损变形.相对于飞行器的其他单元, 执行单元的故障更易发生.Hex-Rotor无人飞行器具有6个执行单元, 这在一定程度上大大增加了故障发生的可能性.对原型机在飞行作业过程中发生过的执行单元故障进行总结, 得到执行单元的常见故障, 如表 2所示.
| 表 2 执行单元常见故障 Table 2 Common fault of execution units |
为了对故障进行分类, 引入执行单元的升力模型.通常飞行器执行单元提供的升力模型[19]可以描述为
| $ f = k{\mathit{\Omega }^2}. $ | (1) |
式中:f为由执行单元所提供的升力, k为执行单元的升力因子, Ω为旋翼电机的转速.当执行单元发生故障时, f通常会表现为明显减小甚至是接近于零的现象.由式(1)可知, 执行单元发生故障, 会表现为2种情况, 即Ω无法达到期望转速或升力因子k明显小于正常值.鉴于此, 将执行单元的故障划分为增益性故障和失效性故障两大类.
1) 执行单元的增益性故障通常表现为在Ω相同的情况下, k明显小于正常值, 进而执行单元所提供的升力呈现减小的趋势.
引入损伤比例系数βi, 且0 < βi < 1, 其中i表示第i个执行单元, 且i=1, 2, …, 6, 则增益性故障的模型可以描述为
| $ \begin{array}{l} \\ {f_i}\left( t \right) = \left( {1 - {\beta _i}} \right){{\bar k}_i}\mathit{\Omega }_i^2. \end{array} $ | (2) |
式中:fi(t)为第i个执行单元在增益性故障条件下实际提供的升力, Ωi为第i个旋翼电机的转速, ki为在室内标准大气压下实测的升力因子.表 2中, 旋翼故障中的旋翼面破损、旋翼松浮动及连接件受损均属于该类故障.
考虑到在实际飞行中, 实测的升力因子受海拔高度、风速、风向、空气密度等环境因素的影响.结合实际的测试经验可知, 当βi < 0.15时, 升力因子的波动是由环境干扰引起;当0.15 < βi < 1时, 执行单元发生增益性故障.
2) 执行单元发生失效性故障通常表现为在正常飞行过程中, 执行单元突然不再提供升力, 丧失了升力的提供能力, 即f=0.表 2中, 驱动电路板故障、旋翼电机故障以及旋翼脱落均属于该类故障.
于是, 失效性故障的模型可以描述为
| $ {f_i}\left( t \right) = 0. $ | (3) |
根据上述分析, 得到Hex-Rotor无人飞行器执行单元的故障模型为
| $ {f_i}\left( t \right) = \left( {1 - {\beta _i}} \right){{\bar k}_i}\mathit{\Omega }_i^2;i = 1,2, \cdots ,6. $ | (4) |
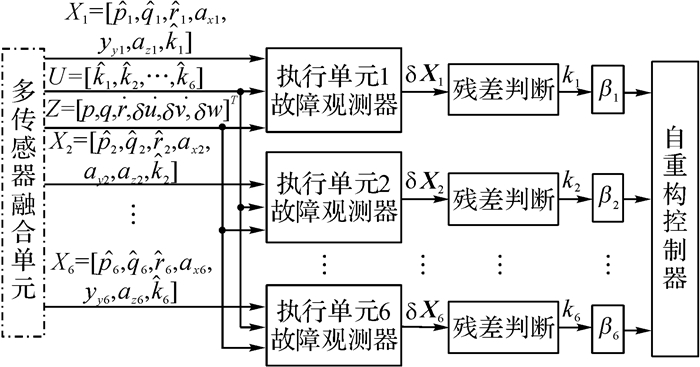
依据执行单元的故障分类, 对执行单元FFD系统进行设计, FDD系统的框图如图 4所示.可以看出, 故障观测器的状态转移矩阵与控制输入矩阵通过飞行器的动力学模型得到, 测量矩阵由多传感器融合单元获取, 实现对旋翼的升力因子的在线估计.基于扩展卡尔曼算法(extended Kalman filter, EKF)的故障观测器(fault observer, FOB)通过在线估计对应执行单元的升力因子, 实现失效性故障与增益性故障的检测.当执行单元故障发生时, 采用不同故障激活对应的自重构算法, 有效地保证飞行器系统的安全.
|
图 4 执行单元的故障检测与诊断系统架构 Fig. 4 Architecture of FDD system |
根据Hex-Rotor无人飞行器的结构特点, 忽略反扭力矩对滚转、俯仰通道控制力矩的影响以及旋翼的转动惯量矩.将各个旋翼转速当作飞行器动力学模型的输入, 得到Hex-Rotor无人飞行器的动力学模型如下:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\dot \eta }} = \mathit{\boldsymbol{T\omega }},\\ \mathit{\boldsymbol{J\dot \omega }} = - \mathit{\boldsymbol{S}}\left( \mathit{\boldsymbol{\omega }} \right)\mathit{\boldsymbol{J\omega }} + \mathit{\boldsymbol{M}}. \end{array} \right\} $ | (5) |
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\dot P}} = {\mathit{\boldsymbol{R}}_{{\rm{b}} - {\rm{e}}}}\mathit{\boldsymbol{V}},\\ \mathit{\boldsymbol{\dot V}} = - \mathit{\boldsymbol{S}}\left( \mathit{\boldsymbol{\omega }} \right)\mathit{\boldsymbol{V}} + {\rm{diag}}\left[ {\frac{1}{m},\frac{1}{m},\frac{1}{m}} \right]\mathit{\boldsymbol{F}}. \end{array} \right\} $ | (6) |
式中:η为姿态欧拉角速度,
Hex-Rotor无人飞行器的状态方程与观测方程为
| $ \mathit{\boldsymbol{\dot X}} = f\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{U}}} \right) + \mathit{\boldsymbol{W}}, $ | (7) |
| $ \mathit{\boldsymbol{Z}} = h\left( \mathit{\boldsymbol{X}} \right) + \mathit{\boldsymbol{V}}. $ | (8) |
式中:X为系统的状态向量,
| $ \left. \begin{array}{l} {a_x} = \left( {\dot u - rv + qw} \right) - G\sin \theta /m,\\ {a_y} = \left( {\dot v - pw + ru} \right) + G\cos \theta \sin \phi /m,\\ {a_z} = \left( {\dot w - qu + pv} \right) + G\cos \theta \cos \phi /m, \end{array} \right\} $ | (9) |
G为当地的重力加速度.
对式(7)、(8)进行离散化处理, 利用Taylor展式进行线性化, 有
| $ {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}{\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k,k - 1}}\left( {{\mathit{\boldsymbol{U}}_{k - 1}} + {\mathit{\boldsymbol{W}}_{k - 1}}} \right), $ | (10) |
| $ {\mathit{\boldsymbol{Z}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{V}}_k}. $ | (11) |
式中:Hk=diag[1, 1, …, 1], Zk来自于陀螺仪和加速度计的测量值, Ts为采样时间间隔, Φk, k-1为离散转移矩阵, Γk, k-1为离散控制输入矩阵.
将
| $ {{\mathit{\boldsymbol{\bar X}}}_i} = \left[ \begin{array}{l} {X_i}\\ {{\hat k}_i} \end{array} \right]. $ | (12) |
Xi的状态方程如下:
| $ {{\mathit{\boldsymbol{\bar X}}}_{i,k}} = {{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{i,k,k - 1}}{{\mathit{\boldsymbol{\bar X}}}_{i,k - 1}} + {{\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}}_{i,k,k - 1}}\left( {{\mathit{\boldsymbol{U}}_k} + {{\mathit{\boldsymbol{\bar W}}}_{k - 1}}} \right), $ | (13) |
| $ {\mathit{\boldsymbol{Z}}_{i,k}} = {{\mathit{\boldsymbol{\bar H}}}_{i,k}}{{\mathit{\boldsymbol{\bar X}}}_{i,k}} + {\mathit{\boldsymbol{V}}_k}. $ | (14) |
式中:增广的离散转移矩阵为
| $ {{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{i,k,k - 1}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}}&{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k,k - 1}^{\left( j \right)}}\\ 0&1 \end{array}} \right]. $ | (15) |
Γk, k-1(j)为控制输入矩阵Γk, k-1的第j列.增广的控制输入矩阵为
| $ {{\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}}_{i,k,k - 1}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k,k - 1}^{\left( {0,j} \right)}}\\ 0 \end{array}} \right]. $ | (16) |
其中, Γk, k-1(0, j)为控制输入矩阵Γk, k-1的第j列清零后的矩阵.增广的测量矩阵为
| $ {{\mathit{\boldsymbol{\bar H}}}_{i,k}} = \left[ {\begin{array}{*{20}{c}} {{H_k},}&0 \end{array}} \right]. $ | (17) |
采用S加权衰减记忆卡尔曼滤波算法[20], 得到执行单元i的故障观测器:
| $ \left. \begin{array}{l} {{\mathit{\boldsymbol{\hat X}}}_{k\left| {k - 1} \right.}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k\left| {k - 1} \right.}}{{\mathit{\boldsymbol{\hat X}}}_{k - 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k,k - 1}}{{\mathit{\boldsymbol{\dot X}}}_{k - 1}},\\ {{\mathit{\boldsymbol{\hat X}}}_k} = {{\mathit{\boldsymbol{\hat X}}}_{k\left| {k - 1} \right.}} + {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{Z}}_k} - {\mathit{\boldsymbol{H}}_k}{{\mathit{\boldsymbol{\hat X}}}_{k\left| {k - 1} \right.}}} \right),\\ {\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_k}\mathit{\boldsymbol{H}}_k^{\rm{T}}{\left[ {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}} \right]^{ - 1}},\\ {\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}} = S{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k\left| {k - 1} \right.}}{\mathit{\boldsymbol{P}}_{k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k\left| {k - 1} \right.}^{\rm{T}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k,k - 1}}{\mathit{\boldsymbol{Q}}_{k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k,k - 1}^{\rm{T}},\\ {\mathit{\boldsymbol{P}}_k} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{H}}_k}} \right){\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{H}}_k}} \right)^{\rm{T}}} + {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{R}}_k}\mathit{\boldsymbol{K}}_k^{\rm{T}} \end{array} \right\}. $ | (18) |
对通过故障观测器得到的残差向量δXi(i=1, 2, …, 6)取二阶范数‖δXi‖2, 判断当前观测值
| $ {\beta _i} = 1 - {{\hat k}_i}/{{\bar k}_i}. $ | (19) |
依据定义的执行单元故障模型, 结合式(19)得到的βi, 自重构控制器将对该执行单元是否有故障发生及发生故障的类型进行判断.在故障发生的第一时间, 进行相应的容错重构;无故障发生时, 则对控制器中的相关参数进行修正.
在通过FDD系统得到的观测信息, 经由式(19)求解得到各个执行单元的损伤比例系数βi之后, 定义如下损伤比例系数矩阵β, 用以表示估计得到的
| $ \mathit{\boldsymbol{\beta }} = {\rm{diag}}\left[ {1 - {\beta _1},1 - {\beta _2}, \cdots ,1 - {\beta _6}} \right]. $ | (20) |
考虑到飞行器通常处于小角度运动状态, 认为姿态角变化率
| $ \mathit{\boldsymbol{\ddot \eta = }}F\left( {\mathit{\boldsymbol{\dot \eta }},t} \right) + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}_\beta }{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^2}. $ | (21) |
式中:Kβ=βK, 其中K=diag [k1, …, k6]T为各执行单元在室内标准大气压下测得的升力因子组成的矩阵;η为姿态角, η=[ϕ, θ, ψ]T;Ω2为旋翼转速向量, Ω2=[Ω12, Ω22, Ω32, Ω42, Ω52, Ω62]T;B为控制输入矩阵,
| $ \mathit{\boldsymbol{B}} = \\ \left[ {\begin{array}{*{20}{c}} { - \frac{{l\cos \gamma }}{{2{I_x}}}}&{ - \frac{{l\cos \gamma }}{{{I_x}}}}&{ - \frac{{l\cos \gamma }}{{2{I_x}}}}&{\frac{{l\cos \gamma }}{{2{I_x}}}}&{\frac{{l\cos \gamma }}{{{I_x}}}}&{\frac{{l\cos \gamma }}{{2{I_x}}}}\\ { - \frac{{\sqrt 3 l\cos \gamma }}{{2{I_y}}}}&0&{\frac{{\sqrt 3 l\cos \gamma }}{{2{I_y}}}}&{\frac{{\sqrt 3 l\cos \gamma }}{{2{I_y}}}}&0&{ - \frac{{\sqrt 3 l\cos \gamma }}{{2{I_y}}}}\\ {\frac{{l\sin \gamma + {\chi _1}\cos \gamma }}{{{I_z}}}}&{ - \frac{{l\sin \gamma + {\chi _2}\cos \gamma }}{{{I_z}}}}&{\frac{{l\sin \gamma + {\chi _3}\cos \gamma }}{{{I_z}}}}&{ - \frac{{l\sin \gamma + {\chi _4}\cos \gamma }}{{{I_z}}}}&{\frac{{l\sin \gamma + {\chi _5}\cos \gamma }}{{{I_z}}}}&{ - \frac{{l\sin \gamma + {\chi _6}\cos \gamma }}{{{I_z}}}} \end{array}} \right]. $ |
以执行单元1为例, 其他执行单元处理方法与之类似.假设执行单元1发生增益性故障, 采用伪逆算法求解各旋翼的期望转速, 即
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{d}}^2 = {{\mathit{\boldsymbol{\hat K}}}^{ - 1}}{\left( {{\mathit{\boldsymbol{B}}_{4 \times 6}}} \right)^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{\rm{d}}}}\\ {{F_z}} \end{array}} \right]. $ | (22) |
式中:B4×6为控制输入矩阵B的增广矩阵;Md=[Mx, My, Mz]T为保持姿态稳定的期望控制力矩;Fz为期望的升力.代入表 1的相关参数, 可得
依据式(22), 可以求得各旋翼的期望转速Ωd2=[Ω1.d2, …, Ω6.d2]T.在执行单元1的当前转速无法达到Ω1.d2, 只能保持最高转速
| $ {{\tilde k}_1} = \mathit{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \Omega } }_1^2{k_i}/\mathit{\Omega }_{1.{\rm{d}}}^2. $ | (23) |
随着β1的逐渐增大,
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot V}}}_2} = - \left\| {{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}} \right\|\left( {\left\| {\mathit{\boldsymbol{H\alpha }}} \right\| - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \rho } \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \xi } \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \rho } \left\| {\mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{z}}_2} - \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{z}}_1}} \right)} \right. + } \right.\\ \;\;\;\;\;\;\left. {\left. {\mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{\dot \eta }},t} \right) - {{\mathit{\boldsymbol{\ddot \eta }}}_{\rm{d}}} + \mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\dot z}}}_1}} \right\|} \right) - {\mathit{\boldsymbol{Z}}^{\rm{T}}}\mathit{\boldsymbol{QZ}} \le 0. \end{array} $ | (24) |
式中:H=diag[h1, h2, h3];α=[α1, α2, α3]T表示反演滑模控制器的设计参数;
根据失效性故障的定义可知, 当执行单元1发生失效性故障时, β1=1, 执行单元1失去升力的提供能力.此时, 增广矩阵B4×6奇异, 降阶后, 求得伪逆矩阵(B4×5)-1.引入表 1的相关参数得到:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat K}}}^{ - 1}}{\left( {{\mathit{\boldsymbol{B}}_{4 \times 5}}} \right)^{ - 1}} = \\ \;\;\;\left[ {\begin{array}{*{20}{c}} { - 0.179}&{ - 0.0619}&{ - 0.285}&{0.877}\\ { - 0.107}&{0.0619}&{0.853}&{0.877}\\ {0.143}&{0.248}&{ - 1.138}&0\\ {0.107}&{ - 0.0619}&{0.853}&{0.877}\\ {0.0357}&{ - 0.1857}&{ - 0.285}&{0.877} \end{array}} \right] \times {10^3}. \end{array} $ | (25) |
式(25)表明, 执行单元4的期望转速非常小并且可能为负.将B4×6修改为3×5的矩阵B3×5, 伪逆矩阵为(B3×5)-1, 有
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\left( 1 \right){\rm{,d}}}^2 = \mathit{\boldsymbol{\hat K}}_{\left( 1 \right)}^{ - 1}{\left( {{\mathit{\boldsymbol{B}}_{3 \times 5}}} \right)^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{M_x}}\\ {{M_y}}\\ {{F_z}} \end{array}} \right]. $ | (26) |
式中:Ω(1).d2=[Ω22, Ω32, Ω42, Ω52, Ω62]T,
为了避免修改后的B3×5在滚转与俯仰通道上的不对称性引起的控制器发散的问题, 须通过坐标转换的方法重新定义飞行器的机体坐标系.坐标转换的具体过程如下:执行单元1的连杆与Obxb轴重合, 指向外为正方向, Obzb轴保持不变, 且Obyb轴与Obxb轴、Obzb轴构成右手笛卡尔坐标系.重新定义机体坐标系后的控制输入矩阵B3×5可以描述为
| $ {{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}} = \left[ {\begin{array}{*{20}{c}} {\frac{{ - \sqrt 3 l\cos \gamma }}{{2{I_x}}}}&{\frac{{ - \sqrt 3 l\cos \gamma }}{{2{I_x}}}}&0&{\frac{{\sqrt 3 l\cos \gamma }}{{2{I_x}}}}&{\frac{{\sqrt 3 l\cos \gamma }}{{2{I_x}}}}\\ {\frac{{ - l\cos \gamma }}{{2{I_y}}}}&{\frac{{l\cos \gamma }}{{2{I_y}}}}&{\frac{{l\cos \gamma }}{{{I_y}}}}&{\frac{{l\cos \gamma }}{{2{I_y}}}}&{\frac{{ - l\cos \gamma }}{{2{I_y}}}}\\ {\cos \gamma }&{\cos \gamma }&{\cos \gamma }&{\cos \gamma }&{\cos \gamma } \end{array}} \right]. $ | (27) |
可得用于姿态稳定控制的反演滑模控制器:
| $ \begin{array}{l} \mathit{\boldsymbol{U}} = {\left( {{{\mathit{\boldsymbol{\hat K}}}_{\left( 1 \right),{\rm{d}}}}} \right)^{ - 1}}{\left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right)^{ - 1}}\left[ { - {\mathit{\boldsymbol{A}}_{\left( 1 \right)}}\left( {{\mathit{\boldsymbol{z}}_{\left( 1 \right).2}} - {\mathit{\boldsymbol{C}}_{\left( 1 \right)}}{\mathit{\boldsymbol{z}}_{\left( 1 \right).1}}} \right) - {F_{\left( 1 \right)}}\left( {{{\mathit{\boldsymbol{\dot \eta }}}_{\left( 1 \right)}},t} \right) + {{\mathit{\boldsymbol{\ddot \eta }}}_{\left( 1 \right),{\rm{d}}}} - {\mathit{\boldsymbol{C}}_{\left( 1 \right)}}{{\mathit{\boldsymbol{\dot z}}}_{\left( 1 \right).1}} - } \right.\\ \;\;\;\;\;\;\left. {{\mathit{\boldsymbol{H}}_{\left( 1 \right)}}\left( {{\mathit{\boldsymbol{\sigma }}_{\left( 1 \right)}} + {\mathit{\boldsymbol{\alpha }}_{\left( 1 \right)}}{\mathop{\rm sgn}} \left( \sigma \right)} \right)} \right]. \end{array} $ | (28) |
式中:A(1)、C(1)、H(1)为降阶后的矩阵, z(1).2、z(1).1、
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot V}}}_2} \le - \left\| {\mathit{\boldsymbol{\sigma }}_{\left( 1 \right)}^{\rm{T}}} \right\|\left[ {\left\| {{\mathit{\boldsymbol{H}}_{\left( 1 \right)}}{\mathit{\boldsymbol{\alpha }}_{\left( 1 \right)}}} \right\| - \left\| {\left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right)\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_{\left( 1 \right)}}\mathit{\boldsymbol{\hat K}}_{\left( 1 \right)}^{ - 1}} \right){{\left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right)}^{ - 1}}} \right\| \times \left\| {{\mathit{\boldsymbol{A}}_{\left( 1 \right)}}\left( {{\mathit{\boldsymbol{z}}_{\left( 1 \right).2}} - {\mathit{\boldsymbol{C}}_{\left( 1 \right)}}{\mathit{\boldsymbol{z}}_{\left( 1 \right).1}}} \right) - {{\mathit{\boldsymbol{\ddot \eta }}}_{\left( 1 \right),d}} + } \right.} \right.\\ \;\;\;\;\;\;\left. {\left. {{\mathit{\boldsymbol{F}}_{\left( 1 \right)}}\left( {{{\mathit{\boldsymbol{\dot \eta }}}_{\left( 1 \right)}},t} \right) + {\mathit{\boldsymbol{C}}_{\left( 1 \right)}}{{\mathit{\boldsymbol{\dot z}}}_{\left( 1 \right).1}}} \right\|} \right] - \mathit{\boldsymbol{Z}}_{\left( 1 \right)}^{\rm{T}}{\mathit{\boldsymbol{Q}}_{4 \times 4}}{\mathit{\boldsymbol{Z}}_{\left( 1 \right)}}. \end{array} $ | (29) |
式中:
| $ \begin{array}{l} \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} {\mathit{\boldsymbol{C}}_{\left( 1 \right)}} + \mathit{\boldsymbol{A}}_{\left( 1 \right)}^{\rm{T}}\left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right){\mathit{\boldsymbol{K}}_{\left( 1 \right)}}\mathit{\boldsymbol{\hat K}}_{\left( 1 \right)}^{ - 1}{\left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}_{\left( 1 \right)}}{\mathit{\boldsymbol{A}}_{\left( 1 \right)}}\\ {{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}{\mathit{\boldsymbol{K}}_{\left( 1 \right)}}\mathit{\boldsymbol{\hat K}}_{\left( 1 \right)}^{ - 1}{\left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}_{\left( 1 \right)}}{\mathit{\boldsymbol{A}}_{\left( 1 \right)}} - \mathit{\boldsymbol{N}} \end{array}&\begin{array}{l} \mathit{\boldsymbol{A}}_{\left( 1 \right)}^{\rm{T}}\left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right){\mathit{\boldsymbol{K}}_{\left( 1 \right)}}\mathit{\boldsymbol{\hat K}}_{\left( 1 \right)}^{ - 1}{\left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}_{\left( 1 \right)}} - \mathit{\boldsymbol{N}}\\ \left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right){\mathit{\boldsymbol{K}}_{\left( 1 \right)}}\mathit{\boldsymbol{\hat K}}_{\left( 1 \right)}^{ - 1}{\left( {{{\mathit{\boldsymbol{\bar B}}}_{3 \times 5}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}_{\left( 1 \right)}} \end{array} \end{array}} \right],\mathit{\boldsymbol{N}} = {\rm{diag}}\left[ {\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2}} \right],\\ {\mathit{\boldsymbol{K}}_{\left( 1 \right)}}\mathit{\boldsymbol{\hat K}}_{\left( 1 \right)}^{ - 1} = {\rm{diag}}{\left[ {\Delta {k_1}, \cdots ,\Delta {k_6}} \right]^{\rm{T}}},\Delta {k_i} = {k_i}/{{\hat k}_i} \in \left[ {0.85,1.15} \right]. \end{array} $ |
构造矩阵H(1), 使得
| $ {R_1} = \sum\limits_{i \ne 1,4}^6 {0.25\Delta {k_i}} > 0, $ | (30) |
| $ {R_2} = \sum\limits_{i = 2}^5 {\left( {\sum\limits_{j > i,j \ne i + 3}^6 {0.125\Delta {k_i}\Delta {k_j}} } \right)} > 0. $ | (31) |
经由式(30)、(31)证明,
| $ {{\mathit{\boldsymbol{\dot V}}}_2} \le - \left\| {{\mathit{\boldsymbol{H}}_{\left( 1 \right)}}{\mathit{\boldsymbol{\alpha }}_{\left( 1 \right)}}} \right\|\left\| {\mathit{\boldsymbol{\sigma }}_{\left( 1 \right)}^{\rm{T}}} \right\| - \mathit{\boldsymbol{Z}}_{\left( 1 \right)}^{\rm{T}}{\mathit{\boldsymbol{Q}}_{4 \times 4}}{\mathit{\boldsymbol{Z}}_{\left( 1 \right)}} \le 0. $ | (32) |
根据LaSalle不变性定理可知, 当
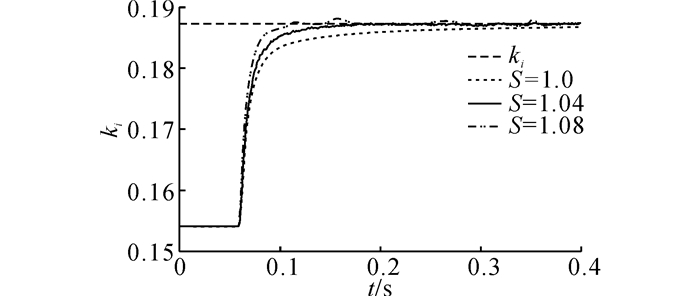
为了提高基于EKF的故障观测器的收敛速度, 采用S加权衰减记忆卡尔曼滤波算法.通过S加权衰减记忆参数对升力因子的影响实验, 合理选择S参数的数值.控制器设定的升力因子为0.19, 故障观测器在S参数取值不同的条件下估计得到的升力因子曲线如图 5所示.
|
图 5 S加权衰减记忆参数对故障观测器的影响 Fig. 5 Effect of S parameters on fault observer |
从图 5可以看出, 当t = 0.06 s时, 故障观测器对控制器设定的升力因子进行估计.当S参数取值为1.0时, 跟踪曲线很光滑, 但是收敛速度较缓慢, 到达设定值所用的时间大于0.2 s.当S参数取值为1.04时, 故障观测器能够在0.14 s左右到达升力因子的设定值, 此时升力因子跟踪曲线变得不再光滑, 有少量噪音出现.当S参数取值为1.08时, 故障观测器能够在0.11 s左右达到升力因子的设定值, 收敛速度较之前有所提升, 但是存在较大噪音, 在实际系统中表现为观测值的精度降低.综合考虑采用S=1.04的加权衰减记忆参数.
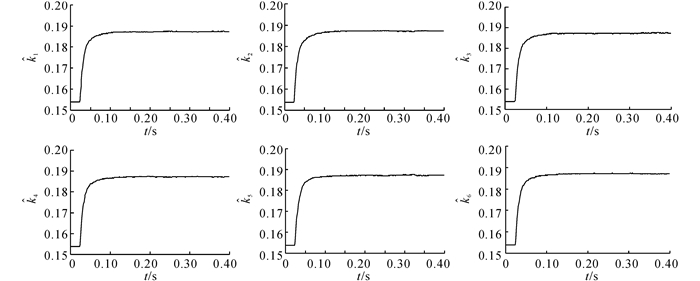
在选定S参数之后, 假设Hex-Rotor无人飞行器在飞行过程中, 控制器设定的升力因子存在一定的误差, 所有执行单元对应的故障观测器组对每个执行单元的升力因子同时进行估计的仿真实验, 实验结果如图 6所示.可以看出, 故障观测器组均在0.025 s时对各执行单元的升力因子进行估计, 在0.10 s左右接近升力因子的设定值.所设计的故障观测器组能够同时对各执行单元的升力因子进行准确跟踪.以某个执行单元发生突发性故障或渐变性故障为例, 通过故障观测器组对各个执行单元升力因子的跟踪实验, 进而验证故障观测器组对单个故障或多个故障发生时的故障准确定位与跟踪性能.实验结果如图 7所示.
|
图 6 故障观测器组对各执行单元升力因子的估计 Fig. 6 Estimation of lift factor for each execution unit |
|
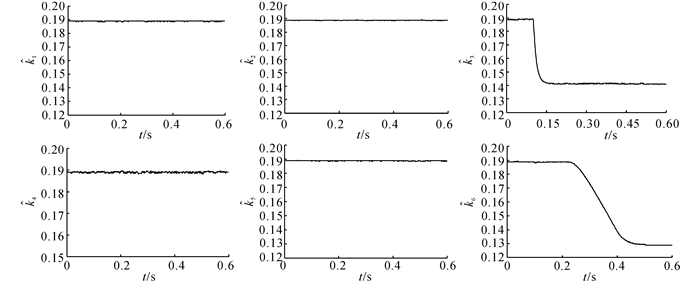
图 7 故障观测器组对突发性故障与渐变性故障的估计效果 Fig. 7 Estimation of sudden fault and gradual fault of fault observer group |
从图 7可以看出, 在0.1 s时, 执行单元3有突发性故障发生, 升力因子迅速下降至设定值的74%;在0.25 s左右, 执行单元6有渐变性故障发生, 升力因子以某一速度约下降至设定值的68%.执行单元3和执行单元6相对应的故障观测器均实现了故障执行单元的准确定位和升力因子的稳定跟踪.
为了验证所设计的自重构控制器在执行单元故障条件下的重构控制性能, 开展原型机的室外飞行实验, 如图 8所示.选定飞行器的初始姿态角为

|
图 8 原型机的飞行测试实验 Fig. 8 Flight test experiment of prototype |

|
图 9 执行单元增益性故障姿态角跟踪曲线 Fig. 9 Attitude angle tracking curve of gain type faults of execution unit |
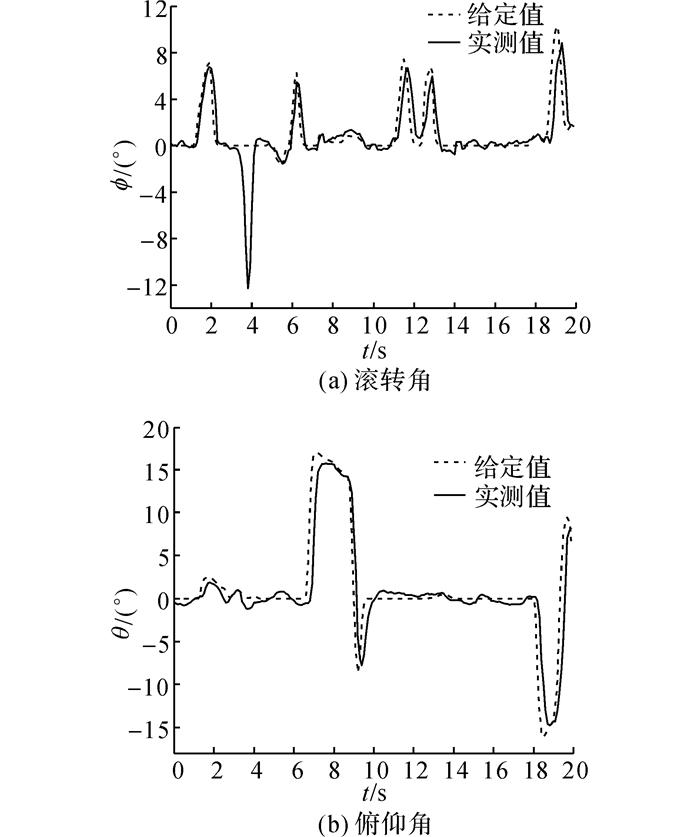
当执行单元5发生失效性故障时的实验结果如图 10所示.此时, 执行单元5完全丧失了提供升力的能力, 并使得控制输入矩阵发生变化;为了保持飞行器的稳定性, 确保安全飞行, 控制器将放弃对偏航角的控制, 仅保持对飞行高度、俯仰角以及滚转角的控制.图 10(a)中, 当t=3.8 s时, 原型机在滚转通道出现一个12°的突变, 执行单元5不再提供驱动力, 使得飞行器有失稳的危险, 自重构控制器在经过0.5 s左右完成容错重构, 使得控制器重新将滚转角稳定控制.由于飞行器这一非线性系统的耦合关系, 即使执行单元5不直接进行俯仰角的控制, 俯仰角控制效果也会下降, 如图 10(b)所示.
|
图 10 执行单元失效性故障姿态角跟踪曲线 Fig. 10 Attitude angle tracking curve of failure type faults of execution unit |
(1) 数值仿真结果表明, 所设计的故障检测器组经过0.08 s后能够准确地估计与跟踪各个执行单元的升力因子, 可以快速地检测到故障的发生位置和类型, 并实现故障隔离.
(2) 原型机实际飞行的实验结果表明, 自重构控制器能够在Hex-Rotor无人飞行器执行单元发生增益性故障和失效性故障之后, 保证Hex-Rotor无人飞行器姿态控制的稳定性和控制品质, 有效地提高了飞行器的可靠性和安全性.
| [1] |
AVRAM R C, ZHANG X, MUSE J. Quadrotor actuator fault diagnosis and accommodation using nonlinear adaptive estimators[J]. IEEE Transactions on Control Systems Technology, 2017, 25(6): 2219-2226. DOI:10.1109/TCST.2016.2640941 |
| [2] |
QI X, QI J, THEILLIOL D, et al. A review on fault diagnosis and fault tolerant control methods for single-rotor aerial vehicles[J]. Journal of Intelligent and Robotic Systems, 2014, 73(1-4): 535-555. DOI:10.1007/s10846-013-9954-z |
| [3] |
XU D, WHIDBORNE J F, COOKE A. Fault tolerant control of a quadrotor using 1 adaptive control[J]. International Journal of Intelligent Unmanned Systems, 2016, 4(1): 43-66. DOI:10.1108/IJIUS-08-2015-0011 |
| [4] |
PARK P, KHADILKAR H, BALAKRISHNAN H, et al. High confidence networked control for next generation air transportation systems[J]. IEEE Transactions on Automatic Control, 2014, 59(12): 3357-3372. DOI:10.1109/TAC.2014.2352011 |
| [5] |
MERHEB A R, NOURA H, BATEMAN F. Design of passive fault-tolerant controllers of a quadrotor based on sliding mode theory[J]. International Journal of Applied Mathematics and Computer Science, 2015, 25(3): 561-576. |
| [6] |
ZEGHLACHE S, SAIGAA D, KARA K. Fault tolerant control based on neural network interval type-2 fuzzy sliding mode controller for octorotor UAV[J]. Frontiers of Computer Science in China, 2016, 10(4): 657-672. DOI:10.1007/s11704-015-4448-8 |
| [7] |
SØRENSEN M E N, HANSEN S, BREIVIK M, et al. Performance comparison of controllers with Fault-Dependent Control Allocation for UAVs[J]. Journal of Intelligent and Robotic Systems, 2017, 87(1): 187-207. DOI:10.1007/s10846-017-0494-9 |
| [8] |
RANJBARAN M, KHORASANI K. Generalized fault recovery of an under-actuated quadrotor aerial vehicle[C]//Proceedings of 2012 American Control Conference Montreal. Montreal: IEEE, 2012: 2515-2520. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6315526
|
| [9] |
SHARIFI F, MIRZAEI M, GORDON B W, et al. Fault tolerant control of a quadrotor UAV using sliding mode control[C]//Control and Fault-Tolerant Systems. Nice: IEEE, 2010: 239-244. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5675979
|
| [10] |
ZEGHLACHE S, KARA K, SAIGAA D. Fault tolerant control based on interval type-2 fuzzy sliding mode controller for coaxial trirotor aircraft[J]. ISA Transactions, 2015, 59(11): 215-231. |
| [11] |
DU G X, QUAN Q, CAI K Y. Controllability analysis and degraded control for a class of hexacopters subject to rotor failures[J]. Journal of Intelligent and Robotic Systems, 2015, 78(1): 143-157. DOI:10.1007/s10846-014-0103-0 |
| [12] |
ROTONDO D, NEJJARI F, PUIG V. Robust quasi-LPV model reference FTC of a quadrotor UAV subject to actuator faults[J]. International Journal of Applied Mathematics and Computer Science, 2015, 25(1): 7-22. |
| [13] |
王俭臣, 齐晓慧, 单甘霖. 一类参数不确定非线性系统的故障检测与重构[J]. 系统工程与电子技术, 2015, 37(1): 155-162. WANG Jian-chen, QI Xiao-hui, SHAN Gan-lin. Fault detection and reconstruction for a class of nonlinear systems with parametric uncertainties[J]. Systems Engineering and Electronics, 2015, 37(1): 155-162. |
| [14] |
刘晓东, 钟麦英, 柳海. 基于EKF的无人机飞行控制系统故障检测[J]. 上海交通大学学报, 2015, 49(6): 884-888. LIU Xiao-dong, ZHONG Mai-ying, LIU Hai. EKF-based fault detection of unmanned aerial vehicle flight control system[J]. Journal of Shanghai Jiaotong University, 2015, 49(6): 884-888. |
| [15] |
JIANG H, YU Y, DING X, et al. A fault tolerant control strategy for quadrotor UAVs based on trajectory linearization approach[C]//Proceedings of 2012 IEEE International Conference on Mechatronics and Automation. Chengdu: IEEE, 2012: 1174-1179. http://ieeexplore.ieee.org/document/6283417/
|
| [16] |
BARGHANDAN S, BADAMCHIZADEH M A, JHAED-MOTLAGH M R. Improved adaptive fuzzy sliding mode controller for robust fault tolerant of a quadrotor[J]. International Journal of Control, Automation and Systems, 2017, 15(1): 427-441. DOI:10.1007/s12555-015-0313-7 |
| [17] |
PENG L, ERIK V K, BIN Y. Actuator fault detection and diagnosis for quadrotors[C]//International Micro Air Vehicle Conference and Competition. Netherlands: Delft University of Technology, 2014: 58-36. http://dx.doi.org/10.4233/uuid:0181d3dd-fa3b-4abf-8587-60faa6e8c17d
|
| [18] |
宫勋, 白越, 赵常均, 等. Hex-Rotor无人飞行器及其飞行控制系统设计[J]. 光学精密工程, 2012, 20(11): 1995-2002. GONG Xun, BAI Yue, ZHAO Chang-jun, et al. Hex-rotor aircraft and its autonomous flight control system[J]. Optics and Precision Engineering, 2012, 20(11): 1995-2002. |
| [19] |
赵常均. Hex-Rotor无人飞行器执行单元的故障分析与飞行控制[D]. 北京: 中国科学院大学, 2015. ZHAO Chang-jun. Fault analysis of execution units and flight control for hex-rotor unmanned aerial vehicle[D]. Beijing: University of Chinese Academy of Sciences, 2015. http://cdmd.cnki.com.cn/Article/CDMD-80139-1015330272.htm |
| [20] |
付梦印, 邓志红, 张继伟. Kalman滤波理论及其在导航系统中的应用[M]. 北京: 科学出版社, 2003, 74-79.
|
| [21] |
赵常均, 白越, 宫勋, 等. 气动干扰下的Hex-Rotor无人飞行器控制器及其飞行实验[J]. 光学精密工程, 2015, 23(4): 1088-1095. ZHAO Chang-jun, BAI Yue, GONG Xun, et al. Hex-rotor unmanned aerial vehicle controller and its flight experiment under aerodynamic disturbance[J]. Optics and Precision Engineering, 2015, 23(4): 1088-1095. |


