无人机(unmanned aerial vehicle, UAV)的飞行环境日益复杂、飞行任务要求越来越高, 利用信息共享和资源优化建立多平台自主任务协同成为无人机技术发展的趋势[1-2].四维航迹规划方法可以严格满足时间上的约束, 航迹在空间维度上通过协调避碰可以进行交叉或重叠,因此在多UAV群组的自主集群、编队组成、同步攻击等任务执行时具有广阔的应用前景[3].
目前,关于多UAV的四维航迹规划方法相关研究大体分为离散型和连续型航迹规划两种方法.Supatcha等[4]通过混合元启发算法对一系列离散航路点坐标进行优化, 时间约束通过为航路点进行到达时间分配来满足;Wu等[5]采用多步A*算法找到初始点到目标点的四维航迹, 再进行航迹点的速度分配.离散型航迹规划主要通过求解考虑时间约束的三维航迹规划问题, 对航迹点的速度分配通常非连续, 不考虑速度变化的过渡过程.不连续的分配速度在实际应用中会造成较大的航迹误差, 须花费大量计算开销用于航迹搜索和速度分配的采样过滤[6-7].
连续型航迹规划方法建立关于位置和时间变量的连续运动方程的数学表达式, 利用启发式算法来搜索满足约束条件下的航迹最优航迹参数[8].为了保证速度和加速度的时域连续, 通常采用时间变量的高阶多项式表示平滑的四维航迹.同时为了满足运动各约束条件, 需要提升多项式阶次, 使得表达式系数的优化求解较难.如Berry等[9]采用6阶Bezier多项式描述航迹运动, 每条航迹需要求解21个参数.
近年来, 关于生物运动规划机制启发的Tau理论在四维运动规划中得到了广泛关注. Lee[10]提出Tau理论, 该理论是在生态心理学理论的基础上发展而来的[11].Tau理论指出, 观察者的重要信息源是由运动物体视觉影像相对扩张率的倒数提供, 即Tau变量.Tau变量可以表示为目标与观察者的距离和二者相对运动速度的比值. Lee[12]通过录像拍照分析鸽子着陆过程的行为, 证实了Tau信息在运动规划中的指导作用.对于不同运动中Tau信息如何协调, Tau信息如何指导人和动物进行运动等一系列问题, Lee[13]经过研究, 提出广义Tau理论, 使Tau可以应用于目标朝向的运动规划.
本文基于Tau运动策略, 推导一种耦合简谐运动的改进的Tau-H运动策略公式.利用该运动策略,结合滚动时域优化算法应用于多UAV四维协同任务中, 能够规划出合理的多无人机四维航迹, 同时满足航迹的连续性、可飞性和安全性.
1 基础理论 1.1 Tau耦合策略在广义Tau理论中, 在t时刻的Tau变量τχ(t)被定义为运动间距χ(t)与运动间距变化率
| $ {\tau _\chi }\left( t \right) = \left\{ \begin{array}{l} \chi \left( t \right)/\dot \chi \left( t \right),\;\;\;\;\;\left| {\dot \chi \left( t \right)} \right| \ge {{\dot \chi }_{\min }};\\ {\tau _{\min }},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {\dot \chi \left( t \right)} \right| < {{\dot \chi }_{\min }}. \end{array} \right. $ | (1) |
在运动的过程中, τχ(t)通常定义为负值.对UAV航迹规划运动空间来说, χ具体可以为三维位置、速度等物理运动状态间距.
Lee等[12]发现,若生物运动想要在目标点停驻,须保持Tau变量的一阶导数
| $ \chi \left( t \right) = {\chi _0}{\left( {\frac{{{{\dot \chi }_0}}}{{{\chi _0}}}kt + 1} \right)^{\frac{1}{k}}}. $ | (2) |
式中:χ0为初始间距,
随着人们对广义Tau理论的不断认识, 研究人员进一步提出导引多个运动间距闭合, 即耦合虚拟运动间距在时间T到达零时, 真实运动间距也到达零的Tau耦合策略. Lee等[14]提出耦合自由落体运动为制导运动的Tau-G运动策略.
Yang等[15]提出耦合简谐运动的Tau-H运动策略, 在UAV点对点的运动规划中得到应用.Tau-H运动策略中的耦合简谐运动可以表达为
| $ H\left( t \right) = {H_0}\left[ {\frac{1}{{2{\rm{ \mathsf{ π} }}}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}t}}{T}} \right) - \frac{t}{T} + 1} \right]. $ | (3) |
式中:H0为初始参考间距.根据Tau耦合策略,求解τχ(t)=kχτH(t)=kχH(t)/Ḣ(t), 实际运动间距及导数表达式为
| $ \left. \begin{array}{l} \chi \left( t \right) = {\chi _0}{h^{1/{k_\chi }}},\\ \dot \chi \left( t \right) = \frac{{{\chi _0}}}{{{k_\chi }}}\dot h{h^{1/{k_\chi } - 1}},\\ \ddot \chi \left( t \right) = \frac{{{\chi _0}}}{{{k_\chi }}}\left( {\frac{{1 - {k_\chi }}}{{{k_\chi }}}{{\dot h}^2} + h\ddot h} \right){h^{1/{k_\chi } - 2}}. \end{array} \right\} $ | (4) |
式中:h=H/H0=sin(2πt/T)/(2π)-t/T+1.
为了导引运动的平稳闭合, Tau-G运动策略须满足耦合系数kχ∈(0, 0.5), Tau-H运动策略须满足kχ∈(0, 1], 意味着kχ的取值范围扩大了一倍, 相应的航迹空间形状调整范围更大.此外,Tau-G运动策略存在初始加速度无法从零开始,初始加加速度趋于无穷的不足, 不适用于从静止或悬停初始状态运动的UAV[16-17].Tau-H制导策略可以避免该缺陷, 能够实现UAV从静止初始状态运动出发的航迹规划. Tau-G和Tau-H等现有的Tau运动策略几乎均要求物体的始末静止,这不能适用于UAV尤其是固定翼UAV的编队形成、调速等更广泛的具有始末速度的运动任务.
1.2 改进的Tau-H运动策略 1.2.1 改进的Tau-H运动策略为了适应具有非零始、末速度的问题, 希望在保留Tau-H运动策略优点的基础上对运动策略进行改进.改进后的参考运动间距表达式为
| $ {H_I}\left( t \right) = \frac{2}{{\rm{ \mathsf{ π} }}}\sin \left( {\frac{{{\rm{ \mathsf{ π} }}t}}{{2T}}} \right) - \frac{t}{T} + {V_H}t + {H_0}. $ | (5) |
式中:H0为参考运动初始间距, VH为参考运动初始速度, T为运动期望到达时间, 在T时刻参考运动闭合. H0、VH为可变虚拟参数.用Ẋ0和ẊT来分别表示运动物体已知的初始速度和到达目标末速度.根据Tau耦合策略,可得实际间距闭合时的运动速度为
| $ {{\dot X}_I}\left( t \right) = {{\dot X}_T} - \frac{{{R_{x0}}}}{{{k_x}H_0^{1/{k_x}}}}{H_I}\dot H_I^{1/{k_x} - 1}. $ | (6) |
式中:ΔẊ=ẊT-ẊI, ẊT不一定为零, 因此
| $ \left. \begin{array}{l} {X_I}\left( t \right) = {X_T} + {{\dot X}_T}\left( {t - T} \right) - \frac{{{R_{x0}}}}{{H_0^{1/{k_x}}}}H_I^{1/{k_x}},\\ {{\dot X}_I}\left( t \right) = {{\dot X}_T} - \frac{{{R_{x0}}}}{{{k_x}H_0^{1/{k_x}}}}{H_I}\dot H_I^{1/{k_x} - 1},\\ {{\ddot X}_I}\left( t \right) = - \frac{{{R_{x0}}H_I^{1/{k_x} - 2}}}{{{k_x}H_0^{1/{k_x}}}}\left( {\frac{{1 - {k_x}}}{{{k_x}}}\dot H_I^2 + {H_I}{{\ddot H}_I}} \right). \end{array} \right\} $ | (7) |
求解条件XI(0)=X0, ẊI(0)=Ẋ0, HI(T)=0并代入式(5)、(7), 可得
| $ \left. \begin{array}{l} {R_{x0}} = {X_T} - {X_0} - {{\dot X}_T}T,\\ {H_0} = \frac{{\left( {{\rm{ \mathsf{ π} }} - 2{R_{x0}}} \right)}}{{{\rm{ \mathsf{ π} }}\left[ {{R_{x0}} + {k_x}T\left( {{{\dot X}_T} - {{\dot X}_0}} \right)} \right]}},\\ {V_H} = \frac{{{k_x}{H_0}\left( {{{\dot X}_T} - {{\dot X}_0}} \right)}}{{{R_{x0}}}}. \end{array} \right\} $ | (8) |
通过真实运动参数Rx0和T, 将H0和VH相互联系起来, 得到改进后的Tau-H运动策略的运动表达式.分析式(7)可知, 若kx∈(0, 0.5), t→T时HI(T)→0, (XI, ẊI, ẌI)→(XT, ẊI, 0), 运动速度和位置将收敛于目标值.
设计2种运动任务来进一步说明改进的Tau-H运动策略的制导效果.以一维运动为例, 如表 1所示, 横向参数分别表示为初始位置、速度和目标位置、速度、运动总时间等, τ < 0表明初始时刻物体朝向目标移动.任务1表示初始时刻物体速度朝向目标移动,任务2表示初始时刻物体速度背离目标移动.各自的运动状态变化如图 1所示.
| 表 1 改进的Tau-H策略验证任务参数 Table 1 Parameters of tasks to verify improved Tau-H movement strategy |

|
图 1 改进的Tau-H策略下运动状态随耦合系数的改变状况 Fig. 1 State changes of different coupling coefficients of improved Tau-H movement strategy |
从图 1可以看出,不管初时刻物体的运动是朝向目标还是背离目标, 在合理的耦合系数(0, 0.5)的范围内, χ和v都能够在T收敛于期望值, 且加速度a趋于0, 制导策略均可以使用;在其他取值范围下, 如k=1.3时, a较大且振荡,并不能使用.
1.2.2 参数有效取值范围改进的Tau-H运动策略虽然能够应用于始末时刻速度非零的任务中, 但不是在所有参数下均能够正常应用, 在实际的应用中需要注意以下几点.
1) H0需要为正值, 否则在式(8)中, 当kx∈(0, 0.5)时, 分母存在负数的非整数次幂的情况, 导致结果可能出现虚数, 会产生结果的误差.
2) 由式(8)可以得出, H0和VH的分母可能会取到零, 此时kx=-Rx0/(ẊT-Ẋ0)T.若Rx0(ẊT-Ẋ0)>0, 奇点不在kx∈(0, 0.5)内取得; 若Rx0×(ẊT-Ẋ0) < 0, 当Rx0/(ẊT-Ẋ0)>-0.5T时, kx取值可能导致奇点.当取值导致奇点时, 由式(8)可得,此时VH=-H0/T, 将式(5)的参考运动转化为匀速直线运动:
| $ {H_I}\left( t \right) = - \frac{{{H_0}t}}{T} + {H_0}. $ | (9) |
结合耦合策略, 转化后的改进的Tau-H运动策略仍适用.
3) 根据Tau耦合策略, 为了使间距严格按照到达时间T闭合, 需要保证HI(t)=0在[0, T]上有且仅有唯一的解t =T, 否则间距会提前达到闭合.分析式(5)可以发现, ḦI(t) < 0, ḢI(t)递减, ḢI(t)=0最多只有一个解, 则HI(t)=0最多只有一个极值.结合H0需要为正值的条件, 可以求出间距严格闭合条件为Rx0(ẊT-Ẋ0)>0或Rx0/(ẊT-Ẋ0) < -0.5T.
综上所述, 耦合系数有效取值的条件为
| $ \left. \begin{array}{l} {R_{x0}}\left( {{{\dot X}_T} - {{\dot X}_0}} \right) > 0,\\ {R_{x0}}/\left( {{{\dot X}_T} - {{\dot X}_0}} \right) < - 0.5T. \end{array} \right\} $ | (10) |
当多无人机开展同步集群、编队飞行等任务时,在某状态下获取任务指标,进行航迹重规划.基于改进的Tau-H运动策略,可以满足具有初、末速度的状态改变, 同时实现规划时三维空间和时间的同步开展;通过建立运动表达式来对航迹进行求解, 方便物理实现, 降低运动过程中的姿态波动和精度损失.
2.1 多无人机体系在含N架次无人机的多UAV体系中, 定义北东地坐标系即NED坐标系下, 第i架UAV的三维位置集合为xi={Xi, Yi, Zi}, 速度集合为ui={Ẋi, Ẏi, Żi}, 则在t时刻系统的状态集可以表示为x(t)={x1(t), …, xN(t)}.将速度集u(t)={u1(t), …, uN(t)}作为UAV的速度和姿态指令, 利用航迹优化算法,为多UAV系统规划一组可以导引各UAV从某一初始时刻状态x(t0)经运行时间T到达目标状态x(t0+T)的航迹.
在进行四维多无人机路径规划中, 各UAV的运动可以在NED坐标系下分解为三维运动, 通过改进的Tau-H制导策略可以描述为
| $ \left. \begin{array}{l} X\left( t \right) = {X_T} + {{\dot X}_T}\left( {t - T} \right) - \frac{{{R_{x0}}}}{{H_0^{1/{k_x}}}}H_I^{1/{k_x}},\\ Y\left( t \right) = {Y_T} + {{\dot Y}_T}\left( {t - T} \right) - \frac{{{R_{y0}}}}{{H_0^{1/{k_y}}}}H_I^{1/{k_y}},\\ Z\left( t \right) = {Z_T} + {{\dot Z}_T}\left( {t - T} \right) - \frac{{{R_{z0}}}}{{H_0^{1/{k_z}}}}H_I^{1/{k_z}}. \end{array} \right\} $ | (11) |
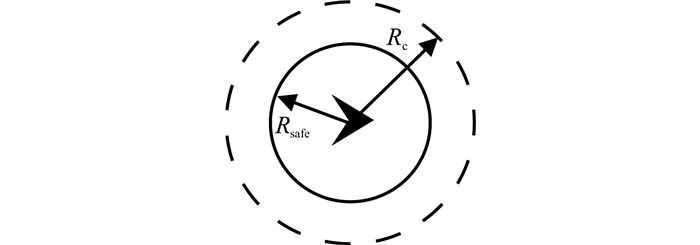
通过对耦合系数k=[kx, ky, kz]T和到达时间T进行取值, 可以得到不同的四维航迹.通过建立通信拓扑来描述多UAV间的相互通信的连接关系.如图 2所示, 各UAV的飞行间距须大于安全半径Rsafe.由于在实际中通信距离Rc是有限的,随着各UAV间的位置不断变化,通信拓扑结构相应地发生动态改变.
|
图 2 UAV冲突检测示意图 Fig. 2 Sketch illustrating conflict detection of UAV |
定义多UAV系统的通信拓扑结构为有向图G={V, E, A},其中顶点集V={1, …, N}表示各UAV所在节点的位置编号, E为图G的边集合, 有向边eij∈E表示UAVi到UAVj的信息流向, A=[aij]NUAV×NUAV为邻接矩阵.以图 3为例, V={1, 2, 3, 4}, 对应的边集合可以表示为E={(3, 1), (3, 4), (4, 3), (2, 3), (2, 4)}, 对应的邻接矩阵A表示为
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0\\ 0&0&1&1\\ 1&0&0&1\\ 0&0&1&0 \end{array}} \right]. $ | (12) |

|
图 3 4架UAV通信拓扑结构示意图 Fig. 3 Sketch illustrating communication topology of three UAVs |
N架次多UAV协同航迹规划方法的输入信息包括初时刻各UAV运动状态xi(t0)和速度ui(t0), 来自目标点末状态xi(t0+T)和速度ui(t0+T)、期望运动时间T和约束条件等.
主要约束条件如下.1)航迹长度.为了减少导航误差和燃油消耗等, 航迹不希望迂回行进和频繁转弯, 可行航迹尽可能短.2)时间约束.对飞行任务往往规划时间需要在一定范围内.3)速度约束.飞行器速度往往保持在某个有限区间, 取决于动力系统和环境、任务要求.4)加速度约束.受飞行器动力以及承受过载能力的影响,也与转弯角度有关.5)还有高度约束、方向约束等.通过输入的信息,利用航迹协同算法对航迹参数进行优化,消解航迹间的冲突, 为每架UAV提供可飞航迹.
| $ \left. \begin{array}{l} \min \;\;\;S = \sum\limits_{i = 1}^N {{l_i}} .\\ {\rm{s}}.\;{\rm{t}}.\;\;\;{v_{ik}} < {v_{\max }},{a_{ik}} < {a_{\max }},\\ \;\;\;\;\;\;\;g\left( {{s_i},{s_j}} \right) \le 0,\\ i,j = 1, \cdots ,N,k = X,Y,Z. \end{array} \right\} $ | (13) |
包含N架UAV的四维航迹优化问题可以表述为式(13).式中:S表示优化目标, 为系统中所有UAV总航迹长度需要达到最小;li为第i条航迹长度;vik和aik分别为第i架UAV在k轴上的速度和加速度, 需要满足最大速度和最大加速度约束.g(si, sj)表示航迹i和j之间的冲突, 表达式为
| $ \left. \begin{array}{l} \mathit{\boldsymbol{g}}\left( {{s_i},{s_j}} \right) = \left[ \begin{array}{l} g\left( {{x_i}\left( {{t_0}} \right),{x_j}\left( {{t_0}} \right)} \right)\\ g\left( {{x_i}\left( {{t_0} + 1} \right),{x_j}\left( {{t_0} + 1} \right)} \right.\\ \;\;\;\;\;\;\;\;\;\; \vdots \\ g\left( {{x_i}\left( T \right),{x_j}\left( T \right)} \right). \end{array} \right];\\ i,j = 1, \cdots ,N,\\ g\left( {{x_i}\left( {{t_0}} \right),{x_j}\left( {{t_0}} \right)} \right) = R_{{\rm{safe}}}^2 - \sum\limits_{k = X,Y,Z} {{{\left[ {{k_i}\left( {{t_0}} \right) - {k_j}\left( {{t_0}} \right)} \right]}^2}} . \end{array} \right\} $ | (14) |
根据式(14)的优化问题, 综合考虑优化目标和各约束条件,经过简化后, 多UAV系统协同四维航迹费用函数可以表示为
| $ \begin{array}{l} J = {\omega _1}\sum\limits_{i = 1}^N {{l_i}} + {\omega _2}\sum\limits_{{A_{ij = 1}}} {\int\limits_{t = {t_0}}^T {\frac{1}{{\sigma + \sum\limits_{k = X,Y,Z} {{{\left( {{k_i}\left( t \right) - {k_j}\left( t \right)} \right)}^2}} }}{\rm{d}}t} } + \\ \;\;\;\;\;\;{\omega _3}\sum\limits_{k = X,Y,Z} {\sum\limits_{i = 1}^N {\left\{ {\max \left[ {0,\left( {\left| {{v_{ik}}} \right| - \left| {{v_{\max }}} \right|} \right)} \right]} \right\}} } + \\ \;\;\;\;\;\;{\omega _4}\sum\limits_{k = X,Y,Z} {\sum\limits_{i = 1}^N {\left\{ {\max \left[ {0,\left( {\left| {{a_{ik}}} \right| - \left| {{a_{\max }}} \right|} \right)} \right]} \right\}} } + \\ \;\;\;\;\;\;{\omega _5}\sum\limits_{m = 1}^{{N_o}} {{o_{im}}} . \end{array} $ | (15) |
式中:No为障碍数目.在J的加权组成项中,第1项表示航迹长度项;第2项为系统内每架UAV的相互冲突项, 其中σ为较小值, 避免分母为零;第3项和第4项分别为航迹的速度和加速度惩罚项;最后一项为环境障碍项.
2.3 航迹优化方法将多UAV四维航迹规划问题转化为目标费用函数, 结合改进的Tau-H运动制导策略, 通过求解最优耦合系数得到各UAV的航迹规划.
采用粒子群算法,对四维航迹规划问题进行求解.目标是找到合适的耦合系数[kx, ky, kz]和期望时间T, 使得目标函数值达到最小.在进行优化之前, 需要进行规范化,确保期望时间Ti和ki具有相同的取值范围.规范化方法采用线性变换, 变换后的表达式为
| $ \left. \begin{array}{l} {k_i} = \frac{{{k_{\max }} - {k_{\min }}}}{{{T_{\max }} - {T_{\min }}}}{T_i} + \frac{{{T_{\max }}{k_{\min }} - {T_{\min }}{k_{\max }}}}{{{T_{\max }} - {T_{\min }}}},\\ {T_i} = \frac{{{T_{\max }} - {T_{\min }}}}{{{k_{\max }} - {k_{\min }}}}{k_i} - \frac{{{T_{\max }}{k_{\min }} - {T_{\min }}{k_{\max }}}}{{{k_{\max }} - {k_{\min }}}}. \end{array} \right\} $ | (16) |
在选取算法初值时, 考虑参数有效范围的条件, 需要调整Ti的上、下限取值来满足式(10), 也可以调整Ti来实现时间自主协同分配.
通过以上优化算法得到的四维航迹为全局状况下的优化解.考虑航迹规划的复杂性, 初始时刻各UAV间距离可能不在通信范围内, 随着时间的变化,通信拓扑结构和环境等会发生变化;各UAV间冲突会发生改变, 需要对航迹在一定时间周期内保持重规划,以修正航迹参数,消解彼此间的冲突,提高航迹的可行性和安全性.
结合滚动时域优化算法,对航迹参数进行周期重规划.滚动优化理论是预测控制理论中的一个基本思想, 不采用不变的全局最优目标, 而是采用滚动式的采样时刻一步步进行.滚动优化虽然难以获得全局最优性能指标, 但经过各采样时刻进行反复优化, 可以对航迹进行及时修正.为了简化滚动优化的过程, 在每个采样时刻, 根据运动状态方程进行下个采样时刻点的相互冲突预测判断.若产生冲突,则在当前时刻进行航迹重规划来消解下个采样时刻冲突, 重复该过程至冲突完全消解;若预测下一采样时刻没有发生冲突, 则跳过重规划过程, 到达下一采样点.通过简化后, 减少了每个采样时刻都要重规划的计算代价, 能够保持航迹的安全可行.
在滚动优化算法运行前, 先通过全局优化得到初始参数, 通过无线通信网络发送并接收通信拓扑内各个UAV的xi(t0)、ui(t0)、ki等信息,随后开展滚动优化过程.
该算法的具体流程如下.
算法1 基于滚动优化的多UAV四维航迹规划算法
1 全局规划给出各UAV初始三维ki和Ti.
2 网络通信发送ki、xi(t0)、xi(t0+Ti), 获取其他UAV信息
3 for 每个采样时刻或发生冲突事件
4 以当前点为起始,计算发送并获取下一采样时刻点各通信拓扑内UAV状态,进行相互冲突检测
5 if 发生冲突, 以当前点为初始时刻进行航迹重规划, 求解优化问题
6 更新各航迹参数, 通信发送和获取各UAV信息
7 重复步骤4至冲突消解
8 else各UAV到达下一航迹采样点
9 end if
10 until 达到最大迭代次数或停止条件
11 end for
3 算例仿真 3.1 算例设计不同于单移动机器人的路径规划, 针对多UAV的四维协同航迹规划问题, 目前尚未提出有关的标准测试算例[18], 需要设计可靠且具有说服性的飞行任务来对仿真进行验证.经过简化并结合固定翼UAV的工程实际, 采用的仿真场景为3架同型号UAV群组, 在80 m×80 m×80 m的三维空间内协同执行任务, UAV的动态约束为vmax=15 m/s, amax=5 m/s2, 各UAV间的安全距离为2 m, 各UAV的始、末状态如表 2所示.在上述场景中, 协同任务为多架UAV在收到任务后, 从各自位置进行集合, 通过自主规划顺序经过共同的集合点, 而后同时在T=15 s时到达编队形成位置, 组成编队后继续飞行15 s.采样周期为1 s, 仿真采用Matlab/Simulink R2016b软件设计完成.
| 表 2 航迹规划任务参数 Table 2 Parameters of task for route planning |
设计通过的集合点:位置为(20, 0, 25)m, 速度为(5, -5, 5) m/s.
采用OAAT(one-at-a-time)策略来作为对照方法[19].OAAT策略通过规划航迹点后进行速度分配来满足期望时间约束, 采用粒子群算法来实现, 是一种传统的带有时间约束的离散航迹规划方法.
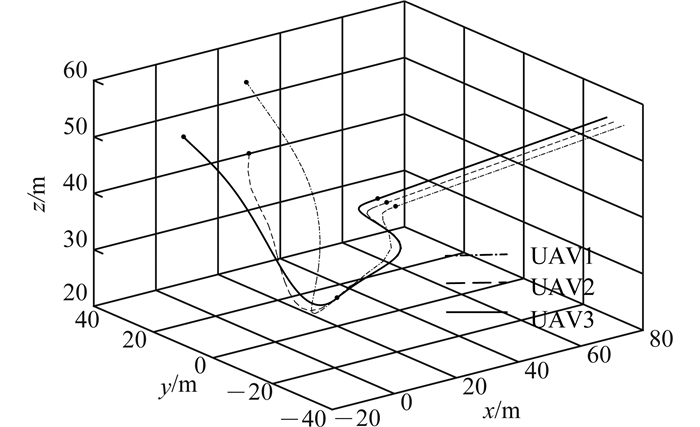
3.2 仿真结果用于得到初始航迹的全局规划过程在决定航迹的整体初始性能中起到了重要作用.全局规划后得到合理的初始航迹耦合系数,可以大大降低后续滚动优化过程进入航迹重规划的频率,减少算法搜索代价.对全局航迹规划进行10次迭代仿真, 取其中使目标费用函数达到最小的Ti和ki作为全局航迹规划的初值.得到的全局航迹图如图 4所示.
|
图 4 3架UAV全局航迹规划 Fig. 4 Global route planning for three UAVs |
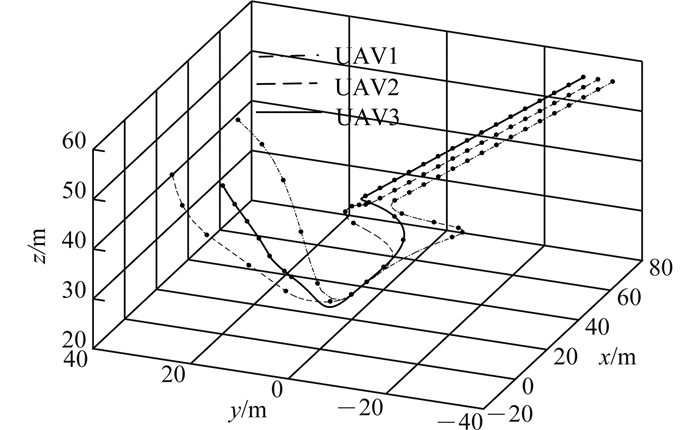
在全局规划完成后, 由于未考虑通信拓扑、其他UAV决策和相互环境变化等原因,得到的航迹在集合处附近不能保证能够做到各UAV无冲突要求.在全局规划基础上, 采用滚动时域优化算法,通过周期重规划来实现冲突消解.航迹优化结果如图 5所示.为了便于显示结果, 图 5舍去一些运动速度较低的采样点,以免过于密集.
|
图 5 3架UAV滚动时域航迹重规划 Fig. 5 Receding horizon route planning for three UAVs |
仿真任务具体分为编队集合和编队组成两部分, 在编队集合过程中, 各UAV须考虑通信拓扑与相互间的动态冲突, 以期望速度顺序通过集合点.任务执行如表 3所示, 各UAV经过优化后通过集合点的自主运行时间分别为(5.31 s, 5.78 s, 9.28 s), 通过的顺序恰好和UAV的编号一致.在通过集合点后, 各UAV在剩余时间内调整航迹, 在总期望时间时刻到达编队形成位置, 实现位置、速度和时间的同步闭合.
| 表 3 航迹规划的主要协同任务 Table 3 Major cooperative tasks for route planning |
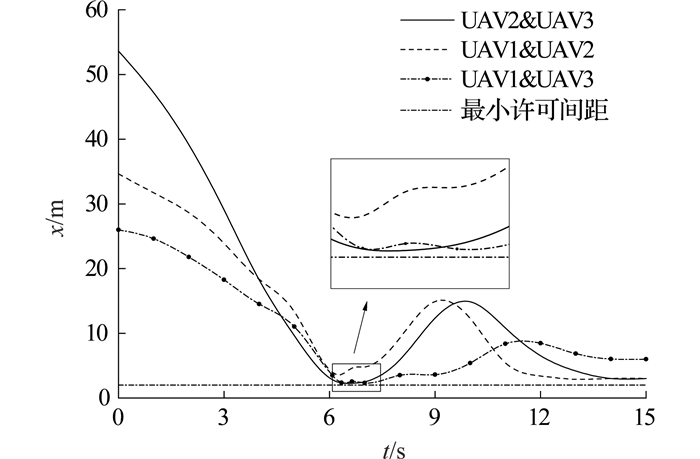
在各航迹规划过程中, 需要考虑航迹距离的可飞安全性.由于静态冲突易于施加约束和处理, 同时仿真任务设计时侧重于满足固定翼UAV的旷野飞行任务环境, 仿真中主要考虑各UAV相互间的动态冲突.在航迹规划中,各UAV间的距离如图 6所示.可以看出,各UAV间的最小位置出现在t=6.64 s附近, 此时第2架UAV和第3架UAV间的距离最近为x=2.330 5 m, 大于安全距离, 可以安全飞行.
|
图 6 航迹重规划中各UAV之间的距离 Fig. 6 Mutual distance between UAVs for route replanning |
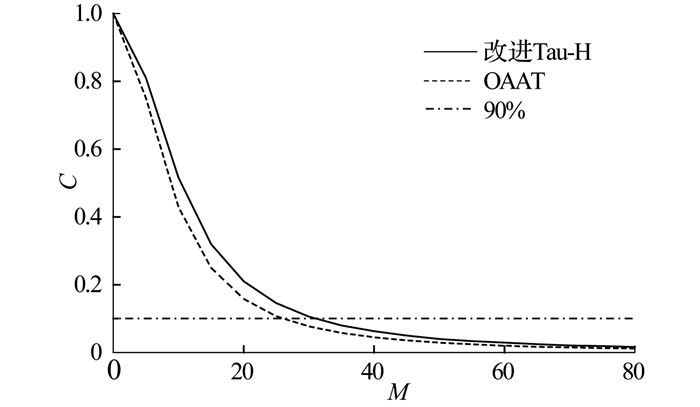
如图 7所示为采用平均航迹标准化费用C与迭代次数M的关系,说明粒子群算法的收敛性[19].标准化的过程通过采用不同的迭代次数进行仿真计算, 目的是当平均标准化航迹费用减少至最初费用的10%时,比较2种方法所需的迭代次数.在3架UAV的运行条件下, 改进的Tau-H方法需要的迭代次数约为31次, OAAT方法需要的迭代次数约为27次.对比结果说明,改进的Tau-H方法的收敛性类似于OAAT方法, 均能够实现快速收敛;OAAT方法的平均标准化费用较低,是由于航迹费用离散化求解导致的.
|
图 7 平均标准化费用与迭代次数的关系 Fig. 7 Relationship between median normalized cost and number of iteration |
如图 8所示为仿真执行时间的对比(此处为i3 2310M处理器的电脑运行时间).因为OAAT方法通过规划离散航迹点,然后进行飞行速度的分配来描述航迹, 不涉及利用积分求解航迹长度过程, 迭代速度更快;滚动优化的过程为实时采样求解, 遇到航迹冲突时需要进行重规划求解航迹, 航迹的求解为连续化过程, 迭代速度稍慢.两者的迭代时间都随着粒子群算法种群数的增加而增加.

|
图 8 仿真过程中不同种群数的时间代价 Fig. 8 Time cost of different population size in simulation procedure |
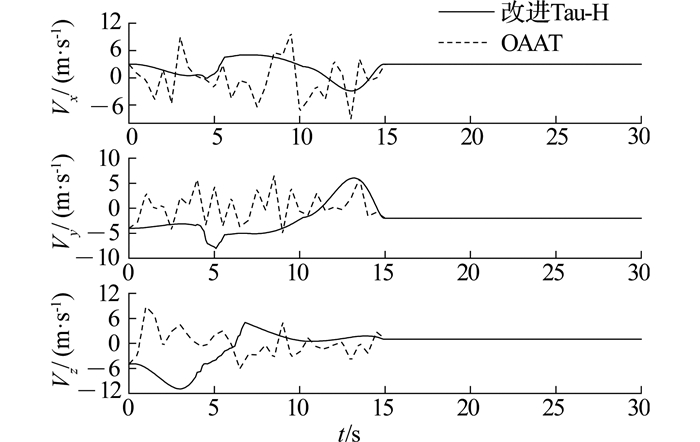
尽管改进的Tau-H方法的迭代速度比OAAT方法慢, 该不足可以通过提高硬件计算能力或使用地面计算站的方法来解决, 但在航迹连续性上,改进的Tau-H方法有着明显优势.以UAV1为例, 航迹运行的各方向速度Vx、Vy、Vz如图 9所示.在改进的Tau-H方法所设计的航迹中, 各方向速度更平滑, OAAT方法不考虑速度的变化, 波动较大.连续的运行速度对于UAV实际运动中姿态、升力及航迹等控制和实现尤为重要, 特别对于固定翼UAV来说, 苛刻的飞行要求不允许速度发生振荡变化.这使得改进的Tau-H方法规划的4D航迹可飞行性更好.
|
图 9 航迹规划中UAV1的各方向速度 Fig. 9 Velocity in each direction of UAV1 in route planning |
(1) 在常用的Tau-H运动策略上, 结合UAV始、末状态速度非零的运动条件,推导改进的Tau-H运动策略公式, 可以满足UAV在期望时间,航迹位置、速度等运动状态达到平稳闭合, 同时自主进行时间分配,为多UAV 4D连续航迹规划提供了方法基础.
(2) 采用改进的Tau-H策略规划4D航迹, 将多UAV航迹规划问题转化为目标费用函数极值问题, 简化求解难度, 建立通信拓扑结构.采用滚动优化方法进行冲突消减,可以实现多UAV协同航迹生成.
(3) 通过飞行任务仿真,对改进的Tau-H策略规划4D航迹的有效性进行验证.本文给出的连续型航迹规划算法在计算速度上虽然逊于OAAT离散型方法, 但在航迹和速度等运动状态上具有良好的连续性.仿真结果表明,基于改进的Tau-H策略的4D航迹规划方法具有良好的收敛性,在协同4D航迹的可飞行性方面明显占优, 能够更好地满足多UAV协同4D航迹规划的任务需求.
| [1] |
RADMANESH M, KUMAR M. Flight formation of UAVs in presence of moving obstacles using fast-dynamic mixed integer linear programming[J]. Aerospace Science and Technology, 2016, 50: 149-160. DOI:10.1016/j.ast.2015.12.021 |
| [2] |
肖刘. 基于多智能体的多无人机编队算法[J]. 航空电子技术, 2014, 45(2): 4-7. XIAO Liu. Multiple uav formation arithmetic based on multi-agent[J]. Avionics Technology, 2014, 45(2): 4-7. |
| [3] |
TANG X M, HAN Y X. 4D trajectory estimation for air traffic control automation system based on hybrid system theory[J]. Promet-Traffic and Transportation, 2012, 24(2): 91-98. |
| [4] |
SUPATCHA C, DANIEL D, MARCEL M. A hybrid metaheuristic optimization algorithm for strategic planning of 4D aircraft trajectories at the continental scale[J]. Computational Intelligence Magazine, 2014, 9(4): 46-61. DOI:10.1109/MCI.2014.2350951 |
| [5] |
WU P P, CAMPBELL D, MERZ T. Multi-objective four-dimensional vehicle motion planning in large dynamic environments[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cyberbetics, 2011, 41(3): 621-634. DOI:10.1109/TSMCB.2010.2061225 |
| [6] |
杨祖强. 生物启发的多无人机协同四维航迹规划方法研究[D]. 杭州: 浙江大学, 2016. YANG Zu-qiang. Bio-inspired 4D trajectory generation for multi-uav cooperation[D]. Hangzhou: Zhejiang University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10335-1016293293.htm |
| [7] |
MOON S, OH E, SHIM D H. An integral framework of task assignment and path planning for multiple unmanned aerial vehicles in dynamic environments[J]. Journal of Intelligent and Robotic Systems, 2013, 70(1-4): 303-313. DOI:10.1007/s10846-012-9740-3 |
| [8] |
BARRIENTOS A, GUTIERREZ P, COLORADO J. Advanced uav trajectory generation: planning and guidance[M]//Aerial Vehicles. : in-tech, 2009. https://www.researchgate.net/publication/221787552_Advanced_UAV_Trajectory_Generation_Planning_and_Guidance
|
| [9] |
BERRY A J, HOWITT J, GU D W. A continuous local motion planning framework for unmanned vehicles in complex environments[J]. Journal of Intelligent and Robotic Systems, 2012, 66(4): 477-494. DOI:10.1007/s10846-011-9633-x |
| [10] |
LEE D N. A theory of visual control of braking based on information about time-to-collision[J]. Perception, 1976, 5(4): 437-459. DOI:10.1068/p050437 |
| [11] |
冯建立, 张宏杰. 运动技能操作的知觉理论辨析-基于间接知觉和直接知觉理论[J]. 成都体育学院学报, 2013, 39(2): 15-19. FENG Jian-li, ZHANG Hong-jie. Analysis on the perception theory of sports skill operation-based on indirect perception and direct perception theory[J]. Journal of Chengdu Sport University, 2013, 39(2): 15-19. |
| [12] |
LEE D N, MARK N D, PATRICK R G. Visual control of velocity of approach by pigeons when landing[J]. Journal of Experimental Biology, 1993, 180(1): 85-104. |
| [13] |
LEE D N. General tau theory:evolution to date[J]. Perception, 2009, 38(6): 837-858. DOI:10.1068/pmklee |
| [14] |
SCHOGLER B, PEPPING G J, LEE D N. Tau-G guidance of transients in expressive musical performance[J]. Experimental Brain Research, 2008, 189(3): 361-372. DOI:10.1007/s00221-008-1431-8 |
| [15] |
YANG Zhu-qiang, FANG Zhou, LI Ping. Bio-inspired collision-free 4D trajectory generation for uavs using tau strategy[J]. Journal of Bionic Engineering, 2016, 13(1): 84-97. DOI:10.1016/S1672-6529(14)60162-1 |
| [16] |
张书涛, 张震, 钱晋武. 基于Tau理论的机器人抓取运动仿真轨迹规划[J]. 机械工程学报, 2014, 50(13): 42-51. ZHANG Shu-tao, ZHANG Zhen, QIAN Jin-wu. Bio inspired trajectory planning for robot catching movements based on the tau theory[J]. Journal of Mechanical Engineering, 2014, 50(13): 42-51. |
| [17] |
ZHANG Z, ZHANG S T, XIE P, et al. Bioinspired 4D trajectory generation for a UAS rapid point-to-point movement[J]. Journal of Bionic Engineering, 2014, 11(1): 72-81. DOI:10.1016/S1672-6529(14)60021-4 |
| [18] |
ALEJO D, COBANO J A, HEREDIA G, et al. Particle swarm optimization for collision-free 4D planning in unmanned aerial vehicles[C]//International Conference on Unmanned Aircraft Systems. Piscataway: IEEE, 2013: 298-307. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6564702
|
| [19] |
ALEJO D, COBANO J A, HEREDIA G, et al. Collsion-free 4D trajectory planning in unmanned aerial vehicles for assembly and structure construction[J]. Journal of Intelligent and Systems, 2014, 73(1-4): 783-795. |



