随着纤维增强复合材料在各个领域的推广应用, 高昂的制造成本成为越发突出的问题[1], 自动铺放工艺是实现复合材料高效低成本制造的有效途径之一[2-3].铺放工艺研究的重点在于探寻适宜的工艺参数[4], 其中铺放温度作为铺放工艺参数之一, 不仅影响预浸料的热学[5]和力学特性[6], 而且对预浸料的固化特性[7]及表面黏结性能[8-9]有较大的影响.准确控制铺放温度是高效、高质完成自动铺放[10-11]、获取力学性能优异的复合材料固化构件[12]的必要前提.
为了建立科学合理的铺放温度控制策略, Tierney等[13-21]开展了大量的研究工作.在真实的铺放传热过程中, 预浸料的力学和热学性质是各向异性的, 且与温度存在耦合关系;压辊、预浸料和模具之间存在复杂的热传导和非线性接触关系, 增加了铺放传热问题求解的复杂性[5], 故学者们对该问题进行简化, 提出不同类型的传热模型.Tierney等[13-15]研究预浸料在厚度方向的传热行为, 将该问题简化为一维问题.Grove等[16-17]认为在宽度方向受热均匀时, 该问题可以简化为预浸料厚度和长度方向的二维问题.当预浸料较宽时, 宽度方向的传热行为不能被忽略, Nejhad等[18-21]建立了三维铺放传热模型.铺放传热问题的求解方法包括解析法[22]、有限差分法[23]和有限元法[24].
自动铺放中的加热方式一般包括热气加热、红外加热和激光加热[25].热气加热因为存在响应速度慢、加热效率低、加热范围难以控制以及可能吹偏预浸料等缺点,逐渐被后两种加热方式所取代[26]; 红外加热和激光加热同属于辐射加热, 由于激光加热的功率远大于红外加热, 主要被用于热塑性预浸料的铺放加热, 红外加热主要用于热固性预浸料[27].
在传热模型中, 热源方程一般作为边界条件输入到模型中, 是铺放温度准确求解的关键.James等[28]假设红外灯辐射到被加热表面的热流是均匀分布的, 仅用一个参数描述红外灯的热流分布.Grove等[29-31]通过引入角系数, 考虑非均匀分布的辐射热流, 但没有考虑热源参数.由于铺放温度的控制主要是热源参数的控制, 包含热源参数的热源方程是探究铺放温度控制策略的前提.Hörmann等[32-33]考虑红外灯相对于被加热表面的距离和方向, 将这两个参数和红外灯辐射功率都引入到角系数中, 建立包含热源参数的热源方程, 但是该模型假设红外灯构型是一个均匀辐射的表面, 没有考虑红外灯的实际构型.
国内关于自动铺放红外传热的研究工作相对较少[34-35], 余永波等[34]采用近似等效的方法简化了自动铺放红外传热问题, 建立预浸带在稳态和非稳态的温度控制方程, 得到预浸带匀速运行时的温度控制律.文立伟等[35]利用该温度控制规律, 搭建红外加热控制系统.该模型将红外热源简化为单个圆柱体辐射的问题, 而实际中的红外热源是由多根灯管和灯罩一起向被加热表面辐射热量的.
本文分析自动铺放红外热源, 建立考虑热源参数的热源方程.该方程包含红外灯长度与安装高度、灯罩各面宽度与角度以及灯管辐射功率与安装位置等参数.采用自主设计的圆筒试验,测定不同电压下灯管的辐射功率, 结合红外灯的具体尺寸, 编制三维红外热源的DFLUX子程序.将该程序导入到ABAQUS中, 开展红外灯动态和静态加热仿真.温度仿真结果与动静态加热试验结果基本吻合, 验证了该红外热源方程的准确性.基于红外热源方程, 借助Matlab计算软件, 探讨红外灯安装高度、灯罩顶面宽度、灯罩侧面角度等参数对红外灯有效辐射强度和均匀度的影响.
1 红外热源方程的建立建立红外热源方程, 描述红外灯在被加热表面上的辐射热流分布情形.如图 1所示, 定义铺放方向为x方向, 红外灯高度方向为y方向, 红外灯管长度方向为z方向.红外灯对模具或预浸料表面进行辐射加热, 被加热表面上某点的热流密度是空间位置和时间的函数.

|
图 1 红外灯辐射示意图 Fig. 1 Diagram of radiation of infrared lamp |
红外灯的构型如图 1所示, 包括灯管和灯罩两部分.灯罩一般为梯形, 有顶面、左侧面和右侧面共3个反射表面;灯管一般成排安装在灯罩内部.整个红外灯一般安装在距离被加热表面一定高度的位置, 灯罩顶面在大多数情况下与被加热表面平行, 偶尔呈现一定的角度, 但仅讨论平行安装的普遍情况.
考虑到直接建立三维情形下的热源方程存在一定的难度, 为了分析和描述问题的方便, 首先建立二维情形下的红外热源方程, 然后推广到三维情形.红外灯的构型在长度方向上是基本均匀的, 主要的构型参数均在xy平面内.首先建立xy平面内的二维红外热源方程, 求解沿x方向的辐射热流分布;然后考虑热流沿z方向的分布, 将红外热源方程推广到三维空间.
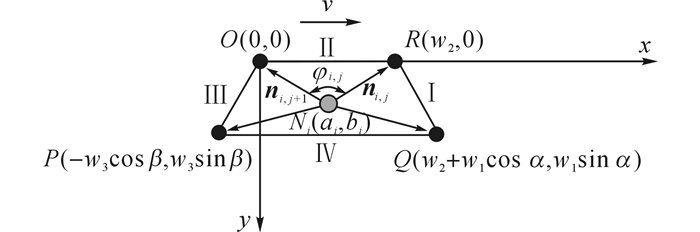
1.1 灯管辐射功率的分配如图 2所示, 灯管辐射出的红外线可以分为两部分:一部分直接射向被加热表面, 称为直接辐射;另一部分射向灯罩, 经过3个灯罩平面的若干次反射后再射向被加热表面, 称为间接辐射.假设红外灯以速率v匀速移动, 以O点为原点, 水平向右为x轴正向, 建立随红外灯移动的动直角坐标系.
|
图 2 灯管的功率分配示意图 Fig. 2 Diagram of power distribution of lamp tube |
各部分辐射功率的分配与相对灯管的角度有关, 称为有效辐射角.由图 2可知,
| $ {\varphi _{i,j}} = \arccos \frac{{{\mathit{\boldsymbol{n}}_{i,j}} \cdot {\mathit{\boldsymbol{n}}_{i,j + 1}}}}{{\left| {{\mathit{\boldsymbol{n}}_{i,j}}} \right|\left| {{\mathit{\boldsymbol{n}}_{i,j + 1}}} \right|}}. $ | (1) |
式中:φi, j为第i根灯管第j部分的有效辐射角, 其中i=1, 2, …, k, j=1, 2, 3, 4, k为灯管根数;ni, j和ni, j+1分别为φi, j的两侧边向量,
| $ {\mathit{\boldsymbol{n}}_{i,1}} = {\mathit{\boldsymbol{n}}_{i,5}} = \left[ {{w_2} + {w_1}\cos \alpha - {a_i},{w_1}\sin \alpha - {b_i}} \right], $ | (2) |
| $ {\mathit{\boldsymbol{n}}_{i,2}} = \left[ {{w_2} - {a_i}, - {b_i}} \right], $ | (3) |
| $ {\mathit{\boldsymbol{n}}_{i,3}} = \left[ { - {a_i}, - {b_i}} \right], $ | (4) |
| $ {\mathit{\boldsymbol{n}}_{i,4}} = \left[ { - {w_3}\cos \beta - {a_i},{w_3}\sin \beta - {b_i}} \right], $ | (5) |
其中w1为灯罩右侧面的宽度, w2为灯罩顶面的宽度, w3为灯罩左侧面的宽度, α为灯罩右侧面与顶面的角度, β为灯罩左侧面与顶面的角度, ai为第i根灯管的x坐标, bi为第i根灯管的y坐标.
由于灯管在周向的辐射强度是均匀的, 各部分的辐射功率为
| $ {P_{i,j}} = {P_i}\left( {{\varphi _{i,j}}/\left( {2{\rm{ \mathsf{ π} }}} \right)} \right). $ | (6) |
式中:Pi, j为第i根灯管对第j部分的辐射功率, Pi为第i根灯管的总辐射功率.
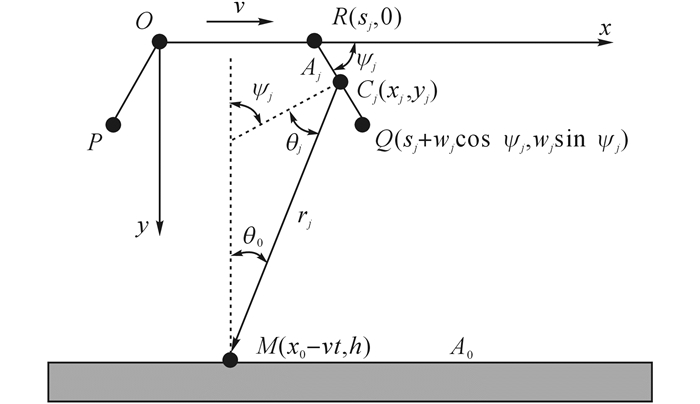
1.2 灯罩间接辐射的热流密度如图 3所示, 虽然部分红外线会在3个灯罩平面之间反射多次才到达被加热表面, 但与被加热表面相比, 灯罩平面的面积很小, 接受的来自其他灯罩平面的辐射相对很小;3个灯罩平面会相互反射, 导致彼此的反射相互抵消, 因此仅考虑经灯罩反射一次即到达被加热表面的辐射.为了简化问题, 假设灯罩平面的辐射功率密度是基本均匀的[32-33], 灯罩与被加热表面的辐射问题可以简化为二面辐射问题.根据传热学基本原理可知, 2个表面之间的辐射角系数[36]为
| $ {F_{{A_j},{A_0}}} = \frac{1}{{{A_j}}}\int_{{A_j}} {\int_{{A_0}} {\frac{{\cos {\theta _j}\cos {\theta _0}}}{{{\rm{ \mathsf{ π} }}r_j^2}}{\rm{d}}{A_j}{\rm{d}}{A_0}} } . $ | (7) |
|
图 3 灯罩在xy平面内的间接辐射示意图 Fig. 3 Diagram of indirect radiation of lampshades in xy plane |
式中:FAj, A0为表面Aj对表面A0的辐射角系数, Aj为发射辐射表面的面积, A0为接受辐射表面的面积, rj为两表面微元面中心的距离, θj为rj与微元面dAj法向的夹角, θ0为rj与微元面dA0法向的夹角.
根据式(7), 可以推导出角系数面密度:
| $ \frac{{{F_{{A_j},{\rm{d}}{A_0}}}}}{{{\rm{d}}{A_0}}} = \frac{1}{{{A_j}}}\int_{{A_j}} {\frac{{\cos {\theta _j}\cos {\theta _0}}}{{{\rm{ \mathsf{ π} }}r_j^2}}{\rm{d}}{A_j}} . $ | (8) |
式中:FAj, dA0为表面Aj对微元面dA0的角系数.
如图 3所示, 定义被加热表面在t时刻受到的第j个灯罩平面辐射的角系数线密度为fj(x0, t).根据式(8), 有
| $ {f_j}\left( {{x_0},t} \right) = \left| {\frac{1}{{{w_j}\cos {\psi _j}}}\int_{{s_j}}^{{s_j} + {w_j}\cos {\psi _j}} {\frac{{\cos {\theta _j}\cos {\theta _0}}}{{{\rm{ \mathsf{ π} }}r_j^2}}{\rm{d}}{x_j}} } \right|. $ | (9) |
式中:
| $ {r_j} = \sqrt {{{\left( {{x_j} - {x_0} + vt} \right)}^2} + {{\left( {h - {y_j}} \right)}^2}} ; $ | (10) |
| $ \cos {\theta _j} = \left[ {\left( {h - {y_j}} \right)\cos {\psi _j} + \left( {{x_j} - {x_0} + vt} \right)\sin {\psi _j}} \right]/{r_j}; $ | (11) |
| $ \cos {\theta _0} = \left( {h - {y_j}} \right)/{r_j}; $ | (12) |
| $ {y_j} = \left( {{x_j} - {s_j}} \right)\tan {\psi _j}; $ | (13) |
fj(x0, t)为表面A0在t时刻受表面Aj辐射的角系数线密度;x0为微元面dA0中心在零时刻的x坐标;l为灯管的长度;h为灯罩顶面距被加热表面的高度;wj为第j个灯罩平面的宽度, j=1, 2, 3;ψj为第j个灯罩平面与x轴正向的夹角;sj为第j个灯罩平面起点的x坐标, xj为微元面dAj中心的x坐标;yj为微元面dAj中心的y坐标.式(9)~(13)中, 3个灯罩平面的具体宽度和位置参数如表 1所示.
| 表 1 3个灯罩平面的宽度和位置 Table 1 Width and position of three lampshade planes |
灯管射向灯罩的红外线一部分被灯罩吸收, 另一部分被灯罩反射到被加热表面.灯罩在吸收红外辐射的同时也在发射红外辐射, 在实际使用中, 灯罩外表面通常被隔热层包裹.假设灯罩是漫射灰体, 当灯罩达到稳态时, 发射的辐射能够与吸收的相互平衡, 即基本不损耗辐射功率[32].考虑到被加热表面(假设被加热表面为漫射灰体, 吸收率等于发射率)的辐射吸收能力, 最终被加热表面在t时刻受到的灯罩平面间接辐射功率线密度为
| $ {{q'}_i}\left( {{x_0},t} \right) = {\varepsilon _0}\sum\limits_{j = 1}^3 {{P_{i,j}}{f_j}\left( {{x_0},t} \right)} . $ | (14) |
式中:q′i(x0, t)为第i根灯管在t时刻通过灯罩平面间接辐射到被加热表面的辐射功率线密度, i=1, 2, …, k;ε0为被加热表面的吸收率.
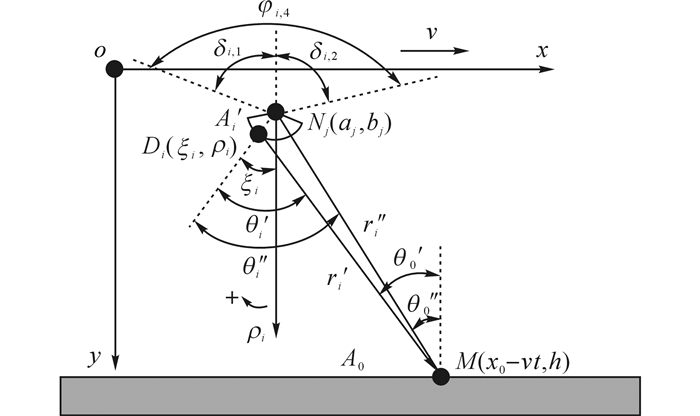
1.3 灯管直接辐射的热流密度如图 4所示, 灯管与被加热表面的辐射问题是一个二面辐射问题.与灯罩平面不同的是, 灯管表面是一个圆弧面, 因此建立以灯管中心Ni点为原点的极坐标, 极轴与y轴平行, 以顺时针方向为正.
|
图 4 灯管在xy平面内的直接辐射示意图 Fig. 4 Diagram of direct radiation of lamp tube in xy plane |
定义被加热表面在t时刻受到的第i根灯管直接辐射的角系数线密度为gi(x0, t), 根据式(8), 有
| $ {g_i}\left( {{x_0},t} \right) = \frac{l}{{{\varphi _{i,4}}}}\int_{ - {\delta _{i,1}}}^{{\delta _{i,2}}} {\frac{{\cos {{\theta '}_i}\cos {{\theta '}_0}}}{{{\rm{ \mathsf{ π} }}r{'}_i^2}}{\rm{d}}{\xi _i}} . $ | (15) |
式中:
| $ \begin{array}{l} {\delta _{i,1}} = \\ \arccos \frac{{{w_1}\sin \alpha - {b_i}}}{{\sqrt {{{\left( {{w_2} + {w_1}\cos \alpha - {a_i}} \right)}^2} + {{\left( {{w_1}\sin \alpha - {b_i}} \right)}^2}} }}, \end{array} $ | (16) |
| $ {\delta _{i,2}} = {\varphi _{i,4}} - {\delta _{i,1}}. $ | (17) |
灯管半径相对于微元面间的距离很小, 因此
| $ \cos {{\theta '}_0} \buildrel\textstyle.\over= \cos {{\theta ''}_0} = \frac{{h - {b_i}}}{{{{r''}_i}}}, $ | (18) |
| $ {{r'}_i} \buildrel\textstyle.\over= {{r''}_i} = \sqrt {{{\left( {{x_0} - vt - {a_i}} \right)}^2} + {{\left( {h - {b_i}} \right)}^2}} , $ | (19) |
| $ {{\theta '}_i} \buildrel\textstyle.\over= {{\theta ''}_i} = {\xi _i} + {{\theta ''}_0}, $ | (20) |
| $ \cos {{\theta '}_i} = \frac{{\left( {h - {b_i}} \right)\cos {\xi _i} - \left( {{x_0} - vt - {a_i}} \right)\sin {\xi _i}}}{{{{r''}_i}}}. $ | (21) |
式中:gi(x0, t)为表面A0在t时刻受灯管i直接辐射的角系数线密度, i=1, 2, …, k;δi, 1为第i根灯管右边界与极轴ρi间的夹角;δi, 2为第i根灯管左边界与极轴ρi的夹角;ξi为第i根灯管的微元面dA′i法向与极轴ρi的夹角;r′i为两表面微元面间的距离;θ′i为r′i与微元面dA′i法向的夹角;θ′0为r′i与微元面dA0法向的夹角;r″i为微元面dA0与灯管中心的距离;θ″i为r″i与微元面dA′i法向的夹角;θ″0为r″i与微元面dA0法向的夹角.
考虑到被加热表面的辐射吸收能力, 被加热表面在时刻接受到的灯管i直接辐射功率线密度为
| $ {{q''}_i}\left( {{x_0},t} \right) = {\varepsilon _0}{P_{i,4}}{g_i}\left( {{x_0},t} \right). $ | (22) |
式中:q″i(x0, t)为第i根灯管在t时刻直接辐射到被加热表面的辐射功率线密度, i=1, 2, …, k.
1.4 红外热源方程在二维情形下, 被加热表面在t时刻受到的来自红外灯的总辐射功率线密度(即二维热源方程)可以联立式(6)、(14)、(22)得到:
| $ \begin{array}{l} q\left( {{x_0},t} \right) = \\ \;\;\;{\varepsilon _0}\sum\limits_{i = 1}^k {{P_i}\left[ {\sum\limits_{j = 1}^3 {\frac{{{\varphi _{i,j}}}}{{2{\rm{ \mathsf{ π} }}}}{f_j}\left( {{x_0},t} \right)} + \frac{{{\varphi _{i,4}}}}{{2{\rm{ \mathsf{ π} }}}}{g_i}\left( {{x_0},t} \right)} \right]} . \end{array} $ | (23) |
式中:q(x0, t)为二维红外热源方程.
将二维红外热源方程中的角系数线密度换成角系数面密度, 可得三维情形下的红外热源方程:
| $ \begin{array}{l} Q\left( {{x_0},{z_0},t} \right) = \\ {\varepsilon _0}\sum\limits_{i = 1}^k {{P_i}\left[ {\sum\limits_{j = 1}^3 {\frac{{{\varphi _{i,j}}}}{{2{\rm{ \mathsf{ π} }}}}{F_j}\left( {{x_0},{z_0},t} \right)} + \frac{{{\varphi _{i,4}}}}{{2{\rm{ \mathsf{ π} }}}}{G_i}\left( {{x_0},{z_0},t} \right)} \right]} . \end{array} $ | (24) |
式中:Q(x0, z0, t)为三维红外热源方程, z0为微元面dA0中心在零时刻的z坐标, Fj(x0, z0, t)为表面A0在t时刻受表面Aj辐射的角系数面密度, Gi(x0, z0, t)为表面A0在t时刻受灯管i直接辐射的角系数面密度.
对于给定的铺放设备, 式(23)、(24)中除了pi需要通过试验进行测定外, 其余各项都是已知的.其中, ε0与被加热表面的材料及状态有关;φi, j与灯管相对灯罩的位置有关, j=1, 2, 3, 4;fj(x0, t)、Fj(x0, z0, t)、gi(x0, t)和Gi(x0, z0, t)与红外灯的外形尺寸、安装位置及被加热表面某点相对红外灯的位置等有关.
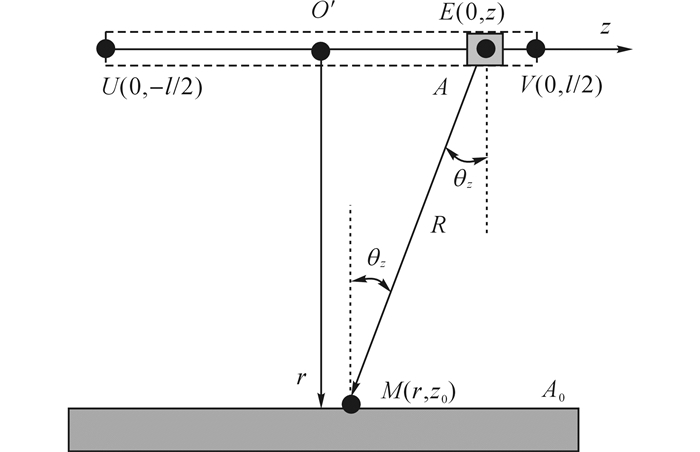
为了求解角系数面密度, 需要将xy平面内的角度和距离推广到三维空间.如图 5所示, 以红外灯罩左上角侧边中点O′为原点, 以灯管长度方向为z方向, 建立rz平面内的直角坐标系.对于灯罩间接辐射的情形, 根据式(9), 有
| $ \begin{array}{l} {F_j}\left( {{x_0},{z_0},t} \right) = \\ \left| {\frac{1}{{l{w_j}\cos {\psi _j}}}\int_{{s_j}}^{{s_j} + {w_j}\cos {\psi _j}} {\int_{ - l/2}^{l/2} {\frac{{\cos {\mathit{\Theta }_j}\cos {\mathit{\Theta }_0}}}{{{\rm{ \mathsf{ π} }}R_j^2}}{\rm{d}}{x_j}{\rm{d}}{z_j}} } } \right|. \end{array} $ | (25) |
|
图 5 红外灯在rz平面内的辐射示意图 Fig. 5 Diagram of radiation of infrared lamp in rz plane |
式中:Rj为两表面微元面dAj和dA0中心的空间距离,
| $ {R_j} = \sqrt {{{\left( {{x_j} - {x_0}} \right)}^2} + {{\left( {h - {y_j}} \right)}^2} + {{\left( {{z_j} - {z_0}} \right)}^2}} , $ | (26) |
其中zj为微元面dAj中心的z坐标;Θj为Rj与微元面dAj法向的空间夹角,
| $ \cos {\mathit{\Theta }_j} = \cos {\theta _j}\cos {\theta _z}; $ | (27) |
Θ0为Rj与微元面dA0法向的空间夹角,
| $ \cos {\mathit{\Theta }_0} = \cos {\theta _0}\cos {\theta _z}, $ | (28) |
其中θz为空间距离Rj与xy面内距离rj的夹角,
| $ \cos {\theta _z} = \frac{{{r_j}}}{{{R_j}}}. $ | (29) |
对于灯管直接辐射的情形, 根据式(15), 有
| $ {G_i}\left( {{x_0},{z_0},t} \right) = \frac{1}{{l{\varphi _{i,4}}}}\int_{ - {\delta _{i,1}}}^{{\delta _{i,2}}} {\int_{ - l/2}^{l/2} {\frac{{\cos {{\mathit{\Theta '}}_i}\cos {{\mathit{\Theta '}}_0}}}{{{\rm{ \mathsf{ π} }}R{'}_i^2}}{\rm{d}}{\xi _i}{\rm{d}}{{z'}_i}} } . $ | (30) |
式中:z′i为微元面dA′i中心的z坐标;R′i为两表面微元面dA′i和dA0中心的空间距离,
| $ {{R'}_i} = \sqrt {{{\left( {{x_0} - vt - {a_i}} \right)}^2} + {{\left( {h - {b_i}} \right)}^2} + {{\left( {{{z'}_i} - {z_0}} \right)}^2}} ; $ | (31) |
Θ′i为R′i与微元面dA′i法向的空间夹角,
| $ \cos {{\mathit{\Theta '}}_i} = \cos {{\theta '}_i}\cos {{\theta '}_z}, $ | (32) |
其中θ′z为空间距离R′i与xy面内距离r′i的夹角,
| $ \cos {{\theta '}_z} = \frac{{{{r'}_i}}}{{{{R'}_i}}}; $ | (34) |
Θ′0为R′i与微元面dA0法向的空间夹角,
| $ \cos {{\mathit{\Theta '}}_0} = \cos {{\theta '}_0}\cos {{\theta '}_z}. $ | (33) |
红外灯管的辐射功率与灯丝温度、尺寸及发射率等众多因素有关, 理论计算相对复杂, 需要通过试验的方法测定红外灯管的辐射功率.
2.1 圆筒试验方法如图 6所示, 通过自行设计的圆筒试验测定灯管的辐射功率.具体方法如下:打开红外灯管, 待功率稳定后, 快速置于等厚不锈钢圆筒的中心;利用热电偶, 记录圆筒底面和柱面在一段时间内的温度变化.根据传热平衡方程[36], 有
| $ P{t_1}\varepsilon = c\rho e\left( {\frac{{{\rm{ \mathsf{ π} }}{d^2}}}{2}\Delta {T_1} + {\rm{ \mathsf{ π} }}dl\Delta {T_2}} \right). $ | (35) |

|
图 6 圆筒试验示意图 Fig. 6 Diagram of cylinder test |
式中:P为灯管辐射功率, t1为辐射时间, ε为圆筒内表面的吸收率, c为不锈钢比热容, ρ为不锈钢密度, e为圆筒厚度, d为圆筒外径, ΔT1为圆筒底面的温度变化值, ΔT2为圆筒柱面的温度变化值.
试验装置如图 7所示, 为了减少圆筒外表面的散热, 在圆筒上粘贴了聚四氟乙烯隔热胶带.为了提高圆筒内表面的辐射吸收率, 在圆筒内表面上喷涂了黑色油漆.圆筒试验的各项参数如表 2所示.

|
图 7 圆筒试验装置 Fig. 7 Setup of cylinder test |
| 表 2 圆筒试验参数 Table 2 Parameters of cylinder test |
试验时, 利用万用表测量灯管的电压与电流, 从而推算电功率, 可知灯管的电-辐射转化效率为
| $ \eta = P/{P_{\rm{E}}}. $ | (36) |
式中:PE为电功率.
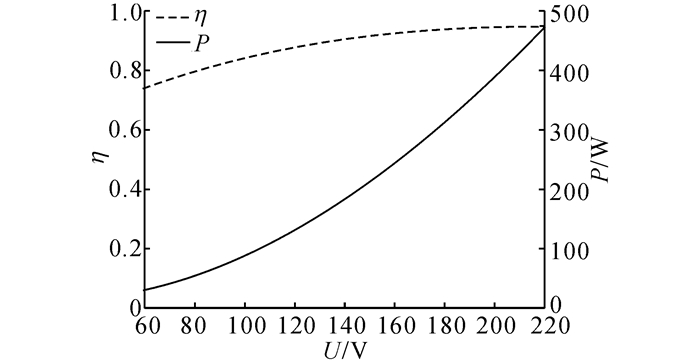
2.2 圆筒试验结果测量灯管在不同电压U下的辐射功率和电-辐射转化效率, 结果如图 8所示.可见, 随着灯管电压的增大, 电-辐射转化效率逐渐升高, 表明红外灯应尽量在额定电压下工作.当电压为220 V时, 红外灯的辐射功率和电-辐射转化效率分别为480 W和0.95.
|
图 8 灯管在不同电压下的辐射功率和电-辐射转化效率 Fig. 8 Radiation power and conversion efficiency of lamp tube at different voltages |
由于热流密度无法直接测出, 通过测量被加热表面的温度来验证热源方程的准确性.设计红外灯动态加热试验, 利用热电偶测量被加热表面上固定点的温度随时间的变化曲线.温度分布一般用红外热像仪测量, 由于红外灯动态加热时, 温度分布很难测准, 设计红外灯静态加热试验, 用以测量被加热表面的温度分布.将式(23)所描述的三维红外热源方程导入有限元模型中, 计算被加热表面上的温度, 并与试验结果对比.
3.1 红外灯加热试验为了验证上述红外热源方程的准确性, 设计红外灯动态加热试验.如图 9(a)所示, 将一块Q235钢板固定在匀速移动平台上, 钢板的尺寸为490 mm×400 mm×8 mm, 移动平台的移动速率为0~120 mm/s.首先, 打开红外灯, 待功率稳定后, 快速置于Q235钢板的右上方并保持不动;迅速启动移动平台, 让钢板从红外灯下方匀速通过.利用热电偶, 记录钢板表面上固定点的温度随时间的变化曲线, 一共设置了3个测试点, 位置如图 9(a)所示.

|
图 9 红外灯加热试验 Fig. 9 Heating test with infrared lamp |
为了测量被加热表面的温度分布, 设计红外灯静态加热试验.如图 9(b)所示, 具体方法如下:打开红外灯, 待功率稳定后, 快速置于Q235钢板的正上方, 对钢板加热1 min后迅速撤去红外灯(避免红外灯发出的红外线对红外热像仪产生干扰), 利用Fluke Ti95红外热像仪记录钢板表面的温度分布.为了抑制钢板底面的热传导, 在底部放置铁氟龙隔热胶带或石棉隔热垫;为了提高钢板表面的辐射吸收率, 并保证红外热像仪的测量准确性, 在钢板表面上喷涂了黑色油漆, 吸收率ε0=0.95[36].试验中所用红外灯的其他参数如表 3、4所示.
| 表 3 红外灯灯罩参数 Table 3 Parameters of infrared lampshades |
| 表 4 红外灯灯管参数 Table 4 Parameters of infrared lamp tubes |
为了求解上述钢板表面的温度变化和温度分布情况, 在ABAQUS仿真平台上对红外灯动态和静态加热模型开展有限元仿真, 并将式(24)编写到ABAQUS的DFLUX子程序中.其中, ε0=0.95;Pi通过圆筒试验进行测定, 具体如表 4所示;φi, j通过式(1)~(5)确定;Fj(x0, z0, t)通过式(25)~(29)、(10)~(13)确定;Gi(x0, z0, t)通过式(30)~(34)、(16)~(21)确定;式(1)~(5)、(10)~(13)、(16)~(21)、(25)~(29)、(30)~(34)中参数的具体值见表 1、3、4.当静态加热仿真时, 令v=0, 并将红外灯中心与钢板中心竖直对齐;当动态加热仿真时, 分别令v=20、40和80 mm/s, 并将红外灯的初始原点设置在钢板最右端.
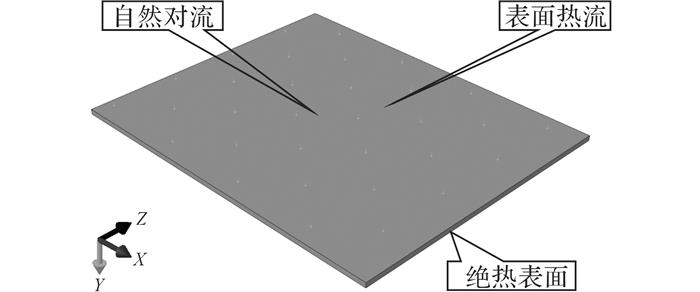
如图 10所示, 将子程序导入到ABAQUS中, 并添加DFLUX到钢板表面上;考虑钢板表面的空气自然对流作用和钢板底面的绝热边界, 空气对流系数为6 W/(m2·K)[36], 钢板的尺寸和热学参数如表 5所示.表中,ls为钢板长度, ws为钢板宽度, es为钢板厚度, ρs为钢板密度, cs为钢板比热容, κs为钢板热导率.
|
图 10 红外灯加热有限元仿真 Fig. 10 FEM simulation of heating with infrared lamp |
| 表 5 钢板参数 Table 5 Parameters of steel plate |
对不同速率下红外灯动态加热的情形进行试验和有限元仿真, 3个测试点的温度θ-时间t曲线结果如图 11所示.可见, 3个测试点的温度均随着红外灯的靠近而升高, 随着红外灯的远离而降低;在红外灯正下方矩形区域即将离开测试点的时刻, 测试点的温度达到峰值, 各测试点的温度峰值随着移动速率的增大而减小.1~3号测试点的温度峰值呈逐渐升高的趋势, 这是因为红外灯在加热1号测试点时, 热量通过钢板传到了前方的2~3号测试点, 导致峰值温度略高.

|
图 11 不同移动速率下3个测试点的温度-时间曲线 Fig. 11 Temperature-time curves of three test points under different moving velocities |
由图 11可知, 在温度上升阶段, 仿真曲线与试验曲线基本吻合, 并且温度峰值的差异均在5%以内, 表明有限元仿真能够较好地模拟钢板表面上固定点的升温过程.在温度下降的前半阶段, 仿真结果与试验结果吻合较好;在温度下降的后半阶段, 仿真曲线普遍比试验曲线高, 表明有限元仿真对测试点后半段降温过程的模拟存在一定的误差, 可能原因是钢板底面虽然设置了隔热层, 但是不能完全隔绝热量的传递, 导致钢板的实际降温速率偏快.
在实际的铺放过程中, 影响铺放质量的因素主要是黏合点的温度, 黏合点随着红外灯的移动而移动[3].由计算可知, 当黏合点到达测试点时, 测试点的温度正处于前半降温阶段, 上述有限元仿真能够较好地模拟该阶段的温度变化, 表明通过仿真可以计算出黏合点的温度, 说明了上述动态热源方程的有效性.
对红外灯在不同高度下静态加热的情形开展试验和有限元仿真, 钢板表面的温度分布结果如图 12所示.可见, 有限元计算的结果与试验结果吻合良好.结合动态加热试验和仿真的对比结果可知, 上述热源方程能够较好地描述红外灯在被加热表面上的热流分布, 验证了所建热源方程的准确性.
对比结果显示, 试验测量温度普遍比有限元计算温度稍低, 可能是在撤走红外灯与拍摄热图的时间间隔内, 钢板温度下降造成的.另外, 钢板底面的传热和灯罩上的功率损耗可能是试验温度偏低的原因之一.

|
图 12 不同红外灯高度下钢板表面的温度分布 Fig. 12 Temperature distribution of steel plate surface under different infrared lamp heights |
为了指导自动铺放红外热源的设计, 需要得知红外灯参数对其热流分布的影响规律.红外灯的可控参数包括红外灯安装高度、灯罩顶面宽度、灯罩侧面角度及灯管安装位置等, 红外灯热流分布的定量描述指标包括热流密度的平均大小和均匀性等.由于红外灯的移动仅仅改变了在被加热表面上的热流密度峰值的位置, 在红外灯下方的某一固定大小的区域内, 热流密度的平均大小和均匀性与移动速率无关, 因此利用静态红外热源方程对红外灯的设计参数进行讨论.
4.1 红外灯热流分布的描述指标在确定了红外灯的尺寸、功率和安装位置后, 可以根据式(24), 利用Matlab直接求解红外灯的热流分布.其中, 通过式(1)~(5)确定;Fj(x0, z0, t)通过式(25)~(29)、(10)~(13)确定;Gi(x0, z0, t)通过式(30)~(34)、(16)~(21)确定.式(1)~(5)、(10)~(13)、(16)~(21)、(25)~(29)、(30)~(34)中参数的具体值如表 1、3、4所示, 令v=0, 求解结果如图 13所示.可知, 红外灯辐射到被加热表面上的热流不是均匀分布的, 呈现出单峰性, 功率密度峰值为26 904 W/m2.

|
图 13 红外灯在被加热表面上的辐射热流分布 Fig. 13 Radiative heat flux distribution of infrared lamp on heated surface |
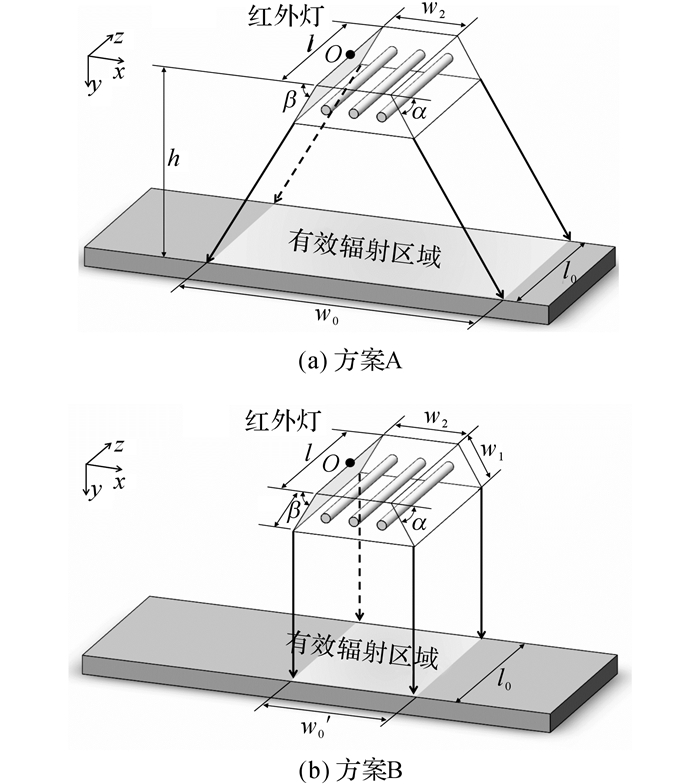
为了定量描述红外灯的热流分布情形, 首先需要定义红外灯的有效辐射区域;然后利用该区域上的热流密度均值衡量有效辐射的强度, 利用该区域上的热流密度离散系数衡量有效辐射的分散性.如图 14所示, 有效辐射区域的定义方法一般有2种:1)灯罩左、右两侧面延伸面与被加热表面的相交线之间的区域;2)红外灯正下方的矩形区域[32].
|
图 14 红外灯的有效辐射区域 Fig. 14 Effective radiation area of infrared lamp |
如图 14所示, 方案A和方案B定义的有效辐射区域的长度都与灯管的长度相同, 即
| $ {l_0} = l. $ | (37) |
式中:l0为有效辐射区域的长度.
如图 14所示, 方案A和方案B定义的有效辐射区域的宽度分别为
| $ {w_0} = h\cot \alpha + {w_2} + h\cot \beta , $ | (38) |
| $ {{w'}_0} = {w_1}\cot \alpha + {w_2} + {w_3}\cot \beta . $ | (39) |
式中:w0为方案A定义的有效辐射区域的宽度, w′0为方案B定义的有效辐射区域的宽度.
在探讨红外灯安装高度和灯罩侧面角度对红外灯热流分布的影响时, 方案A定义的有效辐射区域的宽度随着上述各个变量的变化而差异显著, 无法划定相对一致的有效辐射区域.方案B定义的有效辐射区域的宽度与红外灯安装高度无关, 且由于灯罩左、右两侧面的宽度较小, 随着灯罩侧面角度的变化, 有效辐射区域的宽度仅会产生很小的改变, 因此能够划定相对一致的有效辐射区域, 对有效辐射的强度和分散性进行定量对比分析.选择方案B来定义有效辐射区域.
定义有效辐射区域上的热流密度均值为有效辐射强度:
| $ U = \frac{1}{{{w_0}{l_0}}}\left\{ \begin{array}{l} - {w_3}\cos \beta \\ {w_2} + {w_1}\cos \alpha \end{array} \right.\int_{ - l/2}^{l/2} {Q\left( {{x_0},{z_0}} \right){\rm{d}}{x_0}{\rm{d}}{z_0}} . $ | (40) |
式中:U为有效辐射的强度.
定义有效辐射区域上的热流密度离散系数为有效辐射离散系数:
| $ V = \frac{1}{U}\sqrt {\frac{1}{{{w_0}{l_0}}}\left\{ \begin{array}{l} - {w_1}\cos \alpha \\ {w_2} + {w_3}\cos \beta \end{array} \right.\int_{ - l/2}^{l/2} {{{\left[ {Q\left( {{x_0},{z_0}} \right) - U} \right]}^2}{\rm{d}}{x_0}{\rm{d}}{z_0}} } . $ | (41) |
式中:V为有效辐射的离散系数.
定义有效辐射均匀度:
| $ W = 1 - V. $ | (42) |
式中:W为有效辐射的均匀度, 0 < W≤1.
根据式(40)~(42), 可以计算图 13所示辐射热流的有效辐射强度为15 697 W/m2, 有效辐射均匀度为0.54.该结果表明, 即使在红外灯正下方的矩形有效辐射区域内, 红外灯的辐射热流也不是均匀的, 而是有较大的离散性.应当合理设计红外灯的构型, 使有效辐射的强度更高, 均匀度更大.
4.2 红外灯辐射热流的来源红外灯的辐射包括4个部分:3个灯罩平面的间接辐射及灯管的直接辐射.对这4部分辐射热流进行对比, 确定被加热表面辐射热流的主要来源, 为红外灯的设计提供初步依据.为了便于描述和对比, 主要探讨二维、单根灯管的情形.由于红外灯在被加热表面上的热流分布是通过角系数密度来描述的, 主要分析对角系数线密度.
在分析灯罩的间接辐射和直接辐射的角系数线密度时, 都是参照灯罩或者灯管的一部分辐射功率进行计算.为了便于对比, 统一参照整根灯管的辐射功率进行分析, 即定义归一化角系数线密度:
| $ {\lambda _{i,j}}\left( {{x_0}} \right) = \left\{ \begin{array}{l} \frac{{{\varphi _{i,j}}}}{{2{\rm{ \mathsf{ π} }}}}{f_j}\left( {{x_0}} \right),j = 1,2,3;\\ \frac{{{\varphi _{i,4}}}}{{2{\rm{ \mathsf{ π} }}}}{g_i}\left( {{x_0}} \right),j = 4. \end{array} \right. $ | (43) |
式中:λi, j(x0)为被加热表面受灯管i第j部分辐射的归一化角系数线密度.
利用式(43)、(1)~(5)、(9)~(13)、(15)~(21)和表 1、3、4的灯罩和灯管参数, 可以求解灯管i(以i=2为例)各部分的归一化角系数线密度, 结果如图 15所示.可知, 从角系数线密度的峰值来看, 在红外灯的各部分辐射中, 灯管直接辐射占49.63%, 为主要部分;其次是灯罩顶面的辐射, 占25.33%;灯罩左、右两侧面的辐射功率相对较小, 各占12.52%.

|
图 15 红外灯各部分辐射的归一化角系数线密度 Fig. 15 Normalized view factor per unit length of each part of infrared lamp |
参照式(40)~(42), 可以定义二维的归一化有效辐射强度:
| $ {\sigma _{i,j}} = \frac{1}{{{w_0}}}\int_{{w_2} + {w_1}\cos \alpha }^{ - {w_3}\cos \beta } {{\lambda _{i,j}}\left( {{x_0}} \right){\rm{d}}{x_0}} . $ | (44) |
式中:σi, j为被加热表面受灯管i第j部分辐射的归一化有效辐射强度.
定义二维的归一化有效辐射均匀度:
| $ {\tau _{i,j}} = 1 - \frac{1}{{{\sigma _{i,j}}}}\sqrt {\frac{1}{{{w_0}}}\int_{{w_2} + {w_1}\cos \alpha }^{ - {w_1}\cos \alpha } {{{\left[ {{\lambda _{i,j}}\left( {{x_0}} \right) - {\sigma _{i,j}}} \right]}^2}{\rm{d}}{x_0}} } . $ | (45) |
式中:τi, j为被加热表面受灯管i第j部分辐射的归一化有效辐射均匀度.
利用式(43)~(45)、表 1、3、4的相关参数, 可以求解灯管i(以i=2为例)各个部分的归一化有效辐射强度和均匀度, 结果如表 6所示.
| 表 6 第2根灯管各部分的归一化有效辐射强度和均匀度 Table 6 Normalized effective radiation strength and uniformity of each part of second tube |
从表 6可见, 从有效辐射强度来看, 在红外灯的各部分辐射中, 灯管的直接辐射、灯罩顶面、灯罩左侧面和灯罩右侧面的间接辐射依次降低, 各占47.71%、28.22%、12.04%和12.04%.从有效辐射的均匀度来看, 灯罩顶面的间接辐射相对更加均匀, 均匀度为0.86;另外3部分的有效辐射均匀度分别为0.73、0.72和0.72.
在探讨红外灯设计参数对红外灯热流分布的影响之前, 首先定义被加热表面受灯管i辐射的总归一化角系数线密度, 为灯管各部分归一化角系数线密度的和:
| $ {\lambda _i}\left( {{x_0}} \right) = \sum\limits_{j = 1}^4 {{\lambda _{i,j}}\left( {{x_0}} \right)} . $ | (46) |
式中:λi(x0)为被加热表面受灯管i辐射的总归一化角系数线密度.
类似地, 可以定义被加热表面受灯管i辐射的总归一化有效辐射强度:
| $ {\sigma _i} = \frac{1}{{{w_0}}}\int_{{w_2} + {w_1}\cos \alpha }^{ - {w_3}\cos \beta } {{\lambda _i}\left( {{x_0}} \right){\rm{d}}{x_0}} . $ | (47) |
式中:σi为被加热表面受灯管i辐射的总归一化有效辐射强度.
定义被加热表面受灯管i辐射的总归一化有效辐射均匀度:
| $ {\tau _i} = 1 - \frac{1}{{{\sigma _i}}}\sqrt {\frac{1}{{{w_0}}}\int_{{w_2} + {w_3}\cos \beta }^{ - {w_1}\cos \alpha } {{{\left[ {{\lambda _i}\left( {{x_0}} \right) - {\sigma _i}} \right]}^2}{\rm{d}}{x_0}} } . $ | (48) |
式中:τi为被加热表面受灯管i辐射的总归一化有效辐射均匀度.
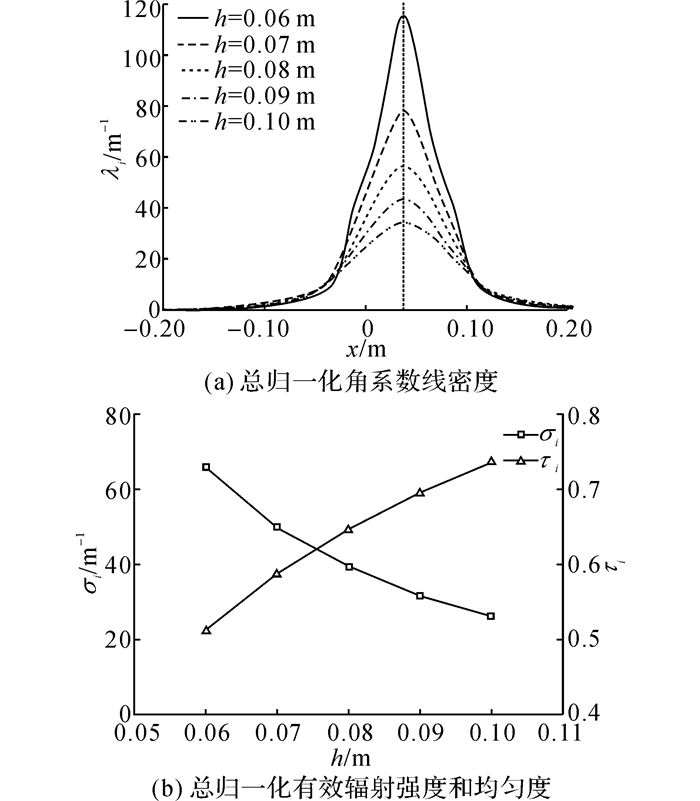
4.3 红外灯安装高度红外灯的安装高度是红外灯的主要设计参数之一, 对红外灯的辐射功率和辐射范围均有影响.利用式(46)、(43)、(1)~(5)、(9)~(13)、(15)~(21)和表 1、3、4的相关参数, 调整红外灯的安装高度, 可以求解红外灯在不同安装高度下的总归一化角系数线密度, 结果如图 16(a)所示.根据式(47)、(48)可知红外灯在不同安装高度下的总归一化有效辐射强度和均匀度, 结果如图 16(b)所示.
|
图 16 红外灯在不同安装高度下的总归一化有效辐射强度和均匀度 Fig. 16 Total normalized effective radiation strength and uniformity of infrared lamp under different installation heights |
由图 16可知, 随着红外灯安装高度从0.10 m降低到0.06 m(底边高度从0.06 m降低到0.02 m), 有效辐射强度从26.07 m-1升高到65.84 m-1, 即升高了1.5倍;有效辐射均匀度从0.74降低到0.51, 即降低了31.08%.结果表明, 适当降低红外灯的安装高度, 可以显著提高红外灯的有效辐射强度, 但会降低有效辐射均匀度.
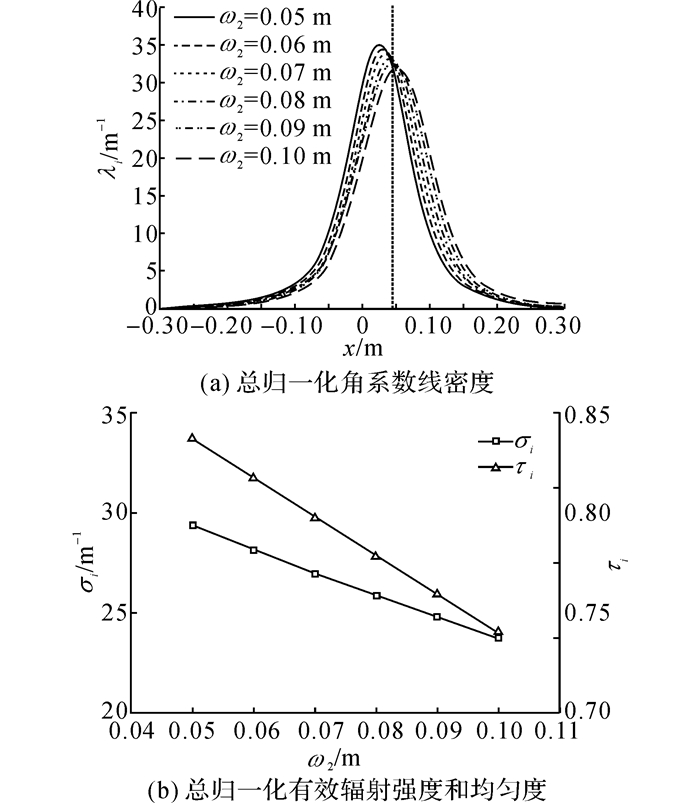
4.4 灯罩顶面宽度梯形灯罩有3个反射表面, 受铺放设备实际安装尺寸的限制, 主要的可设计参数包括顶面宽度和侧面与顶面的角度, 首先探讨灯罩顶面宽度对总归一化有效辐射强度和均匀度的影响.参照4.3节的求解方法, 调整红外灯的灯罩顶面宽度, 可以求解红外灯在不同灯罩顶面宽度下的总归一化角系数线密度以及有效辐射强度和均匀度, 结果如图 17所示.
|
图 17 红外灯在不同灯罩顶面宽度下的总归一化有效辐射强度和均匀度 Fig. 17 Total normalized effective radiation strength and uniformity of infrared lamp under different widths of top lampshade |
由图 17可知, 当灯罩顶面宽度从0.05 m增大到0.10 m时, 红外灯的有效辐射强度从29.41 m-1降低到23.79 m-1, 改变了19.11%;红外灯的有效辐射均匀度从0.84降低到0.74, 改变了11.90%;上述变化趋势均近似为线性.结果表明, 随着灯罩顶面宽度的增加, 红外灯的有效辐射强度和均匀度均近似线性下降.
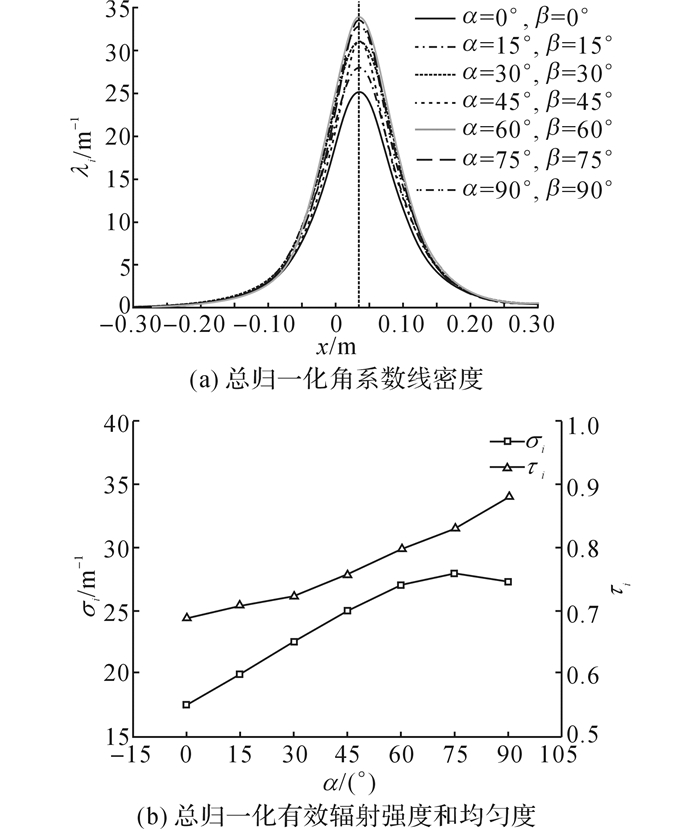
4.5 灯罩侧面角度红外灯罩的两侧面与顶面的角度(简称灯罩侧面角度)对红外灯的辐射范围有较大的影响, 是红外灯罩的主要参数之一.实际中的灯罩一般对称设计, 因此主要考虑左、右侧面与顶面的角度相等的情形.参照4.3节的求解方法, 调整红外灯罩侧面角度, 可知红外灯在不同灯罩侧面角度下的总归一化角系数线密度及有效辐射强度和均匀度, 结果如图 18所示.图中,α=β.
|
图 18 红外灯在不同灯罩侧面角度下的总归一化有效辐射强度和均匀度 Fig. 18 Total normalized effective radiation strength and uniformity of infrared lamp under different angles of side lampshades |
由图 18可知, 随着灯罩侧面角度从0°增加到90°, 红外灯的有效辐射强度先从17.49 m-1上升到27.92 m-1, 改变了59.68%;再从27.92 m-1下降到27.27 m-1, 改变了2.33%;有效辐射均匀度从0.69单调上升到0.88, 改变了27.54%.红外灯有效辐射强度的峰值大概在灯罩侧面角度为60°~75°时取得.结果表明, 将灯罩侧面角度设计为60°~75°, 有利于提高红外灯的有效辐射强度, 且能够取得较高的有效辐射均匀度(约为0.83).
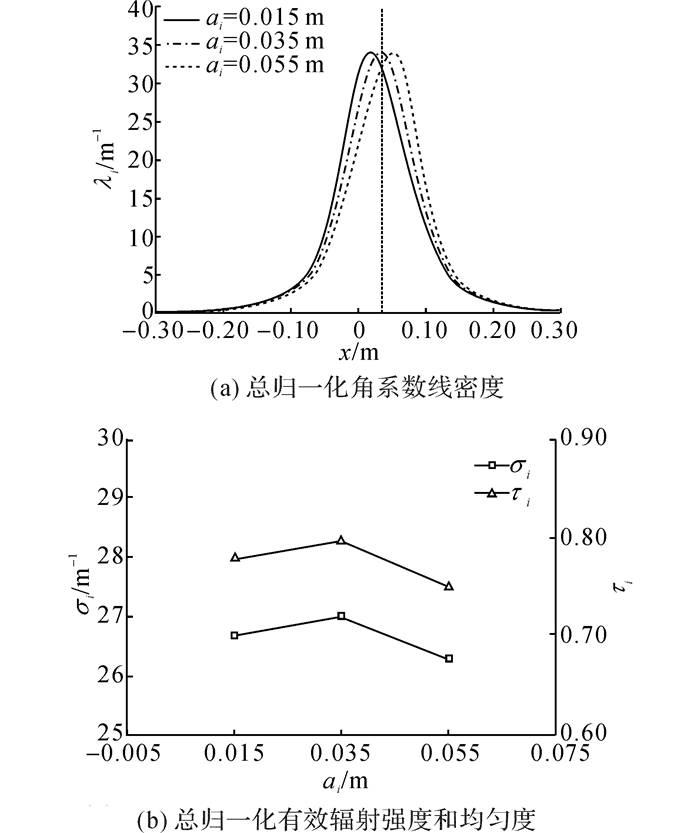
4.6 灯管位置灯管相对灯罩的位置主要影响灯管各部分的辐射功率分配, 受铺放设备的空间限制, 灯管的y方向位置变化不大, 主要是x方向的平行移动.主要探讨灯管的x坐标对总归一化角系数线密度以及有效辐射强度和均匀度的影响, 结果如图 19所示.
|
图 19 红外灯在不同灯管位置下的总归一化有效辐射强度和均匀度 Fig. 19 Total normalized effective radiation strength and uniformity of infrared lamp under different positions of lamp tube |
由图 19可知, 灯管在x方向的位置从0.015 m平行移动到0.055 m时, 红外灯有效辐射强度的最大值和最小值分别为27.02 m-1和26.31 m-1, 变化范围小于3%;红外灯有效辐射均匀度的最大值和最小值分别为0.80和0.75, 变化范围小于7%.结果表明, 在红外灯管水平安装的情形下, x方向安装位置对有效辐射强度和均匀度的影响很小.
5 结论(1) 建立自动铺放红外热源方程.该方程考虑了红外灯长度与安装高度、灯罩各面宽度与角度以及灯管辐射功率与安装位置等设计参数.
(2) 包含热源方程的红外灯动静态加热有限元仿真与试验结果基本一致, 热源方程得到验证.
(3) 在红外灯的各部分辐射中, 灯管直接辐射、灯罩顶面、灯罩左侧面和灯罩右侧面间接辐射的有效辐射强度各占47.71%、28.22%、12.04%和12.04%.
(4) 在红外灯水平安装的情形下, 当红外灯安装高度从0.10 m降低到0.06 m时, 有效辐射强度升高1.5倍, 均匀度降低31.08%;将灯罩侧面角度设计为60°~75°, 可以使红外灯的有效辐射强度提高59.68%, 且能够达到约0.83的均匀度;当灯罩顶面宽度从0.05 m增大到0.10 m时, 红外灯有效辐射强度降低19.11%, 均匀度降低11.90%;当灯管x方向位置从0.015 m增大到0.055 m时, 红外灯有效辐射强度和均匀度的变化均在7%以内.
本文通过所建的红外热源方程探讨红外灯设计参数对热流分布的影响规律, 实际被加热表面(模具或者预浸料铺层的表面)的铺放温度分布与红外灯的热流分布和移动速率均有较大关系.下一步的研究工作是将该热源方程导入铺放传热模型, 开展动态铺放仿真, 探究红外热源参数与铺放速率对铺放温度的影响规律.
| [1] |
顾轶卓, 李敏, 李艳霞, 等. 飞行器结构用复合材料制造技术与工艺理论进展[J]. 航空学报, 2015, 36(8): 2773-2797. GU Yi-zhuo, LI Min, LI Yan-xia, et al. Progress on manufacturing technology and process theory of aircraft composite structure[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2773-2797. |
| [2] |
文立伟, 肖军, 王显峰, 等. 中国复合材料自动铺放技术研究进展[J]. 南京航空航天大学学报, 2015, 47(5): 637-649. WEN Li-wei, XIAO Jun, WANG Xian-feng, et al. Progress of automated placement technology for composites in china[J]. Journal of Nanjing University of Aeronautics Astronautics, 2015, 47(5): 637-649. |
| [3] |
LUKASZEWICZ D H, WARD C, POTTER K. The engineering aspects of automated prepreg layup:history, present and future[J]. Composites Part B:Engineering, 2012, 43(3): 997-1009. DOI:10.1016/j.compositesb.2011.12.003 |
| [4] |
LUKASZEWICZ D H, Adrian H J. Optimisation of high-speed automated layup of thermoset carbon-fibre preimpregnates[D]. Bristol: University of Bristol, 2011. http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.541610
|
| [5] |
SCHLEDJEWSKI R, LATRILLE M. Processing of unidirectional fiber reinforced tapes-fundamentals on the way to a process simulation tool (ProSimFRT)[J]. Composites Science and Technology, 2003, 63(14): 2111-2118. DOI:10.1016/S0266-3538(03)00108-8 |
| [6] |
LUKASZEWICZ D H, POTTER K. Through-thickness compression response of uncured prepreg during manufacture by automated layup[J]. Journal of Engineering Manufacture, 2012, 226(10): 193-202. |
| [7] |
GUAN X, PITCHUMANI R. Modeling of spherulitic crystallization in thermoplastic tow-placement process:heat transfer analysis[J]. Composites Science and Technology, 2004, 64(9): 1123-1134. DOI:10.1016/j.compscitech.2003.08.011 |
| [8] |
CROSSLEY R J, SCHUBEL P J, WARRIOR N A. The experimental determination of prepreg tack anddynamic stiffness[J]. Composites Part A:Applied Science and Manufacturing, 2011, 43(3): 423-434. |
| [9] |
陆楠楠, 肖军, 齐俊伟, 等. 面向自动铺放预浸料动态黏性实验研究[J]. 航空学报, 2014, 35(1): 279-286. LU Nan-nan, XIAO Jun, QI Jun-wei, et al. Experimental research on prepreg dynamic tack based on automated placement process[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 279-286. |
| [10] |
文琼华, 王显峰, 何思敏, 等. 温度对预浸料铺放效果的影响[J]. 航空学报, 2011, 32(9): 1740-1745. WEN Qiong-hua, WANG Xian-feng, HE Si-min, et al. Influence of temperature on placement effect of prepreg[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1740-1745. |
| [11] |
黄志军, 王显峰, 戴振东, 等. 动铺放过程双马树脂预浸料温度与黏度[J]. 复合材料学报, 2012, 29(3): 49-53. HUANG Zhi-jun, WANG Xian-feng, DAI Zhen-dong, et al. Temperature and viscosity of bismaleimide resin prepregs in automated tape laying process[J]. Acta Materiae Compositae Sinica, 2012, 29(3): 49-53. |
| [12] |
段玉岗, 刘芬芬, 陈耀, 等. 纤维铺放压紧力及预浸带加热温度对复合材料力学性能的影响[J]. 复合材料学报, 2012, 29(4): 148-156. DUAN Yu-gang, LIU Fen-fen, CHEN Yao, et al. Effects of compaction force and heating temperature of prepreg on composite mechanical properties during fiber placement process[J]. Acta Materiae Compositae Sinica, 2012, 29(4): 148-156. |
| [13] |
TIERNEY J, GILLESPIE J. Modeling of heat transfer and void dynamics for the thermoplastic composite tow-placement process[J]. Journal of Composite Materials, 2003, 37(19): 1745-1768. DOI:10.1177/002199803035188 |
| [14] |
GROUVE W. Weld strength of laser-assisted tape-placed thermoplastic composites[D]. Enschede: University of Twente, 2012. http://dx.doi.org/10.3990/1.9789036533928
|
| [15] |
KHAN M A, MITSCHANG P, SCHLEDJEWSKI R. Parametric study on processing parameters and resulting part quality through thermoplastic tape placement process[J]. Journal of Composite Materials, 2013, 47(4): 485-499. DOI:10.1177/0021998312441810 |
| [16] |
GROVE S M. Thermal modelling of tape laying with continuous carbon fibre-reinforced thermoplastic[J]. Composites, 1988, 19(5): 367-375. DOI:10.1016/0010-4361(88)90124-3 |
| [17] |
SARRAZIN H, SPRINGER G. Thermomechanical and mechanical aspects of composite tape laying[J]. Journal of Composite Materials, 1995, 29(29): 1908-1943. |
| [18] |
NEJHAD M, COPE R, GUCERI S. Thermal analysis of in-situ thermoplastic composite tape laying[J]. Journal of Thermoplastic Composite Materials, 1991, 4(1): 20-45. DOI:10.1177/089270579100400102 |
| [19] |
KIM H J, SUN K K, LEE W I. A study on heat transfer during thermoplastic composite tape lay-up process[J]. Experimental Thermal and Fluid Science, 1996, 13(4): 408-418. DOI:10.1016/S0894-1777(96)00095-7 |
| [20] |
HASSAN N. A heat transfer analysis of the fiber placement composite manufacturing process[J]. Journal of Reinforced Plastics and Composites, 2005, 24(8): 869-888. DOI:10.1177/0731684405047773 |
| [21] |
CHINESTA F, LEYGUE A, BOGNET B, et al. First steps towards an advanced simulation of composites manufacturing by automated tape placement[J]. International Journal of Material Forming, 2014, 7(1): 81-92. DOI:10.1007/s12289-012-1112-9 |
| [22] |
SONMEZ F O, HAHN H T. Modeling of heat transfer and crystallization in thermoplastic composite tape placement process[J]. Journal of Thermoplastic Composite Materials, 1997, 10(3): 198-240. DOI:10.1177/089270579701000301 |
| [23] |
TUMKOR S, TURKMEN N, CHASSAPIS C, et al. Modeling of heat transfer in thermoplastic composite tape lay-up manufacturing[J]. International Communications in Heat and Mass Transfer, 2001, 28(1): 49-58. DOI:10.1016/S0735-1933(01)00212-3 |
| [24] |
STOKES C M, COMPSTON P, MATUSZYK T I, et al. Thermal modelling of the laser-assisted thermoplastic tape placement process[J]. Journal of Thermoplastic Composite Materials, 2015, 45(10): 1-18. |
| [25] |
SCHLEDJEWSKI R. Thermoplastic tape placement process-in situ consolidation is reachable[J]. Plastics Rubber and Composites, 2009, 38(10): 379-386. |
| [26] |
ORTH T. A review of radiative heating in automated layup and its modeling[J]. Journal of Plastics Technology, 2017, 2(2): 91-125. |
| [27] |
CALAWA R, NANCARROW J. Medium wave infrared heater for high-speed fiber placement[C]//Aerospace Technology Conference and Exposition. Los Angeles: [s. n. ], 2007.
|
| [28] |
JAMES D L, BLACK W Z. Thermal analysis of continuous filament-wound composites[J]. Journal of Thermoplastic Composite Materials, 1996, 9(1): 54-75. DOI:10.1177/089270579600900105 |
| [29] |
GROVE S M. Thermal modelling of tape laying with continuous carbon fibre-reinforced thermoplastic[J]. Composites, 1988, 19(5): 367-375. DOI:10.1016/0010-4361(88)90124-3 |
| [30] |
CHERN B C, MOON T J, HOWELL J R. On-Line processing of unidirectional fiber composites using radiative heating:Ⅰ. model and Ⅱ. radiative properties, experimental validation and process parameter selection[J]. Journal of Composite Materials, 2002, 36(16): 1905-1965. DOI:10.1177/0021998302036016236 |
| [31] |
CHERN B C, MOON T J, HOWELL J R. Thermalanalysis of in-situ curing for thermoset, hoop-wound structures using infrared heating:Part I-predictions assuming independent scattering and Part Ⅱ-dependent scattering effect[J]. Journal of Heat Transfer, 1995, 117(3): 674-686. DOI:10.1115/1.2822629 |
| [32] |
HÖRMANN P, STELZL D, LICHTINGER R, et al. On the numerical prediction of radiative heat transfer for thermoset automated fiber placement[J]. Composites Part A:Applied Science and Manufacturing, 2014, 67: 282-288. DOI:10.1016/j.compositesa.2014.08.019 |
| [33] |
LICHTINGER R, H?RMANN P, STELZL D, et al. The effects of heat input on adjacent paths during automated fiber placement[J]. Composites Part A:Applied Science and Manufacturing, 2015, 68: 387-397. DOI:10.1016/j.compositesa.2014.10.004 |
| [34] |
余永波, 文立伟, 肖军, 等. 自动铺带中红外加热技术研究[J]. 航空学报, 2011, 32(6): 1124-1131. YU Yong-bo, WEN Li-wei, XIAO Jun, et al. Study of infrared heating technology in automatic tape-laying[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(6): 1124-1131. |
| [35] |
文立伟, 余永波, 齐俊伟, 等. 基于自动铺放成型的红外加热系统研究[J]. 航空学报, 2011, 32(10): 1937-1944. WEN Li-wei, YU Yong-bo, QI Jun-wei, et al. Study on infrared heating system based on automatic tape laying[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10): 1937-1944. |
| [36] |
INCROPERA F P, DEWITT D. Fundamentals of heat and mass transfer[M]. New York: Katson, 1990, 12-13, 492-500, 581-582.
|



