为了适应当今工业4.0环境下客户对产品日益增长的数量与个性化需求, 近年来许多飞机制造企业逐步引入了全新的移动式装配线, 以替代过去低效的固定装配方式.由于飞机装配涉及的物料种类复杂且数量巨大, 物料配送的延迟已成为飞机制造企业提高生产能力的瓶颈[1-2].为了保证移动装配线能稳定运作, 需要一套高效、可靠的物料配送系统支持.
目前, 以飞机移动装配线为背景研究物料供给问题的文献较少, 但针对汽车装配线进行物料配送的研究相对成熟, 可以借鉴汽车装配线中物料配送问题的模型与算法作为参考.Dong等[3]在给定装配顺序与工位布局的条件下决策多载量小车的配送工位、时间及物料量, 建立以配送成本最小化为目标函数的数学模型, 设计动态规划算法与贪婪算法求解.Chen等[4]开发一套强化学习的方法, 对汽车总装线物料供给问题中的小车配送时刻与配送工位进行决策, 以总装线的产出与配送距离最短为评价指标, 通过仿真实验证明了该方法的有效性.周炳海等[5]针对准时化顺序供应的混流装配生产线物料补给问题, 提出以线边库存成本最小化为目标函数的单小车物料配送模型;针对小规模与大规模问题, 分别设计反向动态算法和改进蜂群算法.Emde[6]研究从中央仓库到物料线边超市的准时化物料配送问题, 考虑库存成本与配送成本, 构建多目标的混合整数规划模型, 采用禁忌搜索算法求解问题.上述文献在对汽车装配线物料配送问题进行优化时, 由于每个工位的装配作业少且物料类型单一, 物料存储方式相对简单, 因此装配线旁的空间容量通常仅给定一个上限值而不考虑物料具体存储位置.在类似飞机等大型工业品的装配环境下, 受作业装配时间长、并行装配作业多等因素影响, 有限的线边区域需要同时摆放多个作业的不同物料且同一线边存储区在时间维度上会被重复使用.事实上, 物料配送阶段与线边存储阶段在决策上存在相互依赖关系, 物料的配送方案决定了每个时刻各线边存储单元所需要容纳的物料量, 影响物料的摆放决策;另一方面, 科学合理地安排物料在线边空间的存放位置, 可以有效提高线边空间的利用率, 从而为多物料的组批提前配送提供支持.物料配送问题与线边存储问题相互耦合, 共同构成了飞机移动装配线的物料供给问题, 本文将该类问题称为物料配送与线边存储集成决策问题(integrated material delivery and line-side storage problem, IMDLSP).
综合上述分析, 本文以飞机移动生产线的一个装配节拍为决策周期, 综合考虑物料的组批配送与线边空间重复使用、共享等因素, 建立物料配送与物料在线边存储的集成优化模型, 以最小化物料配送成本, 设计基于蚁群算法的混合启发式算法求解该模型.构建一套以线边空间稠度为指标的算例集, 通过数值实验验证提出算法在求解IMDLSP问题时的有效性.
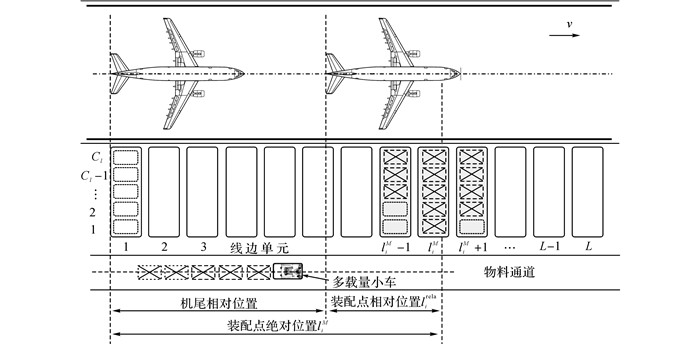
1 问题描述及数学模型 1.1 问题描述及问题假设以飞机移动装配线的物料供给为应用背景, 一方面需要决策装配作业物料的配送过程, 对不同作业装配所需物料进行组批配送, 以最小化配送小车出行总次数;另一方面需要考虑装配线边有限的空间来制定物料摆放计划, 避免小车将物料运抵线边后空间不足导致物料无法存放的情况发生.如图 1所示为飞机移动装配线的物料供给示意图.装配作业物料通过多载量小车组批配送至装配线旁, 并存放在相应的线边空间处, 直至该作业装配完成.
|
图 1 飞机移动装配线物料供给示意图 Fig. 1 Schematic diagram of material supply mode for aircraft moving assembly lines |
涉及的假设可以分为物料相关假设、配送相关假设以及线边空间相关假设3部分.
1) 物料相关假设.
a) 飞机装配过程中所需的物料可以分为4类:通用标准件、大型结构件、装配件和自制件.通用标准件(如螺栓等)一般采用定期补货的方式供给;大型结构件(如发动机、机翼等)由于体积较大且形状不规则, 通常使用行车、叉车和机械臂等其他方式直接配送.本文研究问题中的物料主要指体积中等、种类复杂的装配件和自制件.
b) 任一作业所需物料通过齐套(kitting)方式提前装入一个(或多个)标准料箱中, 等待后续装载和配送.假设仓库的备件能力充足.
2) 配送相关假设.
a) 料箱通过多载量小车进行配送, 单辆小车一次可以配送多个作业所需物料.为了防止配送过程中出现物料混乱, 任一作业所需的全部物料由一辆小车一次配送完成.
b) 小车配送时间主要包括小车从仓库到装配线边的时间和物料的装卸时间, 小车在工位旁物料通道的移动时间可以忽略不计.
3) 线边空间相关假设.
a) 装配线边的存储区域用于存放提前送达和正在使用的物料.整个线边区域被划分为若干个规则的线边存储单元, 假设每个存储单元的空间容量是标准料箱大小的整数倍.
b) 物料送达线边时只能存放在作业装配工位附近的存储单元内.如图 1所示, 定义作业i装配点的绝对位置liM所对应的线边单元为物料中心存储单元.为了作业人员取料的方便, 要求作业i所需物料只能存放在该中心存储单元及左右各一个单元的范围内, 如图 1的阴影区域所示.为了使得线边存储整齐有序, 任一装配作业的所有料箱必须连续地摆放在同一个存储单元内, 不可跨单元摆放, 也不可离散摆放.
1.2 数学模型 1.2.1 符号定义κ={k|k=1, 2, …, K}:多载量小车集合.装配车间内的小车数量为K.
J={i|i=1, 2, …, N}:装配作业集合, 共有N项装配作业.
Δ={d|d=1, 2, …, D}:离散的时间点编号集合.
Λ={l|l=1, 2, …, L}:线边空间存储单元集合, 最大编号为L.
Γl={c|c=1, 2, …, Cl}:线边存储单元l中的存储位置集合, 最大编号为Cl.
(ai, bi), ∀i∈J:装配作业i开始时间为ai, 结束时间为bi, ai, bi∈Δ.
mi, ∀i∈J:装配作业i所需的物料量(下称物料i), 以料箱的数量为计数单位.
v:飞机在装配线上的移动速度, 其值等于单位时间内飞机移动过的线边存储单元数.
Q:多载量小车的运载能力上限.
(k, r), ∀k∈κ, r∈
T:小车从仓库到装配线边的单程耗时.
TLoad:小车装卸物料耗时.
lirela, ∀i∈J:装配作业i在飞机上相对于机尾的装配位置.
liM∈Λ, ∀i∈J:作业i装配过程的中间时刻装配点在移动装配线上所处的绝对位置, 即对应物料i在线边空间的中心存储单元.
1.2.2 决策变量和辅助变量决策变量如下.
xikr∈{0, 1}, ∀i∈J, k∈κ, r∈
skr∈Δ, ∀k∈κ, r∈
(di0, li0, ci0), ∀i∈J:分别表示物料i送达线边的时刻、被安排存储的线边单元编号和在线边单元内存储的最小位置编号.
辅助变量如下.
λkr∈{0, 1}, ∀k∈κ, r∈
si∈Δ, ∀i∈J:物料i的配送时刻.
1.2.3 目标函数和约束条件目标函数为最小化小车配送总次数:
| $ \min \sum\limits_{k \in \kappa } {\sum\limits_{r \in \Re } {{\lambda _{kr}}} } . $ | (1.1) |
约束条件如下.
1) 辅助约束.若小车k的第r次配送决策没有配送任何物料, 小车不发车;否则小车发车:
| $ {\lambda _{kr}} = \left\{ \begin{array}{l} 1,\;\;\;\;\;\sum\limits_{i \in J} {x_i^{kr}} \ge 1;\\ 0,\;\;\;\;\;\sum\limits_{i \in J} {x_i^{kr}} = 0. \end{array} \right. $ | (1.2) |
根据小车各次发车的发车时刻, 计算各装配作业所需物料的配送时刻:
| $ {s_i} = {s_{kr}};\;\;\;\;{\rm{s}}.\;{\rm{t}}.\;\;x_i^{kr} = 1. $ | (1.3) |
物料i的配送时刻与送达线边时间的对应关系为
| $ d_i^0 = {s_i} + T;\;\;\;\;i \in J. $ | (1.4) |
2) 配送问题相关约束.任一装配作业所需的物料必须由一辆小车一次配送完成:
| $ \sum\limits_{k \in \kappa } {\sum\limits_{r \in \Re } {x_i^{kr}} } = 1;\;\;\;i \in J. $ | (1.5) |
每次配送的物料量不超过小车的运载能力上限Q:
| $ \sum\limits_{i \in J} {x_i^{kr}{m_i}} \le Q;\;\;\;k \in \kappa ,r \in \Re . $ | (1.6) |
对于小车k, 若第r次配送包含物料并发车, 则第r+1次配送时刻必须在第r次配送完成后才能执行:
| $ \left. \begin{array}{l} {s_{k,r + 1}} - {s_{k,r}} \ge 2T + {T^{{\rm{Load}}}};\\ {\rm{s}}.\;{\rm{t}}.\;\;{\lambda _{kr}} = 1,k \in \kappa ,r \in \Re \backslash \left\{ R \right\}. \end{array} \right\} $ | (1.7) |
各物料送达线边的时间均不晚于对应装配作业的开始时间:
| $ {s_i} + T \le {a_i};\;\;\;i \in J. $ | (1.8) |
3) 物料存储问题相关约束.计算各装配作业相应物料的中心存储单元编号:
| $ l_i^{\rm{M}} = l_i^{{\rm{rela}}} + \frac{{{a_i} + {b_i}}}{2}v;\;\;\;\;i \in J. $ | (1.9) |
各物料必须存放在相应的中心存储单元或中心存储单元左右各一格的线边单元内:
| $ \left| {l_i^0 - l_i^{\rm{M}}} \right| \le 1;\;\;\;\;i \in J. $ | (1.10) |
物料占用的空间不得超过各线边单元的容量上限:
| $ c_i^0 + {m_i} - 1 \le {C_i};\;\;\;i \in J. $ | (1.11) |
在任意时刻, 任意两个物料所占空间不重叠:
| $ \begin{array}{*{20}{c}} {{b_i} < d_j^0 \vee {b_j} < d_i^0 \vee l_i^0 \ne l_j^0 \vee \left( {c_i^0 + {m_i} - 1} \right) < }\\ {c_j^0 \vee \left( {c_j^0 + {m_j} - 1} \right) < c_i^0;{\rm{s}}.\;{\rm{t}}.\;i,j \in J,i \ne j.} \end{array} $ | (1.12) |
由于小车装载调度问题和线边物料存储问题(即三维装箱问题)均为NP-Hard问题, IMDLSP问题需要对两者进行联合优化, 享有较高的计算复杂度.在大规模问题中, 精确算法难以在合理的时间内获得理想的解.蚁群算法以全局搜索能力和较好的鲁棒性被广泛应用于路径规划、生产线调度、故障诊断等问题中[7-10], 因此针对IMDLSP问题的特点, 设计基于蚁群算法的混合启发式算法进行求解.该算法借助蚁群算法的全局搜索能力搜寻较优的物料组批方式, 对任一包含特定物料分批方案的蚂蚁设计一套联合决策物料配送时间与线边存储方案的解码算法.若解码获得的物料配送与存储方案满足所有约束条件, 说明此前的物料批次划分方式存在对应的可行解, 小车出行总次数可以被接受作为整个问题的目标值;否则此前得到的分批方案无效, 须继续搜寻更优的物料组批方式.为了提高线边空间的利用率, 在解码算法中嵌入物料存储修复算法, 进一步优化物料在线边的存储方案, 为物料的组批配送提供更高的柔性.以下分别对蚁群算法框架、基于物料批次划分的解生成算法以及物料存储修复算法进行阐述.
2.1 蚁群算法框架借鉴精华蚂蚁系统(elitist ant system, EAS)和最大-最小蚂蚁系统(max-min ant system, MMAS)的特点, 基于改进蚁群算法设计混合启发式算法来求解所研究问题.EAS的特点在于对目标函数值最大的一些蚂蚁留下的信息素进行奖励, 抑制种群中“较差”蚂蚁对信息素的贡献, MMAS在进化过程中对信息素浓度的范围进行限定.基于上述思想, 算法中设定仅目标函数值排名前p的蚂蚁允许释放信息素, 且各路径上的信息素浓度不得低于下限pher_lb, 以提高种群多样性并避免种群过早陷入局部最优.
蚁群算法采用变长度编码方式, 以物料的批次划分方案进行编码.数值为0的码位表示小车返回仓库进行下一批次的物料装载, 其余码位表示物料的编号, 因此任意两个0码位之间表示一个批次所需配送的物料.以图 2为例, 作业1和作业2所需物料由小车第1次出行配送, 小车第2次出行仅配送作业3所需物料, 依次类推.由于装配作业总量为N, 编码长度最长为2N+1.

|
图 2 物料组批方式编码示意图 Fig. 2 Coding schematic diagram of material batching |
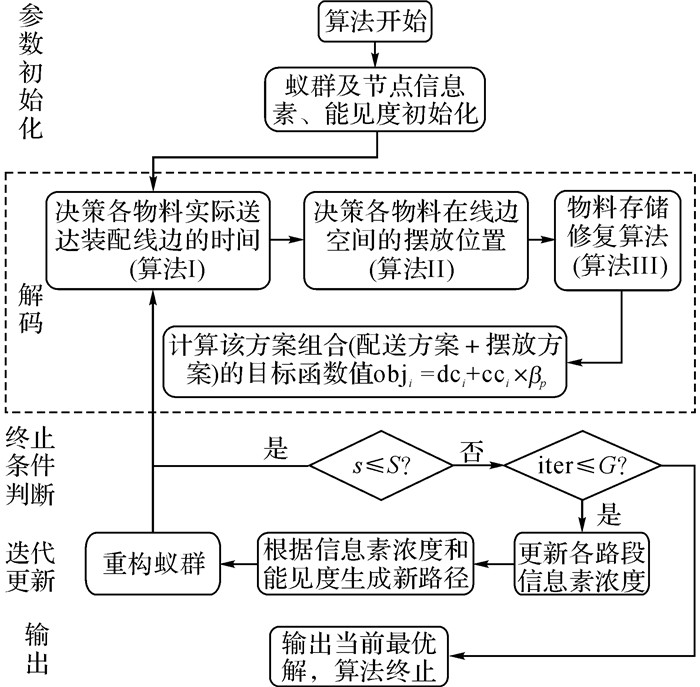
设定蚁群大小为S, 最大进化代数为G, 信息素释放速率为ratea, 信息素挥发速率为rateb, 每一代释放信息素的蚂蚁数为p, 信息素浓度下限为pher_lb, 能见度相对信息素的指数权重因子为β, 出现不可行方案时惩罚因子为βp.算法框架如图 3所示, 蚁群算法的通用部分不再赘述, 解码算法部分在2.2和2.3节中重点介绍.
|
图 3 蚁群算法框架 Fig. 3 Ant colony algorithm framework |
对于2.1节中生成的任意一只“蚂蚁”, 可以获取物料的分批方案.基于该“蚂蚁”的物料批次划分方式, 需要决策各批次物料的具体配送时刻.为了保证小车调度得到可行解, 采用先确定各批次物料的配送顺序, 再根据小车资源从晚到早依次确定具体配送时刻的策略.
定义批次为f的物料配送时刻为Tf, 小车k最晚的可用时刻为TkLA, 算法Ⅰ的具体步骤如下.
1) 为已组批完成的物料确定配送顺序, 将各个批次的物料按照最晚送达时刻升序排列:
| $ \left. \begin{array}{l} {\rm{Batch}} = \left\{ {\left( {{B_1},a_1^{\rm{B}}} \right),\left( {{B_2},a_2^{\rm{B}}} \right), \cdots ,\left( {{B_F},a_F^{\rm{B}}} \right)} \right\};\\ a_f^{\rm{B}} = \min \left\{ {{a_i}\left| {i \in f} \right.} \right\}. \end{array} \right\} $ |
2) 初始化各小车最晚可用时刻TkLA, ∀k∈κ, 初始化f=F.
3) 更新最晚小车可用时刻
| $ T_\kappa ^{{\rm{LA}}} = \max \left\{ {T_k^{{\rm{LA}}}\left| {\forall k \in \kappa } \right.} \right\}. $ |
4) 计算批次f物料的配送时刻Tf=min {TkLA, afB}, 记批次f物料的配送时刻与车次为Tf, k.
5) 更新小车k最晚可用时刻
| $ T_k^{{\rm{LA}}} = {T_{f,k}} - 2T - {T^{{\rm{Load}}}}. $ |
6) 若f>1, 则f=f-1并返回4);否则输出各批次物料配送时刻序列Tf=1, 2, …, F, 算法结束.
对算法Ⅰ给出如下性质及证明.首先定义Tf, kLPA为通过算法Ⅰ所得配送方案H下得到的小车k配送批次为f的物料最晚可能送达时刻, Tf, kLPA′为任意其他方案H′得到的小车k配送批次为f的物料最晚可能抵达时刻.
性质:
在确定物料分批方案及各批次的配送先后顺序的前提下, 若算法Ⅰ输出的配送时间方案在对应的物料存储问题中不存在可行解, 则其他任何配送时间方案均不能在物料存储问题中找到可行解.
证明:
根据假设可知, 一个配送批次的物料由单辆多载量小车完成配送.定义“小车-物料批次”二元组(f, k).在物料组批方案及配送先后顺序确定的前提下, 批次为f的物料最晚需求时刻为afB.在对批次f进行配送时间规划时, 所有小车中最晚可用的时间为TfLA;小车k的最晚可能的送达时间Tf, kLPA不超过小车k的最晚可用时间Tf, kLA与由配送顺序决定的后一车次的实际送达时间af+1A之间的较小值, 各符号间的对应关系如下:
| $ T_f^{{\rm{LA}}} = \min \left\{ {\max \left\{ {T_{f,k}^{{\rm{LA}}}\left| {\forall k} \right.} \right\},a_f^{\rm{B}}} \right\}, $ | (2.1) |
| $ T_{f,k}^{{\rm{LPA}}} = \min \left\{ {T_{f,k}^{{\rm{LA}}},a_{f + 1}^{\rm{A}}} \right\}, $ | (2.2) |
| $ a_f^{\rm{A}} \le T_{f,k}^{{\rm{LPA}}}. $ | (2.3) |
在算法Ⅰ中, 从批次编号为F的物料开始向前对各批物料的配送时间进行规划.若在配送时间规划进行过程中, 出现H′与H不一致的情况, 则H′必然造成小车运输时间浪费, 由此可以证明此时方案H中各小车的可安排时段必然可以在调整顺序后完全覆盖方案H′中的可安排时段.当H′与H方案产生分歧时, H方案必优于H′方案, 且这种优势在后续的配送时间规划中持续存在.综合上述分析可知, H方案中各物料批次的配送时间均晚于H′方案, 因此H′方案对应的物料摆放时间段必然覆盖H方案.显然, 若H方案对应的摆放问题无可行解, 则H′方案将找不到对应的可行摆放方案.
证毕.
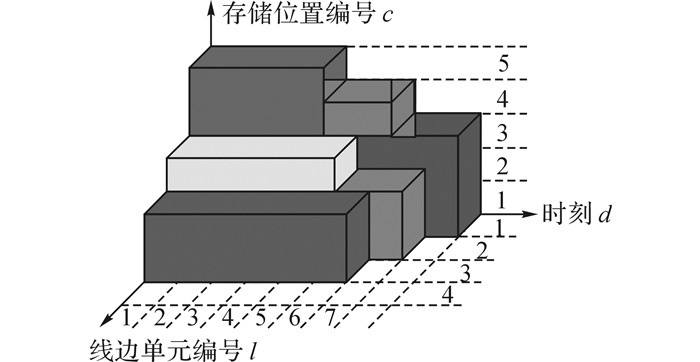
2.2.2 线边空间摆放位置决策(算法Ⅱ)在对各项装配作业所需物料进行配送时刻规划后, 物料将在预定的时间被配送至装配线边存储.线边区域为有限的二维空间, 容量为标准料箱大小的整数倍.由于线边空间需要在时间维上被重复利用, 且任一作业的物料必须连续存放在同一个线边单元内, 物料在线边空间的摆放问题可以抽象为带时间窗三维装箱问题的一类特例.如图 4所示, 一个装配作业的物料可以看作一个形状规则的三维箱体, 长等于物料在线边暂存区存放的时间段长度, 宽为占据的线边单元(恒为1), 高为物料量.目前三维装箱问题的求解方法主要可以分为精确算法[11-12]、启发式算法[13-14]和元启发式算法[15-16]三类, 这些求解方法可以为本文的线边物料存放问题提供借鉴.区别于一般的三维装箱问题, IMDLSP问题的物料存放存在以下特点:物料的存放位置受到较严格的约束, 存放开始和结束时刻已经由配送方案决定, 因此每个“三维箱体”都无法在长度方向上移动;此外, 由于物料存放的线边单元必须为位于作业装配点附近的线边单元, “三维箱体”在宽度方向上的存储位置仅能够有限地浮动.
|
图 4 线边物料存储示意图 Fig. 4 Schematic diagram of line-side material storage |
算法Ⅱ基于物料的优先级, 通过角点法产生初始物料存储方案.定义物料i的“左下后”点(di0, li0, ci0)为所占据的所有时空域中时刻最早、线边单元编号最小和线边单元内存储位置编号最小的点.假设已确定存储位置的物料集合为I, 未确定的物料集合为U, 无法存放的物料集合为Ω.算法Ⅱ的具体步骤如下.
1) 输入各物料配送时刻序列, 初始化无法存放的物料集合Ω=∅.
2) 依次按下列子优先级从高到底对物料进行优先级排序.a)按物料送达线边的时间di0从小到大排序;b)按作业装配点对应的中心存储单元编号liM从小到大排序;c)按物料体积mi(bi-di0+1)从小到大排序.
3) 若|U|=0, 则转6);否则转4).
4) 选择U中优先级最高的物料i, 将物料i按以下规则放入线边空间中.a)线边单元编号尽量小;b)占据的位置尽可能低(ci0尽可能小).
5) 若物料在中心存储单元liM及左右一格范围内无法找到不发生空间冲突的摆放位置, 则Ω=Ω+i.更新集合U、I, 返回3).
6) 若|Ω|=0, 则存在可行解, 否则不存在可行解.
7) 输出物料在线边的存储方案I, 算法结束.
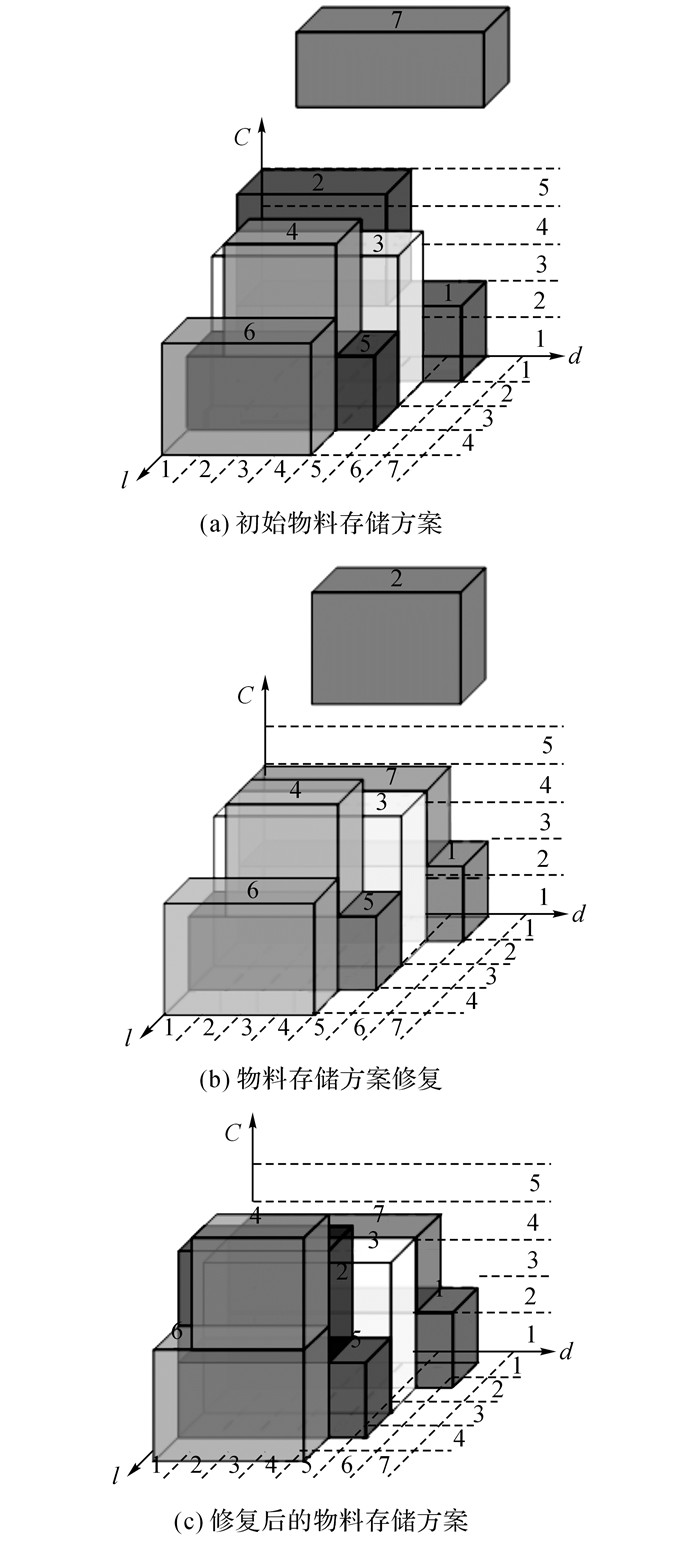
2.3 物料存储修复算法(算法Ⅲ)在线边暂存区空间相对紧张的情况下, 算法Ⅱ中基于优先级和启发式规则可知, 物料存储方案可能无法得到问题的可行解.为了进一步提高线边空间的利用率, 提出物料存储修复算法.通过局部调整多作业间的物料存放位置, 使得线边空间分配更加合理, 以修复初始解中得到的不可行解.如图 5所示为物料存储修复算法的调整机理.假设有7个装配作业所需物料需要在线边存储, l表示线边空间单元, d为时间, C为线边单元内的存储位置集合, 图 5中的方块表示各自作业的物料需求量.对于物料7, 假设中心存储线边单元为li=7M=2, 则该物料可以在任一线边单元li=70∈{1, 2, 3}内存储.由于物料7的存放时间段d∈[1, 5]内线边单元1、2、3均有其他物料存放导致线边容量不足, 物料7暂时无法存储(见图 5(a)).首先随机生成物料7的可插入位置li=70=1, 将物料7存入线边单元1中, 此时弹出物料2(见图 5(b)), 再为物料2随机生成插入位置li=20=3(假设物料2可存放线边单元为li=20∈{2, 3, 4}), 则将物料2插入线边单元3中.由于线边单元3容量不足, 物料4被弹出.继续为物料4随机生成插入位置li=40=4(假设物料4可存放线边单元为li=40∈{2, 3, 4}), 将物料4存入线边单元4内.由于线边单元容量充足, 完成物料存储修复(见图 5(c)).
|
图 5 物料存储修复算法优化机理 Fig. 5 Optimization mechanism of material storagerepairing algorithm |
算法Ⅲ的具体步骤如下.
1) 从无法存放的物料集合Ω中随机选出一个物料i, 初始化当前迭代次数为0.
2) 在物料i允许存放的线边单元{liM-1, liM, liM+1}中随机选出一个, 设其为li0.
3) 从方向集合{ascending, descending}中随机选出一个方向, 依据该方向在bi时刻的线边单元li0内寻找第一个空置的料箱位置ci.
a) 当方向为“ascending”时, 物料占用线边单元内的最小位置编号为ci0=min{ci, Cli0-mi+1};若无法找到足够的空间存储, 令ci=1.
b) 当方向为“descending”时, 物料占用线边单元内的最小位置编号为ci0=max{ci-mi+1, 1};若无法找到足够的空间存储, 则令ci=Cli0-mi+1.
4) 将物料i放入线边单元li0中, 摆放在[ci0, ci0+mi-1]料箱位置, 检查是否与原摆放方案中的物料发生空间冲突;将发生冲突的物料集合Ω′取出, 并入Ω中.
5) 设新摆放方案为I′, 更新后的冲突集合为Ω=(Ω\{i})∪Ω′.
6) 若|Ω|=0, 则转8);若|Ω|≠0且迭代次数达到上限, 则转7);否则转1).
7) 修复算法失败, 不存在可行解.
8) 输出物料在线边的存储方案I′或不可行解, 算法结束.
3 数值实验 3.1 算例集的构建为了方便后续研究中对算法的有效性进行验证并与其他算法对比, 针对影响IMDLSP问题求解性能的多个因素构建一套算例集.该算例集共包含7 705个由不同参数组合而成的算例.影响算例潜在模式和求解性能的主要因素包括装配作业数量N、各作业所需的物料量mi、各作业的持续时间及其波动情况等.对上述因素进行简化和整合, 结合飞机移动装配方式的特点, 对算例提出以线边空间稠度(line-side area density, LAD)为核心的评价指标体系.该指标综合体现了线边空间存放物料量的密集程度.以下给出空间稠度的定义.
定义线边单元l的空间稠度为ρl, 满足式(3.1).
| $ {\rho _l} = \frac{{\sum\limits_{i \in {\mathit{\Pi }_l}} {{m_i}} }}{{3{C_l}}}. $ | (3.1) |
式中:Πl={i|liM∈{l-1, l, l+1}}, 表示装配点对应的线边存储单元位于线边单元l及左右一格范围内的作业集合;Cl为线边单元l的容量上限.整个线边空间的空间稠度等于各单元空间稠度的平方均值:
| $ {\rm{LAD}} = \sum\limits_{l \in \mathit{\Lambda }} {\rho _l^2} /L. $ | (3.2) |
算例集在构建过程中, 尽可能地覆盖各类参数组合的算例, 以保证对算法有效性和敏感性进行准确定位.算例集的结构和组成如表 1所示.表中, m_ub表示生成算例时各作业的物料量mi的上界, SN为算例数.算例集中各装配作业的开始时间服从参数为λ的泊松分布, 持续时间、所需物料量、相对机尾的位置分别服从区间[0, duration_ub]、[0, m_ub]、[0, position_ub]上的均匀分布.算例集的构建过程采取设置m_ub和作业数N的方式, 开展多次随机实验, 计算生成算例的空间稠度指标.为了保证算例集的多样性, 限制各类算例数量不超过50.
| 表 1 IMDLSP问题算例集结构与组成 Table 1 Structure and composition of example set of IMDLSP |
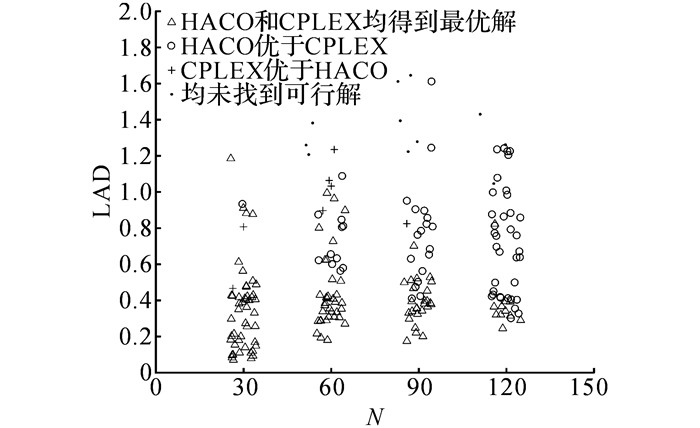
为了验证设计的基于蚁群算法的混合启发式算法(HACO)的精确性和求解效率, 通过MATLAB(2016b)对HACO算法编程进行测试与分析, 将得到的结果与通过CPLEX软件(版本12.7.1)求解的结果进行对比.实验平台为Intel i7-4790处理器, 3.60 GHz主频, 8 GB内存.由于CPLEX在求解大规模算例时效率较低, 从作业规模为30、60、90、120的算例集中按空间稠度的分布比例, 分别各随机选择50组算例进行测试, 表 2和图 6给出算法的对比结果.图 6中,LAD为空间稠度.表 2中, NOpt和POpt分别为CPLEX求得最优解的算例个数和HACO得到最优解算例个数的比例;RCPLEXL和RCPLEXU分别为CPLEX求得的小车出行次数低界和高界;RHACO为采用HACO算法求得的小车出行次数;TCPLEXCPU和THACOCPU为CPLEX和HACO算法的CPU运行时间, 其中7 200+表示该规模算例采用CPLEX的求解时间基本超过可接受上限(7 200 s);GL和GU分别为采用HACO算法得到的小车配送次数与CPLEX求得结果的低界、高界的偏差百分比,
| 表 2 小规模算例数值实验结果 Table 2 Numerical experiment results of small-scale examples |
|
图 6 HACO与CPLEX求解结果对比 Fig. 6 Comparison results of HACO and CPLEX |
| $ {G_{\rm{L}}} = \frac{{{R_{{\rm{HACO}}}} - R_{{\rm{CPLEX}}}^{\rm{L}}}}{{R_{{\rm{CPLEX}}}^{\rm{L}}}} \times 100\% , $ |
| $ {G_{\rm{U}}} = \frac{{R_{{\rm{CPLEX}}}^{\rm{U}} - {R_{{\rm{HACO}}}}}}{{{R_{{\rm{HACO}}}}}} \times 100\% . $ |
特别说明, 表 2中的配送次数、CPU时间等均为各规模算例下得到的均值.
通过上述数值实验可以发现, 利用HACO算法得到的小车配送次数和CPLEX的低界相比, 偏差均能控制在10%内;CPLEX可以求得最优解的算例, HACO算法大多可以在更短时间内得到最优解.当问题规模较小时, 极个别算例通过CPLEX得到的结果优于HACO算法求得的结果.这是由于蚁群算法框架无法保证遍历所有的物料组批方式, 只能在可接受时间内得到近似最优解.随着算例的作业规模增大, CPLEX的求解性能逐步下降, HACO算法在求得的目标函数值和求解时间上的优势相比于CPLEX逐渐增大;当算例规模为120时, 利用HACO算法求得的目标函数值与CPLEX得到的高界相比, 优化比例达到24.19%, 体现了HACO算法在求解效率和有效性上的优势.
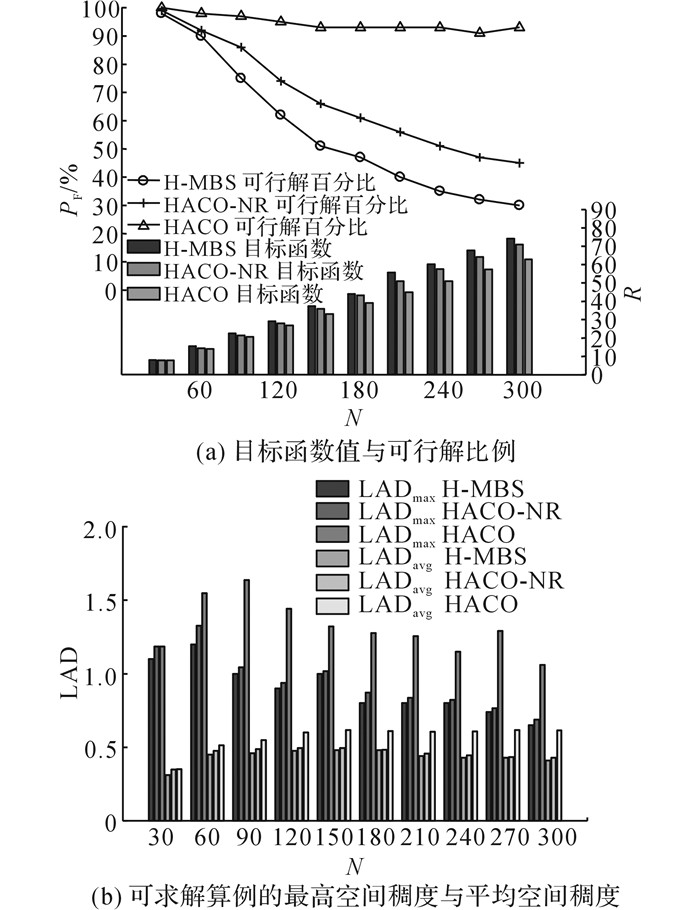
3.3 与其他算法的对比为了检测HACO算法在不同组合算例下的求解性能, 针对全算例集的7 705个算例, 以各规模算例下的目标函数值、算例求解成功率、可求解算例的最高空间稠度和平均空间稠度为评价指标, 将HACO算法和另外2种算法进行对比.H-MBS为基于物料需求时间顺序最小批次规则下的启发式算法, HACO-NR为不加入物料存储修复算法的HACO算法.实验结果如表 3和图 7所示.如表 3所示为3种算法在7 705个算例下的实验结果均值, 如图 7所示为各规模算例下的4类评价指标对比结果.表 3中,R为小车配送次数,PF为求解可行率,LADmax为最高求解空间稠度,LADavg为平均求解空间稠度.
| 表 3 全算例集数值实验结果 Table 3 Numerical experiment results of example set |
|
图 7 全算例集下不同算法结果对比 Fig. 7 Comparison of experimental results of example set between different algorithms |
从表 3可以看出, 与传统的H-MBS算法相比, 所提的HACO算法在物料的组批配送决策中有明显优势, 不仅能够有效地减少小车的配送次数, 而且在全算例集的算例求解中达到了94.60%的求解成功率.与HACO-NR算法相比, 采用HACO算法将算例的最高求解空间稠度和平均求解空间稠度从0.949 5、0.454 8分别提升到了1.307 1和0.569 0, 说明设计的物料存储修复算法在线边物料的摆放规划上有显著效果, 可以通过寻找合理的物料摆放方案为物料组批配送提供更高的柔性.当算例规模为30时, 利用HACO算法得到的结果与其他两种算法的结果相比差距较小.主要原因为当问题规模较小时, 解的搜索空间相对较小, 决策变量的组合方式相对较简单, 其他算法能够搜寻到较优的解, HACO算法的优势不明显.结合图 7可以看出, 随着问题规模的增大, HACO算法在4类指标上的评价值比其他两类算法相比, 差距不断扩大, 证明了HACO算法在飞机装配这类作业规模较大的生产线物料配送问题求解上具有优越性.
4 结论(1) 以飞机移动装配线为应用背景, 对物料配送问题和线边存储问题进行集成优化, 建立集成决策的数学模型, 为物料配送问题在诸如飞机这类大型工业品装配的应用上拓宽了思路.
(2) 设计基于蚁群算法的混合启发式算法求解模型.该算法将物料配送时刻与线边存储位置决策统一到一个联合决策框架下, 可以有效地利用线边空间的存储能力, 减少小车配送次数.
(3) 基于蚁群算法的混合启发式算法在求解小规模问题时优势不明显, 但在诸如飞机这类作业规模较大的大型工业品装配物料供给问题的应用上具有较高的求解效率和较好的求解性能.该算法具有较好的通用性, 适用于工业中其他享有类似IMDLSP问题特性的物料供给问题.
(4) 今后的研究将针对当前算法在物料组批决策中的性质进行分析, 进一步提高算法的求解性能.此外, 为了进一步适应生产实际的需求, 后续将分析飞机移动装配中存在的不确定性因素, 建立动态决策框架, 为IMDLSP问题提供更有效的决策.
| [1] |
CAI H X, MING Y D, TAO Yu. Material coding for aircraft manufacturing industry[J]. Journal of Aerospace Technology and Management, 2014, 6(2): 183-191. DOI:10.5028/jatm.v6i2.315 |
| [2] |
MEI Z, LIU Y, YOUNUS M. Material delivery system for aircraft composite component manufacturing workshop[C]//Proceedings of the International Multi-Conference of Engineers and Computer Scientists. Hongkong: Springer, 2011: 1097-1102. http://www.oalib.com/paper/2162253
|
| [3] |
DONG J, ZHANG L, XIAO T. Part supply method for mixed-model assembly lines with decentralized supermarkets[J]. Tsinghua Science and Technology, 2016, 21(4): 426-434. DOI:10.1109/TST.2016.7536720 |
| [4] |
CHEN C, XIA B, ZHOU B H, et al. A reinforcement learning based approach for a multiple-load carrier scheduling problem[J]. Journal of Intelligent Manufacturing, 2015, 26(6): 1233-1245. DOI:10.1007/s10845-013-0852-9 |
| [5] |
周炳海, 彭涛. 混流装配生产线准时化物料补给调度方法[J]. 控制与决策, 2017, 32(6): 976-982. ZHOU Bing-hai, PENG Tao. Scheduling methods of just-in-time material replenishment inmixed-model assembly lines[J]. Control and Decision, 2017, 32(6): 976-982. |
| [6] |
EMDE S. Scheduling the replenishment of just-in-time supermarkets in assembly plants[J]. Or Spectrum, 2017, 39(1): 321-345. DOI:10.1007/s00291-016-0455-x |
| [7] |
LIU M, ZHANG F, MA Y, et al. Evacuation path optimization based on quantum ant colony algorithm[J]. Advanced Engineering Informatics, 2016, 30(3): 259-267. DOI:10.1016/j.aei.2016.04.005 |
| [8] |
SUN Y, DONG W, CHEN Y. An Improved routing algorithm based on ant colony optimization in wireless sensor networks[J]. IEEE Communications Letters, 2017, 21(6): 1317-1320. DOI:10.1109/LCOMM.2017.2672959 |
| [9] |
SPERANSKII D V. Ant colony optimization algorithms for digital device diagnostics[J]. Automatic Control and Computer Sciences, 2015, 49(2): 82-87. DOI:10.3103/S0146411615020078 |
| [10] |
LU C, YANG Z. Integrated assembly sequence planning and assembly line balancing with ant colony optimization approach[J]. International Journal of Advanced Manufacturing Technology, 2016, 83(1): 243-256. |
| [11] |
MARTELLO S, PISINGER D, VIGO D. The three-dimensional bin packing problem[J]. Operations Research, 2000, 48(2): 256-267. DOI:10.1287/opre.48.2.256.12386 |
| [12] |
TAYLOR G S, CHAN Y, RASOOL G. A three-dimensional bin-packing model:exact multicriteria solution and computational complexity[J]. Annals of Operations Research, 2017, 251(1): 397-427. |
| [13] |
TOFFOLO T A M, ESPRIT E, WAUTERS T, et al. A two-dimensional heuristic decomposition approach to a three-dimensional multiple container loading problem[J]. European Journal of Operational Research, 2016, 257(2): 526-538. |
| [14] |
VIEGAS J L, VIEIRA S M, HENRIQUES E M P, et al. Heuristics for three-dimensional steel cutting with usable leftovers considering large time periods[J]. European Journal of Industrial Engineering, 2016, 10(4): 431-454. DOI:10.1504/EJIE.2016.078141 |
| [15] |
KANG K, MOON I, WANG H. A hybrid genetic algorithm with a new packing strategy for the three-dimensional bin packing problem[J]. Applied Mathematics and Computation, 2012, 219(3): 1287-1299. DOI:10.1016/j.amc.2012.07.036 |
| [16] |
FENG X, MOON I, SHIN J. Hybrid genetic algorithms for the three-dimensional multiple container packing problem[J]. Flexible Services and Manufacturing Journal, 2013, 27(2): 1-27. |


