2. 63983部队, 江苏 无锡 214035
2. Unit 63983 of PLA, Wuxi 214035, China
全方位移动平台大多数以轮式为主, 因具有高度机动性而被广泛应用于狭小空间运输[1-2]、智能服务[3-4]、精确安装[5]等场合, 但该类平台存在运动振动大、路面适应性差等问题.刘勇等[6-8]通过优化辊轮设计、增加减震机构的方法针对运动振动问题进行改进, 取得一定的改善效果.王一治等[9-10]针对全方位平台建立不平路面的运动学模型, 研究楼宇环境下的应用.陶俊杰等[11-12]通过增加运动轮数量使平台具备一定的越野能力, 增强平台的路面适应性.国外学者研究了一些履带式全方位移动平台, 如West等[13]研制的Omnidirectional Spherical Tire Crawler平台、Tadakuma等[14]研制的Cylindrical Track Crawler平台、Damoto等[15]研制的Vuton Ⅰ Crawler平台、Chen等[16]研制的Omnidirectional Crawler-Roller平台等.上述平台多以仿真研究和实验探索为主, 工程应用较少, 且部分平台结构较复杂.Zhang等[17]研制履带式全方位移动平台.该平台既能够实现全方位移动, 还具备一定的越野能力.
Zhang等[17]提出的全方位履带结构结合了Mecanum轮和传统履带的运动原理及机械结构, 将辊轮安装在履带板上, 使履带具备多个运动自由度.平台采用纵向对称布局形式, 4条全方位履带利用独立电驱动技术进行控制.该平台同侧2组履带之间存在一定的间隔, 运行过程中履带不能实现“连续”工作, 在一定程度上削弱了履带机构的运动能力.尤其在越障过程中, 该平台会因为履带中间的间隔而出现“卡顿”、“跳跃”现象, 不利于平台的稳定运行.在体积一定的情况下, 限于平台履带的布局形式, 履带接地长度会受到一定的影响.
本文基于全方位履带结构, 依据传统履带车辆布局形式, 设计新型的全方位移动平台, 建立平台运动学和动力学模型, 针对平台的转向运动进行分析.通过ADAMS软件建立平台虚拟样机, 对平台运动性能进行验证.
1 全方位履带结构及平台布局 1.1 全方位履带结构全方位履带结构如图 1所示, 该结构与传统履带类似, 包括驱动轮、负重轮、托带轮等部分.在履带板外侧安装可自由旋转的辊轮, 辊轮具有一定偏置角α, 一般选取0 < α < π/2.Zhang等[17]分析该履带结构与平台的运动关系, 即平台的逆运动学方程:

|
图 1 全方位履带结构示意图 Fig. 1 Structure of omnidirectional track |
| $ \left. \begin{array}{l} {\left[ {\begin{array}{*{20}{c}} {{\omega _1},}&{{\omega _2},}&{ \cdots ,}&{{\omega _{\rm{n}}}} \end{array}} \right]^{\rm{T}}} = \mathit{\boldsymbol{J}}{\left[ {\begin{array}{*{20}{c}} {{v_y},}&{{v_x},}&{{\omega _z}} \end{array}} \right]^{\rm{T}}},\\ \mathit{\boldsymbol{J}} = \frac{1}{r}\left[ {\begin{array}{*{20}{c}} {\frac{{\sin \left( {{\theta _1} + {\alpha _1}} \right)}}{{\sin {\alpha _1}}}}&{\frac{{\cos \left( {{\theta _1} + {\alpha _1}} \right)}}{{\sin {\alpha _1}}}}&{\frac{{{l_1}\sin \left( {{\theta _1} + {\alpha _1} - {\beta _1}} \right)}}{{\sin {\alpha _1}}}}\\ {\frac{{\sin \left( {{\theta _2} + {\alpha _2}} \right)}}{{\sin {\alpha _2}}}}&{\frac{{\cos \left( {{\theta _2} + {\alpha _2}} \right)}}{{\sin {\alpha _2}}}}&{\frac{{{l_2}\sin \left( {{\theta _2} + {\alpha _2} - {\beta _2}} \right)}}{{\sin {\alpha _2}}}}\\ \vdots&\vdots&\vdots \\ {\frac{{\sin \left( {{\theta _n} + {\alpha _n}} \right)}}{{\sin {\alpha _n}}}}&{\frac{{\cos \left( {{\theta _n} + {\alpha _n}} \right)}}{{\sin {\alpha _n}}}}&{\frac{{{l_n}\sin \left( {{\theta _n} + {\alpha _n} - {\beta _n}} \right)}}{{\sin {\alpha _n}}}} \end{array}} \right],\\ {\left[ {\begin{array}{*{20}{c}} {{v_{r1}},}&{{v_{r2}},}&{ \cdots ,}&{{v_{rn}}} \end{array}} \right]^{\rm{T}}} = \mathit{\boldsymbol{K}}{\left[ {\begin{array}{*{20}{c}} {{v_y},}&{{v_x},}&{{\omega _z}} \end{array}} \right]^{\rm{T}}},\\ \mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\sin {\theta _1}}}{{\sin {\alpha _1}}}}&{\frac{{\cos {\theta _1}}}{{\sin {\alpha _1}}}}&{\frac{{{l_1}\sin \left( {{\theta _1} - {\beta _1}} \right)}}{{\sin {\alpha _1}}}}\\ {\frac{{\sin {\theta _2}}}{{\sin {\alpha _2}}}}&{\frac{{\cos {\theta _2}}}{{\sin {\alpha _2}}}}&{\frac{{{l_2}\sin \left( {{\theta _2} - {\beta _2}} \right)}}{{\sin {\alpha _2}}}}\\ \vdots&\vdots&\vdots \\ {\frac{{\sin {\theta _n}}}{{\sin {\alpha _n}}}}&{\frac{{\cos {\theta _n}}}{{\sin {\alpha _n}}}}&{\frac{{{l_n}\sin \left( {{\theta _n} - {\beta _n}} \right)}}{{\sin {\alpha _n}}}} \end{array}} \right]. \end{array} \right\} $ | (1) |
式中:[vy, vx, ωz]为平台运动速度, (ωi, vri)为驱动轮角速度和辊轮运动速度, αi为辊轮偏置角, li为履带中心到平台中心的距离, r为驱动轮半径, βi为履带分布角, θi为履带坐标系与平台坐标系所成的夹角.
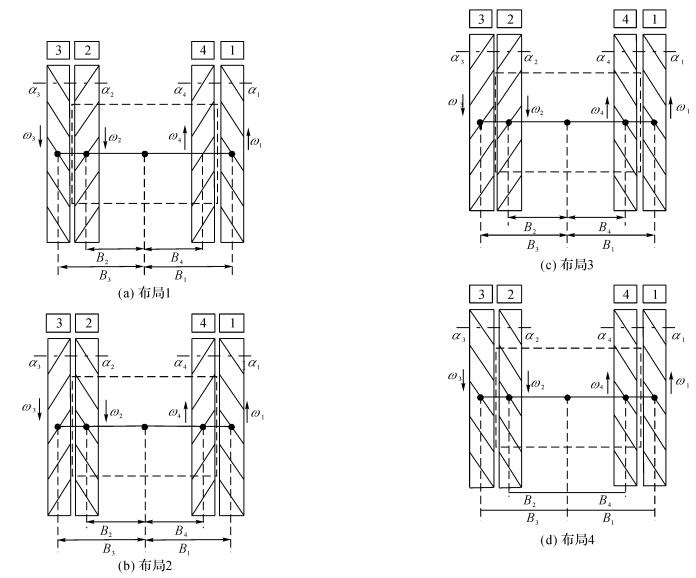
1.2 平台布局设计的平台参照传统履带车辆结构, 采用对称布局形式, 将全方位履带对称放置在平台两侧, 如图 2(a)~(d)所示.为了便于加工安装和驱动控制, 将各条履带的辊轮偏置角选取为±α(0 < α < π/2), 各平台结构参数如表 1所示.平台若要实现全方位运动, 则必须满足必要条件:逆运动学方程的雅克比矩阵列满秩, 即Rank(J)=3[10].表 1给出4种平台对应逆运动学方程的雅克比矩阵秩的值.可以看出, 平台(a)、(b)能够实现全方位移动, 平台(c)、(d)不能.平台(a)的布局对称性更好, 因此选择平台(a)作为研究对象.
|
图 2 履带平台布局示意图 Fig. 2 Layouts of track platform |
| 表 1 履带平台结构参数 Table 1 Parameters of track platform |
将表 1的各参数代入式(1), 可得图 2(a)所示平台的逆运动学方程:
| $ \left[ {\begin{array}{*{20}{c}} {{\omega _1}}\\ {{\omega _2}}\\ {{\omega _3}}\\ {{\omega _4}} \end{array}} \right] = \frac{1}{{r\sin \alpha }}\left[ {\begin{array}{*{20}{c}} {\sin \alpha }&{ - \cos \alpha }&{{B_1}\sin \alpha }\\ { - \sin \alpha }&{ - \cos \alpha }&{{B_2}\sin \alpha }\\ { - \sin \alpha }&{\cos \alpha }&{{B_3}\sin \alpha }\\ {\sin \alpha }&{\cos \alpha }&{{B_4}\sin \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{v_y}}\\ {{v_x}}\\ {{\omega _z}} \end{array}} \right]. $ | (2) |
一般情况下, 若不计履带宽度的影响, 取同侧两条履带几何中点到平台中心的距离作为履带中心距的一半, 则式(2)可以简化为
| $ \left[ {\begin{array}{*{20}{c}} {{\omega _1}}\\ {{\omega _2}}\\ {{\omega _3}}\\ {{\omega _4}} \end{array}} \right] = \frac{1}{r}\left[ {\begin{array}{*{20}{c}} 1&{ - \cot \alpha }&{B'}\\ { - 1}&{ - \cot \alpha }&{B'}\\ { - 1}&{\cot \alpha }&{B'}\\ 1&{\cot \alpha }&{B'} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{v_y}}\\ {{v_x}}\\ {{\omega _z}} \end{array}} \right]. $ | (3) |
式中:B′=(B1+B4)/2=(B2+B3)/2.
由于全方位履带上安装的辊轮具有一定的偏置角且可自由旋转, 使平台在各个方向上平动的速度和加速度各不相同, 该特性称为各向相异性[18].为了使平台具备更好的运动性能, 需要分析辊轮偏置角对平台运动的影响规律.
假定全方位平台的平动方向与x轴夹角为ψ(0≤ψ≤2π), 平动速度可以分解为x轴分量vx和y轴分量vy, 则
| $ {v_y} = V\sin \psi ,{v_x} = V\cos \psi . $ | (4) |
结合式(3)、(4), 可得
| $ V = \frac{{r{\omega _i}}}{{{a_{i1}}\sin \psi + {a_{i2}}\cos \psi }};i = 1,2,3,4. $ | (5) |
式中:
| $ \left[ {{a_{i1}},{a_{i2}}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{ - \cot \alpha }\\ { - 1}&{ - \cot \alpha }\\ { - 1}&{\cot \alpha }\\ 1&{\cot \alpha } \end{array}} \right];i = 1,2,3,4. $ |
假定驱动轮最大线速度为1, 即rωi≤1, 则
| $ {V_{\max }} = 1/{A_{\min }}. $ | (6) |
式中:A=|ai1sin ψ+ai2cos ψ|max(i=1, 2, 3, 4).
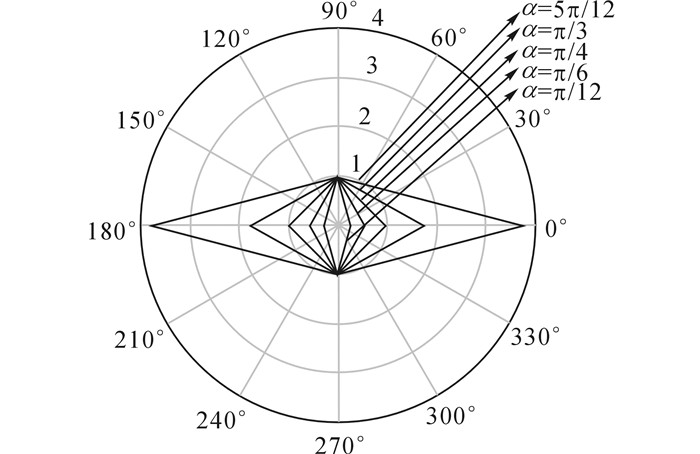
将辊轮偏置角选取5个特征值, 分别为π/12、π/6、π/4、π/3、5π/12, 代入式(6)得到平台各向最大速度, 如图 3所示.
|
图 3 全方位平台各向最大速度 Fig. 3 Maximum speed of omnidirectional platform |
如图 3所示, 当ψ=π/2和ψ=3π/2时, 即平台在纵向上运动时, 最大速度相同, 与辊轮偏置角无关.当ψ=0和ψ=π时, 即平台在横向上运动时, 最大速度与辊轮偏置角的变化趋势成正比, 偏置角越大, 最大速度越大, 且趋势越来越明显.
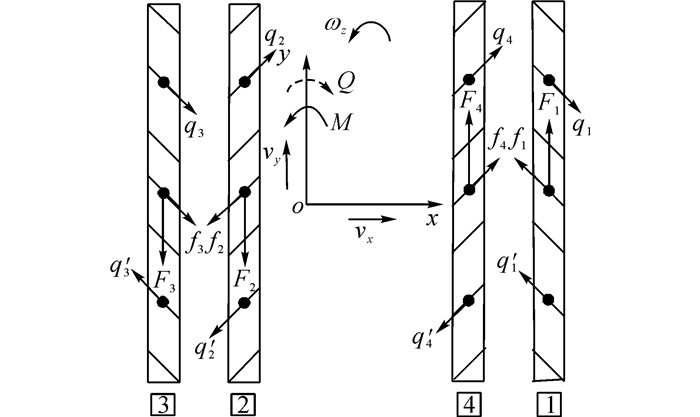
2.2 平台动力学分析全方位履带上的辊轮能够自由旋转, 且具有一定的偏置角度, 因此该履带的动力学特性与传统履带具有较大的差异.全方位履带牵引力可以分解为2个方向的力:平行于辊轮轴线方向的牵引力分量和垂直于辊轮轴线方向的牵引力分量[17].后者通常极小, 尤其是当辊轮发生转动后, 该牵引力分量可以等效为0.全方位履带的牵引力主要是沿辊轮轴线方向的牵引力分量.驱动轮提供的驱动力为Fi (i=1, 2, 3, 4), 则履带牵引力为fi=Fisin α (i=1, 2, 3, 4).其中, α为辊轮偏置角.不考虑滑转、滑移的影响, 对图 2(a)所示平台的转向过程进行受力分析(不计地面变形阻力及滚动阻力), 如图 4所示.
|
图 4 全方位平台受力分析图 Fig. 4 Force analysis of omnidirectional platform |
图 4中, M为平台转向驱动力矩, Q为平台转向摩擦阻力矩, qi、q′i (i=1, 2, 3, 4)为履带转向滑动摩擦阻力.假定m为平台质量, IV为平台转动惯量, μ为平台转向阻力系数, L为履带接地长度, (vy, vx, ωz)为平台运动速度, (ay, ax, az)为平台运动加速度.
在y、x、z轴上分别对平台进行受力分析, 可得
| $ \left. \begin{array}{l} m{a_y} = \left( {{f_1} - {f_2} - {f_3} + {f_4}} \right)\sin \alpha = \\ \;\;\;\;\;\;\;\;\left( {{F_1} - {F_2} - {F_3} + {F_4}} \right){\sin ^2}\alpha ,\\ m{a_x} = \left( { - {f_1} - {f_2} + {f_3} + {f_4}} \right)\cos \alpha = \\ \;\;\;\;\;\;\;\;\left( { - {F_1} - {F_2} - {F_3} + {F_4}} \right)\sin \alpha \cos \alpha ,\\ {I_{\rm{V}}}{a_z} = M - Q. \end{array} \right\} $ | (7) |
式中:
| $ \left. \begin{array}{l} M = \left( {{B_1}{f_1} + {B_2}{f_2} + {B_3}{f_3} + {B_4}{f_4}} \right)\sin \alpha = \\ \;\;\;\;\;\;\;\left( {{B_1}{F_1} + {B_2}{F_2} + {B_3}{F_3} + {B_4}{F_4}} \right){\sin ^2}\alpha ,\\ Q = \left( {\mu mgL{{\cos }^2}\alpha } \right)/4. \end{array} \right\} $ |
综上可得, 平台动力学方程为
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{a_y}}\\ {{a_x}}\\ {{a_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{{\sin }^2}\alpha }}{m}}&0&0\\ 0&{\frac{{\sin \alpha \cos \alpha }}{m}}&0\\ 0&0&{\frac{{{{\sin }^2}\alpha }}{{{I_{\rm{V}}}}}} \end{array}} \right] \times \\ \;\;\;\;\left[ {\begin{array}{*{20}{c}} 1&{ - 1}&{ - 1}&1\\ { - 1}&{ - 1}&1&1\\ {{B_1}}&{{B_2}}&{{B_3}}&{{B_4}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}}\\ {{F_3}}\\ {{F_4}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ { - \frac{{\mu mgL{{\cos }^2}\alpha }}{{4{I_{\rm{V}}}}}} \end{array}} \right]. \end{array} $ | (8) |
可以看出, 履带式全方位平台与传统履带车辆的动力学性能类似.按照平台平动最大速度分析方法, 将辊轮偏置角选取5个特征值, 分别为π/12、π/6、π/4、π/3、5π/12, 可得平台的最大加速度分布, 如图 5所示.

|
图 5 全方位平台各向最大加速度 Fig. 5 Maximum acceleration of omnidirectional platform |
如图 5所示, 当ψ≈π/2和ψ≈3π/2时, 即平台在偏于纵向运动时, 最大加速度与辊轮偏置角的变化趋势成正比, 偏置角越大, 最大加速度越大.当ψ=0和ψ=π时, 即平台在横向上运动时, 最大加速度在α=π/4时达到最大, 而后随着辊轮偏置角的增大, 加速度逐渐减小.
3 平台转向分析 3.1 辊轮偏置角设计对平台进行转向分析, 作如下假设[19]:1)平台转向在坚硬水平路面进行;2)平台履带法向负荷分布均匀;3)不计履带宽度的影响;4)低速均匀转向, 不考虑离心力的影响;5)不计地面变形阻力及滚动阻力.
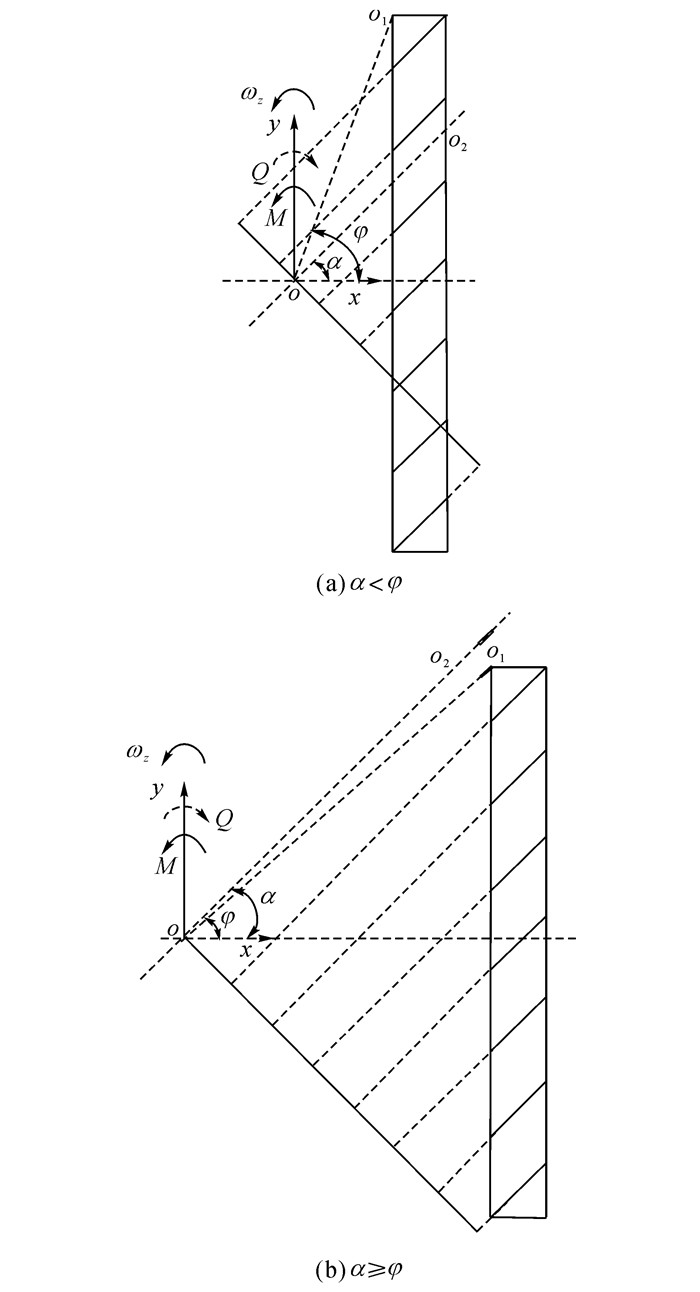
首先, 需要分析辊轮偏置角对平台转向运动的影响.如图 6所示, 定义履带内侧纵向顶点O1与平台中心O连线O1O与x轴的夹角为φ.作一条过O点且与辊轮轴线平行的直线O2O, O2O与x轴的夹角为α.如图 7所示, 当α < φ时, 直线O2O将同侧履带分为上、下两部分;当α≥φ时, 同侧履带位于直线O2O一侧.由2.2节中关于全方位履带动力学特性的分析可知, 全方位履带牵引力方向为辊轮轴线方向.按照判断力矩方向的右手法则可知, 转向过程中平台同侧履带被O2O划分的两部分所形成的力矩方向相反.此时, 不能保证整条履带的全部转向牵引力矩都为同向, 会对平台的转向驱动能力造成影响.为了使平台的转向驱动效果达到最好, 履带上辊轮偏置角的选取应满足如下关系:

|
图 6 辊轮偏置角与平台布局几何关系 Fig. 6 Relationship between roller offset angle and platform layout |
|
图 7 2种履带分割情况 Fig. 7 Two cases of track segmentation |
| $ \alpha \ge \varphi . $ | (9) |
依据履带车辆转向原理可知, 履带接地长度L与履带中心距B的比值一般取L/B≤1.6~1.8[20].由式(9)所示的几何关系, 可得
| $ \left. {\begin{array}{*{20}{c}} {\tan \varphi = \frac{L}{2}/\frac{B}{2},}\\ {\alpha \ge \varphi .} \end{array}} \right\} $ | (10) |
若取L/B=1.6, 可得偏置角取值为
| $ \alpha \ge 0.323{\rm{ \mathsf{ π} }}. $ | (11) |
履带式全方位平台具备纵向、横向等各个方向上的平移能力.理论上, 只有当平台运动中伴有中心转向时, 才会出现履带的相对滑动[17].以硬路面、无滑转、滑移的中心转向为例, 分析履带式全方位平台与传统履带平台的转向特性.
传统履带平台在硬路面上进行低匀速转向运动, 受到的转向阻力主要是指履带相对于地面的横向滑动摩擦力.假定履带法向负荷均匀分布, Q′为传统履带平台转向阻力矩[19], 则
| $ Q' = \mu mgL/4. $ | (12) |
定义ψ为转向摩擦阻力矩比, 表征履带式全方位平台与传统履带平台转向过程中滑动摩擦力矩的比较情况.结合式(7)、(12), 可得
| $ \psi = \frac{Q}{{Q'}} = \frac{{\left( {\mu mgL{{\cos }^2}\alpha } \right)/4}}{{\mu mgL/4}} = {\cos ^2}\alpha . $ | (13) |
从式(13)可以看出, 同等条件下全方位平台比传统履带平台的转向滑动摩擦阻力矩有明显的减小.转向摩擦阻力矩比与履带结构参数、转向半径、转向速度等无关, 只与辊轮偏置角有关.辊轮偏置角越大, 转向滑动摩擦力矩比越小, 则履带式全方位平台转向滑动摩擦力矩越小.
定义ζ为转向驱动力矩比, 表征履带式全方位平台与传统履带平台转向过程驱动力矩的比较情况.M′为传统履带平台在硬路面上进行低匀速转向运动的驱动力矩, 则
| $ M' = B\left( {{F_1} + {F_2} + {F_3} + {F_4}} \right)/2. $ | (14) |
结合式(7)、(14), 可得
| $ \zeta = \frac{M}{{M'}} = \frac{{\left( {{F_1} + {F_2} + {F_3} + {F_4}} \right){{\sin }^2}\alpha \left( {B/2} \right)}}{{\left( {{F_1} + {F_2} + {F_3} + {F_4}} \right)B/2}} = {\sin ^2}\alpha . $ | (15) |
从式(15)可以看出, 同等条件下全方位平台比传统履带平台的转向驱动力矩有明显减小.转向驱动力矩比与履带具体参数、转向半径、转向速度等无关, 只与辊轮偏置角有关.辊轮偏置角越大, 转向驱动力矩比越大, 则履带式全方位平台转向驱动力矩越大.
综上所述, 分析转向摩擦阻力矩比和转向驱动力矩比可以看出, 履带式全方位平台在减小转向滑动摩擦阻力矩的同时, 也减小了转向驱动力矩.因此, 需要分析能够保证全方位平台与传统履带平台具有相同转向能力的结构及运行条件.
3.3 平台几何约束条件由3.2节的分析可知, 同等条件下, 假设传统履带平台在硬路面上进行低匀速转向运动受到的摩擦阻力矩为Q′, 则全方位平台受到的摩擦阻力矩为Q′cos2α;传统履带平台克服摩擦阻力矩Q′需要的驱动力矩为M′, 全方位平台需要的驱动力矩为M′cos2α.此时, 全方位平台能够提供的驱动力矩为M′sin2α.若要保证同等条件下全方位平台具有相同的转向能力, 则必须满足:
| $ \frac{{M'{{\sin }^2}\alpha }}{{M'{{\cos }^2}\alpha }} \ge 1. $ | (16) |
通过计算可得
| $ \alpha \ge 0.25{\rm{ \mathsf{ π} }}. $ | (17) |
该结论表明, 辊轮偏置角必须满足α≥0.25π的条件, 才能确保履带式全方位平台与传统履带平台具有相同的转向能力.
结合式(10)、(17)可知, 履带式全方位平台在结构设计上应满足以下几何条件:
| $ \left. \begin{array}{l} L/B \le 1.6 \sim 1.8,\\ \alpha \ge \arctan \left( {L/B} \right),\\ \alpha \ge 0.25{\rm{ \mathsf{ π} }}. \end{array} \right\} $ | (18) |
在满足式(18)的条件下, 结合式(13)、(15)可知, 履带式全方位平台具有和传统履带平台相同的转向驱动能力, 但转向过程中的滑动摩擦力矩大大减小.α越大, 平台转向越容易, 所以在设计时可以根据应用条件, 适当选取较大的α以利于转向.若考虑传统履带结构的设计要求, α的选取还与平台结构中的L、B有关.
3.4 平台转向功率比定义ε为转向功率比, 表征履带式全方位平台转向与直行时所需的功率比.P为平台直行所需功率, P′为平台转向所需功率(这里以硬路面, 无滑转、滑移的中心转向为例), 则
| $ \left. \begin{array}{l} P = fmg{v_0},\\ P' = Q{\omega _0} = \left( {\mu mgL{\omega _0}{{\cos }^2}\alpha } \right)/4. \end{array} \right\} $ | (19) |
式中:v0为平台直行速度, 即左右两侧履带速度v0=v1=v2;ω0为平台中心转向角速度, ω0=2v1/B=2v2/B;f、μ分别为平台纵向行驶滚动阻力系数、转向行驶阻力系数.
| $ \varepsilon = P'/P = \left( {\mu L{{\cos }^2}\alpha } \right)/\left( {2fB} \right). $ | (20) |
除地面因素影响外, 平台的转向功率比与B、L和α有关.履带中心距越大, 履带接地长度越小, 辊轮偏置角越大, 则平台转向越容易; 反之, 转向越困难.由式(20)可知, 履带式全方位平台的转向特性与传统履带平台相似, 大大改善了转向性能.
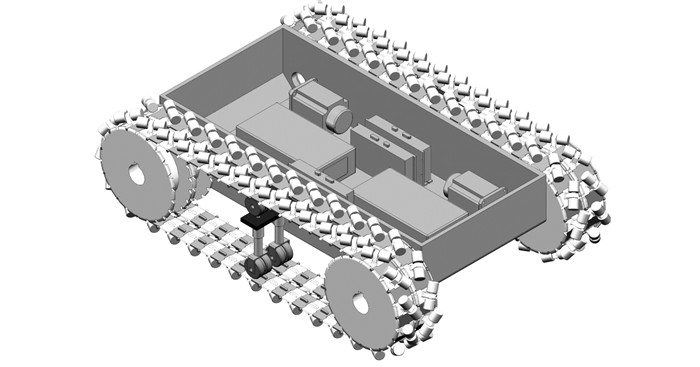
4 仿真验证 4.1 虚拟样机建模按照图 2(a)所示的平台布局形式, 利用ADAMS建立平台虚拟样机, 如图 8所示.样机中设计了电机、驱动器、电池等平台内部主要部件和简易悬架装置.结合图 3、5、式(18), 将平台辊轮偏置角选取为π/3, 能够确保平台具有和传统履带平台相同的转向驱动能力, 且在纵向上具备更好的速度和加速度性能, 利于平台纵向越野行驶.
|
图 8 平台虚拟样机 Fig. 8 Virtual prototype of platform |
平台样机的结构参数如表 2所示.
| 表 2 平台样机结构参数 Table 2 Parameters of prototype |
将表 2的各参数代入式(3), 可得平台逆运动学方程:
| $ \left[ {\begin{array}{*{20}{c}} {{\omega _1}}\\ {{\omega _2}}\\ {{\omega _3}}\\ {{\omega _4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {8.92}&{ - 5.15}&{2.34}\\ { - 8.92}&{ - 5.15}&{2.34}\\ { - 8.92}&{5.15}&{2.34}\\ {8.92}&{5.15}&{2.34} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{v_y}}\\ {{v_x}}\\ {{\omega _z}} \end{array}} \right]. $ | (21) |
针对平台的全方位移动性能, 分别对纵向直行、横向直行、45°斜行和中心转向4种运动状态进行仿真(忽略电机加速时间的影响).将平台目标速度分别设置为[1, 0, 0]T、[0, 1, 0]T, [1, -1, 0]T、[0, 0, 1]T, 分别代入式(21), 得到驱动轮理论转速.将仿真时间设置为4 s, 0~0.5 s为平台静稳定时间, 0.5~1.5 s为平台加速时间, 1.5~4.0 s为平台稳态运动时间, 样机运动轨迹及速度曲线如图 9所示.

|
图 9 平台运动轨迹及速度曲线 Fig. 9 Motion trajectory and velocity curve of omnidirectional platform |
在仿真开始阶段, 速度曲线有较小波动, 为平台落地时引起的微小振动, 而后进入静稳定阶段.设计一定时长的静稳定阶段主要是为了消除仿真中平台落地时的波动对后续运动的影响.经过加速阶段, 平台在1.5 s后达到稳态运动阶段, 对该阶段平台运动平均速度和质心位置偏移误差进行统计, 如表 3所示.结合图 9的运动轨迹和速度曲线, 总体来看, 履带式全方位平台可以较好地实现全方位移动性能, 稳态后的平均速度都接近期望速度1, 平台质心位置的偏移误差较小, 与理论分析相符.由于履带在运动过程中存在滑移、滑转现象, 导致平台运动轨迹发生一定的偏移.此外, 在平台运动学和动力学分析中忽略了履带宽度的影响, 对驱动轮实际速度的给定造成影响, 使平台运动存在一定的误差.
| 表 3 样机稳态运动平均速度及位置误差 Table 3 Average velocity and position errors of prototype |
履带式全方位平台除具有全方位移动性能外, 还具备较强的路面适应性.分别选取不平路面和楼梯两种常见不规则路面进行仿真验证.
在国标GB/T 7301-2005《机械振动 道路路面谱测量数据报告》中, 将不平路面分为A-H等级[21].日常生活中常见的路面多以B、C级为主, 石块路、搓板路等路面起伏较大, 可以达到E级路面[22].设计的平台模型不能利用ADAMS软件中.rdf路面文件, 因此利用谐波叠加法, 通过拉伸方式对E级路面进行重构.平台的纵向直行仿真轨迹和速度曲线如图 10所示.根据住宅建设规范的要求可知, 一般楼梯台阶宽度不小于260 mm, 高度不大于175 mm.结合表 2的平台结构参数, 选取楼梯宽度为320 mm, 高度为150 mm, 坡度约为25°.平台运动轨迹及重心变化曲线如图 11所示.图中,H为重心高度.从仿真结果来看, 平台在E级路面和楼梯两种不规则路面都具有较好的通过性.

|
图 10 平台E级路面运动轨迹及速度曲线 Fig. 10 Motion trajectory and velocity curve of omnidirectional platform on E-road |

|
图 11 平台爬越楼梯运动轨迹及重心变化曲线 Fig. 11 Motion trajectory and gravity centre curve of omnidirectional platform on climbing stairs |
(1) 基于全方位履带结构, 设计新型的履带式全方位移动平台.通过对纵向、横向、45°斜行和中心转向4种运动进行仿真, 平均速度都接近期望速度1, 质心位置的偏移误差较小, 与理论分析相符, 验证了平台的全方位移动性能.通过对E级路面纵向直行和爬越楼梯进行仿真, 验证了平台在不规则路面具有较好的通过性.
(2) 分析全方位平台转向性能, 确定平台设计的几何约束条件:α≥arctan (L/B)(L/B≤1.6~1.8)和α≥0.25π.在满足该条件的情况下, 履带式全方位移动平台具有和传统履带平台相同的转向驱动性能, 但滑动摩擦力矩明显减少.
(3) 履带式全方位平台为多履带平台, 当各履带分配速度的差异较大时, 由于电机驱动性能、履带机械结构、路面情况等影响, 会造成运动误差.履带上安装的辊轮可以自由旋转, 会影响平台运动精度.平台的运动控制将是下一步的研究重点.
| [1] |
孙强, 王文涛, 周璇. 基于kinect传感器的全方位运输平台控制系统研究[J]. 电子设计工程, 2015, 23(24): 99-102. SUN Qiang, WANG Wen-tao, ZHOU Xuan. Development of omnidirectional mobile system based on thekinect sensor[J]. Electronic Design Engineering, 2015, 23(24): 99-102. DOI:10.3969/j.issn.1674-6236.2015.24.030 |
| [2] |
曹其新, 杜建军, 冷春涛, 等. 用于协作搬运的全方位移动式多AGV系统[J]. 华中科技大学学报:自然科学版, 2013, 41(增Ⅰ): 550-556. CAO Qi-xin, DU Jian-jun, LENG Chun-tao, et al. Omnidirectional moving multi-AGVs system for cooperation transport[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2013, 41. |
| [3] |
CAVESTANY P, RODRIGUEZ A L, MARTINEZ H, et al. Improved 3D sparse maps for high-performance SFM with low-cost omnidirectional robots[C]//IEEE International Conference on Image Processing. Quebec City: IEEE, 2015: 4927-4931. http://ieeexplore.ieee.org/document/7351744/
|
| [4] |
JIANG S Y, LIN C Y, HUANG K T, et al. Shared control design of a walking-assistant robot[J]. IEEE Transactions on Control Systems Technology, 2017(99): 1-8. |
| [5] |
叶长龙, 佟泽卉, 于苏洋, 等. 全方位移动装配机器人运动学分析[J]. 机器人, 2016, 38(5): 550-556. YE Chang-long, TONG Ze-hui, YU Su-yang, et al. Kinematic analysis of an omnidirectional mobile assembly robot[J]. Robot, 2016, 38(5): 550-556. |
| [6] |
刘勇. 狭小空间内的全向移动平台关键技术研究[D]. 镇江: 江苏科技大学, 2016. LIU Yong. Research on omnidirectional mobile platform in narrow workspace[D]. Zhenjiang: Jiangsu University of Science and Technology, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D01036289 |
| [7] |
杨天旭. 全方位移动AGV智能控制技术研究[D]. 南京: 南京航空航天大学, 2016. YANG Tian-xu. Intelligent control technology for the omnidirectional mobile AGV[D]. Nanjing: NanjingUniversity of Aeronautics and Astronautics, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D01155863 |
| [8] |
王双双. 全方位移动平台运动仿真与控制研究[D]. 北京: 装甲兵工程学院, 2012. WANG Shuan-shuang. Research on simulation and motion control of omnidirectional platform[D]. Beijing: Academy of Armored Force Engineering, 2012. |
| [9] |
王一治, 钱晋武, 常德功. 不平路面上Mecanum轮全方位运动系统通用运动学模型[J]. 机械工程学报, 2009, 45(9): 77-82. WANG Yi-zhi, QIAN Jin-wu, CHANG De-gong. General kinematics model of motion system with Mecanum wheels on uneven floor[J]. Journal of Mechanical Engineering, 2009, 45(9): 77-82. |
| [10] |
王一治. 适于楼宇环境的全方位移动技术研究[D]. 上海: 上海大学, 2009. WANG Yi-zhi. Research on omnidirectional moving technology for building environment[D]. Shanghai: Shanghai University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-11903-2010252907.htm |
| [11] |
陶俊杰, 臧红彬, 蔡勇. 新型多功能越障机器人设计与功能仿真[J]. 机械设计与制造, 2016(1): 228-237. TAO Jun-jie, ZANG Hong-bin, CAI Yong. Design and functional simulation of a multi-functional obstacle robot[J]. Machinery Design and Manufacture, 2016(1): 228-237. |
| [12] |
田鹏. 8×8全方位移动平台运动性能仿真及控制研究[D]. 北京: 装甲兵工程学院, 2013. TIAN Peng. Research on motion performance simulation and control of the 8×8 omnidirectional platform[D]. Beijing: Academy of Armored Force Engineering, 2013. |
| [13] |
WEST M, ASADA H. Design of a holonomic omnidirectional vehicle[C]//Proceedings of the 1992 International Conference on Robotics and Automation. Nice: IEEE, 1992: 97-103. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=220328
|
| [14] |
TADAKUMA K, TADAKUMA R, KINOSHITA H, et al. Mechanical design of cylindrical track for sideways motion[C]//Proceedings of 2008 IEEE International Conference on Mechatronics and Automation. Takamatsu: IEEE, 2008: 161-167. http://ieeexplore.ieee.org/document/4798744/
|
| [15] |
DAMOTO R, CHENDY W, HIROSE S. Holonomic omnidirectional vehicle with new omniwheel mechanism[C]//Proceedings of the 2001 IEEE International Conference on Robotics and Automation. Seoul: IEEE, 2001: 773-778. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=932644
|
| [16] |
CHEN P, MITSUTAKE S, ISODA T, et al. Omni-directional robot and adaptive control method for off-road running[J]. IEEE Transactions on Robotics and Automation, 2002, 18(2): 251-256. DOI:10.1109/TRA.2002.999654 |
| [17] |
ZHANG Y N, HUANG T. Research on a tracked omnidirectional and cross-country vehicle[J]. Mechanism and Machine Theory, 2015, 87: 18-44. DOI:10.1016/j.mechmachtheory.2014.12.016 |
| [18] |
冷春涛, 曹其新. 四轮全方位移动机器人各向相异性研究[J]. 智能系统学报, 2007, 2(3): 45-51. LENG Chun-tao, CAO Qi-xin. Anisotropy of 4-wheeled omnidirectional mobile robots[J]. CAAI Transactions on Intelligent Systems, 2007, 2(3): 45-51. |
| [19] |
王良曦, 王红岩. 车辆动力学[M]. 北京: 国防工业出版社, 2008, 111-124.
|
| [20] |
闫清东, 张连第, 赵毓芹, 等. 坦克构造与设计[M]. 北京: 北京理工大学出版社, 2007, 570-573.
|
| [21] |
GB/T 7301-2005, 机械振动道路路面谱测量数据报告[S]. 北京: 中国标准出版社, 2005: 19-24.
|
| [22] |
喻凡, 林逸. 汽车系统动力学[M]. 北京: 机械工业出版社, 2008, 140-150.
|



