2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
滑坡治理的关键问题之一在于抗滑结构拟承担推力的确定[1-4].滑坡设计推力与采用的滑带土强度参数及计算方法密切相关.当选择较低的滑带强度参数和保守的滑坡推力计算方法时, 所计算的滑坡推力偏大, 抗滑支挡设计的安全储备推力增加, 防治工程不够经济.相反, 则会造成抗滑支挡结构的安全储备推力不足.如赵家塘大型岩石滑坡治理工程[5]中采用的抗滑桩截面尺寸为3.5 m×7.0 m, 治理工程实施后成功治理了该大型滑坡, 但可能存在设计偏于保守、治理工程不经济的问题.如攀枝花机场12#滑坡[6]在暴雨作用下, 在坡体自重增加、滑带土强度弱化、动静水压增加等综合作用下, 抗滑桩、阻滑键等结构被逐步剪断, 最终滑动面贯通, 滑坡整体失稳.忠万高速公路ZK38+316至ZK38+575处, 因边坡堑顶截水沟及坡面排水沟未能施工, 最终造成了桩身岩土分界线起点附近开始剪断、抗滑桩失效[7].滑带参数和滑坡设计推力是滑坡治理中的2个重要参数, 滑带参数的选取目前多是通过室内试验、原位试验、统计法[8-9]、反算法[10-11]、强度折减法[12-13]等方法确定, 但均存在一定的离散性;不平衡推力法由于计算简单, 可以考虑复杂形状的滑动面, 在滑坡稳定性计算中被广泛应用, 但是当滑动面为非规则折线型时, 存在不确定性[14].在设计中, 对于复杂滑坡, 多采取分段取值法确定滑带强度参数, 滑坡设计推力多采用规范推荐的不平衡推力法进行求解.利用不平衡推力显示法求解的滑坡推力过大, 利用不平衡推力隐示法求解的滑坡推力过小[15-16], 造成产生误差的主要原因是不平衡算法未考虑桩土之间的相互作用.基于上述不足, 本文采取基于监测位移的滑带土参数分析确定方法和考虑桩土耦合作用的不平衡推力法, 对设计推力定量化计算, 最终通过实例进行对比分析.
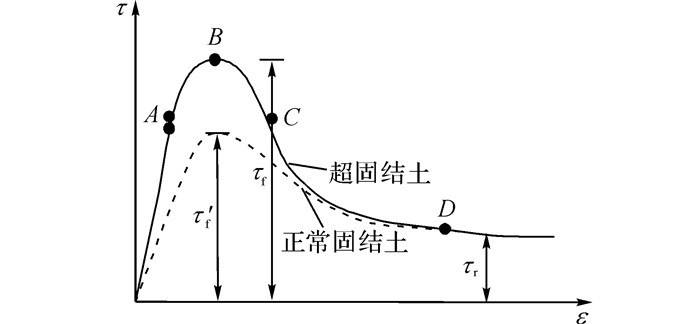
1 滑坡滑带土强度特征 1.1 滑带土强度的时效性当滑坡防治工程设计时, 滑带强度参数选取应结合滑坡发育阶段, 不同发育阶段滑带土的抗剪强度不同, 主要由滑带土的强度曲线控制.黏性滑带土具有峰值强度和残余强度, 即原状土剪切过程中达到峰值强度后随着剪切距离的增加和剪切破坏带的膨胀吸水, 强度会降低到软化点强度, 相当于重塑土的峰值强度.随着剪切位移的增加, 剪切面处土颗粒定向排列, 强度逐渐降低, 最后至残余强度后几乎不再增长, 黏性滑带土的典型抗剪强度曲线如图 1所示.图中,τf为峰值强度;τ′f为软化点强度;τr为残余强度.
|
图 1 黏性滑带土抗剪强度与剪切位移关系曲线 Fig. 1 Relationship between viscous sliding zone soil shear strength and displacement |
根据滑坡的发育过程可知, 在蠕动、挤压、滑动、剧滑和固结阶段, 结合滑带土必须分段选取的原则, 从时间和空间二维角度上确定滑带土的抗剪强度如表 1所示.表中, τ→τf, 其中τr分别表示滑带土强度接近于峰值强度、残余强度, τf、τr应取相同或相近含水率时的抗剪强度.
| 表 1 滑带土抗剪强度取值范围参照表 Table 1 Range reference of shear strength of slide zone soil |
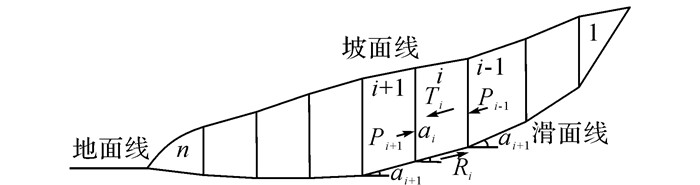
不平衡推力显示法不考虑支护结构与滑坡岩土体的相互作用, 仅增大滑坡下滑力, 不考虑支护作用下抗滑力的提高.推力计算示意图如图 2所示.滑坡的剩余下滑力为下滑力与抗滑力之差, 假设滑坡安全系数为Ks, 则条块的下滑力计算式为
|
图 2 推力计算示意图 Fig. 2 Schematic diagram of thrust calculation |
| $ \left. \begin{array}{l} {P_i} = {K_{\rm{s}}}{T_i} - {R_i} + {P_{i - 1}}{\psi _{i - 1}},\\ {\psi _{i - 1}} = \cos \left( {{a_{i - 1}} - {a_i}} \right) - \sin \left( {{a_{i - 1}} - {a_i}} \right)\tan {\varphi _i}. \end{array} \right\} $ | (1) |
式中:Pi为第i条块的剩余下滑推力, Ti为第i条块的下滑力, Ri为第i条块的抗滑力, Ψi-1为第i-1条块对i条块的传递系数, ai为第i条块的滑面倾角, φi为第i条块滑面的内摩擦角.当i=1时, 第1条块后方没有推力传递, 此时P0=0, Ψ0=0, P1=KT1-R1.由数学归纳法可得, 条块n的剩余推力表达式为
| $ {P_n} = {K_{\rm{s}}}{T_n} - {R_n} + {K_{\rm{s}}}\sum\limits_{i = 1}^{n - 1} {{T_i}\prod\limits_{j = i + 1}^n {{\psi _j}} } - \sum\limits_{i = 1}^{n - 1} {{R_i}\prod\limits_{j = i + 1}^n {{\psi _j}} } . $ | (2) |
将式(2)进行变换, 可得
| $ {K_{\rm{s}}} = \frac{{\sum\limits_{i = 1}^{n - 1} {{R_i}\prod\limits_{j = i + 1}^n {{\psi _j}} } + {R_n} + {P_n}}}{{\sum\limits_{i = 1}^{n - 1} {{T_i}\prod\limits_{j = i + 1}^n {{\psi _j}} } + {T_n}}}. $ | (3) |
当Pn=0时, 式(3)是不平衡推力显示法对应的滑坡稳定性计算公式.
1.2.2 隐示解不平衡推力隐示法的原理是将滑带土的抗剪强度进行折减, 即是将内摩擦角c和tan φ折减为c/K、tan φ/K, 以提高滑坡的安全储备.假设滑坡安全系数为Ks, 推导出滑坡条块的下滑力表达式:
| $ \left. \begin{array}{l} {P_i} = {T_i} - {R_i}/{K_{\rm{s}}} + {P_{i - 1}}{\psi _{i - 1}},\\ {\psi _{i - 1}} = \cos \left( {{a_{i - 1}} - {a_i}} \right) - \sin \left( {{a_{i - 1}} - {a_i}} \right)\tan {\varphi _i}/{K_{\rm{s}}}. \end{array} \right\} $ | (4) |
根据数学归纳法, 可得条块n的剩余推力表达式:
| $ {P_n} = {T_n} - \frac{{{R_n}}}{{{K_{\rm{s}}}}} + \sum\limits_{i = 1}^{n - 1} {{T_i}\prod\limits_{j = i + 1}^n {{\psi _j}} } - \frac{1}{{{K_{\rm{s}}}}}\sum\limits_{i = 1}^{n - 1} {{R_i}\prod\limits_{j = i + 1}^n {{\psi _j}} } . $ | (5) |
将式(5)进行变换, 可得
| $ {K_{\rm{s}}} = \frac{{\sum\limits_{i = 1}^{n - 1} {{R_i}\prod\limits_{j = i + 1}^n {{\psi _j}} } + {R_n}}}{{\sum\limits_{i = 1}^{n - 1} {{T_i}\prod\limits_{j = i + 1}^n {{\psi _j}} } + {T_n} + {P_n}}}. $ | (6) |
当Pn=0时, 式(6)是不平衡推力隐示法对应的滑坡稳定性计算公式.
2 滑带参数分析与确定 2.1 滑带土抗剪强度的弱化方程滑带本构方程是反映滑带切应力与位移的关系式.由于滑带具有明显的应变软化性质, 且Weibull分布能够很好地反映滑带抗剪强度试验曲线, 引入Weibull分布来描述滑带的切应力和剪切位移关系[17], 如下所示:
| $ \tau \left( u \right) = {G_{\rm{s}}}\left( {u/h} \right)\exp \left[ { - {{\left( {u/{u_0}} \right)}^m}} \right]. $ | (7) |
式中:Gs为初始切变模量, u为滑体沿滑床方向的位移, h为滑带厚度, u0为平均应变的测度, m为曲线形状参数.
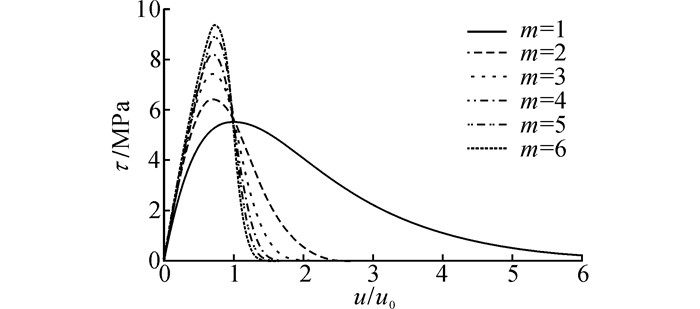
滑带本构曲线形状由Gs、u0和m共同刻画, Gs反映滑带刚度, 控制本构模型曲线的初始斜率;u0反映滑带应力, 法向力越大, 则u0越大, 控制本构模型曲线的峰值点位置. m反映材料的均匀性和脆性, m越大, 则应变软化特征越明显, 如图 3所示.图中,Gs=15 MPa, h=0.1 m, u0=0.1 m.
|
图 3 不同m下的Weibull分布本构曲线 Fig. 3 Weibull distribution constitutive curves underdifferent m values |
对滑带本构模型公式进行一阶、二阶求导, 则有
| $ \begin{array}{l} \tau ''\left( u \right) = \frac{{{G_{\rm{s}}}}}{h}\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]\left[ { - \frac{m}{{{u_0}}}{{\left( {\frac{u}{{{u_0}}}} \right)}^{m - 1}}} \right] \times \\ \;\;\;\;\;\;\;\;\;\;\;\left[ {1 + m - m{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right], \end{array} $ | (8) |
| $ \tau '\left( u \right) = \frac{{{G_{\rm{s}}}}}{h}\exp \left[ { - {{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]\left[ {1 - m{{\left( {\frac{u}{{{u_0}}}} \right)}^m}} \right]. $ | (9) |
令τ′(u)=0, τ"(u)=0, 分别得到曲线峰值强度相应的位移uf和曲线拐点对应位移ut:
| $ {u_{\rm{f}}} = {u_{\rm{0}}}{\left( {\frac{1}{m}} \right)^{1/m}}, $ | (10) |
| $ {u_{\rm{t}}} = {u_{\rm{0}}}{\left( {1 + \frac{1}{m}} \right)^{1/m}}. $ | (11) |
由滑带土切应力-剪位移曲线可以获得Gs、uf和残余强度相对应的位移ur.由于ur接近于ut, 令ur≈ut, 代入式(10)、(11), 求解出u0和m.由不同m下的滑带本构曲线可知, m越大, 则相对误差越小, 相对误差表达式为
| $ \delta = \left( {{u_{\rm{r}}} - {u_{\rm{t}}}} \right)/{u_{\rm{r}}}. $ | (12) |
滑带本构方程表明, 滑带土在剪切力作用下, 随着位移的增加, 抗剪强度先增加后减小.在滑坡防治工程设计中, 重点关注滑带土抗剪强度超过峰值后滑带土的弱化情况, 通常不考虑滑带土在峰值前随着位移的增加、强度增长的硬化过程.将滑带土本构曲线向左移动uf个单位, 得到以滑带土峰值强度对应位移为起点的强度变化曲线.将不同位移处对应的抗剪强度除以峰值强度, 可以推导出滑带土在渐变软化带的名义弱化系数ξ′(u), 具体表达式如下:
| $ \begin{array}{l} \xi '\left( u \right) = \frac{{\tau \left( {u + {u_{\rm{f}}}} \right)}}{{{\tau _{\rm{f}}}}} = \\ \;\;\;\;\;\;\;\;\;\;{G_{\rm{s}}}\frac{{u + {u_{\rm{f}}}}}{{h{\tau _{\rm{f}}}}}\exp \left[ { - {{\left( {\frac{{u + {u_{\rm{f}}}}}{{{u_{\rm{0}}}}}} \right)}^m}} \right];u \ge 0. \end{array} $ | (13) |
式(13)表明, 在滑带土强度弱化阶段, 随着剪切位移的增加, 切应力最终会趋近于零.黏性土类滑带的应变软化特征表现为, 在超过峰值强度后, 滑带土抗剪强度随着位移的增加而呈现非线性降低的趋势, 并最终趋向相对稳定的残余强度.可以看出, 滑带本构方程可以刻画滑带土剪切位移和剪切强度间的非线性关系, 但存在随着位移的增加而极限值不同的问题.本质上, 滑带土的弱化指峰值强度至残余强度间的弱化, 弱化至残余值后强度不再降低.借鉴滑带本构方程软化阶段非线性变化的特点, 结合实际滑带土具有相对稳定的残余强度的特征, 可以得到实际弱化系数ξ(u), 具体表达式为
| $ \begin{array}{l} \xi \left( u \right) = \frac{{\xi '\left( u \right)\left( {{\tau _{\rm{f}}} - {\tau _{\rm{r}}}} \right) + {\tau _{\rm{r}}}}}{{{\tau _{\rm{f}}}}} = \\ \;\;\;{G_{\rm{s}}}\frac{{u + {u_{\rm{f}}}}}{h}\exp \left[ { - {{\left( {\frac{{u + {u_{\rm{f}}}}}{{{u_{\rm{0}}}}}} \right)}^m}} \right]\frac{{{\tau _{\rm{f}}} - {\tau _{\rm{r}}}}}{{\tau _{\rm{f}}^2}} + \frac{{{\tau _{\rm{r}}}}}{{{\tau _{\rm{f}}}}};\;\;\;\;u \ge 0. \end{array} $ | (14) |
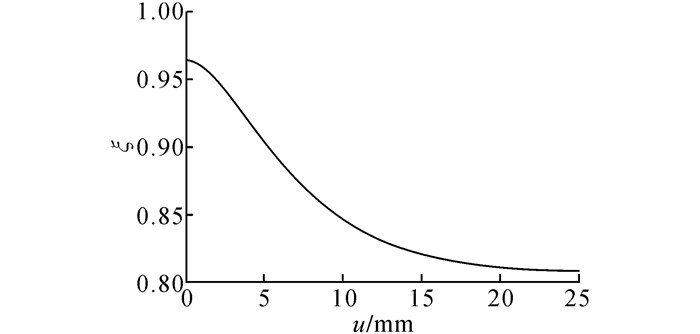
以文献[18]的试验数据为基础, 当正应力σ=120 kPa时, 从滑带土的切应力-切应变曲线可得, Gs=15.0 MPa, uf =4.0 mm, ut =7.9 mm, h=0.5 m, τf =57 kPa, τr=46 kPa.将上述数据代入式(10)、(11)进行联立求解, 可得m=1.06, u0=4.2 mm.滑带弱化系数与剪切位移的关系如图 4所示.
|
图 4 剪切位移和弱化系数的关系曲线 Fig. 4 Relationship between shear displacement and weakening coefficient |
通过弱化系数法求解得到的理论值和试验值之比如表 2所示.表中, 位移以滑带土峰值位移为零点起算,τe、τt分别为抗剪强度的理论值和试验值,ε为误差.从表 2可以看出, 利用弱化系数法求解所得到的理论值与试验值较接近, 最大误差不超过7%, 表明弱化系数法能够较好地反映滑带土的弱化规律.根据弱化系数的推导原理及过程, 得到滑带土不同位移情况下的抗剪强度表达式:
| 表 2 弱化系数法求解滑带土抗剪强度理论值与试验值对比 Table 2 Comparison of shear strength in slide zone between test results and theoretical results obtained by weakening coefficient method |
| $ \tau \left( u \right) = \xi \left( u \right){\tau _{\rm{f}}}. $ | (15) |
根据摩尔库仑准则, 可得抗剪强度表达式:
| $ \tau \left( u \right) = \xi \left( u \right)\left( {\sigma \tan {\varphi _{\rm{f}}} + {c_{\rm{f}}}l} \right). $ | (16) |
由式(15)、(16)可知, 抗剪强度的弱化最终反映到滑带土抗剪强度参数中黏聚力和内摩擦角的弱化.事实上, 黏聚力与内摩擦角的弱化系数不一样, 为了更合理地表达黏聚力和内摩擦角的差异性弱化性质, 引入差异弱化因子, 刻画黏聚力和内摩擦角的不同弱化程度, 则弱化后的抗剪强度参数c和φ的表达式为
| $ c\left( u \right) = k\xi \left( u \right){c_{\rm{f}}},\varphi \left( u \right) = \arctan \left[ {\xi \left( u \right)\tan {\varphi _{\rm{f}}}} \right]. $ | (17) |
式中:k为差异弱化因子.
2.2 滑带抗剪强度演化规律对于简单滑坡, 往往采取单一滑带土参数进行稳定性评价或者推力计算.对于正在孕育的滑坡, 分段取值来评价滑坡稳定性或者计算滑坡设计推力更符合实际情况.分段取值带来的直接后果是滑带土参数的离散化, 与实际情况不符.根据以上不足, 提出滑带土参数连续取值的方法.基于滑带土实验室结果中位移与强度的本构关系, 认为在实际的滑坡治理工程中, 滑带土强度存在残余带、峰值带和渐变软化带, 其中渐变软化带的强度介于残余强度和峰值强度之间, 滑带土强度的变化服从Weibull分布.引入渐变软化段位置函数f(t)和放大系数λ分别反映实际滑带的渐变软化段位置和规模放大效应, 即分别将弱化曲线沿x轴方向右移f(t)个单位;沿x轴拉伸λ倍, 得到考虑时空效应的弱化系数方程ξ(x, t), 如图 5所示.

|
图 5 典型滑带土强度分布示意图 Fig. 5 Typical diagram of strength distribution in slide zone |
| $ \left. \begin{array}{l} \xi \left( {x,t} \right) = \frac{{{G_{\rm{s}}}}}{h}\left( {\frac{{f\left( t \right) - x}}{\lambda } + {u_{\rm{f}}}} \right) \times \\ \;\;\;\exp \left[ { - {{\left( {\frac{{f\left( t \right) - x + \lambda {u_{\rm{f}}}}}{{\lambda {u_0}}}} \right)}^m}} \right] \times \frac{{{\tau _{\rm{f}}} - {\tau _{\rm{r}}}}}{{\tau _{\rm{f}}^2}} + \frac{{{\tau _{\rm{r}}}}}{{{\tau _{\rm{f}}}}};\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \le x \le f\left( t \right). \end{array} \right\} $ | (18) |
式中:x为滑带任意点位置, 坐标起点在滑坡后缘(推移式)/前缘(牵引式);t为滑坡不同发育程度对应的实际时间;f(t)为滑带初始峰值位置, 由滑坡的发展阶段确定;λ为规模放大效应系数, λ=Δx/(ur-uf), 物理意义为工程实践中介于峰值强度和残余强度的实际滑带长度与滑坡滑带土室内试验得到的残余位移和峰值位移差值的倍数;Δx为渐变带宽度, 在滑带弱化系数方程中, 定义渐变带宽度为从某一极值到另一个极值的距离.
2.3 基于监测位移的滑带弱化方程根据滑体厚度, 估算滑体的平均正应力强度, 通过实验确定在该正应力作用下的剪切强度和剪切位移关系曲线, 给出峰值强度和残余强度对应的剪切位移uf、ur.在某一时刻, 从滑坡后缘的第一个孔开始, 将ur逐个与监测孔在滑带处的位移比较, 则存在一个i满足u(t)i-1 < ur < u(t)i, 此时说明在深部位移测斜孔SKi-1和SKi之间存在一个点, 在该点右侧为渐变软化段, 左侧为残值段.假设该点位置按u(t)i-1、ur和u(t)i进行线性比例分配, 则残值段与渐变段分界点xc1的表达式为
| $ {x_{{\rm{c1}}}} = {x_{i - 1}} + \left( {{x_i} - {x_{i - 1}}} \right)\frac{{{u_{\rm{r}}} - u{{\left( t \right)}_{i - 1}}}}{{u{{\left( t \right)}_i} - u{{\left( t \right)}_{i - 1}}}}. $ | (19) |
式中:xi为深部位移监测孔SKi在横坐标上的位置, u(t)i为某一时刻深部位移监测孔SKi在滑带处的累积位移.存在一个j, 满足u(t)j-1 < uf < u(t)j, 说明在深部位移测斜孔SKj-1和SKj之间存在一个点, 在该点右侧为峰值段, 左侧为渐变软化段.假设该点位置按u(t)j、uf和u(t)j-1进行比例分配, 则渐变软化带位置f(t)的表达式为
| $ f\left( t \right) = {x_{j - 1}} + \left( {{x_j} - {x_{j - 1}}} \right)\frac{{{u_{\rm{f}}} - u{{\left( t \right)}_{j - 1}}}}{{u{{\left( t \right)}_j} - u{{\left( t \right)}_{j - 1}}}}. $ | (20) |
式中:xj为深部位移监测孔SKj在横坐标上的位置, u(t)j为某一时刻深部位移监测孔SKj在滑带处的累积位移.
由式(19)可知, xc1为残值段和渐变软化段的估算分界点, xc2为渐变软化段和峰值段的估算分界点, 则规模放大系数λ的估算表达式为
| $ \begin{array}{l} \lambda = \frac{1}{{{u_{\rm{r}}} - {u_{\rm{f}}}}}\left\{ {\left[ {{x_{j - 1}} + \left( {{x_j} - {x_{j - 1}}} \right)\frac{{{u_{\rm{f}}} - u{{\left( t \right)}_{j - 1}}}}{{u{{\left( t \right)}_j} - u{{\left( t \right)}_{j - 1}}}}} \right] - } \right.\\ \;\;\;\left. {\left[ {{x_{i - 1}} + \left( {{x_i} - {x_{i - 1}}} \right)\frac{{{u_{\rm{r}}} - u{{\left( t \right)}_{i - 1}}}}{{u{{\left( t \right)}_i} - u{{\left( t \right)}_{i - 1}}}}} \right]} \right\};j > i. \end{array} $ | (21) |
由此, 考虑时效性的滑带土弱化表达式为
| $ \left. \begin{array}{l} c\left( {x,t} \right) = \xi \left( {x,t} \right){c_{\rm{f}}},\\ \varphi \left( {x,t} \right) = \arctan \left[ {\xi \left( {x,t} \right)\tan {\varphi _{\rm{f}}}} \right]. \end{array} \right\} $ | (22) |
在工程设计中, 作用于抗滑桩上的滑坡推力等于采用不平衡推力法所求得的滑坡剩余下滑力与对应滑动面倾角余弦值之积, 如下所示:
| $ {F_i} = {P_i}\cos {a_i}. $ | (23) |
式中:Fi为抗滑桩拟承担的滑坡推力, Pi为设桩处滑坡剩余下滑力, ai为设桩处滑面倾角.
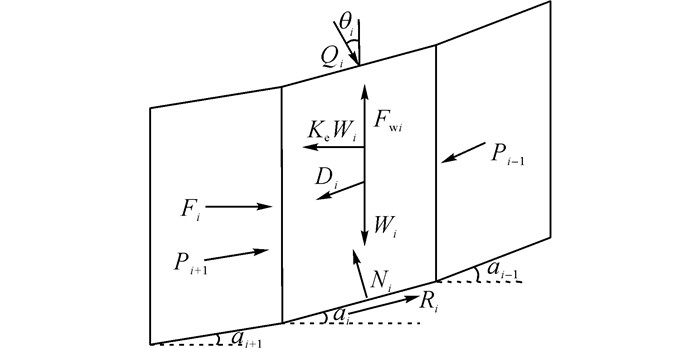
利用不平衡推力法计算滑坡推力的总体思路是先计算出Pi, 将滑坡推力沿水平方向的分力Fi作为抗滑桩的设计推力.在滑坡安全系数的表达式中, 显示法将Pn放在表达式分子中, 隐示法将Pn放在分母中, 这是由于显示法与隐示法对Pn的定性不同, 从而导致两种计算方法结果上的差异.不管是显示法还是隐示法, 均未考虑桩土之间的相互作用.在抗滑桩的设计中, 抗滑桩的主要作用是阻止抗滑桩上部土体的下滑.实际上, 滑坡土体在对桩产生推力的同时, 桩将同时产生一个反作用力.对于某一个条块而言, 滑坡除受到上级条块的推力、滑体自身重力、地震力、动静水压力和抗滑力外, 还受到桩对条块的反作用力, 从而使治理后的滑坡整体保持一个相对平衡的状态.本文不考虑下部土体的反力作用, 下部土体的反力作为一定的安全储备, 这点和传统抗滑桩推力计算是一致的.在传统不平衡推力法条块力系分析的基础上, 将抗滑桩拟承担滑坡推力的反作用力Fi水平作用于抗滑桩位置上方条块.根据力的矢量分解和条块力传递原则, 求解出使Pi=0时对应的力Fi作为抗滑桩的设计推力, 如图 6所示.
|
图 6 考虑桩土耦合作用的滑坡条块受力示意图 Fig. 6 Diagram of landslide block force with pile-soil coupling |
假设抗滑桩布置在条块i与条块i+1之间, 将滑坡设计推力Fi作用于条块i上, 则考虑桩土耦合作用的条块i的下滑力和抗滑力公式如下:
| $ \begin{array}{l} {T_i} = \left( {{W_i} - {F_{{\rm{w}}i}}} \right)\sin {a_i} + \left( {{K_{\rm{e}}}{W_i} - {F_i}} \right)\cos {a_i} + \\ \;\;\;\;\;\;{D_i}\cos \left( {{a_i} - {\beta _i}} \right) + {Q_i}\sin \left( {{a_i} - {\theta _i}} \right), \end{array} $ | (24) |
| $ \begin{array}{l} {R_i} = \left[ {\left( {{W_i} - {F_{{\rm{w}}i}}} \right)\cos {a_i} + \left( {{F_i} - {K_{\rm{e}}}{W_i}} \right)\sin {a_i} - } \right.\\ \;\;\;\;\;\;\left. {{D_i}\sin \left( {{a_i} - {\beta _i}} \right) + {Q_i}\cos \left( {{a_i} - {\theta _i}} \right)} \right]\tan {\varphi _i} + {c_i}{l_i}. \end{array} $ | (25) |
式中:Fi为设置于条块i处抗滑桩所承担的滑坡推力;Wi为设置于条块i处抗滑桩的重力;Di为第i块条块的下滑力;Fwi为第i块条块的静水浮力;Qi为建构筑物荷载;Ke为稳定系数;θi为建构筑物荷载方向与重力方向的夹角;βi为第i块条块的下滑力方向与水平方向的夹角;ci为第i块条块所在滑面的单位黏聚力;li为条块i所在滑面上的长度, 其他参数与前文相同.
将式(24)、(25)代入式(2)、(5), 得到考虑桩土作用的滑坡推力计算公式.当Pi=0时所对应的Fi是满足设计安全系数Ks时拟设桩位处抗滑桩的设计滑坡推力, 滑坡推力计算与现行规范推荐的滑坡推力求解公式主要有以下两点不同:1)改进的滑坡推力计算公式中出现抗滑桩水平支护力Fi来考虑支护结构对岩土体的反作用力;2)改进的滑坡推力计算公式可以计算不同高程处的滑坡推力, 对于滑坡来说, 当桩位设置的相互影响较小时, 可以直接确定不同桩排的设计推力, 不再像传统的推力计算公式需要根据对滑坡的认识和经验将剩余下滑力按照不同比例分配至不同高程位置的抗滑桩排.
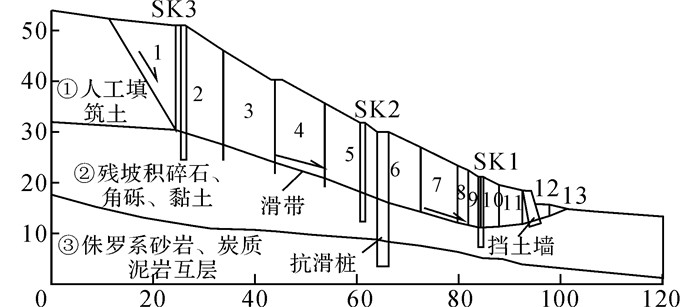
4 工程实例分析如图 7所示为攀枝花机场一滑坡的地质模型.滑坡体物质为人工填筑体, 天然密度ρ=1.95 g/cm3.滑床物质为残坡积碎石、角砾、黏土以及下层的侏罗系砂岩与泥岩互层岩体.滑面后缘较陡, 中部滑带产状相对稳定, 前缘滑带呈弧形反翘.滑带为强-中风化碳质泥岩, 含水量高呈软塑状态, 具有明显的应变软化性质, 揭露厚度为1.0~5.0 m, 前缘较薄, 后缘稍厚.深部位移数据采集仪器产自于SINCO公司, 测量误差为±0.002 mm.通过前期现场钻孔结果和监测数据绘制的主滑方向合位移量曲线特征, 可以清晰、较直观地对滑带位置进行判定.剖面附近的深部位移监测孔监测数据显示, 在2016年11月中旬, 滑坡从后缘至前缘监测孔SK3~SK1在滑面处的深部位移量分别为17、12和8 mm, 为一典型推移式滑坡.室内试验表明, 主滑段和抗滑段范围内的滑带土黏聚力c=6~10 kPa, 内摩擦角φ=12.8~15.0°.
|
图 7 攀枝花机场次级滑坡的滑坡推力计算模型 Fig. 7 Landslide thrust calculation model of secondary landslide at Panzhihua Airport |
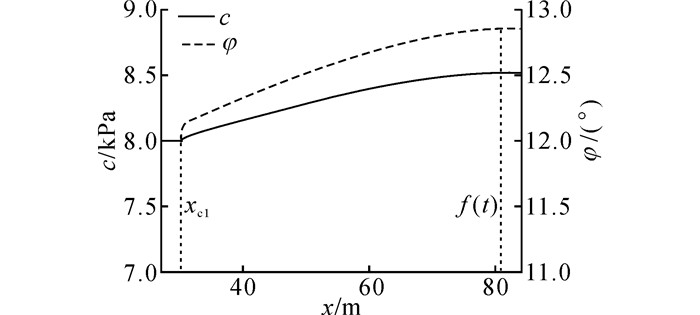
根据现场大剪试验结果得出, 当σ=100 kPa时, 从滑带土切应力-切应变曲线可得, Gs=14.0 MPa, uf=8.5 mm, ut=16.5 mm, h=2.0 m, τf=47 kPa, τr=32 kPa.通过式(10)、(11)求解可得, m=1.16, u0=9.66 mm.根据式(19)、(20)可得, xc1=30.42 m, f(t)=81.82 m.通过式(21)可得, λ=6 424.656.为了简化计算, 式(17)中, 差异弱化因子k=1.在计算中, 滑带参数根据监测位移情况和滑带取值, 考虑到滑坡后缘已发现张拉室内试验以及现场变形迹象分段裂隙, 因此第1条块对应的滑面抗剪强度参数为c=0 kPa, φ=30°;第2~9条抗剪强度参数c、φ取值如图 8所示, 自滑坡后缘向前缘方向滑带土强度以非线性分布逐渐增加;第10~13条块抗剪强度为c=8.51 kPa, φ=12.85°.
|
图 8 滑带抗剪强度参数图 Fig. 8 Shear strength parameter diagram on sliding zone |
根据滑坡地质模型, 结合现场地形条件, 在第5条块处设置一排桩长为30 m、桩截面为2.2 m×3.4 m的抗滑桩.结合滑坡各级条块的几何参数, 采用不平衡推力显示法、隐式法和考虑桩土耦合作用的改进方法, 得出不同安全系数下抗滑桩的设计推力, 如表 3所示.表中, F1、F2分别为显示解和改进显示解,F3、F4为隐示解和改进隐示解.
| 表 3 不平衡推力法改进前后抗滑桩设计推力计算对比 Table 3 Comparison of design thrust calculation of anti-slide pile before and after improvement of imbalance thrust method |
从表 3可以看出, 不平衡推力法显示解和隐示解在相同的计算安全系数下, 相应求解的抗滑桩设计推力差别较大, 且随着安全系数的增加, 抗滑桩设计推力之差不断增加.利用改进显示法和隐示法求解得到的抗滑桩设计推力相差不大, 且除安全系数Ks=1.05外, 当Ks=1.10、1.15和1.20时, 利用改进显示法和隐示法求解得到的抗滑桩设计推力介于不平衡推力显示法和隐示法所求解的抗滑桩设计推力之间, 较好地解决了工程设计中采用显示法时求解的抗滑推力偏大, 采用隐示法求解的抗滑推力偏小的难题.随着安全系数的增加, 采用改进的显示法求解的抗滑推力逐渐降低, 且推力百分比增幅较大;改进的隐示法对应的抗滑桩推力百分比增幅相对较小.
安全系数是指滑坡治理后应该达到的稳定程度, 是一个主观目标值;稳定系数指滑坡当前的稳定程度, 是一个客观分析值, 两者的主要区别在于治理前和治理后.将显示法和隐式法改进前、后的抗滑桩设计推力反作用于滑坡条块上, 得到加固后分别采用改进显示法和隐示法计算得到的稳定系数, 如表 4所示.表中, F为设计推力, K为稳定系数.
| 表 4 不同推力加固后的滑坡稳定系数对比表 Table 4 Comparison of landslide stability coefficient after different thrust reinforcement |
从表 4可知, 当采用不平衡推力显示法和隐示法计算所得的抗滑桩推力作用于滑坡体上时, 加固后的稳定系数与计算采用的安全系数不同;当采用改进的显示法和隐示法计算所得的抗滑桩推力作用于滑坡体上时, 相应加固后的滑坡稳定系数恰好等于抗滑桩推力计算时采用的安全系数.对于显示计算法, 当Ks=1.05时, 采用不平衡推力显示法和改进显示法求得的推力来加固滑坡后对应的稳定系数相近, 本例计算显示解加固后的稳定性系数略低于改进显示解加固后的稳定系数;当Ks=1.10、1.15和1.20时, 显示解加固后的滑坡稳定性系数均较改进显示加固后的滑坡稳定性系数高, 表明采用不平衡推力显示法求解抗滑桩设计推力时计算值偏大, 且随着安全系数的增加, 显示解和改进显示解对应加固后的滑坡稳定性系数之差逐渐增加.对于隐示法, 隐示解加固后的滑坡稳定性系数均比改进隐示解低, 表明采用不平衡推力隐示解法求解抗滑桩设计推力时计算值偏小.
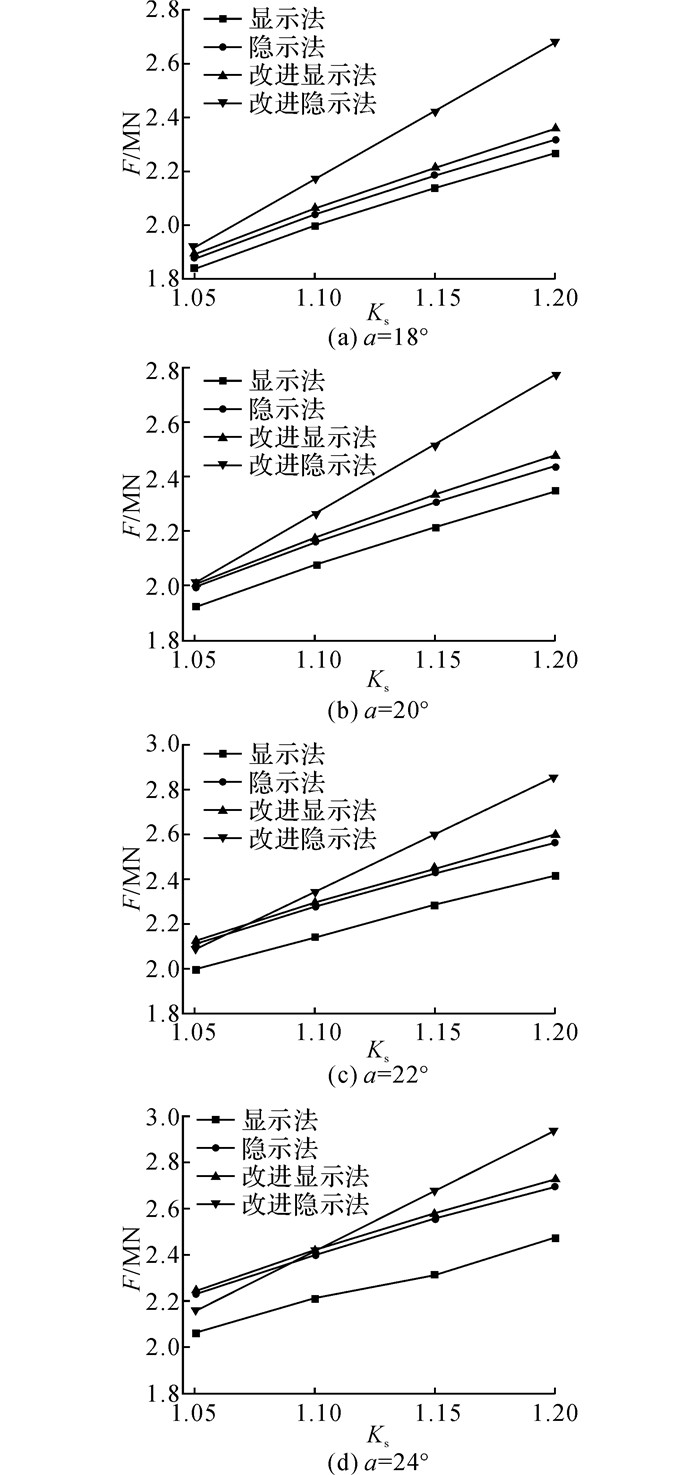
利用改进的不平衡推力法计算得到的设计推力与设桩处滑动面倾角a和Ks紧密相关, 如图 9所示为不同滑面倾角和安全系数下滑坡的设计推力.
|
图 9 设桩处不同滑面倾角a下设计推力与安全系数的关系 Fig. 9 Relationship between design thrust and safety factor at different sliding angles a on pile foundation |
从图 9可以看出, 设桩处的滑面倾角越大, 抗滑桩设计推力越大.当设桩处的滑面倾角固定时, 设计推力随着计算安全系数的增加呈正比例增长, 其中显示法对应的设计推力与设计安全系数的关系曲线斜率较陡, 即随着安全系数的增加, 设计推力增长显著;隐示法、改进的显示法和改进的隐示法对应的设计推力与设计安全系数关系曲线斜率一致, 且较显示法对应的设计推力与设计安全系数关系曲线的斜率较缓, 表明后3种方法对应的设计推力随着设计安全系数的增长幅度较小.当设桩处滑面倾角较小时, 利用改进的显示法和隐示法求解所得的设计推力介于显示法和隐式法求解设计推力之间, 如图 9(a)、(b)所示.当设桩处滑面倾角较大时, 利用改进的显示法和隐示法求解所得的设计推力在较小的设计安全系数区间内, 设计推力稍大于显示法和隐示法所求的设计推力, 表明利用改进的显示法和改进的隐示法所求解的设计推力有更大的安全储备.在该种情况下, 考虑到现有的不平衡推力显示法求解对应的设计推力已相对保守, 建议采用不平衡推力显示法求解对应的推力作为抗滑桩设计推力.在设计安全系数较大的区间内, 改进的显示法和改进的隐示法的设计推力均介于显示法和隐示法所求解的设计推力之间, 且计算结果较接近.在该种情况下, 考虑到利用显示法计算得到的推力过大, 利用隐示法计算得到的推力过小, 此时建议采用改进显示法或隐式法求解得到的推力作为滑坡下滑推力.
5 结论(1) 滑带土强度参数对滑坡稳定性的计算至关重要.本文在滑带土本构方程的基础上, 引入渐变软化段位置函数和规模放大系数λ, 反映实际滑带土的时效性.提出基于监测位移确定各点滑带土强度的量化方法, 避免了参数取值经验化所带来的不足, 为大型复杂滑坡滑带的参数取值提供了新思路.
(2) 利用改进显示法和隐示法所求解的抗滑桩设计推力介于不平衡推力显示法和隐示法所求解的抗滑桩设计推力之间, 较好地解决了工程设计中采用显示法时求解的抗滑推力偏大、隐示法求解的抗滑推力偏小的难题.
(3) 在设计安全系数较大的区间内, 改进的显示法和改进的隐示法的设计推力均介于显示法和隐示法所求解的设计推力之间, 且计算结果较接近.
(4) 利用本文的改进方法可以初步确定相互影响桩排各自的抗滑推力.工程应用算例表明, 改进的显示法和隐式法是一种折中的定量化计算方法, 可以为滑坡防治工程中抗滑桩设计推力的确定提供参考.
| [1] |
张健, 胡瑞林, 李志清. 堆积体滑坡抗滑桩所受推力计算及分布特征研究[J]. 岩土工程学报, 2012, 34(11): 2005-2010. ZHANG Jian, HU Rui-lin, LI Zhi-qing. Distribution laws of thrust of talus slide on anti-sliding pile[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2005-2010. |
| [2] |
徐骏, 李安洪, 肖世国. 折线型滑面滑坡桩排推力分布规律研究[J]. 岩土力学, 2012, 33(11): 3479-3488. XU Jun, LI An-hong, XIAO Shi-guo. Study of landslide thrust distribution law of row of piles in reinforced landslide with polygonal line slip surface[J]. Rock and Soil Mechanics, 2012, 33(11): 3479-3488. |
| [3] |
刘永莉, 孙红月, 于洋, 等. 基于BOTDR监测技术抗滑桩上滑坡推力确定[J]. 浙江大学学报:工学版, 2012, 46(5): 798-803. LIU Yong-li, SUN Hong-yue, YU Yang, et al. Determining landslide thrust on anti-sliding pile by BOTDR monitoring technology[J]. Journal of Zhejiang University:Engineering Science, 2012, 46(5): 798-803. |
| [4] |
杨涛, 周德培, 张俊云, 等. 抗滑桩滑坡推力分布形式的计算确定[J]. 岩土工程学报, 2006, 28(3): 322-326. YANG Tao, ZHOU De-pei, ZHANG Jun-yun, et al. Distribution of land-slide thrust on anti-slide pile[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 322-326. |
| [5] |
王恭先, 马惠民, 王红兵, 等. 大型复杂滑坡和高边坡变形破坏防治理论与实践[M]. 北京: 人民交通出版社, 2016, 45.
|
| [6] |
GONG Z. Remediation measures on the landsliede in fill slopes in north-east part of Panzhihua airport[J]. Journal of Engineering Geology, 2007, 15(2): 237-243. |
| [7] |
陈中学, 邵树强, 李文广. 抗滑桩支挡边坡失效实例分析[J]. 公路交通技术, 2016, 32(3): 31-34. CHEN Zhong-xue, SHAO Shu-qiang, LI Wen-guang. Failure analysis of retaining slope with anti slide piles[J]. Technology of Highway and Transport, 2016, 32(3): 31-34. |
| [8] |
李远耀, 殷坤龙, 柴波, 等. 三峡库区滑带土抗剪强度参数的统计规律研究[J]. 岩土力学, 2008, 29(5): 1419-1424. LI Yuan-yao, YIN Kun-long, CHAI Bo, et al. Study on statistical rule of shear strength parameters of soil in landslide zone in Three Gorges Reservoir area[J]. Rock and Soil Mechanics, 2008, 29(5): 1419-1424. |
| [9] |
张红琼, 欧阳涛. 重庆地区滑带土抗剪强度参数概率统计分析[J]. 灾害与防治工程, 2008(4): 143-145. ZHANG Hong-qiong, OUYANG Tao. Probability distribution statistics analysis of shear strength parameters in sliding zone along horizontal-stratum landslides in Chongqing City[J]. Disaster and Control Engineering, 2008(4): 143-145. |
| [10] |
卢坤林, 朱大勇, 许强, 等. 滑带土抗剪强度参数的三维反分析[J]. 岩土力学, 2010, 31(10): 3319-3323. LU Kun-lin, ZHU Da-yong, XU Qiang, et al. 3D back analysis of shear strength parameters of slip soil[J]. Rock and Soil Mechanics, 2010, 31(10): 3319-3323. DOI:10.3969/j.issn.1000-7598.2010.10.046 |
| [11] |
易朋莹, 王凯, 任佳, 等. 基于传递系数法的滑坡滑带土强度参数反分析研究[J]. 中国地质灾害与防治学报, 2008, 19(4): 23-26. YI Peng-ying, WANG Kai, REN Jia, et al. Research on anti-analysis of the landslide's strength parameter through transferring coefficient method[J]. The Chinese Journal of Geological Hazard and Control, 2008, 19(4): 23-26. |
| [12] |
邓建辉, 魏进兵, 闵弘. 基于强度折减概念的滑坡稳定性三维分析方法(Ⅰ):滑带土抗剪强度参数反演分析[J]. 岩土力学, 2003, 24(6): 896-900. DENG Jian-hui, WEI Jin-bing, MIN Hong. 3D stability analysis of landslides based on strength reduction (Ⅰ):back analysis for the shear strength of slip soils[J]. Rock and Soil Mechanics, 2003, 24(6): 896-900. |
| [13] |
李维树, 邬爱清, 丁秀丽. 三峡库区滑带土抗剪强度参数的影响因素研究[J]. 岩土力学, 2006, 27(1): 56-60. LI Wei-shu, WU Ai-qing, DING Xiu-li. Study on influencing factors of shear strength parameters of slide zone clay in Three Gorges Reservoir area[J]. Rock and Soil Mechanics, 2006, 27(1): 56-60. |
| [14] |
张玉, 徐卫亚, 李德亮. 大型滑坡演化机制及滑带剪切特性试验研究[J]. 岩石力学与工程学报, 2013, 31(增1): 2606-2616. ZHANG Yu, XU Wei-ya, LI De-liang. Experimental study on evolution mechanism and shear characteristics of slip zone of large-scale landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 31(supple.1): 2606-2616. |
| [15] |
时卫民, 郑颖人, 唐伯明, 等. 边坡稳定不平衡推力法的精度分析及其使用条件[J]. 岩土工程学报, 2004, 26(3): 313-317. SHI Wei-min, ZHENG Ying-ren, TANG Bo-ming, et al. Accuracy and application range of imbalance thrust force method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(3): 313-317. |
| [16] |
张鲁渝, 郑颖人, 时卫民. 边坡稳定分析中关于不平衡推力法的讨论[J]. 岩石力学与工程学报, 2005, 24(1): 177-182. ZHANG Lu-yu, ZHENG Ying-ren, SHI Wei-min. On slope stability analysis by imbalance thrust force method[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(1): 177-182. |
| [17] |
QIN S, JIAO J J, LI Z. Nonlinear evolutionary mechanisms of instability of plane-shear slope:catastrophe, bifurcation, chaos and physical prediction[J]. Rock Mechanics and Rock Engineering, 2006, 39(1): 59-76. DOI:10.1007/s00603-005-0049-4 |
| [18] |
张昆, 郭菊彬. 滑带土残余强度参数试验研究[J]. 铁道工程学报, 2007, 24(08): 13-15. ZHANG Kun, GUO Ju-bin. Experimental research on the residual strength parameters of slip soils[J]. Journal of Railway Engineering Society, 2007, 24(08): 13-15. DOI:10.3969/j.issn.1006-2106.2007.08.004 |



