雾气会降低图像的对比度与景物的能见度, 严重影响了户外图像采集系统的正常工作[1-4];因此, 研究具有实时性和鲁棒性的实时视频去雾算法具有理论研究意义和实际应用价值.
近年来, 国内外学者主要研究单幅图像的去雾, 在该领域取得较大的突破.目前, 对于雾天图像的处理方法主要划分成两大类[5-6]:基于图像增强去雾算法和基于物理模型的图像复原去雾算法.图像增强的典型方法如基于Retinex理论的去雾算法[7-9], 该类算法能够有效增加对比度, 突出细节, 在一定程度上去雾和提高雾天图像的视觉效果;由于没有考虑到图像的退化问题, 还原图像信息能力有限, 容易导致图像的部分信息丢失, 没能从根本上去雾且处理后的图像容易出现灰度化;基于Retinex理论的去雾算法的算法的复杂度高, 达不到实时性的要求.基于物理模型图像复原典型的方法如He等[10]的暗原色先验去雾算法(dark channel prior theory, DCP), He等[10]的暗原色先验去雾算法中假设大气散射模型中的大气光为定值, 通过暗原色先验理论求透射率图来复原雾天图像;对于一般的户外雾天图像可以取得较好的去雾效果, 但去雾后图像的天空区域容易出现过饱和、彩色失真和图像整体偏暗等问题.
为了解决He的暗原色先验算法出现的问题, 本文基于大气散射模型[11-12], 提出以透射率为定值, 通过引导滤波求大气光图来复原雾天图像.大量实验证明, 本文算法对于薄雾、中雾和浓雾图像, 不仅有着非常好的去雾效果, 而且处理速度快, 具有实时性、鲁棒性和实用性.
1 求取大气光图 1.1 大气散射模型在计算机视觉领域中, 单色大气光散射模型[11-12]被广泛用来描述雾霾图像的形成过程, 表达式为
| $ I\left( x \right) = J\left( x \right)t\left( x \right) + A\left( {1 - t\left( x \right)} \right). $ | (1) |
式中:I(x)为雾天图像, J(x)为无雾图像, t(x)为透射率, A为大气光强度.对式(1)进行变换, 可得复原图像的表达式:
| $ J\left( x \right) = \frac{{I\left( x \right) - A}}{{t\left( x \right)}} + A. $ | (2) |
在He的暗原色先验去雾算法中, 假设大气散射模型中的A为定值, 通过暗原色先验理论求透射率图来复原雾天图像, 但去雾后图像的天空区域容易出现过饱和和彩色失真问题.为了解决该问题, 从另一角度思考大气光散射模型, 对大气光散射模型进行修改.假设t为定值, 通过引导滤波求大气光图来复原雾天图像, 表达式为
| $ J\left( x \right) = \frac{{I\left( x \right) - A\left( x \right)}}{t} + A\left( x \right). $ | (3) |
以雾天图像的灰度图作为大气光图的估计, 假设透射率为某个定值, 利用式(3)求出复原结果, 实验结果如图 1所示.直接使用雾天图像的灰度图作为大气光图估计, 没有明显的去雾效果, 原因在于由原图转化成灰度图, 灰度图保持与原图一样的雾气, 将彩色图像转化成黑白图像, 所以复原出来的图像有雾气;若能够在复原图像之前, 对灰度图进行去雾处理, 则复原图像应该有明显的去雾效果.

|
图 1 灰度图作为大气光图估计复原结果 Fig. 1 Restoration result of gray-scale image as atmospheric light map |
对于灰度图的去雾, 最简单的方法是采用均值滤波.均值滤波可以将图像中覆盖在物体上的雾气当作噪声给平滑过滤掉, 从而达到去雾的效果, 但是均值滤波会平滑过滤掉物体边缘, 造成图像的边缘信息丢失.灰度图的去雾需要用到一种既能平滑过度处理、又能保持图像边缘的图像滤波器来去雾, 因此采用具有边缘保持和平滑去噪作用的引导滤波[13].
引导滤波算法基于局部线性模型实现, 处理效果如图 2所示.可知, 经过引导滤波处理后, 猫的毛被均匀平滑了, 猫的轮廓被完整地保留下来, 由此可见, 引导滤波既能够平滑图像, 又能够利用引导图像来保持边缘信息.

|
图 2 引导滤波处理结果 Fig. 2 Results of guided filtering |
在该模型中, 设输入图像为J, 引导图像为I, 滤波输出图像为q, 该模型假设在以中心像素为k的领域窗口ωk存在如下线性关系:
| $ {q_i} = {a_k}{I_i} + {b_k};i \in {\omega _k}. $ | (4) |
式中:ωk为以半径为r的方形窗口, ak和bk为窗口ωk中的线性系数.ak和bk可以通过求取p和q的最小化差值确定, 即
| $ E\left[ {{a_k},{b_k}} \right] = \sum\limits_{i \in {\omega _k}} {\left\lfloor {{{\left( {{a_k}{I_i} + {b_k} - {j_i}} \right)}^2} + \varepsilon a_k^2} \right\rfloor } , $ | (5) |
使E(ak, bk)达到最小.式中:ε为调节参数, 目的是为了防止ak取值过大.通过线性回归求解式(5), 可得
| $ {a_k} = \frac{{\frac{1}{{\left| \omega \right|}}\sum\limits_{i \in {\omega _i}} {{I_i}{j_i}} - {\mu _k}\overline {{j_k}} }}{{\sigma _k^2 + \varepsilon }}, $ | (6) |
| $ {b_k} = \overline {{j_i}} - {a_k}{\mu _k}. $ | (7) |
式中:μk和σk2分别为I在ωk的均值和方差, |ω|为ωk中的像素个数,
由于每个像素点会包含在多个领域窗口ωk中, 在不同ωk中计算得到的qi不同, 需要对qi进行平均处理.通过计算所有窗口中的ak和bk, 滤波输出如下:
| $ {q_i} = \frac{1}{{\left| \omega \right|}}\sum\limits_{k:i \in {\omega _k}} {\left( {{a_k}{I_i} + {b_k}} \right)} = \overline {{a_i}} {I_i} + \overline {{b_i}} . $ | (8) |
式中:
| $ \overline {{a_i}} = \frac{1}{{\left| \omega \right|}}\sum\limits_{k \in {\omega _k}} {{a_k}} ,\overline {{b_i}} = \frac{1}{{\left| \omega \right|}}\sum\limits_{k \in {\omega _k}} {{b_k}} . $ |
采用雾天图像的灰度图作为引导滤波的引导图像, 对灰度图进行滤波, 将引导滤波后的灰度图作为大气光图.假设透射率为某个定值, 利用式(3)复原图像, 处理结果如图 3所示.

|
图 3 提出算法的去雾结果 Fig. 3 Dehazing results of proposed algorithm |
通过与He的暗原色去雾算法比较可见, 利用He算法处理后的图像由于最小值滤波采用块状滤波器, 块的大小影响透射率图的精细程度.块的大小选择不当, 容易出现边缘残雾, 即白边现象, 如图 3(b)所示;天空区域由于不符合暗原色先验的理论而容易出现彩色失真现象, 如图 3(b)所示;去雾后图像整体偏暗, 如图 3(g)所示.该算法避免了这些问题, 采用引导滤波是一种既能平滑滤波、又能边缘保持的滤波器, 滤波半径不会影响到边缘的保持, 不会出现He算法的边缘残雾问题和天空彩色失真问题;只要透射率取值合适, 就可以得到清晰、明亮的去雾图像, 如图 3(c)、(h)所示.该算法的去雾效果彻底, 恢复了很多细节信息, 处理后的色彩鲜艳明亮有着良好的视觉效果.通过不断地改变透射率发现, 复原图像的去雾程度与透射率有密切关系.透射率过大, 则去雾效果不明显, 如图 3(d)、(i)所示;透射率过小, 则会去雾过度, 色彩过于饱和, 如图 3(e)、(j)所示;只有透射率取值在合适范围内, 才能够取得理想的去雾效果.
2 透射率估计在该算法中, 透射率的取值与复原图像的去雾程度密切相关, 透射率的估计至关重要;在现实生活中, 透射率与雾气浓度是反相关关系, 雾气浓度越大, 透射率越小, 在利用该算法估计透射率时, 估计透射率越小, 去雾浓度越高.对于透射率的估计, 借用He等[10]的暗原色先验理论来计算.
2.1 暗原色先验理论He等[10]通过统计大量的户外无雾图像特性, 发现暗像素的统计规律.任意一副图像J的暗原色定义为
| $ {J^{{\rm{dark}}}} = \mathop {\min }\limits_{y \in \mathit{\Omega }\left( x \right)} \left( {\mathop {\min }\limits_{c \in \left\{ {r,g,b} \right\}} {J^{\rm{c}}}\left( y \right)} \right). $ | (9) |
式中:Jc为J的一个颜色通道, Ω(x)为以x为中心的一个局部区域.
户外无雾图像的非天空区域Jdark总是趋向于零的, 即
| $ {J^{{\rm{dark}}}} \to 0. $ | (10) |
该统计规律被称为暗原色先验理论.利用暗原色先验理论, 结合式(1)的大气散射模型, 对式(1)两边进行两次最小值滤波, 移项可得透射率t(x)的估计表达式:
| $ t\left( x \right) = 1 - \mathop {\min }\limits_{y \in \mathit{\Omega }\left( x \right)} \left( {\mathop {\min }\limits_{C \in \left\{ {\rm{r,g,b}} \right\}} \frac{{{I^C}\left( x \right)}}{{{A^C}}}} \right). $ | (11) |
由暗原色先验理论可知, 无雾图像的非天空区域的暗原色总是趋于零, 若有雾气, 则图像的非天空区域的暗原色不是趋于零的.在真实环境中, 雾气是均匀的, 但是相对于成像设备的视觉角度而言, 雾气浓度不均匀, 与景深有关;距离成像设备近则显得雾气较薄, 距离成像设备远则显得雾气较浓, 暗原色的强度与覆盖在物体上的雾气浓度有关, 雾气浓度越大, 暗原色强度越大, 如图 4(b)所示.图中, 覆盖在近处绿叶的雾气薄, 暗原色强度低;远处建筑雾气较浓, 暗原色强度较大, 天空区域是最远的, 雾气浓度应该是最大的.若浓雾区域能够去雾彻底, 则其他区域可以去雾彻底;要想复原图像能够去雾彻底, 则应该利用暗原色图找到浓雾区域或天空区域, 再用式(11)算出该区域的平均透射率, 作为本文算法的透射率估计.

|
图 4 原色图 Fig. 4 Dark channel map |
基于四叉树分割思想[14-15]来寻找浓雾区域.当估计透射率时, 应该在浓雾区域或天空区域中取得透射率估计值.首先利用四叉树法分割暗原色图像, 使用暗原色图是为了避免局部图像在某通道存在极大值时引起对透射率的错误估计, 天空区域或雾气浓度区域的平均值较大, 但为了避免图中较大白色物体的影响, 需要计算标准差.若区域中有较大的白色物体, 则标准差较大;若是天空区域或雾气浓度均匀区域, 则标准差较小, 可以用区域的均值减去标准差的差值来准确地确定浓雾区域, 差值最大的区域为浓雾区域或天空区域, 可以表示为
| $ D\left( i \right) = {\rm{Avg}}\left( i \right) - S\left( i \right). $ | (12) |
式中:i为其中某一区域, i=1, 2, 3, 4;Avg(i)和S(i)分别为该区域的平均值和标准差;D(i)为平均值与标准差之间的差值.
为了提高准确率, 取D(i)最大块继续四等分分割.如此重复迭代, 直到图像的块大小小于给定阀值, 将该图像块作为浓雾区域或天空区域.
根据He的暗原色先验理论可知, 式(11)中A应该在浓雾区域或天空区域中取得.在利用四叉树法获得的浓雾区域或天空区域中寻找强度最大的像素点的位置, 将对应原图位置的强度作为大气光的估计值;利用式(11)求出该浓雾区域的透射率, 将该区域的透射率的平均值作为该算法的透射率估计值.
使用该算法对图 3(a)、(e)进行处理, 求得透射率分别为0.350和0.115, 处理结果与图 3(c)、(h)差不多;使用该算法对大雾、中雾、小雾情况的图像进行处理, 取得了较好的去雾效果, 结果如图 3(d)所示.由此可见, 利用该方法用来估计透射率是行之有效的, 不会出现因为以浓雾区域的透射率作为全局的透射率而造成薄雾区域去雾程度过高的情况.
3 实验分析与比较 3.1 实验环境和去雾流程该算法的结果均在CPU为Intel i5-3337U @ 1.8 GHz、内存为4 GB的PC机上运行所得, 操作系统为Win7家庭版, 开发语言为C++和OpenCV, 开发平台为Visual Studio 2010.
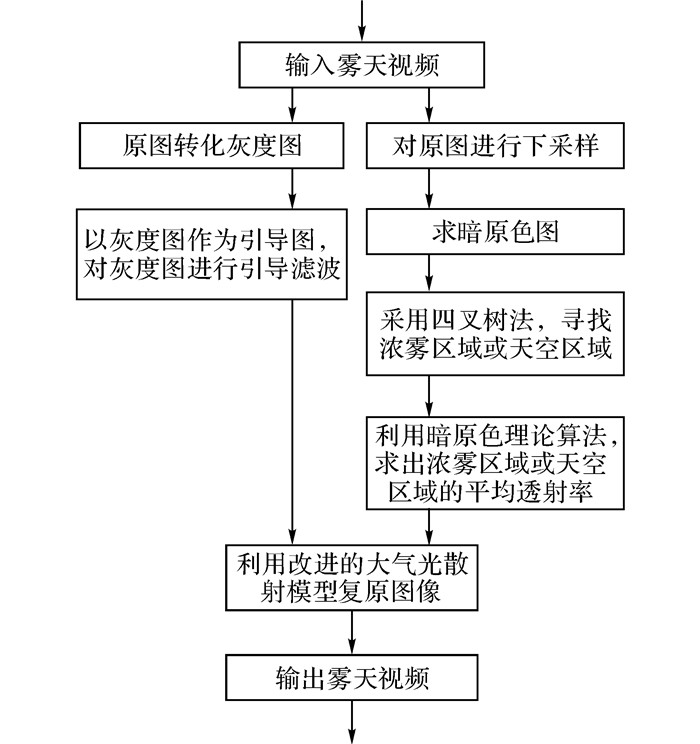
去雾流程如图 5所示.
|
图 5 视频去雾流程图 Fig. 5 Flowchart of image/video dehazing |
如图 6所示为该算法对小雾、中雾和大雾图像(从上到下)的去雾效果.为了验证该算法的去雾效果, 将该算法与图像复原典型算法、He的暗原色先验算法和图像增强典型算法、多尺度Retinex算法[9]进行比较, 其中He算法使用引导滤波优化透射率, 该算法对原图进行0.2倍的下采样.

|
图 6 雾天图像复原结果对比(图像从上到下分别为小雾、中雾和大雾) Fig. 6 Comparison of dehazing image by different methods (images from top to bottom are small fog, moderate fog and heavy fog) |
从图 6可见, 利用He暗原色先验算法处理后, 图像的天空区域偏亮, 还出现了少许的彩色失真而且非天空区域偏暗, 整体的视觉效果欠佳.多尺度Retinex算法对于近景的去雾效果好, 去雾彻底, 色彩自然;对于远景的去雾效果欠佳, 去雾不彻底, 远景处保留大量的残雾, 呈现灰度化, 还原远景信息能力有限, 视觉效果欠佳.该算法对远景和近景的去雾效果极佳, 景深变化大的地方不会出现白边现象, 天空区域不会出现彩色失真现象, 还原出了较多的细节信息, 去雾后的图像清晰, 色彩鲜艳明亮, 视觉效果好.
3.2.2 去雾效果客观对比评价为了更加客观地评价该算法的有效性, 采用信息熵、平均梯度和方差等指标对图像进行质量评价, 利用处理时间tp评价算法的处理速度[16-18].
图像信息熵H表示为图像灰度级集合的比特平均数, 描述了图像的平均信息量,
| $ H = - \sum\limits_{i = 0}^{255} {{p_i}\log {p_i}} . $ | (15) |
式中:pi为像素i出现的概率.从表 1可以看出, 利用该算法复原出更多的图像信息, 复原的结果大大优于He算法和多尺度Retinex算法, 即利用该算法还原图像的信息能力最强.
| 表 1 各方法相关评价指标的对比 Table 1 Value of evaluation indicators by dehazing with different algorithms |
图像的平均梯度A可以反映对图像微小细节反差的表达能力, 同时可以反映图像的纹理变换特征, 大小可以表征图像的清晰度, 如下所示:
| $ A = \frac{{\sum\limits_{i = 1}^{r - 1} {\sum\limits_{j = 1}^{c - 1} {\sqrt {\frac{{{{\left( {{J_{i,j}} - {J_{i + 1,j}}} \right)}^2} + {{\left( {{J_{i,j}} - {J_{i,j + 1}}} \right)}^2}}}{2}} } } }}{{\left( {r - 1} \right)\left( {c - 1} \right)}}. $ | (16) |
式中:Ji, j为第i行、第j列的像素;c与r为图像的行数和列数.该算法的复原图像的平均梯度远远高于He算法高和多尺度Retinex算法, 即利用本文算法复原图像是最清晰的, 去雾效果是最好的.
图像的方差σ反映图像灰度相对于灰度平均值的离散情况, 其大小表示图像的对比度,
| $ \sigma = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i} - \mu } \right)}^2}} . $ | (17) |
式中:xi为像素的灰度, μ为图像的灰度平均值.由于利用该算法处理后的图像方差较大, 在处理大雾图像中稍低于多尺度Retinex算法, 可见该算法处理后的图像视觉效果较好.
在3种算法中, 多尺度Retinex算法的处理速度最慢, 该算法比He的暗原色算法稍快, 2种算法的复杂度差不多, 都需要引导滤波和求取暗原色图;在求取暗原色图之前, 对原图进行下采样处理, 大大减少了运算量.
综合来看, 提出算法不仅去雾效果好, 而且处理速度快.提出算法的远景和近景去雾效果都极佳, 天空区域不会出现彩色失真, 景深变化大的地方不会出现白边现象, 且还原出了较多的细节信息;去雾后的图像清晰, 色彩鲜艳明亮, 视觉效果好.提出的去雾算法对于小、中和大雾图像, 都有良好的去雾效果.对于一幅240×357的图像只需要22 ms, 完全能够满足视频实时处理的要求.
3.3 视频实时去雾利用该算法解决单幅图像的快速去雾问题, 将该算法应用到视频实时去雾中.图 7给出该算法对一段雾天无人机航拍视频的去雾效果的部分截图.视频的大小为605×340, 平均每帧处理时间为32 ms, 已达到视频实时处理的速度要求.从图 7可以看出, 该算法对于视频中大雾、中雾和小雾情况都有较好的去雾效果, 去雾效果细节清晰, 色彩真实自然, 适用性广, 鲁棒性强.

|
图 7 雾天无人机航拍视频去雾效果截图 Fig. 7 Dehazing results of video taken by UAV in foggy weather |
本文从He的暗原色先验理论中得到启发, 从另一角度思考大气光散射模型, 提出以灰度图引导滤波后作为大气光图.利用四叉树法, 在点暗原色图中寻找浓雾区域, 求得透射率的估计值, 最后利用大气光散射模型的复原图像.大量实验表明, 该算法的去雾效果好, 视觉效果佳, 处理速度快, 适合实时视频去雾.当然, 该算法存在不足, 对于1 080和720像素的视频, 达不到实时处理的要求.今后的研究方向主要是用FPGA和DSP硬件语言来实现算法, 提高处理速度, 真正将该算法应用到生产生活中去.
| [1] |
王多超, 王永国, 董雪梅, 等. 贝叶斯框架下的单幅图像去雾算法[J]. 计算机辅助设计与图形学学报, 2010, 22(10): 1756-1761. WANG Duo-chao, WANG Yong-guo, DONG Xue-mei, et al. Single image dehazing based on Bayesian framework[J]. Journal of Computer-Aided Design and Computer Graphics, 2010, 22(10): 1756-1761. |
| [2] |
薛模根, 周浦城, 张洪坤. 利用方向延伸专家场的单幅雾天图像复原[J]. 计算机辅助设计与图形学学报, 2014, 26(05): 782-787. XUE Mo-gen, ZHOU Pu-cheng, ZHANG Hong-kun. Single foggy image restoration using orientation extended field of experts[J]. Journal of Computer-Aided Design and Computer Graphics, 2014, 26(05): 782-787. |
| [3] |
陆健强, 王卫星, 胡子昂, 等. 基于改进暗通道先验算法的农田视频实时去雾清晰化系统[J]. 农业工程学报, 2016, 32(10): 143-148. LU Jian-qiang, WANG Wei-xing, HU Zi-ang, et al. Real time defogging system used for video image of farmland based on modified dark channel prior algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(10): 143-148. DOI:10.11975/j.issn.1002-6819.2016.10.020 |
| [4] |
张万绪, 袁永德, 闫阳, 等. 基于暗原色先验的快速视频去雾优化算法[J]. 西北大学学报:自然科学版, 2016, 46(01): 43-47. ZHANG Wan-xu, YUAN Yong-de, YAN Yang, et al. Fasting video haze removal algorithm using dark channel prior[J]. Journal of Northwest University:Natural Science Edition, 2016, 46(01): 43-47. |
| [5] |
吴迪, 朱青松. 图像去雾的最新研究进展[J]. 自动化学, 2015, 41(02): 221-239. WU Di, ZHU Qing-song. The latest research progress of image dehazing[J]. Acta Automatica Sinica, 2015, 41(02): 221-239. |
| [6] |
郭璠, 蔡自兴, 谢斌, 等. 图像去雾技术研究综述与展望[J]. 计算机应用, 2010, 30(09): 2417-2421. GUO Fan, CAI Zi-xing, XIE Bin, et al. Review and prospect of image dehazing techniques[J]. Journal of Computer Applications, 2010, 30(09): 2417-2421. |
| [7] |
刘茜, 卢心红, 李象霖. 基于多尺度Retinex的自适应图像增强方法[J]. 计算机应用, 2009, 29(08): 2077-2079. LIU Qian, LU Xin-hong, LI Xiang-lin. Adaptive image enhancement method based on multi-scale Retinex algorithm[J]. Journal of Computer Applications, 2009, 29(08): 2077-2079. |
| [8] |
杨万挺, 汪荣贵, 方帅, 等. 滤波器可变的Retinex雾天图像增强算法[J]. 计算机辅助设计与图形学学报, 2010, 22(06): 965-971. YANG Wan-ting, WANG Rong-gui, FANG Shuai, et al. Variable filter Retinex algorithm for foggy image enhancement[J]. Journal of Computer-Aided Design and Computer Graphics, 2010, 22(06): 965-971. |
| [9] |
刘海波, 杨杰, 吴正平, 等. 基于暗通道先验和Retinex理论的快速单幅图像去雾方法[J]. 自动化学报, 2015, 41(07): 1264-1273. LIU Hai-bo, YANG Jie, WU Zheng-ping, et al. A fast single image dehazing method based on dark channel prior and Retinex theory[J]. Acta Automatica Sinica, 2015, 41(07): 1264-1273. |
| [10] |
HE K, SUN J, TANG X. Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2341-2353. DOI:10.1109/TPAMI.2010.168 |
| [11] |
NARASIHAM S G, NAYAR S K. Vision and the atmosphere[J]. International Journal of Computer Vision, 2002, 48(3): 233-254. DOI:10.1023/A:1016328200723 |
| [12] |
OAKLEY J P, SATHERLEY B L. Improving image quality in poor visibility conditions using a physical model for contrast degradation[J]. IEEE Transaction on Image Processing, 1998, 7(2): 167-179. DOI:10.1109/83.660994 |
| [13] |
HE K, SUN J, TANG X. Guide image filtering[J]. IEEE Transactions on Pattern Analysis and MachineIntelligence, 2013, 35(6): 1397-1409. DOI:10.1109/TPAMI.2012.213 |
| [14] |
KIM J, JANG W, SIM J, et al. Optimized contrast enhancement for real-time image and video dehazing[J]. Journal of Visual Communication and Image Presentation, 2013, 24(3): 410-425. DOI:10.1016/j.jvcir.2013.02.004 |
| [15] |
曾浩, 尚媛园, 丁辉, 等. 基于暗原色先验的图像快速去雾[J]. 中国图象图形学报, 2015, 20(07): 914-921. ZENG Hao, SHANG Yuan-yuan, DING Hui, et al. Fast image haze removal base on dark channel prior[J]. Journal of Image and Graphics, 2015, 20(07): 914-921. |
| [16] |
郭璠, 蔡自兴. 图像去雾算法清晰化效果客观评价方法[J]. 自动化学报, 2012, 38(09): 1410-1419. GUO Fan, CAI Zi-xing. Objective assessment method for the clearness effect of image defogging algorithm[J]. Acta Automatica Sinica, 2012, 38(09): 1410-1419. |
| [17] |
李大鹏, 禹晶, 肖创柏. 图像去雾的无参考客观质量评测方法[J]. 中国图象图形学报, 2011, 16(09): 1753-1757. LI Da-peng, YU Jing, XIAO Chuang-bai. No-referencequality assessment method for defogged images[J]. Journal of Image and Graphics, 2011, 16(09): 1753-1757. |
| [18] |
刘海波, 汤群芳, 杨杰. 改进直方图均衡和Retinex算法在灰度图像增强中的应用[J]. 量子电子学报, 2014, 31(05): 525-532. LIU Hai-bo, TANG Qun-fang, YANG Jie. Application of improved histogram equalization and Retinex algorithm in gray image enhancement[J]. Chinese Journal of Quantun Electronics, 2014, 31(05): 525-532. |



