储集层的孔隙结构对于岩石的各种物理性质及运移规律起着决定性的作用, 对此进行定量计算与参数分析是石油勘探开发中的重要工作之一.利用CT扫描建立的岩心三维图像, 能够清晰地观察到岩样的孔隙空间分布情况;通过阈值分割, 能够直观地显示储集层岩心孔隙微观结构、连通特性等储集层岩样的重要特征. CT技术成为当前石油地质中常用的岩心三维图像构建方法.随着科学技术的发展, CT的分辨率不断提高, 目前已有nm级的CT;然而分辨率高低与岩样尺寸大小存在矛盾, 分辨率越高, 扫描的样本尺寸越小.利用超分辨率重建技术提升岩心三维CT图像分辨率, 对改善岩心图像的质量有着重要的研究意义.
超分辨重建是图像处理领域的一大研究热点, 近几年国内外有大量的研究成果.这些算法大都针对二维图像或者视频.三维图像的超分辨率是针对体素放大的算法, 不同于针对像素的单幅图像超分辨率重建.目前较多的针对体素的超分辨率研究集中在核磁共振成像(magnetic resonance imaging, MRI)的超分辨率重建[1-5].如Manjón等[4]提出非局部MRI上采样方法(non-local MRI upsampling), 利用非局部相似性正则化约束重建MRI图像, 通过不断的迭代求解, 时间复杂度较高. Iwamoto等[5]提出基于稀疏表示和自相似性的方法来提升MRI图像切片方向的分辨率, 该方法只在切片方向作了分辨率提升.本文研究的岩心三维CT图像的超分辨率重建, 不同于MRI图像的超分辨率重建, 须对图像的x、y、z 3个方向同时进行分辨率提升.
Timofte等[6-7]提出A+(adjusted anchored neighborhood regression, A+)算法将低分辨率(low resolution, LR)空间到高分辨率(high resolution, HR)空间的非线性映射关系转换为映射矩阵, 把超分辨率重建操作转换为矩阵乘法, 大大提升重建速度.该算法目前是针对二维图像, 无法开展三维图像超分辨率重建.本文将A+算法扩展到三维, 实现三维A+(three-dimensional adjusted anchored neighborhood regression, 3DA+)算法.为了进一步提升重建效果, 本文提出三维高频修正A+算法, 对输入的岩心三维模型进行3个方向的分辨率提升.为了评估该算法的性能, 本文对多组岩心CT图像进行实验, 选择双三次插值、非局部MRI上采样算法和本文实现的3DA+算法作为基准算法.实验证明, 本文算法的重建结果取得相对最高的峰值信噪比(peak signal to noise ratio, PSNR)和结构相似度(structural similarity, SSIM).
1 ANR算法在超分辨率重建研究中, 图像降质数学模型通常表示如下:
| $ {\mathit{\boldsymbol{Y}}_{\rm{l}}} = \mathit{\boldsymbol{SB}}{\mathit{\boldsymbol{X}}_{\rm{h}}} + \mathit{\boldsymbol{n}}. $ | (1) |
式中:Yl表示降质后的LR图像, Xh表示期望的HR图像, S为下采样操作算子, B表示模糊滤波器,n表示加性噪声.超分辨率重建是在已知LR图像的基础上求解HR图像的逆过程.
提出的算法是在Timofte等[6-7]提出的A+算法的基础上进行扩展并改进的.A+是基于字典学习的方法, Timofte在他最开始提出的ANR上作了改进, 其中最简单的全局回归方法如下.
ANR将基于学习的方法中常用的L1范数约束的最优化问题改为如下L2范数约束的最优化问题:
| $ \mathop {\min }\limits_\beta \left\| {\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{D}}_1}\mathit{\boldsymbol{\beta }}} \right\|_2^2 + \lambda \left\| \mathit{\boldsymbol{\beta }} \right\|_2^2. $ | (2) |
式中:Y表示输入的LR特征;Dl表示LR字典;β为系数向量;λ为正则化参数, 用以减轻解的奇异性并稳定解.式(2)的代数解为
| $ \mathit{\boldsymbol{\beta }} = {\left( {\mathit{\boldsymbol{D}}_1^{\rm{T}}{\mathit{\boldsymbol{D}}_1} + \lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}\mathit{\boldsymbol{D}}_1^{\rm{T}}\mathit{\boldsymbol{Y}}. $ | (3) |
HR特征块X可以用同样的系数向量在相应的高分辨率字典Dh表示出来, 即
| $ \mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{D}}_{\rm{h}}}\mathit{\boldsymbol{\beta }}, $ | (4) |
| $ \mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{D}}_{\rm{h}}}{\left( {\mathit{\boldsymbol{D}}_1^{\rm{T}}{\mathit{\boldsymbol{D}}_1} + \lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}\mathit{\boldsymbol{D}}_1^{\rm{T}}\mathit{\boldsymbol{Y}}. $ | (5) |
式中:Dh、Dl是提前训练好的, 因此可以将LR特征与HR特征之间的非线性映射关系转化为映射矩阵:
| $ \mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{D}}_{\rm{h}}}{\left( {\mathit{\boldsymbol{D}}_1^{\rm{T}}{\mathit{\boldsymbol{D}}_1} + \lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}\mathit{\boldsymbol{D}}_1^{\rm{T}}. $ | (6) |
重建时, 对于输入LR特征Yi, 可以用下式直接重建出HR特征Xi:
| $ {\mathit{\boldsymbol{X}}_i} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{Y}}_i}. $ | (7) |
这是全局回归的方式, 所有输入LR特征都对应同一个映射矩阵, 重建过程转换为矩阵乘法操作, 极大地降低了时间消耗, 但重建效果不佳.在A+算法中, 优化问题为
| $ \mathop {\min }\limits_\mathit{\boldsymbol{\beta }} \left\| {\mathit{\boldsymbol{Y}} - {\mathit{\boldsymbol{S}}_1}\mathit{\boldsymbol{\beta }}} \right\|_2^2 + \lambda \left\| \mathit{\boldsymbol{\beta }} \right\|_2^2. $ | (8) |
式中:Sl为离输入的LR特征块匹配的字典原子最近的K个样本组成的矩阵.
假设字典中有n个原子, 在A+算法中, 为对偶字典中的每一个原子都计算一个映射矩阵.具体来说, 分别以Dl中的n个字典原子为中心, 搜索出K个离该字典原子最近的LR特征样本构成邻域矩阵Sl, 对应的HR特征样本构成矩阵Sh.利用式(9)在训练阶段计算字典原子di(i=1, 2, 3, …, n)对应的映射矩阵Pi(i=1, 2, 3, …, n):
| $ \mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{S}}_{\rm{h}}}{\left( {\mathit{\boldsymbol{S}}_{\rm{l}}^{\rm{T}}{\mathit{\boldsymbol{S}}_{\rm{l}}} + \lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}\mathit{\boldsymbol{S}}_{\rm{l}}^{\rm{T}}. $ | (9) |
重建时, 搜索输入LR特征块Yi匹配的字典原子dj与映射矩阵Pj;利用式(10)将Yi映射到HR空间, 重建出HR特征块Xi, 从而重建出HR的图像.该算法相当于用字典原子将特征空间分为n个子空间, 为每个空间利用样本训练LR与HR之间的映射关系, 比全局回归重建效果有较大的提升.
| $ {\mathit{\boldsymbol{X}}_i} = {\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{Y}}_i}. $ | (10) |
针对具有三维体数据的岩心三维图像的分辨率提升问题, 在A+的基础上提出三维高频修正A+算法.算法中使用的图像块和特征块均为三维立方体结构.在训练字典的时候, 增加训练高频修正字典及对应的高频修正映射矩阵ΔP的过程.对于三维LR特征块, 重建时同时搜索对应的映射矩阵P和高频修正映射矩阵ΔP, 于是重建的三维结构中拥有了更多的高频信息, 能够提升重建效果.该算法的整体框架如图 1所示, 主要包括字典训练及映射矩阵计算过程、高频修正字典训练及高频修正映射矩阵计算过程和三维超分辨率重建过程.

|
图 1 三维高频修正A+算法框架 Fig. 1 Framework of three-dimensional high-frequency correction A + algorithm |
在离线训练字典过程中, 将多组三维HR图像作为训练图像Xh.用式(1)的简化的降质模型得到三维LR图像, 对三维LR图像插值放大后进行特征提取, 并分解为三维LR特征集Cl{pli}i(i=1, 2, …, m).由于成像设备的限制, 岩心三维CT图像通常含有较严重的噪声.为了降低噪声影响, 该算法使用三维高斯拉普拉斯滤波器, 提取LR图像的三维特征.利用KSVD[8]算法得到LR字典Dl和稀疏系数矩阵α, 根据Yang等[9]的理论可知, 与LR三维特征样本集相应的三维HR图像的图像特征样本集Ch{phi}i (i=1, 2, …, m)可以在HR字典Dh上用相同的α进行稀疏表示:
| $ {\mathit{\boldsymbol{C}}_{\rm{h}}}{\left\{ {p_{\rm{h}}^i} \right\}_i} = {\mathit{\boldsymbol{D}}_{\rm{h}}}\mathit{\boldsymbol{\alpha }}. $ | (11) |
HR超完备字典可以由伪逆计算求得:
| $ {\mathit{\boldsymbol{D}}_{\rm{h}}} = {\mathit{\boldsymbol{C}}_{\rm{h}}}{\left\{ {p_{\rm{h}}^i} \right\}_i} \cdot {\mathit{\boldsymbol{\alpha }}^{ - 1}}. $ | (12) |
此时可以获得用于重建的2个字典:Dl和Dh.
利用A+的理论, 为字典中的每个原子按欧氏距离的准则搜索最近的K个三维特征样本, 构成邻域矩阵Sl及对应的Sh.用式(9)计算每个原子对应的映射矩阵P, 具体步骤如下:
1) 对输入的三维HR图像Xh进行模糊和下采样, 得到降质的三维模型;利用双三次插值算法放大相同倍数,作为三维LR图像Xl.
2) 提取三维LR图像特征Fl, Fl=F(Xl), F是特征提取算子.本文采用三维高斯拉普拉斯滤波器.
3) 将Fl分解为三维特征集Cl, 利用KSVD算法训练DT和α.
4) 提取三维HR图像特征, Fh=Xh-Xl.
5) 将Fh分解为三维特征集Ch, 利用式(12)计算Dh.
6) 搜索离Dl中字典原子di(i=1, 2, 3, …, n)最近的K个三维LR特征样本, 得到邻域矩阵Sl, 对应的三维HR特征块组成邻域矩阵Sh.
7) 对于每个字典原子, 利用式(9)计算映射矩阵Pj.
2.2 高频修正字典训练和高频映射矩阵计算从式(8)可知, 超分辨率重建是一个求最优解的过程, 对于输入特征Y, 求解在LR字典上最近似的表达;利用训练好的映射关系, 估计HR特征X.估计出的HR特征与真实的HR特征存在误差, 对于三维训练图像Xh, 经过下采样后得到的三维图像利用2.1节训练出来的字典和映射矩阵进行重建, 重建出的三维图像
| $ {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_{\rm{h}}} = {\mathit{\boldsymbol{X}}_{\rm{h}}} - {{\mathit{\boldsymbol{\hat X}}}_{\rm{h}}}, $ | (13) |
| $ \Delta \mathit{\boldsymbol{P}} = \Delta {\mathit{\boldsymbol{S}}_{\rm{h}}}{\left( {\mathit{\boldsymbol{S}}_1^{\rm{T}}{\mathit{\boldsymbol{S}}_1} + \lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}\mathit{\boldsymbol{S}}_1^{\rm{T}}. $ | (14) |
算法的具体步骤如下.
1) 利用已训练好的映射矩阵P, 对降质后的三维图像进行一次3DA+重建, 得到估计的三维HR图像
2) 以Δh为三维HR特征, 分解为三维特征集ΔCh.
| $ \Delta {\mathit{\boldsymbol{D}}_{\rm{h}}} = \Delta {\mathit{\boldsymbol{C}}_{\rm{h}}}{\mathit{\boldsymbol{\alpha }}^{ - 1}}. $ | (15) |
3) 搜索离Dl中字典原子di(i=1, 2, 3, …, n)最近的K个三维LR特征样本, 得到邻域矩阵Sl, 对应的三维高频修正特征样本组成邻域矩阵ΔSh.
4) 对于每个字典原子di(i=1, 2, 3, …, n), 利用式(14)计算ΔPi.
2.3 三维超分辨重建当Dl、Dh、ΔDh、P和ΔP都训练学习之后, 对于一个三维LR特征块Ili, 利用欧氏距离准则在Dl中搜索与之最匹配的字典原子dj, 则可用下式将Ili映射到三维HR空间得到Ihi:
| $ \mathit{\boldsymbol{I}}_{\rm{h}}^i = {\mathit{\boldsymbol{P}}_j}\mathit{\boldsymbol{I}}_{\rm{l}}^i + \Delta {\mathit{\boldsymbol{P}}_j}\mathit{\boldsymbol{I}}_{\rm{l}}^i. $ | (16) |
从而重建出三维HR图像.重建的三维HR增加了高频信息, 取得了更好的重建结果.
重建的具体步骤如下.
1) 采用双三次插值算法, 将输入的LR三维图像Yl放大得到Y′l, 放大倍数同超分辨率放大倍数.
2) 对Y′l进行特征提取, 得到三维LR特征Fl.
3) 将特征Fl分解成为三维特征集Cl{Ili}i(i=1, 2, …, m).
4) 直接将Y′l分解为三维LR图像块集合Cll{Illi}i(i=1, 2, …, m).
5) 搜索与三维LR特征块Ili匹配的字典原子dj和相应的P、ΔP, 利用式(16)计算三维HR特征Ihi.
6) 重建出三维HR图像块集合Chh{Ihhi}i(i=1, 2, …, m), 其中Ihhi=Illi+Ihi.
7) 将三维HR图像块聚合获得三维HR图像Yh.
3 实验与分析通过实验分析提出的三维高频修正A+算法中的重要参数对重建质量的影响, 选择合适的参数开展更多的实验.与传统的双三次插值算法、非局部MRI上采样方法以及本文实现的3DA+算法进行对比, 验证算法的有效性.
3.1 实验基础及评价标准所有的实验图像均为在不同岩心CT图像上截取的400×400×400像素大小的立方体结构, 如图 2、3所示.如图 2所示为本文实验训练字典所用的训练集, 其中图 2(a)~(c)为砂岩岩心, 图 2(d)为致密碳酸盐岩, 图 2(e)为致密砂岩.如图 3所示为算法验证实验样本.其中样本1、2、3为砂岩岩心, 样本4为致密碳酸盐岩岩心, 样本5为致密砂岩岩心.

|
图 2 训练字典所用的训练集 Fig. 2 Training sets used in training dictionary |

|
图 3 验证算法实验所用的测试集 Fig. 3 Test sets used in experiment of verification algorithm |
对实验结果采用PSNR和SSIM进行评价.对于W×H×L大小的重建的三维图像f(x, y, z), PSNR计算如下:
| $ {\rm{PSNR}} = 10\lg \left( {\frac{{{{255}^2}}}{{{\rm{MSE}}}}} \right), $ | (17) |
| $ {\rm{MSE}} = \sum\limits_{z = 1}^L {\sum\limits_{y = 1}^H {\sum\limits_{x = 1}^W {\frac{{{{\left[ {\hat f\left( {x,y,z} \right) - f\left( {x,y,z} \right)} \right]}^2}}}{{W \times H \times L}}} } } . $ | (18) |
式中:
PSNR是基于像素点误差的图像质量评价方法, 未考虑人眼视觉特征, 可能出现评价结果与人眼主观感觉不一致的情况.Wang等[10]提出从图像的亮度、对比度和结构度来表征图像的结构信息, 建立的结构相似度(SSIM)模型相较于PSNR更符合人眼的主观感知.采用Wang等[10]提出的结构相似度(SSIM)来评价重建效果, SSIM取值为[0, 1], SSIM越大表示与原图越接近, 重建效果越好.
3.2 重要参数对重建的影响在算法中, 特征块的尺寸、字典大小和训练映射矩阵时邻域样本个数对重建质量和重建速度均有影响.为了分析这些参数的影响, 选取样本2放大2倍进行实验与讨论.
3.2.1 特征块尺寸当放大倍数为f时, 在字典训练过程中, HR特征块尺寸是LR特征块尺寸的f3倍.当放大2倍时, 若LR特征块尺寸为2×2×2像素, 则HR特征块尺寸为4×4×4像素.对于超完备字典D∈Rm×n(n≫m), 其中m为三维特征的维度, n为字典原子个数, 在没有降维的情况下, m等于特征块的尺寸.为了满足超完备字典的条件, 若m大幅增大, 则应增加字典原子个数, 可见增大特征块尺寸将会大大增加字典的大小.为了测试特征块尺寸对重建质量与运行时间的影响, 对样本2开展特征块尺寸为2×2×2、3×3×3、4×4×4的3组实验.考虑到计算机内存的限制, 字典原子个数设为1 024.实验结果如表 1所示.表中,t为重建时间.可以看出, 增大特征块的尺寸, PSNR有所提升, 重建时间大幅提升.当特征块尺寸为4×4×4时, PSNR比特征块为3×3×3的情况下提升0.07 dB, SSIM相当, 但重建时间多98.08 min.权衡重建质量和运行时间, 在后续实验中, 特征块尺寸设置为3×3×3.
| 表 1 不同特征块尺寸重建质量与时间的比较 Table 1 Comparison of quality and time of reconstruction of different feature block size |
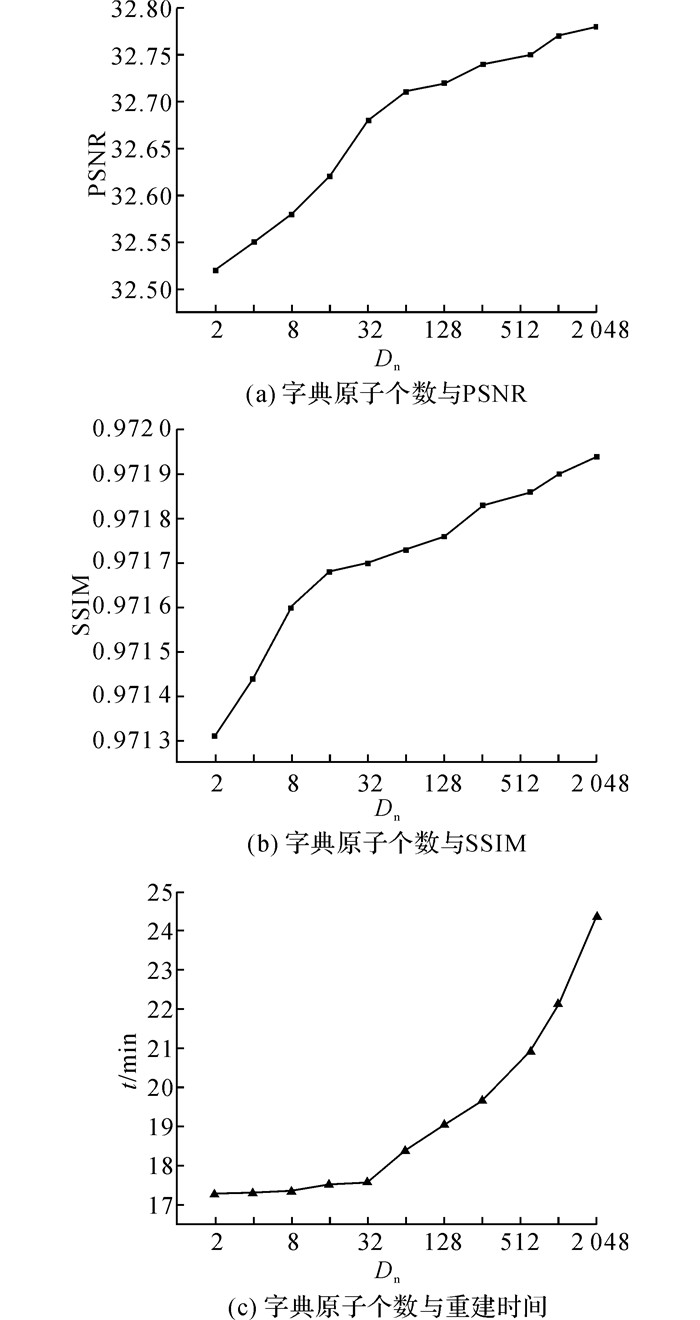
在该算法中, n决定字典的完备性和映射矩阵的个数, 相当于字典原子将特征空间分为n个子空间, 每个空间都有各自的映射关系.理论上,n越大, 字典完备性越高, 空间划分越细, 重建效果越好.为了选择合适的字典原子个数, 对样本2开展字典原子个数为2~2 048的重建实验, 重建结果的PSNR及对应的重建时间如图 4所示.图中, Dn为字典原子个数, 采用对数坐标.从图 4可以看出, 随着字典原子个数的增加, PSNR和SSIM都有所提升, 重建时间相应增加;当字典原子个数为1 024~2 048时, PSNR与SSIM提升较小, 重建时间急剧增加, 后续实验将字典原子设置为1 024.
|
图 4 字典原子个数对重建结果的影响 Fig. 4 Effect of number of atoms on reconstruction results |
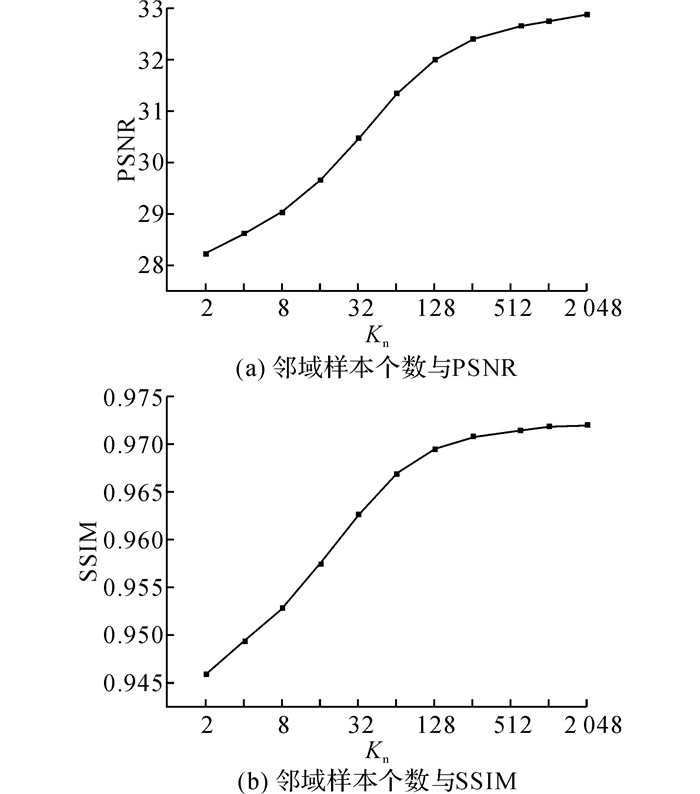
当计算字典原子di的映射矩阵Pi和高频修正映射矩阵ΔPi时, 需要搜索与di最近的K个样本构成邻域矩阵Sl、Sh和ΔSh.从理论上来讲, K越大, 计算的映射矩阵越精确, 重建出的结果越接近真实三维高分率图像.为了确定合适的邻域样本个数K, 对样本2开展K为2~2 048的重建实验, 重建结果的PSNR和SSIM如图 5所示.图中, Kn为邻域样本个数, 采用对数坐标.当K为2~512时, PSNR提升比较明显;当K为512~2 048时, 上升趋势趋于平缓.K在512之后, SSIM变化趋于平缓.选取1 024作为邻域样本数.
|
图 5 邻域样本个数对重建结果的影响 Fig. 5 Effect of number of neighborhood samples on results |
为了评估算法的性能, 采用双三次插值算法、非局部MRI上采样方法、3DA+算法以及提出的三维高频修正A+算法这4种算法, 对5个实验样本开展放大2倍和放大4倍的验证实验, 实验所采用的硬件与软件平台一致.在3DA+算法和本文算法字典训练阶段选用同样的参数设定, 特征块大小为3×3×3, 字典原子个数为1 024, 每个原子的邻域样本个数为1 024.如图 6、7所示分别为4种算法对样本1放大2倍和放大4倍的实验结果以及序列中的一张切片图.可以看出, 利用双三次插值算法和非局部MRI上采样算法得到的重建结果边缘模糊, 高频信息缺失, 3DA+和本文算法重建结果从视觉效果来看较清晰, 且本文算法最接近原始HR图.

|
图 6 4种算法对样本1放大2倍的三维图像及切片图对比 Fig. 6 Comparison of three-dimensional images and slices for four algorithms magnified 2 times on test image 1 |

|
图 7 4种算法对样本1放大4倍的三维图像及切片图对比 Fig. 7 Comparison of three-dimensional images and slices for four algorithms magnified four times on test image 1 |
对比4种算法重建结果的PSNR与SSIM, 如表 2、3所示.可以看出, 提出算法取得最好的重建结果, 平均PSNR和SSIM均最高.当放大2倍时, 该算法的PSNR比双三次插值算法、非局部MRI上采样算法和3DA+算法分别提升3.30、2.23和0.50 dB, SSIM分别提升0.032 9、0.017 6、0.003 7.当放大4倍时, 该算法的PSNR比双三次插值算法、非局部MRI上采样算法和3DA+算法分别提升2.1、1.48和0.27 dB, SSIM分别提升0.089 9、0.028 9、0.009 2.与现有的三维超分辨率重建算法相比, 本文算法重建结果的PSNR和SSIM有明显的提升.
| 表 2 4种算法对测试集放大2倍的比较 Table 2 Comparison for four algorithms magnified 2 times on test sets |
| 表 3 4种算法对测试集放大4倍的比较 Table 3 Comparison for four algorithms magnified 4 times on test sets |
本文在单幅图像A+算法的基础上, 针对岩心三维CT图像, 提出三维高频修正A+算法.与传统的二维超分辨率重建技术不同, 本文算法在三维图像的x、y、z方向上同时提升分辨率.该算法以5组HR岩心三维图像为训练图像, 将降质后的估计HR岩心三维图像与原始HR岩心三维图像的误差作为高频修正信息, 训练高低分辨字典和高频修正字典.利用字典原子将特征空间分为若干个子空间, 利用训练图像样本计算对应子空间的映射矩阵和高频修正映射矩阵, 将重建过程转换为矩阵乘法操作.针对多组岩心三维图像进行实验, 与双三次插值算法、非局部MRI上采样算法和3DA+算法进行对比.实验结果表明, 该算法取得良好的视觉效果和相对最高的PSNR与SSIM.该算法可以应用到实际的岩心三维图像分辨率提升工作中, 同时对其他三维图像的超分辨率重建具有一定的研究意义和应用价值.
| [1] |
PELED S, YESHURUN Y. Super resolution in MRI:application to human white matter fiber tract visualization by diffusion tensor imaging[J]. Magnetic Resonance in Medicine, 2001, 45(1): 29-35. DOI:10.1002/(ISSN)1522-2594 |
| [2] |
GREENSPAN H, OZ G, KIRYATI N, et al. MRI inter-slice reconstruction using super-resolution[J]. Magnetic Resonance Imaging, 2002, 20(5): 437-446. DOI:10.1016/S0730-725X(02)00511-8 |
| [3] |
KORNPROBST P, PEETERS R, NIKOLOVA M, et al. A super resolution framework for fMRI sequences and its impact on resulting activation maps[C]//International Conference of Medical Image Computing and Computer-Assisted Intervention. Montréal: Springer, 2003: 117-125. http://www.springerlink.com/content/lr02gxd9yb04av8l
|
| [4] |
MANJÓN J V, COUPÉ P, BUADES A, et al. Non-local MRI upsampling[J]. Medical Image Analysis, 2010, 14(6): 784-792. DOI:10.1016/j.media.2010.05.010 |
| [5] |
IWAMOTO Y, HAN X H, SASATANI S, et al. Super-resolution of MR volumetric images using sparse representation and self-similarity[C]//International Conference on Pattern Recognition. Tsukuba, Japan: IAPR, 2012: 3758-3761. https://www.researchgate.net/publication/261333847_Super-resolution_of_MR_volumetric_images_using_sparse_representation_and_self-similarity?ev=auth_pub
|
| [6] |
TIMOFTE R, DE V, GOOL L V. Anchored neighborhood regression for fast example-based super-resolution[C]//IEEE International Conference on Computer Vision. Sydney: IEEE, 2013: 1920-1927. http://ieeexplore.ieee.org/document/6751349/
|
| [7] |
TIMOFTE R, SMET V D, GOOL L V. A+:adjusted anchored neighborhood regression for fast super-resolution[J]. Lecture Notes in Computer Science, 2015, 9006: 111-126. DOI:10.1007/978-3-319-16817-3 |
| [8] |
ZEYDE R, ELAD M, PROTTER M. On single image scale-up using sparse-representations[C]//International Conference on Curves and Surfaces. Avignon: Springer, 2010: 711-730. http://www.researchgate.net/publication/229001796_On_Single_Image_Scale-Up_using_Sparse-Representation
|
| [9] |
YANG J, WRIGHT J, HUANG T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873. DOI:10.1109/TIP.2010.2050625 |
| [10] |
WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment:from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |



