2. 浙江广播电视大学 信息学院, 浙江 杭州 310012
2. College of Information Engineering, Zhejiang Radio and Television University, Hangzhou 310012, China
共享自行车系统(bike sharing system, BSS)在世界各地得到了广泛的应用, 目前分为锁桩式BSS(公共自行车系统)和无锁桩式BSS(共享单车).锁桩式BSS系统通过固定自助服务站提供租还服务, 共享单车通过电子围栏方式来解决无序停放问题.无论是固定服务站还是电子围栏, 都有停放自行车容量的限制, 由于交通出行的潮汐时空分布不均衡特性, 租还车难将成为BSS发展中突出的长期问题.通过调度车辆对BSS进行再平衡, 可以有效地缓解租还车难的现象.
目前, 国内外对共享自行车系统调度问题的研究成果较多, 如董红召等[1]提出城市公共自行车系统的滚动时域调度算法, 基于大样本历史数据对公共自行车服务点自然租赁需求进行估算及验证[2].Salaken等[3-5]对公共自行车站点需求量进行预测, 以降低调度成本.Adham等[6-8]对BSS调度方案提出改进的调度算法, 优化调度路径, 提高调度效率, 但这些成果缺少调度区域划分的研究.尤其是大型BSS系统, 若不采用分区调度, 则往往算法求解耗时长, 调度实时性差, 成本增加, 因此有必要对BSS调度区域进行科学划分, 实行分区调度.
研究BSS调度分区的文献较少, Come等[9]根据公共自行车站点的使用情况进行聚类分区, 分析用户出行特征与站点地理位置之间的关系, 但未涉及到BSS调度区域的划分.陈昕昀等[10]利用K-means聚类划分调度区域, 使得各站点离调度中心的平均距离最短, 但没有考虑各区域调度需求量的平衡.董红召等[11]基于服务点之间的关联特性进行调度区域的划分, 但划分的每个调度区域比较笼统, 不同区域之间出现不平衡后不能进行协调互补.徐建闽等[12]的多层次分区调度方法虽然采用了区域划分和分层调度, 但调度小区的划分停留在经验和行政区划阶段, 缺少区域内自行车租/还自平衡的考虑.
本文针对上述问题, 提出基于分形树的自平衡调度区域划分模型[13], 即根据分形树的自相似性特征, 从叶子节点开始, 将租/还需求互补的节点层层聚类形成多级分形自平衡区域, 使得每层调度区域的需求尽量达到自平衡来减少跨区调度.根据不同时段调度需求量的动态变化, 提出基于周转率杠杆系数的共协矩阵聚类融合算法.对聚类结果进行优化融合[14], 提高了分区结果的鲁棒性.
1 基于分形树的自平衡调度区域划分模型BSS自行车处于分区、分级调度模式下, 调度车辆首先负责所属区域内的自行车调度.只有当区域内租还总量差距较大、无法平衡时, 开展跨区域间调度.为了尽量减少区域间调度的次数, 划分的每一个调度区域都需要能够尽量达到租/还自平衡, 因此在开展调度区域划分时, 将在某时间区间内具有自行车调入需求的服务点/区域和调出需求的服务点/区域放入同一个上级区域, 这样调度车辆可以在这两个不同需求的服务点/区域间进行自行车运送, 从而达到该级区域内的自平衡.
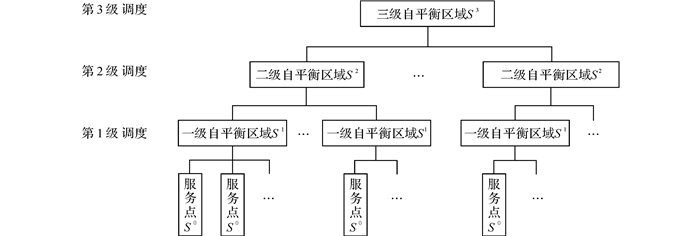
BSS自平衡分级调度区域划分模型如图 1所示.先划分一级自平衡区域S1, 按照服务点的自行车调入和调出需求的互补关系, 将距离较近且有需求互补关系的服务点划在同一区域形成自平衡区域S1;再将具有调入和调出需求的互补区域S1合并形成二级自平衡区域S2, 以此类推, 最终形成最高级自平衡区域, 即整个BSS系统.定义为:对于一个H级分区调度BSS, 每个级别区域定义为Sn(n=0, 1, 2, …, H), 其中, 当n=H时, 最高级SH表示整个BSS, BSS已达到自平衡;当n=0时, 最低级S0表示服务点, 服务点平衡是调度系统服务的最终目标.
|
图 1 共享自行车系统自平衡分区分级调度模型 Fig. 1 Bike sharing system hierarchical scheduling model for self-balanced regions |
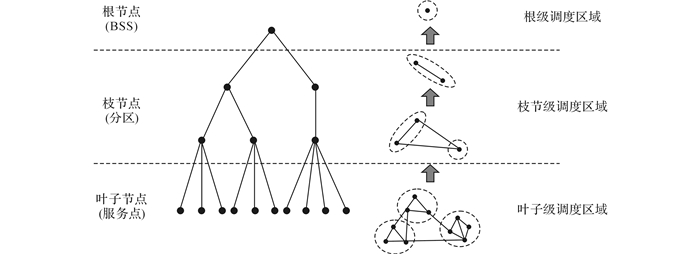
分形理论是非线性科学的一种方法论和认识论, 它可以依靠简单结构与规则的迭代来生成复杂系统, 这种系统具有鲜明的整体与局部结构的自相似特性[12].显然, 上述划分的BSS自平衡区域各个层级的组织和调度方法具有自相似性, 即鲜明的分形结构特性, 因此, 图 1所示的BSS调度模型可以用一个自平衡分形树表达, 如图 2所示.分形树中, 每个叶子节点表示一个自行车服务点S0, 枝节点表示某一级的自平衡区域Sn(0 < n < H), 根节点表示整个BSS系统SH, 各个层级的调度区域结构和规则根据分形系统的自相似性来生成.图 2中, 所有叶子节点根据地理位置和需求互补关系, 可以形成多个叶子级调度区域;这些叶子级调度区域是形成上一级枝节级调度区域的枝节点, 形成的枝节级调度区域将作为上一级枝节调度区域的枝节点;采用自形似方式层层迭代, 最终可以构成根级调度区域.
|
图 2 共享自行车系统自平衡分形树模型 Fig. 2 Bike sharing system self-balanced fractal tree model |
BSS自平衡分形树区域的生成与划分采用如下关键参数.
1) 叶子节点i的不平衡度Wi(τ)定义为在时间段τ内, 服务点i借出和还入的自行车数量的差值.
| $ {W_i}\left( \tau \right) = Z_i^{{\rm{out}}}\left( \tau \right) - Z_i^{{\rm{in}}}\left( \tau \right). $ | (1) |
式中:Ziout(τ)和Ziin(τ)分别为服务点i在时间段τ的借车和还车总数.可以看出, 当Wi(τ)>0时表示自行车借出量大于归还量, 若Wi(τ)>0持续较长时间, 则服务点将进入空位状态, 借车困难;当Wi(τ) < 0时表示自行车借出量小于归还量, 若Wi(τ) < 0持续较长时间, 则服务点进入满位状态, 还车困难.
2) 枝节点α的不平衡度Wα(τ)定义为在时间段τ内, 区域α中所有服务点不平衡度的总和.
| $ {W_\alpha }\left( \tau \right) = \sum\limits_{i \in \alpha } {{W_i}\left( \tau \right)} . $ | (2) |
3) 叶子节点i、j之间的互平衡强度EWi, j(τ).如果服务点i与j间的距离越近、Wi(τ)+Wj(τ)的绝对值越小, 那么这两个节点的互平衡关系越强.Di, j表示服务点i和j之间的距离, 因此EWi, j(τ)的计算可以设计为
| $ {\rm{E}}{{\rm{W}}_{i, j}}\left( \tau \right) = \frac{1}{{\left| {{W_i}\left( \tau \right) + {W_j}\left( \tau \right)} \right|\gamma + {D_{i, j}}}}. $ | (3) |
式中:γ为不平衡度的距离效应转换常数.
4) 枝节点α、β之间的互平衡强度EWα, β(τ).根据分形自相似性可知, 与叶子节点算法相似, 枝节点区域α、β之间的距离越近且不平衡度总和越小, 则说明这两个区域的互平衡关系越强, 计算公式为
| $ {\rm{E}}{{\rm{W}}_{\alpha , \beta }}\left( \tau \right) = \frac{1}{{\left| {{W_\alpha }\left( \tau \right) + {W_\beta }\left( \tau \right)} \right|\gamma + {D_{\alpha , \beta }}}}. $ | (4) |
式中:Dα, β为两区域中心点间的距离.区域α的中心点坐标(xα, yα)计算公式为
| $ {x_\alpha } = \frac{{\sum {_{i \in \alpha }} {x_i}}}{{N\left( \alpha \right)}}, \;\;\;{y_\alpha } = \frac{{\sum {_{i \in \alpha }} {y_i}}}{{N\left( \alpha \right)}}. $ | (5) |
式中:N(α)为区域α中的服务点个数, (xi, yi)为区域α中服务点i的位置坐标.区域β的中心点坐标计算方式相同.
2 BSS调度的分形树自平衡区域划分算法FSPA构造实现分形树自平衡调度区域划分模型的算法(fractal tree based self-balanced partitioning algorithm, FSPA).FSPA包括调度区域范围设计、基于互平衡强度的动态聚类及引入BSS周转率杠杆的共协矩阵自平衡区域聚类融合.
2.1 考虑快速服务响应的叶子与枝节级调度区域范围设计调度区域范围设计直接影响BSS的快速响应服务特性, 若叶子级区域范围太大, 则会降低调度响应速度;区域越小, 该区域自平衡往往越困难.因此, 需要确定叶子级调度区域的合理范围.
设定调度车在非服务期间停留在该调度区域的中心位置, 以便及时响应调度需求.设叶子级调度区域覆盖半径为R, 调度车平均行驶速度为v, 调度响应时间为[δlow, δupp], 则在最小响应时间δlow内调度车能够到达的距离可以作为叶子级调度区域的最小半径Rmin, 理想情况下Rmin=δlowv, 但调度车沿途经过等待调度的服务点时会停留服务.设每个服务点的平均停留服务时间为t, 道路上站点分布密度为ρ, 极限情况下每个沿途服务点都是需调度服务点, 则Rmin的计算方程为
| $ {R_{\min }} = ({\delta ^{{\rm{low}}}} - {R_{\min }}\rho \bar t)\bar v. $ | (6) |
求解式(6), 可得
| $ {R_{\min }} = \frac{{{\delta ^{{\rm{low}}}}\bar v}}{{1 + \rho \bar t\bar v}}. $ | (7) |
同理可得Rmax, 因此叶子级调度区域面积为[Smin1, Smax1], 计算公式为
| $ \left. \begin{array}{l} S_{\min }^1 = {\rm{ \mathsf{ π} }}{({R_{\min }})^2} = {\rm{ \mathsf{ π} }}{\left( {\frac{{{\delta ^{{\rm{low}}}}\bar v}}{{1 + \rho \bar t\bar v}}} \right)^2}, {\rm{ }}\\ S_{\max }^1 = {\rm{ \mathsf{ π} }}{({R_{\max }})^2} = {\rm{ \mathsf{ π} }}{\left( {\frac{{{\delta ^{{\rm{upp}}}}\bar v}}{{1 + \rho \bar t\bar v}}} \right)^2}. \end{array} \right\} $ | (8) |
BSS服务点发出调度需求到获得调度服务的理想时间范围、即[δlow, δupp]与服务级别的对应关系如表 1所示.
| 表 1 BSS不同服务级别对应的响应时间 Table 1 Response time for different service level of BSS |
对于枝节级调度, 区域的划分需要考虑该层级区域内部的租还需求自平衡和区域面积范围.根据实践经验可知, 上级调度区域负责3~5个下级调度区域, 因此n级调度区域面积范围[Sminn, Smaxn]的计算公式为
| $ \left. \begin{array}{l} S_{\min }^n = 3S_{\min }^{n - 1}, \\ S_{\max }^n = 5S_{\max }^{n - 1}. \end{array} \right\} $ | (9) |
根据某时段τ的各服务点租还数据, 可以计算服务点间的互平衡强度, 开展该时段叶子级调度区域的动态聚类, 算法如下.
1) 将BSS内所有的服务点放入集合C0, 服务点数量为N, 这些服务点是分形树的叶子节点.设叶子级调度区域集合为C1.
2) 计算集合C0中所有节点间的互平衡强度, 找出每个节点对应的最大互平衡强度节点组成互补节点对, 如节点i的最大互平衡强度为EWi, j(τ), 则i和j组成互补节点对.
3) 在这些互补节点对中, 去除其中互平衡强度小于平均值的互补节点对;若剩余节点对中有些节点相交, 则去除其中互平衡强度较小的节点对.
4) 将剩余的节点对形成枝节点并计算面积, 枝节点α的面积Sα计算方法为
| $ \left. {\begin{array}{*{20}{c}} {{S_\alpha } = [\max ({x_i}) - \min ({x_i})][\max ({y_i}) - \min ({y_i})];}\\ {i \in \alpha .} \end{array}} \right\} $ | (10) |
若满足Sα>Smin1, 则将该枝节点放入叶子级调度区域集合C1;若不满足Sα>Smin1, 则用α替换集合C0中α包含的节点.
5) 重复2)~4), 直到集合C0中没有剩余节点.
集合C1中枝节点是时间段τ的叶子级自平衡区域聚类结果.对于BSS的某一服务周期T, 该周期内可以得到T/τ个聚类结果, 而且不同时段的聚类结果对调度的影响程度不同, 因此需要实现多个聚类结果的融合, 提出导入周转率杠杆的共协矩阵聚类融合改进算法.
2.3 导入周转率杠杆的共协矩阵聚类融合改进算法将BSS周转率杠杆导入共协矩阵聚类融合算法, 实现多个聚类结果的融合.令m=T/τ为服务周期T内的时段个数, τk表示第k个时段(k=1, 2, …, m), N为BSS的服务点数量, 则BSS第k时段的自行车周转率ωk的计算公式为
| $ {\omega _k} = \frac{{\sum {_{i \in {\rm{BSS}}}} Z_i^{{\rm{out}}}({\tau _k}) + \sum {_{i \in {\rm{BSS}}}} Z_i^{{\rm{in}}}({\tau _k})}}{N}. $ | (11) |
生成N×N维共协矩阵U, 矩阵的元素ui, j表示服务点i和j共同出现在同一个聚类区域中的概率和对应时段周转率的乘积.设置阈值, 若ui, j大于阈值, 则认为服务点i与j属于最终聚类结果中的同一区域.m个不同时段聚类结果形成的序列集合为L={Lk, k=1, 2, …, m}, 其中每一个聚类结果包括多个叶子级调度区域Lk={Ck1(l), l=1, 2, …, σk}, σk为第k个时段聚类出的叶子级调度区域个数.U定义为
| $ \mathit{\boldsymbol{U}} = {[{u_{i, j}}]^{N \times N}} = \left[ {\begin{array}{*{20}{c}} {{u_{1, 1}}}& \cdots &{{u_{1, N}}}\\ \vdots &{}& \vdots \\ {{u_{N, 1}}}& \cdots &{{u_{N, N}}} \end{array}} \right], $ | (12) |
| $ {u_{i, j}} = \frac{1}{m}\sum\limits_{k = 1}^m {{\omega _k}{\delta _k}\left( {i, j} \right)} . $ | (13) |
式中:δk(i, j)为阶跃函数, 表示服务点i和服务点j在k时段是否属于同一个叶子级调度区域, 判别公式为
| $ {\delta _k}\left( {i, j} \right) = \left\{ {\begin{array}{*{20}{c}} {1, }&{i, j \in C_k^1\left( l \right);}\\ {0, }&{i \in C_k^1\left( l \right), j \notin C_k^1\left( l \right).} \end{array}} \right. $ | (14) |
以周转率均值和平均聚类概率为判断阈值θ, 计算公式为
| $ \theta = \frac{{\sum {_{k = 1}^m} {\omega _k}}}{m} \times 50\% . $ | (15) |
ui, j>θ, 则认为服务点i、j属于同一个叶子级调度区域, 据此可以形成多个新的聚类区域.若有面积小于Smin1的区域, 则将该区域划分到与其地理位置最近的区域中;最后可以形成服务周期T的叶子级调度区域划分结果:Lnew={Cnew1(l), l=1, 2, …, σnew}.
2.4 枝节级调度区域的构建在BSS实际运营过程中, 可能会出现某叶子级区域的服务点自行车都被单向大量借出或还入, 早晚高峰时最容易出现, 这需要在不同的叶子级区域之间进行自行车调配, 称为枝节级区域调度, 即叶子级区域内部出现不平衡时需要实施跨区域调度.对于n级自平衡调度区域的构建, 算法如下.
1) 令n=2, 将聚类融合后的叶子级调度区域作为枝节点放入集合Cnewn-1.
2) 令k=1, τk表示服务周期T内第k个时段.
3) 计算集合Cnewn-1中枝节点在τk时段的互平衡强度EWα, β(τk), 找出每个枝节点对应的最大互平衡强度节点组成互补枝节点.
4) 在互补枝节点集合中, 删除其中互平衡强度小于平均值的互补枝节点和相交节点对中互平衡强度较小的互补枝节点.
5) 剩余互补枝节点将成为新的枝节点, 计算区域面积, 计算方法如式(10).若新枝节点面积>Sminn, 将该枝节点放入n级调度区域集合Ckn;若不满足条件, 则替换集合Cnewn-1中被聚类的节点.
6) 重复3)~5), 直到集合Cnewn-1中没有剩余节点.集合Ckn中的枝节点是τk时段的n级自平衡区域.
7) k=k+1, 重复3)~6), 直到周期T内最后一个时段的n级自平衡区域聚类完成.
8) 针对BSS在不同时段聚类产生的n级调度区域Ckn, 采用周转率杠杆共协矩阵聚类融合算法生成最终的n级调度区域聚类结果, 将最终聚类结果放入集合Cnewn.
9) n=n+1, 若SBSS∈[Sminn, Smaxn], 则结束聚类;否则, 重复2)~9).
3 BSS分形树自平衡调度区域划分的实验与分析 3.1 BSS自平衡区域划分实验以杭州锁桩式BSS下沙地区185个服务点为例, BSS服务级别取二级服务, 对分形树自平衡调度区域的划分方法进行实验验证.
根据杭州BSS历史数据, 调度车每完成一个服务点调度平均行驶0.9 km, 平均调入(或调出)约11量自行车, 因此, 式(3)中γ取0.9/11=0.08.通过式(3)可以计算所有服务点间的互平衡强度, 如表 2所示为某工作日第一个时段(6:00-7:00)的185个服务点与对应的最大互平衡强度服务点信息列表.表中, i为服务点编号, Wi(τ)、Wj(τ)为不平衡度, j为互补服务点, Di, j为服务点间距, EWi, j(τ)为服务点间互平衡强度.
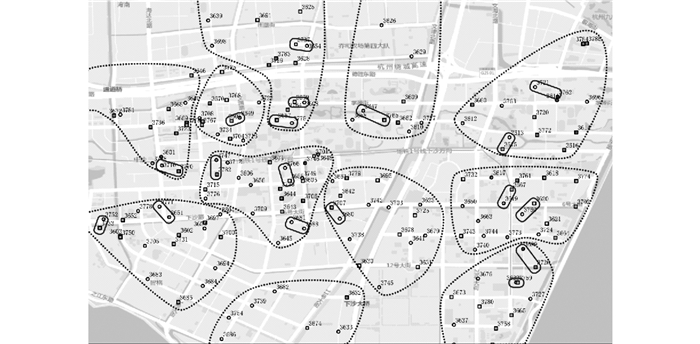
表 2中, 互平衡强度的均值为2.89, 互平衡强度>2.89的互补叶子节点可以进行聚类区域划分.由历史数据可得, 调度机动车平均行驶速度为20 km/h, 每个服务点的平均服务时间为5.5 min, 线路上站点平均分布密度为2.8个/km, 如BSS服务级别取二级服务, 则根据式(8)可知, 叶子级调度区域面积为[3.71, 8.35].根据该面积范围及叶子级自平衡区域划分的动态聚类算法可知, 6:00-7:00时段的叶子级聚类结果如图 3所示.
| 表 2 下沙地区6:00-7:00每个服务点与其互补服务点的互平衡强度 Table 2 Stations and complementary stations in Xiasha district during 6 to 7 am |
|
图 3 下沙地区6:00-7:00叶子级自平衡区域聚类结果 Fig. 3 Clustering diagram of leaf level self-balanced regions in Xiasha district during 6 to 7 am |
图 3中, 圆型图标表示服务点不平衡度Wi(τ) < 0, 需要调出自行车;方型图标表示Wi(τ)>0, 需要调入自行车, 颜色越深则不平衡度绝对值越大.第一轮互补叶子节点聚类结果如图 3的实线矩形框所示.可以看出, 实线框中的聚类节点距离相近, 而且这些节点的自行车调出调入需求相反, 可以互补形成自平衡枝节点.继续计算新枝节点和剩余叶子节点的互平衡强度, 最终聚类形成的叶子级调度区域如图 3的虚线框所示.
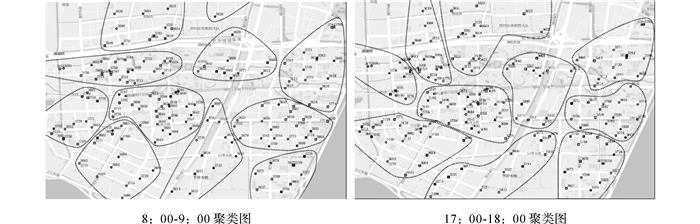
如图 4所示为该地区早晚高峰时段互平衡服务点聚类图.可以看出, 在不同时段获取的叶子级自平衡区域聚类结果不同, 因此在获取6:00-22:00之间16个时段的不同聚类结果后, 可以采用引入周转率杠杆的共协矩阵聚类融合算法进行聚类融合.
|
图 4 下沙地区早晚高峰叶子级自平衡区域聚类图 Fig. 4 Clustering diagram of leaf level self-balanced regions in Xiasha district during morning and evening peak |
如表 3所示为根据式(11)计算出的一天的服务时间中各时段的周转率ωk, 以此作为聚类融合的杠杆系数, 代入各时段聚类结果, 可以建立共协矩阵如下:
| 表 3 BSS不同时段周转率 Table 3 Bicycle turnover rate of BSS in different period of time |
| $ \begin{array}{l} \mathit{\boldsymbol{U}} = {[{u_{i,{\rm{ }}j}}]^{185 \times 185}} = \\ \left[ {\begin{array}{*{20}{c}} {167.56}&{15.50}&{25.51}& \cdots &0\\ {15.50}&{167.56}&{120.55}& \cdots &0\\ \vdots & \vdots & \vdots &{}& \vdots \\ 0&0&0& \cdots &{167.56} \end{array}} \right]. \end{array} $ |
根据式(15)计算θ=83.78, 可得融合的叶子级自平衡调度区域Cnew1.如表 4所示为Cnew1各区域服务点及在6:00-7:00的区域不平衡度, 其中共有12个区域, 区域不平衡度为该聚类区域所有服务点的不平衡度总和.可以看出, 有部分区域的不平衡度的总和为0或者较小的数值;还有部分区域的不平衡度较大, 需要跨区域进行调度.
| 表 4 下沙地区叶子级自平衡区域服务点及6:00-7:00区域不平衡度 Table 4 Stations of leaf level self-balanced regions and regional imbalance in Xiasha district during 6 to 7 am |
根据每个叶子级区域中心点间的距离和不同时段的不平衡度计算区域互平衡强度, 再采用枝节级区域划分聚类算法, 可得融合的二级自平衡调度区域Cnew2.以此类推, 最终的三级聚类结果如图 5所示.
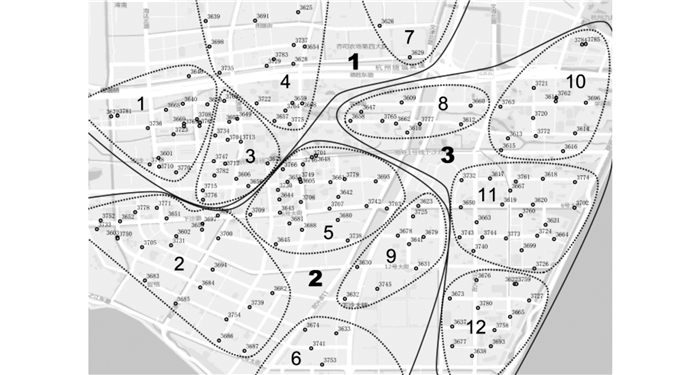
|
图 5 下沙地区三级自平衡调度区域划分结果 Fig. 5 Clustering diagram of three level self-balanced regions in Xiasha district |
图 5中, 下沙地区三级自平衡调度区域划分结果考虑了各服务点及同级调度区域间的需求互补, 将具有自行车调入和调出需求的互补服务点/区域划入同一上级区域, 以达到区域内的调度自平衡.下面对该划分结果进行实验验证和分析.
3.2 BSS自平衡区域划分结果的验证与分析选择下沙地区BSS调度历史数据进行分析, 如表 5所示为该区域在某工作日早高峰9:00的调度需求量.表中, 正数表示需要调入的自行车数量, 负数表示需要调出的自行车数量, 括号内为需要调度的服务点, 共有62个站点需要调度, 它们分别归属于不同叶子级和枝节级调度区域, 如表 5所示.
| 表 5 下沙地区9:00的服务点调度需求量 Table 5 Bicycle demand of stations in Xiasha district at 9 am |
从表 5可以看出, BSS两个叶子级调度区域Cnew1(6)、Cnew1(7)中没有需要调度的服务点, 不需要调度;若叶子级区域调度需求量小于区域服务点个数, 则不参与跨区调度, 因此Cnew1(3)、Cnew1(9)和Cnew1(12) 3个叶子级区域只在自己区域内部平衡;其他叶子级区域需要在枝节级区域内部进行跨区自行车调度.由此计算可得枝节级区域Cnew2(1)、Cnew2(2)与Cnew2(3)的调度需求分别为51、13和-45.当BSS的枝节级区域无法自平衡时, 需要跨区调度, 方法与叶子级区域的平衡调度类似;因为Cnew2(2)调度需求量小于区域服务点个数, 只在自己区域内部平衡, Cnew2(1)与Cnew2(3)两个枝节级区域需要跨区调度, 即在根级区域开展自行车平衡调度.
由历史数据的实验分析可知, 采用BSS分形树自平衡调度区域划分方法, 可以使得各级区域内部服务点的租借与归还趋向于平衡.当出现较小不平衡量时, 可以区域内部消化, 例如表 5的3个叶子级区域和1个枝节级区域;当只有出现较大不平衡时, 开始跨区域调度, 这样不仅有助于减少自行车调度的数量, 还可以较大程度地减少调度车的行驶距离.
将研究结果实验应用于杭州下沙BSS的运营管理, 实验效果良好.结果表明, 研究的BSS分形树自平衡区域划分方法切实可行, 既能够较好地提升BSS运行的调度响应速度和服务质量, 又充分利用BSS系统自行车租借归还的空间相关性, 尽量使得各个区域达到自平衡, 从而降低服务成本.
4 结语科学合理的区域划分和分区调度是大型城市BSS提高车辆调度效果和服务质量的有效方法.提出分形树自平衡调度区域划分模型, 基于服务点租/还需求的互平衡特性进行聚类, 同时采用周转率杠杆共协矩阵聚类融合算法, 分别形成叶子级和枝节级自平衡调度区域.杭州下沙城区共享自行车系统实验结果表明, 自平衡分区算法能够以较低成本满足BSS系统的调度需求.
研究的方法可以推广应用于共享单车, 即无锁桩式BSS.一些城市已经开始试用网格化调度管理共享单车系统, 工作人员各自负责所属网格区域内自行车的有序停放和调度.由于按照行政区划或者经验划分区域, 使得管理效率不高.对于无锁桩式BSS、尤其是电子围栏式BSS的调度分区, 因为这类BSS具有海量出行数据以及与锁桩式BSS相同的调度需求, 采用分形树自平衡调度区域划分模型和方法对管理网格进行划分, 更加有助于提高响应速度和工作效率, 降低调度成本, 从而提升城市管理水平和BSS服务质量.
| [1] |
董红召, 赵敬洋, 郭海锋. 公共慢行系统的动态调度建模与滚动时域调度算法研究的调度[J]. 公路工程, 2009, 34(6): 68-75. DONG Hong-zhao, ZHAO Jing-yang, GUO Hai-feng. Research on the dynamic model and rolling horizon scheduling algorithm for public-use bicycle vehicle scheduling problem[J]. Highway Engineering, 2009, 34(6): 68-75. |
| [2] |
董红召, 吴满金, 刘冬旭, 等. 城市公共自行车系统自然租赁需求的估算方法[J]. 浙江大学学报:工学版, 2016, 50(2): 265-270. DONG Hong-zhao, WU Man-jin, LIU Dong-xu, et al. Estimation method of natural demand of urban public bicycle system[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(2): 265-270. |
| [3] |
SALAKEN S M, HOSEN M A, KHOSRAVI A, et al. Forecasting bike sharing demand using fuzzy inference mechanism[J]. Neural Information Processing, 2015, 9491: 567-574. |
| [4] |
解小平, 邱建东, 汤旻安. 基于Elman神经网络的公共自行车单站点需求预测[J]. 计算机工程与应用, 2017, 53(16): 221-224. XIE Xiao-ping, QIU Jian-dong, TANG Min-an. Demand prediction of public bicycle rental station based on Elman neural network[J]. Computer Engineering and Applications, 2017, 53(16): 221-224. DOI:10.3778/j.issn.1002-8331.1603-0097 |
| [5] |
林燕平, 窦万峰. 基于网络模型的城市公共自行车需求量预测研究[J]. 计算机应用研究, 2017, 34(9): 2692-2695. LIN Yan-ping, DOU Wan-feng. Research on demand prediction of urban bicycle sharing based on network model[J]. Application Research of Computers, 2017, 34(9): 2692-2695. |
| [6] |
ADHAM M T, BENTLEY P J. An ecosystem algorithm for the dynamic redistribution of bicycles in London[J]. Information Processing in Cells and Tissues, 2015, 9303: 39-51. |
| [7] |
杨继伟, 周竹萍, 蔡逸飞. 基于改进蚁群算法的城市公共自行车动态调度模型[J]. 北京理工大学学报, 2016, 36(增2): 121-124. YANG Ji-wei, ZHOU Zhu-ping, CAI Yi-fei. Public bicycle dynamic scheduling model based on improved ant colony algorithm[J]. Transactions of Beijing Institute of Technology, 2016, 36(supple.2): 121-124. |
| [8] |
SCHUIJBROEK J, HAMPSHIRE R C, VAN HOEVE W J. Inventory rebalancing and vehicle routing in bike sharing systems[J]. European Journal of Operational Research, 2017, 257(3): 992-1004. DOI:10.1016/j.ejor.2016.08.029 |
| [9] |
COME E, OUKHELLOU L. Model-based count series clustering for bike sharing system usage mining:a case study with the Velib' system of Paris[J]. ACM Transactions on Intelligent Systems and Technology, 2014, 5(3): 39. |
| [10] |
陈昕昀, 蒋永康, 李牧原, 等. 基于多目标优化模型的城市公共自行车调度研究[J]. 现代交通技术, 2017, 14(1): 61-68. CHEN Xin-yun, JIANG Yong-kang, LI Mu-yuan, et al. Research on urban public bicycle scheduling based on multi objective optimization model[J]. Modern Transportation Technology, 2017, 14(1): 61-68. |
| [11] |
董红召, 史彩霞, 陈宁, 等. 基于关联规则的公共自行车调度区域聚类划分[J]. 科技通报, 2013, 29(9): 209-216. DONG Hong-zhao, SHI Cai-xia, CHEN Ning, et al. Clustering division of public bicycle scheduling regional based on association rules[J]. Bulletin of Science and Technology, 2013, 29(9): 209-216. |
| [12] |
徐建闽, 秦筱然, 马莹莹. 公共自行车多层次分区调度方法研究[J]. 交通运输系统工程与信息, 2017, 17(1): 212-219. XU Jian-min, QIN Xiao-ran, MA Ying-ying. Public bicycle multilevel partition scheduling method[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(1): 212-219. |
| [13] |
董红召, 刘冬旭, 陈鹰, 等. 基于分形理论的企业网络联盟的研究[J]. 浙江大学学报:工学版, 2004, 38(1): 11-16. DONG Hong-zhao, LIU Dong-xu, CHEN Ying, et al. Research on fractal-based extended enterprise[J]. Journal of Zhejiang University:Engineering Science, 2004, 38(1): 11-16. |
| [14] |
冯中慧, 何亮, 王栋. 基于新的成员选择方法的聚类融合算法[J]. 微电子学与计算机, 2016, 33(11): 25-29. FENG Zhong-hui, HE Liang, WANG Dong. Clustering ensemble algorithm based on new members selection method[J]. Microelectronics and Computer, 2016, 33(11): 25-29. |



