移动机器人的出现为解决危险作业问题提供了有效的途径[1].四足仿生机器人躯干大多采用刚性结构, 没有灵活的脊柱[2].四足机器人的脊柱大多利用刚度低、弹性高的柔性材料替代刚性躯体[3]. Kawasaki等[4]利用脊柱的伸展释放弹性势能, 驱动髋关节实现较长的跳跃距离. Miki等[5]利用气动肌肉的可变弹性改变躯干刚度, 机器人的运动稳定性很大程度上取决于机构的机械性能. Aoi等[6]通过数值分析证明, 横滚被动脊柱的刚度变化可以引起四足机器人的步态转换.虽然弹性元件可以保护机械系统免受突然的振动, 但脊柱的变形量无法主动控制. MIT利用差动齿轮, 将脊柱与机器人后腿髋关节相连, 通过存储和释放势能提高运动速度, 减少能量消耗[7-8]. Pouya等[9]通过实验对比得出, 主动脊柱使机器人的运动速度更快, 足底打滑更少, 稳定性更高. Kuehn等[10]利用Steward平台作为四足机器人脊柱, 实现了爬行到直立行走的进化.甄伟鲲等[11]研制了变胞爬行机器人, 通过腰部构型变化适应不同的应用环境.腿关节与脊柱结合的改进方向符合机构仿生进化的思想, 给四足机器人的发展提供了一个新的思路.
在CPG缺乏传感器反馈的情况下能够产生节律信号输出, 引入非线性振荡器作为CPG的数学模型[12]. Spröwitz等[13]采用粒子群算法优化CPG网络参数, 在仿真和实验中均实现了稳定的对角步态. Fukuoka等[14]在CPG模型中引入前庭反馈控制躯干的俯仰运动, 实现四足机器人自发稳定的行走.
本文通过机构和步态两个方面, 建立四足仿生机器人平台, 阐述脊柱与肢体耦合运动的节律, 为灾难救援机器人的应用提供基础.设计3-RPS并联脊柱, 通过运动学分析和生物观察规划脊柱扭转对角步态, 利用耦合CPG网络输出步态的节律信号;通过仿真和实验验证了主动脊柱对提高四足机器人运行性能的作用.
1 有并联脊柱四足机器人机构四足哺乳动物脊柱是一个复杂的生物力学系统, 可以看作刚性骨骼与柔性肌肉、肌腱、韧带组成的并联网络.并联结构可以提供更高的精度, 是脊柱关节的理想特征;四足动物脊柱的肌肉活动主要是横断面偏航、矢状面俯仰以及前后躯干微小的空间位移.为了简化结构和控制系统, 同时能够达到相应的运动目的, 利用气缸搭建3-RPS(R:转动副,P:移动副,S:球副)的并联平台.测得3个极限角度的数据如表 1所示.表中, θin为初始角度, θlim为极限角度, θc为变化角度.并联脊柱实物及3个极限位置如图 1所示.
| 表 1 并联脊柱实物的测试数据 Table 1 Test data of parallel spine |

|
图 1 并联脊柱实物图及3个极限位置 Fig. 1 Parallel spine entity and three extreme positions |
将并联脊柱应用到气动肌肉刚性躯干四足机器人[15]上, 建立简化的有并联脊柱四足机器人三维模型, 如图 2所示.机器人由前躯、脊柱、后躯和腿关节4部分组成;前、后腿关节采用双肘式配置;每条腿关节有髋关节俯仰、膝关节俯仰2个主动旋转自由度, 脊柱有俯仰、偏航、平移3个主动自由度, 整个机器人共有11个主动自由度.机器人的各参数如表 2所示.

|
图 2 有脊柱四足机器人三维模型图 Fig. 2 Three-dimensional model of quadruped robot with spine |
| 表 2 机器人模型参数表 Table 2 Robot model parameters |
为了简化有脊柱四足机器人的运动模型, 定义以下假设:1)假设只利用并联脊柱yaw方向自由度;2)假设脊柱摆动对前躯和后躯的影响相同, 躯干与地面保持平行;3)假设机器人所处的路面环境已知并且平坦;4)假设地面不打滑, 腿关节在支撑相时, 支撑足端由于地面摩擦力保持不动, 机器人质心会随着支撑足的运动向前.
在一个步态周期内, 有脊柱四足机器人的行走如图 3所示.行走初始的后躯髋关节中点设置为参考坐标系{O}的原点, 前进方向设置为x轴.在一个步态周期内, 后躯髋关节中点设置为坐标系{O0}的原点, 脊柱的旋转中心设为坐标系{O1}的原点, 前躯的髋关节中点设为坐标系{O2}的原点.四肢的髋关节坐标分别为OLF、ORF、OLH、ORH.
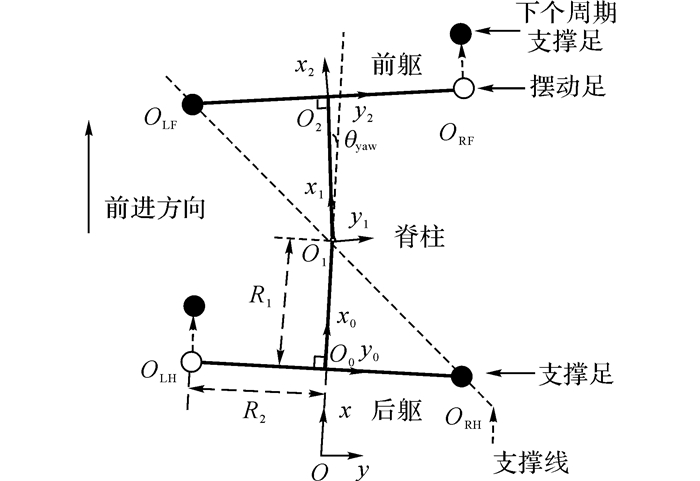
|
图 3 有脊柱四足机器人的运行示意图 Fig. 3 Running diagram of quadruped robot with spine |
设绕脊柱旋转中心的逆时针方向是yaw自由度的正方向.当脊柱关节摆动θyaw时, 四肢的髋关节在参考坐标系{O0}下的坐标分别为
| $ \left. \begin{array}{l} {O_{{\rm{RH}}}} = \left( {0, {R_2}} \right), \\ {O_{{\rm{LH}}}} = \left( {0, - {R_2}} \right), \\ {O_{{\rm{RF}}}} = ({R_1} + {R_1}\cos {\theta _{{\rm{yaw}}}} + {R_2}\sin {\theta _{{\rm{yaw}}}}, \\ \;\;\;\;{R_2}\cos {\theta _{{\rm{yaw}}}} - {R_1}\sin {\theta _{{\rm{yaw}}}}), \\ {O_{{\rm{LF}}}} = ({R_1} + {R_1}\cos {\theta _{{\rm{yaw}}}} - {R_2}\sin {\theta _{{\rm{yaw}}}}, \\ \;\;\;\;2{R_2}\sin {\theta _{{\rm{yaw}}}} - {R_2}\cos {\theta _{{\rm{yaw}}}} + {R_1}\sin {\theta _{{\rm{yaw}}}}). \end{array} \right\} $ | (1) |
当机器人质心向前行进d(t), 脊柱关节摆动θyaw时, 坐标系{O0}在参考坐标系{O}下的坐标为
| $ \left. \begin{array}{l} {x_{{O_0}}} = {R_2}\sin \frac{{{\theta _{{\rm{yaw}}}}}}{2} + d\left( t \right), \\ {y_{{O_0}}} = {R_2}\left( {1 - \cos \frac{{{\theta _{{\rm{yaw}}}}}}{2}} \right). \end{array} \right\} $ | (2) |
由于地面摩擦力的存在, 支撑足足端不会随着脊柱关节的摆动而移动.当左前右后腿关节作为支撑足时, 四肢的髋关节在参考坐标系{O}下的坐标表示如下:
| $ \left. \begin{array}{l} {O_{{\rm{RH}}}} = \left( {d\left( t \right), {R_2}} \right), \\ {O_{{\rm{LH}}}} = \left( {2{R_2}\sin \frac{{{\theta _{{\rm{yaw}}}}}}{2} + d\left( t \right), {R_2}\left( {1 - 2\cos \frac{{{\theta _{{\rm{yaw}}}}}}{2}} \right)} \right), \\ {O_{{\rm{RF}}}} = \left( {2{R_1} + 2{R_2}\sin \frac{{{\theta _{{\rm{yaw}}}}}}{2} + d\left( t \right), {R_2}(2\cos \frac{{{\theta _{{\rm{yaw}}}}}}{2} - 1)} \right), \\ {O_{{\rm{LF}}}} = \left( {2{R_1} + d\left( t \right), {R_2}} \right). \end{array} \right\} $ | (3) |
当右前左后腿关节作为支撑足时, 四肢的髋关节在参考坐标系{O}下的坐标表示如下:
| $ \left. \begin{array}{l} {O_{{\rm{RH}}}} = \left( {2{R_2}\sin \frac{{{\theta _{{\rm{yaw}}}}}}{2} + d\left( t \right), {R_2}\left( {1 - 2\cos \frac{{{\theta _{{\rm{yaw}}}}}}{2}} \right)} \right), \\ {O_{{\rm{LH}}}} = \left( {d\left( t \right), {R_2}} \right), \\ {O_{{\rm{RF}}}} = \left( {2{R_1} + d\left( t \right), {R_2}} \right), \\ {O_{{\rm{LF}}}} = \left( {2{R_1} + 2{R_2}\sin \frac{{{\theta _{{\rm{yaw}}}}}}{2} + d\left( t \right), {R_2}\left( {2\cos \frac{{{\theta _{{\rm{yaw}}}}}}{2} - 1} \right)} \right). \end{array} \right\} $ | (4) |
假设机器人质心高度坐标zg是一个常数, 机器人质心的投影点的坐标(xg, yg)可以表示为
| $ \left. \begin{array}{l} {x_{\rm{g}}} = \frac{{\sum\limits_{i = 1}^4 {{m_{{\rm{leg}}i}}{x_{{\rm{leg}}i}}} + \sum\limits_{j = 1}^2 {{m_{{\rm{body}}j}}{x_{{\rm{body}}j}}} + {m_{{\rm{spine}}}}{x_{{\rm{spine}}}}}}{M}, \\ {y_{\rm{g}}} = \frac{{\sum\limits_{i = 1}^4 {{m_{{\rm{leg}}i}}{z_{{\rm{leg}}i}}} + \sum\limits_{j = 1}^2 {{m_{{\rm{body}}j}}{z_{{\rm{body}}j}}} + {m_{{\rm{spine}}}}{z_{{\rm{spine}}}}}}{M}. \end{array} \right\} $ | (5) |
零力矩点(zero moment point, ZMP)是判定动态稳定性的常用方法, ZMP的坐标可以通过下式[16]获得:
| $ \left[ {\begin{array}{*{20}{c}} {{x_{{\rm{zmp}}}}}\\ {{y_{{\rm{zmp}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_{\rm{g}}}}\\ {{y_{\rm{g}}}} \end{array}} \right] - \frac{{{z_{\rm{g}}}}}{g}\left[ {\begin{array}{*{20}{c}} {{{\ddot x}_{\rm{g}}}}\\ {{{\ddot y}_{\rm{g}}}} \end{array}} \right]. $ | (6) |
式中:xg为机器人在x轴的质心坐标, yg为机器人在y轴的质心坐标,
假设t时刻腿关节的重心在地面的投影位置和髋关节的投影重合.在参考坐标系{O}下, 随脊柱摆动角θyaw∈[-10°, 10°], 在一个步态周期内质心投影点的x轴和y轴坐标变化曲线如图 4所示.

|
图 4 质心随脊柱摆动θyaw的曲线图 Fig. 4 Curves of centroid with rotating angle θyaw of yaw joint |
设定当速度vd=0.3 m/s时, 分别取加速度ad=4×10-5、2×10-5和0 m2/s, ZMP随时间变化的相平面图如图 5所示.

|
图 5 随时间变化的ZMP相平面图 Fig. 5 Phase-plane diagram of ZMP and time |
由图 4和5可知, 无论机器人加速度如何变化, 随着yaw自由度的转动, 有脊柱关节的机器人ZMP点都是平滑移动.脊柱关节的周期性转动不会引起质心位置的突变.
2.2 脊柱扭转对角步态在中速步态模式中:trot步态协调性好, 适应性强和运行速度较快, 是一种十分有效的移动方式.机器人在trot步态下行走时, 支撑相和摆动相周期一致, 可以减少计算量, 节约计算时间.四足机器人trot步态四条腿关节的相序关系可以表示为
| $ \mathit{\Delta }_j^i = {\varphi _i} - {\varphi _j};\;\;\;i, j = 1, 2, \cdots , 4. $ | (7) |
| $ \left[ {\mathit{\Delta }_2^1, \mathit{\Delta }_3^2, \mathit{\Delta }_4^3, \mathit{\Delta }_1^4} \right] = \left[ {{\rm{ \mathsf{ π} }}, - {\rm{ \mathsf{ π} }}, {\rm{ \mathsf{ π} }}, - {\rm{ \mathsf{ π} }}} \right]. $ | (8) |
式中:Δji为第i条腿关节和第j条腿关节之间的相位差, 1为左前腿(LF), 2为右前腿(RF), 3为左后腿(RH), 4为右后腿(LH).
在trot步态模式运动期间, 脊柱的肌肉活动主要作用在横断面上, 产生偏航弯曲, 用来抵抗足底接触力导致的身体扭转.Nyakatura等[17]结合高速X射线视频和断层扫描重建骨骼元素, 得到树懒对角步态两个连续平均步态周期的骨盆相对运动.针对有主动脊柱的四足机器人, 仿照自然界生物的脊柱波动, 将脊柱层的律动与肢体层trot步态相耦合, 得到一种新的脊柱偏转对角步态:当LH处于支撑相时, 脊柱运动使身体向左侧弯曲;当RH处于支撑相时, 脊柱使身体向右侧弯曲;偏转的最大值发生在换相后处于支撑相的一侧.脊柱偏转对角步态模式的ZMP轨迹分析如图 6所示.

|
图 6 脊柱扭转对角步态模式的ZMP轨迹分析 Fig. 6 ZMP trajectory analysis for twisting trot gait |
纵向稳定性是指机器人在抵抗重力和惯性力作用下躯体翻滚的能力. trot步态腿部在一个步态周期内只有2个支撑足, 定义纵向稳定裕度(longitudinal stability marlin, LSM)SL为换相时刻机器人零力矩点在运动方向上到支撑线的距离, SL越小, 机器人的稳定性越高.当支撑足为LF和RH时, θyaw>0;当支撑足为RF和LH时, θyaw < 0.脊柱偏转最大值发生在换相时刻, 保证行走过程具有最大的纵向稳定性. ZMP在一个步态周期内跨过对角支撑线两次, 脊柱层和4个肢体层的相位关系为
| $ [\mathit{\Delta }_5^1, \mathit{\Delta }_5^2, \mathit{\Delta }_5^3, \mathit{\Delta }_5^4] = \left[ {0, - {\rm{ \mathsf{ π} }}, 0, - {\rm{ \mathsf{ π} }}} \right]. $ | (9) |
式中:5为脊柱关节.
2.3 CPG运动控制模型在四足机器人步态规划中, CPG可以用来产生关节运动的节律信号[18], 步态模式由振荡器之间的相位耦合关系决定. Hopf振荡器可以产生类似于动物肢体谐波运动的自稳定正弦振荡[19], 选用Hopf振荡器作为节律发生器.为了肢体之间运动的协调性, 建立环状高度耦合的CPG网络模型:
| $ \left. \begin{array}{l} {{\dot x}_i} = \alpha \left( {\mu - r_i^2} \right){x_i} - {\omega _i}{y_i} + k\sum\limits_j {\left( {{x_j}\cos \Delta _j^i - {y_i}\sin \Delta _j^i} \right)} ,\\ {{\dot y}_i} = \alpha \left( {\mu - r_i^2} \right){y_i} - {\omega _i}{x_i} + k\sum\limits_j {\left( {{y_j}\cos \Delta _j^i + {x_i}\sin \Delta _j^i} \right)} ,\\ \omega = \frac{{{\omega _{{\rm{stance}}}}}}{{\exp ( - b{x_i}) + 1}} + \frac{{{\omega _{{\rm{swing}}}}}}{{\exp (b{x_i}) + 1}}. \end{array} \right\} $ | (10) |
式中:k为振荡器之间的耦合强度, 当k具有非零值时, 振荡器之间具有耦合关系;xj和yj为第j条关节振荡器的状态变量;ωswing为摆动相角频率;ωstance为支撑相角频率.
脊柱扭转对角步态网络拓扑结构图如图 7所示.利用5个振荡器搭建CPG网络, 髋关节、膝关节和脊柱关节的节律信号由映射函数生成:

|
图 7 肢体与脊柱耦合的CPG网络拓扑结构图 Fig. 7 Topological structure diagram of CPG network coupled between limbs and spine |
| $ \left. \begin{array}{l} {\theta _{{\rm{h}}i}}\left( t \right) = {A_{\rm{h}}}{x_i};\\ {\theta _{{\rm{k}}i}}\left( t \right) = \left\{ \begin{array}{l} {A_{\rm{k}}}{y_i}, \;\;\;{y_i} \ge 0;\\ 0, \;\;\;\;\;{y_i} < 0; \end{array} \right.\\ {\theta _{{\rm{yaw}}}}\left( t \right) = {A_{{\rm{sp}}}}{x_5}. \end{array} \right\} $ | (11) |
式中:θhi(t)、θki(t)、θyaw(t)和Ah、Ak、Asp分别为髋、膝和脊柱关节的角度和关节幅值.
脊柱扭转对角步态的CPG网络输出如图 8所示, 具体的参数如表 3所示.
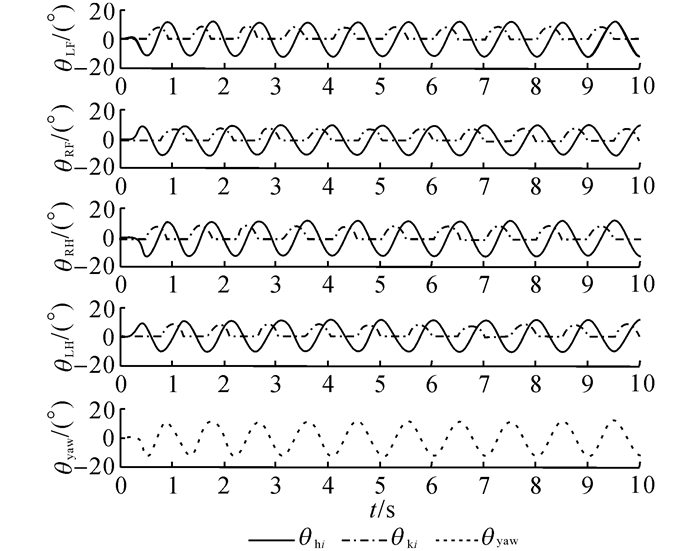
|
图 8 肢体与脊柱耦合的CPG网络输出图 Fig. 8 Output diagram of CPG network coupled between limbs and spine |
| 表 3 肢体与脊柱耦合的CPG网络参数表 Table 3 Parameters of CPG network coupled between limbs and spine |
利用ADAMS对有脊柱四足机器人进行运动仿真, 设置坐标系如下:x轴的正方向是前进方向, 俯仰运动被定义为绕y轴的旋转, z轴的负方向是重力方向.若脊柱关节的驱动设置为0, 机器人具有刚性躯体.当刚性躯干和主动脊柱机器人运行10 s时, 质心波动幅度分别如图 9(a)、(b)所示.图中,φ为偏航角度,θroll为扭转角度,θpitch为俯仰角度.机器人在z轴方向的偏航位移如图 9(c)所示.
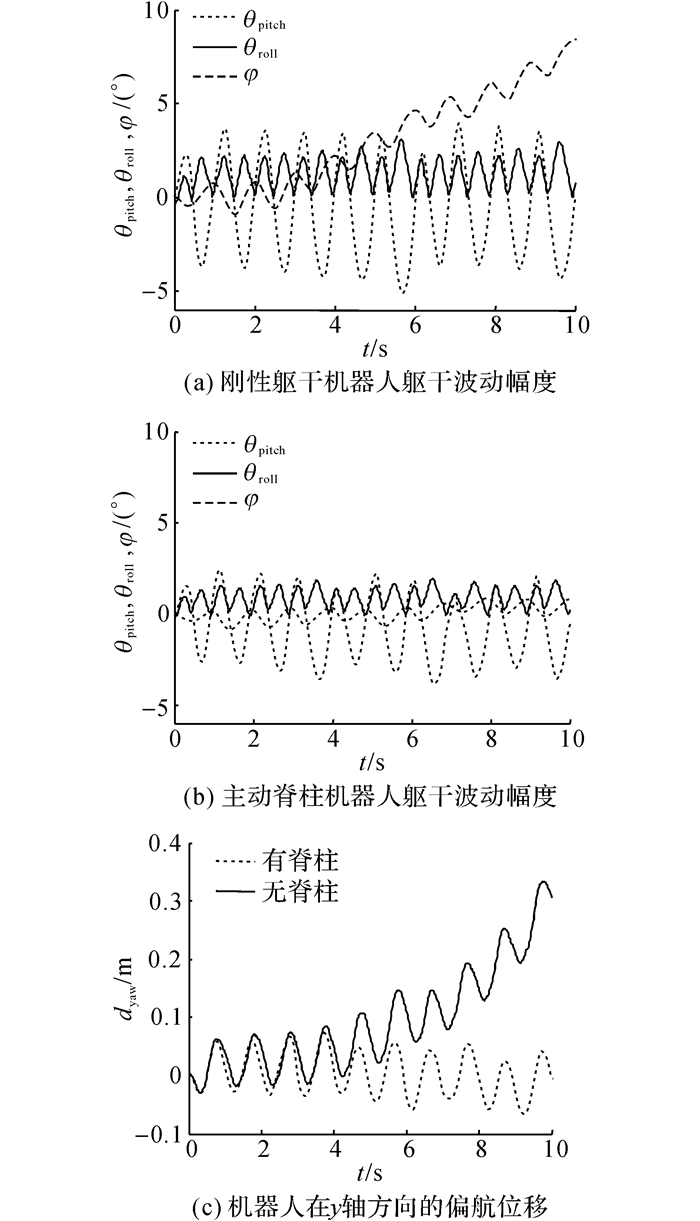
|
图 9 四足机器人运动仿真曲线 Fig. 9 Simulation trajectories with quadruped robot |
刚性躯干、主动脊柱机器人运行10 s, 分别行进了2.73 m和2.85 m;通过质心位置、加速度和足端位置得到, 刚性躯干四足机器人最大的纵向稳定裕度SLMAX=0.25 m, 主动脊柱四足机器人在脊柱扭转对角小跑步态下SLMAX=0.07 m, 四足机器人需要脊柱的动作来配合快速的腿部运动, 脊柱关节使得机器人的稳定性和运行速度增强.
刚性躯干四足机器人的动力学分析如图 10所示, 此时LF和RH处于支撑相.ZMP到支撑足的垂直距离l可以表示为
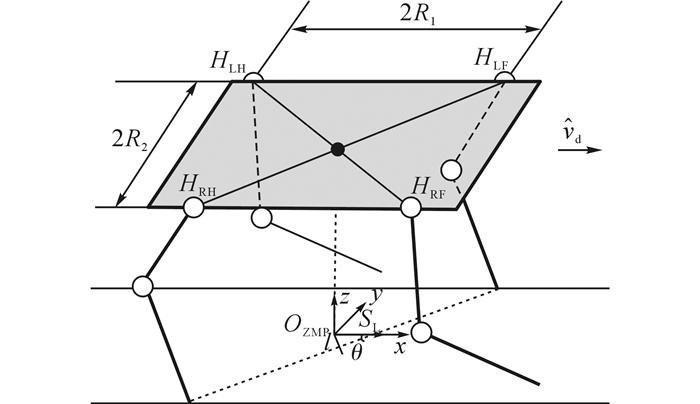
|
图 10 刚性躯干四足机器人动力学分析图 Fig. 10 Dynamic analysis of quadruped robot with rigid torso |
| $ l = {S_{\rm{L}}}\sin \theta , $ | (12) |
| $ \tan \theta = \frac{{2{R_2}}}{{2{R_1}}}. $ | (13) |
式中:θ为支撑线与前进方向形成的夹角, SL为纵向稳定裕度, 2R1为前躯到后躯同侧髋关节的距离, 2R2为前躯或后躯两侧髋关节的距离.由式(13)可以看出, 支撑线与运动方向的夹角θ可由机器人的机构尺寸确定.
将机器人的行走看作是匀速运动, ZMP与质心投影点重合.支撑线在换相时刻ZMP点为原点的{OZMP}坐标系下的方程为
| $ x\sin \theta - y\cos \theta = \left[ {{S_{\rm{L}}} - \smallint v\left( t \right){\rm{d}}t} \right]\sin \theta . $ | (14) |
假设速度
| $ x\sin \theta - y\cos \theta = ({S_{\rm{L}}} - {{\hat v}_{\rm{d}}}t)\sin \theta . $ | (15) |
由欧拉定理可得, 在运动过程中, 四足机器人绕支撑对角线翻转的角加速度为
| $ \varepsilon \left( t \right) = \frac{{gl}}{{{C_{\rm{b}}}}} = \frac{g}{{{C_{\rm{b}}}}}\left( {{S_{\rm{L}}} - \smallint v\left( t \right){\rm{d}}t} \right)\sin \theta . $ | (16) |
式中:Cb为与机器人本体结构有关的参数, 包括高度、质量、转动惯量等参数.由式(16)可知, l越大, 机器人绕支撑对角线翻转的角加速度越大.
在运动过程中, 四足机器人绕支撑对角线翻转的角速度为
| $ \begin{array}{l} \omega \left( t \right) = \smallint \frac{{gl}}{{{C_{\rm{b}}}}}{\rm{d}}t = \smallint \frac{{g({S_{\rm{L}}} - {{\hat v}_{\rm{d}}}t)\tan \theta }}{{{C_{\rm{b}}}}}{\rm{d}}t = \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{g}{{{C_{\rm{b}}}}} \times \left[ {\left( {{S_{\rm{L}}}\tan \theta } \right)t - \left( {\frac{1}{2}{{\hat v}_{\rm{d}}}\tan \theta } \right){t^2}} \right]. \end{array} $ | (17) |
机器人前后腿关节采用双肘式配置, 在trot步态模式下运行.腿关节在换相时刻, ZMP会位于支撑线一侧, 产生不平衡力矩.由式(17)可知, 由于起步时刻机器人的速度为0, 惯性力使得ZMP必然位于支撑线的后方, 方向与起步阶段的姿态有关.
因为绕支撑对角线翻转速度的存在, 刚性躯干的四足机器人纵向稳定性必然会受到限制.由于没有横向可控自由度, 在机器人行走过程中, 会在偏航方向产生不必要的位移.主动脊柱可以利用yaw自由度的运动矫正偏航位移, 小跑步态模式更加类似于真正的四足动物.
搭建有并联脊柱四足机器人实物, 对规划的脊柱扭转对角步态进行步态实验验证.行走实验图如图 10所示, 机器人的前进方向向左.
图 11(a)中, 机器人LF和RH处于摆动相;RF和LH处于支撑相, 随传送带向后移动;气缸2伸出, 气缸3缩回, 身体向左侧偏转.图 11(b)中, LF和RH放下, 接触传送带, 同时RF和LH准备抬起;气缸3伸出, 气缸2缩回, 身体随脊柱向右侧最大摆动.图 11(c)中, LF和RH抬起, 处于摆动相;RF和LH处于支撑相;身体向左侧偏转.图 11(d)中, RF和LH处于摆动相, LF和RH处于支撑相, 身体向右侧偏转.

|
图 11 四足机器人行走实验 Fig. 11 Quadruped robot's walking experiment |
在机器人运动过程中, 将脊柱关节偏航角度设置为0°、3°、5°.利用MPU6050测得机器人躯干各方向角度波动幅度分别如图 12(a)~(c)所示, 3种情况下的躯干波动如表 4所示.

|
图 12 机器人运行过程中的躯干波动幅度 Fig. 12 Torso fluctuation during walking experiment |
| 表 4 机器人运行中的躯干波动数据 Table 4 Extent data of centroid in walking experiment |
利用质心的俯仰波动间接反映行走稳定性, 与刚性躯干相比, 主动脊柱的加入使俯仰波动降低45.79%, 对四足机器人的运行稳定性有明显影响.在目前的四足平台上加入主动脊柱关节, 可以积极地矫正机器人在运动过程中的偏航和降低俯仰波动, 从而获得更高的稳定性.
4 结论(1) 并联结构可以提供更高的精度, 是脊柱关节的理想特征.
(2) 建立有脊柱四足机器人的运动模型, 脊柱关节的周期性转动不会引起质心位置的突变.
(3) 利用脊柱波动、肢体摆动间的协调, 设计脊柱扭转对角步态, 主动脊柱可以提高四足机器人行走过程中的稳定性和运行速度, 矫正偏航位移.
由于该机器人主要用于灾后救援, 后续对于不平坦的路面环境的适应性需要进行改善.根据机器人被应用的场合不同, 选择不同的步态, 脊柱多自由度的加入可以实现更加丰富的步态模式.
| [1] |
KAR D C, KURIEN ISSAC K, JAYARAJAN K. Minimum energy force distribution for a walking robot[J]. Journal of Field Robotics, 2015, 18(2): 47-54. |
| [2] |
孟健, 李贻斌, 李彬. 四足机器人对角小跑步态全方位移动控制方法及其实现[J]. 机器人, 2015, 37(1): 74-84. MENG Jian, LI Yi-bin, LI Bin. Control method and its implementation of quadruped robot in omni-directional trotting gait[J]. Robot, 2015, 37(1): 74-84. |
| [3] |
WANG C, ZHANG T, WEI X. Dynamic characteristics and stability criterion of rotary galloping gait with an articulated passive spine joint[J]. Advanced Robotics, 2016, 31(4): 1-16. |
| [4] |
KAWASAKI R, SATO R. Development of a flexible coupled spine mechanism for a small quadruped robot[C]//IEEE International Conference on Robotics and Biomimetics. Bali: IEEE, 2017: 71-76. http://ieeexplore.ieee.org/document/7866300/
|
| [5] |
MIKI K, TSUJITA K. A study of the effect of structural damping on gait stability in quadrupedal locomotion using a musculoskeletal robot[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Tivoli: IEEE, 2012: 1976-1981. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6386256
|
| [6] |
AOI S, KATAYAMA D, FUJIKI S. Cusp catastrophe embedded in gait transition of a quadruped robot driven by nonlinear oscillators with phase resetting[C]//IEEE International Conference on Robotics and Biomimetics. Guangzhou: IEEE, 2012: 384-389. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6490997
|
| [7] |
DONG J H, SANG O S, LEE J, et al. High speed trot-running:Implementation of a hierarchical controllerusing proprioceptive impedance control on the MIT Cheetah[J]. International Journal of Robotics Research, 2015, 33(11): 1417-1445. |
| [8] |
SEOK S, WANG A, MENG Y C. Design principles for energy-efficient legged locomotion and implementation on the MIT cheetah robot[J]. IEEE/ASME Transactions on Mechatronics, 2014, 20(3): 1-13. |
| [9] |
POUYA S, KHODABAKHSH M, SPRÖWITZ A, et al. Spinal joint compliance and actuation in a simulated bounding quadruped robot[J]. Autonomous Robots, 2017, 41(2): 437-452. DOI:10.1007/s10514-015-9540-2 |
| [10] |
KUEHN D, BEINERSDORF, BERNHARD F. Active spine and feet with increased sensing capabilities for walking robots[C]//International Symposium on Artificial Intelligence. Germany: [s. n. ], 2012: 1204-1210. https://www.researchgate.net/publication/257925163_Active_spine_and_feet_with_increased_sensing_capabilities_for_walking_robots
|
| [11] |
甄伟鲲, 康熙, 张新生. 一种新型四足变胞爬行机器人的步态规划研究[J]. 机械工程学报, 2016, 52(11): 26-33. ZHEN Wei-kun, KANG Xi, ZHANG Xin-sheng. Gait planning of a novel metamorphic quadruped robot[J]. Journal of Mechanical Engineering, 2016, 52(11): 26-33. |
| [12] |
HU Y, LIANG J, WANG T. Parameter synthesis of coupled nonlinear oscillators for CPG-based roboticlocomotion[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6183-6191. DOI:10.1109/TIE.2014.2308150 |
| [13] |
SPRÖWITZ A, TULEU A, VESPIGNANI M. Towards dynamic trot gait locomotion:design, control, and experiments with Cheetah-cub, a compliant quadruped robot[J]. International Journal of Robotics Research, 2013, 32(8): 932-950. DOI:10.1177/0278364913489205 |
| [14] |
FUKUOKA Y, HABU Y, FUKUI T. Analysis of the gait generation principle by a simulated quadruped model with a CPG incorporating vestibular modulation[J]. Biological Cybernetics, 2013, 107(6): 695-710. DOI:10.1007/s00422-013-0572-4 |
| [15] |
王斌锐, 王涛, 郭振武. 气动肌肉四足机器人建模与滑模控制[J]. 机器人, 2017, 39(5): 620-626. WANG Bin-rui, WANG Tao, GUO Zhen-wu. Modeling and sliding mode control of quadruped robot driven by pneumatic muscles[J]. Robot, 2017, 39(5): 620-626. |
| [16] |
HU Y, LIANG J, WANG T. Parameter synthesis of coupled nonlinear oscillators for CPG-based robotic locomotion[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6183-6191. DOI:10.1109/TIE.2014.2308150 |
| [17] |
NYAKATURA J A, FISCHER M S. Functional morphology and three-dimensional kinematics of the thoraco-lumbar region of the spine of the two-toed sloth[J]. Journal of Experimental Biology, 2010, 213(24): 4278-4290. DOI:10.1242/jeb.047647 |
| [18] |
IJSPEERT A J, CABELGUEN J M. Control of aquatic and terrestrial gaits in salamander[M]. New York: Springer, 2015, 1-9.
|
| [19] |
SANTOS C P, ALVES N, MORENO J C. Biped locomotion control through a biomimetic CPG-based controller[J]. Journal of Intelligent and Robotic Systems, 2016, 85(1): 1-24. |



