2. 北京宇航系统工程研究所, 北京 101300
2. Beijing Institute of Astronautical System Engineering, Beijing 101300, China
淬火是较高温度的固体直接接触后较低温度的液体工质后所发生的快速冷却现象.当固体壁面温度远高于冷却工质的饱和温度时, 工质中的传热过程一般将依次经历膜态沸腾、过渡沸腾以及核态沸腾等阶段.淬火在工业领域中有着广泛的应用, 如金属材料热处理和核反应堆堆芯冷却[1].
沸腾传热特性不仅受工质热物性的影响, 与沸腾表面的特性(例如粗糙度、浸润性和孔隙结构等)也密切相关[1].当表面具有微细的中空/孔道结构时(例如凹腔结构[2]、肋化结构[3]和多孔结构[4]等), 不仅会造成粗糙度和宏观浸润性的变化, 还可能表现出由于毛细效应所导致的芯吸性.类似于纺织材料纤维结构内的毛细管体系对液体所产生的导流作用[6], 芯吸表面具有一般粗糙表面甚至是超亲水(超铺展)表面所不具备的面内液体输运能力.液体工质与芯吸表面接触后在毛细压力[5]的作用下会迅速渗入、铺展并浸润周围的未润湿区域.
由于上述特殊的液体输运能力, 芯吸表面在强化沸腾传热领域的应用近年来已越来越受到国内外学者们的关注.Kim等[7]将氧化钛纳米颗粒沉积于镍铬合金丝上, 制得芯吸表面.实验观察到表面芯吸性有效地增大了固液接触面积并抑制蒸干区域的形成, 推迟了临界热流密度(CHF)的出现.芯吸表面的最大CHF为2 500 kW·m-2, 相比于原始表面(1 924 kW·m-2)提高约260%.Hendricks等[8]采用氧化锌纳米颗粒沉积的方法制得具有芯吸性的铝表面, 并指出表面上的芯吸结构能有效增大表面汽化核心密度和汽泡脱离频率, 增强该表面在核态沸腾阶段换热性能.相较于原始表面的CHF(~232 kW·m-2), 铝基芯吸表面的CHF显著提高了约4倍(~825 kW·m-2).此外, Rahman等[9]将包裹有镍壳的烟草花叶病毒沉积于铝、铜、硅以及不锈钢表面上得到了多种超亲水的芯吸表面.实验中在硅基芯吸表面上所得到的最高CHF为2 570 kW·m-2, 并发现CHF随表面芯吸性能参数的提高有线性增长的趋势.
上述工作主要关注的是表面芯吸性对核态池沸腾阶段传热特性的影响.本文尝试将芯吸表面应用于淬火过程的强化, 在常压下的饱和水中进行了芯吸表面的淬火冷却实验研究, 并着重研究芯吸表面膜态和过渡态阶段的沸腾传热特性.
1 实验方法与过程 1.1 芯吸表面的制备和形貌表征本研究选用直径为10 mm的304不锈钢球为实验试样.原始的不锈钢球在实验前依次经过丙酮、酒精和去离子水的仔细清洗.参考Li等[10]的化学腐蚀方法, 将洗净的不锈钢球试样取出后放入浓度为49±2%的氢氟酸溶液中进行腐蚀.通过控制腐蚀时间得到了具有不同芯吸能力的表面.本文将腐蚀时间分别为1.5和3 min的表面记为芯吸表面1和芯吸表面2.整个腐蚀过程在50 ℃的恒温水浴中进行.腐蚀完毕的不锈钢球试样取出后在常温环境中自然风干备用.
如图 1所示为上述3种表面的扫描电镜图.较为光滑的原始表面(见图 1(a))在于氢氟酸溶液反应之后出现了微尺度表面形貌.如图 1(b)所示, 芯吸表面1上的局部区域形成了微米级的花瓣状结构, 与周围较大的碎片结构之间形成不规则的凹腔.由于不锈钢的成分偏析, 在与氢氟酸的反应中有的部分容易被腐蚀而形成深的凹腔, 而其他不容易被腐蚀的部分则形成浅的凹腔或者不形成凹腔.随着腐蚀时间的增加, 芯吸表面2上形成如图 1(c)所示的孢子状团聚结构.由于不锈钢球表面被腐蚀程度加深, 该孢子状团聚结构(直径约为1~5 μm)之间形成了更大尺度的凹腔, 且表面粗糙度显著增大.

|
图 1 表面形貌特征图 Fig. 1 Surface morphology images on |
图 1中同时给出了3种表面的表面粗糙度测试结果.与扫描电镜图片一致, 表面粗糙度随腐蚀时间的增加而逐渐增大, 轮廓算术平均偏差Ra从0.062±0.004 μm依次增长到0.814±0.046和2.871±0.105 μm, 而轮廓最大高度Rz则从0.305±0.041 μm依次增长到5.260±0.424和14.717±0.662 μm.
1.2 芯吸性测量原理与实验装置本研究中参考Ann等[11]所采用的毛细管液柱高度法对所制备表面的芯吸能力进行定量表征, 其测量装置如图 2所示.因为所采用的内径d为500 μm的PFA毛细管具有疏水特性(即去离子水与毛细管壁面接触角较大), 所以在重力和毛细力的作用下管内去离子水液面垂直于毛细管内壁, 并在下端管口产生一个直径约等于毛细管内径的悬垂液滴.在与试样表面接触之后, 利用高速摄像机对芯吸过程中毛细管内液位的瞬时下降高度Δh进行监测.
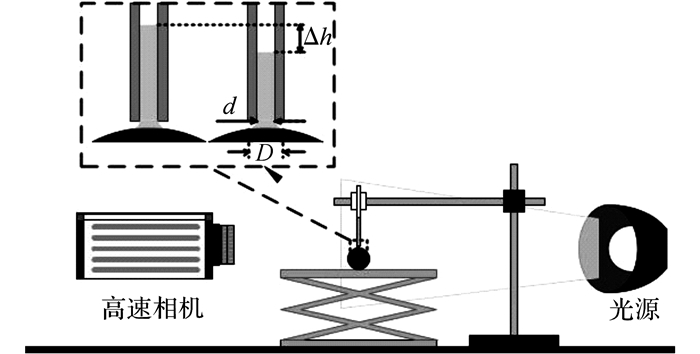
|
图 2 芯吸性测量装置示意图 Fig. 2 Schematic diagram of wicking measurement setup |
试样表面芯吸量为
| $ V = \frac{1}{4}{\rm{ \mathsf{ π} }}{d^2}\Delta h. $ | (1) |
在芯吸过程中, 悬垂液滴与表面接触后转变为连通毛细管内去离子水和试样表面的液桥.假设液桥与表面的接触面为圆形(直径为D), 则表面的瞬时芯吸通量为
| $ u = \frac{4}{{{\rm{ \mathsf{ π} }}{D^2}}}\frac{{\Delta V}}{{\Delta t}}. $ | (2) |
式中:ΔV为在液滴与表面接触时间Δt内毛细管中液体减少的体积.
由式(2)可得, 芯吸量和芯吸通量的测量误差主要来源于液位变化高度Δh的测量误差(±0.07 mm)和液桥底面直径D的测量误差(±0.04 mm).根据误差传递公式可以估算出芯吸量V的相对误差约为2.5%, 而瞬时芯吸通量u的相对误差约为4.7%.
1.3 淬火实验过程及数据处理本研究采用文献[12]中所使用的可视化淬火沸腾实验台进行实验研究, 具体的实验台构成在此不再赘述.通过平板加热器加热石英玻璃制的透明沸腾池, 使池内的去离子水保持在常压下的饱和温度(100 ℃).不锈钢球试样在竖直放置的管式辐射炉中加热升温至恒定后, 通过电动导轨迅速浸没入沸腾池中.在淬火过程中通过K型铠装热电偶采集球心温度, 并使用高速摄像机进行可视化观察.
根据球心过热度Δθc(球心温度θc与水温θw之差), 通过求解导热反问题可得球面过热度Δθs(球面温度θs与水温θw之差)和球面热流密度qs[13].截取解析解的前三项级数, 近似求得球面过热度为
| $ \begin{array}{l} \Delta {\theta _{\rm{s}}}\left( t \right) \approx \Delta {\theta _{\rm{c}}}\left( t \right) + \frac{1}{6}\left( {\frac{{{R^2}}}{\alpha }} \right)\frac{{{\rm{d}}\Delta {\theta _{\rm{c}}}\left( t \right)}}{{{\rm{d}}t}} + \\ \;\;\;\;\frac{1}{{120}}{\left( {\frac{{{R^2}}}{\alpha }} \right)^2}\frac{{{{\rm{d}}^2}\Delta {\theta _{\rm{c}}}\left( t \right)}}{{{\rm{d}}{t^2}}} + \frac{1}{{5\;040}}{\left( {\frac{{{R^2}}}{\alpha }} \right)^3}\frac{{{{\rm{d}}^3}\Delta {\theta _{\rm{c}}}\left( t \right)}}{{{\rm{d}}{t^3}}}, \end{array} $ | (3) |
球面热流密度为
| $ \begin{array}{l} q”{_{\rm{s}}}\left( t \right) \approx- \rho {c_{\rm{p}}}[\left( {\frac{R}{3}} \right)\frac{{{\rm{d}}\Delta {\theta _{\rm{c}}}\left( t \right)}}{{{\rm{d}}t}} + \frac{1}{{30}}\left( {\frac{{{R^3}}}{\alpha }} \right)\frac{{{{\rm{d}}^2}\Delta {\theta _{\rm{c}}}\left( t \right)}}{{{\rm{d}}{t^2}}} + \\ \;\;\;\;\frac{1}{{840}}\left( {\frac{{{R^5}}}{\alpha }} \right)\frac{{{{\rm{d}}^3}\Delta {\theta _{\rm{c}}}\left( t \right)}}{{{\rm{d}}{t^3}}}]. \end{array} $ | (4) |
式中:α、R分别为不锈钢球的热扩散系数和半径.密度ρ约为7 817 kg/m3, 导热系数k约为17 W/mK, 定压比热容cp约为460 J/(kg·K).
由上式可知, 不锈钢球表面热流密度的计算误差主要来源于球直径的测量误差(±0.03 mm)和热电偶温度测量误差(±2.0 ℃), 因此可估算得到热流密度的相对误差约为2.8%[14].本研究中对任一工况均进行了多次平行实验, 以保证结果的可重复性.
2 实验结果及讨论 2.1 芯吸性测量结果如图 3所示为3种表面在芯吸过程中的液位变化图.在原始表面上(见图 3(a)), 虽然悬垂液滴与表面接触后转变为液桥, 但是毛细管内液位几乎不变.这一现象表明原始表面不具有芯吸性.液滴与表面接触后只是在表面张力的作用下转变为液桥, 但是管内液体并未被抽吸进入表面.

|
图 3 芯吸过程中的液位变化 Fig. 3 Variations of liquid level during wicking process |
如图 3(b)所示, 在芯吸表面1的测试中, 毛细管内的液位明显下降.随着时间的推移, 管内液位下降变缓, 表明固液接触区域周围的芯吸性结构逐渐趋于饱和.相比之下, 悬垂液滴与芯吸表面2接触后在相同时间内管内液位下降更多(见图 3(c)), 表明该表面的芯吸能力有了进一步的增强.
如图 4所示为芯吸量随时间变化的曲线图.与图 3中所观察到的现象一致, 原始表面的芯吸量只有极小的变化.如前所述这是由液体表面张力所引起的, 仅约0.07 μL.芯吸表面1在与悬垂液滴接触后, 芯吸量迅速增大, 至约20 ms后, 曲线斜率迅速减小至趋近于0.在100 ms内, 芯吸表面1的总芯吸量约为0.26 μL.与芯吸表面1相比较, 芯吸表面2在初始阶段芯吸量提升更快, 在约40 ms后曲线斜率迅速减小至趋近于0.这使得在100 ms内芯吸表面2的芯吸量(约0.63 μL)远大于芯吸表面1, 提升约140%.由图 4可见, 芯吸表面1和芯吸表面2在初始阶段芯吸量的增量趋向于线性变化, 因此取初始芯吸阶段根据公式(2)可计算得到表面的初始芯吸通量.芯吸表面2的初始芯吸通量约为20 μL/(mm2·s), 相比于芯吸表面1提升了约50% (约13 μL/(mm2·s)), 定量地说明表面芯吸能力随着腐蚀时间的延长而增强.
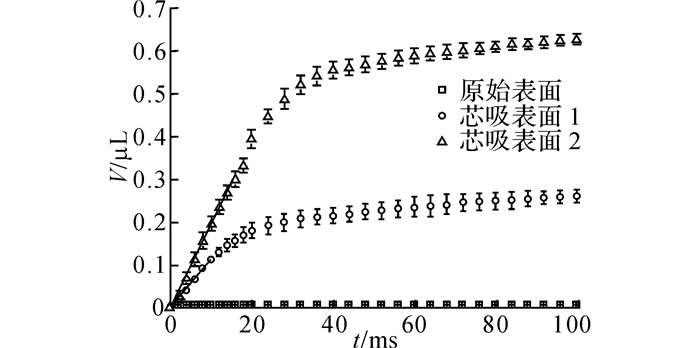
|
图 4 芯吸量曲线 Fig. 4 Transient variations of wicking volume |
如图 5所示为3种表面的淬火冷却曲线图.对于原始表面而言, 随着表面温度降低淬火冷却速率逐渐减慢.当θs≈235 ℃时, 冷却速率迅速加快, 最大约为85 ℃/s.随着表面温度逐渐接近饱和水温, 其冷却速率又逐渐下降, 整个冷却过程用时约57 s.与原始表面相比, 芯吸表面1在初始阶段的冷却速率更快, 且随着表面温度降低逐渐增大, 最大约为110 ℃/s.随后芯吸表面1的冷却速率同样变慢, 相比于原始表面, 冷却时间缩短约60% (约23 s).芯吸性更强的芯吸表面2进入饱和液态水后, 冷却速率远大于前两者.与芯吸表面1相同, 其冷却速率随表面温度降低而逐渐增大, 最大约为160 ℃/s.芯吸表面2的整个冷却过程仅用时约11 s, 相比于原始表面缩短约80%.随着表面芯吸性的增强, 淬火冷却速率加快, 总冷却时间显著缩短.
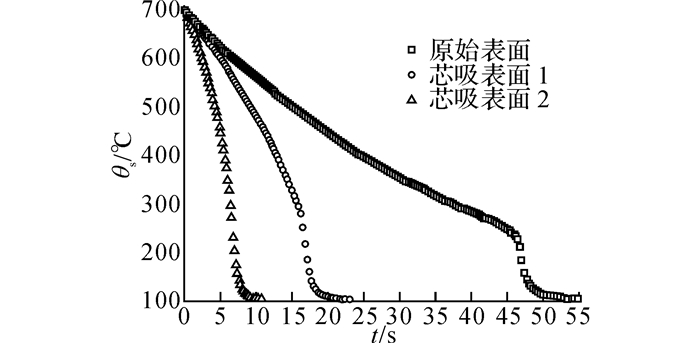
|
图 5 淬火冷却曲线 Fig. 5 Quenching curves |
为进一步分析淬火过程中的传热特性, 3种表面的沸腾传热曲线如图 6所示.原始表面依次经历了膜态沸腾、过渡沸腾以及核态沸腾, 得到的是一条典型的沸腾曲线.原始表面的最小热流密度Leidenfrost点(LFP)出现在Δθs≈170 ℃处, 随后沸腾曲线斜率由正转负, 标志着表面由膜态沸腾进入过渡沸腾阶段.在Δθs≈140 ℃ (如图 6中A点所示)前后, 曲线斜率发生明显变化.文献[14]中将此点定义为临界过渡点(CTP), 并根据该点前后“点接触”和“面接触”特征的不同将过渡沸腾区分为过渡-膜态沸腾和过渡-核态沸腾这2个阶段.在Δθs≈90 ℃时, 原始表面达到CHF, 约为560 kW·m-2.

|
图 6 沸腾传热曲线 Fig. 6 Boiling curves |
芯吸表面1在Δθs≈530 ℃处(B点)沸腾曲线斜率由正转负.如果直接按照斜率推断, 表示表面由膜态沸腾进入过渡沸腾阶段.然而, 随着表面过热度继续降低, 当Δθs≈480 ℃时(C点)曲线斜率重新变为正值, 意味着表面再次进入膜态沸腾阶段.下文将借助对淬火过程的可视化观察对这一现象进行分析判断.在芯吸表面1的沸腾曲线中也出现了CTP(D点, Δθs≈200 ℃), 然而其过渡-膜态沸腾的温区范围远大于原始表面.在Δθs≈120 ℃时, 芯吸表面1达到CHF(约720 kW·m-2), 较之原始表面提高约30%.
如图 6所示, 芯吸表面2在淬火开始后直接进入过渡沸腾阶段.与前两者不同的是, 芯吸表面2的过渡沸腾曲线斜率变化平缓, 因此难以判断是否存在CTP.芯吸表面2的CHF(约1 030 kW·m-2)出现在Δθs ≈ 130 ℃处, 远高于原始表面(提高约84%).显然, 采用芯吸表面可以大幅度提高过渡沸腾阶段的传热和CHF, 从而显著提升淬火冷却速率.
2.4 淬火过程可视化分析原始表面的汽膜演化过程如图 7(a)所示, 分别为其在初始时刻、LFP、过渡沸腾和CHF时的汽膜形貌.在初始时刻, 原始表面被一层稳定的汽膜所覆盖, 汽膜厚度随着表面过热度降低而逐渐减小.在Δθs≈170 ℃时表面到达LFP, 此时表面汽膜开始波动且波动幅度逐渐增大, 导致饱和液态水与原始表面发生点接触.此时球体表面温度依旧远大于饱和水温, 因此点接触的去离子水瞬间汽化体积增大, 在表面上发生剧烈的过渡沸腾.随着表面过热度继续降低, 固液接触方式逐渐由点接触转变为面接触(如图 7(a)Δθs≈130 ℃时所示), 表面由过渡-膜态沸腾进入过渡-核态沸腾阶段.

|
图 7 汽膜演化过程图 Fig. 7 Evolution process diagram of vapor film |
如图 7(b)所示, 相比于原始表面, 芯吸表面1在初始时刻(如图 6所示B点)即被一层不稳定的汽膜所覆盖.这是由于表面粗糙度增大, 轮廓峰顶与谷底之间距离增大使得峰顶温度小于谷底, 产生局部冷却作用[15]导致表面汽膜更容易破裂.另一方面, 汽膜内蒸汽被吸收进入表面芯吸性结构内[15], 减小了汽膜整体厚度, 也将造成沸腾过程提前达到LFP.由图可知, 芯吸表面1在Δθs≈460 ℃时与周围液体间存在着固液点接触现象, 此时表面应处于过渡沸腾阶段.这一现象表明, 芯吸表面1在Δθs≈530 ℃ (B点)时即达到LFP.表面固液点接触频率随着过热度降低而逐渐加快, 且在表面芯吸性的影响下接触面积不断增大, 导致芯吸表面1的CTP (Δθs≈200 ℃)相较于原始表面提早出现.在Δθs ≈ 200 ℃时, 饱和液体水与表面大范围接触产生大量气泡, 其中部分气泡在成形后迅速脱离表面, 另外部分气泡生长变大后聚集合并在一起形成大块汽膜包裹在表面上.随着表面过热度继续降低, 在Δθs≈120 ℃时, 表面达到CHF.
与前两者不同的是, 芯吸表面2进入沸腾池后直接周围饱和液态水发生点接触, 标志着表面进入过渡沸腾阶段.因为芯吸性更强的芯吸表面2在与液体接触的瞬间能抽吸更多液体进入表面芯吸性结构内, 所以表面即使在高温状态下(如图 7(c)中Δθs≈600 ℃和Δθs≈420 ℃时所示)也能与液体发生较大面积的接触, 使得其沸腾曲线在初始阶段即保持着较大的斜率并缓慢增大.与芯吸表面1相同的是, 高温芯吸表面2与饱和液态水接触后, 同样产生大量气泡而不是如原始表面一般产生大块汽膜.到Δθs≈300 ℃时, 表面与周围液体大范围接触后产生的气泡仅有极少部分合并聚集形成小块汽膜覆盖在表面上.这意味着虽然在芯吸表面2的过渡沸腾曲线中难以明确指定CTP, 但是在其过渡沸腾阶段仍然存在着点接触和面接触2种不同的固液接触方式.
综上所述, 饱和液态水与高温的芯吸表面接触后所产生的大量气泡会迅速脱离球体表面, 使得液态水和芯吸表面的接触面积增大, 表面传热性能迅速增强.部分与芯吸表面接触的液体在毛细力的作用下被抽吸进入表面芯吸性结构内, 并侧向流入周围未润湿区域, 进一步增大了有效的固液接触面积.同时, 吸入的液体在高温表面芯吸结构内的瞬间局部蒸发将导致周围液体剧烈波动, 抑制了稳定膜态沸腾的出现.因此, 构建微尺度的表面芯吸结构是进一步增强沸腾传热性能的有效手段.
3 结论(1) 采用化学腐蚀法制备了不锈钢芯吸表面, 测量了原始表面和芯吸表面在水中的冷却曲线.
(2) 芯吸表面的淬火冷却时间相较于原始表面明显缩短, 芯吸表面的临界热流密度与原始表面相比较提高了约84%.
(3) 表面芯吸性可以有效增大固液接触面积并加剧汽膜波动, 抑制稳定膜态沸腾的出现, 从而显著强化了过渡态沸腾传热.
| [1] |
BUONGIORNO J. Can corrosion and CRUD actually improve safety margins in LWRs?[J]. Annals of Nuclear Energy, 2014, 63(1): 9-21. |
| [2] |
VOROBYEV A Y, GUO C. Metal pumps liquid uphill[J]. Applied Physics Letters, 2009, 94(22): 986. |
| [3] |
COURBIN L, BIRD J C, REYSSAT M, et al. Dynamics of wetting:from inertial spreading to viscous imbibition[J]. Journal of Physics Condensed Matter, 2009, 21(46): 464127. DOI:10.1088/0953-8984/21/46/464127 |
| [4] |
LITER S G., KAVIANY M. Pool-boiling CHF enhancement by modulated porous-layer coating:theory and experiment[J]. International Journal of Heat and Mass Transfer, 2001, 44(22): 4287-4311. DOI:10.1016/S0017-9310(01)00084-9 |
| [5] |
WASHBURN E W. The Dynamics of Capillary Flow[J]. Physical Review, 1921, 17(3): 273-283. DOI:10.1103/PhysRev.17.273 |
| [6] |
纪峰, 李娜, 宋冉风, 等. 纺织材料芯吸性能建模预测研究进展[J]. 纺织学报, 2016, 37(9): 162-168. JI Feng, LI Na, SONG Ran-feng, et al. Review of studies on textile wicking modeling[J]. Journal of Textile Research, 2016, 37(9): 162-168. |
| [7] |
KIM H D, KIM M H. Effect of nanoparticle deposition on capillary wicking that influences the critical heat flux in nanofluids[J]. Applied Physics Letters, 2007, 91(1): 718. |
| [8] |
HENDRICKS T J, KRISHNAN S, CHIOI C, et al. Enhancement of pool-boiling heat transfer using nanostructured surfaces on aluminum and copper[J]. International Journal of Heat and Mass Transfer, 2010, 53(15-16): 3357-3365. DOI:10.1016/j.ijheatmasstransfer.2010.02.025 |
| [9] |
RAHMAN M M, OLCEROGLU E, MCCARTHY M. Role of wickability on the critical heat flux of structured superhydrophilic surfaces[J]. Langmuir, 2014, 30(37): 11225-11234. DOI:10.1021/la5030923 |
| [10] |
LI L, BREEDVELD V, HESS D W. Creation of superhydrophobic stainless steel surfaces by acid treatments and hydrophobic film deposition[J]. ACS Applied Materials and Interfaces, 2012, 4(9): 4549. DOI:10.1021/am301666c |
| [11] |
AHN H S, PARK G, KIM J M, et al. The effect of water absorption on critical heat flux enhancement during pool boiling[J]. Experimental Thermal and Fluid Science, 2012, 42(5): 187-195. |
| [12] |
FAN L W, LI J Q, LI D Y, et al. Regulated transient pool boiling of water during quenching on nanostructured surfaces with modified wettability from superhydrophilic to superhydrophobic[J]. International Journal of Heat and Mass Transfer, 2014, 76(6): 81-89. |
| [13] |
BURGGRAF O R. An Exact Solution of the Inverse Problem in Heat Conduction Theory and Applications[J]. ASME Journal of Heat Transfer, 1964, 86(3): 373. DOI:10.1115/1.3688700 |
| [14] |
FAN L W, LI J Q, ZHANG L, et al. Pool boiling heat transfer on a nanoscale roughness-enhanced superhydrophilic surface for accelerated quenching in water[J]. Applied Thermal Engineering, 2016, 109: 630-639. DOI:10.1016/j.applthermaleng.2016.08.131 |
| [15] |
KANG J Y, LEE G C, KAVIANY M, et al. Minimum film-boiling quench temperature increase by CuO porous-microstructure coating[J]. Applied Physics Letters, 2017, 110(4): 043903. DOI:10.1063/1.4974923 |
| [16] |
FATEHI M, KAVIANY M. Analysis of levitation of saturated liquid droplets on permeable surfaces[J]. International Journal of Heat and Mass Transfer, 1990, 33(5): 983-994. DOI:10.1016/0017-9310(90)90079-A |



