2. 中电建路桥集团有限公司, 北京 100048;
3. 华东电力设计院, 上海 200333;
4. 北京科技大学 土木与环境工程学院, 北京 100083
2. Power China Road Bridge Group Linited Compang, Beijing 100048, China;
3. East China Electric Power Design Institute, Shanghai 200333, China;
4. School of Civil and Environmental Engineering, Beijing University of Science and Technology, Beijing 100083, China
近年来, 我国公路、铁路建设事业高速发展, 隧道建设中常遭遇硬石膏岩层.在地下水作用下, 硬石膏岩中CaSO4水化成CaSO4·2H2O, 导致体积膨胀[1-2].理论上, 硬石膏岩水化膨胀后, 体积最大可增加61%, 造成隧道围岩位移增大, 可导致垮塌和侵限等事故, 严重影响隧道稳定性[3].因此有必要探究硬石膏膨胀性对围岩位移的影响.
围岩位移是隧道工作状态表征和控制的重要指标[4], 在进行围岩位移理论求解分析时, 通常将各类隧道假设为圆形, 并以轴对称平面应变问题进行处理, 形成了具有实用意义的圆形轴对称理论.
圆形轴对称理论广泛应用于各类隧道围岩位移解析解研究, 并不断得到深化, 张宇纶[5]考虑应变硬化及软化特性, 得到圆形隧道的弹塑性解;张良辉等[6]考虑了围岩应变软化、剪胀特性及蠕变作用, 得到相应的弹塑黏性解析解;吴建勋等[7]建立了考虑软化效应的隧道自稳时间评价模型.基于圆形轴对称模型的理论解, 多针对弹性、弹塑性或黏弹性围岩, 少有针对膨胀类围岩.
缪协兴受温度应力场理论启发, 提出湿度应力场理论[8], 为膨胀类围岩隧道解析模型提供了严谨的数学、力学理论基础.朱珍德[9]提出了基于湿度应力场理论的膨胀岩弹塑性本构模型;王凯等[10]基于湿度应力场理论, 修正并推导了差分格式下的弹塑性膨胀本构模型.
湿度应力场理论多用于泥岩、页岩或黏土岩类含强吸水矿物的膨胀岩.相较于这类岩石, 硬石膏岩膨胀机理更复杂, 膨胀时间更漫长, 它膨胀性的时变特征不能被忽略.本文基于湿度应力场理论, 考虑膨胀性的时变特征, 建立含时间效应的隧道硬石膏围岩的弹-膨胀解析模型, 并应用于礼让隧道硬石膏段.分析了模型各参数对隧道临空面位移影响规律及其权重, 得出一些对硬石膏隧道工程设计和施工具有指导意义的结论.
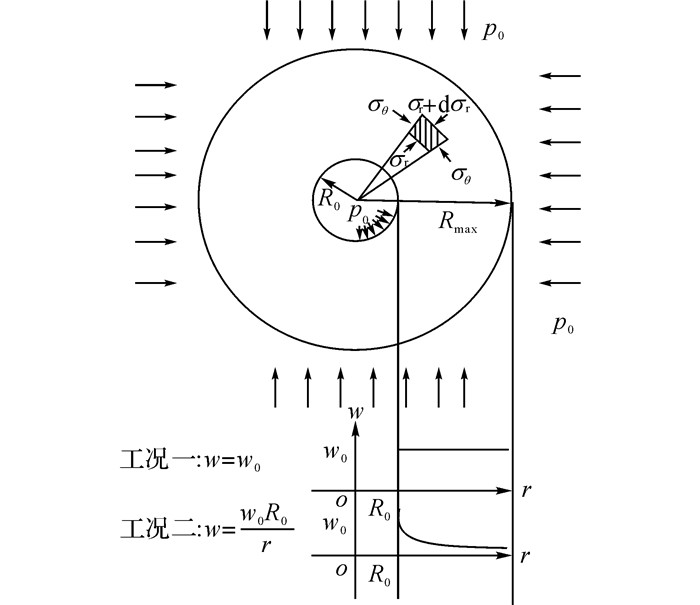
1 模型建立 1.1 圆形轴对称理论1) 基本假定
经典的圆形轴对称模型示意图如图 1所示, 包括如下假设:
|
图 1 圆形隧道示意图 Fig. 1 Sketch of circular tunnel |
a) 隧道断面为圆形, 半径为R0, 外边界固定, 且半径记为Rmax, (本文Rmax=100 m);
b) 隧道围岩为连续、均匀的各向同性介质体;
c) 隧道地应力为p0且隧道内壁受到均匀分布的支护抗力ps.
2) 基本方程
对于圆形轴对称模型, 其平面应变问题的基本方程如下所示.
平衡微分方程:
| $ \frac{{{\rm{d}}{\sigma _{\rm{r}}}}}{{{\rm{d}}r}} + \frac{{{\sigma _{\rm{r}}} - {\sigma _\theta }}}{r} = 0. $ | (1) |
几何方程:
| $ \left. \begin{array}{l} {\varepsilon _{{ { θ} }}} - \frac{{{u_{\rm{r}}}}}{r} = 0,\\ {\varepsilon _{\rm{r}}} - \frac{{{\rm{d}}{u_{\rm{r}}}}}{{{\rm{d}}r}} = 0. \end{array} \right\} $ | (2) |
本构方程:
| $ \left. \begin{array}{l} {\varepsilon _{{ { θ} }}} = \frac{{1 - {\nu ^2}}}{E}\left( {{\sigma _\theta } - \frac{\nu }{{1 - \nu }}{\sigma _{\rm{r}}}} \right),\\ {\varepsilon _{\rm{r}}} = \frac{{1 - {\nu ^2}}}{E}\left( {{\sigma _{\rm{r}}} - \frac{\nu }{{1 - \nu }}{\sigma _\theta }} \right). \end{array} \right\} $ | (3) |
式中:εθ为环向应变, εr为径向应变, σr为径向应力, σθ为环向应力, E为弹性模量, ν为泊松比, ur为径向位移, r为围岩到隧道圆心径向距离.由以上方程, 代入边界条件, 可解得隧洞应力分布和位移分布.
1.2 含时间效应的硬石膏岩弹-膨胀本构1) 硬石膏弹-膨胀本构模型
缪协兴等[8, 11]得出了黏土类膨胀岩膨胀本构关系, 如式(4)所示.
| $ {\varepsilon _{{\rm{tot}}}} = {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{s}}} = \frac{{{\sigma _{\rm{e}}}}}{E} + \alpha \Delta w. $ | (4) |
式中:εtot为湿度条件下的总应变, εe为弹性应变部分, εs为膨胀应变部分, σe为弹性应力, α为线膨胀系数, Δw为湿度变化.
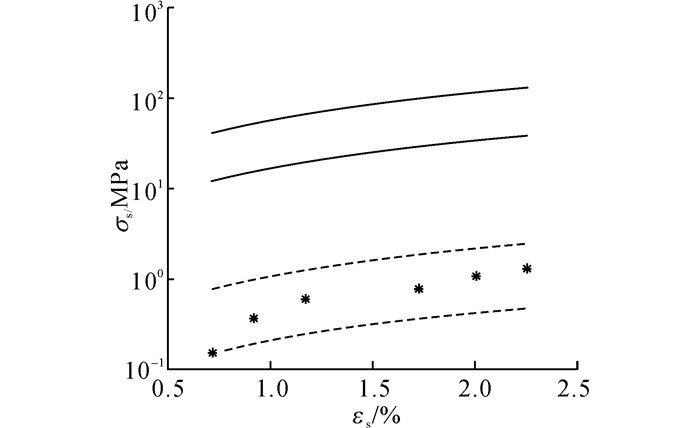
式(4)中, 潜在假设是:围岩膨胀阶段的变形模量与自身弹性模量相等(等式右半部分), 即εs=EαΔw/E.然而, 膨胀试验结果表明, 这个假设并不适合于硬石膏岩.如图 2所示, 散点为试验数据, 而实线纵坐标所示应力范围, 是由膨胀应变与弹性模量之积而得.可见该计算结果远大于试验所得结果.因此, 结合文献[12], 把膨胀试验所得的膨胀应力与膨胀应变的比值, 定义为膨胀模量, 记作Es.则硬石膏相应的膨胀本构关系变为式(5).由该式计算的膨胀应力范围如图 2中虚线范围所示.可见, 改进后的膨胀本构模型更能描述试验结果.
|
图 2 不同变形模量膨胀应力计算值与实测值对比 Fig. 2 Comparison of different deformation modulus employed for estimating swelling stress |
| $ {\varepsilon _{{\rm{tot}}}} = {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{s}}} = \frac{{{\sigma _{\rm{e}}}}}{{{E_{\rm{e}}}}} + \frac{{{E_{\rm{s}}}\alpha \Delta w}}{{{E_{\rm{e}}}}}. $ | (5) |
式中:Ee代替E为弹性模量, Es为膨胀模量.
2) 硬石膏吸水率时变模型
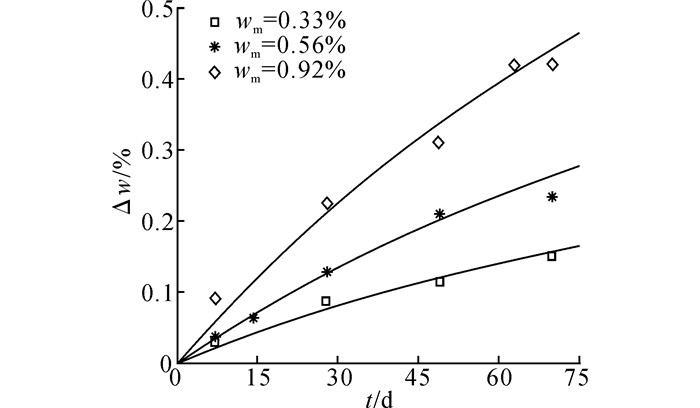
由于地下水在岩层中分布具有不均匀性, 导致不同含水量下围岩吸水特性具有一定差异[13-14].本文采用100 mm×50 mm高径的标准试件, 进行40 ℃烘干.将试件分成3组, 每组至少4个试件, 组间设置初始含水量不同, 组内设置浸泡时间不同[15-16], 测其含水率, 以此研究硬石膏吸水特性, 结果如图 3所示.吸水率与时间的相对关系式如下:
|
图 3 吸水特性试验所得硬石膏吸水时变曲线 Fig. 3 Humidity absorption over time obtained from swelling versus water absorption test |
| $ \Delta w = {w_t} - {w_{\rm{i}}} = \left( {{w_{\rm{m}}} - {w_{\rm{i}}}} \right)\left[ {1 - \exp \left( { - at} \right)} \right]. $ | (6) |
式中:t为时间, wt为岩石在t时刻的吸水率, wi为岩石初始含水量, wm为岩石饱和含水量, a为一与岩石吸水性能有关的系数.
联立式(5)和(6), 可得含时间效应的硬石膏岩膨胀本构模型如下:
| $ {\varepsilon _{{\rm{tot}}}} = {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{s}}} = \frac{{{\sigma _{\rm{e}}}}}{{{E_{\rm{e}}}}} + \frac{{{E_{\rm{s}}}\alpha \left( {{w_{\rm{m}}} - {w_{\rm{i}}}} \right)\left[ {1 - \exp \left( { - at} \right)} \right]}}{{{E_{\rm{e}}}}}. $ | (7) |
该本构在平面应变问题中的极坐标表达式如下:
| $ \begin{array}{l} {\varepsilon _{\rm{r}}} = \frac{{1 - {\nu ^2}}}{{{E_{\rm{e}}}}}\left( {{\sigma _{\rm{r}}} - \frac{\nu }{{1 - \nu }}{\sigma _\theta }} \right) + \\ \;\;\;\;\;\;\frac{{{E_{\rm{s}}}}}{{{E_{\rm{e}}}}}\left( {1 + \nu } \right)\alpha W\left[ {1 - \exp \left( { - at} \right)} \right]. \end{array} $ | (8) |
| $ \begin{array}{l} {\varepsilon _\theta } = \frac{{1 - {\nu ^2}}}{{{E_{\rm{e}}}}}\left( {{\sigma _\theta } - \frac{\nu }{{1 - \nu }}{\sigma _{\rm{r}}}} \right) + \\ \;\;\;\;\;\;\frac{{{E_{\rm{s}}}}}{{{E_{\rm{e}}}}}\left( {1 + \nu } \right)\alpha W\left[ {1 - \exp \left( { - at} \right)} \right]. \end{array} $ | (9) |
式中:W为地下水分布函数.
1.3 地下水分布函数目前地下水量分布形式多通过现场测获得, 或在计算时对其进行假设[17].在此, 假设围岩地下水分布函数W是r的函数, 选取2种常见工况, 分别为:各处围岩均匀吸水(工况一), 围岩吸水随临空面距离增加而减少(工况二), 具体表达式如下:
| $ \left. \begin{array}{l} W = {w_0} = {w_{\rm{m}}} - {w_{\rm{i}}}\;\;\;\;\;\;\left( {工况一} \right),\\ W = \frac{{{w_0}{R_0}}}{r} = \frac{{\left( {{w_{\rm{m}}} - {w_{\rm{i}}}} \right){R_0}}}{r}\;\;\left( {工况二} \right). \end{array} \right\} $ | (10) |
式中:w0为r=R0处围岩吸水率, 反映其吸水饱和后的含水量变化.
1.4 边界条件对隧道进行开挖及支护后, 其临空面径向应力等于支护力;外边界处, 环向应力为膨胀应力与地应力之和.
| $ \left. \begin{array}{l} {\sigma _\theta } = {p_0} + {E_{\rm{s}}}{\varepsilon _{\rm{s}}},\\ {\sigma _{\rm{r}}} = {p_{\rm{s}}}. \end{array} \right\} $ | (11) |
由式(1)、(2)、(8)、(9), 可得解析解通解的表达式如下:
| $ {\sigma _{\rm{r}}} = \frac{{{E_{\rm{e}}}\alpha }}{{\left( {1 - {\nu ^2}} \right){r^2}}}\left( {\int_{{R_0}}^r {\frac{{{E_{\rm{s}}}}}{{{E_{\rm{e}}}}}Wr{\rm{d}}r} + A} \right) + C. $ | (12) |
| $ {\sigma _\theta } = \frac{{E\alpha }}{{\left( {1 - {\nu ^2}} \right){r^2}}}\left( {\int_{{R_0}}^r {\frac{{{E_{\rm{s}}}}}{{{E_{\rm{e}}}}}Wr{\rm{d}}r} + A - \frac{{{E_{\rm{s}}}}}{{{E_{\rm{e}}}}}W{r^2}} \right) + C. $ | (13) |
| $ {u_{\rm{r}}} = \frac{{1 - {\nu ^2}}}{{{E_{\rm{e}}}}}\left( {{\sigma _\theta } - \frac{\nu }{{1 - \nu }}{\sigma _{\rm{r}}}} \right)r + \alpha \left( {1 + \nu } \right)\frac{{{E_{\rm{s}}}}}{{{E_{\rm{e}}}}}Wr. $ | (14) |
式中:A, C为通解参数, 可通过代入地下水分布函数(式(10))和边界条件(式(11))确定.
2 应用示例 2.1 模型参数重庆梁忠高速礼让隧道硬石膏段为三心圆曲墙结构, 拱高7.05 m, 上半圆5.45 m半径, 洞径宽10.66 m, 如图 4所示.隧道采用复合式衬砌支护, 模拟用各参数取值如表 1所示.

|
图 4 礼让隧道主洞断面内轮廓图 Fig. 4 Inner contour of Lirang Tunnel |
| 表 1 模拟用参数取值 Table 1 Values employed for simulation |
1) 不同时间不同工况结果
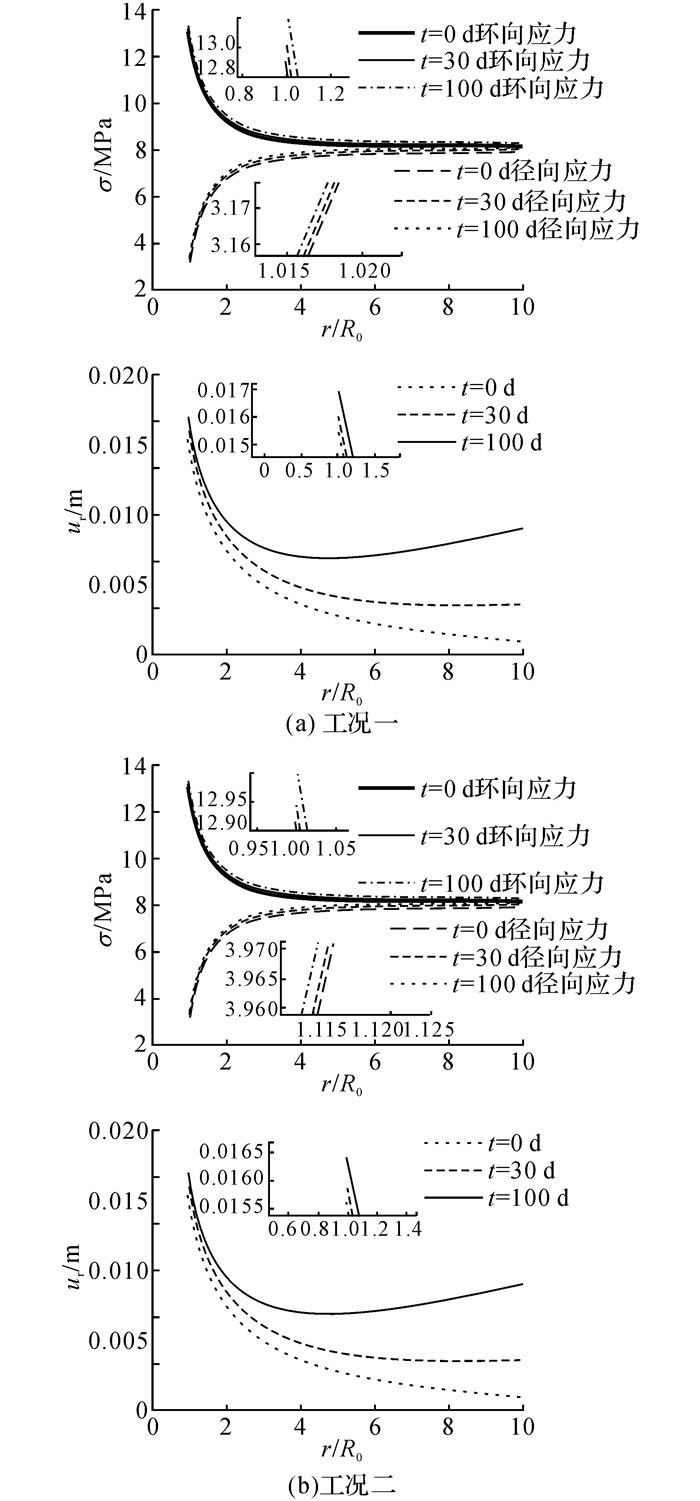
根据式(10)所示的2种工况, 保持相同的隧道洞径R0=10 m, 外界Rmax=100 m, 得隧道未开挖、隧道开挖30 d、开挖100 d后围岩应力、位移与径向距离r的关系, 如图 5所示.横坐标r/R0为隧道洞径倍数, 以此表征隧道临空面径向影响范围.2种工况下, 对于同一位置的围岩, 其径向应力、环向应力及径向位移均随着时间的增加而增大.距隧道越远, 受开挖影响越小, 相应位移较临空面更小.
|
图 5 各工况下隧道应力场及位移场变化 Fig. 5 Stress field and displacement field of tunnel under different conditions |
2) 相同时间不同支护力结果
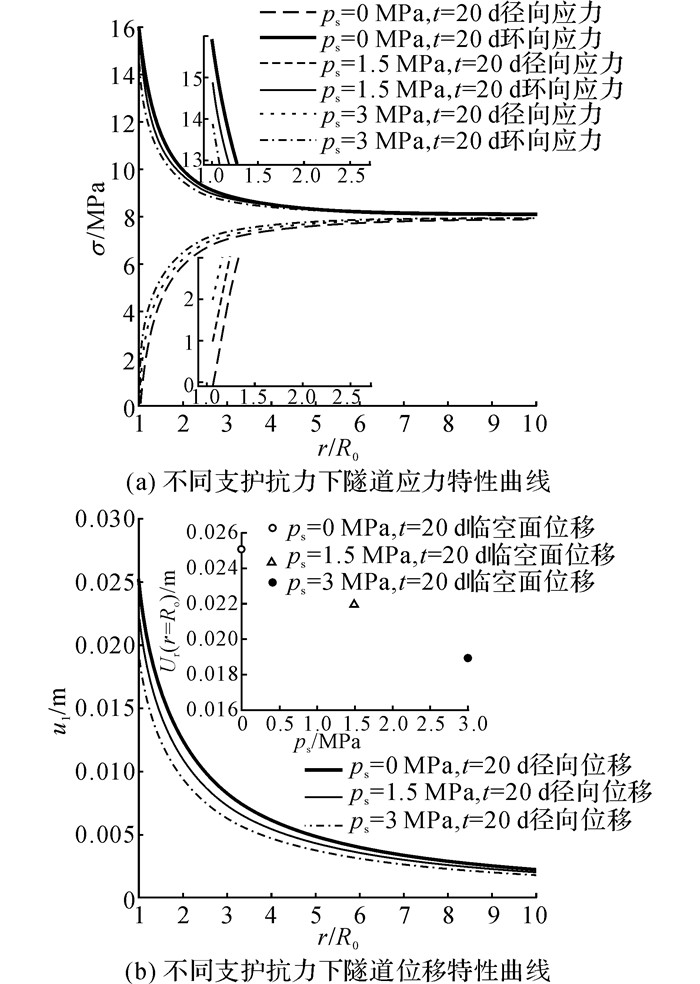
基于表 1中参数, 在工况二条件下, 保持相同时间(t=20 d), 代入不同的支护抗力ps, 得隧道围岩应力及径向位移分布, 如图 6所示.由图可知, 临空面附近围岩径向应力、径向位移随ps增大而减小, 环向应力随之增大.这表明实际施工过程中, 支护材料及支护方式越好, 临空面位移越小, 隧道也越稳定.模型所得临空面附近围岩受不同支护抗力影响结果与实际情况一致.
|
图 6 不同支护抗力对隧道应力场及位移场影响 Fig. 6 Stress field and displacement field of tunnel under different support stress |
对于本文理论模型, 围岩径向位移由隧道开挖变形及其自身膨胀变形2部分组成, 且围岩与临空面距离一定时, 环向应变越大, 隧道径向位移越大.在隧道2~3倍洞径范围内, 围岩径向位移主要受开挖变形影响;该范围外围岩的径向位移则受自身膨胀影响更大.因此, 在工况二条件下, 隧道深部围岩径向位移很小.
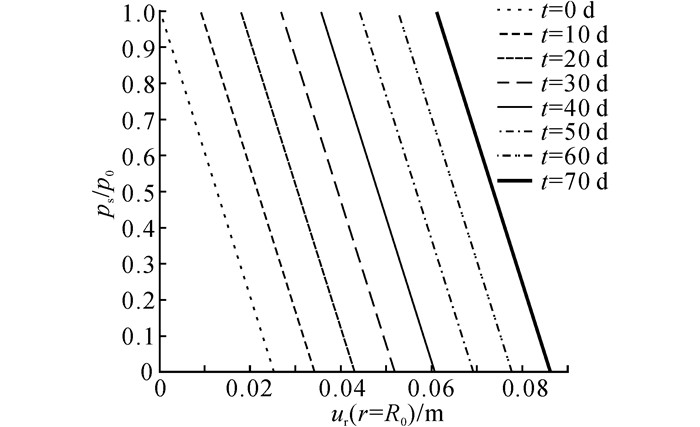
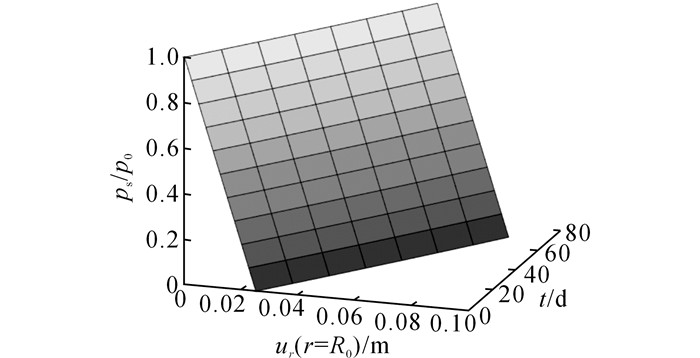
2.3 硬石膏围岩响应曲面及位移特性曲面围岩响应曲线(Ground reaction curve, GRC)可以反映支护力与隧道周边位移的关系[18].根据以上分析, 不同支护应力及膨胀时间可以得到不同的临空面径向位移, 如图 7所示.在其基础上考虑时间的连续性, 可得硬石膏围岩响应曲面(Ground reaction surface, GRS), 如图 8所示.根据GRS, 当支护条件确定后, 结合位移特性曲线(图 6(a)), 还能得到不同时间, 各个位置处的径向位移, 即位移特性曲面(Displacement characteristic surface, DCS), GRS及DCS能够很好地体现围岩整体稳定性及其与支护结构的相互作用随时间的变化规律.由于不同参数对GRS和DCS的影响不同.因此, 针对工况二, 逐个分析表 1中各参数对它们的影响.分析过程中, 其余参数采用基准值, 分析结果如下:
|
图 7 不同膨胀时间硬石膏围岩响应曲线 Fig. 7 GRCs of anhydrite rock with different swelling time |
|
图 8 硬石膏围岩响应曲面 Fig. 8 GRS of anhydrite rock |
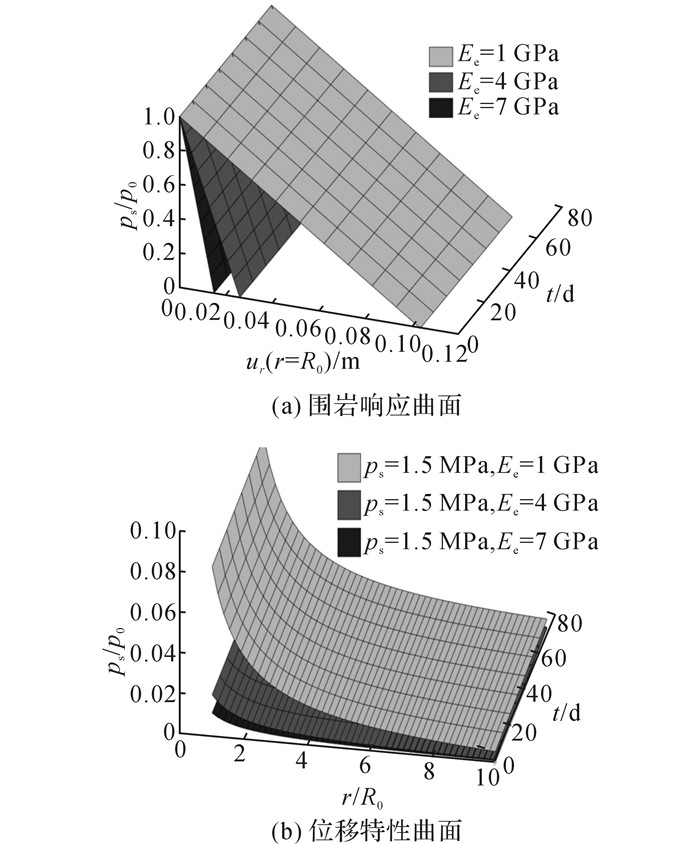
1) 弹性模量对GRS和DCS影响
如图 9(a)所示为不同弹性模量下的硬石膏围岩响应曲面, 在同一时间及支护作用条件下, 隧道临空面位移及其变化速率均随着弹性模量增大而减小, 围岩响应曲面整体向位移零点偏移.如图 9(b)所示为1.5 MPa支护应力下相应的DCS.由图知, 临空面附近位移受弹性模量变化影响最大, 离临空面径向距离越远, 位移所受影响也越小.
|
图 9 不同弹性模量硬石膏围岩响应曲面及位移特性曲面 Fig. 9 GRS and DCS of anhydrite rock with different Ee |
2) 膨胀模量对GRS和DCS影响
如图 10(a)所示为不同膨胀模量下的GRS.可知, 在同一时间及支护条件下, 隧道临空面位移及其变化速率均随膨胀模量增大而增大, 围岩响应曲面整体向远离位移零点处偏移.图 10(b)为1.5 MPa支护应力下相应的DCS, 可知, 临空面位移受膨胀模量变化影响最小, 围岩与隧道临空面径向距离越远, 位移所受影响越大.
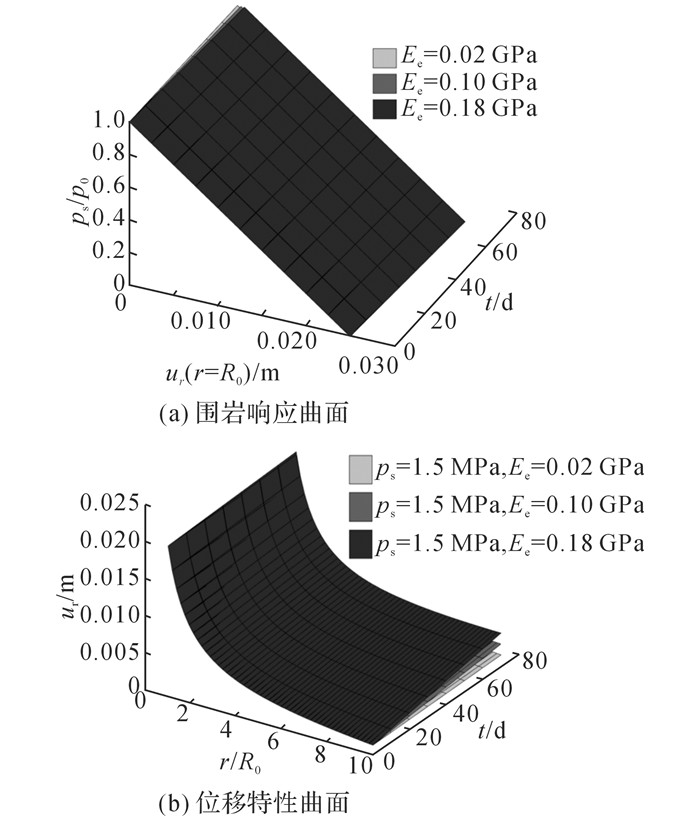
|
图 10 不同膨胀模量硬石膏围岩响应曲面及位移特性曲面 Fig. 10 GRS and DCS of anhydrite rock with different Es |
3) 吸水系数对GRS和DCS影响
如图 11(a)所示为不同吸水系数下的GRS.在同一时间及支护作用条件下, 隧道临空面位移及其变化速率均随着吸水系数增大而增大, 围岩响应曲面整体向远离位移零点处偏移.如图 11(b)所示为1.5 MPa支护应力下相应的DCS, 临空面受吸水系数变化影响最小, 围岩与隧道临空面径向距离越远, 其位移所受影响也越大.
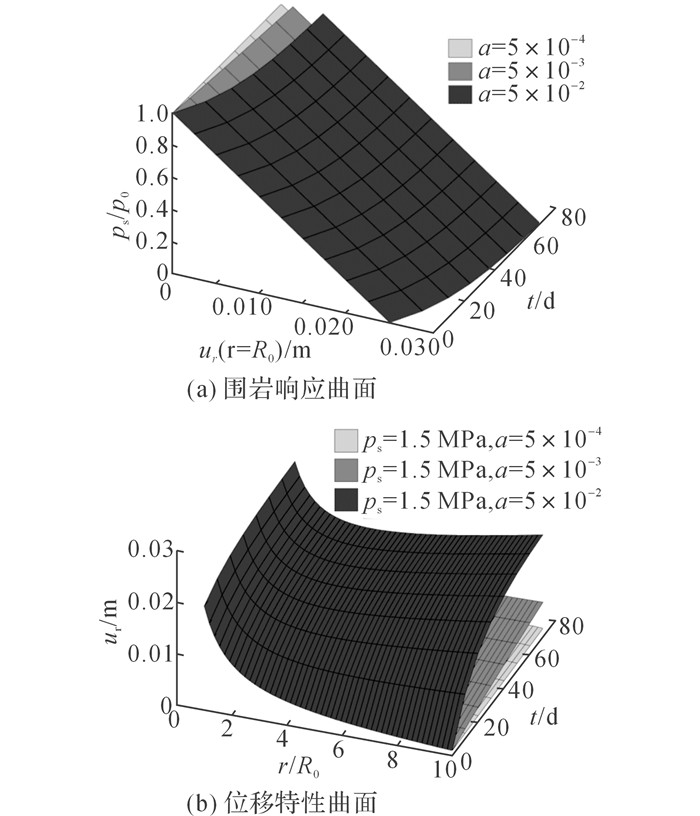
|
图 11 不同吸水性系数硬石膏围岩响应曲面及位移特性曲面 Fig. 11 GRS and DCS of anhydrite rock with different a |
4) 线膨胀系数对GRS和DCS影响
如图 12(a)为线膨胀系数对GRS的影响.在同一时间及支护作用条件下, 隧道临空面位移及其变化速率均随着线膨胀系数增大而增大, 围岩响应曲面整体向远离位移零点处偏移.如图 12(b)所示为1.5 MPa支护应力下相应的DCS, 临空面受线膨胀系数变化影响最小, 围岩与隧道临空面径向距离越远, 其位移所受影响也越大.
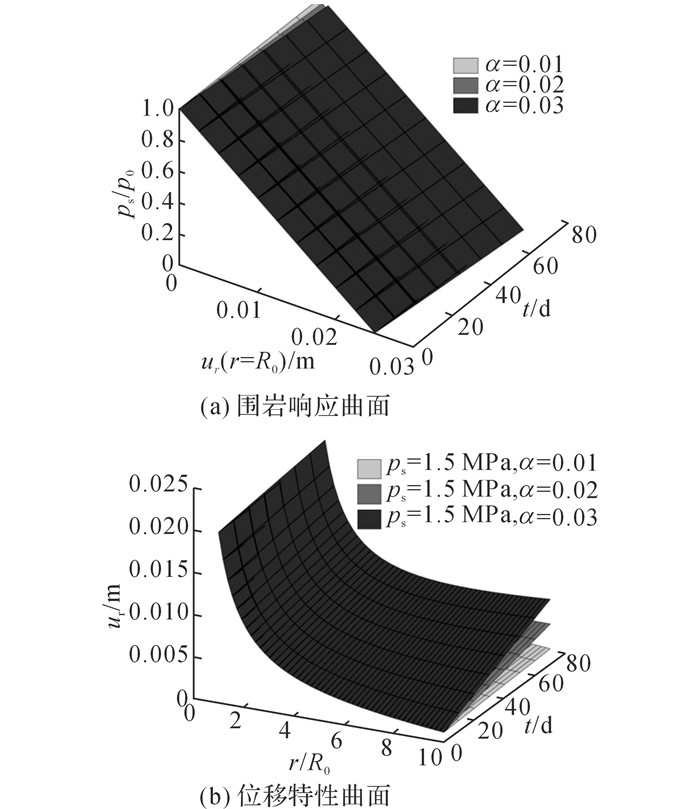
|
图 12 不同线膨胀系数硬石膏围岩响应曲面及位移特性曲面 Fig. 12 GRS and DCS of anhydrite rock with different α |
5) 开挖洞径对GRS和DCS影响
如图 13所示为不同隧洞半径硬石膏围岩响应曲面及位移特性曲面图,从图 13(a)中可以看出, 在无支护条件下, 隧道开挖洞径越大, 其初始位移也越大, 且需要更大的支护应力.但由于模型外边界范围固定, 对于工况二, 当隧道洞径增大时, 膨胀相对范围也减小, 当模型外边界范围不固定时, 不同开挖洞径对硬石膏围岩响应曲面的影响也将发生变化.

|
图 13 不同隧洞半径硬石膏围岩响应曲面及位移特性曲面 Fig. 13 GRS and DCS of anhydrite rock with different R0 |
如图 13(b)所示为1.5 MPa支护应力下相应的DCS, 由于外边界范围固定, 相同的外边界条件(Rmax=100 m)下, 临空面附近围岩受洞径变化影响最小, 围岩与隧道临空面径向距离越远, 其位移所受影响也越大.
综上所述, 就围岩自身条件影响而言, 当围岩性越软弱, 围岩响应曲面越向远离位移零点处偏移, 即临空面位移也越大.另外, 实际工程中, 隧道断面越大, 其临空面变形也越大, 可见, 模型所得各参数影响结果与实际情况相符, 表明模型在硬石膏具有自洽性, 且其在围岩稳定性影响因素分析上是适用的, 考虑时间效应的硬石膏围岩响应曲面及位移特性曲面也值得推广应用.
3 敏感性分析 3.1 敏感性分析方法敏感性分析, 能够出鉴别出一个模型的关键输入变量.偏秩相关性系数(PRCC)作为敏感性指标, 能定量各输入参数对模型输出结果的影响[19].在本模型各输入参数研究区间(列于表 1)内, 采用均匀分布函数, 通过拉丁方抽样法, 设置样本容量为1 000[20], 分别计算各参数与隧道临空面位移之间的偏秩相关性系数及其P值[21].
3.2 敏感性分析结果如图 14所示为各参数灵敏性分析散点图, 每一个点代表特定样本值下的临空面位移值, 对于每个子图, 这些点都定性描述了对应参数在其他参数共同变化下, 对临空面位移的影响.从图中可以看出, 临空面位移随Ee, ps, R0增加明显减小, 随Es, w0, a, t增加而明显增加, 而p0和α的影响相对不明显.
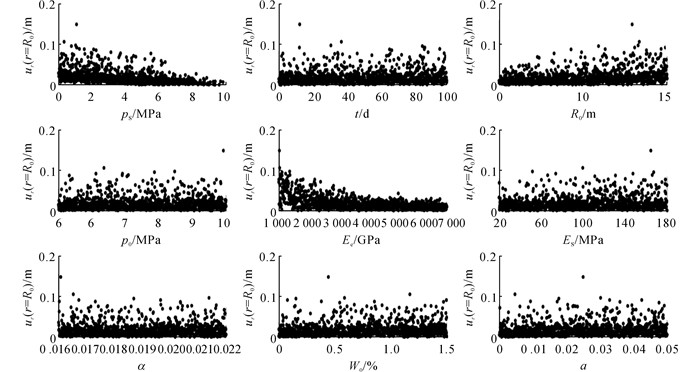
|
图 14 各参数敏感性分析散点图 Fig. 14 Sensitivity analysis scatter plot of parameters |
如图 15所示为各参数偏秩相关系数直方图, 用以定量反映各输入参数对临空面位移的影响.柱状图中数值大的参数, 对临空面位移影响大;柱状图的正负则用以反映参数与结果的定性关系.结果显示, 临空面位移与ps, Ee呈显著负相关;临空面位移与p0, R0, Es, w0, t, a显著正相关;与α也呈正相关, 但显著性相对低, 这与图 9~13所描述的结果一致.
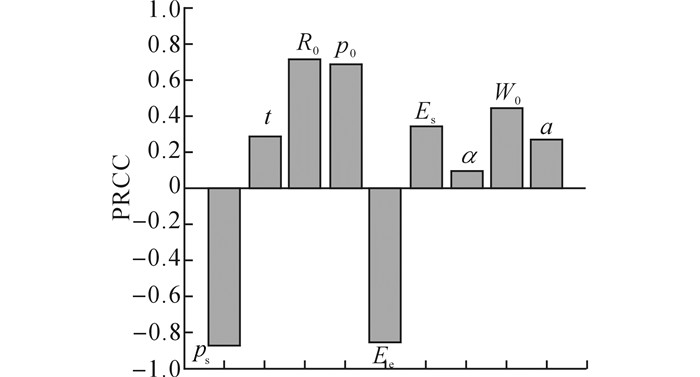
|
图 15 各参数偏秩相关系数直方图 Fig. 15 Partial correlation coefficient histogram ofparameters |
综上所述, 结合表 2结果可知, 各参数对隧道临空面位移影响程度从大到小排列, 依次为:ps, Ee, R0, p0, w0, Es, t, a, α.
| 表 2 各参数隧道临空面位移相关系数及P值 Table 2 Partial correlation coefficient of tunnel face displacement and P value of parameters |
在建模过程中, 本文保持外边界固定, 并采用了式(10)假设的2种工况, 得到各工况下硬石膏岩隧道径向位移与其围岩沿临空面径向距离关系.在实际情况中, 地下水分布形式多样, 若进一步考虑地下水的渗流及蒸发作用, 其分布也能表示为一与时间有关的函数, 文献[22]针对此问题提出了相应的地下水体积平衡方程, 如式(11)所示:
| $ {{\dot V}_{\rm{w}}} = - {E_{\rm{v}}} + I - {{\dot C}_{{\rm{DH}}}}. $ | (15) |
式中:
在后续研究中, 可参考上述方程, 首要分析在何种工况下, 地下水渗流及蒸发作用能对硬石膏膨胀产生明显影响, 再结合对参数Ev、I、
(1) 基于湿度应力场理论, 考虑膨胀的时变特征,建立了含时间效应的硬石膏岩隧道弹-膨胀解析模型.
(2) 当围岩强度越高, 隧道临空面位移越小, 围岩受湿度影响越小, GRS及DCS整体向零点偏移.在同一外边界条件下, 隧道断面越大, 临空面位移受开挖影响越大, 围岩整体受湿度影响越小, 模型计算结果与实际情况相符.
(3) 隧道临空面位移随围岩弹性模量Ee及隧道支护应力ps呈负相关, 临空面位移与隧道洞径R0、膨胀时间t、静水压力p0、围岩膨胀模量Es、吸水性系数a、吸水率w0及线膨胀系数α呈正相关, 且影响程度由高到低排列依次为:ps, Ee, R0, p0, w0, Es, t, a, α.
| [1] |
蒲文明, 陈钒, 任松, 等. 膨胀岩研究现状及其隧道施工技术综述[J]. 地下空间与工程学报, 2016, 12(增刊1): 232-239. PU Wen-Ming, CHEN Fan, REN Song, et al. Research of swelling rock and summarize of tunnel construction[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(suppl 1): 232-239. |
| [2] |
吴建勋, 任松, 欧阳汛, 等. 石膏质岩膨胀性及其对隧道仰拱影响研究[J]. 湖南大学学报:自然科学版, 2018, 45(1): 142-149. WU Jian-xun, REN Song, OU-YANG Xun, et al. Research on swelling of gypsiferous rock and its influence on invert arch of tunnel[J]. Journal of Hunan University:Natural Sciences, 2018, 45(1): 142-149. |
| [3] |
AZAM S. Study on the geological and engineering aspects of anhydrite/gypsum transition in the Arabian Gulf coastal deposits[J]. Bulletin of Engineering Geology & the Environment, 2007, 66(2): 177-185. |
| [4] |
崔芳, 高永涛, 吴顺川. 轴对称荷载作用下圆形隧道围岩变形解析[J]. 北京科技大学学报, 2011, 33(9): 1043-1047. CUI Fan, GAO Yong-tao, WU Shun-chuan. Analytic solutions for surrounding rock mass deformation of circular tunnels subjected to axisymmetric loads[J]. Journal of University of Science and Technology Beijing, 2011, 33(9): 1043-1047. |
| [5] |
张宇纶. 圆形隧道的弹塑性解[J]. 工程力学, 1988, 5(2): 110-119. ZHANG Yu-lun. The elastoplastic solution of circular tunnel[J]. Engineering mechanics, 1988, 5(2): 110-119. |
| [6] |
张良辉, 张清. 隧道围岩位移的弹塑粘性解析解[J]. 岩土工程学报, 1997, 19(4): 66-72. ZHANG Liang-hui, ZHANG Qing. Analytical solution for displacements of Elasto-viscoplastic ground around tunnel[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(4): 66-72. |
| [7] |
吴建勋, 任松, 范金洋, 等. 考虑软化效应的隧道围岩自稳时间解析模型[J]. 工程科学与技术, 2017, 49(3): 68-75. WU Jian-xun, REN Song, FAN Jin-yang, et al. Analytical model for stand-up time of rock mass surrounding tunnel with consideration of softening effect[J]. Adanced Engineering Sciences, 2017, 49(3): 68-75. |
| [8] |
缪协兴, 杨成永, 陈至达. 膨胀岩体中的湿度应力场理论[J]. 岩土力学, 1993, 14(4): 49-55. MIAO Xie-xing, YANG Cheng-yong, CHEN Zhi-da. Humidity stress field theory in swelling rock mass[J]. Rock and Soil Mechanics, 1993, 14(4): 49-55. |
| [9] |
朱珍德, 张爱军, 张勇, 等. 基于湿度应力场理论的膨胀岩弹塑性本构关系[J]. 岩土力学, 2004, 25(5): 700-702. ZHU Zhen-de, ZHANG Ai-jun, ZHANG Yong, et al. Elastoplastic constitutive law of swelling rock based on humidity stress field theory[J]. Rock and Soil Mechanics, 2004, 25(5): 700-702. |
| [10] |
王凯, 刁心宏. 膨胀岩湿度应力场本构模型二次开发研究[J]. 岩石力学与工程学报, 2015, 34(增刊2): 3781-3792. WANG Kai, DIAO Xin-hong. Secondary development study of swelling rock humidity stress field constitutive model[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(suppl 2): 3781-3792. |
| [11] |
郁时炼, 茅献彪, 卢爱红. 湿度场对膨胀岩巷道围岩变形影响规律的研究[J]. 采矿与安全工程学报, 2006, 23(4): 402-405. YU Shi-lian, MAO Xian-biao, LU Ai-hong. Study of deformation rule of swelling rock roadway under the humidity field[J]. Journal of Mining & Safety Engineering, 2006, 23(4): 402-405. |
| [12] |
PIMENTEL E. Existing methods for swelling tests-a critical review[J]. Energy Procedia, 2015, 76(1): 96-105. |
| [13] |
EINSTEIN H. Suggested methods for laboratory testing of argillaceous swelling rocks[J]. International Journal of Rock Mechanics & Mining Science & Geomechanic Abstract, 1989, 26(5): 415-426. |
| [14] |
WEI B X. Experimental research on lateral restricted swelling strain of expansive soil[J]. Journal of Highway & Transportation Research & Development, 2008, 3(1): 10-15. |
| [15] |
任松, 邓高岭, 吴建勋, 等. 石膏岩淡水浸泡软化试验研究[J]. 岩土力学, 2017, 38(4): 943-950. REN Song, DENG Gao-ling, WU Jiian-xun, et al. Immersion tests on gypsum rocks using fresh water[J]. Rock and Soil Mechanics, 2017, 38(4): 943-950. |
| [16] |
任松, 文永江, 姜德义, 等. 泥岩夹层软化试验研究[J]. 岩土力学, 2013, 34(11): 3110-3116. REN Song, WEN Yong-jiang, JIANG De-yi, et al. Experimental research on softening in mudstone interlayer[J]. Rock and Soil Mechanics, 2013, 34(11): 3110-3116. |
| [17] |
付平勇. 膨胀岩中巷道围岩湿度场相似材料模型试验研究[D]. 南昌: 华东交通大学, 2013. FU Ping-yong. Simial material model test study on the humidity field of tunnel surrounding rocks within swelling rocks[D]. Nanchang: East China Jiaotong University, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D373961 |
| [18] |
蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社, 2013.
|
| [19] |
FISHMAN G S. Monte Carlo. Concepts, algorithms, and applications[J]. Series in Operations Research, 1996, 75(2):N3-N4., 1996, 75(2): N3-N4. |
| [20] |
MARINO S, HOGUE I B, RAY C J, et al. A methodology for performing global uncertainty and sensitivity analysis in systems biology[J]. Journal of Theoretical Biology, 2008, 254(1): 178. DOI:10.1016/j.jtbi.2008.04.011 |
| [21] |
SHEN M, XIAO Y, ZHOU W, et al. Global Dynamics and applications of an epidemiological model for hepatitis c virus transmission in China[J]. Discrete Dynamics in Nature & Society, 2015, 1-13. |
| [22] |
BERDUGO I R, ALONSO E, Ramon A. Extreme expansive phenomena in anhydritic-gypsiferous claystone:the case of Lilla tunnel[J]. Géotechnique, 2013, 63(7): 584-612. DOI:10.1680/geot.12.P.143 |



