2. 义乌工商职业技术学院 机电信息学院, 浙江 义乌 322000
2. School of Mechanical Information, Yiwu Industrial & Commercial College, Yiwu 322000, China
图形间的交线在机械加工制造、建筑、电力和冶金等行业有广泛运用[1].由于交线形式多样形状复杂,其坐标提取一直以来是数控切割系统中核心技术之一[2].近些年,国内外学者对此展开了广泛的研究.韩淑洁[3]提出了一种快速准确作截交线的通用方法.杨绪利[4]对圆锥截交线的形状及投影进行了全面分析,但该方法只适用于手工作图,实际工程应用范围受限.朱建宁等[5]提出了一种快速计算平面与高精度细分曲面交线的方法,利用Catmull-Clark细分曲面计算与平面的交线.类似地,李慧莹等[6]基于四边形网格细分提出了一种平面与自由曲面求交算法,两者只能解决单曲面求交问题.曹斌等[7]在文献[5]的基础上,将Catmull-Clark细分曲面法应用于双曲面求交问题上,将曲面细分思想作了进一步推广.孙殿柱等[8]针对三角网格曲面,提出了一种采用R*S树索引结构快速查询相交区的三角面包围盒,并对其进行排序求交的算法.李宁等[9]在AABB法的基础上,构造层次包围盒来定位求交区域,对三角网格求交算法作了进一步的优化.付明珠等[10]基于微分几何理论,提出了一种隐式曲面交线跟踪方法,可得到隐式曲面的数值解,但该方法需已知曲面方程,这一条件约束了该法在自由曲面求交问题上的应用.Skoda[11]提出了一种新的多面体线相交算法,Marina等[12]提出了一种用平面内两线之间最近点来计算交点的新方法.段明德等[13]在利用逆向几何求交算法时,采用全局搜索三角面片顶点坐标的方式进行分层体素化,这种遍历搜索法耗时较大.Sabharwal等[14]通过对三角形的相交分类(点交、线交、面交),根据其各自的相交边界条件,提出了一种简单快速三角形求交算法,该方法为三角网格面求交问题提供了思路.Wang等[15]通过数值解析法给出了一种双次曲面的的求交算法,但其解析过程较为复杂.Teixeira等[16]采用有限元方法,将曲面划分成四叉树结构,并三角面片逼近求交.Chrismianto等[17]利用三次贝塞尔曲线和曲线平面交线法对实体造型过程中球头弓进行参数化设计.Jia等[18]提出了一种检测两个二次曲面交线的拓扑和代数性质的典型算法.Fu等[19]提出了一种求解B样条曲线交点的基础算法.Shen等[20]基于矩阵表示法提出了一种直线/修剪NURBS曲面求交算法.Aléssio等[21]提出了一种在欧式四维空间中计算三参数超曲面非横截相交曲线的微分几何特性的算法.Seo等[22]利用计算机仿真模型提出了一种网格曲面自动求交算法.
综上所述,目前的曲面求交算法大致可分为三类:几何作图法、解析法、有限元法.作图法又可分为画法几何法和软件作图法,其中,画法几何作图法是根据正投影法则及三等原则,用表面取点法或辅助面法求作交线上的若干点的投影,再将这些投影点光滑连接而成.该法的作图结果精度较低,作图过程耗时较多,效率低.软件作图法对图形进行造型建模并求交法虽然精度较好,但其求解内核或原理无从知晓.而且,在建模过程须已知图形的相关参数,否则无法精确建模.若采用点云数据进行曲面拟合建模再求交的方式,虽然能解决实际工程中图形相关参数未知的问题,但拟合求交会造成误差二次累积.解析法通过联立相交两图形的方程组,求其公共解即为交线方程,或者利用微分几何原理,通过约束条件对交线进一步优化迭代.但该方法的数值求解过程相当复杂,有时甚至无法求解.另一缺点是,该法需要已知两相交曲面的显式或隐式表达式,这在实际中常常无法满足,因此也限制了解析法的适用范围.有限元法则通过曲面的网格划分(多为四边形、三角形),将曲面求交问题转换为平面交线问题加以解决,但该法的求解精度与网格划分方式有关,且网格划分过程耗时成本较多.在当今点云数据获取最为便捷的环境下,通过点云拟合成曲面,然后进行网格划分求交的方法,无疑增加了过程的冗余与时间的浪费.
为了避开复杂的数学计算和放弃借助未知内核的三维软件作图法,提出一种点云曲面空间网格化加密求交算法,采用几何问题几何解,用几何元素离散化方法求解几何图形间的度量与定位问题.通过点云信息直接进行相交区的快速定位求交,省去网格划分阶段,得到的结果亦是点云显示,更符合目前的快速成型、3D打印等先进制造技术的需求.
1 几何图形离散化表达两图形相交的形式是多样的,如线与面、面与面、面与体相交,线包括直线、曲线,面包括平面、曲面,体包括平面立体、曲面立体,其图形维度有一维、二维、三维.为了简化图形计算复杂度,采用图形降维的方式,设计统一化的图形表达形式,用低维度的图元特征表示高维度的复杂图形.将图形(一维、二维、三维)离散成坐标点,以图形最小单元——点来表示各种维度,各种形状的图形,实现方法归一化的目的.
图形离散化的方法不仅能将图形表达简单化,通过各数据点之间的位置关系来反应图形的类型和复杂程度,还能通过调整离散点密度来关联图形显示与计算的精度.另一方面,几何图形离散化表达方式也符合工程实际中的未知曲面数据来源特征,只需控制点云扫描密度就可以得到相应精度的曲面离散化模型.如图 1所示,分别列出了直线、曲线、平面、曲面、平面立体、曲面立体等几何图形的离散化表达效果.

|
图 1 线、面、体的离散化表达 Fig. 1 Discrete expression of line, plane and bodies |
由于截交线、相贯线是相交两图形的共有点所构成的交线,将图形均采用点云表示后,计算两相交图形的交线就转变为计算两点云的重合点组过程,这也是几何图元交集求解算法的构建基础.
2.1 构建包络点云的三维空间网格相交两图形的点云密度越高,得到的共有点就越多,但通过遍历两图形的数据点信息,求解两图形的共有点计算量也会越大,计算耗时久,导致算法的效率较低,因此,有必要设计一些优化规则,对该算法进行优化,以提高其实用性,减少资源浪费.两图形相交,并不是所有图形数据点都在相交范围内,可通过设置包围盒来筛选两图形的相交区域,仅在该区域内加密点云达到既能获得大量共有点又不普遍增长原始数据点数量的目的.通过检测图形的x, y, z方向最大、最小坐标值, 计算该图形的最小立体包围盒,利用2个图形的最小包围盒来判断其相交区域的三方向坐标值范围.具体方法如下:将图形1的x向最大、最小坐标值x1min、x1max,与图形2的x向最大、最小坐标值x2min、x2max进行合并排序,若排序结果为
| $ {x_{1\min }} < {x_{2\min }} < {x_{1\max }} < {x_{2\max }}, $ |
则其x向坐标范围是x2max~x1min.同理,对两图形的y、z向坐标范围进行计算,并以该三向坐标范围值进行三维包围盒的绘制.此时,位于该包围盒内的数据点即为优化后的原始数据点信息,该方式可大大降低原始数据点数量,达到初步优化算法的效果.
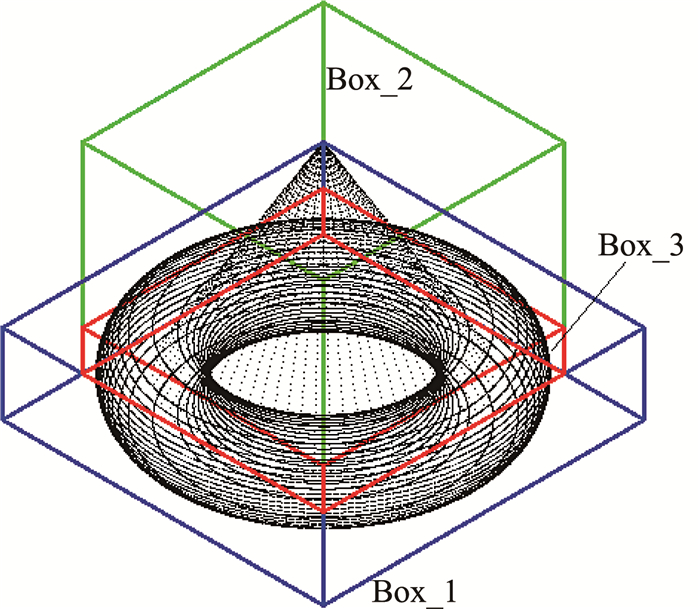
如图 2所示,图形1的包围盒为Box_1,位于该包围盒内的点集为pdata_1.图形2的包围盒为Box_2,位于该包围盒内的点集为pdata_2.通过该交叉筛选法处理之后,可构建一个交叉包围盒Box_3,位于包围盒Box_3内的数据点集为pdata_3,将其作为初始备选数据,再进行下一步的提取交线共有点的算法设计.经检测,pdata_1的数据量为3 213,pdata_2的数据量为158 400,pdata_3的数据量为53 143.其中,pdata_3中属于图形1的数据量为693,该数据称为pdata_4,属于图形2的数据量为52 450,该数据称为pdata_5.由此可见,包围盒交叉筛选法可将有用数据对比计算量缩减至原计算量的7%,大大提高了计算速度,降低了时间复杂度.
|
图 2 包围盒交叉提取相交区域 Fig. 2 Intersection region extraction by intersection of bounding boxes |
为了提高点云计算效率,快速定位曲面相交区域,现设计一种三维空间网格包络盒.如图 3所示,Box_3为经过上一步包围盒交叉处理后的相交包围盒,将Box_3包围盒按三坐标方向均匀划分成m×n×h个立体包络盒.通过读取每个立体包络盒中的点属性,即可快速定位到两曲面相交区域.具体方法是若某包络盒中存在属于pdata_1的点,也存在属于pdata_2的点,则该包络盒位于两曲面相交区域,存入intersection_box集.若某包络盒仅存在属于一类数据点集的点,则丢弃该包络盒数据点,减少后续计算量.

|
图 3 三维空间网格包络盒表示法 Fig. 3 Representation of 3D space mesh envelope box |
为了进一步缩小相交搜索范围,减少后期求交判别次数,根据三维空间网格包络盒的迭代计算思路,现将该优化迭代过程详述如下:根据点云曲面整体三维尺寸,初定迭代计算步长x_step、y_step、z_step,及步长最小精度值ε.
1) 计算包含曲面点云整个包围盒Box_1,根据设定的各向步长,将其划分为m×n×h个立体包络盒,并将其存入Box_set1;
2) 读取Box_set1中每个盒子中的点属性,提取包含2个点集元素的包络盒,存入inter_Box_set;
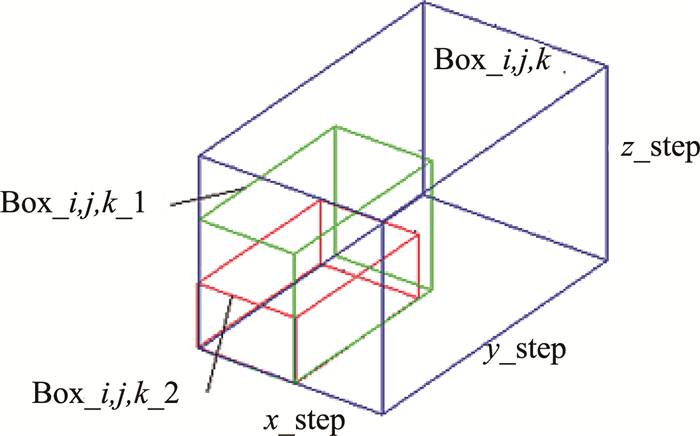
3) 读取inter_Box_set中盒内容,如图 4所示的Box_i, j, k,提取包含点集1的最大包络盒Box_i, j, k_1,包含点集2的最大包络盒Box_i, j, k_2,计算两包络盒所含点数,将点数少者Box_i, j, k_2(为了后续降低计算量)存入Box_set2;
|
图 4 包络盒优化迭代过程 Fig. 4 Optimum iterative process of envelope box |
4) 读取Box_set2中每个盒子box_i, 将其替代Box_1,并将步长x_step,y_step,z_step减半,转入1),继续迭代计算;
5) 若步长 < ε,则停止迭代;
6) 若步长>ε,则转入1)继续迭代,直至满足5);
通过网格包络盒优化迭代之后,小尺寸包络盒即可快速定位到两曲面相交区域,如图 5所示.利用三维空间网格包络盒的方式可将点对点的单一、大量计算,替换为盒与盒的异类、少量计算.并在此基础上,利用包络盒迭代缩小的方式,进一步细化相交区域包络盒,减少每一包络盒内的数据点,从而大大减少计算量,降低时间消耗量.同时,该方法与曲面形状等因素无关,适用于任意复杂曲面求交问题.

|
图 5 细化相交区包络盒 Fig. 5 Subdividing envelope boxes in intersection |
由于网格包络盒迭代计算仅有利于快速定位并缩小曲面相交区域,并不能优化原始点云密度,在计算两曲面交线点坐标之前,还须提高相交区域的点云密度,以利于提高计算精度,提取更优、更接近的曲面交线.现采用一种点云数据拼片形心加密方法,对相交区域点云进行二次加密处理.在点云加密过程中,为了保证三角片加密拆分前后面片变形量小,采用求三角面的形心作为加密点.形心加密法较之他法有变形量小、精度高的优点.如图 6所示,S1是三角面ABC的形心,加密后,△ABS1、△ACS1、△BCS1的面积差异较小,不会引起三角面的扭曲(如S2),能有效保证加密后形变精度.若三角面片是均质的,则其重心与形心重合,利用形心法加密后,不会引起三角面片的重心偏移而导致加密前后的精度降低.

|
图 6 点云三角形心加密精度分析 Fig. 6 Centroid refinement accuracy analysis of triangle |
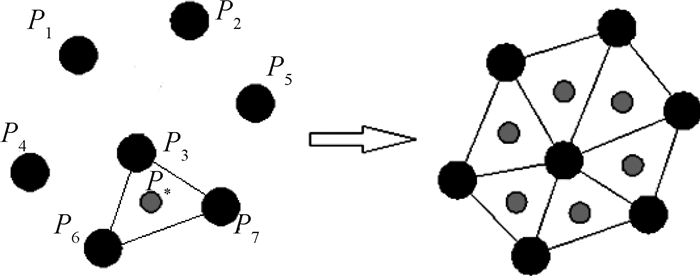
如图 7所示,若位于相交区域的某一包络盒包含坐标点P1, P2, P3, …, P7以点P3为例,其与附近最近点P6, P7拼成一个三角面△P3P6P7,以△P3P6P7的形心P*作为加密点,其坐标计算公式为
|
图 7 点云数据拼片形心加密过程 Fig. 7 Centroid refinement process of point cloud patch |
P*x=(P3x+P6x+P7x)/3,
P*y=(P3y+P6y+P7y)/3,
P*z=(P3z+P6z+P7z)/3.
经过点云数据拼片形心加密,即可将该包络盒内点云进行加密,加密结果如图 7所示.该过程既避免了全局加密点云而造成庞大的运算浪费,又实现了交线区域的靶向点加密,从而为后期交线点的精确计算充实了点云信息.
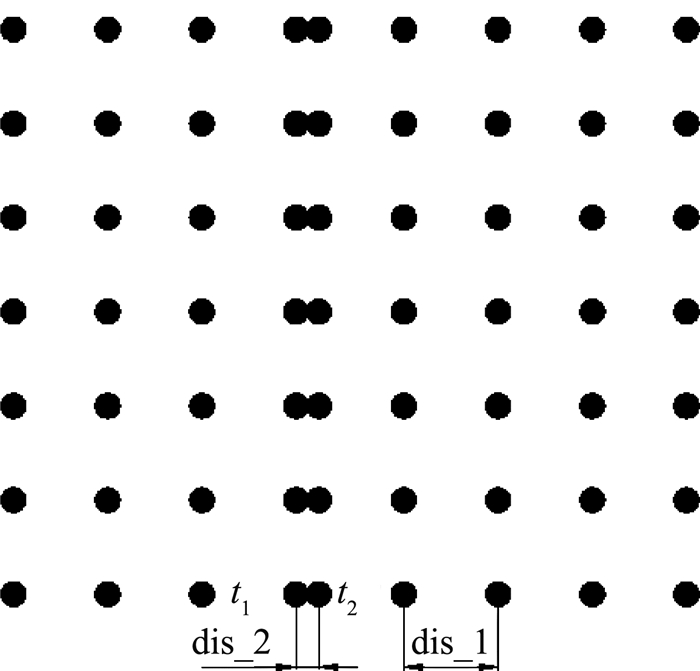
2.4 点云图元求交将高维的图形与几何拓扑关系,转换为低维的数据点之间的几何定位与度量关系,这是几何图元离散化计算的关键.如图 8所示,离散化点云平面P1、P2,其截交线L1为由P1、P2的数据点集中的公共点组成的点组.本法中的图元均由点集表示,求解结果亦是点集,若有需要,可由此点集拟合成曲线.在线、面、体等图形均离散为点云后,点与点之间必然有间隙,该间隙的大小由点云密度参数dis_1表示,如图 9所示.在求解截交线和相贯线时,由于dis_1≠0,则在求解两点集公共数据点时,出现无法得到精确重合点的情况.此时,可通过设置相应的精度阈值dis_2,保证近似求解过程有解,其中该阈值的设置原则为dis_2 < dis_1.如图 9中,图形1的点t1(x1, y1, z1)与图形2的点t2(x2, y2, z2)的间距值为dis_2,且dis_2 < dis_1,故认为t1与t2为两图形的公共数据点,并对其求均值后作为该交线中的数据点:

|
图 8 图元求交模型 Fig. 8 Intersection model of graphic |
|
图 9 点云密度与计算精度的关系 Fig. 9 Relationship between point clouds density and computational accuracy |
| $ {t_0} = \left( {\frac{{{x_1} + {x_2}}}{2}, \frac{{{y_1} + {y_2}}}{2}, \frac{{{z_1} + {z_2}}}{2}} \right). $ |
采用该方法,通过遍历图形1与图形2的所有数据点,即可得到其近似重合点.由于该方法无须考虑图形的复杂性,故具有一般性和广泛的适应性.不管图形的维度高低,其显示的几何信息都为数据点,则其几何计算过程均为数据点坐标值的对比判断.在下文的实际工程案例应用中,经过3次迭代加密后,阈值已达0.05~0.075 mm,此阈值范围能满足该案例的后续注塑模具设计的精度要求,并在后期成品检测中得到了实际验证.
2.5 自适应阈值调整利用本法计算图形交线的过程中,存在来自于原始数据的误差不可避免.由于图形离散化数据本身存在间隙而造成误差,在实际运用中需设置一个合理的精度阈值dis_2,以满足该法的计算结果不是空集,且能满足工程精度要求.但精度阈值受图形点云密度等方面影响,很难一次得到一个合适的数值.需通过反复测试,才能筛选出一个兼顾精度和计算速度的阈值.因此,有必要设计一个自适应阈值调整过程,来帮助使用者选择一个合理的精度阈值.采用原始图形离散点间距求平均的方式计算图形密度值,即dis_1值是一种比较方便的方法.另外再提供两种方法来自适应调整精度阈值dis_2,一种是当所求结果的数据点数大于预先设定值,则通过dis_2自减来重新计算结果,直至结果点数满足预先要求为止.同样地,当所求结果的数据点数小于预先设定值时可通过dis_2自加来修正.另一种是通过结果点数最小化来提高计算精度和自适应调整阈值,该方法先将阈值设置成极小值,此时对应的结果是空集,然后通过阈值小步长逐渐自加,直到结果空集消失,此时对应的阈值即为最精确的阈值.
3 算例验证 3.1 算法实现为了进一步验证本算法的有效性,将该算法在通用软件AutoCAD上加以实现.现通过实例来验证该算法的通用性,利用Vtop扫描仪获取玩具小猫的点云模型和装饰花的点云模型,并对其进行求交计算.其中,小猫点云数据量为313 415点,装饰花点云为240 555点, 如图 10所示.由图可见,两模型的初始点云密度不一致,小猫的点云比较稀疏,装饰花的点云比较密集.此时算法设计以点数少者为加密对象原则,即若在某一相交包络盒中,模型1的点数少于模型2,则对模型1进行加密处理即可.这样既可减少2个模型同时加密的时间,又可减少单个模型加密的时间,就可节省总计算量.利用本法对该算例进行包络盒优化迭代计算,如图 11所示,可见包络盒可快速精确定位到曲面相交区域.由图 12,13可见,所设计的加密求交算法计算可靠,经与软件作图法对比测量,本例与软件法重合度为99.13%.

|
图 10 花与猫的点云模型 Fig. 10 Point cloud models of cat and flowers |

|
图 11 包络盒优化迭代结果 Fig. 11 Optimum and iterative result of envelope box |

|
图 12 花与猫的求交结果 Fig. 12 Result of intersection computing for flowers and cat |
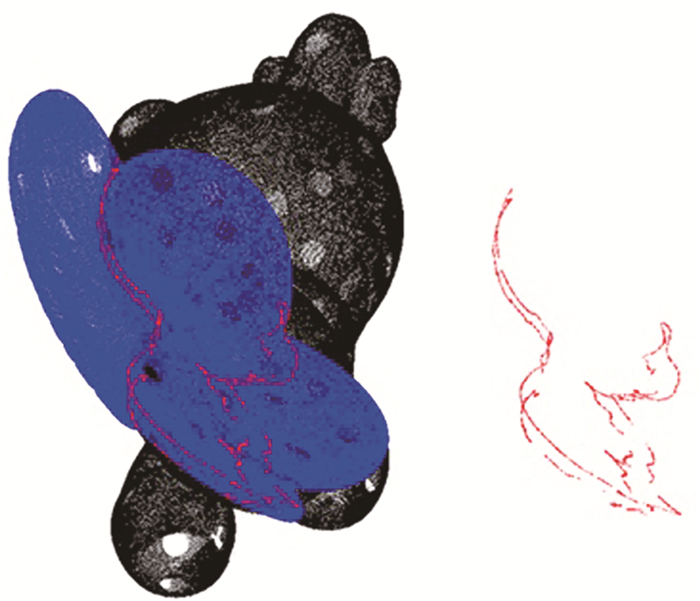
|
图 13 更换求交位置后的求交结果 Fig. 13 Intersection computing for other location |
采用文献[8]和本算法进行效率分析,对于本算例,文献[8-9]交线提取的时间复杂度是o(m·n),本文算法的时间复杂为o(s·k),其中m和n分别为两点云模型的点数,而s和k则分别为两点云模型相交区域的点数.可见,
以本文的小猫模型和装饰花模型为例,测试本算法在不同步长值Lstep、不同迭代次数Nite、不同加密阈值Vadd、相同精度ε条件下的求交效率.由表 1可见,在相同步长值、加密阈值情况下,随着全局迭代次数的增加,相应计算量增加,加密的点数也随之增加.同时加密点数Np也与加密阈值有关,当加密阈值接近点云密度时,加密点数的增加随迭代次数的增加变得缓慢, 交点数Nint越多,计算耗时T越久.
| 表 1 不同全局迭代次数下加密点数变化表(ε=0.1 mm) Table 1 Diversification of refinement points under different global iterations (ε=0.1 mm) |
在上述测试基础上,将本算法进一步与同类算法做横向求交效率对比,将点云模型网格化后,再以文献[8-9]中的算法作求交计算.由表 2所示,可见本算法的求交速度优于全局遍历算法和文献[8-9]算法,且前文中已验证本算法的求交结果是精确的.值得一提的是,本算法省去了复杂耗时的网格划分过程,避开了复杂的解析计算和微分方程,以点数据求点数据,结果也以点数据显示,简单可视.
| 表 2 4种不同算法的求交耗时对比 Table 2 Comparison of time taken in intersection among four different algorithms |
由此,可得出这样的结论:点云曲面空间网格化加密求交算法适用于各类图形相交问题,且计算结果精度可控,能达到工程应用的需求.该算法具有一般性,操作简单,精度高,且有较好的鲁棒性.
4 结语几何图形离散成点云是将复杂问题简单化的前提.通过离散化处理将图形处理成点云,为二维、三维图形求交问题的几何算法奠定了普适基础.通过设计交叉包围盒、三维空间网格包络盒优化迭代计算法,大大降低了原始点云的计算量.通过相交区域的靶向点云加密方式,充实了相交区的点云信息,最大程度上补偿了部分因扫描而丢失的点信息,提高了算法的计算速度和精度,该算法不受图形的复杂度、参数预知性等影响,既避开了复杂的数学计算过程,又满足了计算结果可视性的要求,为解决工程设计、施工安装中所涉及的图形相交问题提供了一种实用方法.
今后的研究工作将在以下几方面开展:对几何图元交集求解算法进一步优化,提高其智能优选数据的效率;研究图形离散化的自适应密度调整方式;将用几何元素离散化方法求解几何图形间的度量与定位问题的思路运用到更多的工程领域,继续不断推进几何图形问题用几何解的理念.
| [1] |
张晓东, 王园宇, 郝鹏飞, 等. 相贯线及其展开曲线的方程构建方法的研究[J]. 机械设计与研究, 2008, 4(2): 21-24. ZHANG Xiao-dong, WANG Yuan-yu, HAO Peng-fei, et al. Study of establishing the equations of intersecting line and its developmental figure[J]. Machine Design and Research, 2008, 4(2): 21-24. |
| [2] |
刘德刚, 吴兴群, 李佳星. 基于VTK的相贯线坐标计算方法研究[J]. 现代制造工程, 2016(3): 59-63. LIU De-gang, WU Xing-qun, LI Jia-xing. Intersection calculation method research based on VTK[J]. Modern Manufacturing Engineering, 2016(3): 59-63. |
| [3] |
韩淑洁. 快速准确作截交线的通用方法研究[J]. 机械工程与自动化, 2012, 10(5): 201-204. HAN Shu-jie. A general method of drawing intersection line rapidly and accurately[J]. Mechanical Engineering & Automation, 2012, 10(5): 201-204. |
| [4] |
杨绪利. 圆锥截交线的形状及投影分析[J]. 东华大学学报:自然科学版, 2005, 8(4): 76-78. YANG Xu-li. On the form and projection analysis of conic cut and hand in line[J]. Journal of Dong-hua University, 2005, 8(4): 76-78. |
| [5] |
朱建宁, 王敏杰, 魏兆成, 等. 快速计算平面与高精度细分曲面交线的方法[J]. 计算机集成制造系统, 2014, 6(20): 1322-1329. ZHU Jian-ning, WANG Min-jie, WEI Zhao-cheng, et al. Efficient algorithm for computing intersection curve between plane and subdivision surface[J]. Computer Integrated Manufacturing Systems, 2014, 6(20): 1322-1329. |
| [6] |
李慧莹, 陈良骥. 基于四边形网格参数细分的平面与自由曲面求交算法[J]. 机电工程, 2013, 8(30): 956-970. LI Hui-ying, CHEN Liang-ji. Algorithm for finding plane & free-form surface intersection curve based on subdivision of quadrilateral mesh parameters[J]. Journal of Mechanical & Electrical Engineering, 2013, 8(30): 956-970. |
| [7] |
曹斌, 王敏杰, 朱建宁. 快速计算高精度细分曲面之间交线的方法[J]. 计算机集成制造系统, 2014, 9(20): 2079-2085. CAO Bin, WANG Min-jie, ZHU Jian-ning. Efficient algorithm for computing intersection curve between subdivision surfaces[J]. Computer Integrated Manufacturing Systems, 2014, 9(20): 2079-2085. |
| [8] |
孙殿柱, 孙永伟, 田中朝, 等. 三角网格曲面模型快速求交算法[J]. 北京工业大学学报, 2012, 8(38): 1121-1135. SUN Dian-zhu, SUN Yong-wei, TIAN Zhong-chao, et al. Rapidly getting intersection algorithm for triangular mesh surface models[J]. Journal of Bei-jing University of Technology, 2012, 8(38): 1121-1135. |
| [9] |
李宁, 田震, 张立华, 等. 优化的三角网格曲面求交算法[J]. 辽宁工程技术大学学报:自然科学版, 2013, 9(32): 1269-1273. LI Ning, TIAN Zhen, ZHANG Li-hua, et al. Optimization algorithm for triangular mesh surface intersection[J]. Journal of Liao-ning Technical University:Natural Science, 2013, 9(32): 1269-1273. |
| [10] |
付明珠, 罗钟铉, 冯二宝. 基于微分几何的隐式曲面交线跟踪方法[J]. 计算机辅助设计与图形学学报, 2016, 4(28): 556-564. FU Ming-zhu, LUO Zhong-xuan, FENG Er-bao. Tracing implicit surface intersection based on differential geometry[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 4(28): 556-564. |
| [11] |
SKODA A. A new algorithm for the intersection of a line with the independent set polytope of a matroid[J]. Bulletin Des Sciences Mathematiques, 2009, 133(2): 169-185. DOI:10.1016/j.bulsci.2008.10.003 |
| [12] |
MARIN G, JON R. Computing line intersections[J]. International Journal of Image and Graphics, 2001, 1(2): 217-230. DOI:10.1142/S0219467801000141 |
| [13] |
段明德, 郑立霞, 李明利, 等. 基于逆向几何求交算法的STL模型多孔结构体素化[J]. 河南理工大学学报:自然科学版, 2017, 1(36): 86-90. DUAN Ming-de, ZHENG Li-xia, LI Ming-li, et al. Porous structure voxelization for STL model based on reverse geometrical intersection[J]. Journal of He-nan Polytechnic University:Nature Science, 2017, 1(36): 86-90. |
| [14] |
SABHARWAL C L, LEOPOLD J L. A triangle-triangle intersection algorithm[J]. Computer Science & Information Technology, 2015, 5(11): 27-35. |
| [15] |
WANG W, GOLDMAN R, TU C. Enhancing Levin's method for computing quadric-surface intersections[J]. Computer Aided Geometric Design, 2003, 20(7): 401-422. DOI:10.1016/S0167-8396(03)00081-5 |
| [16] |
TEIXEIRA F G, CREUS G J. A robust algorithm to determine surface/surface intersection in both parametric spaces[J]. Mecnica Computacional, 2008(41): 3093-3115. |
| [17] |
CHRISMIANTO D, KIM D J. Parametric bulbous bow design using the cubic Bezier curve and curve-plane intersection method for the minimization of ship resistance in CFD[J]. Journal of Marine Science & Technology, 2014, 19(4): 479-492. |
| [18] |
JIA X, WANG W, CHOI Y K, et al. Continuous detection of the variations of the intersection curve of two moving quadrics in 3-Dimensional projective space[J]. Journal of Symbolic Computation, 2016, 73(C): 221-243. |
| [19] |
FU Q, WU Z, WANG X, et al. An algorithm for finding intersection between ball B-spline curves[J]. Journal of Computational & Applied Mathematics, 2017, 327: 260-273. |
| [20] |
SHEN J, ALLIEZ P, DODGSON N. A line/trimmed NURBS surface intersection algorithm using matrix representations[J]. Computer Aided Geometric Design, 2016, 48. |
| [21] |
ALÉSSIO O, DVLDVL M, DVLDVL B U, et al. Differential geometry of non-transversal intersection curves of three parametric hypersurfaces in Euclidean 4-space[J]. Computer Aided Geometric Design, 2014, 31(9): 712-727. DOI:10.1016/j.cagd.2014.09.003 |
| [22] |
SEO D, JUNG H, SUNG W K, et al. Development of the Korean spine database and automatic surface mesh intersection algorithm for constructing e-Spine simulator[J]. Journal of Applied Mathematics, 2014, 2014(9): 1-11. |



