2. 北京航空航天大学 机械工程及自动化学院, 北京 100191
2. School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China
筋是飞机结构件中的典型加工特征,多为槽与槽、槽与外轮廓间的条形结构, 其顶面由一系列满足一定几何约束条件的彼此邻接的面组成[1].根据顶面类型,可分为平顶筋、斜顶筋和曲顶筋.其中,平顶筋是顶面为水平平面(与加工坐标系垂直的平面)的筋,是大型飞机结构件主要的筋特征.筋的数控编程烦琐且易出错.这类结构件的数控加工时间与数控编程时间的比值约为1:10[2].因此提高数控编程效率是提高这类飞机结构件加工效率的关键,而筋特征的自动识别是实现数控编程、特征加工的首要前提.
基于特征的数控加工编程技术的研究开始于1975年剑桥大学的CAD中心,该中心的Grayer等[3]从零件的实体模型中自动提取出几何元素,并将其应用于零件数控刀轨的计算.特征识别的思想在1980年由Kyprianou[4]在博士论文中首次提出,此后,加工特征自动识别技术作为CAD/CAM/CAPP系统间的转换接口,成为基于特征的数控加工自动编程技术的核心.经过近40年的发展,特征识别技术取得了丰硕的成果,除了传统的基于边界匹配的特征识别方法和基于体分解的特征识别方法,近年来也有学者提出一些新的特征识别方法,如分层求交的特征识别方法[5-6],基于知识推理的方法[6],基于广义槽的方法[7-8]等.飞机结构件筋特征识别方面,Li等[1-2]基于加工知识和整体的属性邻接图[2],设计了一系列启发式规则用于识别特征种子面,并对种子面进行扩展以完成单个的局部筋特征元素的识别,最后再将这些筋元素组合起来形成筋加工特征.施建飞等[9]提出了基于属性边点图的筋特征识别方法,该方法以水平筋顶面作为特征种子面提取特征端点,进而构造种子面的属性边点图.作者给出了特征种子面即水平筋顶面所具有的性质,但并未给出具体识别方法和识别效率.而根据文献[9]给出的特征种子面的性质,凸台顶面也可能识别为特征种子面.文献[9]也未说明如何排除这种可能或如何区分特征种子面和凸台顶面.笔者提出了基于约束Delaunay三角剖分的筋特征识别与构建算法[10].该算法中斜筋的识别与构建依赖于平顶筋面的识别,但平顶筋面的识别算法效率相对较低.此外,Zhu等[11-12]提出了一种基于筋特征识别与拆分的分层语义中间面提取方法用于薄壁件模型的简化.其中,筋特征的识别方法主要是根据构成筋特征的面的相邻约束关系和边的平行关系,建立“面组对(FGP)”的识别规则从而识别筋特征.为了在对零件进行有限元分析时生成高质量的网格,Lai等[13]将特征识别技术应用到有限元分析中,对薄壳塑料件的CAD模型的筋特征进行了识别与拆分.其识别方法主要是基于对所定义的具有相互约束关系的筋特征的顶面、端面和基面(即本文所述的主面、侧面和底面/限制面)的搜索,最后将识别出的筋特征结构拆分为适宜实体网格划分的筋元素.这2种筋特征识别方法都不适用于飞机结构件筋加工特征的识别.因此,本文提出基于模糊推理的飞机结构件平顶筋识别方法.首先,给出平顶筋的表示模型;其次,给出基于模糊推理的平顶筋识别方法;最后,给出实例对算法的有效性进行了验证.
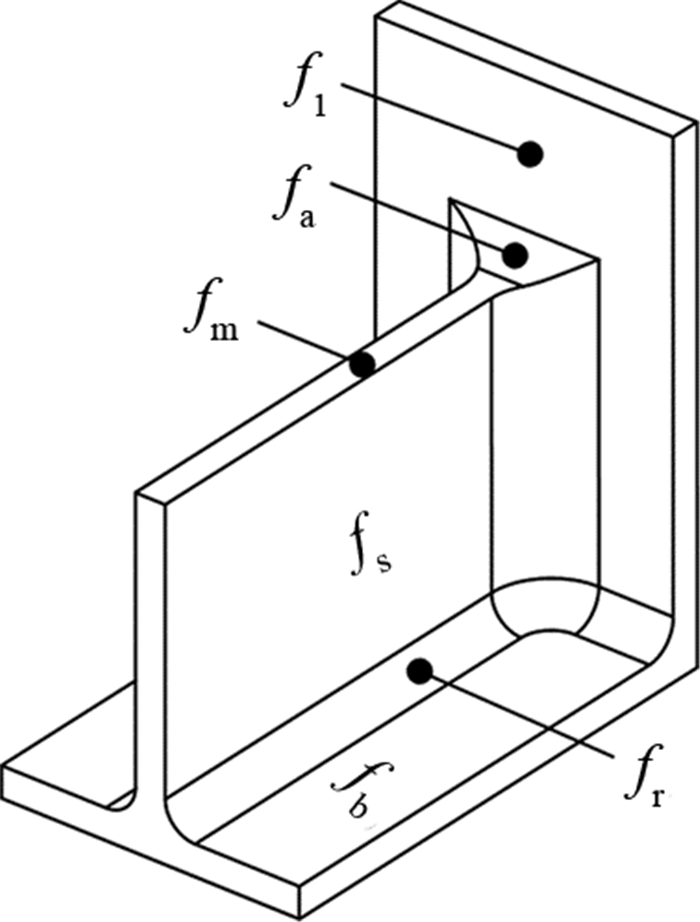
1 平顶筋的表示模型 1.1 几何属性平顶筋的几何属性是依据CAM和CAPP系统需求对平顶筋几何信息的描述,从三维设计模型中提取得到,是对平顶筋进行数控加工编程的依据,也是参数属性和工艺属性的载体.根据常见平顶筋结构的特点,结合数控加工编程过程中对几何信息的需求,将平顶筋的几何属性GA总结为以下特征面的集合:主面fm、侧面fs、限制面fl、过渡面fa、底面fb及底圆面fr的集合,如图 1所示.各特征面的详细定义可参见笔者此前的研究[10].
|
图 1 平顶筋几何属性 Fig. 1 Geometrical attributes of planar-top rib |
几何属性除自身作为平顶筋加工中的几何元素外,还包含平顶筋加工中刀具选取、刀轨计算及加工参数选择等过程所需的相关参数信息,这些参数信息构成平顶筋的参数属性PA,可直接或间接从几何属性中提取或计算获得.为满足实际加工的需要,将平顶筋加工过程所需的参数信息总结如下,主要有位置(Location)、长度(Length)、宽度(Width)、高度(Height)、端头类型(T-Type)、特征面的面积(F-Area)、特征面的轮廓周长(C-Parameter)等.
1.3 工艺属性除几何属性和参数属性外,从加工制造角度出发,对飞机结构件数控加工工艺以及CAM和CAPP系统对工艺信息的处理流程进行分析,将结构形状与工艺信息进行关联和匹配,赋予几何外形域指定的加工方法.
将加工特征赋予几何外形域指定的加工方法定义为加工特征的工艺属性MA,主要包括机床(Machine)、刀具(Tool)、加工方法(Method)、加工策略(Strategy)、切削参数(Parameter)、公差(Tolerance).
1.4 表示模型根据上文分析,结合平顶筋的几何属性、参数属性、工艺属性等,设RF表示一个平顶筋,则RF用巴科斯-诺尔范式(BNF:Backus-Naur Form)定义如下:
〈RF〉::=(〈ID〉, 〈GA〉, 〈PA〉, 〈MA〉),
〈GA〉::=(〈fm〉, 〈Fs〉, 〈Fl〉, 〈Fb〉, [Fa], [Fr]),
〈PA〉::=(〈Location〉, 〈Length〉, 〈Width〉, 〈Hight〉, 〈T-Type〉, {〈F-Aera〉, 〈C-Parameter〉}),
〈MA〉::=(〈Machine〉, 〈Tool〉, 〈Method〉, 〈Strategy〉, 〈Parameter〉, 〈Tolerance〉).
其中,ID表示当前平顶筋的标识符,Fs、Fl、Fb、Fa、Fr分别为fs、fl、fb、fa、fr的集合.
2 基于模糊推理的平顶筋识别模糊理论摆脱经典数学理论中“非此即彼”的精确性,研究的是具有一定模糊性的对象,这种模糊性是由于事物之间差异的中间过渡性所引起的划分上的不确定性[14].在本文所研究的飞机结构件中,平顶筋的特征识别具有一定的不确定性和模糊性.首先,加工特征具有拓扑不确定性[15];其次,不同特征在拓扑结构上具有某些相似性.因此,为有效地识别平顶筋,提高算法的适用性和效率,采用基于模糊推理的平顶筋识别方法,充分考虑并利用平顶筋的特征属性,同时引入一些专家知识并用计算机语言加以表达,通过设计关联规则对知识进行逻辑运算实现具有一定程度模糊性的平顶筋的识别.
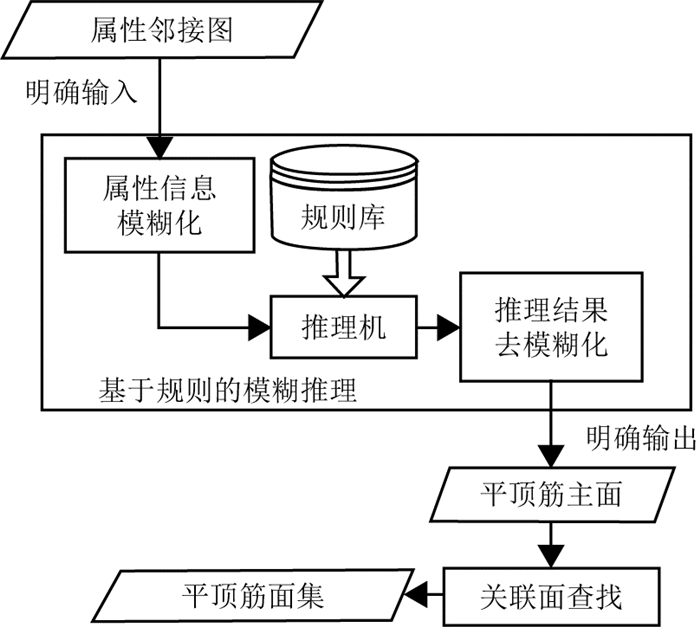
基于模糊推理的平顶筋识别的结构如图 2所示,主要包括属性邻接图的明确输入、基于规则的模糊推理、平顶筋主面的明确输出和关联面查找.在基于规则的模糊推理中,规则库是模糊推理的主体,也是知识表示的核心.
|
图 2 基于模糊推理的平顶筋识别的结构图 Fig. 2 Structure diagram of planar-top rib recognition based on fuzzy inference |
产生式规则表达了自然语言中的一种逻辑结构关系,是人工智能中有效的不确定知识表示方法,其基本结构形如:
A→B或者IF A, THEN B.
其中,A表示产生式规则的前件,为产生式规则的前提条件,B表示产生式规则的后件,当前件在某种程度上为真时,产生式规则得出的结论或作出的响应.
为区分前件中不同条件命题对结论的重要性,使得规则的表达更接近实际情况,引入条件权值、条件真度和结论置信度,设计加权模糊推理规则Ri:
| $ \begin{array}{l} {\rm{IF}}\left( {{P_{i1}}, {w_{i1}}} \right)/{T_{i1}}, \left( {{P_{i2}}, {w_{i2}}} \right)/{T_{i2}}, \cdots, \left( {{P_{in}}, {w_{in}}} \right)/{T_{in}}, \\ \;\;\;\;\;\;\;\;{\rm{THEN}}\left( {{C_i}, {\rm{D}}{{\rm{F}}_i}, {\tau _i}.} \right) \end{array} $ |
其中,n表示条件命题的个数,wij表示规则Ri中条件命题Pij的相对重要程度,即条件命题的权值,
| $ {w_{ij}} \ge 0, \sum\nolimits_{j = 1}^n {{w_{ij}} = 1.} $ |
Tij为条件命题Pij的真度,规则Ri的条件总真度Ti可根据各条件命题间加权逻辑关系所对应的真度计算得出,DFi为规则Ri的置信度(0≤DFi≤1),即所有条件命题均为真时结论的置信度,τi为规则Ri的激活阈值(0≤τi≤1),当规则Ri的条件总真度Ti≥τi时,规则激活并可推出结论Ci,且结论的真度T(Ci)= DFi×Ti.其中,加权逻辑关系的计算采用加权模糊逻辑真值传播算法[16],公式如下.
1) 加权逻辑与:
| $ \begin{array}{l} T_i^ \wedge = \sum\limits_{j = 1}^n {\left( {{w_{ij}}{T_{ij}}} \right)}- \\ \;\;\;\;\;\;\frac{1}{2}\left[{\sum\limits_{j = 1}^n {\left( {{w_{ij}}T_{ij}^2} \right)}-{{\left( {\sum\limits_{j = 1}^n {\left( {{w_{ij}}{T_{ij}}} \right)} } \right)}^2}} \right], \end{array} $ | (1) |
2) 加权逻辑或:
| $ \begin{array}{l} T_i^ \vee = \sum\limits_{j = 1}^n {\left( {{w_{ij}}{T_{ij}}} \right)} + \\ \;\;\;\;\;\;\frac{1}{2}\left[{\sum\limits_{j = 1}^n {\left( {{w_{ij}}T_{ij}^2} \right)}-{{\left( {\sum\limits_{j = 1}^n {\left( {{w_{ij}}{T_{ij}}} \right)} } \right)}^2}} \right]. \end{array} $ | (2) |
如果m(m≥2)个不同的规则同时被激活并推导出同一个结论,且各规则的条件命题相互独立,则采用合成公式计算结论的综合真度[17].对于任意2个规则的合成计算规则为
| $ {T_{i, j}}\left( C \right) = {T_i}\left( C \right) + {T_j}\left( C \right)-{T_i}\left( C \right) \times {T_j}\left( C \right). $ | (3) |
当m>2时,可先任意选取其中2个进行合成计算,再将其计算结果与第3个规则进行合成计算,依次进行,直至全部规则合成完成.
根据图 2,基于模糊推理识别平顶筋的主要步骤包括:1)以三维实体模型作为输入,通过面属性和边属性的计算,构建零件模型的属性邻接图;2)设计主面识别加权关联规则,运用模糊推理从属性邻接图中提取平顶筋主面;3)以平顶筋主面为种子面,搜索其他关联特征面.
2.1 属性邻接图构建属性邻接图是一种用于描述零件几何拓扑信息的图结构,所构建的属性邻接图包含了面与面之间的邻接关系,以及面的属性和连接2个面的公共边的属性,其表示形式如下:
| $ G = \left( {{V_{\rm{f}}}, {E_{\rm{e}}}, {A_{\rm{f}}}, {A_{\rm{e}}}} \right). $ |
其中,Vf和Ee分别为图中顶点的集合和弧的集合,图中的任一顶点唯一对应零件模型上的1个拓扑面;图中的任一弧唯一对应零件模型上的1个拓扑边,表示拓扑面间的相邻关系;Af和Ae分别为Vf和Ee中元素的属性的集合.属性邻接图的构建主要包括:1)零件模型中面和边的自动提取以及邻接关系构建;2)边属性的计算;3)面属性的计算.其中,1)可通过CAD二次开发接口获取三维Brep模型中的拓扑面(Face)以及面与面之间的公共边(Edge),然后以这些拓扑面与边构建邻接图;2)采用下文边属性计算规则自动识别拓扑边的凹凸属性,添加到邻接图的弧属性中,用于识别筋特征;3)采用面属性计算规则自动识别面的几何类型、凹凸性等属性信息,添加到邻接图的顶点属性中,完成属性邻接图的自动构建,用于识别平顶筋.如图 3所示为某零件的三维模型及其属性邻接图,图中弧上的属性值“0”表示该拓扑边为凹边,“1”表示该拓扑边为凸边.

|
图 3 零件模型及其属性邻接图 Fig. 3 Part model and its attribute adjacency graph |
1) 面属性计算.
面属性计算即计算邻接图中各顶点的属性,包括近平面、近圆柱面和面的凹凸性识别等,详细的计算方法可参见文献[14].
2) 边属性计算.
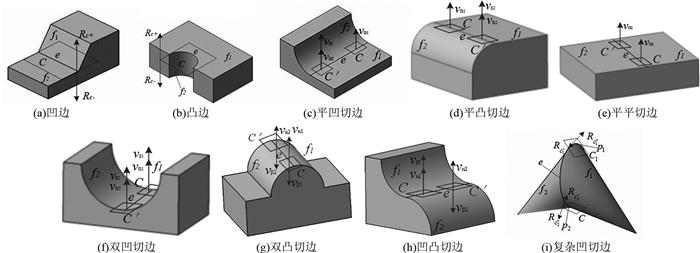
设面f1和面f2为两邻接拓扑面,边e为面f1与f2的公共边,点p为边e上一点,点p在面f1、面f2上的体外法向分别为vn1、vn2,C为面f1在点p处的切平面,平面C将空间分为两部分,其中Rc+表示沿面f1在点p处体外法线正向区域,Rc-表示沿面f1在点p处体外法线负向区域,C′为面f2在点p上的切平面,C为点p在f2上的一无穷小邻域,面f1和面f2与法面(过点p且与点p切向垂直的平面)的交线分别为l1、l2,l1和l2在点p处的曲率为κ1、κ2,l1和l2在点p处的法向(指向曲率圆圆心)为vβ1、vβ2,则边上点的凹凸性计算如下,其中δ为计算精度,取1.0×10-3、1.0×10-4等.
① 若C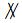
② 若C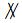
③ 若C//C′∧|κ1-0| < δ∧(κ2>0∧vn2·vβ2>0),则称面f1与f2在点p处为平凹切点;
④ 若C//C′∧|κ1-0| < δ∧(κ2>0∧vn2·vβ2 < 0),则称面f1与f2在点p处为平凸切点;
⑤ 若C//C′∧|κ1-0| < δ∧|κ2-0| < δ,则称面f1与f2在点p处为平平切点;
⑥ 若C//C′∧(κ1>0∧vn1·vβ1>0)∧(κ2>0∧vn2·vβ2>0),则称面f1与f2在点p处为双凹切点;
⑦ 若C//C′∧(κ1>0∧vn1·vβ1 < 0)∧(κ2>0∧vn2·vβ2 < 0),则称面f1与f2在点p处为双凸切点;
⑧ 若C//C′∧(κ1>0∧vn1·vβ1>0)∧(κ2>0∧vn2·vβ2 < 0),则称面f1与f2在点p处为凹凸切点.
基于邻接边上点的凹凸关系,进一步给出邻接边的凹凸关系定义.边e的凹凸性判别如图 4所示.
|
图 4 邻接边的凹凸关系 Fig. 4 concave-convex relationship of adjacency edges |
① 若∀p,p∈e,p为凹点,则称边e为面f1与面f2的凹边;
② 若∀p,p∈e,p为凸点,则称边e为面f1与面f2的凸边;
③ 若∀p,p∈e,p为平凹切点,则称边e为面f1与面f2的平凹切边;
④ 若∀p,p∈e,p为平凸切点,则称边e为面f1与面f2的平凸切边;
⑤ 若∀p,p∈e,p为平平切点,则称边e为面f1与面f2的平平切边;
⑥ 若∀p,p∈e,p为双凹切点,则称边e为面f1与面f2的双凹切边;
⑦ 若∀p,p∈e,p为双凸切点,则称边e为面f1与面f2的双凸切边;
⑧ 若∀p,p∈e,p为凹凸切点,则称边e为面f1与面f2的凹凸切边;
⑨ 若边e上至少存在两点p、q属于不同的凹凸类型,则称边e为面f1与面f2的复杂凹凸边.
2.2 主面识别规则设计主面为平顶筋的主要加工面,也是平顶筋有别于其他特征的主要拓扑面.从加工角度看,平顶筋主面多为狭长型的条状区域,加工方式以轮廓加工方式为主.基于特征面与加工方式的匹配关系,通过模拟外环走刀面积与加工面面积之间的关系建立加工面与加工方式间的匹配规则,具体表述如下.
规则2.1(加工面与加工方式匹配) 设面f为正向水平面,f的面积记为Af,l表示面f的轮廓周长,D为刀具直径,k为外环走刀面积近似系数,若
| $ k \cdot \frac{1}{2}Dl > A, $ |
则称面f与轮廓加工方式匹配,否则称面f与型腔加工方式匹配.
属性邻接图中各结点属性信息为平顶筋识别提供判断依据,作为模糊推理模型的明确输入信息.此外,综合考虑参数属性和工艺属性,给出具有专家经验的主面识别产生式规则建立模糊推理识别规则库.本文对所设计规则中的条件命题的权值及真度、规则的置信度和规则的激活阈值进行多轮预估、调试和修正,得出加权模糊推理规则Ri的最终形式化表达如下,其中Rmin表示面参数域最小的长宽比,Wmax表示最大筋宽,D表示当前刀具直径.
Rule1:IF(水平面或近水平面,0.64)/0.80,(参数域中两参数区间长宽比(ue-us)/(ve-vs)>Rmin或(ve-vs)/(ue-us)>Rmin,0.36)/0.50,THEN(主面,0.40,0.53);
Rule2:IF(水平面或近水平面,0.60)/0.80,(曲面的最狭长包络矩形[18]面积与自身面积之比,0.40)/0.90,THEN(主面,0.52,0.62);
Rule3:IF(水平面或近水平面,0.55)/0.80,(轮廓边中存在两条平行边e1、e2且长度与边间的距离之比le1/Dis(e1, e2)>Rmin∧le2/Dis(e1, e2)>Rmin 0.45)/0.82, THEN(主面,0.54,0.68);
Rule4:IF(水平面或近水平面,0.56)/0.80,(最大连续凹边(平凹边)长度La < Wmax,0.44)/0.52, THEN(主面,0.83,0.58);
Rule5:IF(水平面或近水平面,0.58)/0.80,(最大连续凹边(平凹边)长度La<2D,0.42)/0.52, THEN(主面,0.78,0.60);
Rule6:IF(水平面或近水平面,0.58)/0.80,(最大连续平凸边长度Le < Wmax,0.42)/0.54, THEN(主面,0.76,0.56);
Rule7:IF(水平面或近水平面,0.60)/0.80,(最大连续平凸边长度Le<2D,0.40)/0.70, THEN(主面,0.71,0.62);
Rule8:IF(水平面或近水平面,0.53)/0.80,(轮廓边除平凸切边外仅包含凸边,0.47)/0.60, THEN(主面,0.85,0.58);
Rule9:IF(水平面或近水平面0.52)/0.80,(外环除平凸切边外仅包含凸边,0.28)/0.70,(内环不包含凹边和平凹边,0.20)/0.70, THEN(主面,0.79,0.54);
Rule10:IF(水平面或近水平面,0.52)/0.80,(与轮廓加工方式匹配,0.48)/0.92, THEN(主面,0.94,0.50)
2.3 特征面关联查找在主面识别完成后得到的面集中,每个元素唯一对应1个平顶筋,因此,以主面为起点,通过遍历零件模型的属性邻接图对构成平顶筋的其他拓扑面进行关联搜索,构建完整的平顶筋,具体介绍如下.
首先,访问属性邻接图的主面的相邻顶点,综合面类型、面属性和边属性对平顶筋的过渡面、限制面和侧面进行识别,具体识别规则如下:
规则2.2(过渡面识别) 设零件模型属性邻接图为G=(Vf, Ee),u、v为Vf中两相邻顶点,对应拓扑面分别为fu、fv,公共边为e,其中fu为主面,若fv为圆柱面(近圆柱面)且e为平凹切边或平凸切边,则fv为平顶筋过渡面,即fv∈Fa.
规则2.3(限制面识别) 设零件模型属性邻接图为G=(Vf, Ee),u、v为Vf中两相邻顶点,对应拓扑面分别为fu、fv,公共边为e,e的长度为Le,fv的轮廓边中e的相邻边为ea、eb.
1) 若fu为主面,e为凸边,Le < Wmax(最大筋宽),ea、eb均为凸边,则fv为平顶筋限制面,即fv∈F1;
2) 若fu为过渡面,e//ec(ec为fu与主面的公共边),则fv为平顶筋限制面,即fv∈F1.
规则2.4(侧面识别) 设零件模型属性邻接图为G=(Vf, Ee),u、v为Vf中两相邻顶点,对应拓扑面分别为fu、fv,公共边为e,其中fu为主面,若fv∉Fa∧fv∉F1,则fv为平顶筋侧面,fv∈Fs.
然后,基于已知的侧面和限制面,进一步关联查找底圆面和底面.由于基于限制面的关联查找方法与基于侧面的关联查找方法相同,故下文仅以侧面为例对关联查找方法进行说明.
规则2.5(底圆面识别) 设零件模型属性邻接图为G=(Vf, Ee),u、v为Vf中两相邻顶点,对应拓扑面分别为fu、fv,公共边为e.
1) 若fu为侧面,e为平凹切边,fv为圆柱面(近圆柱面)、圆环面(近圆环面)或球面(近球面),则fv为平顶筋底圆面,即fv∈Fr;
2) 若fu为限制面,e为平凹切边,fv为圆柱面(近圆柱面)、圆环面(近圆环面)或球面(近球面),则fv为平顶筋底圆面,即fv∈Fr.
规则2.6(底面识别) 设零件模型属性邻接图为G=(Vf, Ee),u、v为Vf中2个相邻顶点,对应拓扑面分别为fu、fv,公共边为e.
1) 若fu为底圆面,e为平凹切边,fv为平面(近平面),则fv为平顶筋底面,即fv∈Fb;
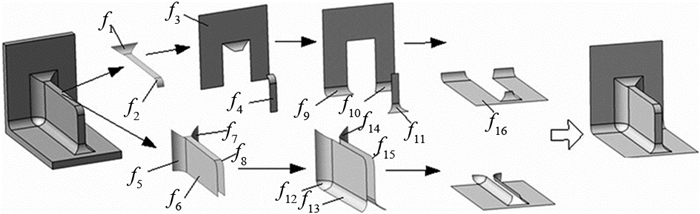
2) 若fv为侧面或限制面,e为凹边,fv为平面(近平面),则fv为平顶筋底面,即∈fv∈Fb.图 5所示为基于上述规则的平顶筋特征面关联查找过程.首先,从主面出发,基于规则2.2和2.3查找得到过渡面(f1、f2)和限制面(f3、f4),同时基于规则2.4找到侧面(f5~f8),然后,遍历侧面和限制面的在属性邻接图中的相邻顶点,通过规则2.5关联底圆面(f9~f15),在此基础上以规则2.6完成底面(f16)的查找,最终的关联识别结果如图 5所示.
|
图 5 特征面关联查找 Fig. 5 Association search of feature surfaces |
基于模糊推理的平顶筋识别的基本流程见图 6,输入为零件模型和加工坐标系,主要分为属性邻接图构建、主面识别和特征面关联查找,步骤如下:

|
图 6 平顶筋特征识别算法 Fig. 6 Algorithm for planar-top rib recognition |
1) 交互选取加工坐标系,从零件模型中提取拓扑面及其相邻边;
2) 属性邻接图构建.依据零件模型上的拓扑面和相邻边构建邻接图,并分别计算面属性和边属性;
3) 依次遍历属性邻接图的顶点,选取顶点对应的拓扑面;
4) 主面识别.将属性信息值转化为加权模糊推理规则中的条件命题,并进行规则匹配与规则中结论的真度计算,通过合成得到结论的总真度;
5) 依据结论的总真度判断是否为主面,若是,则转6);若不是,则转7);
6) 特征面关联查找.从上一步中所得的主面出发,关联查找得到完整的平顶筋面集;
7) 判断属性邻接图中顶点是否全部遍历完,若是,则算法结束;否则,转3).
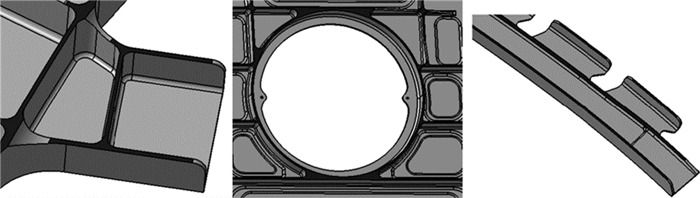
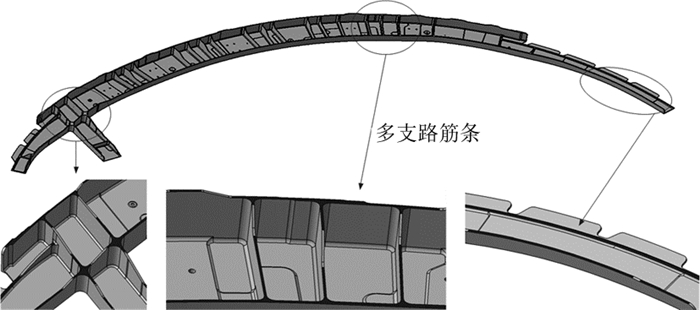
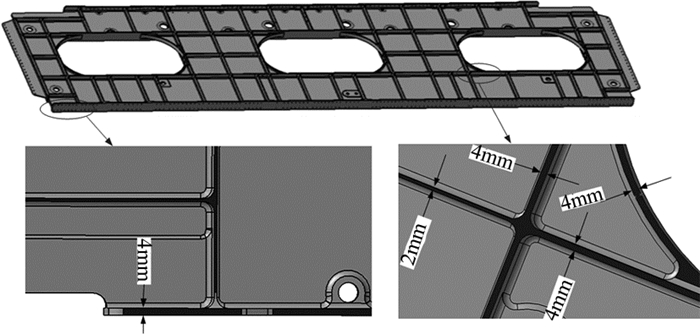
该算法已在CATIA平台上以VC++为编程语言进行了开发和实例验证,并已集成到数控加工系统中.本文实例测试在Windows7系统上进行,电脑配置为Inter(R) Pentium(R) P6000 @1.87 GHz,内存为3 GB.实例测试零件均为飞机大型结构件,包含各种不同顶面类型的筋即平顶筋、斜顶筋和曲顶筋,以及各类不同的端头支撑类型(如图 7所示),且存在复杂的多支路筋条(如图 8细节图所示),而筋的宽度一般为2~5 mm,如图 9所示双面壁板,筋的宽度为2 mm和4 mm两个系列,因此,所测零件类型和筋类型均具有典型性和代表性.
|
图 7 框类模型a及其识别结果 Fig. 7 Frame model a and recognizing results |
|
图 8 框类模型b及其识别结果 Fig. 8 Frame model b and recognizing results |
|
图 9 双面壁板模型c及其识别结果 Fig. 9 Double-face panel model c and recognizing results |
表 1为与平顶筋识别紧密相关的零件参数,包括零件整体尺寸S(零件的长、宽、高)、筋的宽度系列尺寸W和平顶筋面个数Nr.表 2为与识别规则相关的阈值(最大筋宽Wmax,面参数域最小长宽比Rmin、当前刀具直径D)、算法运行时间T和识别出的平顶筋面的个数N′r.如图 7~9所示为典型飞机结构件的框类零件模型和壁板类零件模型,以及相应的识别结果的细节图.由图 7~9和表 1、2可以看出,本文提出的算法可正确识别出所有不同类型的平顶筋,且效率较高.
| 表 1 测试零件尺寸与特征参数 Table 1 Size and feature parameters of test models |
| 表 2 算法参数及识别结果 Table 2 Parameters of algorithm and recognition results |
为识别飞机结构件中广泛存在的平顶筋特征以实现筋加工的自动数控编程,本文提出了模糊推理的飞机结构件平顶筋特征自动识别方法,其实现的主要步骤如下:
1) 构建结构件实体模型的属性邻接图,并计算面属性和边属性,对邻接图中元素进行属性赋值;
2) 设计主面识别加权关联规则,运用模糊推理从属性邻接图中提取平顶筋主面;
3) 以平顶筋主面为种子面,搜索其他关联特征面,识别出平顶筋特征.
与前人的研究相比,本文在构建属性邻接图的基础上提出了采用模糊推理的智能算法对其中关键的面——平顶筋主面进行识别,提取出特征种子面.所述方法及后续平顶筋刀轨自动生成技术已完成开发并集成到数控加工系统中应用于某航空企业,其使用范围已涵盖各类机型超过1 000项零件.经实例测试及应用表明,该算法能正确且快速地识别出飞机结构件中的平顶筋特征,并能直接映射到后续的加工操作中,实现筋特征加工的自动数控编程.
| [1] |
LI Y, WANG W, LIU X, et al. Definition and recognition of rib features in aircraft structural part[J]. International Journal of Computer Integrated Manufacturing, 2014, 27(1): 1-19. |
| [2] |
LI Y G, DING Y F, MOU W P, et al. Feature recognition technology for aircraft structural parts based on a holistic attribute adjacency graph[J]. Proceedings of the Institution of Mechanical Engineers, Part B:Journal of Engineering Manufacture, 2010, 224(2): 271-278. DOI:10.1243/09544054JEM1634 |
| [3] |
GRAYER A R. The automatic production of machined components starting from a stored geometric description[M]. Cambridge: University of Cambridge, 1975.
|
| [4] |
KYPRIANOU L K. Shape classification in computer-aided design[D]. Cambridge: University of Cambridge, 1980. https://www.sciencedirect.com/science/article/pii/B978086103058350018X
|
| [5] |
SHEEN B T, YOU C F. Tool Path generation for arbitrary pockets with islands[J]. Journal of Intelligent Manufacturing, 2006, 17: 275-283. DOI:10.1007/s10845-005-0006-9 |
| [6] |
MARCHETTA M G, FORRADELLAS R Q. An artificial intelligence planning approach to manufacturing feature recognition[J]. Computer-Aided Design, 2010, 42(3): 248-256. DOI:10.1016/j.cad.2009.11.007 |
| [7] |
YU F F, DU B R, REN W J, et al. Slicing recognition of aircraft integral panel generalized pocket[J]. Chinese Journal of Aeronautics, 2008, 21(6): 585-592. DOI:10.1016/S1000-9361(08)60178-8 |
| [8] |
于芳芳. 飞机整体壁板快速数控加工编程系统关键技术研究与开发[D]. 北京: 北京航空航天大学, 2008. YU Fang-fang. Research and development of rapid NC machining programming system for aircraft integral panel[D]. Beijing: Beijing University of Aeronautics and Astronautics, 2008. |
| [9] |
施建飞, 李迎光, 刘旭, 等. 基于属性边点图的飞机结构件筋特征识别方法[J]. 计算机集成制造系统, 2014, 20(3): 521-529. SHI Jian-fei, LI Ying-guang, LIU Xu, et al. Rib feature recognition method for aircraft structural parts based on vertex attributed adjacency graph[J]. Computer Integrated Manufacturing System, 2014, 20(3): 521-529. |
| [10] |
周敏, 郑国磊, 罗智波, 等. 基于约束Delaunay三角剖分的筋特征识别与构建算法[J]. 北京航空航天大学学报, 2016, 42(1): 201-210. ZHOU Min, ZHENG Guo-lei, LUO Zhi-bo, et al. Algorithm for recognizing and constructing rib feature based on constrained Delaunay triangulation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 201-210. |
| [11] |
ZHU H, LIU Y. Abstraction of semantic mid-surface based on rib-feature recognition[C]//ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Boston: ASME, 2015: V01AT02A003.
|
| [12] |
ZHU H, SHAO Y, LIU Y, et al. Automatic hierarchical mid-surface abstraction of thin-walled model based on rib decomposition[J]. Advances in Engineering Software, 2016, 97: 60-71. DOI:10.1016/j.advengsoft.2016.01.007 |
| [13] |
LAI J Y, WANG M H, SONG P P, et al. Recognition and decomposition of rib features in thin-shell plastic parts for finite element analysis[J]. Computer-Aided Design and Applications, 2017, 1-16. |
| [14] |
麻芳兰. 智能设计关键技术的研究及其在甘蔗收获机械中的应用[D]. 重庆: 重庆大学, 2006. MA Fang-lan. Research on the key technologies of intelligent design and application of sugarcane harvester[D]. Chongqing: Chongqing University, 2006. http://d.wanfangdata.com.cn/Thesis_D019223.aspx |
| [15] |
闫海兵, 李迎光, 韩雄. 飞机结构件拓扑不固定特征的自动识别[J]. 中国机械工程, 2010, 21(13): 1567-1571. YAN Hai-bin, LI Ying-guang, HAN Xiong. Automatic recognition of features with variable topology for aircraft structural parts[J]. China Mechanical Engineering, 2010, 21(13): 1567-1571. |
| [16] |
范九伦. 加权模糊逻辑真值传播的计算方法[J]. 系统工程理论与实践, 2002, 9: 15-21. FAN Jiu-lun. A method to compute truth-value propagation in weighed fuzzy logic[J]. System Engineering Theory and Practice, 2002, 9: 15-21. |
| [17] |
蔡自兴, 徐光佑. 人工智能及其应用:第5版[M]. 北京: 清华大学出版社, 2016, 132-133.
|
| [18] |
周敏, 郑国磊, 陈树林. 二维图形最狭长包络矩形的求解原理及方法[J]. 图学学报, 2013, 34: 46-53. ZHOU Min, ZHENG Guo-lei, CHEN Shu-lin. Thesolution to determine the bounding rectangle with maximum aspect ratio for 2D graphics[J]. Journal of Graphics, 2013, 34: 46-53. |



