随着能源、环境问题的日益突出以及电力电子技术的不断发展,基于电压源型变流器(voltage source converter, VSC)的分布式电源得到了推广和应用.传统VSC响应快、控制灵活,但同时存在低阻尼、低惯性的不足.随着新能源对电网渗透率的提高,传统电力系统的转动惯量逐渐下降,阻尼特性逐渐恶化甚至出现负阻尼,电力系统频率稳定性、运行安全性逐渐降低[1-4].
针对上述新问题,学者提出了虚拟同步发电机的控制方法[5-6],即利用同步发电机的数学模型作为变流器功率调节的算法基础,使并网逆变器近似为传统的同步发电机,通过引入虚拟惯量提高系统的阻尼,增强电网稳定性[6].由于采用VSG控制的变流器并不完全等效为同步发电机,且变流器调节快速、灵活,系统仍可能受到不利影响,如:功率振荡.
Ma等[7-9]针对VSG技术在微电网中的应用给出了具体实现方法,表明了VSG在变流器入网控制方面的优势,但未给出相应控制参数的设计方法,同时VSG自身的稳定性未被考虑.吴恒等[10-11]建立了VSG控制的数学模型,给出了控制过程中关键参数的设计方法,但未考虑电网参数对变流器稳定性的影响以及参数导致功率振荡的潜在可能性.Zheng等[12]指出三相不平衡电网中VSG控制的功率振荡现象,并通过引入负序控制抑制了功率振荡的发生,但未阐明平衡系统中是否存在功率振荡.Zhang等[13]通过分析指出,VSG控制在系统基频处存在谐振点,导致系统存在功率振荡的问题.在此基础上,王金华等[14]提出了在VSG磁链方程中加入虚拟阻抗的抑制方法,同时指出加入的虚拟阻抗会加剧有功-无功间的耦合,降低了功率调节的准确度,但未明确虚拟电阻数值的整定方法.李武华等[15]在文献[13]的基础上进一步分析了VSG功率振荡现象,但所提振荡抑制方法同样未给出虚拟电阻数值的设计方法.
针对上述新问题,本文通过建立VSG控制的小信号动态模型,对系统功率振荡的产生机理进行了分析,指出交流侧小线路阻抗比R/X促进了功率振荡的发生.同时通过建立VSG控制的频域模型,在小线路阻抗比情况下分析确定了VSG无功调节参数对功率振荡的影响关系.针对功率振荡的理论分析,在保证系统调节性能的基础上,提出基于相位补偿和交叉前馈补偿的2种功率振荡抑制方法,同时改善了系统阻尼.最后通过搭建Simulink/Matlab仿真模型验证VSG控制存在的同步频率处功率振荡现象以及所提方法的有效性.
1 VSG基本原理与数学模型在应用VSG技术的典型微电网结构中,分布式电源或储能装置采用VSG控制,实现对电网电压和频率的支撑.如图 1所示为采用VSG控制的分布式电源逆变器并网拓扑结构及原理分析矢量示意图.

|
图 1 VSG逆变器并网控制及原理分析图 Fig. 1 Control and schematic analysis diagram of inverter based on VSG |
图中,Uin为直流侧电压,Cdc为直流侧稳压电容;eabc、uabc和ugabc分别为VSG虚拟电动势、输出电压和电网电压,iabc为输出电流;E和U分别表示稳态时的VSG虚拟电势和电网电压;δ和φ分别为VSG虚拟功角与负载功率因数角;Lf和Rf分别为滤波电感和等效电阻,Cf为滤波电容;Lg和Rg分别为并网线路的电感和电阻;Z=R+jX为等效线路阻抗,X=ωL为交流测线路总感抗(L=Lf +Lg),线路总电阻为R=Rf+Rg;Pref和Qref分别为有功功率和无功功率指令;uref为控制输出参考信号.
采用同步发电机的二阶模型作为VSG控制的算法基础,由2部分组成.
1) 机械运动部分.
| $ \left. \begin{array}{l} \frac{{{\rm{d}}\Delta \delta }}{{{\rm{d}}t}} = \omega - {\omega _{\rm{N}}},\\ \frac{{{\rm{d}}\Delta \omega }}{{{\rm{d}}t}} = \frac{{{\omega _{\rm{N}}}}}{{{T_{\rm{j}}}}}\left( {{P_{\rm{m}}} - {P_{\rm{u}}} - {P_{\rm{D}}}} \right). \end{array} \right\} $ | (1) |
式中:Δδ和Δω分别为功角增量和频率增量;ω和ωN分别为VSG同步频率和系统额定频率;Pm、Pu和PD分别为VSG机械功率、电功率和阻尼功率,且PD=D(ω-ωN).D和Tj分别为VSG阻尼功率系数和虚拟惯性时间常数.
2) 电磁部分:
| $ L\frac{{{\rm{d}}{i_{{\rm{abc}}}}}}{{{\rm{d}}t}} = {e_{{\rm{abc}}}} - {u_{{\rm{abc}}}} - {i_{{\rm{abc}}}}R. $ | (2) |
根据图 1(b)所示VSG原理分析矢量图,计算出VSG输出至电网的有功功率和无功功率分别为
| $ {P_{\rm{u}}} = \frac{{EU}}{{\left| Z \right|}}\sin \left( {\delta + \alpha } \right) - \frac{{{U^2}}}{{\left| Z \right|}}\sin \alpha , $ | (3) |
| $ {Q_{\rm{u}}} = \frac{{EU}}{{\left| Z \right|}}\cos \left( {\delta + \alpha } \right) - \frac{{{U^2}}}{{\left| Z \right|}}\cos \alpha . $ | (4) |
式中:α=arctan (R/X).
2 小信号动态模型建立及稳定性分析 2.1 小信号动态模型以电网电压U∠0为d轴参考,建立d-q旋转坐标系,此坐标系下的VSG电磁方程式(2)可表示为
| $ L\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{e_d}}\\ {{e_q}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{u_d}}\\ {{u_q}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} R&{ - \omega L}\\ {\omega L}&R \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right]. $ | (5) |
式中:
| $ \left. \begin{array}{l} {e_d} = E\cos \delta ,{e_q} = E\sin \delta ,\\ {u_d} = U,{u_q} = 0. \end{array} \right\} $ | (6) |
将X=ωL代入式(5)并根据式(3)求得d-q坐标系下的电流表达式为
| $ \left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {sL + R}&{ - X}\\ X&{sL + R} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{e_d} - {u_d}}\\ {{e_q} - {u_q}} \end{array}} \right]. $ | (7) |
根据瞬时无功功率理论计算d-q坐标系下VSG输出电功率为
| $ {P_{\rm{u}}} = {u_d}{i_d} + {u_q}{i_q},{Q_{\rm{u}}} = {u_q}{i_d} - {u_d}{i_q}. $ | (8) |
将式(6)、(7)代入式(8),得出功率的表达式
| $ \left. \begin{array}{l} {P_{\rm{u}}} = \frac{{\left( {sL + R} \right)\left( {EU\cos \delta - {U^2}} \right) + XEU\sin \delta }}{{{{\left( {sL + R} \right)}^2} + {X^2}}},\\ {Q_{\rm{u}}} = \frac{{ - \left( {sL + R} \right)EU\sin \delta + XEU\cos \delta - X{U^2}}}{{{{\left( {sL + R} \right)}^2} + {X^2}}}. \end{array} \right\} $ | (9) |
对比式(3)、(9)可以看出,式(3)中的功率表达式为式(9)在系统稳态时的情况.考虑系统受到小扰动,即e =E0 +ΔE, δ =δ0 +Δδ,代入式(9)进行小扰动并线性化可得
| $ \left[ {\begin{array}{*{20}{c}} {\Delta {P_{\rm{u}}}}\\ {\Delta {Q_{\rm{u}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{H_{{\rm{P \mathsf{ δ} }}}}}&{{H_{{\rm{PE}}}}}\\ {{H_{{\rm{Q \mathsf{ δ} }}}}}&{{H_{{\rm{QE}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta \delta }\\ {\Delta E} \end{array}} \right]. $ | (10) |
状态矩阵表达式如下:
| $ \left. \begin{array}{l} {H_{{\rm{P \mathsf{ δ} }}}}\left( s \right) = \frac{{X{E_0}U\cos {\delta _0} - \left( {sL + R} \right){E_0}U\sin {\delta _0}}}{{{{\left( {sL + R} \right)}^2} + {X^2}}};\\ {H_{{\rm{PE}}}}\left( s \right) = \frac{{\left( {sL + R} \right)U\cos {\delta _0} + XU\sin {\delta _0}}}{{{{\left( {sL + R} \right)}^2} + {X^2}}};\\ {H_{{\rm{Q \mathsf{ δ} }}}}\left( s \right) = \frac{{ - \left( {sL + R} \right){E_0}U\cos {\delta _0} - X{E_0}U\sin {\delta _0}}}{{{{\left( {sL + R} \right)}^2} + {X^2}}};\\ {H_{{\rm{QE}}}}\left( s \right) = \frac{{ - \left( {sL + R} \right)U\sin {\delta _0} + XU\cos {\delta _0}}}{{{{\left( {sL + R} \right)}^2} + {X^2}}}. \end{array} \right\} $ | (11) |
式中:E0和δ0分别为稳态时VSG的虚拟电动势和功角.
由小信号动态模型可以看出,VSG状态矩阵存在式(12)所示共轭极点.在线路阻抗比R/X较小时,2个共轭极点十分靠近虚轴,在控制设计不恰当时,系统极易出现同步频率处的功率振荡.
| $ {s_{1,2}} = - \frac{R}{L} \mp {\rm{j}}\omega . $ | (12) |
由2.1小节的小信号动态模型可以看出,二阶VSG模型在线路总阻抗比较小时,存在靠近虚轴的共轭极点,可能出现功率振荡,导致系统失稳.本小节根据小信号模型建立VSG控制的频域模型,分析小线路阻抗比时控制参数对系统稳定性的影响.
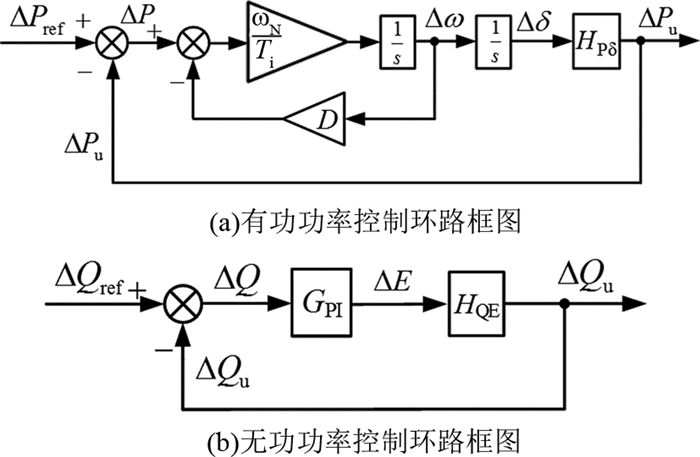
如图 2所示分别为VSG有功和无功控制环路框图,其中无功控制环路中采用PI调节器模拟同步发电机的“励磁调节”环节.
|
图 2 VSG闭环功率控制框图 Fig. 2 Closed-loop power control blocks of VSG |
根据图 2,有功和无功控制的开环传递函数表达式分别为
| $ {H_{\rm{p}}}\left( s \right) = \frac{{\Delta {P_{\rm{u}}}}}{{\Delta {P_{{\rm{ref}}}}}} = \frac{{{\omega _{\rm{N}}}}}{{s\left( {{T_{\rm{j}}}s + {\omega _{\rm{N}}}D} \right)}}{H_{{\rm{P \mathsf{ δ} }}}}\left( s \right), $ | (13) |
| $ {H_{\rm{q}}}\left( s \right) = \frac{{\Delta {Q_{\rm{u}}}}}{{\Delta {Q_{{\rm{ref}}}}}} = \frac{{\left( {{k_{{\rm{pq}}}}s + {k_{{\rm{iq}}}}} \right)}}{s}{H_{{\rm{QE}}}}\left( s \right). $ | (14) |
式中:kpq和kiq分别为无功控制环路PI调节器GPI(s)的比例系数和积分系数.
为便于利用频域模型直观分析VSG控制参数对稳定性的影响,采用如表 1所示系统参数对VSG进行频域分析,同时为保证分析结果的适用性,对上述参数以及控制参数进行标幺处理.
| 表 1 VSG并网变流器系统参数表 Table 1 Parameters of inverter based on VSG |
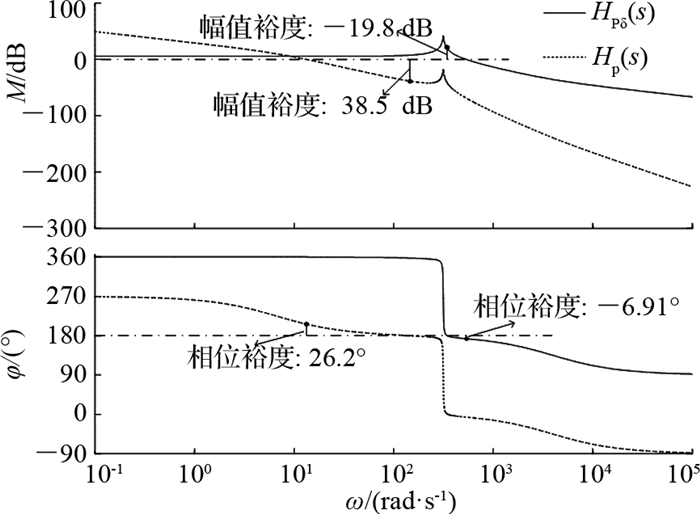
图 3给出了功角-有功传递函数HPδ(s)的bode图,可以看出,HPδ(s)在同步频率处存在谐振点以及180°的相位滞后,稳定裕度为负.同时,图 3给出了虚拟惯性时间常数Tj=1.2 s、D=0.11时的有功控制环Hp(s)的bode图,可以看出在上述参数下,有功环路具有足够的稳定裕度.VSG控制中Tj决定变流器输出惯性和对电网频率的支撑能力,通常依据变流器容量、电压等级进行整定[17].本文主要分析小线路阻抗比时无功控制环路中的参数对系统稳定性的影响.
|
图 3 有功-功角特性及有功控制环的频率响应特性曲线 Fig. 3 Frequency response plots of active-angle and active control transfer function |
图 4为无功-电压传递函数HQE(s)的bode图.在同步频率处同样存在谐振点和180°的相位滞后.结合图 2(b)和(14)得出无功控制环的闭环特征方程为

|
图 4 无功电压特性传递函数的频率响应特性曲线 Fig. 4 Frequency response plots of reactive-voltage transfer function |
| $ {G_{{\rm{PI}}}} \cdot {H_{{\rm{QE}}}} + 1 = 0. $ | (15) |
展开、等效处理后的参数根轨迹方程为
| $ \frac{{{k_{{\rm{iq}}}}U\left( { - L\sin {\delta _0} \cdot s + \left| Z \right|\cos \left( {{\delta _0} + \alpha } \right)} \right)}}{{s\left[ {{L^2}{s^2} + L\left( {2R - {k_{{\rm{pq}}}}U\sin {\delta _0}} \right)s + {Z^2} + {k_{{\rm{pq}}}}\left| Z \right|U\cos \left( {{\delta _0} + \alpha } \right)} \right]}} + 1 = 0. $ | (16) |
为保证系统的稳定性,根据经典控制理论[18],此时无功调节参数须满足下式:
| $ \left. \begin{array}{l} {k_{{\rm{pq}}}} < \frac{{2R}}{{U\sin {\delta _0}}},\\ {k_{{\rm{iq}}}} < \frac{{\left[ {{Z^2} + {k_{{\rm{pq}}}}\left| Z \right|U\cos \left( {{\delta _0} + \alpha } \right)} \right]\left( {2R - {k_{{\rm{pq}}}}U\sin {\delta _0}} \right)}}{{\left( {2R - {k_{{\rm{pq}}}}U\sin {\delta _0}} \right)LU\sin {\delta _0} + L\left| Z \right|U\cos \left( {{\delta _0} + \alpha } \right)}}. \end{array} \right\} $ | (17) |
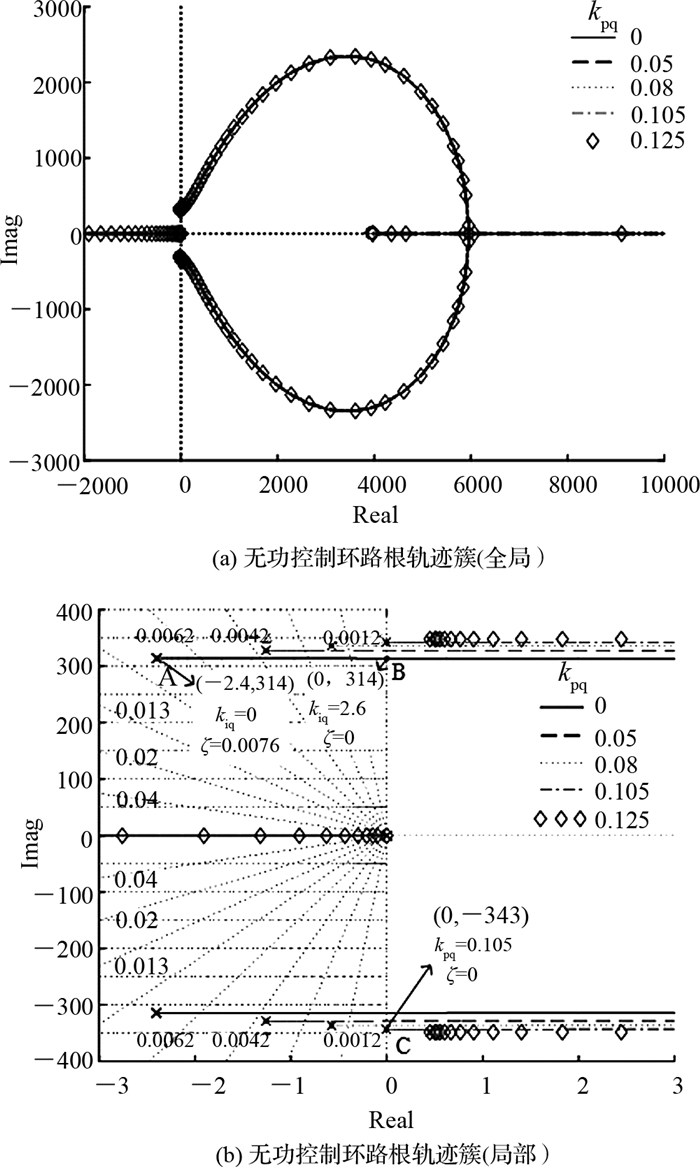
根据式(17),为保证系统稳定,kpq≤0.105且kiq受kpq限制.进一步通过根轨迹簇分析调节参数对无功控制稳定性的影响,如图 5所示,图中,ζ为控制系统阴尼.从图 5(a)可知,Hq(s)存在一个虚轴右侧的零点,在特定参数下,根轨迹存在虚轴右侧的极点,无功控制失稳;图 5(b)表明,kpq越大,根轨迹起始极点越靠近虚轴,且当kpq>0.105 (点C)时,系统始终存在虚轴右侧的极点,验证了式(17)的正确性;同时,由A、B点(kpq=0)可知,即使稳定状态下,无功控制系统阻尼很小(ζmax=0.007 6),且kiq受限(< 2.6),稳定性及调节性能均较差.
|
图 5 无功控制环路的根轨迹簇 Fig. 5 Root loci of reactive control loop |
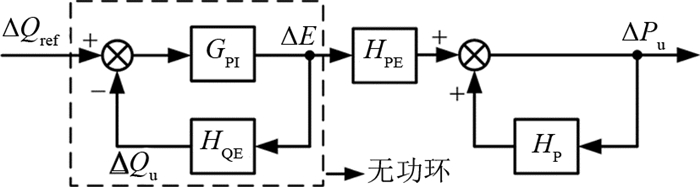
式(10)、(11)表明:无功和有功的控制环路存在耦合.由图 6可知,当无功环路控制失稳时,功率耦合关系将导致有功输出存在波动,反馈到有功控制环路后,对有功控制产生不利影响.同样有功控制会影响到无功调节的稳定性.因此,弱化功率控制间的耦合有助于改善系统控制的稳定性.
|
图 6 Root loci of reactive control loop Fig. 6 Active control block with coupling term from reactive control |
针对2.2节中VSG存在的问题,通过引入谐振点处的相位补偿环节改善系统的相频特性,提高稳定裕度;给出一种基于交叉前馈的补偿方法弱化功率控制间的耦合关系,改善系统稳定性.
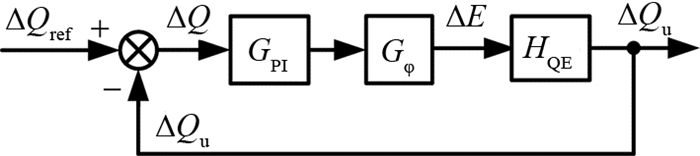
2.3.1 引入相位补偿抑制策略在无功控制环路中引入补偿环节后,控制框图如图 7所示.图中,Gφ(s)为引入的相位补偿网络,其表达式为
|
图 7 补偿后的无功功率控制环路框图 Fig. 7 Reactive control block with phase compensation |
| $ {G_\varphi }\left( {\rm{s}} \right) = \frac{{1 + aTs}}{{1 + Ts}}. $ | (18) |
式中:T为时间常数,a为分度系数(a>1).
补偿相角φc关于频率ω的函数关系表达式为
| $ {\varphi _{\rm{c}}}\left( \omega \right) = \arctan \frac{{\left( {a - 1} \right)T\omega }}{{1 + a{T^2}{\omega ^2}}}. $ | (19) |
对φc求导,求得相角极值所对应频率为
| $ {\omega _{\rm{m}}} = \frac{1}{{T\sqrt a }}. $ | (20) |
相角极值为
| $ {\varphi _{\rm{m}}} = \arcsin \frac{{a - 1}}{{a + 1}}. $ | (21) |
为保证控制系统具有足够的稳定裕度和动态性能,通常设计控制系统的相角裕度为45°~70°[18].考虑初始无功控制环路的负相角裕度,设置补偿器最大补偿相角为50°,且根据(10),选取ωm=ωN.计算得相位补偿器参数T=1.16e-3, a=7.55.
参考2.2节,对引入补偿网络后的无功控制环路进行频域分析.可以计算出,闭环极点均位于虚轴及其左侧情况时,比例系数需满足kpq < 2.1.通过参数根轨迹簇,观察控制参数对系统稳定性的影响,如图 8所示.

|
图 8 相位补偿后无功控制环路的根轨迹簇 Fig. 8 Root loci of reactive loop with phase compensation |
从图 8(b)可以看出,引入补偿环节后,随着kpq增大,根轨迹起始特征根先远离虚轴,而后靠近虚轴,当kpq > 2.1时,极点均位于虚轴右侧,系统失稳.对比图 8(b)可以发现,引入的补偿网络扩大了控制参数的整定范围且提高了控制系统阻尼ζ,有助于提高无功功率的控制精度和响应速度.
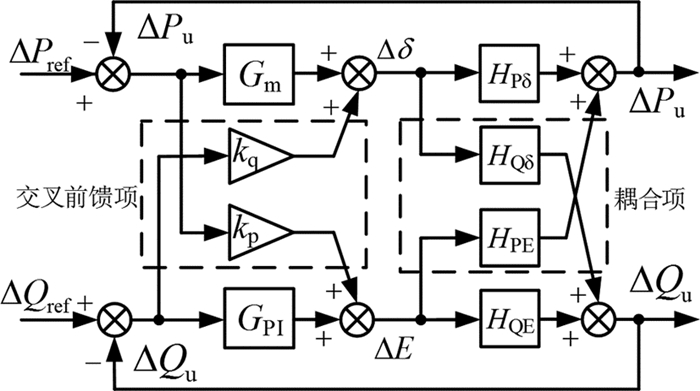
2.3.2 交叉前馈补偿抑制策略为弱化VSG功率耦合对控制稳定性的影响,在VSG控制环路里引入功率波动的交叉前馈补偿环节,如图 9所示.图中kp、kq分别为有功和无功功率波动的交叉前馈补偿系数.Gm(s)为VSG转子运动方程的传递函数,其表达式为
|
图 9 交叉前馈补偿后的VSG整体控制框图 Fig. 9 Control block with cross feed forward compensation of VSG |
| $ {G_{\rm{m}}}\left( s \right) = \frac{{{\omega _{\rm{N}}}}}{{s\left( {{T_{\rm{j}}}s + {\omega _{\rm{N}}}D} \right)}}. $ | (22) |
根据式(10)所示小扰动下功率波动状态矩阵及如图 9所示引入交叉前馈补偿后的VSG控制框图,为降低无功控制对有功控制的耦合影响,引入前馈补偿项后有功控制环中功角小扰动需满足
| $ \Delta \delta = \left( {\Delta {P_{{\rm{ref}}}} - \Delta {P_{\rm{u}}}} \right){G_{\rm{m}}} - \frac{{{H_{{\rm{PE}}}}}}{{{H_{{\rm{P \mathsf{ δ} }}}}}}{G_{{\rm{PI}}}}\left( {\Delta {Q_{{\rm{ref}}}} - \Delta {Q_{\rm{u}}}} \right), $ | (23) |
即kq表达式为
| $ {k_{\rm{q}}} = - \frac{{{H_{{\rm{PE}}}}}}{{{H_{{\rm{P \mathsf{ δ} }}}}}}{G_{{\rm{PI}}}}. $ | (24) |
同理,引入前馈补偿后无功控制环中电动势小扰动需满足
| $ \Delta E = \left( {\Delta {Q_{{\rm{ref}}}} - \Delta {Q_{\rm{u}}}} \right){G_{{\rm{PI}}}} - \frac{{{H_{{\rm{QE}}}}}}{{{H_{{\rm{Q \mathsf{ δ} }}}}}}{G_{\rm{m}}}\left( {\Delta {P_{{\rm{ref}}}} - \Delta {P_{\rm{u}}}} \right). $ | (25) |
即kp表达式为
| $ {k_{\rm{p}}} = - \frac{{{H_{{\rm{Q \mathsf{ δ} }}}}}}{{{H_{{\rm{QE}}}}}}{G_{\rm{m}}}. $ | (26) |
式(24)、(26)分别给出了前馈补偿系数kq、kp的频域表达式,为抑制瞬时有功功率中的脉动量对输出频率和功角的影响,VSG控制截止频率应在基波频率的1/5内[10].补偿系数可依据上述频域表达式在10 Hz内的幅频特性和相频特性整定.
3 仿真验证为了验证上述理论分析的正确性,利用Simulink/Matlab搭建了容量为20 kVA的三相并网逆变器仿真模型.模型具体参数与表 1一致.
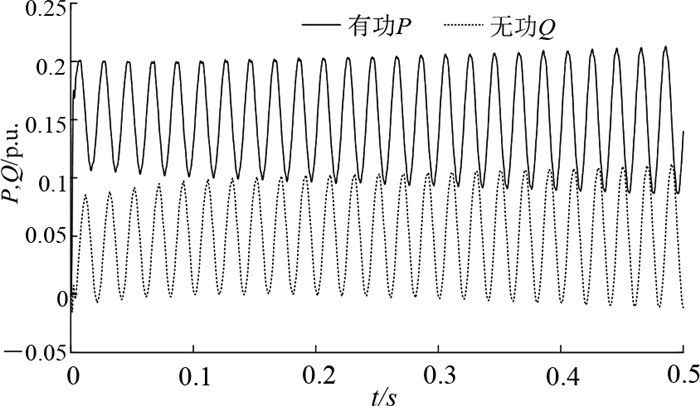
3.1 功率振荡现象验证在没有引入补偿环节情况下运行仿真模型,设定起始时刻VSG变流器功率指令为:有功指令0.15 pu、无功指令0.05 pu.选取功率调节参数kpq=0.01, kiq=5,观察功率动态变化,如图 10所示.
|
图 10 输出功率的同步频率振荡波形 Fig. 10 Power oscillation waveforms at 50 Hz of VSG |
在上述无功调节参数下,VSG变流器输出功率存在同步频率处的振荡现象.验证了2.1小节中关于小线路阻抗时VSG存在功率振荡的理论分析.
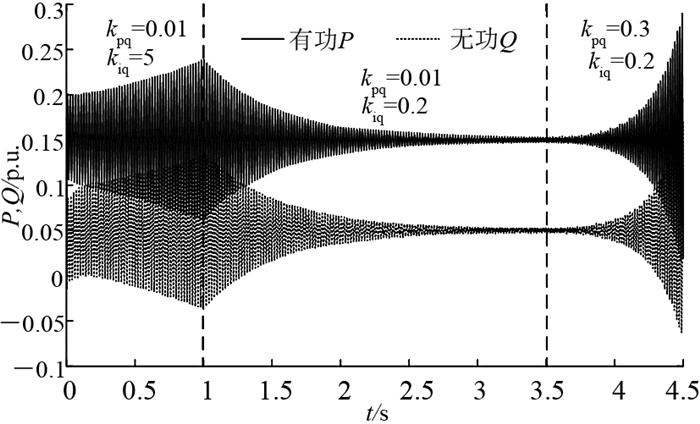
如图 11所示为不同控制参数时,功率的动态过程变化.kiq初值为5,1s后阶跃至0.2;kpq初值为0.01,2s后阶跃至0.3.从图 11可以看出,kpq=0.01且kiq=5时,功率发散振荡,系统失稳;kpq=0.01且kiq=0.2时,功率振荡逐渐收敛,但收敛速度较慢;kpq=0.3且kiq=0.2时,功率发散、振荡加剧,系统失稳.验证了2.2小节的有关小线路阻抗比时调节参数对稳定性影响的分析结果,即kpq一定时,kiq越大,稳定性越差;较大的kpq会加剧功率的发散振荡,系统失稳.稳定状态下,系统的控制阻尼很小,收敛较慢,系统稳定性以及调节性能均较差.
|
图 11 不同控制参数下的输出功率波形 Fig. 11 Power waveforms with different control parameters |
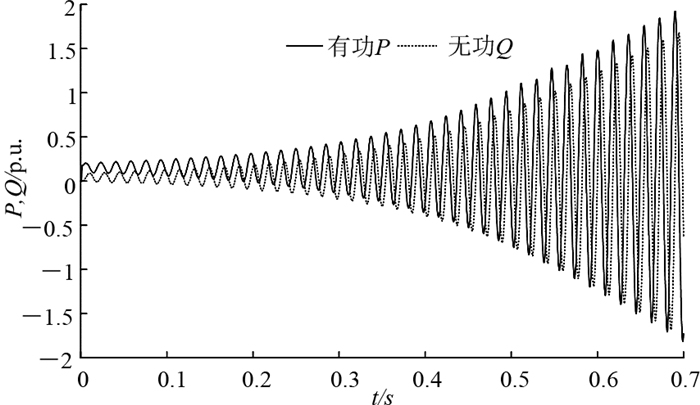
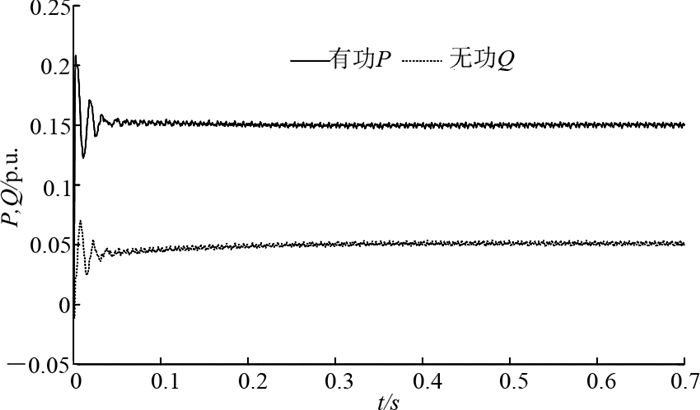
参考图 8中引入补偿环节后PI调节参数对系统稳定性影响的根轨迹图,选取kpq=0.25且kiq=5.在无补偿情况下,运行仿真,VSG输出功率指令分别为Pu=0.15 pu,Qu=0.05 pu,仿真结果如图 12所示.引入2.3.1小节中的相位补偿环节后,同等条件下运行仿真,结果如图 13所示.
|
图 12 无补偿时输出功率波形 Fig. 12 Power waveforms without any compensation |
|
图 13 相位补偿后的输出功率波形 Fig. 13 Power waveform with phase compensation |
对比图 12、13,可以看出相位补偿环节的引入有效抑制了功率振荡的发生,且系统动态过程较短,即控制系统阻尼得到提高,验证了图 8中对引入补偿环节后功率控制稳定性的分析结果,即相位补偿环节的引入扩大了参数选取范围,改善了小线路阻抗比时控制系统的阻尼特性,有利于提高系统稳定性和改善功率的调节性能.
3.2.2 交叉前馈补偿的抑制策略根据2.3.2节中引入交叉前馈补偿后的功率控制框图以及关于补偿系数整定方法的分析,确定kp=0.075、kq=-0.132.在3.2.1节中同等条件且无相位补偿环节的情况下,运行仿真模型,结果如图 14所示.

|
图 14 交叉前馈补偿后的输出功率波形 Fig. 14 Power waveform with cross feedforward compensation |
对比图 12中无补偿时的功率变化波形,VSG控制系统在引入交叉前馈补偿后处于稳定状态.表明引入的交叉前馈补偿使功率间的耦合减弱,系统稳定性得到增强,有效抑制了功率振荡的发生.
4 结语通过建立d-q坐标系下VSG的小信号动态模型,给出了输出功率与虚拟电动势、虚拟功角的关系矩阵,指出VSG功率控制间存在耦合.对状态矩阵的分析表明交流侧较小的线路阻抗比R/X使得功率控制环路存在一对靠近虚轴的极点,表现在bode图上为基波频率处的谐振点,且谐振点处180°的滞后相角降低了系统稳定裕度,导致了功率振荡问题.利用VSG频域模型和根轨迹法给出小线路阻抗比时无功调节参数与功率振荡关系.针对本文VSG功率振荡现象,提出引入相位补偿和交叉前馈补偿的2种功率振荡抑制方法,方法实现简单、有利于扩大参数设计范围、提高控制稳定裕度、弱化功率耦合,整体改善了系统稳定性.对VSG在低线路阻抗比或接入小短路比电网的应用中改善控制稳定性具有一定意义.通过Simulink/Matlab仿真验证了对功率振荡理论分析的正确性,以及上述2种抑制方法的有效性.
| [1] |
王成山, 李鹏. 分布式发电、微网与智能配电网的发展与挑战[J]. 电力系统自动化, 2010, 34(2): 10-14. WANG Cheng-shan, LI Peng. Development and challenges of distributed generation, the micro-grid and smart distribution system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-14. |
| [2] |
CARRASCO J M, FRANQUEDO L G, BIALASIEWICA J T, et al. Power-electronic systems for the grid integration of renewable energy sources:a survey[J]. IEEE Transactions on Industrial Electronics, 2006, 53(4): 1002-1016. DOI:10.1109/TIE.2006.878356 |
| [3] |
SHARMA R, SINGH M, JAIN D K. Power system stability analysis with large penetration of distributed generation[C]//20146th IEEE Power India International Conference. Delhi: PⅡCON, 2014: 1-6. http://ieeexplore.ieee.org/document/7117685/
|
| [4] |
GHEPRGHE S, GOLOVANOV N, CRISTIAN G, et al. The connection of renewable sources to the grid. Influences and power quality issues[C]//10th International Symposium on Advanced Topics in Electrical Engineering. Bucharest: ATEE, 2017: 313-318. http://www.ijera.com/papers/Vol4_issue3/Version%201/DH4301636643.pdf
|
| [5] |
郑天文, 陈来军, 陈天一, 等. 虚拟同步发电机技术及展望[J]. 电力系统自动化, 2015, 39(21): 165-171. ZHENG Tian-wen, CHEN Lai-jun, CHEN Tian-yi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-171. DOI:10.7500/AEPS20150508006 |
| [6] |
ZHONG Q C, WEISS G. Synchronverters:Inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1266. DOI:10.1109/TIE.2010.2048839 |
| [7] |
MA Y W, CAO W C, LIU Y, et al. Virtual synchronous generator control of full converter wind turbines with short term energy storage[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 8821-8830. |
| [8] |
张兴, 朱德斌, 徐海珍. 分布式发电中的虚拟同步发电机技术[J]. 电源学报, 2012, 10(3): 1-6. ZHANG Xing, ZHU De-bin, XU Hai-zhen. Review of virtual synchronous generator technology in distributed generation[J]. Journal of Power Supply, 2012, 10(3): 1-6. |
| [9] |
吕志鹏, 盛万兴, 钟庆昌, 等. 虚拟同步发电机及其在微电网中的应用[J]. 中国电机工程学报, 2014, 34(16): 2591-2603. LV Zhi-peng, SHENG Wan-xing, ZHONG Qing-chang, et al. Virtual synchronous generator and its applications in micro-grid[J]. Proceedings of the CSEE, 2014, 34(16): 2591-2603. |
| [10] |
吴恒, 阮新波, 杨东升, 等. 虚拟同步发电机功率环的建模与参数设计[J]. 中国电机工程学报, 2015, 35(24): 6508-6518. WU Heng, RUAN Xin-bo, YANG Dong-sheng, et al. Modeling of the power loop and parameter design of virtual synchronous generators[J]. Proceedings of the CSEE, 2015, 35(24): 6508-6518. |
| [11] |
孟建辉, 王毅, 石新春, 等. 基于虚拟同步发电机的分布式逆变电源控制策略及参数分析[J]. 电工技术学报, 2014, 29(12): 1-10. MENG Jian-hui, WANG Yi, SHI Xin-chun, et al. Control strategy and parameter analysis of distributed inverters based on VSG[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 1-10. DOI:10.3969/j.issn.1000-6753.2014.12.001 |
| [12] |
ZHENG T W, CHEN L J, ZHANG H N, et al. Control strategy for suppressing power oscillation of virtual synchronous generator under unbalanced grid voltage[C]//International Conference on Renewable Power Generation. Beijing: RPG, 2015: 1-5. http://digital-library.theiet.org/content/conferences/10.1049/cp.2015.0313
|
| [13] |
ZHANG L D, HARNEFORS L, NEE H P. Power synchronization control of grid-connected voltage-source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820. DOI:10.1109/TPWRS.2009.2032231 |
| [14] |
王金华, 王宇翔, 顾云杰, 等. 基于虚拟同步发电机控制的并网变流器同步频率谐振机理研究[J]. 电源学报, 2016, 14(2): 17-23. WANG Jin-hua, WANG Yu-xiang, GU Yun-jie, et al. Synchronous frequency resonance in grid-connected VSCs with virtual synchronous generator technology[J]. Journal of Power Supply, 2016, 14(2): 17-23. |
| [15] |
李武华, 王金华, 杨贺雅, 等. 虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J]. 中国电机工程学报, 2017, 37(2): 381-391. LI Wu-hua, WANG Jin-hua, YANG He-ya, et al. Power dynamic coupling mechanism and resonance suppression of synchronous frequency for virtual synchronous generators[J]. Proceedings of the CSEE, 2017, 37(2): 381-391. |
| [16] |
杜威, 姜齐荣, 陈蛟瑞. 微电网电源的虚拟惯性频率控制策略[J]. 电力系统自动化, 2011, 35(23): 26-31. DU Wei, JIANG Qi-rong, CHEN Jiao-rui. Frequencycontrol strategy of distributed generations based on virtual inertia in a microgrid[J]. Automation of Electric Power Systems, 2011, 35(23): 26-31. |
| [17] |
SHINTAI T, MIURA Y, ISE T. Oscillation damping of a distributed generator using a virtual synchronous generator[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 668-676. DOI:10.1109/TPWRD.2013.2281359 |
| [18] |
胡寿松. 自动控制原理:第5版[M]. 北京: 科学出版社, 2007, 217-244.
|
| [19] |
LIU J, MIURA Y, ISE T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators[J]. IEEE Transactions on Industrial Electronics, 2016, 31(5): 3600-3611. |



