2. 广东电网有限责任公司惠州供电局, 广东 惠州 516003
2. Huizhou Power Supply Bureau of Guangdong Power Grid Co., Huizhou 516003, China
近年来,多次发生的大停电事故[1]引发了人们对电网脆弱性的关注.研究表明,大停电事故的发生过程如下:由外部或内部脆弱源导致电网中某些脆弱线路退出运行,引发大范围潮流转移,进而导致连锁故障的发生,造成大面积停电[2-4].外部脆弱源主要是自然灾害,如台风、地震,内部脆弱源主要是过负荷、元件故障、控制保护及通信系统故障等[4].在电网的日常运行维护过程中,对脆弱线路加强关注与保护,可以减小大停电事故发生的概率;在自然灾害来临之前,在有限的时间、应急物资、队伍储备条件下,通过提高电网中某些脆弱线路的抗灾水平,可以高效、合理地减小灾害损失.因此,准确识别出这些脆弱线路,对保证电网的安全稳定运行具有重要意义.
电网脆弱线路辨识研究最早从暂态稳定分析角度进行.Fouad等[5]通过求取系统暂态能量函数的裕度及其对线路传输功率变化的灵敏度来识别脆弱线路.刘群英等[6]基于能量函数的观点,构建支路势能的函数模型,提出支路脆弱性的评估指标.基于暂态稳定的研究需要对能量函数进行求解,计算复杂.Watts等[7]于1998年提出“小世界网络模型”,并指出美国西部电网属于小世界网络,随后复杂网络理论被应用到电网脆弱线路辨识中,已取得较多研究成果.曹一家等[8]提出用带权重线路介数作为识别电网脆弱线路的指标;倪向萍等[9]基于复杂网络脆弱度理论构建互补脆弱指标集和综合脆弱度指标,提出了一种输电线路脆弱度评估方法.Bompard等[10-11]考虑网络结构、线路的传输容量等,定义了用于识别脆弱线路的扩展介数和网络联通性下降指标.徐林等[12-13]考虑网络拓扑、电源及负荷等因素,定义了电气介数并以此辨识电网关键线路.鞠文云等[14]基于复杂网络理论和图论中的最大流算法,给出了识别脆弱线路的流程.基于复杂网络理论识别脆弱线路的研究更多地从电网拓扑结构的角度出发,和电网本身的物理特征结合不够紧密.近几年,有学者基于熵理论来辨识电网中脆弱线路.蔡晔等[15]基于熵理论,给出电网潮流熵的概念,并结合电压等级及运行状态信息,提出了线路综合脆弱性指标,该方法侧重于从线路切除的后果来考察线路的脆弱性.李勇等[16]借助熵的概念,对过负荷和断线扰动时潮流转移的特征进行描述,提出基于潮流熵的脆弱元件评估模型,但该方法未能在评估的过程中考虑线路传输容量及运行状态
为了更全面地考虑电网拓扑结构、实时运行状态、电源负荷分布及线路传输容量等对系统安全运行有重大影响的电气信息[17],本文提出基于线路开断相对概率和开断后果的电网脆弱线路辨识新方法.首先定义单位熵综合负载率作为衡量电网脆弱性的指标,然后研究电网节点重要度评估方法,用线路两端节点的重要度修正线路开断前后电网单位熵综合负载率的变化,实现线路开断后果的衡量.线路开断相对概率由线路故障率和线路运行时因负荷波动而越限开断的相对概率两部分构成.其中,因负荷波动而越限开断的相对概率是基于直流潮流模型、电源负荷分布、线路传输容量及运行状态进行计算的.最后,以IEEE 39节点系统为例,验证所提方法的有效性.
1 单位熵综合负载率 1.1 电网综合负载率的定义电网中线路的负载率是表征系统输电能力和负荷需求是否匹配的关键性指标.文献[18-19]借助OPA模型和隐性故障模型,指出较小的线路平均负载率能够抑制电网连锁故障的传播,降低电网的脆弱性,减小大停电发生的概率,防止电网进入自组织临界态.为综合反映系统中线路的负载率,突出过负荷的影响,定义电网综合负载率指标为
| $ {\rm{LR = }}-\frac{1}{L}\sum\limits_{l = 1}^L {\mu _l^2 =-} \frac{1}{L}{\sum\limits_{l = 1}^L {\left( {\frac{{{p_l}}}{{{p_{l\;\max }}}}} \right)} ^2}. $ | (1) |
式中:μl为线路l的负载率,Pl为线路l上流过的有功潮流,Pl max为线路l的传输极限值,L为电网中线路总数.
由式(1)可以看出,由于负载率平方项的影响,当电网中没有线路过载时,电网综合负载率较低;当有线路过载时,该指标将变大.公式中负载率采用高次项可以更加突出地反映电网中线路的过载情况,而采用一次项则变为平均负载率.
1.2 单位熵综合负载率的定义电网综合负载率从整体上反映了电网输电能力和负荷需求的关系,但缺乏线路负载率分布信息.对于同样的LR,电网可能存在多种运行状态,即不同的负载率分布.文献[20]采用潮流熵来衡量电网中线路负载率的分布情况,并指出在线路平均负载率相同的情况下,潮流熵越大,电网的脆弱性越高,发生连锁故障的概率就越大.
为了更准确地反映负载率的分布情况,给出潮流熵的定义如下:
| $ {\rm{HS = }}-\sum\limits_{l = 1}^L {({\eta _l}\ln \;{\eta _l})}, {\eta _l} = {\eta _l}/\sum\limits_{l = 1}^L {{\eta _l}} . $ | (2) |
式中:ηl为线路l的负载率在电网所有线路负载率之和中的比例.
按照式(2),当电网中所有线路负载率相同时,即各线路承担的有功潮流和其传输容量成正比,此时线路潮流分布有序程度最高,潮流熵取得最大值-ln (1/L);当线路负载率差异越大,潮流分布的无序性就越高,潮流熵将越小.这虽然和传统意义上熵的含义刚好相反,但依然能够准确地度量电网负载率分布状态.
由于电网综合负载率及负载率分布能较全面地反映电网的脆弱性,定义单位熵综合负载率LSR作为衡量电网脆弱性的指标:
| $ {\rm{LSR}} = \frac{{{\rm{LR}}}}{{{\rm{HS}}}}. $ | (3) |
根据式(3),单位熵综合负载率随着电网综合负载率的增加和潮流熵的减小而增大.系统中线路过载情况越严重,线路负载率分布越无序,LSR就越高,电网的脆弱性越高,发生连锁故障的概率就越大.
2 基于HITS算法的电网节点重要度评估对电网重要节点的攻击会导致电网最大联通能力的剧烈下降,因此进行电网关键线路辨识时,线路两端所连接节点的重要度也是需要考虑的一个重要因素[15].
2.1 电网与互联网的对比电网和互联网都属于复杂网络,存在一定的共性[21].两者的类比关系如下:1)电网中母线可以看作互联网中的网页,对应于有向图的节点;2)电网中的线路可以看作网页之间的超链接,对应于有向图中的边,方向由有功潮流的流向给定;3)母线的进线和出线数目类比于指向某网页的链接数目和某网页指向其他网页的链接数目,对应于有向图中节点的入度和出度.基于此,本文把应用于互联网网页重要度排序的Hypertext-Induced Topic Search (HITS)[22]算法移植到电网中来评估节点重要度.
HITS算法赋予节点2个重要度度量值:权威值和枢纽值.权威值从入度的角度来衡量节点对信息原创性的贡献,等于所有指向该节点的网页的枢纽值之和;枢纽值从出度的角度衡量节点在信息传播中的作用,等于该节点指向的所有网页的权威值之和.当把HITS算法移植到电网中时,权威值是从功率流入的角度衡量节点的重要度,枢纽值是从功率流出的角度来衡量节点的重要度.
2.2 电网节点重要度的计算方法假设电网中节点数目为N,电网拓扑结构所对应有向图G的邻接矩阵为Ho.对电网中某个节点n,记yn为该节点的权威值,zn为该节点的枢纽值,An为节点n的所有进线所连接节点的集合,Bn为节点n的所有出线所连接节点的集合,y*=(y1, y2, …, yN)为电网中所有节点的权威值向量,z*=(z1, z2, …, zN)为电网中所有节点的枢纽值向量,则有
| $ {y_n} = \sum\limits_{i \in {A_n}} {{z_i}}, {\boldsymbol{y}^*} = {\boldsymbol{H}^{\rm{T}}}{z^*}; $ | (4) |
| $ {z_n} = \sum\limits_{i \in {B_n}} {{y_i}}, {\boldsymbol{z}^*} = \boldsymbol{H}{y^*}. $ | (5) |
给定节点权威值初始向量后,HITS算法通过下式迭代计算:
| $ {\boldsymbol{y}^{*k}} = {\boldsymbol{H}^{\rm{T}}}\boldsymbol{H}{y^{*k-1}}. $ | (6) |
式中:k=1, 2, 3,…为迭代次数,得到收敛的权威值向量y*后,枢纽值向量根据z*= Hy*计算.
为弥补HITS算法计算过程中的缺陷,保证解的存在性和唯一性[23],采用式(7)代替式(6)来进行迭代[24]:
| $ {\boldsymbol{y}^{*k}} = {\{ \beta D_{\rm{c}}^{-1}({\boldsymbol{H}^{\rm{T}}}\boldsymbol{H} + p{\boldsymbol{e}^{\rm{T}}}) + (1-\beta )(1/N)\boldsymbol{e}{\boldsymbol{e}^{\rm{T}}}\} ^{\rm{T}}}{\boldsymbol{y}^{*k-1}}. $ | (7) |
其中,Dc、p是为保证迭代过程有解而引入,具体计算过程参见文献[24],β是为保证解的唯一性而引入的阻尼系数,e为N维单位向量.
考虑到电网节点功率的流入和流出相等,本文认为节点的权威值和枢纽值在节点重要度评估中具有相同的地位,采用两者之和来综合衡量节点的重要度,定义Rn为电网节点n的重要度:
| $ {R_n} = {y_n} + {z_n}. $ | (8) |
Rn的值越大,代表电网中该节点的重要度越高.
根据电网和互联网的对应关系,电网可抽象为一个有向图,应用HITS算法可以得到每个节点的权威值和枢纽值.但在电网节点重要度评估中,节点重要度不仅和电网的纯拓扑结构有关,还要结合电力系统的实际运行情况,考虑以下3方面因素进行改进.
(1) 考虑电网运行方式的影响,即线路的潮流大小.将有功潮流大小作为有向边的权重考虑,进而形成带有权重的邻接矩阵H.
(2) 对于电网中节点i所接负荷li,引入一个负荷节点nli进行处理,即在原先根据电网拓扑连接情况生成的有向图的基础上,增加相应的负荷节点nli及一条由节点i指向负荷节点nli的有向边li→nli,li→nli的潮流为负荷容量.
(3) 与负荷的处理类似,节点i上连接的发电机,引入一个发电机节点nGi和一条由发电机节点nGi指向节点i的有向边lnGi→i,边的潮流为发电机有功出力.
综上所述,基于HITS算法的电网节点重要度评估的计算流程如下:
(1) 根据电网拓扑结构以及潮流中有功的方向,生成电网拓扑的原始有向图G.
(2) 对节点所接负荷、电源进行处理,得到修正后的有向图G′.
(3) 根据有向图G′中每条线路的潮流大小,生成该有向图的含权邻接矩阵H.
(4) 给定图中所有节点的初始权威值向量
(5) 根据z*= Hy*,单位化后得到电网节点枢纽值向量z*.根据电网节点重要度的定义,计算得到电网节点的重要度R.
基于HITS算法的电网节点重要度评估模型从功率的流入和流出2个角度全面地衡量节点的重要程度,并综合考虑了负荷、电源分布以及线路潮流,上述因素密切反映了电网实际运行状态.
3 电网脆弱线路识别方法当前电网单一元件故障导致电力系统失稳而引发大停电的事故越来越少.多数大停电事故是由于某些脆弱线路故障或过载引起保护动作导致线路退出运行,引起大范围潮流转移,进而导致其他线路也过载退运,由此引发连锁故障而导致.因此,在识别电网脆弱线路时,需从后果和概率两方面考虑:1)线路开断后引起的潮流转移对电网脆弱性造成的影响.2)线路运行时开断的相对概率,包括线路自身故障率和线路运行时潮流越限的相对概率2个因素.
3.1 基于单位熵综合负载率变化的线路开断后果评估模型线路开断后,系统为维持功率平衡将发生潮流转移动态过程.系统中线路过负荷情况越严重,负载率分布越无序,线路开断对电网脆弱性的影响就越大.通过单位熵综合负载率在线路开断前后的变化,能够反映电网脆弱性的变化,因此能从故障后果角度反映该条线路的脆弱性,即有
| $ \begin{array}{l} \Delta {\rm{LSR}} = {\rm{LSR}}'-{\rm{LSR}} = \\ \frac{{\frac{1}{{L-1}}{{\sum\limits_{l = 1}^{L-1} {\left( {\frac{{P{'_l}}}{{{P_{l\;\max }}}}} \right)} }^2}}}{{ - \sum\limits_{l = 1}^{L - 1} {(\eta {'_l}ln\eta {'_l})} }} - \frac{{\frac{1}{L}{{\sum\limits_{l = 1}^L {\left( {\frac{{{P_l}}}{{{P_{l\;\max }}}}} \right)} }^2}}}{{ - \sum\limits_{l = 1}^L {(\eta {'_l}ln{\eta _l})} }}. \end{array} $ | (9) |
式中:ΔLSR表示线路l开断前后单位熵综合负载率的变化量,其他变量含义不变,带与不带上标的区别是线路l开断后与开断前的相应变量.
在节点重要度评估方法中,节点的重要度反映了节点在网架结构中的位置及拓扑连接情况、电源及负荷分布情况和实时运行方式等.连接2个重要节点的线路通常位于重要的输电通道上,两节点的重要度一定程度上反映了线路的输电功能强度[25].断开电网中2个重要节点之间的线路,将减少这2个重要节点间的电气联系,削弱系统输电能力,增大电网的脆弱性.因此即使开断前后单位熵综合负载率变化量相同的2条线路,也会由于两端节点的重要度不同,致使开断的后果有差异.
为更加全面地衡量线路开断的后果,取线路两端所连接节点重要度的算术平方根来修正线路开断前后电网单位熵负载率的变化,因此线路l开断后果ξl1用下式衡量:
| $ {\xi _{l1}} = \sqrt {{R_m}{R_n}} \times \Delta {\rm{LSR}}. $ | (10) |
式中:Rm和Rn代表线路l两端所连接节点的重要度.
3.2 线路开断相对概率评估模型线路运行时面临的开断相对概率来源于负荷随机波动导致的潮流越限跳闸和线路自身故障跳闸两方面,由以下3因素决定:1)线路抵御由负荷随机波动引起的潮流冲击的能力.线路抵御潮流冲击的能力主要由线路的传输容量、当前的传输功率共同决定. 2)潮流冲击在线路上的分布.线路受到的因负荷随机波动带来的潮流冲击与电网拓扑结构、线路电气参数、电源及负荷分布等因素有关. 3)线路自身的故障率.线路故障率受役龄、健康状态、运行环境、气象及灾害等因素影响[26-29].
为衡量某一条线路受到因负荷随机波动导致的潮流冲击大小,将潮流冲击分为全局冲击和局部冲击[16],考虑线路传输容量,采用潮流冲击与线路传输容量之比的1范数和∞范数来衡量:
| $ {\delta _1}{\rm{ = }}{\omega _1} \times \frac{1}{{{N_T}{N_D}}}\sum\limits_{t \in T} {\sum\limits_{d \in D} {\frac{{f_l^{td}}}{{{p_{l\;\max }}}}} } + {\omega _2}\mathop {\max }\limits_{t \in T, d \in D} \frac{{f_l^{td}}}{{{p_{l\;\max }}}}. $ | (11) |
式中:δl表示线路l受到因负荷随机波动导致的潮流冲击大小;fltd为发电机t注入单位功率,负荷节点d消耗单位功率在线路l上引起的功率变化,可采用直流潮流模型计算;ω1和ω2为全局冲击和局部冲击的权重,本文认为两者均为0.5;T、D为发电机和负荷节点集合,NT、ND为发电机和负荷节点的数量.
线路抵御潮流冲击的能力借助线路的负载率来刻画,因此,用下式来表示线路运行时因负荷冲击导致潮流越限而开断的概率大小:
| $ {\alpha _l} = \frac{{{\delta _l}}}{{1-{\mu _l}}}. $ | (12) |
考虑线路自身故障率,线路运行时开断的相对概率采用下式来衡量:
| $ {\xi _{l2}} = P({\lambda _l} \cup {\alpha _l}). $ | (13) |
式中:λl为线路l自身的故障率;P为概率乘法,λl和αl为2个独立事件,运算前分别进行归一化,代表线路因自身故障或过载而开断的相对概率.
3.3 电网脆弱线路识别指标及流程某些线路开断相对概率较大,但开断后对电网脆弱性影响较小,而另一些线路则可能与之相反.因此准确辨识电网脆弱线路,要综合线路开断相对概率和开断后果两方面因素.辨识电网脆弱线路的指标ξl定义如下:
| $ {\xi _l} = {\xi _{l2}} \times {\xi _{l1}}. $ | (14) |
其中,所得的电网脆弱线路指标ξl也需归一化.
电网脆弱线路识别流程如下:
1) 根据电网的运行状态,计算电网初始的单位熵综合负载率LSR;
2) 将电网抽象为有向有权图,基于HITS算法计算各节点的重要度R;
3) 基于直流潮流模型、线路负载率及传输容量、线路故障率及电源负荷分布,根据式(11)~(13)分别计算线路开断相对概率指标ξl2;
4) 依次开断线路,计算线路开断前后单位熵综合负载率变化量,结合线路两端节点重要度,根据式(10)计算线路的开断后果指标ξl1;
5) 由式(14)计算各线路的脆弱性指标ξl,归一化后从大到小进行排序,排名靠前的线路为脆弱线路.
需强调的是,在进行以上各指标计算时,不同量纲的指标进行运算时,须先进行归一化.
4 算例分析将本文提出的电网脆弱线路识别方法应用于IEEE 39节点系统.该系统有39个节点,其中发电机节点10个,34条线路,12条变压器支路,系统如图 1所示,其中,带圆圈的数字表示线路编号,不带圆圈的数字表示节点编号.本算例中,暂不考虑线路自身故障率的影响,即假设电网中所有线路自身的故障率相同.

|
图 1 IEEE 39节点系统 Fig. 1 IEEE 39-Bus system |
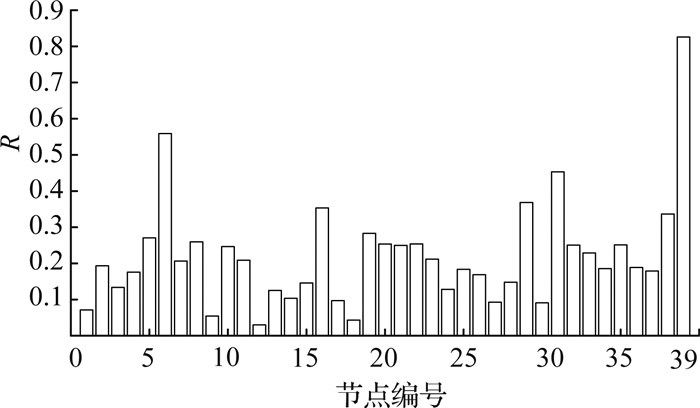
根据基于HITS算法的节点重要度评估模型得出系统中39个节点的重要度,其大小分布如图 2所示.节点39、6、31、29、16、38、19、5、8、22为排名在前10位的节点,这些节点进出线数量较多且潮流值较大,大多连接重要的电源和负荷,是功率传输的重要中枢节点.
|
图 2 IEEE 39系统中各节点重要度 Fig. 2 Node importance of each node in IEEE 39-Bus system |
根据本文方法识别出脆弱性排序在前15位的线路如表 1所示,表中列出了各线路归一化的脆弱性指标ξl,开断后果ξl1以及开断相对概率ξl2.图 3为系统中各条线路的脆弱性分布.

|
图 3 IEEE 39系统中各线路脆弱性 Fig. 3 Vulnerability of each line in IEEE 39-Bus system |
| 表 1 IEEE 39系统中脆弱性排序在前15的线路 Table 1 Top 15 of most vulnerable lines in IEEE 39-Bus system |
表 1中的脆弱线路多位于关键输电通道上,承担较大的功率输送任务,受潮流冲击影响而过载的相对概率和开断后果较大.其中,线路22为电网中最为脆弱的线路,其开断相对概率最大,开断后果位列第4.具体看,该线路为发电机33、34唯一的输电通道,正常运行时线路负载率达到75.7%,位列全网第一位;并且33、34号发电机有功出力占全系统的18.1%,因负荷随机波动对该线路造成的潮流冲击很大,容易导致该条线路过载,因此该线路开断的相对概率最大.该线路开断后,33、34号发电机将与电网失去联系,电网中其余发电机会增加出力以维持系统功率平衡,必然会导致电网中剩余线路负载率升高,因此该线路开断前后单位熵综合负载率的变化量较大,且该线路连接节点16和19,其重要度位列全网的第5、7位,开断后果较为严重.线路12的脆弱性居全网第二位,所连接节点6的重要度位列全网第二位,该线路为发电机32功率外送重要的通道,且为重载线路,其负载率在全系统位于第3位,其面临的开断相对概率及开断后果均很大,分别为系统第3、2位.
线路3、4位于电网潮流输送的关键位置,负荷随机波动带来的潮流冲击对其影响较大,但线路开断引起的潮流转移对电网脆弱性的影响较小.而线路9、27虽然受负荷随机波动的影响较小,但其开断后会大大提升电网脆弱性.因此,本文提出的脆弱指标从开断相对概率和开断后果两方面来衡量线路的脆弱性,更加合理全面.
所提出的脆弱线路辨识方法是从电网连锁故障引发大停电的相关研究出发.为了验证本文所提方法的有效性,采用文献[30]中所提出的电网连锁故障模型进行验证.该连锁故障模型考虑继电保护系统的隐性故障、系统解列、线路重载跳闸、电力系统切机切负荷和最优潮流等因素来进行电网的停电模拟,较为细致准确.在进行脆弱线路辨识时,设定快过程的仿真次数,遍历电网中的所有线路,计算各条线路引发连锁故障而导致的失负荷量.失负荷量越大,线路越脆弱.
采用上述连锁故障仿真模型对IEEE 39节点系统进行脆弱线路辨识.脆弱线路辨识结果见表 2中的方法1.文献[30]认为造成系统解列的支路对系统至关重要,并将辨识出的脆弱线路分为引起系统解列和不引起系统解列2类.为方便比较,本文将引起系统解列的线路列在排序的最前面,并剔除变压器支路19-20.比较本文方法和方法1的结果可见:在脆弱性排名前11位的线路中,本文方法有8条线路和方法1相同,且这8条线路之间的排序大体相同,方法1中的线路21在本文方法中排在第12位;2种方法的辨识结果具有很大的相似性,由此说明了本文方法的有效性.
| 表 2 本文方法和其他方法的对比 Table 2 Comparison between proposed method and other methods |
文献[15]、[16]中也提出了基于潮流熵的电网脆弱线路辨识方法(分别称为方法2、3),只是方法的侧重点有所不同.表 2列出了分别采用本文方法与另外2种方法所识别出的脆弱线路的对比.
比较本文方法和方法2、3可见:在脆弱性排名前11位的线路中,方法2和本文方法有5条相同线路;方法3中,去除变压器支路19-20后有5条和本文方法相同,方法2和方法3中分别有7、8条线路位于采用本文方法的脆弱性排名的前15中;3种方法具有一定的相似性.
进一步比较本文方法和其他方法的结果发现,方法2由于仅侧重于线路切除后果,因而未能辨识出开断相对概率最大的脆弱线路22;方法3由于未考虑线路传输容量和潮流状态,未能辨识出开断后果最大的线路27,该线路开断后会发生较大范围的潮流转移,发生三相接地短路故障后切除会引起系统功角失稳[8].线路9在方法2和方法3的脆弱性排名中位于第1位,而在本文方法中仅排在第14位,原因如下:方法2辨识脆弱线路更多地从线路开断后果进行,并用电压、运行状态等信息进行修正,系统潮流熵在线路9开断前后变化很大,这一点在方法2和本文方法中均得到印证,但方法2未能考虑线路在运行时因潮流冲击过载的可能性,而线路9运行时开断的相对概率很小;方法3在评估线路因潮流冲击而过载开断的相对概率时,未能考虑线路的实时传输功率和传输容量,导致评估得到的线路运行时开断的相对概率偏大,而线路9运行时的负载率仅为44.7%,抵抗潮流冲击的能力较强.以上对比说明采用本文方法来辨识脆弱线路更为全面有效.
5 结语大停电事故多是由于电网中的少部分脆弱线路因故障或过载而导致保护动作切除后,在潮流转移的过程中引发连锁跳闸导致.本文从大停电发生机理出发,综合线路运行时开断的相对概率和开断后果两方面来辨识脆弱线路.定义单位熵综合负载率来表征系统中线路的过载情况和负载率分布,反映电网脆弱性.引入网页排序HITS算法,从功率的流入和流出角度来准确评估电网节点重要度.结合开断前后单位熵综合负载率的变化和两端节点的重要度,能全面刻画线路的开断后果.除考虑线路自身故障率外,负荷随机波动导致线路潮流越限开断的概率也被计及,使线路运行时开断的相对概率和电网实时运行状态密切相关.算例表明,本文所提出的基于开断后果和开断相对概率的线路脆弱性辨识指标合理有效;对脆弱线路加强关注与保护,有利于电网安全稳定运行.
| [1] |
石立宝, 史中英, 姚良忠, 等. 现代电力系统连锁性大停电事故机理研究综述[J]. 电网技术, 2010(3): 48-54. SHI Ying-bao, SHI Zhong-ying, YAO Liang-zhong. A review of mechanism of large cascading failure blackouts of modern power system[J]. Power System Technology, 2010(3): 48-54. |
| [2] |
印永华, 郭剑波, 赵建军. 美加"8·14"大停电事故初步分析以及应吸取的教训[J]. 电网技术, 2003, 27(10): 8-11. YIN Yong-hua, GUO Jian-bo, ZHAO Jian-jun. Preliminary analysis of large scale blackout in interconnected north America power grid on August 14 and lessons to be drawn[J]. Power System Technology, 2003, 27(10): 8-11. |
| [3] |
高翔, 庄侃沁, 孙勇. 西欧电网"11, 4"大停电事故的启示[J]. 电网技术, 2007, 31(1): 25-31. GAO Xiang, ZHUANG Kan-qin, SUN Yong. Lessons and enlightenment from blackout occurred in UCTE grid on November 4, 2006[J]. Power System Technology, 2007, 31(1): 25-31. |
| [4] |
LIU B C C, JUNG J, HEYDT G T, et al. The strategic power infrastructure defense (SPID) system:a conceptual design[J]. Control Systems, IEEE, 2000, 20(4): 40-52. DOI:10.1109/37.856178 |
| [5] |
FOUAD A A, ZHOU Q, VITTAL V. System vulnerability as a concept to assess power system dynamic security[J]. Power Systems, IEEE Transactions on, 1994, 9(2): 1009-1015. DOI:10.1109/59.317643 |
| [6] |
刘群英, 刘俊勇, 刘起方. 基于支路势能信息的电网脆弱性评估[J]. 电力系统自动化, 2008, 32(10): 6-11. LIU Qun-ying, LIU Jun-yong, LIU Qi-fang. Power grid vulnerability assessment based on branch potential energy information[J]. Automation of Electric Power Systems, 2008, 32(10): 6-11. |
| [7] |
WATTS D J, STROGATZ S H. Collective dynamics of 'small-world' networks[J]. Nature, 1998, 393(6684): 440-442. DOI:10.1038/30918 |
| [8] |
曹一家, 陈晓刚, 孙可. 基于复杂网络理论的大型电力系统脆弱线路辨识[J]. 电力自动化设备, 2006, 26(12): 1-5. CAO Yi-jia, CHEN Xiao-gang, SUN Ke. Identification of vulnerable lines in power grid based on complex network theory[J]. Electric Power Automation Equipment, 2006, 26(12): 1-5. |
| [9] |
倪向萍, 梅生伟, 张雪敏. 基于复杂网络理论的输电线路脆弱度评估方法[J]. 电力系统自动化, 2008, 32(4): 1-5. NI Xiang-ping, MEI Sheng-wei, ZHANG Xue-min. Transmission lines' vulnerability assessment based on complex network theory[J]. Automation of Electric Power Systems, 2008, 32(4): 1-5. |
| [10] |
BOMPARD E, NAPOLI R, XUE F. Extended topological approach for the assessment of structural vulnerability in transmission networks[J]. Generation, Transmission and Distribution, IET, 2010, 4(6): 716-724. DOI:10.1049/iet-gtd.2009.0452 |
| [11] |
BOMPARD E, NAPOLI R, XUE F. Analysis of structural vulnerabilities in power transmission grids[J]. International Journal of Critical Infrastructure Protection, 2009, 2(1): 5-12. |
| [12] |
徐林, 王秀丽, 王锡凡. 电气介数及其在电力系统关键线路识别中的应用[J]. 中国电机工程学报, 2010(1): 33-39. XU Lin, WANG Xiu-li, WANG Xi-fan. Electric betweenness and its application in vulnerable line identification in power system[J]. Proceedings of the CSEE, 2010(1): 33-39. |
| [13] |
WANG K, ZHANG B, ZHANG Z, et al. An electrical betweenness approach for vulnerability assessment of power grids considering the capacity of generators and load[J]. Physica A:Statistical Mechanics and its Applications, 2011, 390(23): 4692-4701. |
| [14] |
鞠文云, 李银红. 基于最大流传输贡献度的电力网关键线路和节点辨识[J]. 电力系统自动化, 2012, 36(9): 6-12. JU Wen-yun, LI Yin-hong. Iditification of criticallines and nodes in power grid based on maximum flow transmission contribution degree[J]. Automation of Electric Power Systems, 2012, 36(9): 6-12. |
| [15] |
蔡晔, 曹一家, 李勇, 等. 考虑电压等级和运行状态的电网脆弱线路辨识[J]. 中国电机工程学报, 2014, 34(13): 2124-2131. CAI Ye, CAO Yi-jia, LI yong, et al. Identification of vulnerable lines in urban power grid based on voltage grade and running state[J]. Proceedings of the CSEE, 2014, 34(13): 2124-2131. |
| [16] |
李勇, 刘俊勇, 刘晓宇, 等. 基于潮流熵的电网连锁故障传播元件的脆弱性评估[J]. 电力系统自动化, 2012, 36(19): 11-16. LI Yong, LIU Jun-yong, LIU Xiao-yu, et al. Vulnerability assessment in power grid cascading failures based on entropy of power flow[J]. Automation of Electric Power Systems, 2012, 36(19): 11-16. |
| [17] |
王锡凡. 电网可靠性评估的随机网流模型[J]. 电力系统自动化, 2006, 30(12): 1-6. WANG Xi-fan. Probabilistic network flow models for reliability evaluation of power networks[J]. Automation of Electric Power Systems, 2006, 30(12): 1-6. DOI:10.3321/j.issn:1000-1026.2006.12.001 |
| [18] |
何飞, 梅生伟, 薛安成, 等. 基于直流潮流的电力系统停电分布及自组织临界性分析[J]. 电网技术, 2006, 30(14): 7-12. HE fei, MEI Sheng-wei, XUE An-cheng, et al. Blackouts distribution and Self-organized criticality of power system based on DC power flow[J]. Power System Technology, 2006, 30(14): 7-12. DOI:10.3321/j.issn:1000-3673.2006.14.002 |
| [19] |
CHEN J, THORP J S, DOBSON I. Cascading dynamics and mitigation assessment in power system disturbances via a hidden failure model[J]. International Journal of Electrical Power and Energy Systems, 2005, 27(4): 318-326. |
| [20] |
曹一家, 王光增, 曹丽华, 等. 基于潮流熵的复杂电网自组织临界态判断模型[J]. 电力系统自动化, 2011, 35(7): 1-6. CAO Yi-jia, WANG Guang-zeng, CAO Li-hua, et al. An identification model for self-organized criticality of power grids based on power flowentropy[J]. Automation of Electric Power Systems, 2011, 35(7): 1-6. |
| [21] |
STROGATZ S H. Exploring complex networks[J]. Nature, 2001, 410(6825): 268-276. DOI:10.1038/35065725 |
| [22] |
KLEINBERG J M. Authoritative sources in a hyperlinked environment[J]. Journal of the ACM (JACM), 1999, 46(5): 604-632. DOI:10.1145/324133.324140 |
| [23] |
FARAHAT A, LOFARO T, MILLER J C, et al. Authority rankings from HITS, PageRank, and SALSA:existence, uniqueness, and effect of initialization[J]. SIAM Journal on Scientific Computing, 2006, 27(4): 1181-1201. DOI:10.1137/S1064827502412875 |
| [24] |
XIE Y, HUANG T Z. Amodel based on cocitation for web information retrieval[J]. Mathematical Problems in Engineering, 2014, 2014: 1-6. |
| [25] |
余兴祥, 刘友波, 罗辉, 等. 考虑潮流转移结构特征的输电线路脆弱度在线评估[J]. 电力科学与技术学报, 2011, 26(4): 80-87. YU Xing-xiang, LIU You-bo, LUO Hui, et al. On-line assessment for transmission line vulnerability with structure characteristics of power flow transfer considering[J]. Journal of Electric Power Science and Technology, 2011, 26(4): 80-87. |
| [26] |
王瑞祥, 夏莹, 熊小伏. 计及气象因素的输电线路维修风险分析[J]. 电网技术, 2010(1): 219-222. WANG Rui-xiang, XIA Ying, XIONG Xiao-fu. Riskanalysis method for transmission line maintenance considering meteorological factors[J]. Power System Technology, 2010(1): 219-222. |
| [27] |
杨洪明, 黄拉, 何纯芳, 等. 冰风暴灾害下输电线路故障概率预测[J]. 电网技术, 2012, 36(4): 213-218. YANG Hong-ming, HUANG La, He Chun-fang, et al. Probabilistic prediction of transmission line fault resulted from disaster of ice storm[J]. Power System Technology, 2012, 36(4): 213-218. |
| [28] |
孙羽, 王秀丽, 王建学, 等. 架空线路冰风荷载风险建模及模糊预测[J]. 中国电机工程学报, 2011, 31(7): 21-28. SUN Yu, WANG Xiu-li, WANG Jian-xue, et al. Wind and ice loading risk model and fuzzy forecast for overhead transmission lines[J]. Proceedings of the CSEE, 2011, 31(7): 21-28. |
| [29] |
姚恺丰, 于继来, 徐泰山, 等. 热带气旋引发电网群发性故障的动态事故集生成方法[J]. 电网技术, 2014, 38(6): 1593-1599. YAO Kai-feng, YU Ji-lai, XU Tai-shan, et al. A method to generate dynamic accident set for power grid clustered faults caused by tropical cyclone[J]. Power System Technology, 2014, 38(6): 1593-1599. |
| [30] |
岳贤龙, 王涛, 顾雪平, 等. 基于自组织临界理论的电网脆弱线路辨识[J]. 电力系统保护与控制, 2016, 44(15): 18-26. YUE Xian-long, WANG Tao, GU Xue-ping, et al. Vulnerableline identification of power grid based on self-organized critical theory[J]. Power System Protection and Control, 2016, 44(15): 18-26. |



