2. 北京科技大学 土木与资源工程学院, 北京 100083
2. Civil and Environmental Engineering School, University of Science and Technology Beijing, Beijing 100083, China
准晶具有准周期平移对称性和长程取向对称性[1], 其力、电、磁等特性与晶体有很大差别, 这些特殊性质使其具有重大的理论意义, 得到了广泛的关注[2-4].准晶体呈脆性[5], 对裂纹等缺陷非常敏感, 限制了其本身作为结构件的应用.苛刻的工作环境将使材料产生缺陷, 例如多物理场耦合, 这些缺陷的存在破坏了原材料(或结构)的几何或物理连续性, 故在非连续区附近将产生局部的应力集中, 进而转变为裂纹, 裂纹不断扩展, 最终导致结构非正常失效或破坏.
若考虑力电耦合的情况, 准晶的本构比各向异性纯弹性材料更加复杂.Altay等[6]研究了三维准晶材料的电弹性基本方程.Hu等[7]研究了声子场和相位子场引起的力电耦合效应, 研究表明力电耦合效应可能来自于声子场、相位子场或者同时来自于两者, 并利用群论研究了二维五次、八次、十次、十二次对称的准晶中张量的矩阵形式, 将传统晶体中的力电耦合效应和电致伸缩效应推广到了准晶中.Yu等[8]研究了一维压电准晶的基本方程和反平面裂纹问题, 并且利用复变函数方法求解了反平面椭圆孔问题, 退化之后得到了裂纹的场强度因子和能量释放率的解.
二维压电准晶的本构比一维压电更加复杂, 对考虑力电耦合情况的二维准晶裂纹问题的报道目前相对较少.传统的各向异性弹性方法(Lekhnitskii方法、Stroh方法)用于准晶问题的求解时需要扩展和重建本构, 对具有复杂本构方程的各向异性材料而言, Stroh方法在求解时具有简洁严谨的优势.Gao等[9-10]分别将Stroh方法推广到压电材料和二维准晶中, 文献[11]同样以Stroh方法求解了一维六方压电准晶三角形孔边裂纹反平面问题.
本文利用Stroh公式求得二维压电准晶全平面位移场和应力场的基本解, 采用半逆解法, 得到二维十次对称压电准晶单一Griffith裂纹的尖端场解、场强度因子解, 继而利用裂纹权函数方法求得裂纹尖端的能量释放率等.通过算例分析场强度因子和能量释放率在载荷作用下的变化规律, 并对裂纹尖端附近的应力场进行分析, 得出二维十次对称压电准晶材料裂纹问题的一些规律.
1 基本方程与Stroh公式以二维十次对称准晶为研究对象, 以x1-x2平面为准周期平面, x3方向为周期方向, x2方向为极化方向.根据准晶弹性理论[3, 6-7], 几何方程、本构方程和平衡方程分别表示为
| $ {\mathit{\boldsymbol{\varepsilon }}_{ij}} = \frac{1}{2}\left( {\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial {\mathit{\boldsymbol{x}}_j}}} + \frac{{\partial {\mathit{\boldsymbol{u}}_j}}}{{\partial {\mathit{\boldsymbol{x}}_i}}}} \right),{\mathit{\boldsymbol{w}}_{ij}} = {\partial _j}{\mathit{\boldsymbol{w}}_i},{\mathit{\boldsymbol{E}}_i} = - {\partial _i}\mathit{\boldsymbol{\varphi }}. $ | (1) |
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{ij}} = {\mathit{\boldsymbol{C}}_{ijkl}}{\mathit{\boldsymbol{\varepsilon }}_{kl}} + {\mathit{\boldsymbol{R}}_{ijkl}}{\mathit{\boldsymbol{w}}_{kl}} - \mathit{\boldsymbol{e}}_{ijl}^{\left( 1 \right)}{\mathit{\boldsymbol{E}}_l};\\ {\mathit{\boldsymbol{H}}_{ij}} = {\mathit{\boldsymbol{R}}_{klij}}{\mathit{\boldsymbol{\varepsilon }}_{kl}} + {\mathit{\boldsymbol{K}}_{ijkl}}{\mathit{\boldsymbol{w}}_{kl}} - \mathit{\boldsymbol{e}}_{ijl}^{\left( 2 \right)}{\mathit{\boldsymbol{E}}_l};\\ {\mathit{\boldsymbol{D}}_j} = \mathit{\boldsymbol{e}}_{jkl}^{\left( 1 \right)}{\mathit{\boldsymbol{\varepsilon }}_{kl}} + \mathit{\boldsymbol{e}}_{jkl}^{\left( 2 \right)}{\mathit{\boldsymbol{w}}_{kl}} + {\mathit{\boldsymbol{\xi }}_{jl}}{\mathit{\boldsymbol{E}}_l}. \end{array} \right\} $ | (2) |
| $ {\partial _j}{\mathit{\boldsymbol{\sigma }}_{ij}} = 0,\;\;\;\;{\partial _j}{\mathit{\boldsymbol{H}}_{ij}} = 0,\;\;\;\;{\partial _j}{\mathit{\boldsymbol{D}}_j} = 0. $ | (3) |
式中:ui和wi分别为物理空间中声子场位移和垂直空间中相位子场位移;σij和Hij分别为声子场和相位子场的应力;εij和wij分别为声子场和相位子场的应变;Ei为电场;Dj为电位移;Cijkl和Kijkl分别为声子场和相位子场的弹性常数;Rijkl为声子场-相位子场的耦合弹性常数;eijl(1)和eijl(2)分别为声子场和相位子场的压电常数;ξjl为介电常数.对于不同的点群, 压电常数eijl(1)和eijl(2)可能都不为0, 也可能其中之一为0 [7].
本文研究力电耦合仅存在于电场和声子场之间、电场与相位子场并无直接耦合的准晶点群, 即eijl(2)= 0, 具体弹性常数的形式详见附录(A1).各物理参数有对称性和正定性:
| $ {\mathit{\boldsymbol{C}}_{ijkl}} = {\mathit{\boldsymbol{C}}_{jikl}} = {\mathit{\boldsymbol{C}}_{klij}} = {\mathit{\boldsymbol{C}}_{ijlk}}, $ |
| $ {\mathit{\boldsymbol{K}}_{ijkl}} = {\mathit{\boldsymbol{K}}_{klij}},{\mathit{\boldsymbol{R}}_{ijkl}} = {\mathit{\boldsymbol{R}}_{jikl}}, $ |
| $ \mathit{\boldsymbol{e}}_{ijl}^{\left( 1 \right)} = \mathit{\boldsymbol{e}}_{jil}^{\left( 1 \right)},{\mathit{\boldsymbol{\xi }}_{jl}} = {\mathit{\boldsymbol{\xi }}_{lj}}, $ |
| $ {\mathit{\boldsymbol{C}}_{ijkl}}{\mathit{\boldsymbol{\varepsilon }}_{ij}}{\mathit{\boldsymbol{\varepsilon }}_{kl}} > 0,{\mathit{\boldsymbol{K}}_{ijkl}}{\mathit{\boldsymbol{w}}_{ij}}{\mathit{\boldsymbol{w}}_{kl}} > 0,{\mathit{\boldsymbol{\xi }}_{jl}}{\mathit{\boldsymbol{E}}_j}{\mathit{\boldsymbol{E}}_l} > 0. $ |
将本构方程(式(2))以张量形式统一表示为
| $ {\mathit{\boldsymbol{\sigma }}_{Ij}} = {\mathit{\boldsymbol{E}}_{IjKl}}{\mathit{\boldsymbol{u}}_{K,l}}. $ | (4) |
式中:I, K = 1, 2, 3, 4, 5, 6; j, l = 1, 2, 3.
广义位移uK和广义应力σIj以及弹性常数矩阵EIjKl为
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}_K} = {\mathit{\boldsymbol{u}}_K}\left( {K = 1,2,3} \right);{\mathit{\boldsymbol{u}}_K} = {\mathit{\boldsymbol{w}}_{K - 3}}\left( {K = 4,5} \right);\\ {\mathit{\boldsymbol{u}}_K} = \phi \left( {K = 6} \right);\\ {\mathit{\boldsymbol{\sigma }}_{Ij}} = {\mathit{\boldsymbol{\sigma }}_{Ij}}\left( {I = 1,2,3} \right);\\ {\mathit{\boldsymbol{\sigma }}_{Ij}} = {\mathit{\boldsymbol{H}}_{\left( {I - 3} \right)j}}\left( {I = 4,5} \right);{\mathit{\boldsymbol{\sigma }}_{Ij}} = {\mathit{\boldsymbol{D}}_j}\left( {I = 6} \right);\\ {\mathit{\boldsymbol{E}}_{IjKl}} = {\mathit{\boldsymbol{C}}_{IjKl}}\left( {I,K = 1,2,3} \right);{\mathit{\boldsymbol{E}}_{IjKl}} = {\mathit{\boldsymbol{\xi }}_{jl}}\left( {I,K = 6} \right);\\ {\mathit{\boldsymbol{E}}_{IjKl}} = {\mathit{\boldsymbol{K}}_{\left( {I - 3} \right)j\left( {K - 3} \right)l}}\left( {I,K = 4,5} \right);\\ {\mathit{\boldsymbol{E}}_{IjKl}} = {\mathit{\boldsymbol{R}}_{Ij\left( {K - 3} \right)l}}\left( {I = 1,2,3;K = 4,5} \right);\\ {\mathit{\boldsymbol{E}}_{IjKl}} = {\mathit{\boldsymbol{R}}_{\left( {I - 3} \right)jKl}}\left( {I = 4,5;K = 1,2,3} \right);\\ {\mathit{\boldsymbol{E}}_{IjKl}} = - \mathit{\boldsymbol{e}}_{Ijl}^{\left( 1 \right)}\left( {I = 1,2,3;K = 6} \right);\\ {\mathit{\boldsymbol{E}}_{IjKl}} = \mathit{\boldsymbol{e}}_{jKl}^{\left( 1 \right)}\left( {I = 6;K = 1,2,3} \right). \end{array} $ | (5) |
对于广义二维问题, 考虑场变量仅是x1和x2的函数, 而与x3相互独立, 平衡方程式(3)表示为
| $ {\mathit{\boldsymbol{\sigma }}_{I1,1}} + {\mathit{\boldsymbol{\sigma }}_{I2,2}} = 0. $ | (6) |
将式(4)代入到式(6)中, 得式(6)一般解[12]的形式为
| $ {\mathit{\boldsymbol{u}}_K} = {\mathit{\boldsymbol{a}}_K}\mathit{\boldsymbol{f}}\left( z \right),z = {x_1} + p{x_2}. $ | (7) |
将式(7)代入式(6), 结果以矩阵表示:
| $ \left[ {\mathit{\boldsymbol{Q}} + \mathit{\boldsymbol{p}}\left( {\mathit{\boldsymbol{R}} + {\mathit{\boldsymbol{R}}^{\rm{T}}}} \right) + {\mathit{\boldsymbol{p}}^2}\mathit{\boldsymbol{T}}} \right]\mathit{\boldsymbol{a}} = {\bf{0}}. $ | (8) |
其中, Q、R、T是6×6的矩阵:
| $ \begin{array}{l} \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{i1k1}}}&{{\mathit{\boldsymbol{R}}_{ij11}}}&{\mathit{\boldsymbol{e}}_{11l}^{\left( 1 \right)}}\\ {{\mathit{\boldsymbol{R}}_{ji11}}}&{{\mathit{\boldsymbol{K}}_{i1k1}}}&{\bf{0}}\\ {\mathit{\boldsymbol{e}}_{11l}^{\left( 1 \right){\rm{T}}}}&{\bf{0}}&{{\mathit{\boldsymbol{\xi }}_{11}}} \end{array}} \right],\mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{i1k2}}}&{{\mathit{\boldsymbol{R}}_{ij21}}}&{\mathit{\boldsymbol{e}}_{12l}^{\left( 1 \right)}}\\ {{\mathit{\boldsymbol{R}}_{ji21}}}&{{\mathit{\boldsymbol{K}}_{i1k2}}}&{\bf{0}}\\ {\mathit{\boldsymbol{e}}_{12l}^{\left( 1 \right){\rm{T}}}}&{\bf{0}}&{{\mathit{\boldsymbol{\xi }}_{12}}} \end{array}} \right],\\ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{i2k2}}}&{{\mathit{\boldsymbol{R}}_{ij22}}}&{\mathit{\boldsymbol{e}}_{22l}^{\left( 1 \right)}}\\ {{\mathit{\boldsymbol{R}}_{ji22}}}&{{\mathit{\boldsymbol{K}}_{i2k2}}}&{\bf{0}}\\ {\mathit{\boldsymbol{e}}_{22l}^{\left( 1 \right){\rm{T}}}}&{\bf{0}}&{{\mathit{\boldsymbol{\xi }}_{22}}} \end{array}} \right]. \end{array} $ | (9) |
引入广义应力矢:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\varphi }} = \mathit{\boldsymbol{bf}}\left( z \right),\\ \mathit{\boldsymbol{b}} = \left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}p\mathit{\boldsymbol{T}}} \right)\mathit{\boldsymbol{a}} = - \frac{1}{p}\left( {\mathit{\boldsymbol{Q}} + p\mathit{\boldsymbol{R}}} \right)\mathit{\boldsymbol{a}}. \end{array} \right\} $ | (10) |
式(6)中应力分量可表示为
| $ {\mathit{\boldsymbol{\sigma }}_{I1}} = - {\mathit{\boldsymbol{\varphi }}_{I,2}} = - p{\mathit{\boldsymbol{b}}_I}\mathit{\boldsymbol{f'}}\left( z \right),{\mathit{\boldsymbol{\sigma }}_{I2}} = {\mathit{\boldsymbol{\varphi }}_{I,1}} = {\mathit{\boldsymbol{b}}_I}\mathit{\boldsymbol{f'}}\left( z \right). $ | (11) |
式(8)是二次本征问题, 可以求得六对共轭的复数特征值和特征向量:
| $ {p_{\alpha + 6}} = {{\bar p}_\alpha },{\mathop{\rm Im}\nolimits} {p_\alpha } > 0,{\mathit{\boldsymbol{a}}_{\alpha + 6}} = {{\mathit{\boldsymbol{\bar a}}}_\alpha },{\mathit{\boldsymbol{b}}_{\alpha + 6}} = {{\mathit{\boldsymbol{\bar b}}}_\alpha }, $ | (12) |
其中, α=1, 2, 3, 4, 5, 6. “Im”表示复数的虚数部分, 上标横线表示共轭, 并且aα和bα有关系式(10).叠加各解, 广义位移u和广义应力函数φ的一般解表示为
| $ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{Af}}\left( z \right) + \overline {\mathit{\boldsymbol{Af}}} \left( {\bar z} \right);\mathit{\boldsymbol{\varphi }} = \mathit{\boldsymbol{Bf}}\left( z \right) + \overline {\mathit{\boldsymbol{Bf}}} \left( {\bar z} \right). $ | (13) |
| $ \left. \begin{array}{l} \mathit{\boldsymbol{A}} = \left[ {{\mathit{\boldsymbol{a}}_1},{\mathit{\boldsymbol{a}}_2},{\mathit{\boldsymbol{a}}_3},{\mathit{\boldsymbol{a}}_4},{\mathit{\boldsymbol{a}}_5},{\mathit{\boldsymbol{a}}_6}} \right],\\ \mathit{\boldsymbol{B}} = \left[ {{\mathit{\boldsymbol{b}}_1},{\mathit{\boldsymbol{b}}_2},{\mathit{\boldsymbol{b}}_3},{\mathit{\boldsymbol{b}}_4},{\mathit{\boldsymbol{b}}_5},{\mathit{\boldsymbol{b}}_6}} \right],\\ \mathit{\boldsymbol{f}}\left( z \right) = \left[ {{f_1}\left( {{z_1}} \right),{f_2}\left( {{z_2}} \right),{f_3}\left( {{z_3}} \right),} \right.\\ \;\;\;\;\;\;\;\;\;\;{\left. {{f_4}\left( {{z_4}} \right),{f_5}\left( {{z_5}} \right),{f_6}\left( {{z_6}} \right)} \right]^{\rm{T}}}. \end{array} \right\} $ | (14) |
其中, zα=x1+pαx2.对于各向异性平面, 特征矩阵A、B是非奇异的.为方便裂纹问题的求解, 引入Barnett-Lothe矩阵S、H、L和Hermitian矩阵Y:
| $ \mathit{\boldsymbol{S}} = {\rm{i}}\left( {2\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^{\rm{T}}} - \mathit{\boldsymbol{I}}} \right),\mathit{\boldsymbol{H}} = 2{\rm{i}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{A}}^{\rm{T}}},\mathit{\boldsymbol{L}} = - 2{\rm{i}}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{T}}}. $ | (15) |
| $ \mathit{\boldsymbol{Y}} = {\rm{i}}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{B}}^{ - 1}},{\mathit{\boldsymbol{H}}^{\rm{R}}} = 2{\mathop{\rm Re}\nolimits} \mathit{\boldsymbol{Y}}. $ | (16) |
Suo等[13]对弹性材料和压电材料的Hermitian矩阵Y进行了相关研究, 矩阵Y由3部分组成:与弹性相关的矩阵、与介电常数相关的矩阵以及与压电常数相关的矩阵.式(16)中Hermitian矩阵Y具有类似的组成.
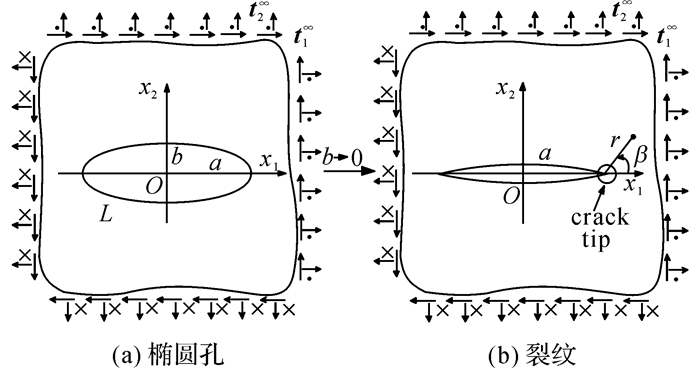
2 裂纹问题的基本解考虑二维十次对称压电准晶含有一椭圆孔L, 其长半轴和短半轴分别为a和b, 在无限远处有均匀的机械载荷和电场, 在孔表面应力和自由电荷为零, 内部充满空气, 如图 1所示.假设椭圆孔内电位移为常量[14], 边界条件采用绝缘边界条件, 孔内不承受机械载荷和电场作用, 孔内空气的介电常数与材料介电常数相比可以忽略不计.裂纹问题可以看作是椭圆孔短半轴退化为0时的极限情况.
|
图 1 准周期平面受无穷远均匀载荷作用 Fig. 1 Quasi-periodic plane with infinite uniform loading |
在无限大平面内, 椭圆孔的边界L表示为
| $ {x_1} = a\cos \psi ,\;\;\;\;{x_2} = b\sin \psi . $ | (17) |
无限远处的载荷表示为
| $ \left. \begin{array}{l} \mathit{\boldsymbol{t}}_1^\infty = {\left[ {\sigma _{11}^\infty ,\sigma _{12}^\infty ,\sigma _{13}^\infty ,H_{11}^\infty ,H_{12}^\infty ,D_1^\infty } \right]^{\rm{T}}},\\ \mathit{\boldsymbol{t}}_2^\infty = {\left[ {\sigma _{21}^\infty ,\sigma _{22}^\infty ,\sigma _{23}^\infty ,H_{21}^\infty ,H_{22}^\infty ,D_2^\infty } \right]^{\rm{T}}}, \end{array} \right\} $ | (18) |
按照叠加原理, 设应力函数矢量为
| $ \mathit{\boldsymbol{\varphi }} = {x_1}\mathit{\boldsymbol{t}}_2^\infty - {x_2}\mathit{\boldsymbol{t}}_1^\infty + \mathit{\boldsymbol{Bf}}\left( \mathit{{\zeta }} \right) + \overline {\mathit{\boldsymbol{Bf}}\left( \mathit{{\zeta }} \right)} . $ | (19) |
其中, 前2项是无穷远处载荷引起的应力, 后2项为全平面内椭圆孔扰动项.为简便, 令ζ=eiψ.由于在椭圆孔边界L上无应力和电位移, 由式(17)和(19)以及保角映射(A2), 应力边界条件为
| $ \mathit{\boldsymbol{Bf}}\left( t \right) + \overline {\mathit{\boldsymbol{Bf}}\left( t \right)} + \frac{a}{2}\left( {t + \frac{1}{t}} \right)\mathit{\boldsymbol{t}}_2^\infty - \frac{b}{{2{\rm{i}}}}\left( {t - \frac{1}{t}} \right)\mathit{\boldsymbol{t}}_1^\infty = 0. $ | (20) |
式(20)两边同时乘以
| $ \mathit{\boldsymbol{f}}\left( {{\zeta _\alpha }} \right) = \frac{1}{2}\left\langle {\zeta _\alpha ^{ - 1}} \right\rangle {\mathit{\boldsymbol{B}}^{ - 1}}\left( {a\mathit{\boldsymbol{t}}_2^\infty - {\rm{i}}b\mathit{\boldsymbol{t}}_1^\infty } \right). $ | (21) |
其中, 〈ζα-1〉=diag[ζ1-1, ζ2-1, ζ3-1, ζ4-1, ζ5-1, ζ6-1]T.
映射式(A2)将ζα平面上椭圆孔外的区域变换成pα平面上单位圆外的区域, 而将椭圆边界Lα上的点变换成单位圆上同一点ζ=eiψ.式(21)在椭圆孔外区域处处解析, 将式(21)代入式(19), 得到椭圆孔外无限远处受均匀载荷时的应力函数:
| $ \begin{array}{l} \mathit{\boldsymbol{\varphi }} = a\cos \psi \mathit{\boldsymbol{t}}_2^\infty - b\sin \psi \mathit{\boldsymbol{t}}_1^\infty + \\ \;\;\;\;\;{\mathop{\rm Re}\nolimits} \left\{ {\mathit{\boldsymbol{B}}\left\langle {\zeta _\alpha ^{ - 1}} \right\rangle {\mathit{\boldsymbol{B}}^{ - 1}}\left( { - a\mathit{\boldsymbol{t}}_2^\infty + {\rm{i}}b\mathit{\boldsymbol{t}}_1^\infty } \right)} \right\}. \end{array} $ | (22) |
当短轴b趋近于0时, 椭圆孔退化为裂纹, 如图 1(b)所示.对裂纹而言, 全纯矢量f(z)和应力函数矢量φ为
| $ \mathit{\boldsymbol{f}}\left( {{z_\alpha }} \right) = - \frac{1}{2}\left\langle {{z_\alpha } - \sqrt {z_\alpha ^2 - {a^2}} } \right\rangle {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{t}}_2^\infty , $ | (23) |
| $ \mathit{\boldsymbol{\varphi }} = {x_2}\mathit{\boldsymbol{t}}_1^\infty - {\mathop{\rm Re}\nolimits} \left\{ {\mathit{\boldsymbol{B}}\left\langle {{z_\alpha } - \sqrt {z_\alpha ^2 - {a^2}} } \right\rangle {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{t}}_2^\infty } \right\}. $ | (24) |
二维压电准晶的裂纹的应力强度因子和电位移强度因子定义为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}} = {{\left[ {K_{{\rm{II}}}^\parallel ,K_{\rm{I}}^\parallel ,K_{{\rm{III}}}^\parallel ,K_{{\rm{II}}}^ \bot ,K_{\rm{I}}^ \bot ,{K_{\rm{D}}}} \right]}^{\rm{T}}} = }\\ {\mathop {\lim }\limits_{{x_1} \to a} \sqrt {2{\rm{ \mathsf{ π} }}\left( {{x_1} - a} \right)} {\mathit{\boldsymbol{t}}_2},{x_2} = 0.} \end{array} $ | (25) |
其中, 下标“Ⅰ、Ⅱ、Ⅲ”代表 3种不同类型裂纹, 上标“‖”和“⊥”分别代表声子场和相位子场, 下标“D”代表电场.
将式(19)对x1微分后代入(25)中, 得到矩阵形式的场强度因子解:
| $ \mathit{\boldsymbol{K}} = \sqrt {{\rm{ \mathsf{ π} }}a} \mathit{\boldsymbol{t}}_2^\infty . $ | (26) |
在裂尖附近, 按照式(17), 有极坐标下复势函数:
| $ {z_\alpha } = a + r\left( {\cos \beta + {p_\alpha }\sin \beta } \right). $ | (27) |
其中, r代表距离裂纹尖端的距离, β表示与x1轴的夹角, 如图 1所示.
根据式(13)和(24), 得到极坐标下裂尖处广义位移和广义应力的场解:
| $ {\mathit{\boldsymbol{t}}_1}\left( {r,\beta } \right) = - \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}r} }}{\mathop{\rm Re}\nolimits} \mathit{\boldsymbol{B}}\left\langle {\frac{{{p_\alpha }}}{{\sqrt {\cos \beta + {p_\alpha }\sin \beta } }}} \right\rangle {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{K}}, $ | (28) |
| $ {\mathit{\boldsymbol{t}}_2}\left( {r,\beta } \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}r} }}{\mathop{\rm Re}\nolimits} \mathit{\boldsymbol{B}}\left\langle {\frac{1}{{\sqrt {\cos \beta + {p_\alpha }\sin \beta } }}} \right\rangle {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{K}}, $ | (29) |
| $ \mathit{\boldsymbol{u}}\left( {r,\beta } \right) = \sqrt {\frac{{2r}}{{\rm{ \mathsf{ π} }}}} {\mathop{\rm Re}\nolimits} \mathit{\boldsymbol{A}}\left\langle {\sqrt {\cos \beta + {p_\alpha }\sin \beta } } \right\rangle {\mathit{\boldsymbol{B}}^{ - 1}}\mathit{\boldsymbol{K}}. $ | (30) |
由(28)和(29)可知, 广义应力在裂纹尖端附近存在明显的奇异现象, 而广义位移在裂纹尖端并没有奇异性.Guo等[15]对十次对称准晶的裂纹问题的研究表明, 在裂尖处应力场具有奇异性, 声子场应力分布和场强度因子与线弹性断裂力学中的结果相同, 与本文得到的结果相似.Gao等[10]对二维准晶不考虑压电情况下的椭圆孔问题做了理论上的推导, 本文若不考虑压电效应, 可退化为与其相同的结果.
式(26)表明在无限远处均匀载荷作用下各应力强度因子是解耦的, 应力强度因子与电载荷无关.Fu等[16]的实验结果表明, 对于压电材料, 电载荷会对裂纹扩展产生影响.因此, 仅由场强度因子作为二维压电准晶断裂特征的判定依据还不够, 还需要分析二维压电准晶裂纹的能量释放率.
根据热动力学的观点, 能量释放率是裂纹整体势能的增量对裂纹扩展区域的全微分, 代表了裂纹整体势能的变化.由McMeeking等[17]对裂纹问题的求解结果, 能量释放率可以表示为
| $ G = \frac{1}{4}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{H}}^{\rm{R}}}\mathit{\boldsymbol{K}}. $ | (31) |
式中:HR由声子场、相位子场和电场的相关物理量组成.式(31)显示相位子场和电场对材料的断裂行为有明显的影响, 能量释放率G包括3部分:弹性场(包括声子场、相位子场、声子-相位子耦合场)的能量释放率、电场的能量释放率和力-电耦合效应的能量释放率.
2.2 裂尖附近作用集中载荷时的基本解在裂纹问题中,裂尖是非常重要的区域。当裂纹受到载荷作用时,裂尖会出现应力奇异现象,裂尖的开裂规律是研究的热点,在裂尖附近作用集中载荷时所表现出来的规律值得探究.
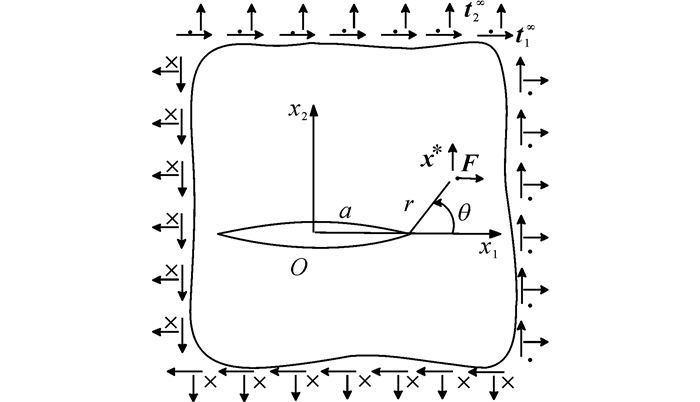
在无限域二维压电准晶中存在一Griffith裂纹, 穿透方向为x3方向, 裂纹长度2a=2 cm, 裂纹尖端附近一点x*=(a+rcos θ, rsin θ)受到集中载荷F作用, 如图 2所示:
| $ \mathit{\boldsymbol{F}} = {\left[ {f_1^\parallel ,f_2^\parallel ,f_3^\parallel ,f_1^ \bot ,f_2^ \bot ,{f_{\rm{D}}}} \right]^{\rm{T}}}. $ | (32) |
|
图 2 在无穷远处均匀载荷和裂尖集中载荷作用下的裂纹 Fig. 2 Crack with infinite uniform loading and concentrated force near crack tip |
其中, f1‖、f2‖、f3‖表示3个方向上的声子场载荷, f1⊥、f2⊥表示相位子场载荷, fD表示外加电载荷.
根据叠加原理, 问题可以分解为2部分:一部分是受到无限远处均匀载荷作用;另一部分是仅在裂纹尖端受到线力载荷作用.第一部分前面已经进行了分析, 下面主要研究第二部分问题.
在叠加了集中载荷后, 场强度因子(式(26))为
| $ \mathit{\boldsymbol{K}} = {\mathit{\boldsymbol{K}}^{\left( 1 \right)}} + {\mathit{\boldsymbol{K}}^{\left( 2 \right)}}. $ | (33) |
其中, K(1)为无限远处均匀载荷作用时的场强度因子, K(2)为在裂尖附近作用集中载荷时的场强度因子.
权函数方法是一种可以有效求解给定几何形状受到任意外加载荷作用时的应力强度因子的方法[17].二维压电准晶材料裂尖附近集中载荷对场强度因子的贡献K(2)表示为
| $ {\mathit{\boldsymbol{K}}^{\left( 2 \right)}} = \mathit{\boldsymbol{hF}}. $ | (34) |
式中:h是一个待定的六阶矩阵.
将式(34)代入式(31)中有
| $ G = \frac{1}{4}{\left( {\sqrt {{\rm{ \mathsf{ π} }}a} \mathit{\boldsymbol{t}}_2^\infty + \mathit{\boldsymbol{hF}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{H}}^{\rm{R}}}\left( {\sqrt {{\rm{ \mathsf{ π} }}a} \mathit{\boldsymbol{t}}_2^\infty + \mathit{\boldsymbol{hF}}} \right). $ | (35) |
裂纹权函数是几何边值问题的一个性质, 相对于外加载荷是独立的.McMeeking等[17]对压电材料的Griffith裂纹权函数进行了推导求解, 可以采用相同的方法得到本文的权函数, 通过势能原理和Betti互易定理,得
| $ \mathit{\boldsymbol{h}} = - \frac{1}{{{\mathit{\boldsymbol{H}}^{\rm{R}}}\sqrt {{\rm{ \mathsf{ π} }}a} }}{\mathop{\rm Re}\nolimits} \mathit{\boldsymbol{A}}\left\langle {\frac{{\sqrt {{z_\alpha } + a} }}{{\sqrt {{z_\alpha } - a} }}} \right\rangle {\mathit{\boldsymbol{B}}^{ - 1}}. $ | (36) |
转化为极坐标(r, θ)的形式为
| $ \mathit{\boldsymbol{h}} = - \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}r}}} \frac{1}{{{\mathit{\boldsymbol{H}}^{\rm{R}}}}}{\mathop{\rm Re}\nolimits} \mathit{\boldsymbol{A}}\left\langle {\frac{1}{{\sqrt {\cos \theta + {p_\alpha }\sin \theta } }}} \right\rangle {\mathit{\boldsymbol{B}}^{ - 1}}. $ | (37) |
将式(37)代入到式(35)可得受到无限远处均匀载荷和裂尖附近集中力共同作用时的能量释放率.
3 数值算例十次对称的二维压电准晶的弹性常数还未能完全获得, 假定以准晶合金Al-Ni-Co的弹性常数[18]为声子场、相位子场和声子场-相位子场耦合场的弹性常数, 以BaTiO3的压电特征参数[19]作为压电常数和介电常数, 之前的研究表明, 假定的弹性常数满足正定性[20].
为避免材料参数处于不同的数量级所导致的矩阵病态, 对材料常数进行无量纲化, 得出无量纲结果u、φ等参数:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{x}}_i^ * = \frac{{{\mathit{\boldsymbol{x}}_i}}}{l},{{\mathit{\boldsymbol{C'}}}_{ij}} = \frac{{{\mathit{\boldsymbol{C}}_{ij}}}}{{{C_{11}}}},{{\mathit{\boldsymbol{R'}}}_i} = \frac{{{\mathit{\boldsymbol{R}}_i}}}{{{R_1}}},{{\mathit{\boldsymbol{K'}}}_i} = \frac{{{C_{11}} \times {\mathit{\boldsymbol{K}}_i}}}{{R_1^2}},\\ {\left( {\mathit{\boldsymbol{e}}_{ijl}^{\left( 1 \right)}} \right)^\prime } = \frac{{\mathit{\boldsymbol{e}}_{ijl}^{\left( 1 \right)}}}{{e_{33}^{\left( 1 \right)}}},{{\mathit{\boldsymbol{\xi '}}}_{jl}} = \frac{{{\mathit{\boldsymbol{\xi }}_{jl}} \times {C_{11}}}}{{{{\left( {e_{33}^{\left( 1 \right)}} \right)}^2}}},\\ \mathit{\boldsymbol{u}} = {\left[ {\frac{{{\mathit{\boldsymbol{u}}_i}}}{l},\frac{{{R_1} \times {\mathit{\boldsymbol{w}}_j}}}{{l \times {C_{11}}}},\frac{{e_{33}^{\left( 1 \right)} \times \phi }}{{l \times {C_{11}}}}} \right]^{\rm{T}}},\\ \mathit{\boldsymbol{\varphi }} = {\left[ {\frac{{{\mathit{\boldsymbol{\sigma }}_{ij}}}}{{{C_{11}}}},\frac{{{\mathit{\boldsymbol{H}}_{mj}}}}{{{R_1}}},\frac{{{\mathit{\boldsymbol{D}}_j}}}{{e_{33}^{\left( 1 \right)}}}} \right]^{\rm{T}}}. \end{array} \right\} $ | (38) |
其中, l=0.01 m.附录(A3)给出了式(12)的特征根的具体数值, 可进一步得出式(14)的特征向量矩阵.
算例分析了分别作用如下集中载荷时的情况:工况1, F =[1,0,0,0,0,0]T;工况2, F =[0,1,0,0,0,0]T; 工况3, F =[0,0,0,0,0,1]T, 依次代表裂纹模式为Ⅱ型(滑开型裂纹)、Ⅰ型(张开型裂纹)Griffith裂纹分别加载1 N/m线力和加载1 C/m线电荷时的情况.另外, 分析加载无限远处载荷σ22∞/C11=1时, 裂纹尖端附近的应力变化情况, 以及椭圆孔退化为裂纹过程中应力和位移变化规律, 并将二维压电准晶退化为压电材料, 对比两者的裂尖位移, 并且在压电耦合系数退化为0后与非压电二维准晶进行对比.
3.1 场强度因子无量纲应力强度因子和电位移强度因子随角θ的变化如图 3所示, 其中线载荷F作用位置与裂纹尖端的距离为r=0.001 m.

|
图 3 不同工况作用下各应力强度因子变化图 Fig. 3 Changing curves of field intensity factors indifferent cases |
如图 3所示为工况1 ~ 3下的场强度因子的变化规律.其中, 纵坐标单位第一项(Pa·m1/2)为声子场应力强度因子的单位, 第二项(10-4Pa·m1/2和10-5Pa·m1/2)为相位子场应力强度因子的单位, 第三项(10-2C·m-3/2和C·m-3/2)为电位移强度因子的单位.从图 3(a)可以看出, 在工况1作用下, 各场强度因子在-π≤θ≤π的区域内均有变化.这说明虽然在远处载荷作用时各场强度因子独立, 但是在裂尖附近的声子场载荷作用下, 声子场载荷对于声子场应力强度因子、相位子场应力强度因子和电位移强度因子均有影响, 并且Ⅱ型裂纹的应力强度因子KⅡ‖变化最为明显, 其次分别是KⅠ‖、KD、KⅡ⊥、KⅠ⊥和KⅢ‖.图 3(b)表明, 工况2对应力强度因子KⅠ‖、KⅡ‖的影响更加明显, 其中KⅠ‖关于θ=0反对称, KⅡ‖曲线关于θ=0对称.图 3(c)显示, 在裂尖附近作用电载荷时, 电位移强度因子在θ=0时最小, 并且随角度θ变化, 电载荷对声子场应力强度因子KⅠ‖、KⅡ‖和KⅢ‖均有较为显著的影响.
在工况1~3作用下, 相位子场应力强度因子要远远小于声子场应力强度因子和电位移强度因子的相应值, 工况1和2的相位子场应力强度因子大于工况3的相应值.在工况1~3分别作用下, Ⅱ型、Ⅰ型以及电位移强度因子分别占了主导地位.
为了探究场强度因子随角度和半径的变化规律, 下面给出场强度因子随半径r和角度θ同时变化的等值线图, 其中0<r≤0.01 m, 0≤θ≤π.如图 4所示为在裂纹尖端附近作用集中载荷时, 应力强度因子KⅡ‖(a)和KⅠ‖(b)随载荷作用位置x*=(a+rcos θ, rsin θ)变化的等值线图.图 4(a)表明, 在工况1作用下, 当θ不变而r趋近于0时, 应力强度因子KⅡ‖逐渐变大;r不变θ趋近于0时, 应力强度因子KⅡ‖逐渐变小, 这与图 3中应力强度因子的变化趋势一致.图 4(b)应力强度因子等值线图的变化规律与图 4(a)类似, 当r增大而θ不变时, KⅠ‖变小, 而r不变θ增大时KⅠ‖先变大后减小, 在θ=2.25附近存在峰值.图 4显示, 在r→0且θ→0时, 等值线越来越密集, 可以反映出集中载荷作用在裂纹尖端时其应力强度因子的急剧变化.
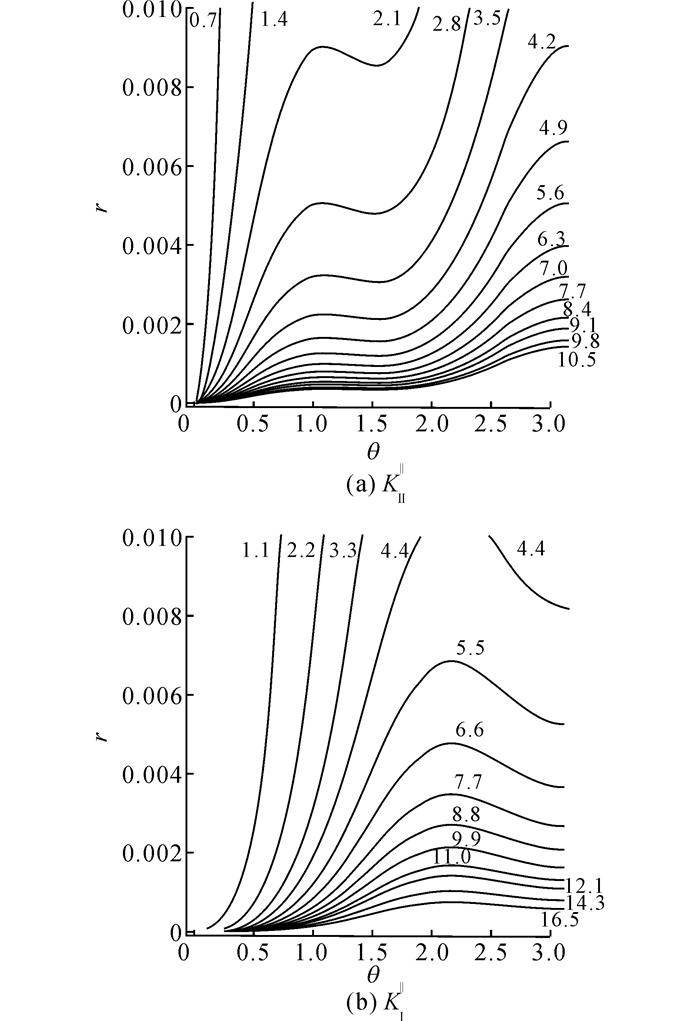
|
图 4 工况1和2作用下应力强度因子等值线图 Fig. 4 Contour maps of stress intensity factor in case 1 and 2 |
在裂尖附近作用集中载荷时(见图 2), 各个工况单独作用或者组合情况下的能量释放率随作用角度θ变化时的曲线如图 5所示.可以看出:
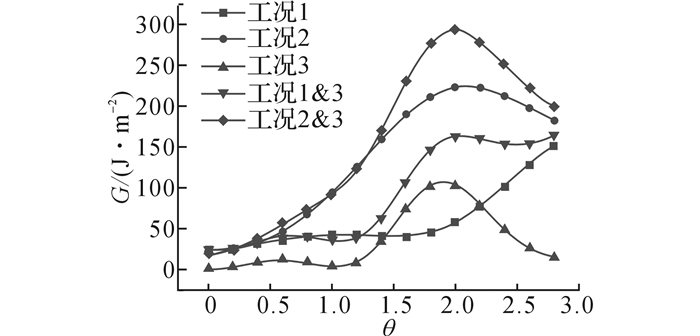
|
图 5 工况1~3、1&3和2&3分别作用下的能量释放率随角度θ变化的曲线图 Fig. 5 Changing curves of energy release rate with angle θ in case 1~3, case 1 & 3, case 2 & 3 |
1) 工况2即Ⅰ型裂纹的能量释放率比之Ⅱ型和电载荷作用时裂纹能量释放率变化更加明显;
2) 三种裂纹的能量释放率均在θ=0时处于最小值;
3) 当工况3电载荷作用时, 能量释放率在θ=0时处于最小值, 并且在θ=2附近存在峰值;
4) 组合工况1&3作用时的能量释放率比工况3单独作用时大;组合工况2&3作用时的能量释放率也明显大于工况3单独作用时.
3.3 无限远处均匀载荷作用下应力变化在无限远处作用均匀载荷时, 裂纹的扩展与作用载荷相关, 对裂纹尖端周边的应力进行分析, 可以进一步探究其变化规律.以在无限远处作用均匀载荷σ22∞/C11=1为例, 裂纹尖端附近应力变化如图 6所示.可以看出, 在无限远处作用均匀载荷时, 裂纹尖端附近的无量纲应力分量σ22/C11随着与裂纹尖端距离的减小而增大, 与裂纹尖端距离越近, 则应力σ22/C11越大, 其最大应力出现在β=1处左右, 当β接近2π时, 应力σ22/C11趋近于0.

|
图 6 无限远处均匀载荷作用下裂尖附近应力σ22/C11随角度β和距离r变化的曲线图 Fig. 6 Changing curves of stress σ22/C11 around crack tip with angle β and distance r under infinite uniform loading |
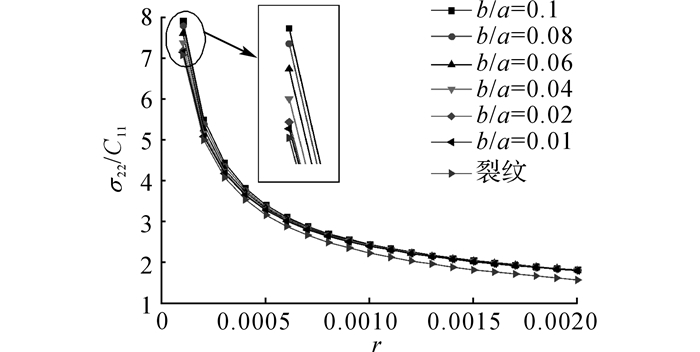
对椭圆孔退化过程中的应力进行求解, 有助于探明裂纹尖端附近的应力变化和形成规律.随着椭圆孔短半轴减小, 椭圆孔长半轴端点的应力会逐渐增大, 逐渐表现出裂纹尖端的应力奇异现象.考虑无限远处仅施加x2方向拉伸载荷σ22∞/C11=1, 椭圆孔长半轴端点附近的应力随短半轴减小时的变化如下图 7所示.
|
图 7 无限远处均匀载荷作用下椭圆孔短轴趋于0时长轴端点附近应力σ22/C11随距离r变化的曲线图 Fig. 7 Changing curves of stress σ22/C11 around endpoint of long axis for elliptical hole with distance r under remote uniform loading when short axis tends to zero. |
图 7中的位置点均位于x1轴上, 应力随r以及b/a而变化.当远离椭圆孔长轴端点时, 应力σ22/C11逐渐减小.随着b/a减小, 椭圆孔逐渐退化为裂纹, 椭圆孔长轴端点附近应力变化逐渐与裂纹尖端附近应力变化趋于一致, 在b/a减小的过程中, 靠近椭圆孔长轴端点时和远离椭圆孔长轴端点时的应力差值越来越大.另外可以发现, 越接近于椭圆孔长轴端点或裂纹尖端, 两者的应力变化规律越趋于一致.在退化为裂纹后, 长半轴端点的应力会呈现奇异性.
如图 8所示为椭圆孔b/a=0.01时长轴端点附近和裂纹尖端附近的应力等值线对比图.图 8(a)为椭圆孔长轴端点附近应力σ22/C11的等值线图, 应力随着r减小而增加.当角度趋近于π时, 位置点接近椭圆孔的边界, 应力逐渐减小为0.当b/a趋于0时, 椭圆孔退化为裂纹, 图 8(b)表明, 裂纹尖端附近应力σ22/C11随着r的增大而减小, 同时当β从0到π变化, 应力先增大后减小, 并且在接近β=2π时, 应力趋近于0.对比可以发现, 裂纹尖端附近应力等值线图的变化趋势与椭圆孔b/a=0.01时相似.

|
图 8 无限远处均匀载荷作用下应力σ22/C11的等值线图 Fig. 8 Contour map of stress σ22/C11 under infiniteuniform loading |
如图 9所示为无限远处均匀载荷作用下裂纹尖端附近位移分量u2/l随角度β变化的曲线图, 可以看出, 在裂纹尖端附近位移u2/l趋近于0, 当β从0趋近于π时, 裂纹尖端附近的位移u2/l逐渐增大, 并且随着距离裂纹尖端的距离r增大, 位移逐渐增大.

|
图 9 无限远处均匀载荷作用下裂纹尖端附近u2/l变化图 Fig. 9 Changing curves of u2/l around crack tip withinfinite uniform loading |
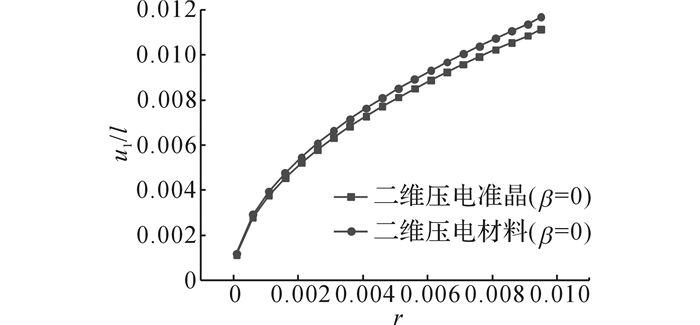
文献[21]给出了压电材料平面裂纹问题的精确解, 将表 1中材料常数代入其中, 对比压电材料与本文二维压电准晶的位移分量, 如图 10所示.可以发现, 加载无限远处均匀载荷σ22∞/C11=1时, 压电材料平面裂纹问题与二维压电准晶材料中裂尖附近位移分量变化趋势是一致的, 相位子场的存在导致的数值差别很小, 并且此差别越靠近尖端越小.
| 表 1 十次对称压电准晶材料常数 Table 1 Material constants of decagonal quasicrystals with piezoelectric effect |
|
图 10 无限远处均匀载荷作用下裂纹尖端附近位移u1/l退化前后对比图 Fig. 10 Comparison curves of displacement u1/l before and after degeneration around crack tip withinfinite uniform loading |
当压电耦合系数为0时, 二维压电准晶材料在理论上应可以退化为非压电准晶材料.本文通过计算文献[10]中的研究结果, 得到非压电二维准晶的应力场分量, 将压电准晶退化解与非压电二维准晶解对比, 可以从数值上验证理论的准确性.
如表 2所示为仅加载无限远处均匀载荷σ22∞/C11=1时, 在裂纹尖端附近, 压电耦合系数退化为0的压电准晶与非压电准晶应力场无量纲分量的对比.通过对比发现, 两者数值一致, 表明本文求得的结果在退化后和非压电的结果是一致的.
| 表 2 耦合系数为0时压电准晶和非压电准晶应力场分量的对比(r=0.1 cm) Table 2 Comparison of stress components between non-piezoelectric quasicrystals and piezoelectric Quasicrystals with coupling coefficients of zero (r=0.1 cm) |
(1) 当受到无限远处载荷作用时, 各个应力强度因子以及电位移强度因子是解耦的, 只与各自对应的载荷有关;
(2) 裂尖附近作用的集中载荷对各应力强度因子以及电位移强度因子均有显著影响;
(3) 受外载荷作用时, 能量释放率是电场、声子场、相位子场、声子场-相位子场耦合效应以及电场-声子场耦合效应共同作用的结果.
附录十次对称压电准晶弹性常数矩阵为
| $ \begin{align} & \mathit{\boldsymbol{e}}_{ijl}^{\left( 1 \right)}=\left[ \begin{matrix} 0 & 0 & 0 & 0 & 0 & e_{15}^{\left( 1 \right)} \\ e_{31}^{\left( 1 \right)} & e_{33}^{\left( 1 \right)} & e_{31}^{\left( 1 \right)} & 0 & 0 & 0 \\ 0 & 0 & e_{15}^{\left( 1 \right)} & 0 & 0 & 0 \\ \end{matrix} \right], \\ & \mathit{\boldsymbol{e}}_{ijl}^{\left( 2 \right)}=0,\ {{\mathit{\boldsymbol{\xi}}_{jl}}}=\left[ \begin{matrix} {{\xi }_{11}} & 0 & 0 \\ 0 & {{\xi }_{22}} & 0 \\ 0 & 0 & {{\xi }_{33}} \\ \end{matrix} \right], \\ & {{\mathit{\boldsymbol{R}}}_{ijkl}}=\left[ \begin{matrix} R & R & 0 & 0 & 0 & 0 \\ -R & -R & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -R & 0 & R \\ \end{matrix} \right], \\ & {{\mathit{\boldsymbol{C}}}_{ijkl}}=\left[ \begin{matrix} {{C}_{11}} & {{C}_{12}} & {{C}_{13}} & 0 & 0 & 0 \\ {{C}_{12}} & {{C}_{11}} & {{C}_{13}} & 0 & 0 & 0 \\ {{C}_{13}} & {{C}_{13}} & {{C}_{33}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {{C}_{44}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{C}_{44}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {{C}_{66}} \\ \end{matrix} \right], \\ & {{\mathit{\boldsymbol{K}}}_{ijkl}}=\left[ \begin{matrix} {{K}_{1}} & {{K}_{2}} & 0 & 0 & 0 & 0 \\ {{K}_{2}} & {{K}_{1}} & 0 & 0 & 0 & 0 \\ 0 & 0 & {{K}_{4}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {{K}_{1}} & 0 & -{{K}_{2}} \\ 0 & 0 & 0 & 0 & {{K}_{4}} & 0 \\ 0 & 0 & 0 & -{{K}_{2}} & 0 & {{K}_{1}} \\ \end{matrix} \right]. \\ \end{align} $ | (A1) |
保角映射:
| $ {{\zeta }_{\alpha }}=\frac{{{z}_{\alpha }}+\sqrt{z_{\alpha }^{2}-{{a}^{2}}-p_{\alpha }^{2}{{b}^{2}}}}{a-i{{p}_{\alpha }}b},\ \ \alpha =1,2,3,4,5,6. $ | (A2) |
式(12)中的特征值pα为
| $ \begin{align} & {{p}_{1}}=1.036\ 9 \text{i};\text{ }{{p}_{2}}=1.007\ 9\text{i};\text{ }{{p}_{3}}=0.734\ 52\text{i}; \\ & {{p}_{4}}=-0.002\text{ }831\ 61+0.999\ 334\text{i}; \\ & {{p}_{5}}=1.123\ 32\text{i};\text{ }{{p}_{6}}=0.002\ 831\ 61+0.999\ 334\text{i}.\text{ } \\ \end{align} $ | (A3) |
式(13)中特征矩阵A和B中各项为如下:
A11=8.886 8i; A12=3.385 9i; A13=0.153 4i;
A15=-1.319 5i; A14=-0.404 18-2.386 8i;
A16=-0.404 18-2.386 8i; A21=-8.156 9;
A22=-3.288 6; A23=-0.267 1;
A25=0.987 001; A24=2.415 6-0.352 2i;
A26=-2.415 6-0.352 2i; A31=3.663 7;
A32=1.284 19; A33=-0.952 8;
A34=-0.915 22+0.124 397i; A35=-1.318 9;
A36=0.915 2+0.124 4i; A41=0.005 92i;
A42=0.011 34i; A43=-0.000 03i;
A44=-0.021 36+0.008 5i; A45=-0.000 2i;
A46=-0.021 4-0.008 5i; A51=-0.006 9;
A52=-0.011 865; A53=6×10-6;
A54=-0.008 75-0.021i; A55=0.000 337;
A56=0.008 75-0.021i; A61=0.132 26;
A62=0.009 786; A63=0.210 72;
A64=0.000 25-0.002 57i; A65=-0.165 9;
A66=-0.000 25-0.002 56i; B11=-6.570 86;
B12=-2.553; B13=-0.143 3;
B14=1.795 6-0.325 3i; B15=0.932 7;
B16=-1.795 6-0.325 3i; B21=-6.311 8i;
B22=-2.486 8i; B23=-0.195 2i;
B24=0.245 9+1.830 4i; B25=0.829 3i;
B26=0.245 9-1.830 4i; B31=1.137 9i;
B32=0.387 7i; B33=-0.209 6i;
B34=-0.036 5-0.274 1i; B35=-0.443 8i;
B36=-0.036 5+0.274 1i; B41=-175.356 6;
B42=-332.556 4i; B43=0.849 27i;
B44=-244.007-629.794i; B45=6.104 6;
B46=244.006 8-629.794i; B51=-202.822 1i;
B52=-348.659 7i; B53=0.314 95i;
B54=613.525-261.167i; B55=9.992i;
B56=613.525+261.167i; B61=3.171 2i;
B62=0.868 3i; B63=1.367 3i;
B64=-0.059 8-0.569 1i; B65=-1.852 4i;
B66=-0.059 8+0.569 1i.
| [1] |
SHECHTMAN D, BLECH I, GRATIAS D, et al. Metallic phase with long-range orientational order and no translational symmetry[J]. Physical Review Letters, 1984, 53(20): 1951-1953. DOI:10.1103/PhysRevLett.53.1951 |
| [2] |
DING D H, YANG W G, HU C Z, et al. Generalized elasticity theory of quasicrystals[J]. Physical Review B, 1993, 48(10): 7003-7010. DOI:10.1103/PhysRevB.48.7003 |
| [3] |
FAN T Y. Mathematical theory of elasticity of quasicrystals and its applications[M]. Berlin: Springer, 2011, 67-69.
|
| [4] |
STADNIK Z M. Physical properties of quasicrystals[M]. New York: Springer Science & Business Media, 1999.
|
| [5] |
董闯. 准晶材料的形成机制, 性能及应用前景[J]. 材料研究学报, 1994, 8(6): 482-490. DONG Chuang. The formation mechanism, properties and application potentials of quasicrystalline materials[J]. Chinese Journal of Materials Research, 1994, 8(6): 482-490. |
| [6] |
ALTAY G, DÖKMECI M C. On the fundamental equations of piezoelasticity of quasicrystal media[J]. International Journal of Solids and Structures, 2012, 49(23): 3255-3262. |
| [7] |
HU C Z, WANG R H, DING D H, YANG W G. Piezoelectric effects in quasicrystals[J]. Physical Review B, 1997, 56(5): 2463-2469. DOI:10.1103/PhysRevB.56.2463 |
| [8] |
YU J, GUO J H, PAN E N, et al. General solutions of plane problem in one-dimensional quasicrystal piezoelectric materials and its application on fracture mechanics[J]. Applied Mathematics and Mechanics-English Edition, 2015, 36(6): 793-814. DOI:10.1007/s10483-015-1949-6 |
| [9] |
GAO C F, WANG M Z. Green's functions for generalized 2D problems in piezoelectric media with an elliptic hole[J]. Mechanics Research Communications, 1998, 25(6): 685-693. DOI:10.1016/S0093-6413(98)00088-3 |
| [10] |
GAO Y, XU B X. Method on holomorphic vector functions and applications in two-dimensional quasicrystals[J]. International Journal of Modern Physics B, 2008, 22(6): 635-643. DOI:10.1142/S021797920803882X |
| [11] |
樊世旺, 郭俊宏. 一维六方压电准晶三角形孔边裂纹反平面问题[J]. 应用力学学报, 2016, 33(3): 421-426. FAN Shi-wang, GUO Jun-hong. The antiplane problem of one-dimensional hexagonal quasicrystals with an edge crack emanating from a triangle hole[J]. Chinese Journal of Applied Mechanics, 2016, 33(3): 421-426. |
| [12] |
HWU C. Anisotropic Elastic Plates[M]. New York: Springer, 2010.
|
| [13] |
SUO Z, KUO C M, BARNETT D M, et al. Fracture mechanics for piezoelectric ceramics[J]. Journal of the Mechanics and Physics of Solids, 1992, 40(4): 739-765. DOI:10.1016/0022-5096(92)90002-J |
| [14] |
SOSA H, KHUTORYANSKY N. New developments concerning piezoelectric materials with defects[J]. International Journal of Solids and Structures, 1996, 33(23): 3399-3414. DOI:10.1016/0020-7683(95)00187-5 |
| [15] |
GUO Y C, FAN T Y. A mode-Ⅱ Griffith crack in decagonal quasicrystals[J]. Applied Mathematics andMechanics-English Edition, 2001, 22(11): 1311-1317. |
| [16] |
FU R, ZHANG T Y. Effects of an electric field on the fracture toughness of poled lead zirconate titanateceramics[J]. Journal of the American Ceramic Society, 2000, 83(5): 1215-1218. |
| [17] |
MCMEEKING R, RICOEUR A. The weight function for cracks in piezoelectrics[J]. International Journal of Solids and Structures, 2003, 40(22): 6143-6162. DOI:10.1016/S0020-7683(03)00366-4 |
| [18] |
FAN T Y. Mathematical theory and methods of mechanics of quasicrystalline materials[J]. Engineering, 2013, 5(4): 407-448. DOI:10.4236/eng.2013.54053 |
| [19] |
LEE J S, JIANG L Z. Exact electroelastic analysis of piezoelectric laminae via state space approach[J]. International Journal of Solids and Structures, 1996, 33(7): 977-990. DOI:10.1016/0020-7683(95)00083-6 |
| [20] |
YANG L Z, GAO Y, PAN E N, et al. An exact solution for a multilayered two-dimensional decagonal quasicrystal plate[J]. International Journal of Solids and Structures, 2014, 51(9): 1737-1749. DOI:10.1016/j.ijsolstr.2014.01.018 |
| [21] |
高存法, 樊蔚勋. 压电介质内裂纹问题的精确解[J]. 应用数学与力学, 1999, 20(1): 47-53. GAO Cun-fa, FAN Wei-xun. A exact solution of crack problems in piezoelectric materials[J]. Applied Mathematics and Mechanics, 1999, 20(1): 47-53. |



