2. 中国城市规划设计研究院, 北京 100037
2. China Academy of Urban Planning & Design, Beijing 100037, China
行程时间是反映道路交通状态的关键指标之一,对于出行诱导也有着重要的作用.近年来,随着城市道路视频采集设备的逐渐普及和数据质量不断提高,通过车牌识别数据实时获取道路行程时间成为可能.付凤杰等[1]研究表明,当前的车牌识别数据匹配得到的行程时间可靠性较高,能够反映出路段的实际情况.如何利用车牌识别数据,来改善城市道路行程时间的预测精度意义重大.
现有的一些预测方法主要可以分为两类.一类是基于统计的预测方法,另一类则是基于机器学习的预测方法.基于统计的有指数平滑法[2]、ARIMA[3]、马尔科夫预测法[4]、混沌理论预测法[5]、卡尔曼滤波预测法[6]等,基于机器学习的有BP神经网络[7]、K近邻算法[8]等.近几年来,更多的学者开始利用机器学习方法对行程时间进行预测.张娟等[9]利用SVM模型对城市快速路行程时间进行预测,并使用遗传算法进行参数调优,取得了显著的效果,但该模型训练时间较长,运算量较大.丁宏飞等[7]则通过BP神经网络对行程时间进行预测,但由于算法是一个黑箱过程,模型解释性不强.在以往的研究中,面临的问题主要是:1)由于交通信息的复杂性,当数据维度较大时,运算时间长且往往容易陷入过拟合的情况,如回归树模型等,且当数据出现缺失的情况下则对模型影响较大;2)由于部分模型是黑箱过程,如神经网络等,模型的解释性不强.3)以往的研究主要是利用行程时间的时间序列上的相关性进行预测,而考虑空间相关性的方法相对较少.
鉴于以上几点,本文提出使用集成学习方法来解决上述问题.集成学习方法在较多领域得到广泛应用,在解决分类和预测问题上有着显著的效果.在近几年的研究中,部分学者逐渐将其应用到交通领域[10-13].梯度提升回归树模型(gradient boosting regression tress,GBRT)作为一种常见而有效的集成学习方法,主要被应用到预测问题上,不容易陷入过拟合,模型的解释性较强,能够帮助使用者更好地理解各变量对于结果的影响,且运算速度快,能够较好地解决以往研究中存在的问题.本文在考虑时间相关性的同时,还考虑了空间相关性对于行程时间的影响,以提高模型的预测精度.
1 梯度提升回归树模型原理 1.1 集成学习方法如图 1所示,集成学习算法的原理是基于一些基础学习器(如:回归树、神经网络),通过一定的处理方式(投票法等)将所有基础学习器产生的结果整合起来.因此集成学习模型得到的结果往往比单一基础模型更加稳定,也更加准确.

|
图 1 集成学习原理示意图 Fig. 1 Sketch map of ensemble learning |
在集成学习方法中,以决策树为基础学习器的方法主要有两种类型,分别是Bagging和Boosting.这2类算法都是将已有的分类或回归算法通过一定方式组合起来,形成一个性能更加强大的模型.两者的主要区别是取样方式不同,Bagging采用均匀取样,而Boosting根据错误率来采样,因此Boosting的预测精度要优于Bagging.GBRT模型则是一种Boosting方法,最早由Friedman[14]在2001年提出,近年来不断发展,在许多领域得到了广泛应用.
1.2 回归树GBRT模型的基础学习器是回归树,为更好地理解其原理,首先应了解回归树的产生过程.回归树模型的原理是将特征空间划分为不同的区域,并且给每个区域以相应的值(常数),通过将数据划分至不同区域进而得到预测值.回归树每次生成树的子节点只有2个,即递归地二分每个特征,采取平方误差作为评价指标,在每一步选择一个最好的特征来分裂,这样将输入空间,即特征空间划分为有限个单元,并对应以相应的数值.
1.3 梯度提升回归树GBRT模型是Boosting算法的一种,也是Boosting算法的一种改进.原始的Boosting算法是在算法开始时,为每一个样本赋上一个相等的权重值,最初所有的基础学习器都有着同样的重要度.在每一次训练中得到的模型,会使得数据点的估计有所差异,所以在每一步结束后,需要对权重值进行处理,而处理的方式就是通过增加错分类点的权重,同时减少正确分类点的权重.这样使得如果某些点长期被分错,就会被“严重关注”,也就被赋上一个很高的权重.等进行了N次迭代后,将会得到N个简单的基础学习器,最后将其组合起来,对其进行加权(错误率越大的基分类器权重值越小,错误率越小的基分类器权重值越大)、或者进行投票得到一个最终的模型.
GBRT与传统的Boosting有着很大的区别,GBRT的核心就在于每一次计算都是为了减少上一次的残差(Residual),而为了减少这些残差,可以在残差减少的梯度(Gradient)方向上建立一个新模型.在GBRT中,每个新模型的建立是为了使得先前模型残差往梯度方向减少,与传统Boosting算法对正确、错误的样本进行加权有着极大的区别.
GBRT模型的具体产生过程如下:假设数据集为D={(x1, y1), (x2, y2), …, (xN, yN)},损失函数为L(y, f(x)),每棵回归树的叶节点数为J,将其输入空间分割成J个不相交区域R1m, R2m, …, Rjm,并为每一个区域估计一个常量值bjm.回归树gm(x)用公式表示为
| $ {g_m}\left( x \right) = \sum\limits_{j = 1}^J {\left( {{b_{jm}}I} \right)} ,x \in {R_{jm}}. $ | (1) |
| $ I\left( {x \in {R_{jm}}} \right) = \left\{ \begin{array}{l} 1,\;\;x \in {R_{jm}};\\ 0,\;\;其他. \end{array} \right. $ | (2) |
步骤1:模型的初始化:
| $ {f_0}\left( x \right) = \mathop {\arg \min }\limits_\rho \sum\limits_{i = 1}^n {L\left( {{y_i},\rho } \right)} $ | (3) |
步骤2:迭代生成M颗回归树,for m=1 to M,m表示第m颗树:
① 对于所有的样本N,for i=1 to N,i表示第i个样本,计算损失函数的负梯度值,并将它作为残差的估计值rim;
| $ {r_{im}} = - {\left[ {\frac{{\partial L\left( {{y_i},{f_{m - 1}}\left( {{x_i}} \right)} \right)}}{{\partial {f_{m - 1}}\left( {{x_i}} \right)}}} \right]_{f\left( x \right) = {f_{m - 1}}\left( x \right)}} $ | (4) |
② 针对上一步产生的残差生成一棵回归树gm(x), 将第m棵树的输入空间分割成J个不相交区域R1m, R2m, …, RJm,并计算梯度下降的步长:
| $ {\rho _m} = \mathop {\arg \min }\limits_\rho \sum\limits_{i = 1}^n {L\left( {{y_i},{f_{m - 1}}\left( {{x_i}} \right) + \rho {g_m}\left( {{x_i}} \right)} \right)} . $ | (5) |
步骤3:更新模型, 其中lr表示学习率;
| $ {f_m}\left( x \right) = {f_{m - 1}}\left( x \right) + {\rm{lr}} * {\rho _m}{g_m}\left( x \right). $ | (6) |
步骤4:输出模型fM(x).
GBRT模型的预测精度主要受到回归树的数量(M),学习效率(lr)的影响,其中回归树的棵树表示基础学习器的数量,而学习率则是为防止模型过度拟合而设置的,以缩减每个基模型对于最终结果的影响.以上2个参数的优化和选择过程将在后文中进行论述.
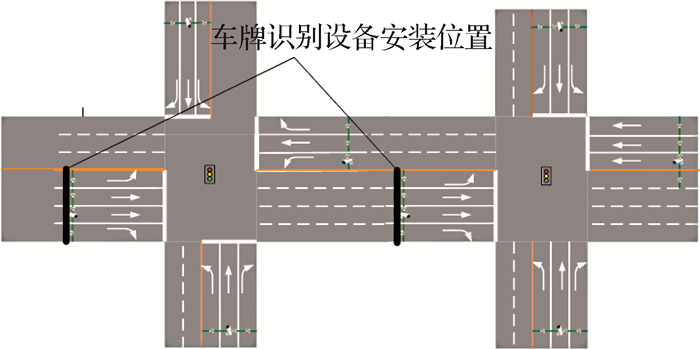
2 城市道路车牌识别数据准备 2.1 车牌识别数据说明贵阳市车牌识别系统的布设位置如图 2所示,一般是在距离各进口道停车线约30 m处,当车辆驶过停车线附近时,会拍摄其尾部,进而获取其相关信息.而单车的行程时间是通过上、下游车牌识别数据匹配得到,即车辆通过路段上、下游的时间差:
| $ {T_i} = {t_{{\rm{down}},i}} - {t_{{\rm{up}},i}}. $ | (7) |
|
图 2 车牌识别设备布设位置 Fig. 2 Location of license plate recognition equipment |
式中:Ti为第i辆车的单车路段行程时间;tdown, i为第i辆车通过下游交叉口的时刻,tup, i为第i辆车通过上游交叉口的时刻.
本文中数据采集时间为2015年12月4日至12月31日,共计6 238 896行数据.
2.2 数据质量控制由于实际数据中存在着大量的异常数据,在使用车牌识别数据前应对数据进行预处理,而这些异常数据产生的原因主要是以下2种情况.
(1) 车牌识别设备存在误识别.
由于车牌识别设备存在一定的误识别几率,会产生部分异常数据.主要是车牌数据缺位或超位,可以通过车牌位数直接剔除掉异常车牌信息;另外一种常见的错误是车牌数据中存在异常字符,可通过简单的判断进行剔除.
(2) 不同的驾驶行为导致异常数据.
由于驾驶员的一些驾驶行为导致行程时间出现异常.如出现长时间停车、车辆抛锚等情况时,将导致行程时间过大;而超速行程则会导致行程时间过小.这些情况对于获取路段的真实平均行程时间有较大的干扰,故应剔除这些数据.本文采取四分位法[15]对数据进行预处理.四分位法的原理是通过上下四分位确定合理的数据区间,将区间外的数据进行剔除.具体步骤如下:
步骤1:将时间窗内全部数据从小到大排列,得到数据上下四分位值Q25%和Q75%.
步骤2:计算该时间窗内的数据合理区间Z;
| $ Z = \left[ {\max \left( {{Q_{25\% }} - 1.5R,0} \right),{Q_{75\% }} + 1.5R} \right], $ | (8) |
| $ R = {Q_{75\% }} - {Q_{25\% }}. $ | (9) |
步骤3:检索时间窗内所有数据,若数据在合理区间Z外,则将该数据进行剔除,在合理区间内则不处理,最终得到数据处理过后的实际数据.
步骤4:计算预处理过后的数据的标准差,如果标准差过大,即大于阈值K(根据周期设定),则认为数据还需要再次剔除,即重复步骤1、2、3,直至标准差小于阈值,则结束步骤4.
步骤5:将预处理过后的数据进行计算,获取其平均行程时间.
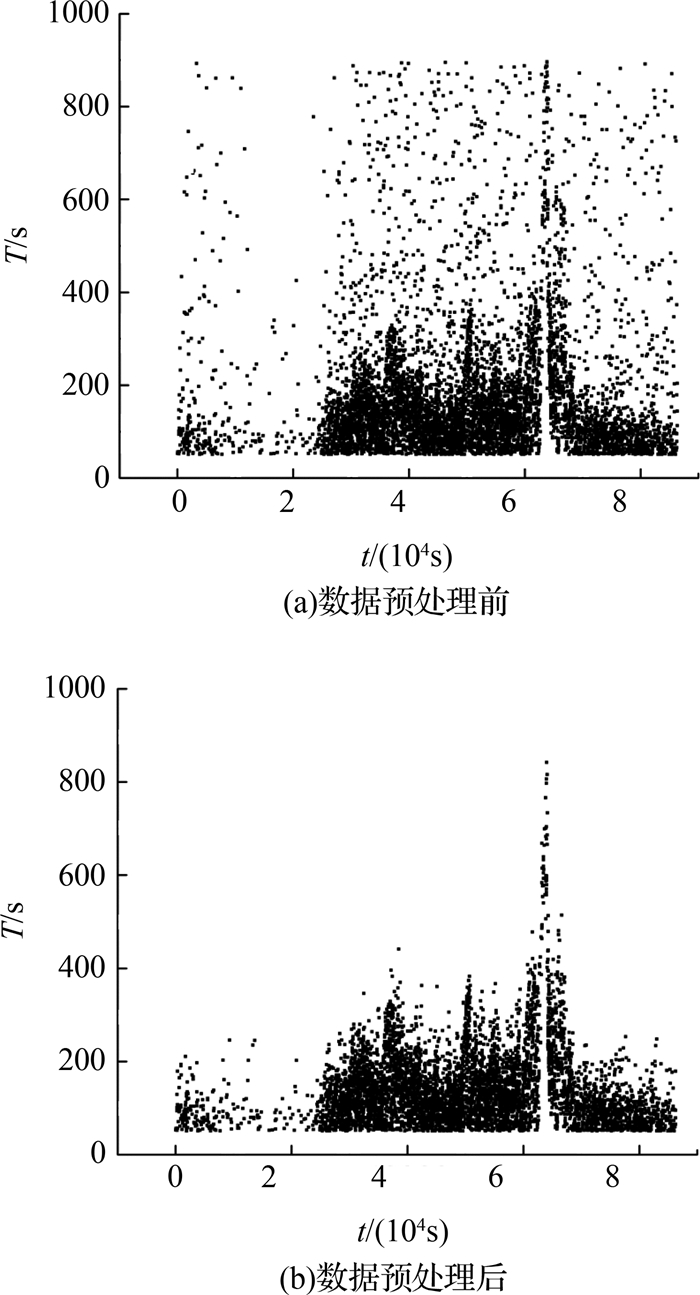
由于四分位法原理相对简单,运算速度较快,如图 3所示,经过数据预处理过后,能够较好地剔除掉其中的异常数据.
|
图 3 四分位数据剔除法效果图 Fig. 3 Effect of quartile division data filting algorithm |
实际情况中,当出现设备故障导致数据缺失时,无法获取该段时间窗内的平均行程时间;而当有效的数据过少时,则又会导致平均行程时间的准确度较低.对于这2种情况需要对数据进行补全,以建立完整的历史数据集.
1) 低峰时段(0:00—6:00)出现数据量较小或者数据量缺失时,按照以下算法进行数据补全,具体步骤如下.
步骤1:判断上一个时间窗的平均行程时间Tt_1是否处于拥堵状态,设路段长度为L,路段交通拥堵速度为v=5 km/h,当Tt_1>L/v1时,则认为路段处于拥堵状态,反之则为非拥堵状态;
步骤2:如果前一个时间窗处于拥堵状态,则认为是由于交通拥堵导致获取的数据量少,用前一个时间窗的平均行程时间Tt_1进行补全;如果前一个时间窗为非拥堵状态,则使用夜间自由流下的行程时间进行补全,设路段长L,自由流的速度为vf,即使用L/vf对当前数据进行补全.
2) 非低峰时段(6:00—24:00)出现数据量较小或者数据量缺失时,按照以下算法进行数据补全,具体步骤如下:
步骤1:判断上一个时间窗的平均行程时间Tt_1是否处于拥堵状态,设路段长度为L,路段交通拥堵速度为v1(取5 km/h),当Tt_1>L/v1时,则认为路段处于拥堵状态,反之则为非拥堵状态;
步骤2:如果前一个时间窗处于拥堵状态,则认为是由于交通拥堵导致获取的数据量少,用前一个时间窗的平均行程时间Tt_1进行补全;如果前一个时间窗为非拥堵状态,则使用前2个时间窗的平均行程时间Tt_1、Tt_2按照式(10)进行补全,T′t为当前时间窗的补全数据.
| $ {{T'}_{t\_1}} = 0.4{T_{t\_1}} + 0.6{T_{t\_2}}. $ | (10) |
城市道路行程时间预测算法如下:构建特征向量,模型参数分析及参数调整,模型解释.本文选择贵阳市4个交叉口从2015年12月4日至12月31日4周数据进行分析(见图 4),通过数据质量控制后得到相邻三条道路的行程时间,并处理成时间间隔为5 min的平均行程时间.

|
图 4 实验道路点位(瑞金南路中段) Fig. 4 Locaion of experiment road (middle of Ruijin South Road) |
在行程时间预测中,预测精度的好坏与特征向量的选择有极大的关系.而与行程时间相关的变量较多,如:时刻,星期,前n个时间窗的行程时间,上、下游的交通状态,因此选取合适的特征向量是预测最为关键的一步.本文采取皮尔逊相关性系数来分析各变量与行程时间的相关性.在统计学当中,皮尔逊相关性系数被广泛应用于测量2个变量X、Y的相关程度.皮尔逊相关性系数的值在(-1.0, 1.0),绝对值越大,则2个变量间的相关性则越强,其具体的计算过程如下:
| $ {\rho _{X,Y}} = \frac{{E\left[ {\left( {X - {\mu _X}} \right)\left( {Y - {\mu _Y}} \right)} \right]}}{{{\sigma _X}{\sigma _Y}}}. $ | (11) |
式中:μX、μY表示X、Y平均值,σX、σY表示X、Y方差.
(1) 时间相关性.
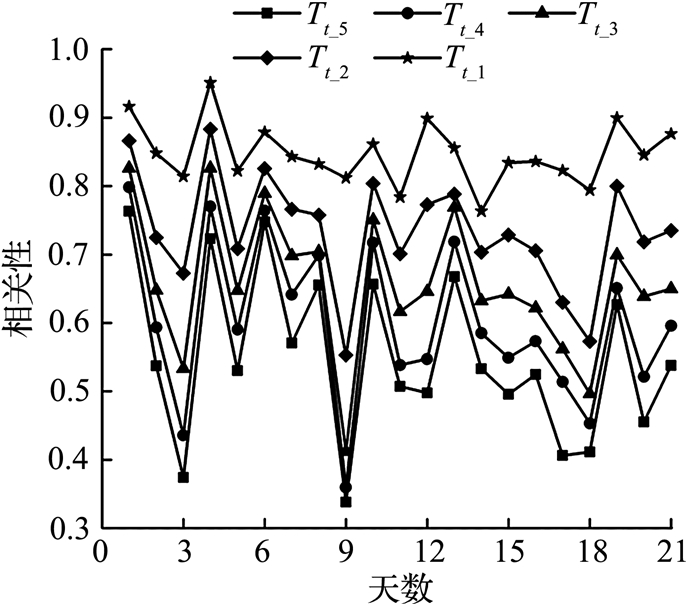
在之前的行程时间预测研究中,往往是利用其时间序列上的相关性来进行分析的.因此在选择特征向量时,优先考虑使用当前时段前n个时间窗的平均行程时间作为预测的特征向量.而以往的研究中往往是根据经验选取前几个时间窗的平均行程时间作为特征向量,并没有较为量化的分析.本文则使用瑞金南路-遵义路与瑞金南路-兴永路2个交叉口,即图 4中路段Ⅱ从2015年12月4日至12月24日共21 d行程时间数据进行分析,将时段t时刻的平均行程时间Tt与其前5个时间窗(Tt_1, Tt_2, Tt_3, Tt_4, Tt_5)的平均行程时间进行相关性分析.结果如图 5所示,当前t时刻的平均行程时间与前5个时间窗的平均行程时间相关性存在着一定的波动性,但是与前4个时间窗的平均行程时间的相关性一直较强,其相关性系数ρX, Y在绝大部分天都高于0.4.而在统计学分析中相关性系数高于0.4则可以认为存在中等程度的相关性.因此采用当前时刻前4个时间窗的平均行程时间作为特征向量.同时,前几个时间窗的行程时间变化趋势也是反映未来交通状态的重要信息,所以将前4个时间窗的行程时间变化量也作为特征向量之一.
|
图 5 前期与当前时段行程时间相关性分析 Fig. 5 Correlation analysis of travel time between prior period and current period |
(2) 空间相关性.
在以往的预测模型中,利用较多的是时间序列的相关性信息,而对于空间上的相关性则涉及的较少.虽然在城市道路中由于受到信号灯的干扰,交通流有一定的间断性,但是路段上下游的交通状态往往能反映出未来状态的演化趋势.实际情况中,有些路段的行程时间增加,常常是因为上、下游交通状态的拥堵蔓延导致的.本文使用图 4中实验路段12月4日至12月11日的数据,分析得到了路段Ⅱ当前时刻平均行程时间Tt和其上游路段Ⅰ前2个时间窗的平均行程时间(Tu_t_2,Tu_t_1)的相关性系数,以及其与下游路段Ⅲ前2个时间窗的平均行程时间(Tdown_t_2, Tdown_t_1)的相关性系数.
如表 1中所示,当前时段行程时间Tt与上游前两个时间窗的平均行程时间Tu_t_2,Tu_t_1相关性较强,绝大数天的相关性系数超过0.4,在12月6日至12月8日,甚至达到0.5以上,存在较强的相关性.而下游路段相关性则较低,相关性系数都在0.4以下,说明该路段较易收到上游交通状态的影响,而下游交通状态则对其干扰较少.因此选择Tu_t_2,Tu_t_1作为其特征向量之一.
| 表 1 当前道路与邻接道路行程时间相关性分析 Table 1 Correlation analysis of travel time between current roads and adjacent roads |
同时,工作日与休息日通行模式具有较大差异,应考虑将此信息作为特征之一.因此得到最终的特征向量是:当天所处的时刻t,星期wk,当前路段前4个时间窗的平均行程时间Tt_4,前3个时间窗的平均行程时间Tt_3,前2个时间窗的平均行程时间Tt_2,前1个时间窗的平均行程时间Tt_1;以及前4个时间窗的变化值ΔTt_3,ΔTt_2,ΔTt_1;路段上游前2个时间窗的平均行程时间Tu_t_2,路段上游前1个时间窗的平均行程时间Tu_t_1,共11个变量.
3.2 参数分析在GBRT模型中最主要的参数为学习率lr和回归树的棵数M,为达到最优的预测模型,理解这2个参数的对于模型的影响显得尤为重要.本文利用贵阳市实验交叉口从2015年12月4日至12月24日的数据,随机地将其中70%的数据作为训练集,剩下30%的数据作为测试集,使用不同数量的回归树(从(1~1000)和不同的学习率(0.005~0.500)来训练模型,以观察各参数对于模型预测精度的影响.同时,为了评估模型的优劣,使用平均绝对百分误差MAPE作为预测模型的评价指标,定义如下:
| $ {\rm{MAPE}} = 100\% \times \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{\left| {{t_{{\rm{predict}},i}} - {t_{{\rm{true}},i}}} \right|}}{{{t_{{\rm{true}},i}}}}.} $ | (12) |
式中:tpredict, i为第i时刻的预测值,ttrue, i为第i时刻的真实值.
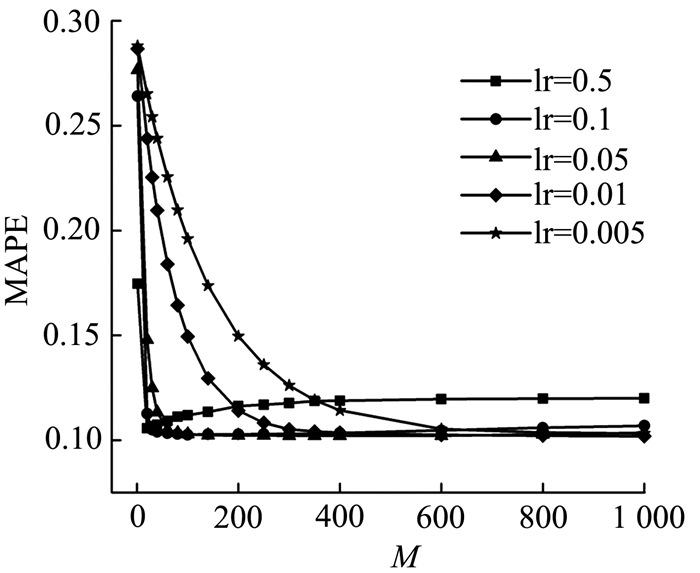
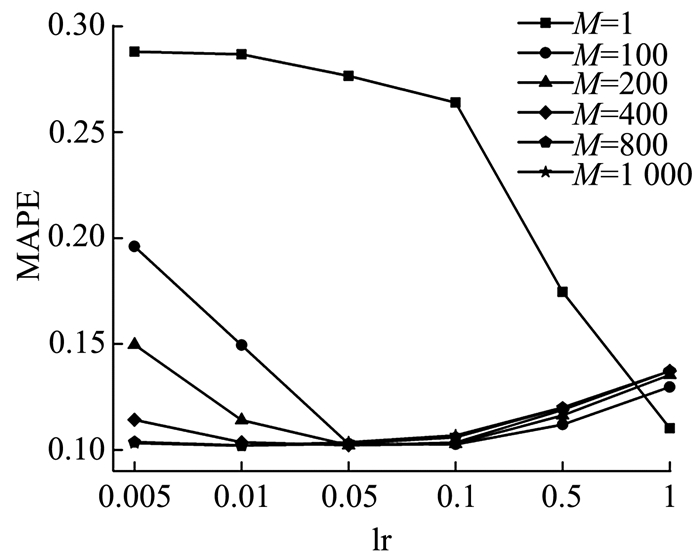
从图 6中可以发现, 不同的学习率曲线有着不同的线形,学习率为0.005的曲线下降速度最慢,而学习率为0.5的曲线则下降最快.同时,在固定了学习率的情况下,随着回归树的棵数不断增加,也就是集成学习中基础模型的数量不断递增,模型的预测精度逐渐提高,但是当回归树的棵数达到一定数量后,则会发生过度拟合的现象,导致模型的预测精度下降.此外更多的回归树意味着更大的运算量.而学习率与模型预测精度关系则如图 7所示.学习率的作用是防止模型过度拟合,通过其来缩减每个模型的贡献程度.因此较小的学习率往往需要更多的回归树来达到最优模型.当回归树的棵数固定时,在不同的学习率下,学习率增大的往往能更快地提升预测精度,但是较低的学习率却能达到更好的预测精度,也就是学习的效果更好.最后,在确定参数对模型的影响后,通过网格搜索法获取最优参数.
|
图 6 回归树的棵数与模型预测精度的关系 Fig. 6 Relation between number of regression tree and model's prediction accuracy |
|
图 7 学习率与模型预测精度的关系 Fig. 7 Relation between learning rate and model's prediction accuracy |
考虑到特征向量中不同的变量对于最终的结果有着不同的影响,本文通过GBRT模型输出每个变量对于预测结果的重要程度,以此更好地理解各变量的影响.表 2给出了各变量对于预测结果的重要程度排序,其中前一个时间窗的交通状态Tt_1对于预测结果的贡献度最大,这与实际情况比较符合,因为前一个时刻的交通状态对未来交通状态有着较大影响.而重要程度第二的变量则是每天所处的时刻t,这反映了城市道路交通状态往往具有一定的周期性,早晚高峰期行程时间将会普遍增加,而平低峰期的行程时间则相对较小.其次对预测结果较为重要的,则是前一个时间窗的行程时间变化ΔTt_1,因为前一个时间窗的行程时间增加还是减少反映了未来交通状态的大体变化趋势.
| 表 2 各特征向量的重要程度 Table 2 Importance of each feature vector |
本文将数据质量控制之后2015年12月4日至2015年12月24日的实验道路的行程时间数据作为训练集,将随后一周2015年12月25日至12月31日的行程时间作为测试集,对全天24 h数据进行预测,预测时间步长是5 min.由于篇幅有限,本文仅给出部分天的预测结果,如图 8所示,T为行程时间.由图 8可知,基于GBRT模型预测的行程时间较为准确,预测值的变化趋势和实际值较为吻合,其中12月29日是工作日,预测值在早晚高峰期能较好地跟随交通状态的变化,且准确度较高.12月26日则是休息日,基于GBRT模型的预测方法也能较好地跟随不同模式下的交通状态变化趋势,但在晚高峰期间,由于交通需求急剧变化,预测结果存在一定误差.

|
图 8 城市道路行程时间预测值与实际值 Fig. 8 Predicted and actual travel time on urban road |
通过比较以下几种方法的预测精度,以验证本文提出方法的有效性和稳定性.
方法1:本文提出的基于GBRT模型的预测方法;
方法2:基于SVM模型的预测方法,该模型在近年来被广泛应用于解决交通预测的问题,本文使用SVM模型的核函数为rbf核,且通过网格搜索法进行了参数调整;
方法3:基于随机森林(RF)的预测方法,是集成学习中,较为典型的算法之一;
方法4:基于时间序列的自回归积分滑动平均模型(ARIMA模型),该方法在预测问题上有着较为稳定的表现,且是多数预测方法的判别标准,本文应用的是滞后阶数为3、差分项为1、p值为3的ARIMA模型;
方法5:未考虑空间相关性的基于GBRT模型的预测方法.
通过测试不同模型的预测精度,得到表 3的预测结果,可以看出GBRT模型在不同天的测试中均有着稳定的表现,且预测精度较好.其中方法1中的GBRT模型在12月25日的预测误差仅为ARIMA模型的64%,且在其他6天的预测结果都是最优的预测模型.而从以上得到的预测结果看,基于集成学习模型的方法1、方法3、方法5有着更好地预测精度,比ARIMA和SVM模型表现也更为稳定.同样使用GBRT模型的方法1和方法5,方法1在考虑空间相关性后比方法5有着更好的预测精度.说明在使用空间信息后,模型能够得到邻接道路的交通状态对于当前路段的影响,并且将其有效地反映到预测结果当中去,提升了模型的预测精度.
| 表 3 各模型在不同天的预测精度MAPE Table 3 Prediction accuracy MAPE of each model in different days |
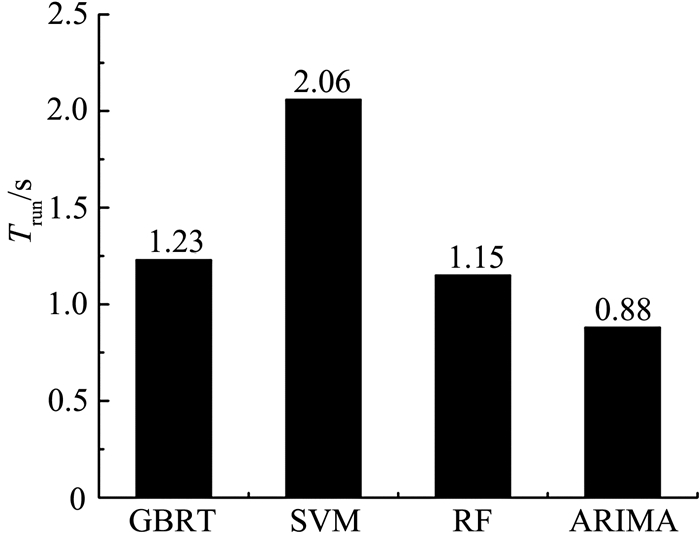
除考虑各模型精度的同时,也应考虑模型的运算效率.本实验使用同等配置的计算机(具体配置为CPU Intel i5-5200,RAM 8 GB).运算所需时间Trun如图 9所示,在相同条件下,虽然基于ARIMA模型的法计算时间最小,但是预测精度较差.而基于GBRT模型的预测方法运算所需时间适中,而预测精度则较高.
|
图 9 各模型运算所需时间 Fig. 9 Computational time required by GBRT, SVM, RF and ARIMA |
利用城市道路中的车牌识别数据,提出了基于GBRT模型的行程时间预测方法,预测结果可用于城市道路交通信息发布,提供出行引导.通过数据质量控制建立了完整的数据集,在考虑时间序列相关性的同时,分析了城市道路中空间相关性,并将其应用到行程时间预测当中,提高了行程时间预测的精度.通过分析特征向量中各变量对于预测精度的重要性,更好地阐明了各变量对于模型的影响.
| [1] |
付凤杰, 龚越, 王殿海, 等. 基于高清智能卡口路段行程时间的数据质量分析[J]. 浙江大学学报:工学版, 2016, 50(9): 1761-1767. FU Feng-jie, GONG Yue, WANG Dian-hai, et al. Data quality analysis of link travel time based on HD smart gate[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(9): 1761-1767. |
| [2] |
WILLIAMS B, DURVASULA P, BROWN D. Urban freeway traffic flow prediction:application of seasonal autoregressive integrated moving average and exponential smoothing models[J]. Transportation Research Record:Journal of the Transportation Research Board, 1998(1644): 132-141. |
| [3] |
WILLIAMS B M, HOEL L A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process:Theoretical basis and empirical results[J]. Journal of transportation engineering, 2003, 129(6): 664-672. DOI:10.1061/(ASCE)0733-947X(2003)129:6(664) |
| [4] |
胡继华, 李国源, 程智锋. 基于马尔科夫链的公交站间行程时间预测算法[J]. 交通信息与安全, 2014, 32(2): 17-22. HU Ji-hua, LI Guo-yuan, CHEN Zhi-feng. Algorithm for predicting bus travel time between stops based on markov chain[J]. Journal of Transport Information and Safety, 2014, 32(2): 17-22. |
| [5] |
JI Y J, TANG D N, GUO W H, et al. Forecasting available parking space with largest Lyapunov exponents method[J]. Journal of Central South University, 2014, 21(4): 1624-1632. DOI:10.1007/s11771-014-2104-3 |
| [6] |
李进燕, 朱征宇, 刘琳, 等. 基于简化路网模型的卡尔曼滤波多步行程时间预测方法[J]. 系统工程理论与实践, 2013, 33(5): 1289-1297. LI Jin-yan, ZHU Zheng-yu, LIU Ling, et al. Multi-step kalman filtering travel time estimation method based on simplified road network model[J]. Systems Engineering:Theory & Practice, 2013, 33(5): 1289-1297. DOI:10.12011/1000-6788(2013)5-1289 |
| [7] |
丁宏飞, 李演洪, 刘博, 等. 基于BP神经网络与SVM的快速路行程时间组合预测研究[J]. 计算机应用研究, 2016, 33(10): 2929-2932. DING Hong-fei, LI Yan-hong, LIU Bo, et al. Expressway's travel time prediction based on combined BP neural network and support vector machine approach[J]. Application Research of Computers, 2016, 33(10): 2929-2932. DOI:10.3969/j.issn.1001-3695.2016.10.012 |
| [8] |
王翔, 陈小鸿, 杨祥妹. 基于K最近邻算法的高速公路短时行程时间预测[J]. 中国公路学报, 2015, 28(1): 102-111. WANG Xiang, CHEN Xiao-hong, YANG Xiang-mei. Short term prediction of expressway travel time based on K nearest neighbor algorithm[J]. China Journal of Highway and Transport, 2015, 28(1): 102-111. |
| [9] |
张娟, 孙剑. 基于SVM的城市快速路行程时间预测研究[J]. 交通运输系统工程与信息, 2011, 11(2): 174-179. ZHANG Juan, SUN Jian. Prediction of urban express way travel time based on SVM[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(2): 174-179. |
| [10] |
AHMED M, ABDEL-ATY M. Application of stochastic gradient boosting technique to enhance reliability of real-time risk assessment:use of automatic vehicle identification and remote traffic microwave sensor data[J]. Transportation Research Record:Journal of the Transportation Research Board, 2013(2386): 26-34. |
| [11] |
CHUNG Y S. Factor complexity of crash occurrence:An empirical demonstration using boosted regression trees[J]. Accident Analysis & Prevention, 2013, 61: 107-118. |
| [12] |
LIU Q C, LU J, CHEN S U. Design and analysis of traffic incident detection based on random forest[J]. Journal of Southeast University, 2014, 1: 88-95. |
| [13] |
ZHANG Y, HAGHANI A. A gradient boosting method to improve travel time prediction[J]. Transportation Research Part C:Emerging Technologies, 2015, 58: 308-324. DOI:10.1016/j.trc.2015.02.019 |
| [14] |
FRIEDMAN J H. Greedy function approximation:a gradient boosting machine[J]. Annals of Statistics, 2001, 1189-1232. |
| [15] |
范金城, 梅长林. 数据分析[M]. 北京: 科学出版社, 2002, 6.
|



