城市隧道是缓解交通拥堵、节约土地资源、改善区域环境的重要举措[1-2].为实现交通立体分流,城市隧道往往在沿线设置多对进出口匝道[3-4],形成分叉结构.出口匝道的存在会产生分流现象[5-6],改变隧道内风量和污染物的分配,直接影响隧道内外环境.掌握分叉隧道分流局部损失特性是研究和控制分流现象的基础和关键.
从结构形式看,分叉隧道类似于三通管道.对分流三通局部损失特性,Iwanami等[7]基于势流理论研究了90°分流三通管中的压力损失机制,认为三通直管的流动类似于突扩流,而侧管为收缩-突扩流.李玲等[8]对64°分流三通管内的水流流动特性进行了数值及试验研究,发现流速方向变化和离心力引起的流速分布变化是造成三通分流局部损失的主要因素.此外,Miller等[9-10]通过大量试验获得了45°~120°夹角范围内三通分流局部损失系数随流量比、面积比及夹角的变化规律.Bassett等[11]进一步基于质量、动量和能量守恒推导出可计算任意夹角、截面积比的三通分流局部损失系数理论公式,在45°~120°夹角范围内,公式预测结果与试验数据吻合良好.应当指出,为保障行车安全,分叉隧道夹角通常在5°~15°,而已有针对分流局部损失特性的研究,其夹角均大于30°,无法为分叉隧道通风设计提供借鉴.
本文针对小角度(5°~15°)分叉隧道,通过比尺模型试验结合CFD模拟,分析分叉隧道流动特征和分流局部损失特性,获得分流局部损失系数随夹角的变化规律及半经验理论公式,从而为分叉隧道的通风排污计算提供重要的参考依据.
1 比尺模型试验基于相似理论[12],按照雷诺(Re)相似及欧拉(Eu)相似准则[13]设计搭建1/20分叉隧道通风比尺模型,速度比尺λu=压力比尺λp=1、长度比尺λl=时间比尺λt=20.为满足Re相似,模型隧道采用绝对粗糙度ks=0.5 mm的镀锌钢板制成,相对粗糙度ks/D≈0.001 08,与实际隧道(水力直径D=9.31 m,沿程损失系数λ≈0.02[14])相同.模型主体包括分流前主线、分流后主线和匝道3部分,如图 1(a)所示,长度分别为19.00 m、10.46 m和9.23 m,截面形状为矩形,尺寸分别为0.675 m×0.355 m、0.487 5 m×0.355 m和0.375 m×0.355 m,分叉夹角θ可在5°~30°范围内调节,如图 1(b)所示.采用变频高压风机通过引流管道连接喷嘴以模拟射流风机,喷嘴由抽气管和射流管组成,如图 1(c)所示,最大射流速度可达50 m/s.

|
图 1 通风比尺模型隧道 Fig. 1 Scale model of tunnel ventilation |
分别采用精度为±0.1 m/s的毕托管式风速变送器和精度为±0.5 Pa的Dwyer差压变送器获取断面风速及压力数据.图 2为不同风速u下模型隧道的沿程损失系数λ变化,由图可以看出,λ随着风速的增大而逐渐减小,当风速>3 m/s后,流动进入阻力平方区[15],λ趋于稳定,此时,λ≈0.02,与实际隧道一致,模型隧道满足阻力相似.

|
图 2 模型隧道沿程损失系数 Fig. 2 Linear loss coefficients of model tunnel |
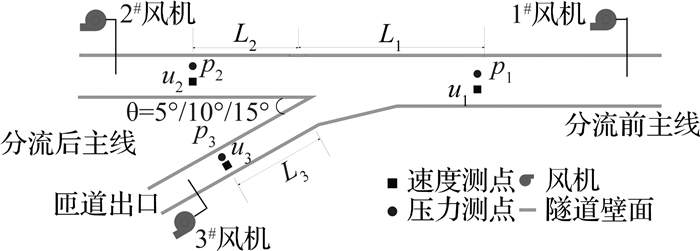
具体试验时,分别针对5°、10°和15°三种夹角进行分叉隧道通风试验.速度及压力测点布置如图 3所示.为了保障数据的可靠性,测点均距离隧道分叉段20倍水力直径以上[16].为满足阻力相似,试验中始终开启1号风机确保模型隧道风速进入自模区,通过调节2、3号风机以实现各种分流比.
|
图 3 速度、压力测点布设示意图 Fig. 3 Location of measuring points for velocity and pressure |
本文采用在模拟分流、回流和旋转时具有较高精度的Realizable k-ε湍流模型[17-18],计算分叉隧道内的空气运动.考虑到隧道内的空气流动属于黏性和密度为定值的不可压缩流[19-20],因此忽略由浮力引起的湍动能产生项和可压缩性引起的扩张耗散项,则湍动能k及湍动能耗散率ε输运方程如下:
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} -\rho \varepsilon . $ | (1) |
| $ \begin{array}{l} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}S\varepsilon -\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }}. \end{array} $ | (2) |
式中,ρ、μ、ν、u分别为空气密度、动力黏性系数、运动黏性系数和速度;t、x分别为时间和空间坐标;Gk为由平均速度梯度引起的湍动能产生项;S为应变率;μt=ρ Cμk2/ε为湍流黏性系数;Cμ、C1为模型系数,计算公式参见文献[21];模型常数σk、σε、C2分别为1.0、1.2、1.9.
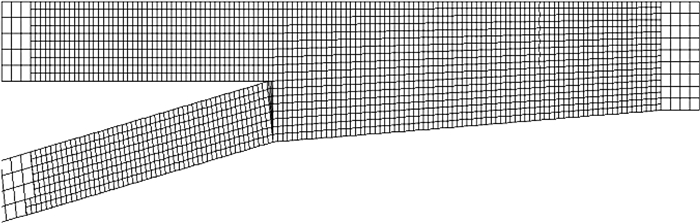
分别建立夹角为5°、10°及15°的比尺分叉隧道CFD模型.采用六面体网格剖分计算域,为保障计算精度并提高计算效率,对隧道分叉区域进行局部加密,如图 4所示,模型网格总数为236万.
|
图 4 分叉隧道网格示意图 Fig. 4 Schematic diagram of gird for bifurcated tunnel |
计算时,隧道壁面取无穿透不可滑移边界;隧道入口为Dirichlet边界条件,给定风速;分流后主线和匝道出口则为Neumann边界条件,自由出流.利用有限体积法离散控制方程,通过SIMPLE算法[22]进行速度场和压力场的稳态迭代求解.
3 结果分析 3.1 分流局部损失特性根据伯努利方程,结合三通局部损失系数计算公式[16, 23]定义分叉隧道分流局部损失系数为
| $ {\xi _{12}} = \frac{{2\left( {{p_1}-{p_2}} \right)-2\left( {\Delta {p_1} + 2\Delta {p_2}} \right) + \rho \left( {v_1^2-v_2^2} \right)}}{{\rho v_1^2}}, $ | (3) |
| $ {\xi _{13}} = \frac{{2\left( {{p_1}-{p_3}} \right)-2\left( {\Delta {p_1} + 2\Delta {p_3}} \right) + \rho \left( {v_1^2-v_3^2} \right)}}{{\rho v_1^2}}. $ | (4) |
式中:ξ12、ξ13分别为主线和匝道的分流局部损失系数;下标1、2、3分别代表位于分流前主线、分流后主线及匝道的测点;p、v分别为测点断面的静压和风速;λ、D为测点所在断面的沿程损失系数和当量直径,L为测点到分叉面的距离;Δpi为测点到分叉面的沿程损失压降:
| $ \Delta {p_i} = {\lambda _i}{L_i}\rho v_i^2/\left( {2{D_i}} \right), i = 1, 2, 3. $ |
如图 5所示为分叉隧道分流局部损失系数随分流比的变化规律,分流比β= Q3/ Q1.其中Q3为匝道风量,Q1为总风量.可以看出,ξ12和ξ13均呈“U”型曲线变化,随β的增大先减小后增大.同时,在相同分流比下,ξ13均大于ξ12;且分流比越大,两者差异越大.对于主线隧道,在5°~15°,ξ12基本不受夹角变化的影响,这与45°~120°三通主管分流局部损失系数的变化规律一致[9];对于匝道,当β<0.5时,ξ13随着夹角的增大而增大,当β>0.5时,ξ13随着夹角的增大而减小.此外,CFD模拟结果与试验值变化趋势一致,平均误差仅为0.022.

|
图 5 分流局部损失系数变化规律 Fig. 5 Chang rule of dividing flow local loss coefficients |
当空气流经隧道分叉处,由于边壁和流量的改变,均匀流遭到破坏,引发流速大小、方向和分布的变化,促使流体质点间发生剧烈的摩擦和动量交换,从而产生局部能量损失.可见,局部损失主要受流速大小和流向变化的影响[24].分流比较小(β=0.1)时,隧道流场结构如图 6所示.
由图 6可以看出,在小分流比下,大部分空气将进入主线隧道,导致流线收缩,由于分流前后主线隧道为直线,整体流态较为平顺,尽管在靠近匝道一侧的主线隧道边壁会出现流动分离,但分离程度较弱、并未产生旋涡,且该分离几乎不受夹角变化的影响,因此不同夹角下的ξ12基本一致.而小部分进入匝道的空气,不仅速度梯度变化明显,而且在惯性力的作用下,将在远离主线隧道一侧的匝道边壁出现流动分离,且夹角越大,分离越明显,因此小分流比下,ξ13随夹角的增大而增大.

|
图 6 β=0.1时隧道流场结构 Fig. 6 Tunnel flow field structure at β=0.1 |
图 7是β=0.9的隧道流场结构.由图可知,当分流比较大时,大部分空气将进入匝道,由于匝道与主线隧道呈一定的夹角,导致主流流动出现明显的转向,这是造成大分流比下匝道分流局部损失明显大于主线的根本原因.同时,流线的收缩将导致靠近主线一侧的匝道边壁出现流动分离,且夹角越大,分离越弱,因此大分流比下,ξ13随着夹角的增大而减小.

|
图 7 β=0.9时隧道流场结构 Fig. 7 Tunnel flow field structure at β=0.9 |
对于进入分流后主线隧道的小部分空气,由于沿流动方向出现减速增压现象,受分叉处空气的剪切与横向环流作用,使得远离匝道一侧的主线隧道边壁出现强烈的流动分离,并产生旋涡.但与小分流比情况类似,该旋涡受夹角变化的影响极为有限,因此不同夹角下的ξ12基本不变.
可见,流速梯度变化和流动分离是产生主线分流局部损失的主因,而匝道分流局部损失还进一步受到流速转向的影响.
3.3 局部损失系数修正公式分流局部损失系数与分流比β呈二阶抛物线关系[25],且当夹角θ在45°~120°时,ξ12基本不受θ的影响,而ξ13与θ呈正相关关系[9].Bassett基于Hagar假设推导出可计算任意夹角、截面积比的三通分流局部损失系数公式[11]:
| $ \left. \begin{array}{l} {\xi _{12}}{\rm{ = }}\alpha {\beta ^2} + b\beta + c, \\ {\xi _{13}} = d{\beta ^2} + e\beta + f + g\beta \cos \left( {h\theta } \right). \end{array} \right\} $ | (5) |
式中:系数a、b、c、e、f和h为常数,分别为1、-0.5、0、0、1、3/4;d=(主管截面积A1/侧管截面积A3)2;g=2(A1/A3).Bassett公式对45°~120°三通分流局部损失系数的预测结果与实验数据吻合良好.分叉隧道结构类似于三通管道,利用Bassett公式计算5°、10°及15°分叉比尺模型隧道的分流局部损失系数,结果如图 8所示.可以看出,预测值与试验结果差异较大,尤其在β>0.5时,公式预测的ξ13随θ的增大而增大,这与试验获得的ξ13随θ的增大而减小的规律相违背.可见,Bassett公式并不适用于小角度分叉隧道.

|
图 8 Bassett公式计算结果与试验结果对比 Fig. 8 Comparison of Bassett's results and experimental data |
基于模型隧道试验数据,利用Mtlab软件采用最小二乘法重新拟合Bassett公式系数,获得修正的Bassett(modified Bassett, MB)公式如下:
| $ \left. \begin{array}{l} {\xi _{12}}{\rm{ = }}1.93{\beta ^2}-2.12\beta + 0.49, \\ {\xi _{13}} = 3.08{\beta ^2} + 6.17\beta \cos 0.75\left. \theta \right)-8.74\beta + 0.508. \end{array} \right\} $ | (6) |
ξ12和ξ13的拟合优度分别为0.96和0.95.图 9为MB公式与5°和15°的分叉隧道试验结果的对比.可以看出,MB公式预测的分叉隧道ξ12和ξ13变化规律与试验结果一致,两者吻合良好.

|
图 9 MB公式计算结果与试验结果对比 Fig. 9 Comparison of MB's results and experimental data |
(1) 分叉隧道分流局部损失主要受流速大小、流向和分布变化的影响.其中,流速梯度变化和流动分离是产生主线分流局部损失的主因,而匝道分流局部损失还进一步受到流速转向的影响.
(2) 对夹角为5°~15°的分叉隧道,分流局部损失系数随分流比β的增大呈先减小后增大的U型曲线变化.其中,主线隧道分流局部损失系数ξ12基本不受夹角的影响;当β<0.5时,匝道分流局部损失系数ξ13随着夹角的增大而增大,当β>0.5时,ξ13随着夹角的增大而减小.
(3) 基于比尺模型试验数据提出修正的Bassett公式,可准确预测夹角为5°~15°分叉隧道的分流局部损失系数,为分叉隧道的通风计算提供理论参考依据.
| [1] |
高广运, 何俊锋, 李佳. 地铁运行引起的饱和地基动力响应[J]. 浙江大学学报:工学版, 2010, 44(10): 1925-1930. GAO Guang-yun, HE Jun-feng, LI Jia. Dynamic response induced by running subway in saturated ground[J]. Journal of Zhejiang University:Engineering Science, 2010, 44(10): 1925-1930. |
| [2] |
吴世明, 王湛, 王立忠. 大断面过江隧道运营期受力变形健康监测分析[J]. 浙江大学学报:工学版, 2013, 47(4): 595-601. WU Shi-ming, WANG Zhan, WANG Li-zhong. Monitoring and analysis of force and deformation of large section crossing-river tunnel during operation period[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(4): 595-601. |
| [3] |
阳东, 赵成梅. 热压与风机动力共同作用下多分支隧道内排烟气流的多解性[J]. 土木建筑与环境工程, 2015, 37(1): 1-6. YANG Dong, ZHAO Cheng-mei. Multiple steady states of exhaust airflow in a multi-branch tunnel with the combined effects of buoyancy and fan power[J]. Journal of Civil, Architectural & Environmental Engineering, 2015, 37(1): 1-6. DOI:10.11835/j.issn.1005-2909.2015.01.001 |
| [4] |
俞明健. 城市地下道路设计理论与实践[M]. 北京: 中国建筑工业出版社, 2014, 25-35.
|
| [5] |
陈玉远. 城市公路隧道多匝道通风系统计算方法的探讨[J]. 现代隧道技术, 2011, 48(5): 97-100. CHEN Yu-yuan. Discussion of calculation method for multiple-ramp ventilation systems in urban highway tunnels[J]. Modern Tunnelling Technology, 2011, 48(5): 97-100. |
| [6] |
LI Q, CHEN C, DENG Y W, et al. Influence of traffic force on pollutant dispersion of CO, NO and particle matter (PM 2.5) measured in an urban tunnel in Changsha, China[J]. Tunnelling and Underground Space Technology, 2015, 49: 400-407. DOI:10.1016/j.tust.2015.04.019 |
| [7] |
IWANAMI S, SUU T, KATO H. Study on flow characteristics in right-angled pipe fittings:1st report on case of water flow[J]. Transactions of the Japan Society of Mechanical Engineers, 2008, 35(269): 97-106. |
| [8] |
李玲, 李玉梁, 黄继汤, 等. 三岔管内水流流动的数值模拟与实验研究[J]. 水利学报, 2001, 3: 49-52. LI Ling, LI Yu-liang, HUANG Ji-tang, et al. Numerical simulation and experimental study on water flow in Y-type tube[J]. Journal of Hydraulic Engineering, 2001, 3: 49-52. |
| [9] |
MILLER D S. Internal flow:a guide to losses in pipe and duct systems[M]. Bedford: BHR Group Limited, 1971, 303-360.
|
| [10] |
IDELCHIK I E, STEINBERG M O, MALYAVSKAYA G R, et al. Handbook of hydraulic resistance, 4th Edition[M]. New York: Begell House Inc, 2008, 483-572.
|
| [11] |
BASSETT M D, WINTERBONE D E, PEARSON R J. Calculation of steady flow pressure loss coefficients for pipe junctions[J]. Proceedings of the institution of mechanical engineers, part C:Journal of Mechanical Engineering Science, 2001, 215(8): 861-881. DOI:10.1177/095440620121500801 |
| [12] |
王亚琼, 谢永利, 刘洪洲, 等. 海底隧道半横向通风孔物理模型试验[J]. 中国公路学报, 2010, 23(3): 76-82. WANG Ya-qiong, XIE Yong-li, LIU Hong-zhou, et al. Physical model experiment on semi-transverse ventilation air inlet and outlet of subsea tunnel[J]. China Journal of Highway and Transport, 2010, 23(3): 76-82. |
| [13] |
孙恒超, 陈国定, 陈薄. 泛结构条件下轴承腔油气两相流动的模化方法[J]. 航空动力学报, 2014, 29(8): 1987-1995. SUN Heng-chao, CHEN Guo-ding, CHEN Bo. Modeling method of bearing chamber oil/air tow-phase flow under multi-geometrical conditions[J]. Journal of Aerospace Power, 2014, 29(8): 1987-1995. |
| [14] |
JTG/T D70/2-02-2014. 公路隧道通风设计细则[S]. 北京, 中华人民共和国交通运输部, 2014: 37. http://www.bookask.com/book/1967699.html
|
| [15] |
归柯庭, 汪军, 王秋颖. 工程流体力学[M]. 北京: 科学出版社, 2007, 183-185.
|
| [16] |
石喜, 吕宏兴, 朱德兰, 等. PVC三通管水流阻力与流动特征分析[J]. 农业机械学报, 2013, 44(1): 73-79. SHI Xi, LV Hong-xing, ZHU De-lan, et al. Flow resistance and characteristics of PVC tee pipes[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1): 73-79. DOI:10.6041/j.issn.1000-1298.2013.01.015 |
| [17] |
朱红钧, 林元华, 谢龙汉. FLUENT流动分析及仿真实用教程[M]. 北京: 人民邮电出版社, 2010, 107-110.
|
| [18] |
SHIH T H, LIOU W W, SHABBIR A, et al. A new k-eeddy viscosity model for high reynolds number turbulent flows[J]. Computers & Fluids, 1995, 24(3): 227-238. |
| [19] |
陈卫忠, 郭小红, 曹传林, 等. 公路分岔隧道循环风相互影响及其对策研究[J]. 岩石力学与工程学报, 2008, 27(6): 1137-1147. CHEN Wei-zhong, GUO Xiao-hong, CAO Chuan-lin, et al. Research on interrelationship of exhaust air of highway forked tunnel and countermeasures[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1137-1147. |
| [20] |
王晓雯, 蒋树屏. 公路长隧道纵向组合通风计算方法及应用[J]. 中国公路学报, 1996, 9(3): 62-71. WANG Xiao-wen, JIANG Shu-ping. Calculating method and application of longitudinally combined ventilation in a long highway tunnel project[J]. China Journal of Highway and Transport, 1996, 9(3): 62-71. |
| [21] |
王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 清华大学出版社, 2004, 125-126.
|
| [22] |
VERSTEEG H K, MALALASEKERA W. An introduction to computational fluid dynamics:the finite volume method[M]. Harlow Essex: Pearson Education Limited, 2007, 186-190.
|
| [23] |
吕宏兴, 裴国霞, 杨玲霞. 水力学[M]. 北京: 中国农业出版社, 2002, 55-66.
|
| [24] |
蔡增基, 龙天渝. 流体力学泵与风机[M]. 北京: 中国建筑工业出版社, 2009, 91-128.
|
| [25] |
GAN G H, RIFFAT S B. Numerical determination of energy losses at duct junctions[J]. Applied Energy, 2000, 67(3): 331-340. DOI:10.1016/S0306-2619(00)00026-X |



