2. 浙江大学 建筑工程学院, 浙江 杭州 310058
2. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
由于城市地下空间的限制,新建隧道将不可避免地接近、穿越既有运营隧道.新建隧道下穿开挖将对既有隧道产生不利的影响,如纵向不均匀沉降、管片开裂、道床脱开、接头破损、渗漏水等,从而严重影响列车运营安全.合理预估隧道下穿施工过程中既有隧道响应及控制隧道施工风险、保护既有隧道结构,是目前城市轨道交通工程面临的重要课题之一.
国内外学者主要通过现场原位监测[1-3]、模型试验[4-5]、有限元分析[6]及简化解析理论[7-11]等手段研究下穿隧道对既有运营隧道的影响.其中,简化理论解析解具有概念明确、运算简单、易于工程应用等优点,在研究隧道响应的初步分析中常常被采用.Klar等[7]基于弹性介质理论推导得到隧道施工对上部管道影响的解析解答.张治国等[8-9]基于Winkler地基模型理论及两阶段分析法,建立了隧道下穿施工引起既有隧道位移及内力理论解,进一步采用层状地基模型并考虑隧道非均匀开挖受力条件下推导得到隧道纵向响应理论解.Zhang等[10]基于Segaseta[12]隧道施工镜像法并通过两阶段分析法,建立了隧道超挖施工对上部隧道影响的解析解.
在简化解析理论上,尽管前人不断通过采用复杂的地基模型及土体位移施加方式来改进理论计算方法,隧道本身的模型没有得到充分的重视.为了简化计算,既有的理论解无一例外把盾构隧道简化为等直梁或Euler-Bernoulli无限长梁[9-11].但城市盾构隧道并非连续筒状结构体,而是由管片及螺栓连接而成的复合结构体.接头的物理力学性能,特别是管片间抗剪刚度,远远弱于隧道管片,是隧道结构中最为薄弱的环节.Wu等[13-14]指出,由于隧道接头的存在,隧道沉降变形基本可以划分为两部分:一是纵向弯曲变形;二是隧道管片间的剪切错台,认为采用Timoshenko梁模型能较好地模拟隧道剪切刚度的削减效应,并能进一步得到管片间的剪切错台量. Liang等[15]通过简化隧道为Timoshenko梁,推导得到考虑隧道剪切效应的基坑开挖卸荷对既有下卧隧道影响的解析解,并通过案例分析进一步验证Timoshenko梁模型的适用性.Li等[16]亦采用Timoshenko梁模拟隧道变形,推导得到在隧道下穿作用下既有隧道响应,但文献[16]没有进一步对隧道剪切错台进行分析,且没有详细给出隧道相关变形参数的获取办法,导致工程应用存在一定的困难.
为进一步模拟盾构隧道在剪切作用下的变形特性,本文采用具有2个广义位移的Timoshenko梁考虑盾构隧道变形.将既有盾构隧道考虑为搁置于Winkler弹性地基上的Timoshenko梁.隧道开挖引起的附加地层位移采用修正的Loganatha及Polous解得到.基于两阶段分析法,把下穿隧道引起的附加地层位移施加于上部隧道之上,通过受力分析,建立地层位移-隧道变形耦合的平衡微分方程.采用有限差分法求解,得到考虑剪切效应的既有盾构隧道响应的解析解,并进一步给出隧道剪切错台量的计算方法.最后通过与2个下盾构隧道工程隧道实测数据进行对比分析,验证本文所提理论的适用性.
1 考虑隧道剪切效应的地层位移-隧道变形理论新建隧道开挖将引起地层损失,导致土体自由位移.既有盾构隧道在土体位移作用下产生沉降变形及内力.如图 1所示为新建隧道下穿对既有盾构隧道纵向变形影响示意图.已有研究在理论分析上基本采用Euler-Bernoulli梁模型模拟隧道的纵向弯曲变形[8-11].Euler-Bernoulli梁假定任意一截面在变形前后均与中性轴垂直相交,如图 2(a)所示,不产生剪切变形.该假定暗含梁剪切刚度无穷大这一内在假定,因而不能考虑隧道接头的存在对整体剪切刚度的削减效应.假如仅把隧道考虑为等直梁或Euler-Bernoulli无限长梁,则只能考虑隧道的弯曲变形,因其不能考虑隧道接头对整体刚度的削减,也就不能进一步得到管片间的剪切变形.此外,基于等直梁或Euler-Bernoulli无限长梁理论,往往过高估计隧道弯矩值及剪力值[13].若采用该方法预测结果对隧道进行加固处理势必导致加固措施过度保守.

|
图 1 隧道开挖对既有盾构影响示意图 Fig. 1 Sketch for influences of existing tunnel due tunnelling |

|
图 2 Euler-Bernoulli梁及Timoshenko梁变形特征 Fig. 2 Deformation characters of Euler-Bernoulli beam and Timoshenko beam |
为进一步考虑隧道接头的存在对整体剪切刚度的削弱,一些研究者指出可以采用Timoshenko梁模型模拟隧道的变形与内力发展[13-16].与Euler-Bernoulli梁理论不同,Timoshenko梁是具有2个广义位移的梁理论模型[17].Timoshenko梁截面变形如图 2(b)所示.Timoshenko梁理论假定:在梁受力变形前,任意一梁截面与中性轴垂直相交(与Euler-Bernoulli梁一样);在受力变形后,截面虽仍然为一平面,而不再与中性轴垂直相交,而是在剪切作用下截面与中性轴法线方向成大小为θ的夹角,并产生剪切变形,如图 2(b)所示.Wu等[13]指出,Timoshenko梁不仅能模拟隧道弯曲变形,并且能够考虑隧道剪切效应,故采用Timoshenko梁理论模拟隧道响应比Euler-Bernoulli梁理论更加符合实际情况.
进一步考虑隧道接头剪切效应,推导得到在下部隧道施工作用下上部既有盾构隧道响应公式.为简化计算,本文计算模型作如下假设:
1) 既有隧道考虑为具有剪切效应的Timoshenko梁;
2) 地层与隧道相互作用通过Winkler地基模型考虑,且隧道与地基弹簧始终连接,不发生脱离;
3) 不考虑隧道既有变形及地层-隧道相互作用的时间效应,如固结、蠕变等.
本文通过两阶段分析法推导求解.“两阶段分析法”具有概念明确、计算简单、易于工程应用等优点,是目前在考虑隧道与邻近施工相互作用分析中应用较为广泛的分析方法[7-11, 15-16, 18-19].根据两阶段分析法的基本原理,首先,估算新建隧道开挖引起的土体自由位移(不考虑隧道存在);其次,把计算得到的土体自由位移当作“位移荷载”施加于隧道上,建立地层位移-隧道变形的纵向微分控制方程,通过有限差分法求解等方法得到隧道的内力及位移解答.
1.1 隧道纵向变形理论推导图 3为新建隧道开挖对既有隧道影响分析模型示意图.地层损失引起的自由土体沉降uz(x)作用于盾构隧道上,从而引起隧道的纵向变形及内力.自由土体沉降uz(x)采用修正的Loganathan及Polous理论[20]进行预估,详见1.2节.

|
图 3 隧道下穿对既有盾构隧道的影响计算模型 Fig. 3 Analysis model of impacts on existing shield tunnel due to down-crossing tunnelling |
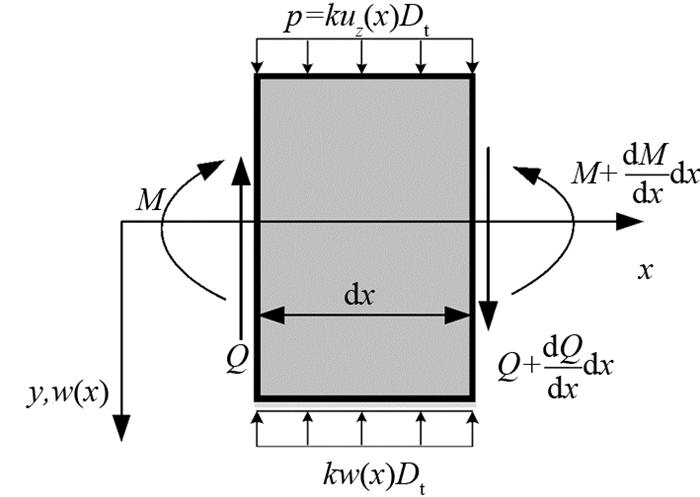
为获得在自由土体沉降uz(x)作用下的隧道变形控制方程,取图 3中任意位置的一微元体进行受力分析,如图 4所示.得到隧道受力及弯矩平衡方程:
| $ \begin{array}{l} Q + kw\left( x \right){D_{\rm{t}}}{\rm{d}}x = \\ \;\;\;\;\;Q + \frac{{{\rm{d}}Q}}{{{\rm{d}}x}}{\rm{d}}x + k{u_z}\left( x \right){D_{\rm{t}}}{\rm{d}}x, \end{array} $ | (1) |
| $ \begin{array}{l} M + Q{\rm{d}}x + kw\left( x \right){D_{\rm{t}}}\frac{{{\rm{d}}{x^2}}}{2} = \\ \;\;\;\;\;M + \frac{{{\rm{d}}M}}{{{\rm{d}}x}}{\rm{d}}x + k{u_z}\left( x \right){D_{\rm{t}}}\frac{{{\rm{d}}{x^2}}}{2}. \end{array} $ | (2) |
|
图 4 微元体受力分析 Fig. 4 Unit element force analysis |
式中:Q为隧道附加剪力(正方向如图 4所示),M为隧道附加弯矩(正方向如图 4所示),k为地基反力系数,Dt为既有隧道外径,w(x)为隧道竖向位移.
根据Timoshenko梁理论,剪力、弯矩与隧道竖向位移、转角θ存在如下关系:
| $ M = - {\left( {EI} \right)_{{\rm{eq}}}}\frac{{{\rm{d}}\theta }}{{{\rm{d}}x}}, $ | (3) |
| $ Q = {\left( {\kappa GA} \right)_{{\rm{eq}}}}\left( {\frac{{{\rm{d}}w\left( x \right)}}{{{\rm{d}}x}} - \theta } \right). $ | (4) |
式中:(EI)eq为隧道纵向等效抗弯刚度,(κGA)eq为隧道等效剪切刚度.
对式(1)和(2)进一步化简,略去高阶微量,并结合式(3)和(4),可得到在Timoshenko梁上的竖向位移w(x)、转角θ的平衡微分方程:
| $ kw\left( x \right){D_{\rm{t}}} = {\left( {\kappa GA} \right)_{{\rm{eq}}}}\left( {\frac{{{{\rm{d}}^2}w\left( x \right)}}{{{\rm{d}}{x^2}}} - \frac{{{\rm{d}}\theta }}{{{\rm{d}}x}}} \right) + k{u_z}\left( x \right){D_{\rm{t}}}, $ | (5) |
| $ {\left( {\kappa GA} \right)_{{\rm{eq}}}}\left( {\frac{{{\rm{d}}w\left( x \right)}}{{{\rm{d}}x}} - \theta } \right) + {\left( {EI} \right)_{{\rm{eq}}}}\frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{x^2}}} = 0. $ | (6) |
对式(5)和(6)解耦,可得到只关于竖向位移w(x)微分方程表达式:
| $ \begin{array}{*{20}{c}} {\frac{{{{\rm{d}}^4}w\left( x \right)}}{{{\rm{d}}{x^4}}} - \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{{{\rm{d}}^2}w\left( x \right)}}{{{\rm{d}}{x^2}}} + \frac{{k{D_{\rm{t}}}}}{{{{\left( {EI} \right)}_{{\rm{eq}}}}}}w\left( x \right) = }\\ {\frac{{k{D_{\rm{t}}}}}{{{{\left( {EI} \right)}_{{\rm{eq}}}}}}{u_z}\left( x \right) - \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{{{\rm{d}}^2}{u_z}\left( x \right)}}{{{\rm{d}}{x^2}}}.} \end{array} $ | (7) |
求解式(7)即可得到在隧道开挖影响下既有隧道纵向变形.由于(7)式为四阶常微分方程,在数学求解上有一定的难度.为简化计算及方便编程,采用有限差分法进行数值求解.既有盾构隧道离散为n+5个节点(隧道两端分别增加2个虚拟节点),每2个节点间距离长度为l.如图 5所示为隧道的离散化示意图.据标准有限差分原理,取微分方程式(7)的有限差分形式:
| $ \begin{array}{l} \frac{{6{w_i} - 4\left( {{w_{i + 1}} + {w_{i - 1}}} \right) + \left( {{w_{i + 2}} + {w_{i - 2}}} \right)}}{{{l^4}}} - \\ \;\;\;\;\;\frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}} \cdot \frac{{{w_{i + 1}} - 2{w_i} + {w_{i - 1}}}}{{{l^2}}} + \frac{{k{D_{\rm{t}}}}}{{{{\left( {EI} \right)}_{{\rm{eq}}}}}}{w_i} = \\ \;\;\;\;\;\frac{{k{D_{\rm{t}}}}}{{{{\left( {EI} \right)}_{{\rm{eq}}}}}}{u_{z,i}} - \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{\left( {{u_{{\rm{z}},i + 1}} - 2{u_{{\rm{z}},i}} + {u_{{\rm{z}},i - 1}}} \right)}}{{{l^2}}}. \end{array} $ | (8) |

|
图 5 盾构隧道离散分析 Fig. 5 Discretization analysis of shield tunnel |
式中:wi、wi-1、wi+1、wi+2及wi-2分别为节点单元i、i-1、i+1、i+2及i-2竖向位移,uz, i、uz, i+1、uz, i-1分别为节点单元i、i+1、i-1处隧道施工引起的地层竖向位移;以此类推.
整理式(6)可得
| $ \frac{{{\rm{d}}w\left( x \right)}}{{{\rm{d}}x}} - \theta = - \frac{{{{\left( {EI} \right)}_{{\rm{eq}}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{x^2}}}. $ | (9) |
将式(9)代入式(4)得到
| $ Q = - {\left( {EI} \right)_{{\rm{eq}}}}\frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{x^2}}}. $ | (10) |
对式(5)求一次导数整理后得
| $ \frac{{{{\rm{d}}^2}\theta }}{{{\rm{d}}{x^2}}} = \frac{{{{\rm{d}}^3}w\left( x \right)}}{{{\rm{d}}{x^3}}} - \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{{\rm{d}}w\left( x \right)}}{{{\rm{d}}x}} + \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{{\rm{d}}{u_z}\left( x \right)}}{{{\rm{d}}x}}. $ | (11) |
式(5)可进一步改写为
| $ \frac{{{\rm{d}}\theta }}{{{\rm{d}}x}} = \frac{{{{\rm{d}}^2}w\left( x \right)}}{{{\rm{d}}{x^2}}} - \frac{{k{D_{\rm{t}}}w\left( x \right)}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}} + \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{u_z}\left( x \right). $ | (12) |
把式(10)、(11)分别代入式(3)、(4)可得到在自由土体沉降作用下既有盾构隧道剪力Q及弯矩M的表达式:
| $ \begin{array}{l} Q = - {\left( {EI} \right)_{{\rm{eq}}}}\left[ {\frac{{{{\rm{d}}^3}w\left( x \right)}}{{{\rm{d}}{x^3}}} - \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{{\rm{d}}w\left( x \right)}}{{{\rm{d}}x}} + } \right.\\ \;\;\;\;\;\;\left. {\frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{{\rm{d}}{u_z}\left( x \right)}}{{{\rm{d}}x}}} \right], \end{array} $ | (13) |
| $ M = - {\left( {EI} \right)_{{\rm{eq}}}}\left[ {\frac{{{{\rm{d}}^2}w\left( x \right)}}{{{\rm{d}}{x^2}}} - \frac{{k{D_{\rm{t}}}w\left( x \right)}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}} + \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{u_z}\left( x \right)} \right]. $ | (14) |
对式(13)和(14)进行有限差分,可得到任意节点i的剪力Qi及弯矩Mi表达式:
| $ \begin{array}{l} {Q_i} = - {\left( {EI} \right)_{{\rm{eq}}}}\left( {\frac{{{w_{i + 2}} - 2{w_{i + 1}} + 2{w_{i - 1}} - {w_{i - 2}}}}{{2{l^3}}} - } \right.\\ \;\;\;\;\;\;\;\left. {\frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{{w_{i + 1}} - {w_{i - 1}}}}{{2l}} + \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}\frac{{{u_{z,i + 1}} - {u_{z,i - 1}}}}{{2l}}} \right) \end{array} $ | (15) |
| $ \begin{array}{*{20}{c}} {{M_i} = - {{\left( {EI} \right)}_{{\rm{eq}}}}\left( {\frac{{{w_{i + 1}} - 2{w_i} + {w_{i - 1}}}}{{{l^2}}} - } \right.}\\ {\left. {\frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{w_i} + \frac{{{u_{z,i}}k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}} \right).} \end{array} $ | (16) |
假定隧道两端自由,则
| $ {M_0} = {M_{\rm{n}}} = 0, $ | (17) |
| $ {Q_0} = {Q_{\rm{n}}} = 0. $ | (18) |
结合式(15)~(18),可得隧道两端位置处附加剪力及弯矩的限差分形式,并联立求解,得到图 4中额外的4个虚拟节点的位移表达式:
| $ {w_{ - 1}} = \left( {\frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2} + 2} \right){w_0} - {w_1} - \frac{{{u_{z,0}}k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2}, $ | (19) |
| $ \begin{array}{l} {w_{ - 2}} = \left( {\frac{{4k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2} + 4 + \frac{{D_{\rm{t}}^2{k^2}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^4}} \right){w_0} - \\ \;\;\;\;\;\;\;\;\left( {\frac{{2k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2} + 4} \right){w_1} + {w_2} - \left( {\frac{{{k^2}D_{\rm{t}}^2{l^4}}}{{\left( {\kappa GA} \right)_{{\rm{eq}}}^2}} + } \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{2k{D_{\rm{t}}}{l^2}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}} \right){u_{z,0}} + \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2}\left( {{u_{z,1}} - {u_{z, - 1}}} \right), \end{array} $ | (20) |
| $ {w_{n + 1}} = \left( {\frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2} + 2} \right){w_n} - {w_{n - 1}} - \frac{{{u_{z,n}}k{D_t}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2}, $ | (21) |
| $ \begin{array}{l} {w_{n + 2}} = \left( {\frac{{4k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2} + 4 + \frac{{D_{\rm{t}}^2{k^2}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^4}} \right){w_n} - \\ \;\;\;\;\;\;\;\;\;\left( {\frac{{2k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2} + 4} \right){w_{n - 1}} + {w_{n - 2}} - \\ \;\;\;\;\;\;\;\;\;\left( {\frac{{{k^2}D_{\rm{t}}^2{l^4}}}{{\left( {\kappa GA} \right)_{{\rm{eq}}}^2}} + \frac{{2k{D_{\rm{t}}}{l^2}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}} \right){u_{z,n}} + \\ \;\;\;\;\;\;\;\;\;\frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}{l^2}\left( {{u_{z,n - 1}} - {u_{z,n + 1}}} \right). \end{array} $ | (22) |
结合4个虚拟位移表达式,式(8)可改写成矩阵表达形式:
| $ \left( {{\mathit{\boldsymbol{K}}_1} - {\mathit{\boldsymbol{K}}_2} + {\mathit{\boldsymbol{K}}_3}} \right)\mathit{\boldsymbol{w}} = {\mathit{\boldsymbol{U}}_1} - {\mathit{\boldsymbol{U}}_2} - {\mathit{\boldsymbol{U}}_3}. $ | (23) |
式中:K1为隧道位移刚度矩阵, K2为隧道剪切刚度矩阵, K3为抗弯刚度矩阵, w为隧道竖向位移列向量, U1为隧道施工引起地层竖向位移列向量, U2为隧道施工引起竖向位移修正列向量, U3为隧道施工引起竖向位移补充列向量.
代入虚节点位移表达式(19)~(22)后,可得到式(23)各个矩阵、列向量的表达式如下:
| $ {\mathit{\boldsymbol{K}}_1} = \frac{1}{{{l^4}}}{\left[ {\begin{array}{*{20}{c}} {{A_1}}&{{A_2}}&2&{}&{}&{}&{}&{}&{}\\ {{A_3}}&5&{ - 4}&1&{}&{}&{}&{}&{}\\ 1&{ - 4}&6&{ - 4}&1&{}&{}&{}&{}\\ {}&1&{ - 4}&6&{ - 4}&1&{}&{}&{}\\ {}&{}& \ddots&\ddots&\ddots&\ddots&\ddots &{}&{}\\ {}&{}&{}&1&{ - 4}&6&{ - 4}&1&{}\\ {}&{}&{}&{}&1&{ - 4}&6&{ - 1}&1\\ {}&{}&{}&{}&{}&1&{ - 4}&5&{{A_3}}\\ {}&{}&{}&{}&{}&{}&2&{{A_2}}&{{A_1}} \end{array}} \right]_{\left( {n + 1} \right) \times \left( {n + 1} \right)}}, $ | (24) |
| $ {\mathit{\boldsymbol{K}}_2} = \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}{l^2}}}{\left[ {\begin{array}{*{20}{c}} B&{}&{}&{}&{}&{}&{}&{}&{}\\ 1&{ - 2}&1&{}&{}&{}&{}&{}&{}\\ {}&1&{ - 2}&1&{}&{}&{}&{}&{}\\ {}&{}&1&{ - 2}&1&{}&{}&{}&{}\\ {}&{}&{}& \ddots&\ddots&\ddots &{}&{}&{}\\ {}&{}&{}&{}&1&{ - 2}&1&{}&{}\\ {}&{}&{}&{}&{}&1&{ - 2}&1&{}\\ {}&{}&{}&{}&{}&{}&1&{ - 2}&1\\ {}&{}&{}&{}&{}&{}&{}&{}&B \end{array}} \right]_{\left( {n + 1} \right) \times \left( {n + 1} \right)}}, $ | (25) |
| $ {\mathit{\boldsymbol{K}}_3} = \frac{{k{D_{\rm{t}}}}}{{{{\left( {EI} \right)}_{{\rm{eq}}}}}}{\left[ {\begin{array}{*{20}{c}} 1&{}&{}&{}&{}&{}&{}&{}&{}\\ {}&1&{}&{}&{}&{}&{}&{}&{}\\ {}&{}&1&{}&{}&{}&{}&{}&{}\\ {}&{}&{}&1&{}&{}&{}&{}&{}\\ {}&{}&{}&{}& \ddots &{}&{}&{}&{}\\ {}&{}&{}&{}&{}&1&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&1&{}&{}\\ {}&{}&{}&{}&{}&{}&{}&1&{}\\ {}&{}&{}&{}&{}&{}&{}&{}&1 \end{array}} \right]_{\left( {n + 1} \right) \times \left( {n + 1} \right)}}, $ | (26) |
| $ \begin{array}{l} {\mathit{\boldsymbol{U}}_1} = \frac{{k{D_{\rm{t}}}}}{{{{\left( {EI} \right)}_{{\rm{eq}}}}}}\left\{ {{u_{z,0}},{u_{z,1}},{u_{z,2}},{u_{z,3}} \cdots {u_{z,n - 3}},{u_{z,n - 2}},} \right.\\ \;\;\;\;\;\;\;{\left. {{u_{z,n - 1}},{u_{z,n}}} \right\}^{\rm{T}}}, \end{array} $ | (27) |
| $ {\mathit{\boldsymbol{U}}_2} = \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}{l^2}}}{\left\{ {\begin{array}{*{20}{c}} {{u_{z,1}} - 2{u_{z,0}} + {u_{z, - 1}}}\\ {{u_{z,2}} - 2{u_{z,1}} + {u_{z,0}}}\\ {{u_{z,3}} - 2{u_{z,2}} + {u_{z,1}}}\\ {{u_{z,4}} - 2{u_{z,3}} + {u_{z,2}}}\\ \vdots \\ {{u_{z,n - 2}} - 2{u_{z,n - 3}} + {u_{z,n - 4}}}\\ {{u_{z,n - 1}} - 2{u_{z,n - 2}} + {u_{z,n - 3}}}\\ {{u_{z,n}} - 2{u_{z,n - 1}} + {u_{z,n - 2}}}\\ {{u_{z,n + 1}} - 2{u_{z,n}} + {u_{z,n - 1}}} \end{array}} \right\}_{\left( {n + 1} \right) \times 1}}, $ | (28) |
| $ {\mathit{\boldsymbol{U}}_3} = {\left\{ {{E_1},{E_2},0,0, \cdots ,0,0,{E_3},{E_4}} \right\}^{\rm{T}}}. $ | (29) |
其中:
| $ {A_1} = \frac{{{k^2}D_{\rm{t}}^2{l^4}}}{{\left( {\kappa GA} \right)_{{\rm{eq}}}^2}} + 2,\;\;\;\;\;{A_2} = - \frac{{2{D_{\rm{t}}}k{l^2}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}} - 4, $ |
| $ {A_3} = \frac{{{D_{\rm{t}}}k{l^2}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}} - 2,\;\;\;\;\;B = \frac{{{D_{\rm{t}}}k{l^2}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}, $ |
| $ \begin{array}{l} {E_1} = {u_{z,0}}\left[ { - \frac{{{k^2}D_{\rm{t}}^2}}{{\left( {\kappa GA} \right)_{{\rm{eq}}}^2}} + \frac{{2k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}{l^2}}}} \right] + \\ \;\;\;\;\;\;\;\frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}{l^2}}}\left( {{u_{z,1}} - {u_{z, - 1}}} \right) + {u_{z,0}}\frac{{{k^2}D_{\rm{t}}^2}}{{\left( {\kappa GA} \right)_{{\rm{eq}}}^2}}; \end{array} $ |
| $ {E_2} = - \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}{l^2}}}{u_{z,0}},\;\;\;{E_3} = - \frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}{l^2}}}{u_{z,n}}, $ |
| $ \begin{array}{l} {E_4} = {u_{z,n}}\left[ { - \frac{{{k^2}D_{\rm{t}}^2}}{{\left( {\kappa GA} \right)_{{\rm{eq}}}^2}} + \frac{{2k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}{l^2}}}} \right] + \\ \;\;\;\;\frac{{k{D_{\rm{t}}}}}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}{l^2}}}\left( {{u_{z,n - 1}} - {u_{z,n + 1}}} \right) + \frac{{{k^2}D_{\rm{t}}^2}}{{\left( {\kappa GA} \right)_{{\rm{eq}}}^2}}{u_{z,n}}. \end{array} $ |
令式(23)中
| $ \mathit{\boldsymbol{K}} = {\mathit{\boldsymbol{K}}_1} - {\mathit{\boldsymbol{K}}_2} + {\mathit{\boldsymbol{K}}_3}, $ |
| $ \mathit{\boldsymbol{U}} = {\mathit{\boldsymbol{U}}_1} - {\mathit{\boldsymbol{U}}_2} - {\mathit{\boldsymbol{U}}_3}, $ |
对式(23)两边同乘取K-1,则可得到隧道竖向位移列向量w的表达式:
| $ \mathit{\boldsymbol{w}} = {\mathit{\boldsymbol{K}}^{ - 1}}\mathit{\boldsymbol{U}}. $ | (30) |
式中:K-1为矩阵K的逆矩阵.
在已知附加土体位移uz(x)分布的情况下,由式(30)可以得到隧道下穿施工引起既有隧道竖向位移w(x)的数值解.进一步把计算得到的隧道竖向位移w(x)值代入式(15)和(16)中,可得到在下穿隧道开挖作用下引起既有隧道的附加剪力Q及弯矩M的数值解.
值得注意的是,当隧道等效剪切刚度取无穷大时,隧道剪切变形趋近于0,该解答退化为基于Euler-Bernoulli梁的隧道下穿引起既有隧道纵向内力及位移响应的解答.
1.2 隧道下穿引起的地层位移众多学者提出了各种预测隧道施工引起土体自由位移的理论解法,其中以Loganathan等[20]的理论解法应用最为广泛.文献[20]提出在软土地层中隧道开挖引起的地层竖向位移uz(x)公式:
| $ \begin{array}{l} {u_z}\left( {x'} \right) = {R^2}\left\{ { - \frac{{z - H}}{{{{x'}^2} + {{\left( {z - H} \right)}^2}}} + \left( {3 - 4\nu } \right) \times } \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{{z + H}}{{{{x'}^2} + {{\left( {z + H} \right)}^2}}} - \frac{{2z\left[ {{{x'}^2} - {{\left( {z + H} \right)}^2}} \right]}}{{{{\left[ {{{x'}^2} + \left( {z + {H^2}} \right)} \right]}^2}}}} \right\} \times \\ \;\;\;\;\;\;\;\;\frac{{4Rg + {g^2}}}{{4{R^2}}}\exp \left\{ { - \left[ {\frac{{1.38{{x'}^2}}}{{{{\left( {H + R} \right)}^2}}} + \frac{{0.69{z^2}}}{{{H^2}}}} \right]} \right\}. \end{array} $ | (31) |
式中:x′为隧道上一点对新旧隧道轴线交点的连线长度,R为开挖隧道的半径,H为新建隧道轴线埋深,z为既有隧道埋深,v为地层泊松比,g为间隙参数[21]:
| $ g = {G_{\rm{p}}} + U_{3{\rm{D}}}^ * + {w^ * }, $ |
其中,Gp为隧道物理间隙参数,Gp=2a+o,a为盾尾厚度,o为管片安装所需间隙,U3D*为隧道开挖面等效三维弹塑性变形,w*为考虑隧道人工施工影响参数.
在实际工程中,地层损失率v1应用范围更加广泛.为方便工程应用,笔者建立了地层损失率与间隙参数间的关系[22]:
| $ {v_1} = \frac{{4gR + {g^2}}}{{4{R^2}}}. $ | (32) |
对于新旧隧道相互垂直情况,可通过式(31)直接计算既有隧道所在位置处由隧道开挖引起的自由土体位移.在城市隧道交叠施工中,新旧隧道往往以一定的夹角相交,若依然采用式(31)进行自由土体位移预测,将导致计算结果与实际情况不符合.为考虑新旧隧道夹角相交的影响,通过坐标轴变换,把式(31)应用范围拓展到新旧隧道任意相交角度的情况.推导过程如下.
如图 6所示为隧道斜交情况下自由土体位移转换示意图.假定新旧隧道间夹角为α,取值为0~90°.由几何关系有
| $ x' = x \cdot \sin \alpha . $ | (33) |

|
图 6 隧道斜交情况下地层附加土体位移变换示意图 Fig. 6 Sketch for transform of additional ground movements due to obliquely tunnelling |
式中:x为隧道上一点对新旧隧道轴线交点的连线长度.
把式(33)代入式(31)中得新旧隧道成任意夹角时既有隧道所在位置处自由土体位移uz(x)表达式:
| $ \begin{array}{l} {u_z}\left( x \right) = {R^2}\left\{ { - \frac{{z - H}}{{{{\left( {x\sin \alpha } \right)}^2} + {{\left( {z - H} \right)}^2}}} + } \right.\\ \left. {\frac{{\left( {3 - 4\nu } \right)\left( {z + H} \right)}}{{{{\left( {x\sin \alpha } \right)}^2} + {{\left( {z + H} \right)}^2}}} - \frac{{2z\left[ {{{\left( {x\sin \alpha } \right)}^2} - {{\left( {z + H} \right)}^2}} \right]}}{{{{\left[ {{{\left( {x\sin \alpha } \right)}^2} - \left( {z + {H^2}} \right)} \right]}^2}}}} \right\}\\ \frac{{4Rg + {g^2}}}{{4{R^2}}} \times \exp \left\{ { - \left[ {\frac{{1.38{{\left( {x\sin \alpha } \right)}^2}}}{{{{\left( {H + R} \right)}^2}}} + \frac{{0.69{z^2}}}{{{H^2}}}} \right]} \right\}. \end{array} $ | (34) |
结合式(32)、(34)可计算得到新旧隧道成任意夹角情况下由隧道开挖引起的既有隧道位置处的自由土体位移.
2 相关参数确定隧道自身等效抗弯刚度(EI)eq及等效剪切刚度(κ GA)eq是影响隧道变形及内力分布的重要参数.盾构隧道是在纵向与环向通过螺栓将管片连接而成的筒体结构.隧道接头的存在致使其整体刚度要远远小于连续的混凝土管片筒体结构.
2.1 纵向等效抗弯刚度日本隧道专家Shiba等[23]提出纵向等效连续化模型,是目前应用较为广泛的确定隧道等效纵向抗弯刚度(EI)eq的方法.如图 7所示为等效连续化模型示意图.图中,ls为环宽,ψ为中性轴位置,t为管片厚度,m为隧道轴线到螺栓位置距离,Δ为管片张开量,φ为管片间张开角.该方法假定隧道在横向为一均质圆环,在纵向上以刚度等效的方法,把由接头和管片组成的盾构隧道等效为均匀连续梁.其等效弹性弯曲刚度表达式为
| $ {\left( {EI} \right)_{{\rm{eq}}}} = \frac{{{{\cos }^3}\psi }}{{\cos \psi + \left( {\psi + {\rm{ \mathsf{ π} }}/2} \right)\sin \psi }}{E_{\rm{c}}}{I_{\rm{c}}}. $ | (35) |

|
图 7 隧道管片等效连续化模型示意图 Fig. 7 Sketch of equivalent continuum model of shield tunnel segmental rings |
式中:Ec为管片弹性模量,Ic为隧道纵向惯性矩.
中性轴的位置ψ如图 7所示,通过下式确定:
| $ \psi + \cot \psi = {\rm{ \mathsf{ π} }}\left( {0.5 + \frac{{n{k_{\rm{b}}}{l_{\rm{s}}}}}{{{E_{\rm{c}}}{A_{\rm{c}}}}}} \right),{k_{\rm{b}}} = {E_{\rm{b}}}{A_{\rm{b}}}/{l_{\rm{b}}}. $ | (36) |
式中:kb为接头螺栓的平均线刚度,Eb为螺栓的弹性模量,Ab为螺栓的横截面积,lb为螺栓长度,n为螺栓个数,Ac为隧道管片横截面积.
由几何关系可进一步得到管片间张开角φ及张开量Δ的表达式:
| $ \varphi = \frac{{{l_{\rm{s}}}}}{{{E_{\rm{c}}}{I_{\rm{c}}}}}\frac{{\cos \psi + \left( {\psi + {\rm{ \mathsf{ π} }}/2} \right)\sin \psi }}{{{{\cos }^3}\psi }}M, $ | (37) |
| $ \Delta = \varphi \left( {r + m} \right) = \frac{M}{{{{\left( {EI} \right)}_{{\rm{eq}}}}}}\left( {r + r\sin \psi } \right){l_{\rm{b}}}. $ | (38) |
式中:r为隧道轴线对螺栓中点的距离.
2.2 等效剪切刚度Wu等[13]提出了盾构隧道等效剪切刚度(κ GA)eq及管片间错台量δ的计算公式,认为隧道单位剪切位移u由管片剪切变形uj及螺栓剪切变形us组成:
| $ u = {u_{\rm{j}}} + {u_{\rm{s}}}. $ | (39) |
其变形量可分别通过下式计算:
| $ u = {l_{\rm{s}}}\tan \frac{Q}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}}, $ | (40) |
| $ {u_{\rm{j}}} = {l_{\rm{b}}}\tan \frac{Q}{{n{\kappa _{\rm{b}}}{G_{\rm{b}}}{A_{\rm{b}}}}}, $ | (41) |
| $ {u_{\rm{s}}} = \left( {{l_{\rm{s}}} - {l_{\rm{b}}}} \right)\tan \frac{Q}{{{\kappa _{\rm{c}}}{G_{\rm{c}}}{A_{\rm{c}}}}}. $ | (42) |
式中:κb及κc分别为螺栓及管片环Timoshenko剪切系数.对于圆形截面螺栓,κb=0.9;对于环形隧道管片环结构,κc=0.5.Gb及Gc为分别螺栓剪切刚度及隧道管片剪切刚度,两者与各自弹性模量的关系为
| $ {G_{\rm{b}}} = \frac{{{E_{\rm{b}}}}}{{2\left( {1 + {v_{\rm{b}}}} \right)}},{G_{\rm{c}}} = \frac{{{E_{\rm{c}}}}}{{2\left( {1 + {v_{\rm{c}}}} \right)}}. $ |
其中,vb及vc分别为螺栓及管片的泊松比.
结合式(39)~(42)可得到隧道等效剪切刚度表达式:
| $ {\left( {\kappa GA} \right)_{{\rm{eq}}}} = \zeta {l_{\rm{s}}}{\left( {\frac{{{l_{\rm{b}}}}}{{n{\kappa _{\rm{b}}}{G_{\rm{b}}}{A_{\rm{b}}}}} + \frac{{{l_{\rm{s}}} - {l_{\rm{b}}}}}{{{\kappa _{\rm{c}}}{G_{\rm{c}}}{A_{\rm{c}}}}}} \right)^{ - 1}}. $ | (43) |
式中:ζ为修正系数,本文取ζ=1.
考虑到管片剪切位移较小(约为5%的螺栓剪切变形)[13],因此忽略管片剪切变形,则管片间错台量δ主要由螺栓剪切变形引起:
| $ \delta = u = {l_{\rm{s}}}\tan \frac{Q}{{{{\left( {\kappa GA} \right)}_{{\rm{eq}}}}}} = {u_{\rm{j}}}. $ | (44) |
在Winkler地基模型中,地基基床系数k的取值对计算结果有重要的影响.Vesic[24]通过搁置于地表上的长梁荷载试验研究证实,地基基床系数明显受到梁的刚度影响,并给出考虑梁刚度、地层特性的地基基床系数表达式:
| $ {k_{{\rm{Vesic}}}} = \frac{{0.65{E_{\rm{s}}}}}{{B\left( {1 - {\nu ^2}} \right)}}\sqrt[{12}]{{\frac{{{E_{\rm{s}}}{B^4}}}{{EI}}}}. $ | (45) |
式中:Es为土体弹性模量,EI为梁抗弯刚度(在本文EI=(EI)eq),B为梁宽度(在本文为隧道外径B=Dt).
Vesic地基基床系数法被广泛应用[7-11, 18-19].但是Attewell等[25]指出,Vesic地基基床系数法是假定长梁位于地表而得到,而对于埋置于一定深度的地基梁,若采用Vesic地基基床系数将导致计算结果与实际不符合.Attewell等[25]建议采用2倍的Vesic地基基床系数大致估算在当长梁埋置于一定深度时地基基床系数,即
| $ k = 2{k_{{\rm{Vesic}}}} = \frac{{1.3{E_{\rm{s}}}}}{{B\left( {1 - {\nu ^2}} \right)}}\sqrt[{12}]{{\frac{{{E_{\rm{s}}}{B^4}}}{{EI}}}}. $ | (46) |
本文采用Attewell等[25]的建议,采用式(46)计算Winkler地基基床系数.
对于地基土模量的取值,Vorster等[26]认为在非均质土中,取隧道或管线埋深位置处的土体模量可以得到较好的计算结果.
3 实例验证 3.1 上海轨道交通11号线下穿4号工程上海轨道交通11号线徐家汇-上海体育馆区间隧道上、下交叠穿越既有4号线隧道[10].其中,上行线隧道率先下穿既有轨道交通4号线,随后下行线隧道上穿4号线隧道,新旧隧道相交角度为75°.本文仅对上行线下穿施工既有4号线盾构隧道响应进行分析.既有4号线盾构隧道结构为典型上海地铁隧道结构,其相关隧道结构参数如表 1所示.表中,Di为隧道内径,Db为螺栓直径,隧道埋深17.1 m,位于⑤1a层砂质粉土地层中.11号线隧道采用盾构法施工,隧道外径为6.2 m,内径为5.5 m,环宽1.2 m,隧道轴线埋深25.1 m,新旧隧道净距仅为1.82 m.由式(35)和(43)计算得到既有轨道4号线隧道等效抗弯刚度及等效剪切刚度分别为7.8×104 MN·m2及2.5×103 MN/m.计算取值如下:根据杨敏等[25]的建议对既有隧道所在砂质粉土弹性模量取2.5倍压缩模量值,即20.5 MPa,泊松比取0.26;考虑到该工程较好的隧道同步注浆控制效果,地层损失率取0.25%.文献[10]给出下穿隧道通过后既有隧道纵向沉降变形实测结果,并采用Sagaseta提出的地层位移公式[12],建立基于Euler-Bernoulli梁的简化计算方法.如图 8所示为采用本文方法计算结果、基于Euler-Bernoulli梁预测值与实测、简化计算方法纵向沉降变形对比曲线.
| 表 1 盾构隧道管片结构相关参数 Table 1 Shield tunnel lining relative parameters |

|
图 8 实测与本文计算、简化计算、Euler-Bernoulli梁方法隧道位移曲线对比 Fig. 8 Tunnel displacements comparison between the measured results and predictions by the proposed, simplified, Euler-Bernoulli method. |
由图 8可见,本文计算方法最大沉降值略大于实测结果,小于简化方法计算结果.与简化方法计算结果相比,本文方法得到的隧道纵向沉降槽宽度明显小于简化方法.其原因为本文计算结果基于Loganatha与Polous位移预测方法,而文献[10]是基于Sagaseta位移理论方法.Schimidt[28]指出在计算地层沉降时,根据Sagaseta理论[12]得到的沉降槽曲线往往宽于实测结果.因此,基于Sagaseta理论方法得到的隧道纵向沉降曲线亦大于实测值.而基于Loganatha及Polous位移预测理论能较好地预测隧道沉降槽宽度,因此计算结果也更加接近实际情况.总体而言,本文计算结果与实测结果更加接近.此外,图中亦给出基于修正的Euler-Bernoulli梁的计算结果,本文方法得到的最大沉降值略大于Euler-Bernoulli梁得到的隧道沉降量,但是整体而言两者曲线趋势基本一致.可见在预测隧道沉降上,合适的自由土体沉降理论是合理预测隧道纵向变形的重要基础,且分别基于Euler-Bernoulli梁与Timoshenko梁的隧道纵向预测理论在评估隧道纵向沉降上区别并不大,得到的计算结果均可被工程接受.
如图 9所示为基于Euler-Bernoulli梁与Timoshenko梁的隧道纵向预测理论得到的隧道弯矩M、剪力Q、张开量Δ及管片间错台量δ分布图.对比发现,两者得到的隧道弯矩及剪力纵向变化趋势基本一致,但是采用Euler-Bernoulli梁模型得到的剪力与弯矩结果均明显大于Timoshenko梁,其中最大弯矩值及最大剪力值分别为Timoshenko梁计算结果的1.7倍和4.0倍.在隧道变形上,Euler-Bernoulli梁模型计算得到的张开量大于Timoshenko梁计算结果,最大张开量值为Timoshenko梁的1.7倍.Timoshenko梁理论可考虑隧道剪切效应,可以进一步得到隧道的管片间错台量δ变化.而Euler-Bernoulli梁理论暗含梁的剪切刚度无穷大这一假定,不能考虑隧道剪切效应,无法进一步得到管片间错台量的变化.可见,基于Euler-Bernoulli梁理论的计算方法往往高估隧道的剪力、弯矩及管片张开量,若应用其结果进行隧道加固处理,势必导致加固处理过度保守,造成不必要的浪费.

|
图 9 Euler-Bernoulli梁与Timoshenko梁理论对隧道内力及变形影响的对比分析 Fig. 9 Comparison of internal forces and deformation in tunnel by Euler-Bernoulli beam and Timoshenko beam theory |
王岩[29]报道了北京某盾构下穿施工过程中既有盾构隧道纵向变形实测结果.新建隧道采用盾构法施工,隧道结构采用复合衬砌形式,隧道外径为6.0 m,内径为4.6 m.既有地铁隧道含左线隧道及右线隧道两条盾构线路.本文仅对右线盾构隧道变形进行分析.既有盾构隧道管片为钢筋混凝土管片,外径为6.0 m,内径为5.4 m,壁厚为0.3 m,环宽1 m,相关参数如表 1所示.新建隧道以24°角下穿既有隧道.在穿越位置处既有盾构轴线埋深19.4 m,位于⑤1粉土地层中.新建隧道在穿越区处轴线埋深约为32.7 m.新旧隧道净距约为7.3 m.为实时掌握下穿施工对既有隧道结构影响,在穿越中心两侧隧道各40.0 m范围内对既有隧道结构进行人工及自动化沉降监测.计算参数取值:根据文献[30]数值分析参数取值表,既有隧道所在粉土层弹性模量取40 MPa,泊松比取0.26;根据文献[30]的统计结果,北京地区在粉质粘土层及粉土层盾构施工引起的地层损失率在0.66%~1.71%,且平均地层损失率为1.17%.参考文献[30]的研究成果,隧道开挖引起的地层损失率取值1%;隧道纵向等效刚度由表 1计算得到7.2×1010 N·m2,隧道等效剪切刚度为2.5×109 N/m.如图 10所示为实测与计算结隧道纵向变形曲线对比图.由图可见,计算结果略大于实测值,但总体而言,本文方法得到结果与实测值趋势一致,证明了本文方法的正确性.

|
图 10 实测隧道位移结果与本文计算结果对比 Fig. 10 Comparison between measured tunnel displacement and computed results by proposed method |
如图 11所示为不同地层损失率条件下隧道内力及变形的变化规律.由图可见,隧道最大沉降量wmax、最大弯矩Mmax、最大剪力Qmax、最大管片张开量Δmax及最大错台量δmax随着地层损失率v1的增加基本成线性趋势增大.隧道开挖导致的地层损失越大,则隧道内力及变形也就越大.因此,在实际施工中,应对盾构机进行精细化操作,避免盾构偏航而引起的额外建筑空隙,并及时注浆填充超挖地层,以减少地层位移,从而减少隧道本身的内力及变形.

|
图 11 不同地层损失率对隧道内力及变形的影响 Fig. 11 Effects of ground volume loss ratio on internal forces and deformations of tunnel |
(1) 隧道开挖引起地层位移预测理论对隧道纵向变形估算有重要的影响.Segaseta位移预测理论往往高估地层沉降槽宽度,以至于在预测隧道纵向沉降时得到的隧道沉降槽宽度大于实测.修正的Loganatha与Polous自由土体沉降预测理论在整体上能够较好地预测地层变形,因而得到的隧道纵向沉降变化与实测结果有较好的一致性.
(2) 基于Euler-Bernoulli梁的隧道纵向预测理论得到的隧道纵向变形趋势与Timoshenko梁理论基本一致.然而,Euler-Bernoulli梁理论高估隧道的弯矩、剪力、管片张开量.通过Timoshenko梁理论可进一步考虑隧道剪切效应,可得到管片间错台位移量,而基于Euler-Bernoulli梁理论并不能得到管片间错台位移.
(3) 隧道开挖引起的地层损失率对隧道变形及内力有重要的影响.隧道的沉降、弯矩、剪力、张开量、错台量随着地层损失率增加而成线性增大.
(4) 本文主要考虑地层较为均匀的情况下,隧道开挖对既有隧道影响.如果新旧隧道之间分层明显时,应进一步考虑地层成层性的影响.总体而言,提出的考虑隧道剪切效应的解析解答可为隧道开挖对既有盾构隧道影响分析提供一定理论支持.
| [1] |
CLAYTON C, BERG J, THOMAS A. Monitoring and displacements at Heathrow Express Terminal 4 station tunnels[J]. Géotechnique, 2006, 56(5): 323-334. DOI:10.1680/geot.2006.56.5.323 |
| [2] |
COOPER M L, CHAPMAN D N, ROGERS C D F, et al. Movements in the piccadilly line tunnels due to the heathrow express construction[J]. Géotechnique, 2002, 52(4): 243-258. DOI:10.1680/geot.2002.52.4.243 |
| [3] |
MOHAMAD H, BENNETT P J, SOGA K, et al. Behaviour of an old masonry tunnel due to tunneling-induced ground settlement[J]. Géotechnique, 2010, 60(12): 927-938. DOI:10.1680/geot.8.P.074 |
| [4] |
NG C W W, BOONYARAK T, MAŠÍN D. Three-dimensional centrifuge and numerical modeling of the interaction between perpendicularly crossing tunnels[J]. Canadian Geotechnical Journal, 2013, 50(9): 935-946. DOI:10.1139/cgj-2012-0445 |
| [5] |
NG C W W, BOONYARAK T, MAŠÍN D. Effects of pillar depth and shielding on the interaction of crossing multitunnels[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, ASCE, 141(6): 04015021. |
| [6] |
LIU H Y, SMALL J C, CARTER J P, et al. Effects of tunnelling on existing support systems of perpendicularly crossing tunnels[J]. Computers and Geotechnics, 2009, 36(5): 880-894. DOI:10.1016/j.compgeo.2009.01.013 |
| [7] |
KLAR A, VORSTER T, SOGA K, et al. Soil-pipe interaction due to tunnelling:comparsion between Winkler and elastic continuum solutions[J]. Géotechnique, 55(6): 461-466. DOI:10.1680/geot.2005.55.6.461 |
| [8] |
张治国, 黄茂松, 王卫东. 邻近开挖对既有软土隧道的影响[J]. 岩土力学, 2009, 30(5): 1373-1380. ZHANG Zhi-guo, HUANG Mao-song, WANG Wei-dong. Responses of existing tunnels induced by adjacent excavation in soft soils[J]. Rock and Soil Mechanics, 2009, 30(5): 1373-1380. |
| [9] |
张治国, 黄茂松, 王卫东. 层状地基中隧道开挖对临近既有隧道的影响分析[J]. 岩土工程学报, 2009, 31(4): 600-608. ZHANG Zhi-guo, HUANG Mao-song, WANG Wei-dong. Analysis on response of existing tunnels due to adjacent tunneling in multi-layered soils[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 600-608. |
| [10] |
ZHANG Z, HUANG M. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil[J]. Computers and Geotechnics, 2014, 56(56): 121-132. |
| [11] |
LIANG R, XIA T, YI H, et al. Effects of above-crossing tunnelling on the existing shield tunnels[J]. Tunnelling and Underground Space Technology, 2016, 58(8): 159-176. |
| [12] |
SAGASETA C. Analysis of undraind soil deformation due to ground loss[J]. Géotechnique, 1987, 37(3): 301-320. DOI:10.1680/geot.1987.37.3.301 |
| [13] |
WU H, SHEN S, LIAO S, et al. Longitudinal structural modelling of shield tunnels considering shearing dislocation between segmental rings[J]. Tunnelling and Underground Space Technology, 2015, 50(8): 317-323. |
| [14] |
SHEN S L, WU H N, CUI Y J, et al. Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai[J]. Tunnelling and Underground Space Technology, 2014, 40(2): 309-323. |
| [15] |
LIANG R, XIA T, HUANG M, LIN C. Simplified analytical method for evaluating the effects of adjacent excavation on shield tunnel considering the shearing effect[J]. Computers and Geotechnics, 2017, 81(1): 167-187. |
| [16] |
LI P, DU S, SHEN S, et al. Timoshenko beam solution for the response of existing tunnels because of tunnelling underneath[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(5): 766-784. DOI:10.1002/nag.v40.5 |
| [17] |
TIMOSHENKO S P. On the correction for shear of the differential equation for transverse vibration of prismatic bars[J]. Philosophical Magazine, 1921, 41(2): 744-746. |
| [18] |
ZHANG Z, HUANG M, WANG W. Evaluation of deformation response for adjacent tunnels due to soil unloading in excavation engineering[J]. Tunnelling and Underground Space Technology, 2013, 38(9): 244-253. |
| [19] |
ZHANG Z, ZHANG M, ZHAO Q. A simplified analysis for deformation behavior of buried pipelines considering disturbance effects of underground excavation in soft clays[J]. Arabian Journal of Geosciences, 2015, 8(10): 1-15. |
| [20] |
LOGANATHAN N, POULOS H. Analytical predicted for tunnelling-induced ground movements in clays[J]. Journal of Geotechnical and Geo environmental Engineering, 1999, 124(9): 846-856. |
| [21] |
LEE K, ROWE R, LO K. Subsidence owing to tunnelling. Ⅰ. Estimating the gap parameter[J]. Canadian Geotechnical Journal, 1992, 29(6): 929-940. DOI:10.1139/t92-104 |
| [22] |
梁荣柱, 夏唐代, 林存刚, 等. 盾构推进引起地表及深层水平位移分析[J]. 岩土力学与工程学报, 2015, 34(3): 583-593. LIANG Rong-zhu, XIA Tang-dai, LIN Cun-gang, et al. Analysis of ground surface displacement and horizontal movement of deep soils induced by shield advancing[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3): 583-593. |
| [23] |
SHIBA Y, KAWASHIMA K, OBINATA N, et al. Evaluation procedure for seismic stress developed in shield tunnels based on seismic deformation method[J]. Doboku Gakkai Ronbunshu, 1989, 1989(404): 385-394. |
| [24] |
VESIC A. Bending of beams resting on isotropic elastic solid[J]. Journal of Soil Mechanics and Foundation Engineering, ASCE, 1961, 87(2): 35-53. |
| [25] |
ATTEWELL P, YEATES J, SELBY A. Soil movements induced by tunnelling and their effects on pipelines and structures[M]. London: Blackie and Son Ltd, 1986, 128-132.
|
| [26] |
VORSTER T, KLAR A, SOGA K, et al. Estimating the effects of tunneling on existing pipelines[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(11): 1399-1410. DOI:10.1061/(ASCE)1090-0241(2005)131:11(1399) |
| [27] |
杨敏, 赵锡宏. 分层土中的单桩分析[J]. 同济大学学报, 1992, 20(4): 421-428. YANG Min, ZHAO Xi-hong. An approach for a single pile in layered soil[J]. Journal of Tongji University:Natural Science, 1992, 20(4): 421-428. |
| [28] |
SCHIMIDT C. Author's reply to Schmidt[J]. Géotechnique, 1988, 38(4): 647-649. DOI:10.1680/geot.1988.38.4.647 |
| [29] |
王岩. 某盾构隧道下穿既有盾构隧道变形超限原因解析及控制研究[D]. 北京: 北京交通大学, 2015: 14-34. WANG Yan. Case analysis and control research on ultra-limit of deformation of the existing tunnel undercrossed by shield tunnel[D]. Beijing: Beijing Jiaotong University, 2015: 14-34. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015611754.htm |
| [30] |
魏纲. 盾构隧道施工引起的土体损失率取值及分布研究[J]. 岩土工程学报, 2010, 32(9): 1354-1361. WEI Gang. Selection and distribution of ground loss ratio induced by shield tunnel construction[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1354-1361. |



