中国竹类植物资源丰富, 竹林面积达500万公顷, 竹子的面积与采伐量均居世界之首[1].竹材成材较木材快, 各项力学指标优良, 作为建筑产品使用有很大的潜力, 有利于可持续发展[2-4].
竹材在建筑领域有广泛的应用.以竹材作为混凝土的加强骨架材料形成的竹筋混凝土, 能够有效提高混凝土构件的承载能力[5-7].竹材经胶合与高温施压等过程后加工而成的结构用胶合竹, 受力性能稳定, 可作为木材的替代材料[8-10].原竹材料形态朴实、价格低廉, 不仅在脚手架等简单的临时结构中有广泛成熟的研究和应用[11-13], 近年来也因其自然典雅的形态越来越受到建筑师的青睐[14].
不同于钢结构、木结构等装配式框架建筑, 竹管之间的连接是制约原竹结构广泛应用的主要障碍.竹管连接处钻孔或开槽都会造成承载力的大幅下降, 铁钉或螺栓直接连接易使竹壁劈裂, 而使用过程中在连接处逐渐产生的间隙会影响结构的牢固性[15].在竹空腔内灌注水泥砂浆可以在一定程度上防止螺栓造成的劈裂破坏[16], 但灌注砂浆会成倍地增大结构的自重, 使原竹结构丧失轻质高强的优势.本文采用不损伤竹子的绑扎方式, 利用麻绳在杆件交叉部位的2个方向上轮流缠绕多圈并扎紧,麻绳可采用桐油浸泡方式提高其强度及耐久性.
解决原竹结构连接问题的方法之一是建立更适合于原竹受力的新型结构体系. Albermani等[17]在杆件试验的基础上, 提出了一种采用PVC节点连接原竹杆件的双层网架体系.由德国艺术家Markus设计的“德中同行”竹结构展馆, 采用了竹桁架与专用钢制节点, 具有可拆建的特点[18].上海世博会印度馆采用多根原竹组成的组合竹拱设计, 建成了跨度达35 m的半球形穹顶结构.
本文提出一种适用于原竹的绑扎节点的直杆叠积螺旋空间结构, 通过几何建模建立相应找形分析方法, 提出有效的逆向安装方法.通过工程实践验证结构的可靠性及安装方法的准确性, 并通过有限元分析得出整体结构的受力特点.
1 直杆叠积螺旋空间结构的构成 1.1 几何构成直杆叠积螺旋空间结构由一组直径相同的直线形杆件组成:在水平方向,各根杆件绕中心点等角度旋转;在垂直方向,每根杆件的一端落地, 另一端搁置在下部的相邻杆件的叠积点上.一定数量的直杆按照这样的几何排布规则相互叠积, 形成一个直杆叠积螺旋空间结构, 如图 1所示为用相同长度的细竹竿搭设的一个直杆叠积螺旋空间结构小模型.该模型没有立柱, 仅靠杆件之间没有连接的相互搁置而形成了一个空间螺旋曲面.

|
图 1 直杆叠积螺旋空间结构小模型 Fig. 1 Simple model of spiral spatial structures with stacked members |
直杆叠积螺旋空间结构的连接可采用不损坏材质的绑扎方法, 只需在叠积点处, 用麻绳、塑料、铅丝等材料绑扎2根相邻的杆件.不破洞开槽的绑扎连接方式保全了竹构件的完整性, 对防止竹管的劈裂、提高原竹结构的承载力具有重要意义.
2 结构的设计方法 2.1 直杆叠积螺旋结构的找形分析直杆叠积螺旋结构的空间形态和杆件数量需通过找形分析得到, 因为每根杆件叠积点的竖向坐标取决于该杆件的几何尺寸以及其下部杆件的竖向坐标和平面位置, 所以每根杆件的竖向坐标值并非按线性规律递增.本文采用空间解析几何方法建立方程组, 用迭代法求解来获得每根杆件叠积点的几何位置, 然后用多项式回归方法拟合得到各杆件竖向坐标的计算公式, 为结构的几何建模提供依据.
2.1.1 建立几何方程组各根直径相同的杆件均为圆柱体, 围绕1根用于导向的虚拟圆柱体形成一个直杆叠积螺旋空间结构.所有杆件在叠积点位置的侧面与虚拟圆柱体侧面相切, 上部杆件的下表面与下部杆件的上表面相切.
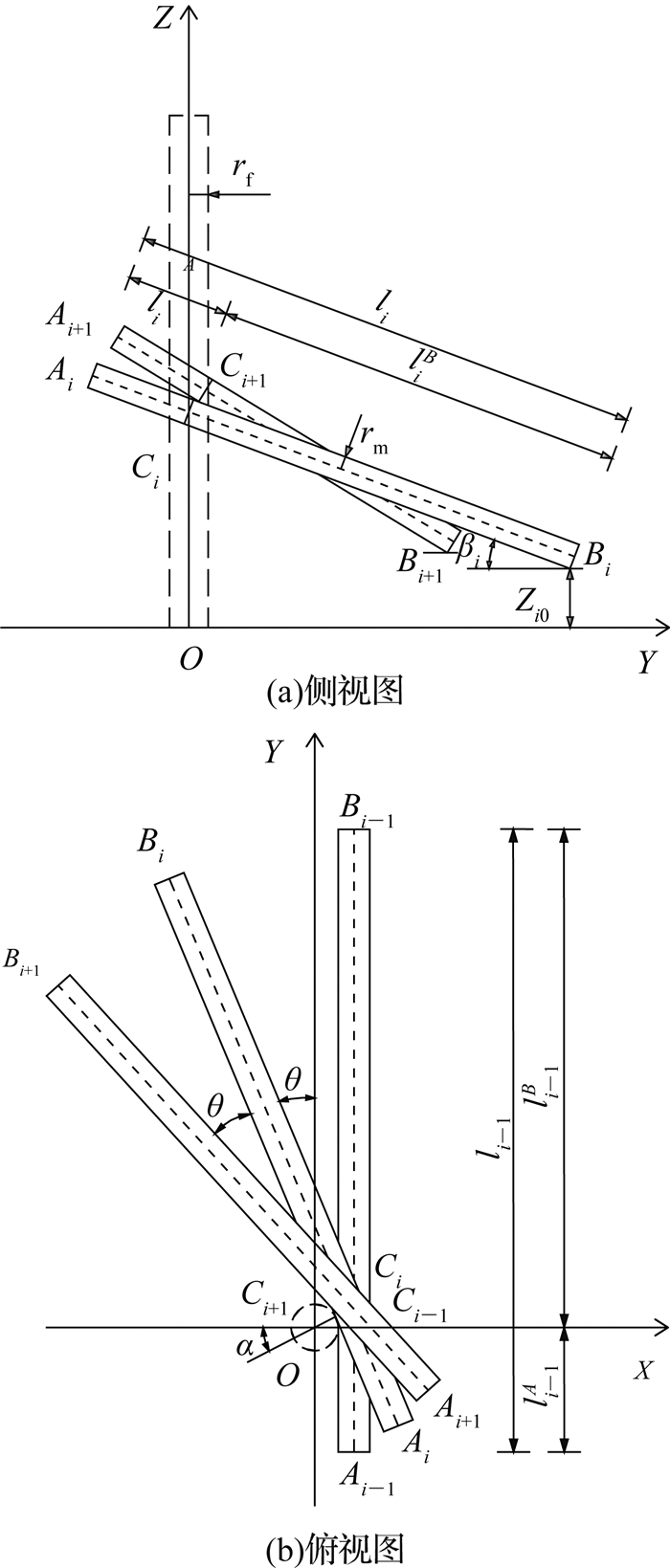
令虚拟圆柱体底部中心为原点O、中轴线为Z轴, 以第一根杆件中轴线垂线方向和中轴线方向分别为X轴和Y轴, 建立空间直角坐标系, 如图 2所示.
|
图 2 结构杆件布置的几何关系图 Fig. 2 Geometric relation diagram of structural member arrangement |
设第i根杆件中轴线的上、下端点分别为Ai、Bi, 叠积点Ci为杆件与虚拟圆柱体切点处截面与其中轴线的交点.杆件长度为li, A为上部端点, B为底部端点, 叠积点Ci将杆件分为liA、liB上下两端.相邻2根杆件之间的水平夹角均为θ.虚拟圆柱体与杆件的半径分别为rf、rm.杆件搁置在高程为Zi0的底座上, 与水平面的竖直夹角为βi.杆件上、下端长度和搁置点高程由函数确定, 假定其与杆件号i的关系为
| $ l_i^A = f\left( i \right),l_i^B = {l_i} - f\left( i \right). $ | (1) |
| $ {Z_{i0}} = h\left( i \right). $ | (2) |
则第i根杆件Ai、Bi、Ci三点的坐标分别为(XiA, YiA, ZiA), (XiB, YiB, ZiB)和(XiC, YiC, ZiC).
第一根杆件垂线与X轴平行, 故第i根杆件垂线与X轴的水平夹角为
| $ {\alpha _i} = \left( {i - 1} \right)\theta . $ | (3) |
则杆件切点处中轴线上点C的坐标为
| $ \left. \begin{array}{l} X_i^C = \left( {{r_{\rm{f}}} + {r_{\rm{m}}}} \right)\cos {\alpha _i},\\ Y_i^C = \left( {{r_{\rm{f}}} + {r_{\rm{m}}}} \right)\sin {\alpha _i},\\ Z_i^C = l_i^B\sin {\beta _i} + {r_{\rm{m}}}\cos {\beta _i} + {Z_{i0}}. \end{array} \right\} $ | (4) |
通过点C坐标可求得A、B两点的坐标:
| $ \left. \begin{array}{l} X_i^A = X_i^C + l_i^A\cos {\beta _i}\cos \left( {{\alpha _i} - {\rm{ \mathsf{ π} }}/2} \right),\\ Y_i^A = Y_i^C + l_i^A\cos {\beta _i}\sin \left( {{\alpha _i} - {\rm{ \mathsf{ π} }}/2} \right),\\ Z_i^A = Z_i^C + l_i^A\sin {\beta _i}. \end{array} \right\} $ | (5) |
| $ \left. \begin{array}{l} X_i^B = X_i^C + l_i^B\cos {\beta _i}\cos \left( {{\alpha _i} + {\rm{ \mathsf{ π} }}/2} \right),\\ Y_i^B = Y_i^C + l_i^B\cos {\beta _i}\sin \left( {{\alpha _i} + {\rm{ \mathsf{ π} }}/2} \right),\\ Z_i^B = Z_i^C - l_i^B\sin {\beta _i}. \end{array} \right\} $ | (6) |
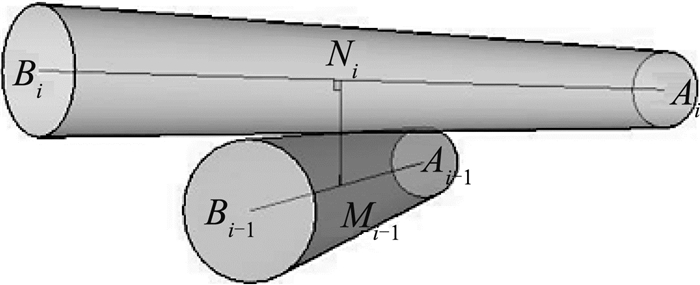
因βi是未知数, 故上述方程组无法确定各根杆件的坐标.本结构中杆件不仅与虚拟圆柱体相切, 而且还与上、下相邻两根杆件相切.如图 3所示, 杆件之间相切可视为2个圆柱中轴线之间的最短距离, 等于2根杆件半径之和, 此问题可转化为2根空间异面直线的距离问题.
|
图 3 杆件相切时叠积点的几何关系图 Fig. 3 Geometric relation diagram of stacking point at two tangent members |
第i根杆件中轴线向量可表示成关于βi的关系式:
| $ {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{A}}_i} = \left( {X_i^A - X_i^B,Y_i^A - Y_i^B,Z_i^A - Z_i^B} \right). $ | (7) |
杆件中轴线向量BiAi与前一根杆件中轴线向量Bi-1Ai-1的公垂线Mi-1Ni向量为
| $ \begin{array}{l} {\mathit{\boldsymbol{M}}_{i - 1}}{\mathit{\boldsymbol{N}}_i} = \\ \left( \begin{array}{l} \left( {Y_i^A - Y_i^B} \right)\left( {Z_{i - 1}^A - Z_{i - 1}^B} \right) - \left( {Y_{i - 1}^A - Y_{i - 1}^B} \right)\left( {Z_i^A - Z_i^B} \right)\\ \left( {Z_i^A - Z_i^B} \right)\left( {X_{i - 1}^A - X_{i - 1}^B} \right) - \left( {Z_{i - 1}^A - Z_{i - 1}^B} \right)\left( {X_i^A - X_i^B} \right)\\ \left( {X_i^A - X_i^B} \right)\left( {Y_{i - 1}^A - Y_{i - 1}^B} \right) - \left( {X_{i - 1}^A - X_{i - 1}^B} \right)\left( {Y_i^A - Y_i^B} \right) \end{array} \right). \end{array} $ | (8) |
又有
| $ {\mathit{\boldsymbol{A}}_{i - 1}}{\mathit{\boldsymbol{A}}_i} = \left( {X_i^A - X_{i - 1}^A,Y_i^A - Y_{i - 1}^A,Z_i^A - Z_{i - 1}^A} \right). $ | (9) |
则2杆件中轴线之间的距离关于βi的函数:
| $ {d_{i - 1,i}}\left( {{\beta _i}} \right) = \frac{{\left| {{\mathit{\boldsymbol{M}}_{i - 1}}{\mathit{\boldsymbol{N}}_i} \cdot {\mathit{\boldsymbol{A}}_{i - 1}}{\mathit{\boldsymbol{A}}_i}} \right|}}{{\left| {{\mathit{\boldsymbol{M}}_{i - 1}}{\mathit{\boldsymbol{N}}_i}} \right|}}. $ | (10) |
杆件与虚拟圆柱体的切点坐标满足式(4), 因此当上、下2根直径相同的杆件相切时,
| $ {d_{i - 1,i}}\left( {{\beta _i}} \right) = 2{r_{\rm{m}}}. $ | (11) |
联立式(10)与(11)可以求得角度βi.根据式(4)~(6)求得各杆件中轴线上Ai、Bi、Ci三点的坐标.
本文采用五次多项式对叠合点坐标进行拟合, 编程时采用拟合方程进行结构的几何建模.
2.1.2 方程的求解由于式(10)、(11)关于βi的联立方程属超越方程, 难以获得解析解, 提出用迭代法求解, 计算流程如图 4所示.

|
图 4 迭代法求解竖向夹角流程图 Fig. 4 Flow chart of iterative method for vertical angle |
1) 一般解法.
由于各杆件叠积过程中的βi∈[-π/2, π/2], 试算角β′i的初始值为-π/2, 每一步迭代都增加一极小的角度值Δβ.当β′i使2个圆柱杆件中轴线距离与杆件直径之差小于一定的误差阈值δ, 即满足条件式(12)时, 可判定杆件i在此竖向角度与杆件相切.然而, 迭代过程中满足式(12)会分别得到杆件i上切和下切于杆件i-1两种情况的计算值:
| $ \left| {{d_{i - 1,i}}\left( {{{\beta '}_i}} \right) - 2{r_{\rm{m}}}} \right| < \delta . $ | (12) |
显然, 叠积结构的几何特征决定了杆件i必上切于杆件i-1, 因此, 竖向夹角βi的输出值只需取相应的计算值.
2) 快捷解法.
上述一般解法可适用于各种形式的叠积结构, 但所有杆件的初始试算角都从-π/2开始的迭代策略非常耗时.对于工程应用较多出现的杆件长度、搁置点高程以及水平夹角等变化均较小的情况, 可通过缩小试算范围的方法优化迭代过程.快捷解法的优化策略.
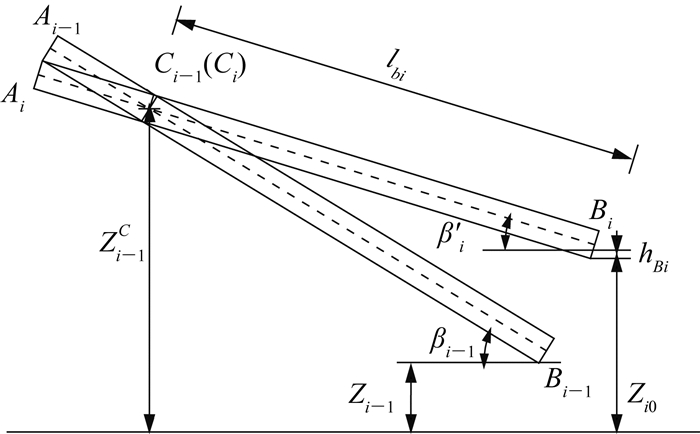
1) 杆件i试算角β′i的初始值可用如图 5的方式取值, 由于杆件之间叠积点接近于杆件与虚拟圆柱体的切点, 可假定杆件i与虚拟圆柱体切点Ci的纵坐标近似等于Zi-1C, 并以此时杆件i位置作为其试算角初始值.
|
图 5 快捷解法试算角初始值确定原理图 Fig. 5 Schematic diagram for initial value determination of trial angle in fast algorithm |
2) 因相邻杆件竖向夹角相差较小, 故杆件i中轴线下端距搁置点高度:
| $ {h_{Bi}} = {r_{\rm{m}}}\cos {{\beta '}_i} \approx {r_{\rm{m}}}\cos {\beta _{i - 1}}. $ |
再根据图 5中的几何关系可以得到杆件i的试算角初始值:
| $ {{\beta '}_i} = \arcsin \frac{{Z_{i - 1}^C - {r_{\rm{m}}}\cos {\beta _{i - 1}} - {Z_{i0}}}}{{l_i^B}}. $ | (13) |
3) 由于相邻2根杆件中轴线距离小于2rm时表示试算角β′i的初始值处于上切角与下切角之间, 由式(13)计算杆件i的试算角β′i的初始值应大于杆件i在杆件i-1的下切角且小于βi, 迭代时把β′i代入式(10)满足判定条件(式(14)), 即可使用快捷解法, 使迭代效率大幅度提高:
| $ {d_{i - 1,i}}\left( {{{\beta '}_i}} \right) < 2{r_{\rm{m}}}. $ | (14) |
为“2016艺术北京”提供的参展作品为直纹双曲面造型、直杆叠积螺旋空间结构, 主结构用51根长为6 m的毛竹搭建, 2道柔软的螺旋竹片与50道交叉竹片将所有竹管联系成一个整体.
采用本文快捷算法建立几何方程, 杆件等长且长度li=6 m, 叠积点处杆件直径为5 cm, 虚拟圆柱体直径为10 cm;杆件上端伸出虚拟圆柱体liA=1 m, 下端长度liB=5 m, 杆件之间水平夹角θ=6°, 且全部搁置于地面.
由于liB与Zi0为定值, β′i等于前一杆件的竖直夹角βi-1.令杆件1初始竖直角度β1=0, 且放置方向平行于如图 3(b)坐标系的Y轴, 则
1) 杆件1各点的坐标:A1(0.075, -1, 0.025)、B1(0.075, 5, 0.025), 叠积点C1(0.075, 0, 0.025).
2) 杆件2的水平夹角:α2=(2-1)θ=6°.
根据式(4)~(7)得:
| $ \begin{array}{l} X_2^{BA} = l_i^A\cos {\beta _2}\cos \left( {{\alpha _2} - \frac{{\rm{ \mathsf{ π} }}}{2}} \right) - l_i^B\cos {\beta _2}\cos \left( {{\alpha _2} + \frac{{\rm{ \mathsf{ π} }}}{2}} \right) = \\ \;\;\;\;\;0.627\cos {\beta _2}. \end{array} $ |
类似地,
| $ Y_2^{BA} = - 5.967\cos {\beta _2},Z_2^{BA} = 6\sin {\beta _2}. $ |
得到向量B2A2关于其竖直夹角β2的关系式:
| $ {\mathit{\boldsymbol{B}}_2}{\mathit{\boldsymbol{A}}_2} = \left( {0.627\cos {\beta _2}, - 5.967\cos {\beta _2},6\sin {\beta _2}} \right). $ |
已知B1A1=(0, -6, 0), 则可求出杆件1和杆件2中轴线的公垂线向量M1N2:
| $ {\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{N}}_2} = \left( {36\sin {\beta _2},0, - 3.762\cos {\beta _2}} \right). $ |
由式(9)得杆件1、2上端点间的向量:
| $ {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} {0.105\cos {\beta _2} - 0.004}\\ { - 0.995\cos {\beta _2} + 1.008}\\ {6\sin {\beta _2} + 0.025\cos {\beta _2} - 0.025} \end{array}} \right]. $ |
将上述结果代入式(10)与(11):
| $ {d_{1,2}}\left( {{\beta _2}} \right) = \frac{{\left| {{\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{N}}_2} \cdot {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{A}}_2}} \right|}}{{\left| {{\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{N}}_2}} \right|}} = 0.05. $ |
取β′2=β1=0, 并根据经验取δ=rm/10 000, Δβ=10-7.采用图 5的迭代法流程解得β2=0.575°, 代入式(3)~(6)可求得杆件2各点坐标:A2(0.179, -0.987, 0.085)、B2(-0.448, 4.980, 0.025), 叠积点C2(0.075, 0.008, 0.075).
同理, 可用迭代法计算出余下叠积杆件的几何位置, 当试算角超过90°即可认为杆件已排满, 迭代结束.此结构共能叠积78根杆件, 取第28~78号共51根杆件组成结构的斜向杆,再添加环向杆及装饰竹条,得到的结构几何如图 6所示.

|
图 6 结构设计杆件轴线示意图 Fig. 6 Axis of structural members diagram |
(1) 测量定位.依据设计结果并结合场地的实际情况, 计算确定竹结构旋转中心点的合理位置, 然后在地面标出每根斜向杆落地点的平面位置.
(2) 构件进场.对竹材进行分类、分区堆放.依据设计值在每根竹杆上标注连接点的位置.
(3) 主结构安装.采用如图 7(a)所示的逆向安装法, 即:先安装场地中心的垂直导向杆后, 再安装叠积点竖向坐标最大的斜向杆, 然后依次向下安装各根杆件.该方法化解了竹子直径和安装误差对结构形态的不利影响, 确保了结构的形态尤其是高宽比完全符合设计, 且安装过程简捷.

|
图 7 结构安装过程与成形后实景 Fig. 7 Installation process and complete scene of structure |
(4) 次结构安装.如图 7(b)所示, 用麻绳将环向杆与各根斜向杆捆扎, 使竹结构连接形成一个整体.竹杆之间再用交叉竹片连接, 使结构形成一个稳定的几何不变体.
3 直杆叠积螺旋空间结构的受力特性 3.1 算例工程概况直杆叠积螺旋空间结构高5.2 m, 平面长轴9 m、短轴7.8 m. 51根斜向杆均为长度6 m、直径与壁厚Ф80×6 mm竹管.因原竹杆件间采用绑扎连接, 叠积点处可沿各向转动, 而转动刚度远远小于相对杆件刚度, 故均按铰接计算.杆件上端铰接于立柱, 下端铰接于基础;2道环向杆共50根均为Ф80×6 mm竹管, 铰接于两侧的斜向杆;原竹杆件简化为标准圆管, 根据对安吉毛竹的试验结果取抗压强度为25 N/mm2, 抗弯强度为45 N/mm2, 并根据规范取弹性模量Ew=15×103 N/mm2[19].中间立柱为Ф102×10 mm钢管, 立柱下端与基础刚接, 钢管弹性模量Es=200×103 N/mm2.
永久荷载标准值:原竹杆件0.014 kN/m, 耐力板0.035 kN/m2, 压条0.005 kN/m;可变荷载标准值0.3 kN/m2;基本雪压、风压同取0.3 kN/m2.风荷载采用虚面方式加载, 即加载到杆件间一个虚拟的无刚度的面上再导荷到杆件各个节点.其他荷载按杆件受荷面积以梯形线荷载的形式直接加载于斜向杆上.
3.2 计算结果分析采用有限元软件SAP2000对永久荷载、可变荷载、雪荷载及四向的风荷载组合下结构的内力、变形进行分析.经验算[20], 各工况下杆件内力均满足强度要求, 其中1.2倍的永久荷载加上1.4倍的可变荷载为最不利工况组合, 斜向杆部分编号见图 6,最下部斜向杆编号为1,并依次递增,环向杆编号规则相同,2种杆件的内力分布如图 8所示.其中,n为杆件编号,FNS为斜向杆轴力,FVS为斜向杆剪力,MS为斜向杆弯矩,FNS为环向杆轴力.

|
图 8 结构在均布荷载下斜向杆件内力分布图 Fig. 8 Internal force distribution of structural members under uniformly distributed load |
1) 图 8(a)~(c)为斜向杆内力的分布情况, 开口形的直杆叠积螺旋结构会削弱承载力, 并导致结构上部斜向杆轴力、弯矩和剪力分布的畸变.结构下部斜向杆的受力最为不利, 弯曲应力已接近限值, 而轴力和剪力较限值仍处于较低水平.
2) 图 8(d)为环向杆的轴力分布图, 环向杆将各斜向杆拉结可提高结构的整体刚度从而减小斜向杆的竖向变形, 而上部环向杆的轴力均大于相应位置下部环向杆, 且显著大于斜向杆上的轴力.
3) 原竹具有良好的弹性, 弹性模量远小于钢材, 即使挠度达到构件长度的1/100仍能可靠地工作[21].本算例屋面最大挠度为4 cm(构件长度的1/125), 宜采用膜材或塑料耐力板等柔性屋面材料.
4) 立柱刚度远大于斜向杆, 其作用可近似看作斜向杆的支座, 其轴力向下逐步递增.立柱传递斜向杆之间的水平力并使之平衡, 故立柱上部与斜向杆连接处存在较大的剪力和弯矩.
4 结论(1) “直杆叠积螺旋空间结构”不会破坏杆件截面的绑扎连接方式,可提高原竹结构的承载力.该结构叠积杆件的数量和叠积点的竖向坐标需要结合杆件的粗细、相邻两杆的水平夹角、叠积点到杆件下端点长度、杆件搁置点的高程等参数,通过找形分析来获得.建立杆件的几何方程组并结合迭代法是找形分析的有效方法.
(2) 斜向杆的最大应力受弯矩控制, 故不宜采用过长的单根原竹.当结构跨度较大时, 斜向杆可采用桁架形式, 以充分发挥竹材的轴向强度.
(3) 简捷的逆向安装方法可将材料及安装误差消化在结构的底部, 使结构的形态尤其是高宽比符合建筑设计.
| [1] |
柳菁, 张家亮, 郭军, 等. 现代竹结构建筑的发展现状[J]. 森林工程, 2013, 29(5): 126-130. LIU Jing, ZHANG Jia-liang, GUO Jun, et al. The development status of the modern bamboo structure buildings[J]. Forest Engineering, 2013, 29(5): 126-130. |
| [2] |
FLANDER K D, ROVERS R. One laminated bamboo-frame house per hectare per year[J]. Construction and Building Materials, 2009, 23(1): 210-218. DOI:10.1016/j.conbuildmat.2008.01.004 |
| [3] |
AHMAD M, KAMKE F A. Analysis of Calcutta bamboo for structural composite materials:surface characteristics[J]. Wood Science and Technology, 2003, 37(3): 233-240. |
| [4] |
AHMAD M, KAMKE F A. Analysis of Calcutta bamboo for structural composite materials:physical and mechanical properties[J]. Wood Science and Technology, 2005, 39(6): 448-459. DOI:10.1007/s00226-005-0016-y |
| [5] |
王慧英, 赵卫锋, 补国斌. 竹筋混凝土技术在建筑结构中的应用[J]. 建筑技术, 2012, 43(7): 605-607. WANG Hui-ying, ZHAO Wei-feng, BU Guo-bin. Application technology of bamboo reinforced concrete in building structures[J]. Architecture Technology, 2012, 43(7): 605-607. |
| [6] |
GHAVAMI K. Bamboo as reinforcement in structural concrete elements[J]. Cement and Concrete Composites, 2005, 27(6): 637-649. DOI:10.1016/j.cemconcomp.2004.06.002 |
| [7] |
SALAU M A, ADEGBITE I, IKPONMWOSA E E. Characteristic strength of concrete column reinforced with bamboo strips[J]. Journal of Sustainable Development, 2011, 5(1): 133. |
| [8] |
肖岩, 杨瑞珍, 单波, 等. 结构用胶合竹力学性能试验研究[J]. 建筑结构学报, 2012, 33(11): 150-157. XIAO Yan, YANG Rui-zhen, SHAN Bo, et al. Experimental research on mechanical properties of glubam[J]. Journal of Building Structures, 2012, 33(11): 150-157. |
| [9] |
XIAO Y, ZHOU Q, SHAN B. Design and construction of modern bamboo bridges[J]. Journal of Bridge Engineering, 2010, 15(5): 533-541. DOI:10.1061/(ASCE)BE.1943-5592.0000089 |
| [10] |
SHARMA B, GATÍO A, BOCK M, et al. Engineered bamboo for structural applications[J]. Construction and Building Materials, 2015, 81: 66-73. DOI:10.1016/j.conbuildmat.2015.01.077 |
| [11] |
CHUNG K F, YU W K. Mechanical properties of structural bamboo for bamboo scaffoldings[J]. Engineering Structures, 2002, 24(4): 429-442. DOI:10.1016/S0141-0296(01)00110-9 |
| [12] |
YU W K, CHUNG K F, CHAN S L. Column buckling of structural bamboo[J]. Engineering Structures, 2003, 25(6): 755-768. DOI:10.1016/S0141-0296(02)00219-5 |
| [13] |
YU W K, CHUNG K F, CHAN S L. Axial buckling of bamboo columns in bamboo scaffolds[J]. Engineering Structures, 2005, 27(1): 61-73. DOI:10.1016/j.engstruct.2004.08.011 |
| [14] |
张达光. , 浅谈竹材建筑[J]. 中国西部科技, 2007(7): 65-67. ZHANG Da-guang. Views on developing bamboo buildings[J]. Science and Technology of West China, 2007(7): 65-67. |
| [15] |
张楠, 柏文峰. 原竹建筑节点构造分析及改进[J]. 科学技术与工程, 2008, 8(18): 5318-5326. ZHANG Nan, BAI Wen-feng. Analysis and improvement of the construction technology of the bamboo building house node[J]. Science Technology and Engineering, 2008, 8(18): 5318-5326. DOI:10.3969/j.issn.1671-1815.2008.18.048 |
| [16] |
陈溪, 许清风, HARRIESK A. 竹材力学性能及其在土木工程中应用的研究进展[J]. 结构工程师, 2015, 31(6): 209-215. CHEN Xi, XU Qing-feng, HARRIES K A. Research on mechanical properties and application of bamboo in civil engineering:state-of-the-art[J]. Structural Engineers, 2015, 31(6): 209-215. |
| [17] |
ALBERMANI F, GOH G Y, CHAN S L. Lightweight bamboo double layer grid system[J]. Engineering Structures, 2007, 29(7): 1499-1506. DOI:10.1016/j.engstruct.2006.09.003 |
| [18] |
沈之容, 倪阳, 胡志凌, 等. "德中同行"竹结构展馆的材料试验与结构分析[J]. 结构工程师, 2009, 25(1): 51-54. SHEN Zhi-rong, NI Yang, HU Zhi-ling, et al. Material test and structural analysis for "germany and china together cooperation" bamboo structure exhibition hall[J]. Structural Engineers, 2009, 25(1): 51-54. |
| [19] |
CECS434: 2016, 圆竹结构建筑技术规程[S]. 北京: 中国计划出版社, 2016. http://www.zzguifan.com/webarbs/book/88362/2769490.shtml
|
| [20] |
王修通. 基于结构分析的原竹屋架构造技术研究[D]. 昆明: 昆明理工大学, 2013. WANG Xiu-tong. Study on the constructional measures of the bamboo roof based on structural analysis[D]. Kunming: Kunming University of Science and Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10674-1013346400.htm |
| [21] |
刘中伟. 云南农村竹木结构原竹构件试验研究[D]. 昆明: 昆明理工大学, 2012. LIU Zhong-wei. Experimental study on bamboo cane component of bamboo and wood structure used in rural houses of yunnan province[D]. Kunming: Kunming University of Science and Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10674-1012430733.htm |


