2. 华南理工大学 土木与交通学院, 广东 广州 510641
2. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou, Guangdong 510641, China
盾构隧道纵向计算模型对于隧道结构设计与安全评估是至关重要的.目前,盾构隧道纵向结构分析模型主要以纵向梁-弹簧模型[1]和纵向等效连续化模型[2]为主.其中纵向等效连续化模型概念明确、计算相对简单,是研究盾构隧道纵向结构性能的常用方法.
基于盾构隧道纵向等效连续化模型,田敬学等[3]提出了纵向拉压刚度和弯曲刚度的计算式,并用于上海地铁区间隧道的计算;叶飞等[4]将横向弯曲刚度有效率引入到纵向等效连续化模型中,得到了考虑横向特性的纵向等效刚度计算式;张文杰等[5]提出了广义的纵向等效连续化模型,同时考虑了隧道横向特性和环缝影响范围的影响;李翔宇等[6]综合考虑了螺栓所处的受力状态、隧道横向特性及环缝影响范围,建立新型的纵向等效连续化模型.
上述研究为盾构隧道纵向分析提供了思路和方法,但依然存在尚需改进完善的问题.田敬学等[3]将盾构隧道纵、横向孤立为2个平面问题进行分析,未考虑隧道的空间结构特性,忽视了2个方向特性的相互作用和影响[7].叶飞等[4]定义盾构衬砌结构横向刚度有效率为均质圆环与实际衬砌变形后的直径比,该定义合理性值得商榷.叶飞等[4-6]均应用了横向刚度影响系数,定义为衬砌变形后的短、长轴比,该系数推导基于椭圆状变形和长短轴方向变形相同的假定,而实际上,尽管衬砌本体沿环向是同性的,但受内、外部非均匀和非对称的作用,结构受力变形具有典型的差异性特征,假定长短轴方向变形相等存在不足.此外现有研究均将点状、非连续分布的纵向接头等效成均匀连续分布的环状螺栓,与实际情况有偏差.
本文借鉴修正惯用法思路,定义了考虑错缝拼装增强的横向刚度有效率.针对盾构管片变形特性与纵向接头特征对隧道纵向等效刚度的影响,引入等效螺栓刚度修正系数和衬砌差异变形系数,而后推导了修正纵向计算模型,并通过算例分析隧道纵向等效刚度对横向刚度有效率、接头等效刚度修正系数和衬砌变形差异系数的敏感性.研究可弥补现有成果的不足,为盾构隧道设计计算提供参考.
1 修正纵向等效刚度计算式的推导 1.1 衬砌横向抗弯刚度有效率的定义对于盾构隧道横向特性,主要通过横向抗弯刚度有效率表征.黄宏伟等[8-9]采用模型试验分析了横向刚度有效率,但单纯从结构角度出发,未考虑地层抗力的影响;Lee等[10-11]考虑地层抗力作用,探讨了横向刚度有效率,但未计入管片错缝拼装的影响.本文借鉴修正惯用法[12]弯曲刚度的分析思路定义衬砌横向刚度有效率,且通过错缝拼装增强系数来体现错缝拼装对横向刚度的影响.
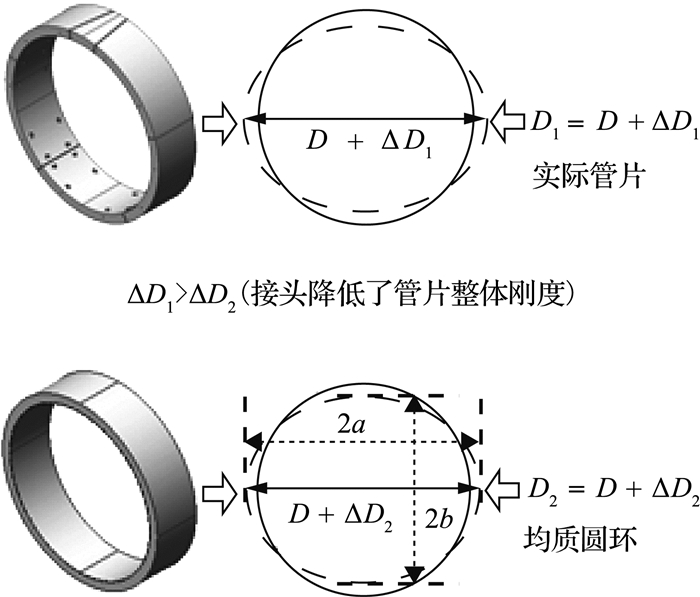
假定衬砌管片在周围荷载作用下近似呈“椭圆变形”,如图 1所示.图中D为衬砌外径、ΔD1、ΔD2为2种情况直径的变化量,a、b为变形后椭圆的长短轴.横向弯曲刚度有效率为
| $ \eta = \Delta {D_2}/\Delta {D_1}. $ | (1) |
|
图 1 衬砌横向刚度有效率计算示意 Fig. 1 Transverse rigidity calculation of lining |
考虑到管片错缝拼装的影响,引入错缝拼装刚度增强系数β,该系数为错缝拼装较通缝拼装横向刚度有效率提高值.则横向等效刚度为
| $ E{I^ * } = \left( {1 + \beta } \right)\eta EI. $ | (2) |
式中:EI为均质衬砌横向抗弯刚度,EI*为考虑实际接头衬砌横向等效抗弯刚度.
1.2 衬砌环差异变形系数与纵向接头等效刚度修正系数的提出当前盾构隧道为数不多的在纵向计算中考虑横向特性的研究[4-6]均假定隧道衬砌结构水平与竖向变形一致,即认为图 1中D=a+b,忽视了实际工程水文地质、地形地貌、外部荷载及建筑环境的非均匀性,由此势必造成与实际情况的偏差.因此有必要探索衬砌受荷差异变形特性,并分析该特性对隧道纵向等效刚度的影响;本文通过定义差异变形系数来表征实际衬砌竖向与水平变形的差异特性及其对隧道纵向等效刚度的影响.差异变形系数为
| $ \xi = \frac{{\left( {D - 2b} \right)}}{{\left( {2a - D} \right)}}. $ | (3) |
现有盾构隧道纵向结构理论分析与数值计算大多将纵向接头等效为均质连续的螺栓环,并通过式(4)进行刚度等效[13].
| $ {k_{\rm{j}}} = \frac{{n{k_{{\rm{j1}}}}}}{{2{\rm{ \mathsf{ π} }}r}} = \frac{{n{E_{\rm{b}}}{A_{\rm{b}}}}}{{2{\rm{ \mathsf{ π} }}rt{l_{\rm{b}}}}}. $ | (4) |
式中:kj为螺栓等效刚度系数,kj1为单个螺栓线刚度系数,n为环向螺栓数量,Eb为螺栓弹性模量,Ab为螺栓的作用面积,r为衬砌半径,t为衬砌厚度,lb为螺栓作用长度.
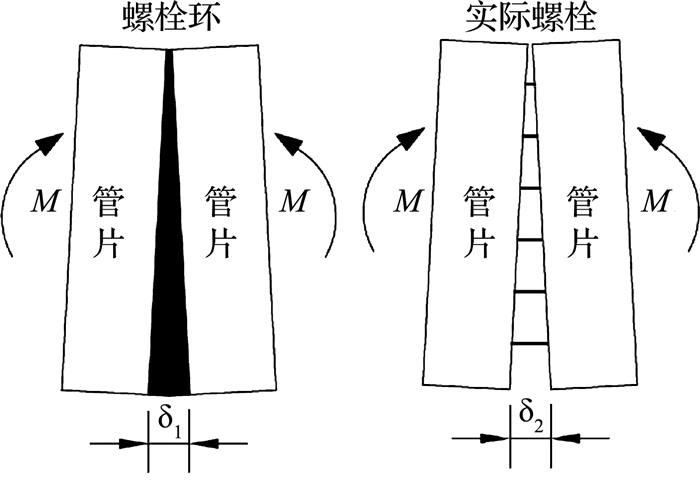
为了阐述盾构隧道采用等效螺栓环与实际接头间的误差并进行修正,本文提出管片螺栓等效刚度修正系数λ,定义为λ=δ1/δ2,δ1为等效螺栓环后管片环缝最大张开量,δ2为实际接头螺栓对应的管片环缝张开量,如图 2所示.
|
图 2 隧道受弯变形示意图 Fig. 2 Bending deformation of shield tunnel |
基于上述分析,在常规接头等效刚度式(4)的基础上提出修正等效螺栓环刚度计算公式:
| $ {k_{\rm{j}}} = \lambda \frac{{n{E_{\rm{b}}}{A_{\rm{b}}}}}{{2{\rm{ \mathsf{ π} }}rt{l_{\rm{b}}}}}. $ | (5) |
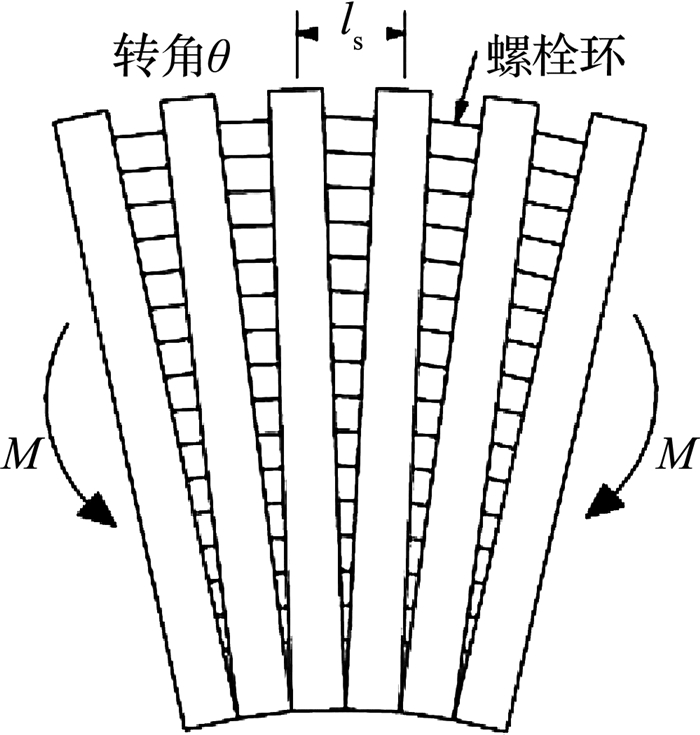
取衬砌环结合面为中心的一环管片宽度ls的变形来考虑,当衬砌环受到纵向弯矩M时,在接缝处求解出相邻管片的2个面之间有相对转角θ,θ/ls相当于梁弯曲的理论曲率,如图 3所示.
|
图 3 衬砌环受弯变形示意图 Fig. 3 Bending deformation of lining |
为求衬砌受力与变形的关系,假定:1)中性轴以上受拉且拉力由螺栓和管段共同承担,受压侧的压力由管片承担;2)衬砌结构变形后为椭圆形.
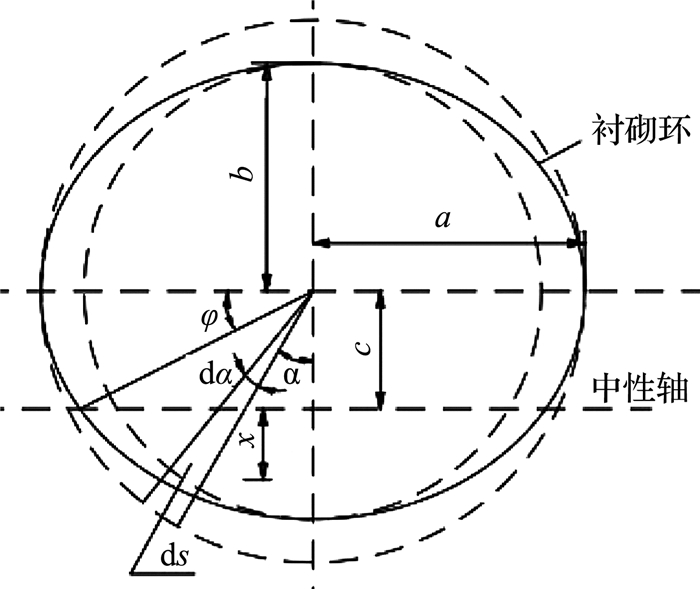
如图 4所示,c、φ为中性轴位置与角度,ds为管片上任意微元,α为微元与短轴夹角,dα为微元ds对应圆心角,x和x′分别为压拉侧微元ds到中性轴的距离.
|
图 4 衬砌环受弯变形示意图 Fig. 4 Bending deformation of lining |
由图 4可以得到ds、近似的c及ds到拉、压侧中性轴位置的距离满足:
| $ \left. \begin{array}{l} {\rm{d}}s = \frac{{\left( {a + b} \right)}}{2}{\rm{d}}\alpha ,\\ c = \frac{{\left( {a + b} \right)}}{2}\sin \varphi ,\\ x = - b\cos \alpha + c,\\ x' = b\cos \alpha - c. \end{array} \right\} $ | (6) |
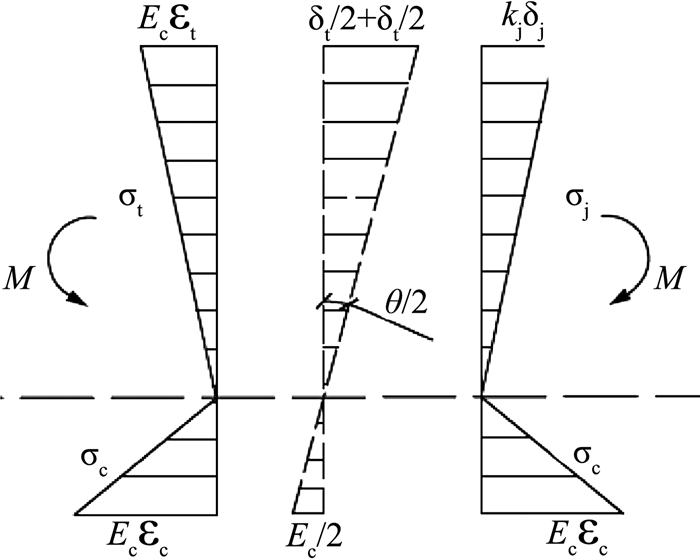
衬砌环在纵向弯矩作用下,连接螺栓单元处于弹性状态,管片纵向变形与受力如图 5所示.
|
图 5 隧道纵向受弯变形示意图 Fig. 5 Longitudinal bending deformation of tunnel |
由变形协调条件可得
| $ \left. \begin{array}{l} {\varepsilon _{\rm{t}}}\frac{{{l_{\rm{s}}}}}{2} + \frac{{{\delta _{\rm{j}}}}}{2} = \left( {b + c} \right)\frac{\theta }{2},\\ {\varepsilon _{\rm{c}}}\frac{{{l_{\rm{s}}}}}{2} = \left( {b - c} \right)\frac{\theta }{2}. \end{array} \right\} $ | (7) |
式中:εt、εc分别为管片的拉应变和压应变;δj为接头的变形量.
根据力的平衡条件有
| $ \left. \begin{array}{l} 2\frac{{{E_{\rm{c}}}{\varepsilon _{\rm{c}}}}}{{b - c}}\int_0^{{\rm{ \mathsf{ π} /2}} - \varphi } {x{\rm{d}}\alpha } = 2\frac{{{E_{\rm{c}}}{\varepsilon _{\rm{t}}}}}{{b + c}}\int_{{\rm{ \mathsf{ π} /2}} - \varphi }^{\rm{ \mathsf{ π} }} {x'{\rm{d}}\alpha } \\ 2\frac{{{E_{\rm{c}}}{\varepsilon _{\rm{c}}}}}{{b - c}}\int_0^{{\rm{ \mathsf{ π} /2}} - \varphi } {x{\rm{d}}\alpha } = 2\frac{{{k_{\rm{j}}}{\delta _{\rm{j}}}}}{{\left( {b + c} \right)}}\int_{{\rm{ \mathsf{ π} /2}} - \varphi }^{\rm{ \mathsf{ π} }} {x'{\rm{d}}\alpha } \end{array} \right\} $ | (8) |
式中:Ec为管片弹性模量;
由式(6)~(8)换算得到
| $ \begin{array}{*{20}{c}} {\frac{{{E_{\rm{c}}}}}{{{l_{\rm{s}}}}}\int_0^{{\rm{ \mathsf{ π} /2}} - \varphi } {\left( {b\cos \alpha - c} \right){\rm{d}}\alpha } = }\\ {\frac{{{k_{\rm{j}}}{E_{\rm{c}}}}}{{{k_{\rm{j}}}{l_{\rm{s}}} + {E_{\rm{c}}}}}\int_{{\rm{ \mathsf{ π} /2}} - \varphi }^{\rm{ \mathsf{ π} }} {\left( { - b\cos \alpha + c} \right){\rm{d}}\alpha } .} \end{array} $ | (9) |
解得中性轴位置φ满足
| $ \frac{{{k_{\rm{j}}}{l_{\rm{s}}}}}{{{E_c}}} = \frac{{\frac{{a + b}}{2}\sin \varphi \left( {\varphi - \frac{{\rm{ \mathsf{ π} }}}{2}} \right) + b\cos \varphi }}{{{\rm{ \mathsf{ π} }}\frac{{a + b}}{2}\sin \varphi }}. $ | (10) |
把式(5)代入(10)得到
| $ \frac{{\lambda n{E_{\rm{b}}}{A_{\rm{b}}}{l_{\rm{s}}}}}{{{E_{\rm{c}}}{A_{\rm{c}}}{l_{\rm{b}}}}} = \frac{{\frac{{a + b}}{2}\sin \varphi \left( {\varphi - \frac{{\rm{ \mathsf{ π} }}}{2}} \right) + b\cos \varphi }}{{{\rm{ \mathsf{ π} }}\frac{{a + b}}{2}\sin \varphi }}. $ | (11) |
式中:Ac为衬砌管片横向面面积.
根据力矩的平衡条件可得
| $ \begin{array}{l} 2\frac{{{E_{\rm{c}}}{\varepsilon _{\rm{c}}}}}{{b - c}}\int_0^{{\rm{ \mathsf{ π} /2}} - \varphi } {{x^2}\frac{{a + b}}{2}t{\rm{d}}\alpha } + \\ 2\frac{{{E_{\rm{c}}}{\varepsilon _{\rm{t}}}}}{{b + c}}\int_{{\rm{ \mathsf{ π} }}/2 - \varphi }^{\rm{ \mathsf{ π} }} {{{\left( {x'} \right)}^2}\frac{{a + b}}{2}t{\rm{d}}\alpha } = M. \end{array} $ | (12) |
通过式(6)~(7)转换代入式(12)得到
| $ \begin{array}{l} 2\frac{{{E_{\rm{c}}}\theta }}{{{l_{\rm{s}}}}}\int_0^{{\rm{ \mathsf{ π} /2}} - \varphi } {{{\left( {b\cos \alpha - c} \right)}^2}\frac{{a + b}}{2}t{\rm{d}}\alpha } + \\ \;\;\;\;\;\;\;2\frac{{{k_{\rm{j}}}{E_{\rm{c}}}\theta }}{{{E_{\rm{c}}} + {k_{\rm{j}}}{l_{\rm{s}}}}}\int_{{\rm{ \mathsf{ π} /2}} - \varphi }^{\rm{ \mathsf{ π} }} {{{\left( { - b\cos \alpha + c} \right)}^2}\frac{{a + b}}{2}t{\rm{d}}\alpha } = M. \end{array} $ | (13) |
求解式(13),得到纵向弯曲下环缝转角为
| $ \theta = \frac{M}{{\frac{{{E_{\rm{c}}}{R_1}}}{{{l_{\rm{s}}}}} + \frac{{{E_{\rm{c}}}{k_{\rm{j}}}{R_2}}}{{{E_{\rm{c}}} + {k_{\rm{j}}}{l_{\rm{s}}}}}}}. $ | (14) |
式中:
| $ \begin{array}{l} {R_1} = \left( {a + b} \right)t\left\{ {\left[ {\frac{{{b^2}}}{2} + \frac{{{{\left( {a + b} \right)}^2}}}{4}{{\sin }^2}\varphi } \right]\left( {\frac{{\rm{ \mathsf{ π} }}}{2} - \varphi } \right) + } \right.\\ \;\;\;\;\;\left. {\frac{{{b^2}}}{4}\sin 2\varphi - \frac{{b\left( {a + b} \right)\sin 2\varphi }}{2}} \right\}. \end{array} $ | (15) |
| $ \begin{array}{l} {R_2} = \left( {a + b} \right)t\left\{ {\left[ {\frac{{{b^2}}}{2} + \frac{{{{\left( {a + b} \right)}^2}}}{4}{{\sin }^2}\varphi } \right]\left( {\varphi + \frac{{\rm{ \mathsf{ π} }}}{2}} \right) - } \right.\\ \;\;\;\;\;\left. {\frac{{{b^2}}}{4}\sin 2\varphi + \frac{{b\left( {a + b} \right)\sin 2\varphi }}{2}} \right\}. \end{array} $ | (16) |
根据曲率公式可知等效连续梁的转角为
| $ \theta = \frac{{M{l_{\rm{s}}}}}{{{{\left( {EI} \right)}_{{\rm{eq}}}}}}. $ | (17) |
式中:(EI)eq为纵向等效刚度,由式(14)、(17)可得到
| $ \frac{{M{l_{\rm{s}}}}}{{{{\left( {EI} \right)}_{{\rm{eq}}}}}} = M/\left( {\frac{{{E_{\rm{c}}}{R_1}}}{{{l_s}}} + \frac{{{E_{\rm{c}}}{k_{\rm{j}}}{R_2}}}{{{E_{\rm{c}}} + {k_{\rm{j}}}{l_{\rm{s}}}}}} \right). $ | (18) |
进而得到等效刚度为
| $ {\left( {EI} \right)_{{\rm{eq}}}} = {E_{\rm{c}}}{I_{\rm{c}}}\left[ {\frac{{{R_1}}}{{{I_{\rm{c}}}}} + \frac{{{l_{\rm{s}}}{k_{\rm{j}}}{R_2}}}{{\left( {{E_{\rm{c}}} + {k_{\rm{j}}}{l_{\rm{s}}}} \right){I_{\rm{c}}}}}} \right]. $ | (19) |
式中:Ic为隧道管片截面惯性矩.
纵向刚度有效率为
| $ \eta ' = \frac{{{R_1}}}{{{I_{\rm{c}}}}} + \frac{{{l_{\rm{s}}}{k_{\rm{j}}}{R_2}}}{{\left( {{E_{\rm{c}}} + {k_{\rm{j}}}{l_{\rm{s}}}} \right){I_{\rm{c}}}}}. $ | (20) |
差异变形系数表征了衬砌结构不同方向变形的组合和匹配关系,与横向刚度有效率的影响通过上式中R1、R2体现,纵向接头等效刚度修正系数的影响则由kj值体现.
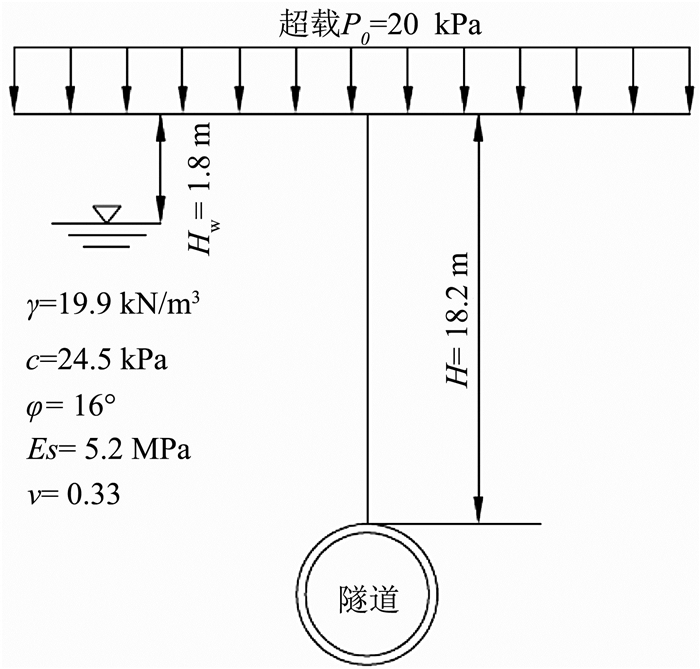
2 算例分析算例地层为典型珠三角黏土层,场地的稳定地下水位埋深总体变化不大,均深位于地面以下1.8 m处,具体围岩和超载情况如图 6所示, 图中γ为土层的重度,c为黏聚力,ϕ为土体的内摩擦角,Es为压缩模型, ν为泊松比,H为上覆土厚度.盾构隧道管片含1封顶块、2相邻块及3标准块,纵向采用错缝拼装,具体结构参数如表 1所示.表中d为衬砌内径,db为螺栓直径,γb为螺栓重度.
|
图 6 结构计算地层条件 Fig. 6 Formaton condition of structure calculation |
| 表 1 隧道部分结构参数 Table 1 Structure parameters of shield tunnel |
盾构隧道结构力学特性受诸多因素的影响,通过试验观察异常困难,理论分析也极其复杂,因此对隧道结构受力变形特性研究往往借助数值法.本文借助有限元软件,根据不同参数的计算思路,且充分考虑计算精度和可行性,利用地层-结构法计算衬砌差异变形与纵向螺栓等效刚度修正值,通过荷载-结构法分析衬砌横向刚度有效率和错缝拼装增强系数.
1) 衬砌差异变形与接头等效刚度修正计算
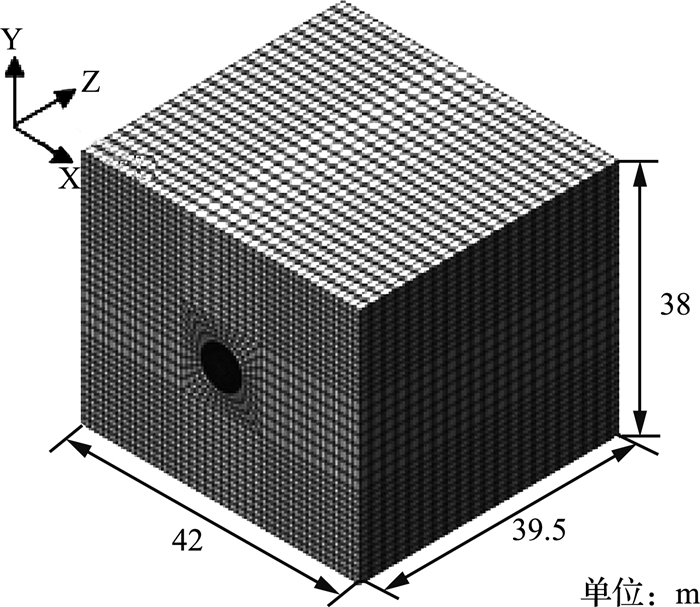
地层-结构法整体计算模型如图 7所示,模型含21环管片,其中管片、土层及接头采用实体单元模拟,管片与土层间设无厚度的goodman接触单元[14].土层用Mohr-coulumb模型,管片和接头则用弹性模型.计算工况:初始应力场计算(位移清零)→隧道开挖且管片施作→地面超载20 kPa.
|
图 7 地层结构法计算模型 Fig. 7 Calculation model of stratum structure |
如图 8所示为衬砌结构变形图,定义位移沿坐标正向为正,反之为负.可见,衬砌结构呈现近似椭圆状的变形,水平方向总的变形量为2a=4.9 mm,相应的竖直方向总的变形值为2b=5.63 mm,两者相差15%,且根据差异变形系数定义可知ζ=1.15.通过计算,结合理论分析不难发现,实际工程中水文地质、作用荷载及建筑环境非均匀性、非对称性愈明显引起的衬砌变形差异系数愈大.

|
图 8 衬砌结构变形计算结果(局部模型) Fig. 8 Deformation results of lining (local model) |
以图 7计算模型为基础,设置计算工况:初始应力场计算→盾构隧道开挖与管片施作(位移清零)→隧道中部施加向下附加位移10 mm.通过计算取第10环与11环间张开量进行分析(见图 9).定义隧道轴向位移向坐标正轴为正,反之为负,通过螺栓两侧管片相对位移计算环缝张开量.

|
图 9 2种接头模型张开变形(放大3倍) Fig. 9 Displacement nephogram of two kinds of joints |
通过计算得到采用实际接头时管片张开量约为2.55 mm,而等效螺栓环隧道对应的管片张开量约为3 mm,两者相差17.6%,说明采用等效螺栓环表征实际管片接头存在不容忽视的误差,隧道纵向设计计算中应给予充分考虑.根据等效螺栓环刚度修正系数的定义可知λ=1.176.
2) 横向刚度有效率和错缝拼装增强系数计算
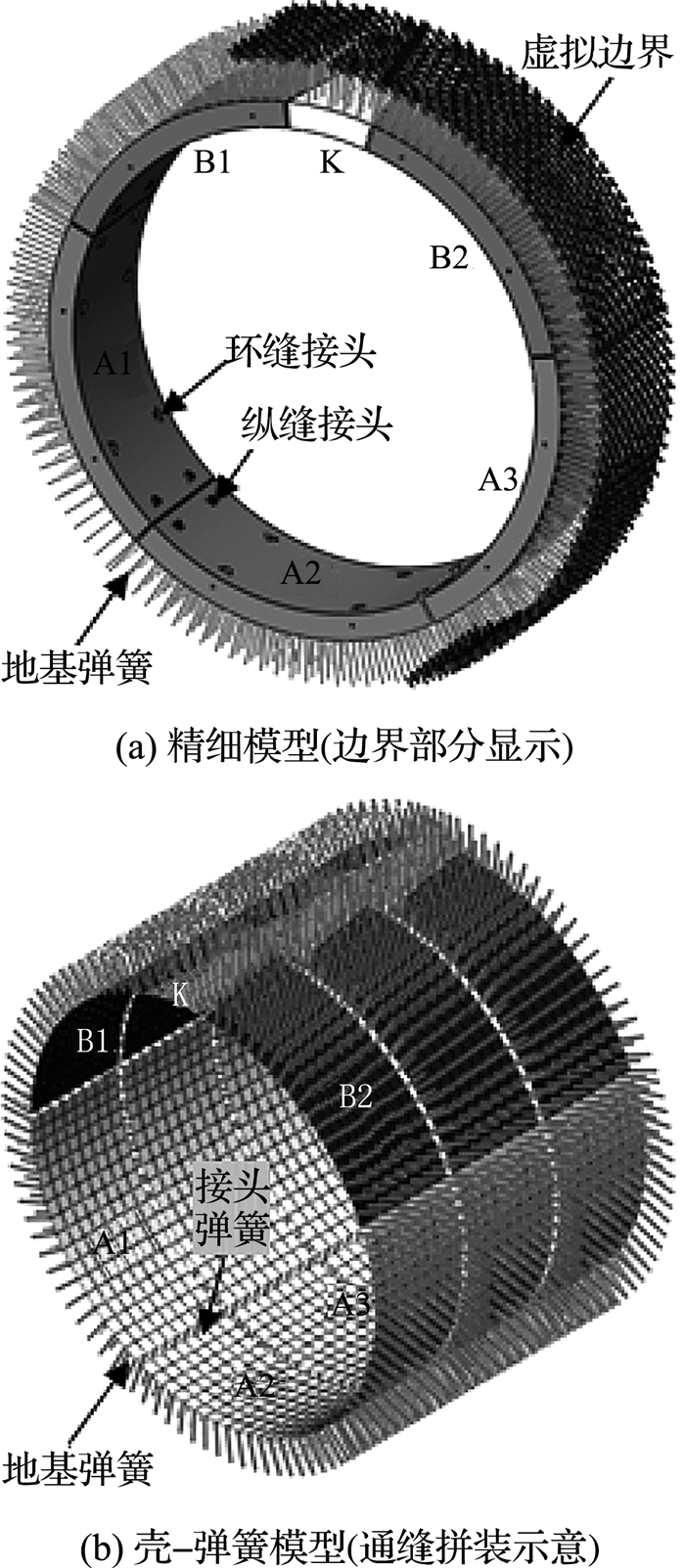
建立精细的三维计算模型(见图 10(a))分析横向刚度有效率,考虑到计算的可行性,采用壳-弹簧模型(图 10(b))计算错缝拼装增强系数;由于错缝拼装时管片变形主要受前后两环的剪切作用,故壳-弹簧模型包含三环管片,并取中间环变形计算横向刚度有效率.精细模型中管片、接头及衬垫均用实体单元模拟,壳-弹簧模型管片则用壳单元模拟,纵、横向连接用接头单元模拟,接头正、负弯曲刚度分别为kθ+= 30 000 kN/rad和kθ-=10 000 kN/rad.地层对结构的作用通过地基弹簧体现,地基系数k=14.6 MPa/m.
|
图 10 荷载-结构法计算模型 Fig. 10 Calculation model of load structure |
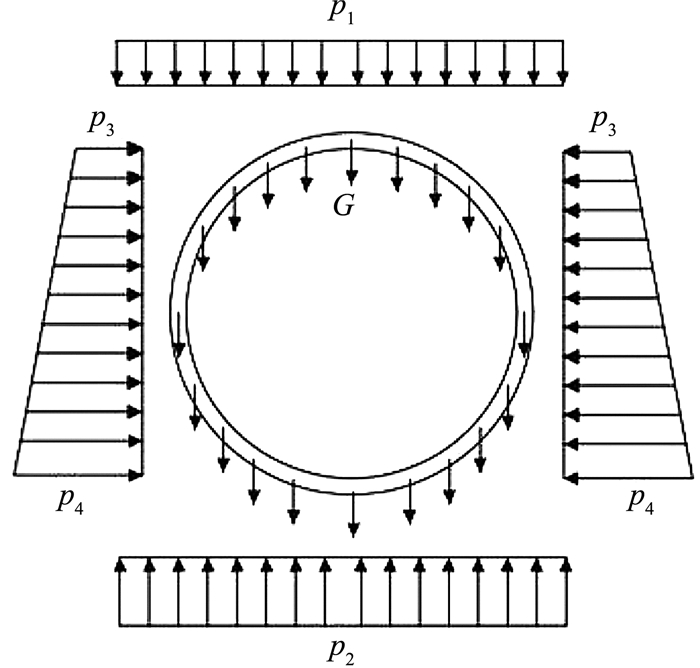
图 10精细模型与壳-弹簧模型计算均采用荷载-结构法的思路,隧道相应的围岩压力分布形式如图 11所示.图中p1为衬砌顶部所受上覆水土压力,p2为衬砌环底部受到的地层抗力,p3为衬砌环顶部侧向水土压力,p4为衬砌环底部侧向水土压力,G为管片自重.采用Terzaghi松弛土压力理论[15]计算图 11中的各压力值.
|
图 11 隧道围岩压力分布形式 Fig. 11 Pattern of surrounding pressure of tunnel |
松动半宽和高度分别为
| $ {B_1} = {R_0}\cot \left( {\frac{{{\rm{ \mathsf{ π} }}/4 + \varphi /2}}{2}} \right). $ | (21) |
| $ \begin{array}{l} {h_0} = \frac{{{B_1}\left( {1 - \frac{c}{{{B_1}\gamma }}} \right)}}{{{K_0}\tan \varphi }}\left[ {1 - \exp \left( { - {K_0}\tan \varphi \frac{H}{{{B_1}}}} \right)} \right] + \\ \;\;\;\;\;\;\frac{{{p_0}}}{\gamma }\exp \left( { - {K_0}\tan \varphi \frac{H}{{{B_1}}}} \right). \end{array} $ | (22) |
式中:R0为管片外半径(m);K0为土层侧压力系数,K0=1-sin φs′=0.72;p0为地面超载(kPa),荷载为20 kPa.将图 6中参数代入式(21)、(22)计算可得B1=6.02 m,h0=13.07> 2D=12 m,由此得到p1=γh0+p0=280 kPa,p2=p1+πg= 280+3.14× 10.68=313.5 kPa,p3=k0p1= 201.6 kPa;p4= k0(p1+γR0) =280 kPa.
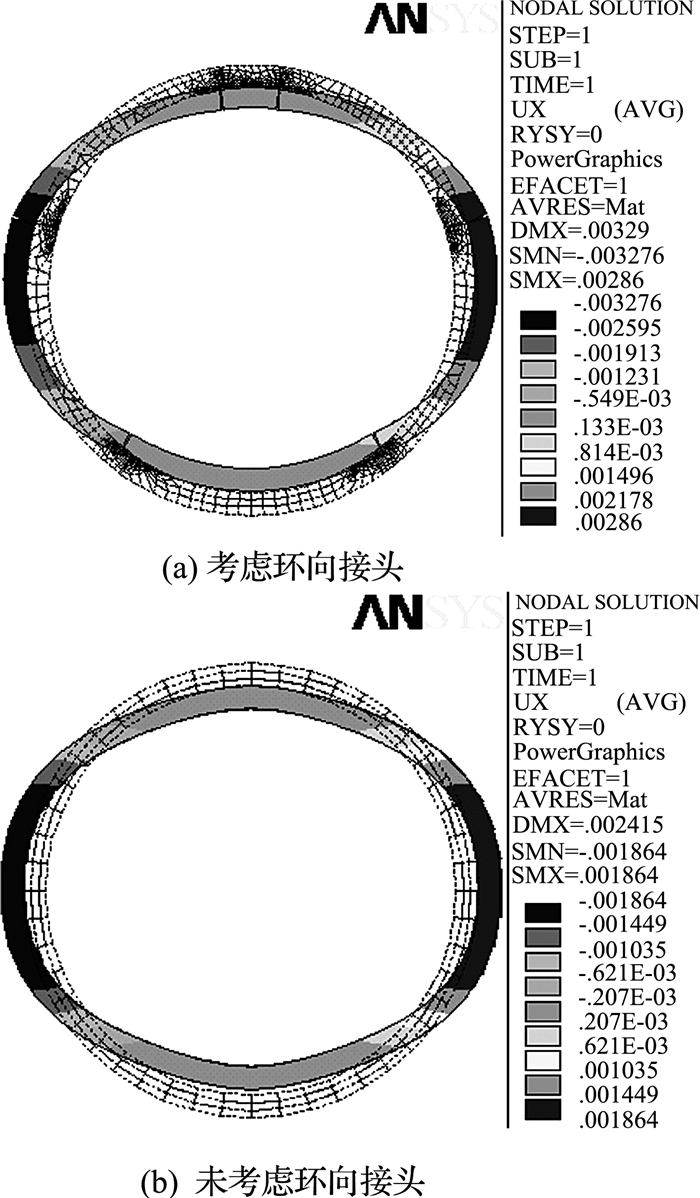
如图 12所示为衬砌考虑实际接头与均质圆环2种情况对应的水平位移云图,定义位移指向坐标正向为正.由位移结果,利用横向刚度有效率公式(1)计算得到η=0.6.如图 13所示为通、错缝拼装衬砌整体模型水平位移与中间环水平位移云图.错缝拼装时管片变形主要受前后两环的剪切作用,因此取中间环变形计算横向刚度有效率.通缝计算水平变形为5.86 mm与实际管片精细分析结果6.14 mm相差5%,且错缝水平变形为5.16 mm,较地层结构法4.9 mm也相差5%,说明本文计算模型具备一定合理性.根据横向刚度有效率公式计算得到通缝拼装刚度有效率η=0.63,错缝拼装刚度有效率η=0.74,错缝拼装刚度有效率较通缝拼装提高了17.5%,可见错缝拼装引起的纵向剪切约束对横向抗弯刚度影响明显.综合考虑精细计算刚度有效率和错缝拼装的增强效应结果,取横向刚度有效率η=0.6×1.175 =0.71,且考虑到错缝拼装增强效应在纵向计算中是由横向刚度有效率体现,故后续分析将其抽象概括为横向刚度有效率的影响.
|
图 12 考虑环向接头与否管片水平位移云图(m) Fig. 12 Displacement considering actual joint or not (m) |

|
图 13 三维壳—弹簧模型计算位移云图(放大3倍) Fig. 13 Displacement nephogram of shell-spring model (3 x amplification) |
将隧道结构参数代入式(5)计算螺栓的平均弹性刚度系数kj=709 704.4 kPa.将等效接头刚度、考虑差异变形和横向刚度有效率的变形值代入式(10)得到管片中性轴位置的角度φ=54°,将上述参数代入式(20)计算得到隧道纵向等效刚度有效率为0.088.同理计算得到未考虑衬砌差异变形、接头等效刚度误差及错缝拼装影响时衬砌中性轴的位置φ=55.8°,计算纵向刚度有效率为0.077,较修正模型计算刚度小14.3%.由于盾构隧道纵向受弯变形程度取决于隧道纵向等效抗弯刚度[16-17],修正前后纵向刚度误差会显著影响隧道结构力学行为,说明修正现有计算模型是必要的.
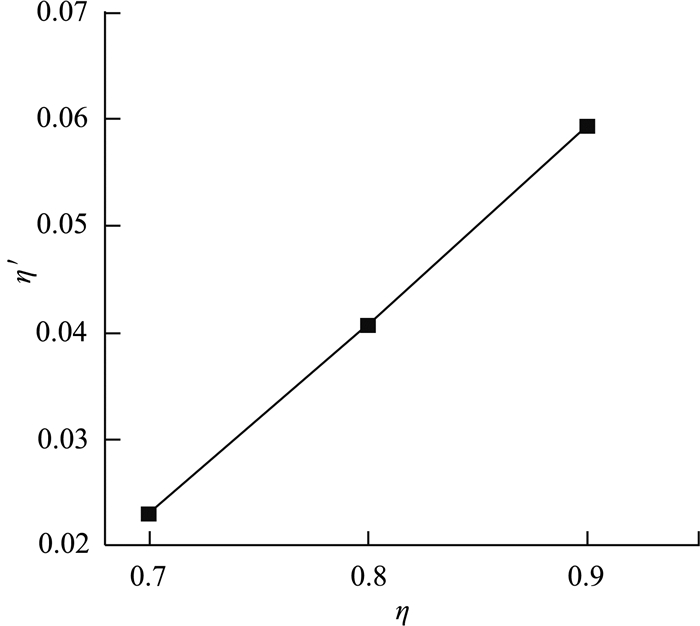
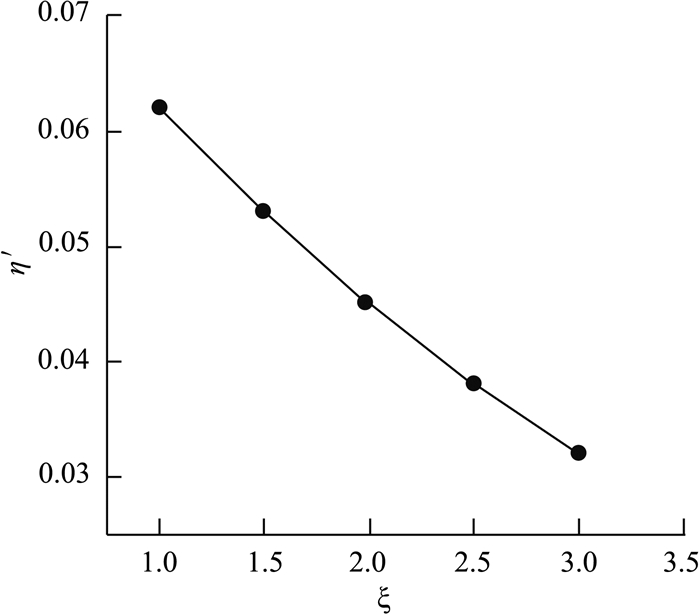
本文分析的算例为硬质黏性土场地中的深埋隧道,考虑了土拱效应,因此隧道结构整体位移较小;为了考察本文修正后的纵向计算模型与已有模型的差异,引用文献[4]的算例作分析,具体计算如表 2所示并得到如图 14所示纵向刚度与横向刚度间的关系曲线,其中差异变形系数和纵向接头等效刚度修正系数取本文算例计算结果.此外以表 2中横向刚度有效率0.9为例,其他参数不变,改变差异变形系数与纵向接头等效刚度修正系数,以探索隧道等效纵向刚度对其敏感性,结果见图 15~16.
| 表 2 本文成果与既有研究纵向刚度有效率计算对比 Table 2 Comparison of longitudinal equivalent rigidity between this work and existing research |
|
图 14 纵向等效刚度与横向刚度有效率关系曲线 Fig. 14 Relation between longitudinal equivalent rigidity and transverse rigidity ratio |
|
图 15 纵向等效刚度与差异变形系数关系曲线 Fig. 15 Relation between longitudinal equivalent rigidity and differential deformation |
|
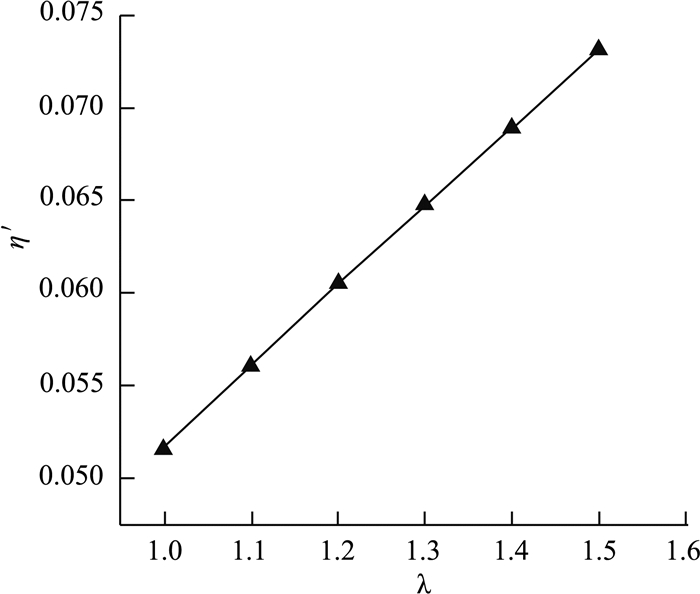
图 16 纵向等效刚度与接头等效刚度修正系数关系曲线 Fig. 16 Relation between longitudinal equivalent rigidity and joint rigidity correction coefficient |
表 2和图 14表明,由本文修正模型计算所得的盾构隧道纵向等效刚度随横向刚度的变化规律与既有模型计算结果一致,均表现为同向线性关系;但本文修正后的纵向等效刚度值比现有常规模型计算结果明显更小.图 15~16显示,盾构隧道纵向等效刚度随着衬砌差异变形的增大近线性减小,而随接头修正系数的增大呈线性增大.实际衬砌差异变形受隧道本体和环境作用的影响,如衬砌结构横向变柔,即横向刚度减小,会引起差异变形增大,从而使纵向等效刚度减小,与纵、横向刚度表征的关系是吻合的;衬砌纵向接头等效刚度修正会增大衬砌环间连接刚度,使纵向等效刚度增大.通过对比和修正参数的敏感性分析,进一步说明衬砌沿环向的差异变形和纵向接头特征对盾构隧道纵向等效刚度产生了可观的影响.
3 结论针对盾构隧道纵向计算理论,提出现有研究存在的不足并作了完善,后用于算例分析,得到如下认识:
(1) 在相同荷载作用下,衬砌环间采用实际纵向接头与等效螺栓环计算管片张开量相差17.6%,因此采用等效螺栓环表征实际盾构管片接头存有不容忽视的误差.
(2) 衬砌环横向承载时,竖向变形较水平向大15%,假定衬砌2个方向变形相同存在不足;衬砌横向刚度有效率受纵向错缝拼装影响显著,刚度提高了17.5%.
(3) 考虑衬砌差异变形、纵向接头特征及横向刚度影响时,计算所得隧道纵向刚度有效率较未考虑时分析结果大14.3%,对隧道结构纵向特性产生明显的影响.
(4) 盾构隧道纵向等效刚度随着衬砌差异变形的增大近线性减小,且与接头等效刚度修正值和横向刚度有效率同向线性变化;等效刚度对不同因素的敏感性依次为:横向刚度有效率大于衬砌差异变形大于接头等效刚度修正值.
实际工程水文地质、外部荷载及建筑环境的非均匀性、非对称性愈明显,引起的衬砌环差异变形愈大;同时衬砌纵向接头型式发生变化会放大环间连接初始刚度环向分布的不均匀性,从而增大等效螺栓环产生的误差.这些因素的影响在实际工程盾构隧道纵向分析时要充分考虑,本文分析方法耦合了上述因素,比现有模型更具合理性和适用性.
| [1] |
MURAKAMI, KOIZUMI A. Study on load bearing eapacity and mechanics of shield segment ring[J]. Proc for the Japan Society for Civil Engineering, 1978, 272(4): 103-115. |
| [2] |
YUKIS S K N. Evaluation procedure for seismic stress developed in shield tunnels based on seismic deformation method[J]. Proceedings of the Japan Society of Civil Engineering, 1988, 385-394. |
| [3] |
田敬学, 张庆贺. 盾构法隧道的纵向刚度计算方法[J]. 中国市政工程, 2001(3): 37-39. TIAN Jing-xue, ZHANG Qing-he. Calculation of longitudinal rigidity of shield tunnels[J]. China Municipal Eng-Ineering, 2001(3): 37-39. |
| [4] |
叶飞, 何川, 朱合华, 等. 考虑横向性能的盾构隧道纵向等效刚度分析[J]. 岩土工程学报, 2011, 12(3): 1870-1876. YE Fei, HE Chuan, ZHU He-hua, et al. Longitudinal equivalent rigidity analysis of shield tunnel considering transiverse characteristics[J]. Chinese Journal of Geote-chnical Engineering, 2011, 12(3): 1870-1876. |
| [5] |
张文杰, 徐旭, 李向红, 等. 广义的盾构隧道纵向等效连续化模型研究[J]. 岩石力学与工程学, 2009, 28(增2): 3938-3944. ZHANG Wen-jie, XU Xu, LI Xiang-hong, et al. Research on generalized longitudinal equivalent continous model of shield tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Supp2): 3938-3944. |
| [6] |
李翔宇, 刘国彬, 杨潇, 等. 基于修正纵向等效连续化模型的隧道变形受力研究[J]. 岩土工程学报, 2014, 36(4): 662-670. LI Xiang-yu, LIU Guo-bin, YANG Xiao, et al. Deformation and stress of tunnel structures based on modified longitudinal equivalent continuous model[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 662-670. DOI:10.11779/CJGE201404010 |
| [7] |
廖少明, 侯学渊, 彭乐芳. 隧道纵向剪切传递效应及其一维解析[J]. 岩石力学与工程学报, 2006, 24(7): 1110-1116. LIAO Shao-ming, HOU Xue-yuan, PENG Le-fang. Longitudinal shear transfer of tunnel and its 1d analytical solution[J]. Chinese Journal of Rock Mechanics and Eng ineering, 2006, 24(7): 1110-1116. |
| [8] |
黄宏伟, 徐凌, 严佳梁, 等. 盾构隧道横向刚度有效率研究[J]. 岩土工程学报, 2006, 28(1): 11-18. HUANG Hongwei, XU Ling, YAN Jialiang, et al. Study on transverse effective rigidity ratio of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(1): 11-18. |
| [9] |
叶飞, 杨鹏博, 毛家骅, 等. 基于模型试验的盾构隧道纵向刚度分析[J]. 岩土工程学报, 2015, 37(1): 83-90. YE Fei, YANG Peng-bo, MAO Jia-hua, et al. Longitudinal rigidity of shield tunnels based on model tests[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1): 83-90. DOI:10.11779/CJGE201501009 |
| [10] |
LEE K M, Y H X, GE X W, et al. An analytical solution for a jointed shield-driven tunnel lining[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(4): 365-390. DOI:10.1002/(ISSN)1096-9853 |
| [11] |
LEE K M, GE X W. The equivalence of a jointed shield-driven tunnel lining to a continuous ring structure[J]. Journal of Canadian Geotechnical Engineering, 2001, 38: 461-483. DOI:10.1139/t00-107 |
| [12] |
彭益成, 丁文其, 闫治国, 等. 修正惯用法中弯曲刚度有效率的影响因素分析及计算方法[J]. 岩土工程学报, 2013, 35(增1): 495-500. PENG Yi-cheng, DING Wen-qing, YAN Zhi-guo, et al. Analysis and calculation method of effective bending rigidity ratio in modified routine method[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Supp1): 495-500. |
| [13] |
杨春山, 莫海鸿, 陈俊生, 等. 盾构隧道先隧后井施工法对管片张开量的影响研究[J]. 岩石力学与工程学报, 2014, 33(增1): 2870-2877. YANG Chun-shan, Mo Hai-hong, Chen Jun-sheng, et al. Influence of shield tunneling with tunnels followed by well excavation on segment opening[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Supp1): 2870-2877. |
| [14] |
YANG Chun-shan, MO Hai-hong, CHEN Jun-sheng, et al. Numerical analysis of influence caused by lining cracks on dynamic response of shield tunnel during metro operation[J]. Journal of information and computational science, 2014, 11(11): 3835-3846. DOI:10.12733/issn.1548-7741 |
| [15] |
YANG Chun-shan, MO Hai-hong, CHEN Jun-sheng, et al. Numerical study on material optimization of the composite lining of shield tunneling[J]. Electronic Journal of Geotechnical Engineering, 2013, 18R: 3813-3824. |
| [16] |
莫海鸿, 杨春山, 陈俊生, 等. 盾构隧道先隧道后井施工中工作井支护结构优化[J]. 中南大学学报:自然科学版, 2016, 47(4): 1346-1352. MO Hai-hong, YANG Chun-shan, CHEN Jun-sheng, et al. Supporting optimization of working well in shield construction with tunnel followed by well excavation[J]. Journal of Central South University:Science and Technology, 2016, 47(4): 1346-1352. |
| [17] |
钟小春, 张金荣, 秦建设, 等. 盾构隧道纵向等效弯曲刚度的简化计算模型及影响因素分析[J]. 岩土力学, 2011, 32(1): 132-136. ZHONG Xiao-chun, ZHANG Jin-rong, QIN Jian-she, et al. Simplified calculation model for longitudinal equivalent bending stiffness of shield tunnel and its influence factors' analysis[J]. Rock and Soil Mechanics, 2011, 32(1): 132-136. |



