2. 天津市交通科学研究院, 天津 300074
2. Tianjin Transportation Research Institute, TianJin 300074, China
当前,社会力模型分为2类,不加入路径选择模型和加入路径选择模型.第1类模型中,Helbing等[1]考虑行人的行走机制,将行人与环境之间的相互作用量化为吸引力和斥力,然后利用这些力的合力驱动行人运动.这些模型能够重现许多行人聚集现象,如“自动渠化”、“出口拱形”、“快即是慢”[2-5, 7]等.然而因为它们并未考虑行人路径选择行为,导致行人运动受到其他行人和外界环境的严重干扰,行人在仿真中更像“无目的”的粒子而非会思考的人.有效的路径选择模型不仅能够有效避免仿真中出现的“振荡”现象,也能提高行人寻找最优路径运动的能力,提高人群疏散效率.
第2类模型中,路径选择模型也分2类:静态路径选择模型和动态路径选择模型.静态路径选择模型在仿真开始给行人分配一条直线最短路径,然后在仿真过程中行人自主选择路径前往目的地.而动态路径选择模型允许行人根据周围环境时刻调整最优路径.Kretz等[8]建立了保证运行时间最小的路径选择模型;Patil等[9]建立了行人相互作用算法来控制行人的路径选择行为;Treuille等[10]通过设置一系列动态速度势能场的方法控制行人的路径选择行为;Asano等[11]引入路径/出口选择模型赋予行人提前选择路径的能力.现有路径选择模型大多只能保证路径最短或者运行时间最短[8-9],然而,实际情况下,最优路径在当前时刻可能无法获得,比如视野受到遮挡的情况,此时现有路径选择模型很难得到有效的最优路径.
鉴此,本文设置了一系列处于行人可视范围内的中间目的地,并在此基础上,综合考虑行人视野范围、行人当前位置,前方行人速度、密度、空间占有率,利用离散网格来提高行人对周围环境的判断能力,建立了动态路径选择模型,模型保证行人在每个仿真步长内都能够得到未被占用的目的地和最佳运动方向.
1 社会力模型因本文的动态路径选择模型是社会力模型的扩展,所以本节简单介绍社会力模型.基本社会力模型包括:驱动力fα0(t),障碍物的作用力foα(t),行人之间在t时刻的相互作用力fαβ(t),其他行人的作用力和随机波动力εα(t).εα(t)表示行人无法预测的随机行为,它的大小服从正态分布,方向垂直于速度方向.社会力模型的基本公式如下:
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{v}}_\alpha }\left( t \right)}}{{{\rm{d}}t}} = \mathit{\boldsymbol{f}}_\alpha ^0\left( t \right) + \sum\limits_\beta {{\mathit{\boldsymbol{f}}_{\alpha \beta }}\left( t \right)} + \sum\limits_o {{\mathit{\boldsymbol{f}}_{o\alpha }}\left( t \right)} + {\varepsilon _\alpha }\left( t \right). $ | (1) |
其中,
| $ {\varepsilon _\alpha }\left( t \right) = {\mathit{\boldsymbol{e}}_\alpha }\left( t \right) \times {\mathit{\boldsymbol{f}}_\alpha }\left( t \right)x\mathit{\boldsymbol{e}}_\alpha ^{{\rm{norm}}}\left( t \right). $ | (2) |
式中:eα(t)为期望速度方向的单位向量;fα(t)为行人在时刻t受到的合力;eαnorm(t)为垂直于期望速度方向的单位向量;vα(t)为行人α在时刻t的速度向量;α,β表示不同的行人, x为自变量的数值.
x~N(0, 1),N为正态分布符号,概率密度函数为
| $ f\left( x \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\exp \left( {\frac{{ - {x^2}}}{2}} \right). $ | (3) |
行人α在时刻t受到的驱动力为
| $ \mathit{\boldsymbol{f}}_\alpha ^0\left( t \right) = m\frac{{v_\alpha ^0\left( t \right)\mathit{\boldsymbol{e}}_\alpha ^0\left( t \right) - {\mathit{\boldsymbol{v}}_\alpha }\left( t \right)}}{{{\tau _\alpha }}}. $ | (4) |
| $ \mathit{\boldsymbol{e}}_\alpha ^0\left( t \right) = \frac{{\mathit{\boldsymbol{p}}_\alpha ^{\rm{d}}\left( t \right) - \mathit{\boldsymbol{p}}_\alpha ^{\rm{c}}\left( t \right)}}{{\left| {\mathit{\boldsymbol{p}}_\alpha ^{\rm{d}}\left( t \right) - \mathit{\boldsymbol{p}}_\alpha ^{\rm{c}}\left( t \right)} \right|}}. $ | (5) |
式中:m为行人质量,vα0(t)为行人α在时刻t的期望速度;τα为行人的反应时间;eα0(t)为初始期望速度方向的单位向量;pαd(t)为行人的期望目的地;pαc(t)为行人α的当前位置.
行人也受其他行人影响,行人α和β的相互作用力由式(6)计算得到.行人之间的社会心理力fαβsoc(t)可以用公式(7)计算得到,它保证行人拥有一个其他行人无法进入的空间.行人之间的物理力包括物理压力和滑动摩擦力,它用来解释2个人相互接触时产生的相互作用.
| $ {\mathit{\boldsymbol{f}}_{\alpha \beta }}\left( t \right) = \mathit{\boldsymbol{f}}_{\alpha \beta }^{{\rm{soc}}}\left( t \right) + \mathit{\boldsymbol{f}}_{\alpha \beta }^{{\rm{PH}}}\left( t \right). $ | (6) |
| $ \mathit{\boldsymbol{f}}_{\alpha \beta }^{{\rm{soc}}}\left( t \right) = {\mathit{\boldsymbol{A}}_{\alpha \beta }}\exp \left[ {\frac{{\left( {{r_{\alpha \beta }} - {d_{\alpha \beta }}} \right)}}{{{B_{\alpha \beta }}}}} \right]{\mathit{\boldsymbol{n}}_{\alpha \beta }}{F_{\alpha \beta }}. $ | (7) |
| $ {\mathit{\boldsymbol{n}}_{\alpha \beta }} = \left( {n_{\alpha \beta }^1,n_{\alpha \beta }^2} \right) = \frac{{\left\{ {{\mathit{\boldsymbol{p}}_\alpha }\left( t \right) - {\mathit{\boldsymbol{p}}_\beta }\left( t \right)} \right\}}}{{{d_{\alpha \beta }}}}. $ | (8) |
| $ \mathit{\boldsymbol{f}}_{\alpha \beta }^{{\rm{PH}}}\left( t \right) = Kg\left( {{r_{\alpha \beta }} - {d_{\alpha \beta }}} \right){\mathit{\boldsymbol{n}}_{\alpha \beta }} + kg\left( {{r_{\alpha \beta }} - {d_{\alpha \beta }}} \right)\Delta v_{\alpha \beta }^t{\mathit{\boldsymbol{t}}_{\alpha \beta }}. $ | (9) |
| $ {\mathit{\boldsymbol{t}}_{\alpha \beta }} = \left( { - n_{\alpha \beta }^2,n_{\alpha \beta }^1} \right). $ | (10) |
| $ \Delta v_{\alpha \beta }^t = \left( {{\mathit{\boldsymbol{v}}_\alpha }\left( t \right) - {\mathit{\boldsymbol{v}}_\beta }\left( t \right)} \right) \cdot {\mathit{\boldsymbol{t}}_{\alpha \beta }}. $ | (11) |
| $ g\left( x \right) = \left\{ \begin{array}{l} x,x > 0;\\ 0,其他. \end{array} \right. $ | (12) |
式中:vβ(t)为行人β在时刻t的速度; Aαβ和Bαβ为行人之间作用力强度和作用力影响范围;pα(t), pβ(t)为行人α和β中心的位置;rαβ为行人α的半径rα和行人β的半径rβ的和;dαβ为行人α和β中心距离;nαβ为从行人α指向β的向量;Fαβ为各向异性;Δvαβt为行人与行人之间切线方向的速度差;tαβ为垂直于nαβ的行人切向量; K和k为非常大的常量[17],是决定行人接触时产生的物理作用力影响的参数.
当λα取0≤λα<1之间的值时,Fαβ表示行人受前方行人影响大于后方行人.
| $ {F_{\alpha \beta }} = {\lambda _\alpha } + \left( {1 - {\lambda _\alpha }} \right)\frac{{1 + \cos \left( {{\varphi _{\alpha \beta }}} \right)}}{2}, $ | (13) |
| $ \cos \left( {{\varphi _{\alpha \beta }}} \right) = - {\mathit{\boldsymbol{n}}_{\alpha \beta }}{\mathit{\boldsymbol{e}}_\alpha }\left( t \right), $ | (14) |
| $ {\mathit{\boldsymbol{e}}_\alpha }\left( t \right) = \frac{{{\mathit{\boldsymbol{v}}_\alpha }\left( t \right)}}{{\left\| {{\mathit{\boldsymbol{v}}_\alpha }\left( t \right)} \right\|}}. $ | (15) |
式中:λα为各向异性系数;φαβ为行人α和β速度的夹角.
行人与障碍物之间的作用力类似与行人之间的作用力.行人与障碍物之间的作用力为
| $ {\mathit{\boldsymbol{f}}_{o\alpha }}\left( t \right) = \mathit{\boldsymbol{f}}_{o\alpha }^{{\rm{soc}}}\left( t \right) + \mathit{\boldsymbol{f}}_{o\alpha }^{{\rm{PH}}}\left( t \right). $ | (16) |
| $ \mathit{\boldsymbol{f}}_{o\alpha }^{{\rm{soc}}}\left( t \right) = {A_{o\alpha }}\exp \left[ {\frac{{\left( {{r_{o\alpha }} - {d_{o\alpha }}} \right)}}{{{B_{o\alpha }}}}} \right]{\mathit{\boldsymbol{n}}_{o\alpha }}. $ | (17) |
| $ \mathit{\boldsymbol{f}}_{o\alpha }^{{\rm{PH}}}\left( t \right) = Kg\left( {{r_{o\alpha }} - {d_{o\alpha }}} \right){\mathit{\boldsymbol{n}}_{o\alpha }} - kg\left( {{r_{o\alpha }} - {d_{o\alpha }}} \right)\Delta v_{o\alpha }^t{\mathit{\boldsymbol{t}}_{o\alpha }}. $ | (18) |
| $ \Delta v_{o\alpha }^t = {\mathit{\boldsymbol{v}}_\alpha }\left( t \right) \cdot {\mathit{\boldsymbol{t}}_{o\alpha }}. $ | (19) |
式中:foαsoc为行人与障碍物之间的社会心理力,foαPH为行人与障碍物之间的物理力,Aoα为行人与障碍物之间的作用力强度,Boα为行人与障碍物之间的作用力范围,roα为行人与障碍物的半径之和,doα为行人中心与障碍物中心的距离.Δvoαt为行人与障碍物之间切线方向的速度差, noα为行人指向障碍物中心的向量, toα为平行于障碍物方向的向量.
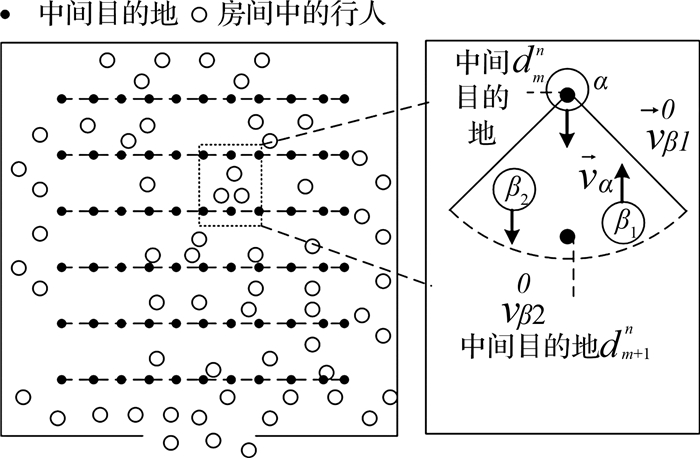
2 路径选择模型建立 2.1 行人期望位置分布在社会力模型中,行人运动轨迹受期望速度方向影响,期望速度方向受目的地影响.行人在目的地吸引下,逐步向目的地移动.但是,因为行人视野受到干扰,导致行人的期望速度方向可能被其他行人所阻挡,而仿真中行人依旧按照该期望速度方向行走,这就导致了潜在的事故和“锁死”现象.因此,本文为了配合路径选择模型,对目的地的分布模型进行了改进.如图 1所示,一系列均匀分布的中间目的地被设置在留有出口的密闭空间内.同行的2个中间目的地之间的间距为0.5 m,同列相邻的2个中间目的地之间的距离为小于4 m的常数.在每个仿真步长里,距离行人当前位置距离最近的中间目的地被暂时选择为下一时刻的目的地,当该中间目的地被遮挡时,行人会随之选择视野看的到的目的地代替.如图 1所示,dmn和dm+1n分别表示当前2个不同的中间目的地,行人根据周围环境选择最优的中间目的地.
|
图 1 中间目的地分布 Fig. 1 Distribution of intermediate destination |
本文模型受Guo等[12]的启发,利用离散网格来分解行人周围环境,以此增强行人对周围环境的理解能力.如图 2(a)所示,离散网格细化行人周围环境,为行人提供多个行走方向.行人周围空间被划分为8个格子,每个格子表示一个可以选择的行走方向,在每个仿真步长内,拥有最大权重的格子被选择为下一仿真步长的期望速度方向.

|
图 2 离散化空间示意图 Fig. 2 Sketch of discretization space |
如图 2(b)所示,每个行人i占有一个真实的半径为Ri空间.η为行人隐私空间.除此以外,每个行人i也存在一个安全空间保持与其他行人的距离PR.每个格子用ck表示,其中k∈[0, 7].L0, L1, …Ln-1表示一系列逆时针排列的边界向量.一个格子由2个边界向量.每个格子ck的张开角度为θ=360°/8.格子ck的方向为dik.
如图 3(a)所示,当在格子c0内不存在行人时,dis作为格子c0的方向向量di0,即di0=dis,其他格子的方向向量逆时针依次排列.而当dis被前方行人遮挡时,需要寻找能够通行的调整dis.如图 3(b)所示,点zj1和zj2表示在dis方向的人群切点,因此,一旦人群切向量rizj1和rizj2确定,与dis夹角最小的切向量就被定义为di0.

|
图 3 格子里在dis方向是否有行人 Fig. 3 Whether there are pedestrians or not indirection of dis in discretization grid |
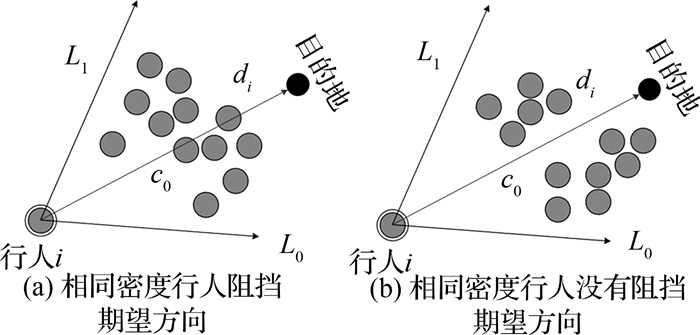
在策略层,路径选择的关键在于各个格子的权重计算,在Saboia等[13]的研究中,权重由行人格子中的行人密度决定,然而实际行走中,格子的权重不仅受到行人密度影响,还会受到周围行人行走速度以及格子中行人的位置分布影响.如图 4所示为2种具有相同行人密度但有不同行人位置分布的格子c0.显然,图 4(b)的格子有利于行人通过,而图 4(a)因为前方行人阻挡无法为行人提供有效的期望方向.因此,行人在格子中的空间分布也是决定权重的关键因素.
|
图 4 相同行人密度不同行人空间分布示意图 Fig. 4 Sketch of pedestrian different space distribution with same density |
对于行人i,每个格子ck的选择权重用wik表示,如式(20)所示.
| $ w_i^k = {N_t}\delta _i^kE_i^kF_i^kB_i^k. $ | (20) |
式中:Nt为需要标定的常数,用来调整所有wik的和为1;δik为表示行人喜欢选择低行人密度且距离目的地近的格子的参数;Eik表示行人喜欢通过与自己速度相差不大的人群的参数,Fik表示行人保持当前速度方向的意愿的参数;Bik表示格子ck的空间可用率Bi, jk.
其中:
| $ \delta _i^k = \frac{1}{{{d_{{\rm{route}}}}\rho }}. $ | (21) |
| $ {d_{{\rm{route}}}} = {\rm{minimum}}\left\{ {\left| {{\mathit{\boldsymbol{p}}_{\rm{c}}}\left( t \right) - {\mathit{\boldsymbol{p}}_{{\rm{in}}}}\left( t \right)} \right|} \right\}. $ | (22) |
式中:droute为当前行人位置距离中间目的地的最短距离;ρ为格子ck的行人密度;pc(t)为行人当前位置坐标;pin(t)为中间目的地坐标.
Eik表示行人i与格子气中其他行人相对速度比的倒数,如式(23)所示.速度差越小,该格子被行人选择的概率就越大.
| $ E_i^k = \frac{1}{{\sum\limits_\beta {\frac{{\left| {{\mathit{\boldsymbol{v}}_\beta }\left( t \right) - {\mathit{\boldsymbol{v}}_\alpha }\left( t \right)} \right|}}{{\left| {{\mathit{\boldsymbol{v}}_\beta }\left( t \right)} \right|}}} }}. $ | (23) |
Fik在0到1之间取值.
| $ F_i^k = {\lambda _r}\frac{{{{\left( {\cos \left( {{\theta _{k,0}}} \right) + 1} \right)}^2}}}{4}. $ | (24) |
式中:λr为在路径选择模型中的各向异性系数,θk, 0为方向向量di0和dik之间的夹角.
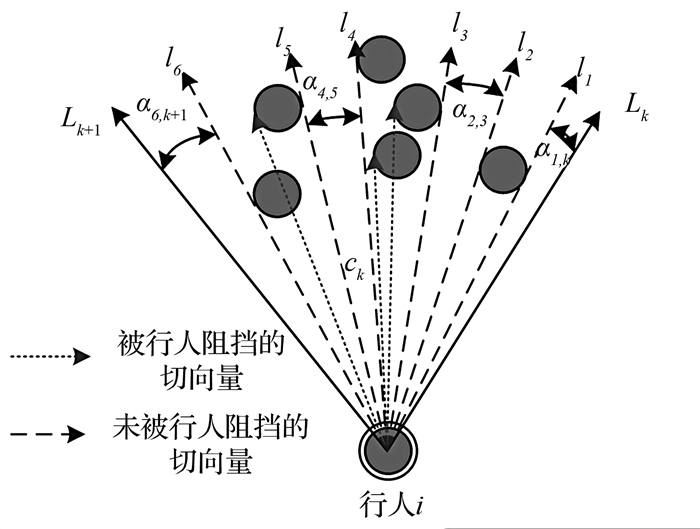
Bi, jk为格子ck中未被行人占用的空间比率.以格子ck作为例子说明.如图 5所示,一个向量从边界Lk到边界Lk+1逆时针扫过格子ck.当扫描向量遇到格子ck中的第一个行人时,开始切向量记为l1.然后,扫描向量继续扫描剩下的区间,扫描向量离开第一个行人后,当第一个行人的结束切向量方向不存在其他行人时,结束切向量记为l2.如果结束切向量方向有行人存在例如,如图 5所示,扫描向量扫描到第2个行人时,第2个行人的开始切向量记为l3,然后扫描向量继续扫描剩下的区域,因为第2个行人的结束切向量被第3个堵塞,所以不记录结束切向量;扫描向量继续扫描,因为第3个行人的结束向量被第4个行人占用,所以第3个行人的结束向量也不记录;扫描向量继续扫描,第4个行人的结束切向量没有被其他行人占用,所以记录得到结束切向量l4.扫描向量继续扫描直到边界向量Lk+1.扫描结束后,得到一系列的开始和结束切向量l1, l2, …ln.向量l1和Lk之间的空间(向量l3和l2,向量l5和l4,向量l6和Lk+1)能够被行人利用.向量l1和Lk(向量l3和l2,向量l5和l4,向量l6和Lk+1)的夹角α1, k(α2, 3, α4, 5, α6, k+1)可以通过计算得到.
|
图 5 格子ck的自由张角 Fig. 5 Free angular α1, k, α2, 3, α4, 5, α6, k+1 oflattice ck |
α1, k, α2, 3, α4, 5, α6, k+1中的最大角度的角平分线被定义为dik.
| $ \mathit{\boldsymbol{d}}_i^k = \frac{{{\mathit{\boldsymbol{L}}_{i + 1}}}}{{\left| {{\mathit{\boldsymbol{L}}_{i + 1}}} \right|}} + \frac{{{\mathit{\boldsymbol{l}}_6}}}{{\left| {{\mathit{\boldsymbol{l}}_6}} \right|}}. $ | (25) |
| $ B_{i,j}^k = \frac{{\alpha _{1,k}^k + \alpha _{2,3}^k + \alpha _{4,5}^k + \alpha _{6,k + 1}^k}}{\theta }. $ | (26) |
行人将选择最大权重的格子ck的方向向量dik作为下一步的期望速度方向.式(27)表示t时刻行人的期望速度计算方法.在决策层,因为行人希望保持当前速度继续行走,所以只有当新格子和当前格子的权重差大于阈值gi时,行人才会决定采用新的运动方向.轨迹选择决策模型如公式(28)所示.
| $ \mathit{\boldsymbol{v}}_i^0\left( t \right) = \mathit{\boldsymbol{v}}_i^0\left( t \right)\mathit{\boldsymbol{e}}_{{\rm{current}},i}^0\left( t \right). $ | (27) |
| $ \mathit{\boldsymbol{e}}_{{\rm{current}},i}^0\left( t \right) = \left\{ \begin{array}{l} \mathit{\boldsymbol{e}}_{{\rm{new}},i}^0\left( t \right),w_{{\rm{current}},i}^k - w_{{\rm{new}},i}^0 \ge {g_i};\\ \mathit{\boldsymbol{e}}_{{\rm{current}},i}^0\left( t \right),其他. \end{array} \right. $ | (28) |
式中:enew, i0为行人在新网格速度方向的单位向量,ecurrent, i0为行人在当前网格里速度方向的单位向量,wcurrent, ik为行人在当前网格k里的权重值,wnew, i0为行人在新的网格里的权重值.
3 仿真和分析 3.1 参数标定本文建立的模型中包含许多参数.为了确定合理的模型参数值,本文采用Zeng等[6]提出的参数标定方法.一些模型参数能直接从实际数据(实际数据采集是在一长10 m,宽10 m,且有宽2 m出口的教室内,数据筛选确保每组数据行人容量大于100,且控制进口不允许行人进入,用于参数标定的行人数共476人)得到,例如行人期望速度和反应时间等,而作用强度和作用范围参数无法直接得到.标定参数分为3个步骤.
1) 参数例如视野范围, 这类参数虽然可以测得,但是却没办法直接从轨迹数据中获取,所以这类参数的取值采用了前人的研究结果(Anvari等[14],Zeng等[6]和Li等[15]).
2) 参数例如速度、反应时间等,这类参数可以通过调查数据直接得到.
3) 上述可测参数标定以后,其他无法直接获取的参数例如作用力强度和作用力范围,这类参数利用Zeng等[6]提出的参数标定方法进行了标定.
参数标定需要获取行人的真实运动轨迹数据,本文利用实验室自主开发的轨迹提取软件进行数据提取,江晟等[16]对软件的实现算法和软件的误差进行了分析研究,最终轨迹误差在7%以内,数据精度能够满足数据要求.参数的标定结果如表 1所示,在95%的置信水平下,p值表明标定结果的准确性.
| 表 1 参数标定结果 Table 1 Calibration results of parameters |
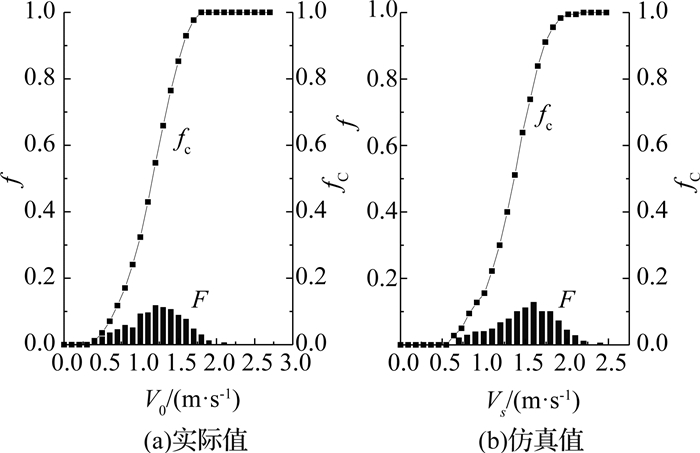
对一个房间的行人疏散进行仿真分析,房间面积10 m×10 m,安全出口的宽度为2 m.为排除偶然误差,进行了100次的仿真实验.仿真开始行人随机分布于房间内.行人的期望速度大小为1.37 m/s.各向异性系数取值0.3,以此保证不受视野范围外的行人干扰.如图 6所示为100次仿真中所有行人的平均速度Vo和实际调查行人(所有调查的行人)的速度Vs分布频率f和累计频率fc的对比,从图中可知,仿真结果和实际数据的速度平均值分别为1.45、1.34 m/s,标准差分别为0.45、0.37.这说明模型参数是有效的.
|
图 6 仿真和实际速度直方图 Fig. 6 Speed histograms of collection and simulation data |
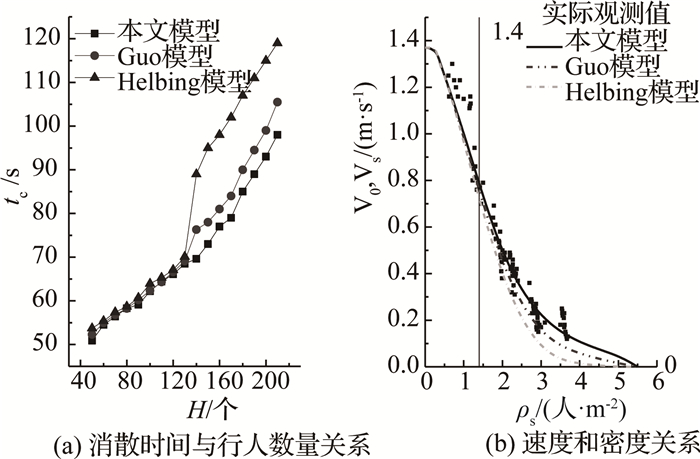
如图 7所示为实际和仿真数据的对比结果,分析了行人消散时间tc随行人数量H的变化规律及行人速度随仿真场景中行人密度ρs的变化规律.
|
图 7 观测数据与3种模型结果对比图 Fig. 7 Diagram of comparison of observed and simulated results based on three models |
从图 7(a)可知,对于相同的行人数,本文模型和Guo模型接近,且在行人数小于130人时,3个模型差别不大,但是当房间中人数超过130时,本文模型所需的消散时间小于Helbing模型和Guo模型.这是因为,虽然Guo模型考虑了路径选择问题,但是因为并没有设置中间目的地,导致在目的地被阻挡的情况下行人运动方向模糊,行人选择最优路径的能力不足;而Helbing模型因为行人完全没有路径选择,其运动更接近于无规律的粒子,所以行人之间的相互作用是最激烈的,消散时间也最长.从消散时间tc来看,本文模型能够一定程度上赋予行人搜寻路径的能力,并使行人更类似于真实行人而非粒子.
从图 7(b)可知,在相同密度下,本文模型结果与实际观测数据更加接近,Guo模型和Helbing模型均小于实际观测值.当ρs<1.4人/m2时,3个模型在相同密度下的速度差别不大,路径选择模型有利于提高人群消散的速度,因为此时行人有足够的空间且与其他行人相互作用较弱;当ρs>1.4人/m2时,因为行人相互作用的增加以及视野的变小,本文结果逐渐大于其他2个模型,这些变化趋势与图 7(a)的规律变化趋势一致.这表明,行人密度越高,路径选择模型越有利于提高人群消散效率.仿真结果更加符合实际.
4 结语本文首先设置了一系列的中间目的地,随后在此基础上,提出了行人的路径选择模型.通过设置中间目的地,增强仿真中行人路径选择的能力.修正模型考虑了行人与周围行人的速度差、周围行人空间占用率等因素,保证行人能够充分利用行人视野内的空间.通过几种模型的对仿真结果对比,本文修正模型能够有效地提高行人的释放效率,尤其是高密度条件下,改进路径选择模型尤为有效,这是因为改进模型提高了行人对周围环境的判别和路径选择能力.本文模型完善了行人社会力仿真模型,为行人仿真的进一步应用打下基础.然而本文并不完善,本文仅从路径选择方面完善社会力模型,其他的行人特性并未考虑,例如行人的随机行为、记忆效应等等,这些因素都影响着行人的消散效率,如何建立这些行为的运动模型是下一步研究亟待解决的问题.
| [1] |
HELBING D, MOLNAR P. Social force model for pedestrian dynamics[J]. Physical review E, 1995, 51(5): 4282-4286. DOI:10.1103/PhysRevE.51.4282 |
| [2] |
YU W J, CHEN R, DONG L Y, et al. Centrifugal force model for pedestrian dynamics[J]. Physical Review E, 2005, 72(2): 026112. DOI:10.1103/PhysRevE.72.026112 |
| [3] |
PARISI D R, DORSO C O. Morphological and dynamical aspects of the room evacuation process[J]. Physica A:Statistical Mechanics and Its Applications, 2007, 385(1): 343-355. DOI:10.1016/j.physa.2007.06.033 |
| [4] |
HELBING D, FARKAS I, VICSEK T. Simulating dynamical features of escape panic[J]. Nature, 2000, 407(6803): 487-490. DOI:10.1038/35035023 |
| [5] |
LAKOBA T I, KAUP D J, FINKELSTEIN N M. Modifications of the Helbing-Molnar-Farkas-Vicsek social force model for pedestrian evolution[J]. Simulation, 2005, 81(5): 339-352. DOI:10.1177/0037549705052772 |
| [6] |
ZENG W, CHEN P, NAKAMURA H, et al. Application of social force model to pedestrian behavior analysis at signalized crosswalk[J]. Transportation Research Part C:Emerging Technologies, 2014, 40: 143-159. DOI:10.1016/j.trc.2014.01.007 |
| [7] |
HELBING D, FARKAS I J, MOLNAR P, et al. Simulation of pedestrian crowds in normal and evacuation situations[J]. Pedestrian and evacuation dynamics, 2002, 21(2): 21-58. |
| [8] |
KRETZ T, GROßE A, HENGST S L, et al. Quickest routes in simulations of pedestrians[J]. Advances in Complex Systems, 2011, 14.05: 733-759. |
| [9] |
PATIL S. J, BERG S, CURTIS M, et al. Manocha. Directing crowd simulations using navigation fields[J]. IEEE Transactions on Visualization and Computer Graphics, 2010, 244-254. |
| [10] |
TREUILLE A, COOPER S, POPOVIC' Z. Continuum crowds[C]//ACM Transactions on Graphics (TOG)[S. l. ]. ACM, 2006, 25(3): 1160-1168. https://link.springer.com/chapter/10.1007/978-3-319-11900-7_2
|
| [11] |
ASANO M, IRYO T, KUWAHARA M. Microscopic pedestrian simulation model combined with a tactical model for route choice behavior[J]. Transportation Research Part C:Emerging Technologies, 2010, 18(6): 842-855. DOI:10.1016/j.trc.2010.01.005 |
| [12] |
GUO R, HUANG H. A mobile lattice gas model for simulating pedestrian evacuation[J]. Physica A, Stat. Mech. Appl, 2008, 387(2-3): 580-586. DOI:10.1016/j.physa.2007.10.001 |
| [13] |
SABOIA P, GOLDENSTEIN S. Crowd simulation:applying mobile grids to the social force model[J]. The Visual Computer, 2012, 28(10): 1039-1048. DOI:10.1007/s00371-012-0731-y |
| [14] |
ANVARI B, BELL M G H, Sivakumar A, et al. Modelling shared space users via rule-based social force model[J]. Transportation Research Part C:Emerging Technologies, 2015, 51: 83-103. DOI:10.1016/j.trc.2014.10.012 |
| [15] |
LI M, SHI F, CHEN D. Analyze bicycle-car mixed flow by social force model for collision risk evaluation[C]//3rd International Conference on Road Safety and Simulation. Transportation Research Board. Washington, DC: [s. n. ]. 2011. http://www.safetylit.org/citations/index.php?fuseaction=citations.viewdetails&citationIds%5b%5d=citjournalarticle_491776_9
|
| [16] |
江晟, 王殿海, 陈永恒, 等. 基于视频的行人运动轨迹再现与过街行为表达[J]. 东南大学学报:自然科学版, 2012, 42(6): 1233-1237. JIANG Sheng, WANG Dian-hai, CHEN Yong-heng, et al. Pedestrian movement trajectory reappearance and crossing feature expression based on video processing[J]. Journal of Southeast University:Natural Science Edition, 2012, 42(6): 1233-1237. |
| [17] |
ZAINUDDIN Z, SHUAIB M. Modification of the decision-making capability in the social force model for the evacuation process[J]. Transport Theory and Statistical Physics, 2010, 39(1): 47-70. DOI:10.1080/00411450.2010.529979 |



 ,
曲昭伟1,
赵利英1,
白乔文1,
杨秋杰2
,
曲昭伟1,
赵利英1,
白乔文1,
杨秋杰2