轨迹可以真实反映车辆的运行状态,进而了解车辆与其他道路使用者的冲突情况;轨迹特性分析是道路交通安全研究的重要手段,也是驾驶员行为分析的重要方面,可以为信号交叉口渠化设计提供参考,同时为交叉口通行能力及延误计算提供依据.其中右转车辆轨迹主要包括以下2种情况: 1)右转保护相位控制交叉口以及行人和非机动车流量较少的信号交叉口,右转车辆轨迹主要受交叉口几何条件、车辆和驾驶员自身条件的影响,轨迹变化范围小,分布较为集中;2)右转许可相位控制交叉口,右转车辆受行人和非机动车的影响,轨迹相对复杂,变化范围广.
国外研究学者对不同交叉口的右转车辆进行调查,结果表明不受行人和非机动车干扰下的轨迹分布较为集中,可以用数学模型进行表示.Stover[1]和Alhajyaseen等[2]在对大量数据进行分析的基础上,提出转弯车辆轨迹与交叉口的几何条件有关;Decabooter等[3]发现转弯车辆轨迹不仅与交叉口几何条件有关,也受车辆类型等因素的干扰;Read[4]和Asano等[5]采集了信号交叉口转弯车辆轨迹坐标,分析轨迹影响因素,并建立转弯轨迹模型.
针对右转许可相位控制的信号交叉口,右转机动车与非机动车的冲突是交叉口的主要冲突类型.关宏志等[6]分析了自行车对机动车的干扰问题,运用交通流理论提出混和交通流模型;景春光等[7]分析信号交叉口直行自行车与右转机动车之间的冲突规律,并以此为基础标定了机动车饱和流率影响参数;陈晓明[8]基于概率和间隙理论分析行人和非机动车对通行能力的影响,并对模型进行修正;王殿海等[9]分析右转机动车与自行车之间的冲突规律,以提高交叉口运行效率为指标,确定右转机动车相位的设置方法.因此,现有机非冲突的研究主要体现在对通行能力以及车辆延误的宏观影响方面,而对机非冲突所造成的车辆轨迹变化和速度波动等微观行为缺乏深入的解析.
本文在当前研究的基础上,利用视频检测技术,对不同交叉口的右转车辆轨迹进行追踪,从微观角度分析车辆的运行规律.首先,选择典型地点,对比有无机非冲突下右转车辆轨迹穿越位置分布;其次,分析无干扰条件下轨迹的影响因素,基于交叉口几何条件及车辆速度,建立无干扰条件下右转车辆轨迹模型;最后,分析有非机动车干扰时右转车辆轨迹变化规律,并对轨迹穿越位置进行聚类,建立机非干扰条件下右转车辆轨迹模型.
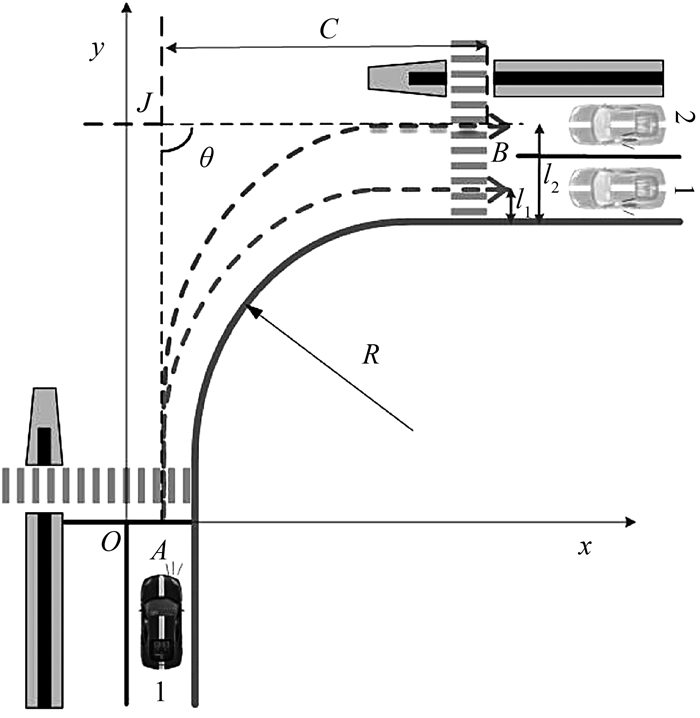
1 数据采集为分析右转车辆轨迹特性,选择苏州市8个信号交叉口32个进口道作为调查地点,信息参照如表 1和图 1所示,图中θ为交叉口转角,单位: rad;R为交叉口转弯半径,单位: m;J为出口道中心线与进口道中心线的交点;A为进口道中心线与停止线交点;B为出口道中心线与人行道内侧边缘线交点;C为J与B两点之间距离,单位: m;l为出口道中心线距路缘石的距离,单位: m.
| 表 1 调查交叉口统计表 Table 1 Surveyed sites characteristics |
|
图 1 交叉口几何参数定义示意图 Fig. 1 Definition of parameters related to intersection layout |
本文在信号交叉口高处建筑进行录像采集,利用Corel Video Studio Pro X7将视频以每秒10帧分割为图片,以左前轮触地点为参考点,利用Track-pro软件获得车辆的位置坐标、速度、位移等数据.该软件是基于视频采集技术获得行人或车辆时空数据的分析软件,通过软件参数设置可以将像素坐标转变为地理坐标,广泛应用于车辆轨迹及速度、加速度等数据的采集,通过验证,软件采集得到的位置坐标与真实坐标的平均相对误差在4%以内[10],满足本文研究需求.本文仅对小型车右转数据进行调查,针对右转车排队通过的情况,仅对右转车流的头车进行统计,避免跟驰行为对轨迹造成的影响.视频观测时间为2015年11月6个工作日早8点到9点,共采集右转机动车15 001辆.
当交叉口为右转机动车保护相位或交叉口内的行人和非机动车流量较少时,右转车辆轨迹主要受交叉口几何条件、车辆和驾驶员自身条件的影响,轨迹分布较为集中,将这种情况称为无干扰条件,因此本文提到的无干扰并非指右转车转弯过程中完全不受到其他道路使用者的干扰.
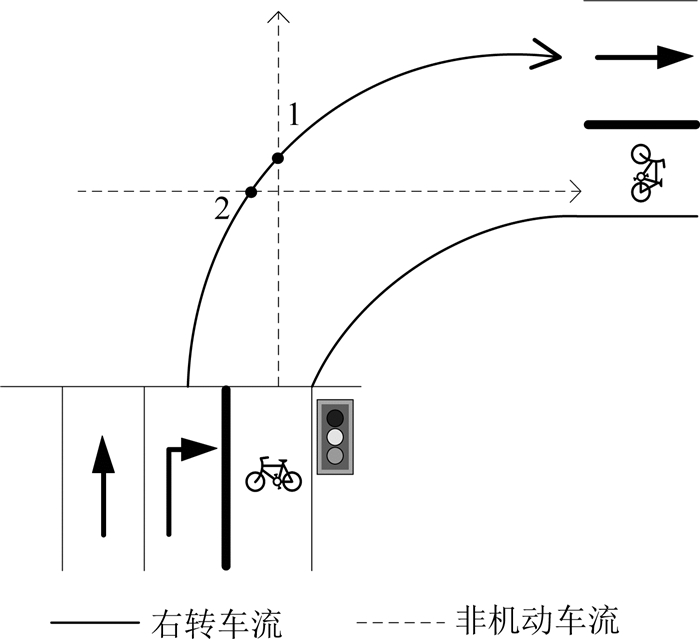
针对右转许可相位控制,右转机非冲突包括以下2种[11-12]: 1)右转机动车与同方向直行非机动车的冲突;2)右转机动车与侧向直行非机动车的冲突,如图 2所示.
|
图 2 右转车受非机动车干扰示意图 Fig. 2 Conflict between right-turning vehicles and bicycles |
当右转机动车与非机动车发生冲突时,二者会发生相应的减速和避让的行为,右转车辆的轨迹会发生变化,当单位时间内冲突次数较多时,该时间段内统计得到的右转车辆轨迹分布越广.因此本文选择小时机非冲突数这一指标对交叉口有无机非冲突情况进行划分,机非冲突数以机动车和非机动车到达率为基础,结合间隙理论,计算单位时间内机动车与非机动车之间的冲突概率,是评价交叉口冲突严重性的重要指标,计算公式如下:
| $ \begin{array}{l} N = \\ \frac{{3600{t_1}}}{T}\frac{{\left[ {{\lambda _{VN}}\Delta t \cdot \exp \left( { - {\lambda _{VN}}\Delta t} \right)} \right]\left[ {1 - \exp \left( { - {\lambda _{BN}}\Delta t} \right)} \right]}}{{\Delta t}}. \end{array} $ | (1) |
式中: N为冲突点机非冲突数;t1为冲突相位绿灯时间(s);T为信号周期(s);λVN为右转机动车到达率;λBN为右转非机动车到达率;Δt为临界间隙,即车流能够穿越的最小间隔(s),建议值1.15 s.
根据前期调查,当小时机非冲突数小于10时,右转车辆轨迹分布较为集中,因此本文选择冲突点1和冲突点2的小时机非冲突数均小于10的交叉口作为无干扰条件右转车辆轨迹研究的样本,调查时段内样本有无干扰划分结果参照表 1.
2 有无机非冲突下右转车辆轨迹分布对比选择几何条件相近的星明街-现代大道交叉口西进口与星湖街-苏虹中路交叉口东进口作为对比组,分析有无机非冲突右转车辆轨迹分布,对比组信息如表 2所示.
| 表 2 对比组基本信息表 Table 2 Basic information about two intersections |
如图 3所示,建立截面1和2,截面1是右转车辆转弯开始位置,是与同向非机动车冲突区边界;截面2为出口道延长线,是右转机动车与侧向非机动车冲突区边界.

|
图 3 对比组基本信息图 Fig. 3 Basic information about the two intersections |
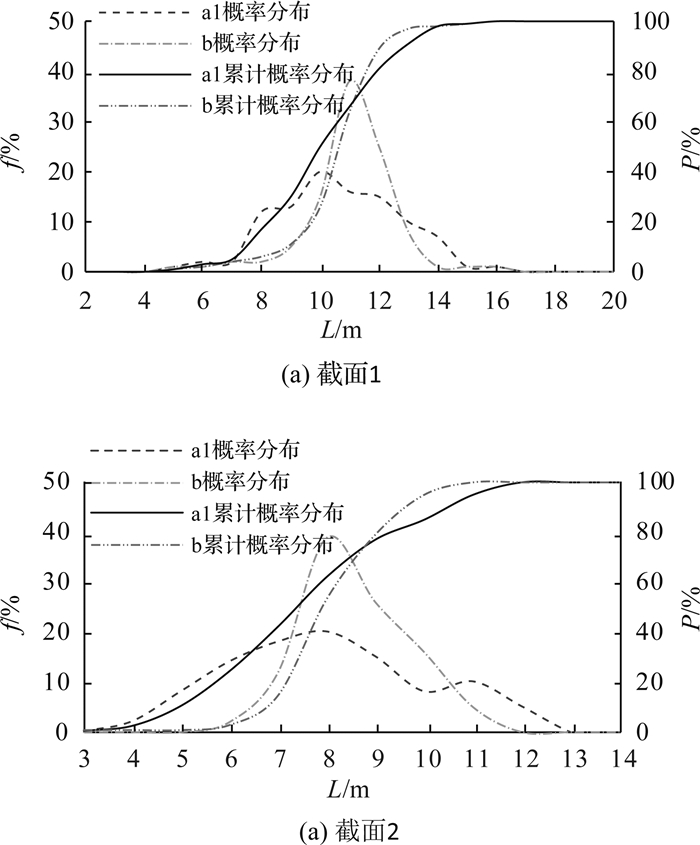
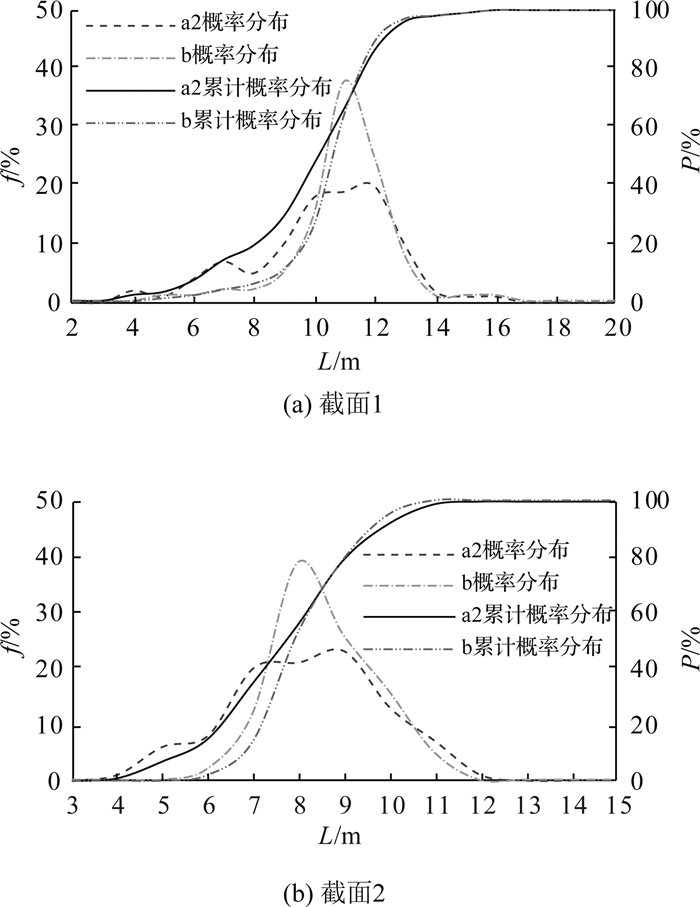
2种冲突下右转机动车在不同截面穿越位置的密度分布和累计概率密度分布如图 4和5所示,坐标原点为图 3中黑点,横坐标正方向为截面箭头方向,用坐标值L表示穿越位置,f为概率值,P为累计概率值,并计算穿越位置分布方差εL,统计结果如表 3所示.
|
图 4 右转车有无同向机非冲突穿越位置分布图 Fig. 4 Trajectory distribution at cross-section of right-turn vehicles with or without same direction bicycles conflict |
|
图 5 右转车有无侧向机非冲突穿越位置分布图 Fig. 5 Trajectory distribution at cross-section of right-turn vehicles with or without side direction bicycles conflict |
| 表 3 穿越位置方差统计表 Table 3 Dispersion of trajectory distribution at cross-section |
通过分析,得到如下结论:
1) 如图 4(a)所示,在受同向非机动车干扰时,车辆在截面1的穿越位置小于10 m的概率接近50%,大于无干扰情况.这是因为同向直行相位绿灯初期,非机动车抢占冲突区,右转机动车为尽快通过交叉口,常常提前转弯通过.
2) 如图 4(b)所示,在受同向非机动车干扰时,右转机动车在截面2的穿越位置分布从3到13 m,且方差为4.11大于无干扰时的0.78,说明右转机动车受同向非机动车干扰比较严重.
3) 如图 5(a)所示,受侧向非机动车干扰的右转车辆在截面1的穿越位置分布与无干扰情况相比更广,穿越位置小于9 m的概率接近15%,与无干扰条件下的5%相比差异较大,说明部分右转机动车为与侧向直行绿灯初期释放的非机动车争夺路权,提前到达潜在冲突区,完成转弯.
4) 如图 5(b)所示,受侧向非机动车干扰的右转机动车在截面2的位置分布在4~13 m,与无干扰条件下相比分布更广;且穿越位置小于7 m的概率与无干扰条件相比较大,穿越位置越靠近原点,说明右转机动车与非机动车争夺路权的欲望越强烈.
5) 星湖街-苏虹中路交叉口南进口道右转车辆在截面1与截面2穿越位置的方差分别为0.62和0.78,说明无干扰条件下右转车辆轨迹分布较为集中.
通过以上分析,当右转车辆与非机动车发生冲突时,右转车辆轨迹变化范围大,影响因素多,无干扰条件下右转车辆轨迹穿越位置分布较为集中.接下来将通过数理统计,分别建立无干扰条件下和有干扰条件下右转车辆轨迹模型.
3 无干扰条件下右转车辆轨迹建模参照表 1,选择星湖街-苏虹中路、华池街-西沈浒路、津梁街-方洲路、华池街-现代大道4处交叉口16个进口道作为无干扰条件右转机动车轨迹建模研究的观测地点,建立如图 6所示坐标轴,利用Track pro软件提取无干扰条件下右转车辆转弯轨迹坐标点,通过观测,在无干扰条件下有90%以上的右转车辆在转弯过程中选择最外侧2个出口道,因此仅采集由最外侧2个出口道驶出的右转车辆数据.

|
图 6 数据获取方法示意图 Fig. 6 Approach of data collection |
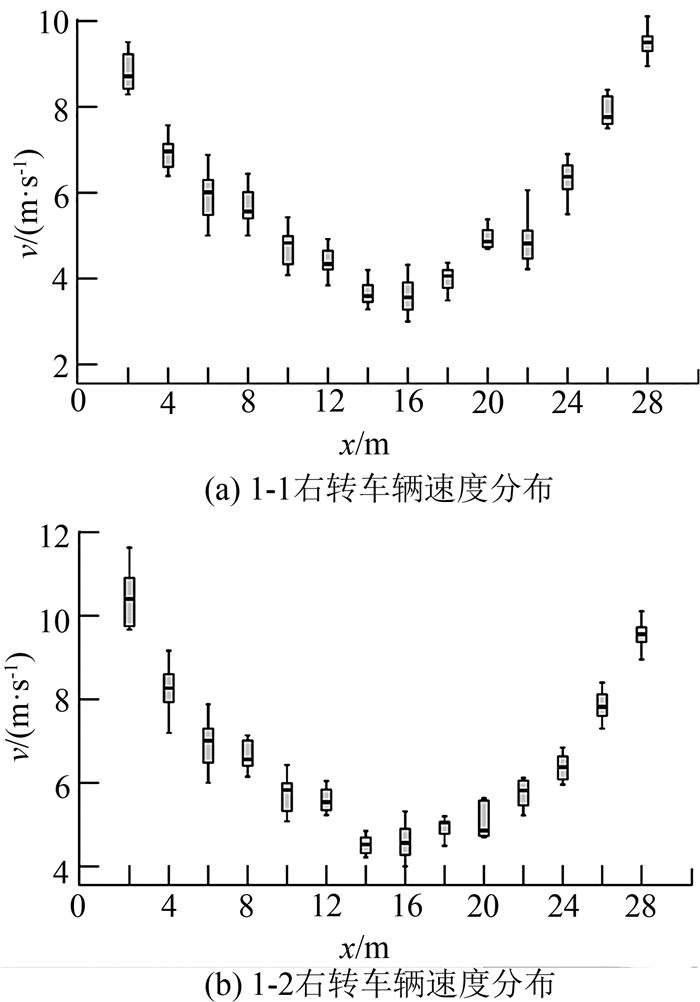
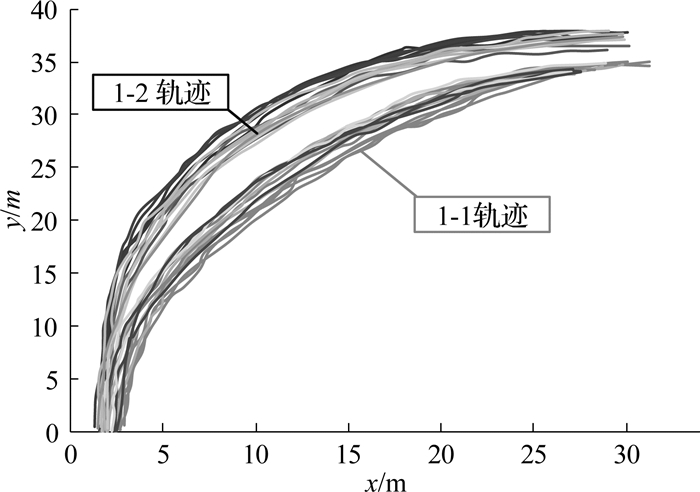
如图 7所示为华池街-西沈浒路南进口右转车辆转弯过程速度v分布图,其中1-1表示最外侧进口道到最外侧出口道,1-2表示最外侧进口道到次外侧出口道,对3 h内右转车辆轨迹进行统计,如图 8所示为轨迹空间变化,分析结果如下:
|
图 7 不同出口道速度分布箱图 Fig. 7 Box plots of speed profiles at differentexit lanes |
|
图 8 不同出口道轨迹分布示意图 Fig. 8 Trajectories of vehicles at differentexit lanes |
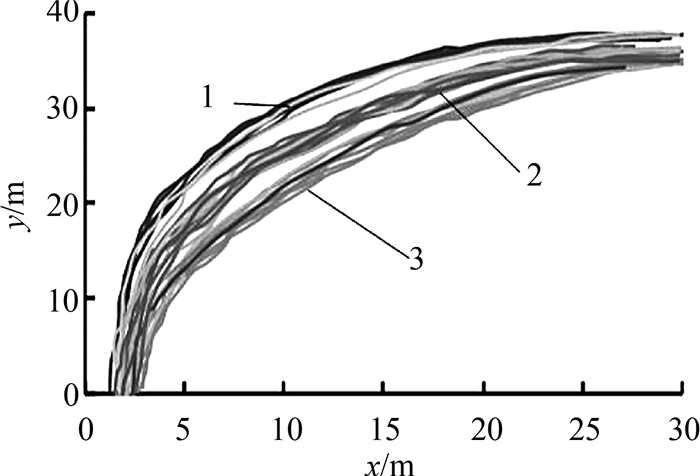
1) 从图 7中可看出,右转车辆转弯过程中速度会发生较为明显的变化,但同一出口道不同车辆在同一横坐标下的速度变化较为集中;不同出口道的右转车辆速度变化符合相似分布,但速度值存在明显不同.
2) 从图 8可看出,同一出口道和同一进口道的右转车辆轨迹集中在一定范围内,相同横坐标下的纵坐标变化范围小;同一进口道不同出口道的右转车辆轨迹存在明显不同,主要集中在2个范围.
3) 通过以上分析,可以对同一出口道进口道的右转车辆轨迹和速度进行统计,通过计算相同横坐标下的平均纵坐标和平均速度对该处右转车辆轨迹和速度变化进行表示,本节对4个交叉口16个进口道无干扰条件下右转车辆轨迹进行统计,最终得到32组平均轨迹数据.
3.1 影响因素分析影响车辆转弯轨迹的主要因素有交叉口几何条件,车辆及驾驶员自身因素,以及其他道路使用者的干扰等.本节针对交叉口无干扰条件下右转车辆轨迹进行建模,因此不考虑行人和非机动车的影响,仅将交叉口几何条件以及车辆速度作为右转轨迹的影响因素,以星湖街-苏虹中路北进口道右转车辆为例,统计调查时段内车辆在进口道停止线的车辆速度,并根据车辆对出口道的选择情况对速度进行分类,统计结果如表 4所示,表中v为统计车辆通过进口道停止线的平均速度,εv为车辆通过进口道停止线速度均值的方差,参照图 1,对出口道由外向内依次编号,例如: 1-1表示右转车辆由最外侧出口道驶出.
| 表 4 进口道停止线车辆速度统计表 Table 4 Vehicle speed at stop line of entrance lane |
由表可知,当车辆进入交叉口速度较大时,更易选择靠内侧出口道,大半径转弯通过交叉口.接下来将重点讨论交叉口几何条件对转弯车辆轨迹的影响.参照图 1,交叉口几何条件主要包括交叉口转角、转弯半径、出口道数目等.利用SPSS软件对转角θ、转弯半径R、距离l和距离C进行相关分析,分析结果如表 5所示.从表中可以看出变量C与变量R之间存在较为显著的相关关系,然而这并不能代表两变量之间的真实相关关系,因此需要控制其他变量的线性影响,进行偏相关分析,分析得到的偏相关系数可以反应2个变量间净相关的强弱程度,分析结果如表 6所示.C与R、θ的偏相关系数较大,且T值得显著性水平为0,说明距离C受转角θ的制约,且与半径R存在很强的正相关关系,因此排除因素C,进一步分析对θ、l、R对轨迹的影响.
| 表 5 变量间相关系数表 Table 5 Variable Correlations coefficients |
| 表 6 偏相关系数表 Table 6 Partial Correlations coefficients |
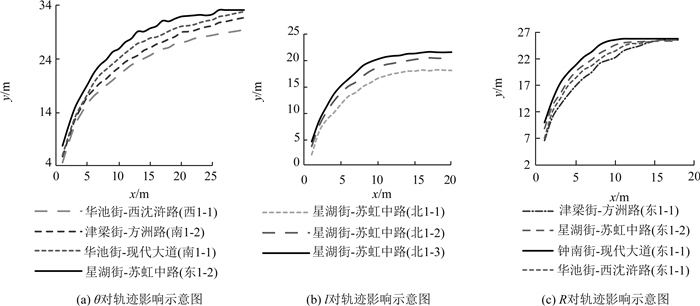
选择3组调查地点,分别在θ、l和R方面存在较大差异,其他几何条件差异不大,调查时段为6个工作日8 : 00-9 : 00,分别计算调查时段内右转车辆的平均轨迹.如图 9(a)所示,当其他几何条件相近时,转角更大的右转车辆的转弯轨迹在相同横坐标下纵坐标更大;如图 9(b)所示,当其他几何条件相近时,l值越大右转车辆的转弯轨迹在相同横坐标下纵坐标越大;如图 9(c)所示,当其他几何条件相近时,R值越大右转车辆的转弯轨迹在相同横坐标下纵坐标越小.由上述关系可知,转弯轨迹受θ值、l值和R值的影响.
|
图 9 几何参数对轨迹影响示意图 Fig. 9 Influence of characteristics on average trajectories |
综上所述,确定影响右转车辆转弯轨迹的因素为车辆速度v、θ、l、R.
3.2 平均轨迹模型建立通过3.1节分析可知,可以通过计算平均轨迹对同一出口道和进口道右转车辆的运行特性进行分析.由图 7可知,右转车辆在转弯过程中速度会出现先减小后增大的趋势,因此选择二次函数对车辆转弯过程中的速度的变化趋势进行拟合,如式(2)所示,拟合结果r2值均大于0.75.
| $ y = {f_1}\left( v \right) = {a_1}{v^2} + {a_2}v + {a_3}. $ | (2) |
式中: a1、a2、a3分别为变量的系数值.
由图 8可知,转弯车辆坐标关系可以用对数函数或二次函数表示.
通过以上分析,分别选取复合函数和二次多项式对平均轨迹进行拟合,基本函数为式(3)、(4).对比拟合结果r2值.0.9以上的占73.7%,略小于二次多项式的80.3%,但复合函数引入4个模型参数,而二次多项式引入5个模型参数.统计分析中,当参数过多时,计算工作量加大,计算误差累计也随之增大,估计出的模型精度不高.因此选择复合函数(3)作为模型基本公式,利用Matlab软件,通过对数值结果的拟合和回归分析,得到复合函数回归方程,依据32组平均轨迹数据,拟合得到32组a值、b值、c值和d值.
| $ y = a + b\ln x + c{v^2} + dv. $ | (3) |
| $ y = {a_1} + {b_1}{x^2} + {c_1}x + {d_1}{v^2} + ev. $ | (4) |
式中: a、b、c、d、a1、b1、c1、d1、e均为变量系数.
3.3 参数回归模型建立通过以上分析,选取交叉口θ,l,半径R作为回归分析模型的自变量,平均轨迹模型参数a, b, c, d为回归模型的因变量.利用SPSS软件,采用不同回归模型分别对平均轨迹模型参数进行回归,对比拟合效果,选择最优模型,以模型参数a为例介绍具体分析过程,其中y=a, x1=R', x2=l, x3=θ.建模过程如下:
1) 线性回归
首先做线性回归,得回归方程为
| $ y = - 0.684 - 0.312{x_1} + 2.831{x_2} + 5.799{x_3}. $ | (5) |
回归方程F检验的r2=0.315.
2) 二次多项式回归
回归方程的具体形式为
| $ \begin{array}{l} \hat y = {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2} + {\beta _3}{x_3} + {\beta _{11}}x_1^2 + {\beta _{22}}x_2^2 + {\beta _{33}}x_3^2 + \\ {\beta _{12}}{x_1}{x_2} + {\beta _{13}}{x_1}{x_3} + {\beta _{23}}{x_2}{x_3} + \varepsilon . \end{array} $ | (6) |
式中: β1、β2、β3、β4、β11、β12、β13、β23、ε均为变量系数.
对此回归方程按下面的方式做变量替换,转化为y对9个自变量的线性回归,使用逐步回归逐个引入变量,输出结果表包括模型汇总表、方差分析表、回归系数表和剔除变量表,从输出的结果表中看到,逐步回归共进行了8步,剔除变量如下:
x1, x11, x22, x33.
结合调整r2和P值,最终确定回归模型如下,其中r2=0.879:
| $ {x_{11}} = x_1^2,{x_{22}} = x_2^2,{x_{33}} = x_3^2,{x_{12}} = {x_1}{x_2}, $ |
| $ {x_{13}} = {x_1}{x_3},{x_{23}} = {x_2}{x_3}. $ |
| $ \begin{array}{l} y = - 2.831 + 3.943{x_1} - 30.412{x_2} - \\ 0.291{x_1}{x_2} - 2.354{x_1}{x_3} + 24.12{x_2}{x_3}. \end{array} $ | (7) |
3) 对数函数回归
| $ y = a\ln {x_1} + b\ln {x_2} + c\ln {x_3} + d. $ | (8) |
利用变量替换,x1=ln x1, x2=ln x2, x3=ln x3,将非线性回归转化为线性回归,得到最优模型,如公式(9)所示,r2为0.158.
| $ a = 1.743 - 3.459\ln R' + 5.48\ln l + 5.589\ln \theta . $ | (9) |
4) 指数函数回归
| $ y = a\exp \left( {{x_1}} \right) + b\exp \left( {{x_2}} \right) + c\exp \left( {{x_3}} \right) + d. $ | (10) |
利用变量替换,x1=exp (x1), x2=exp (x2), x3=exp (x3),将非线性回归转化为线性回归,得到最优模型,如公式(11)所示,r2=0.152.
| $ \begin{array}{l} a = 17.04 - 1.179\exp \left( {R - 14} \right) + 9.321\exp \left( {l - 13} \right)\\ - 1.562\exp \left( \theta \right). \end{array} $ | (11) |
通过以上分析,选取二次多项式回归模型作为模型参数a与影响参数关系模型,利用同样方法,计算其他模型参数回归模型,结合平均轨迹模型,最终确立信号控制交叉口无行人和非机动车干扰情况下的右转车辆轨迹模型如下:
| $ y = a + b\ln x + c{v^2} + dv. $ | (12) |
| $ \begin{array}{l} a = - 2.813 + 3.943R - 30.412l - \\ \;\;\;\;\;0.291Rl - 2.354R\theta + 24.12l\theta . \end{array} $ | (13) |
| $ \begin{array}{l} b = - 52.149 + 4.312R - 27.12l - \\ \;\;\;\;\;2.03Rl + 30.45l\theta . \end{array} $ | (14) |
| $ c = 3.748 - 5.236\theta + 1.841{\theta ^2} + 0.312l. $ | (15) |
| $ \begin{array}{l} d = 3.999 + 8.407R - 60.21l + 0.03{R^2} + \\ \;\;\;\;\;\;4.121{l^2} - 0.854Rl - 4.793R\theta + 41.22\theta l. \end{array} $ | (16) |
选取金鸡湖大道-星波街交叉口南进口作为验证地点,调查时间为15 : 00-16 : 00,该交叉口为两主干路相交,四相位控制,进口道设有一个右转专用车道,几何尺寸如下: θ=1.585 3 rad, l=1.75 m, R'=12.21 m.
对该地点真实车辆轨迹坐标及速度值进行调查,利用调查得到的不同横坐标下对应的速度值计算模型纵坐标,同时利用Asano[13]中提到轨迹分布计算方法,针对调查交叉口计算平均轨迹.分别计算2种方法得到的轨迹与实际轨迹同一横坐标下纵坐标值的相对误差σ,对比结果及误差结果如图 10所示,利用本文模型计算的轨迹坐标点与实际值的最大相对误差为8.18%,最小相对误差为0.15%,平均相对误差为2.14%,M.Asano模型[5]计算的平均相对误差为7.45%,本文模型与之相比误差更小,且在可接受范围内,因此该模型对无行人和非机动干扰条件下右转机动车轨迹的预测具有一定的可靠性.

|
图 10 轨迹计算值与实际值对比及误差分析 Fig. 10 Comparison between calculated and actual value |
为建立右转机动车受非机动车干扰时轨迹模型,本节以第2节数据为基础,利用聚类分析法分析右转车辆受干扰时轨迹穿越位置分布特性.四相位信号控制交叉口右转车与非机动车的干扰主要为同向非机动车的干扰和侧向非机动车的干扰,且2种干扰不会同时发生,因此分别对2种干扰情况的轨迹穿越位置进行聚类,通过聚类可以将右转车辆轨迹穿越位置划分为不同类别,每个类别的右转车辆轨迹符合相似特性[14].
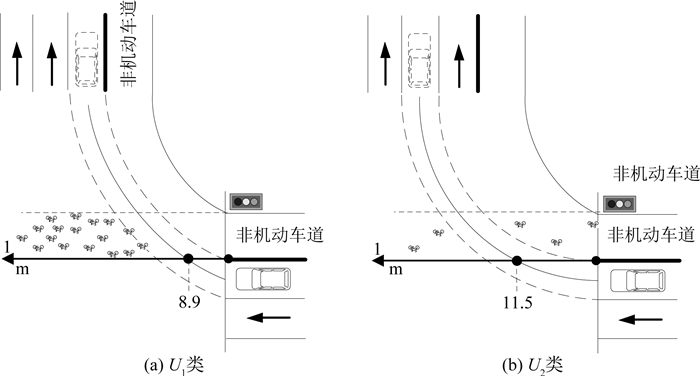
参照表 2,对a1样本右转车辆在截面1的穿越位置进行聚类,利用SPSS软件将数据划分为2类U1和U2,参照如图 11所示,得到如下结论:
|
图 11 受同向非机动车干扰时右转车辆2类轨迹 Fig. 11 Two right-turning maneuvers affected by same direction bicycles |
(1) U1类中心为8.9 m,该类右转车辆穿越位置更靠近原点,表示同方向直行相位绿灯启亮后,非机动车群以饱和流率驶出,非机动车的启动速度与机动车相比更快,且非机动车常常在黄灯启亮时抢占冲突区,绿灯初期非机动车群间隙很小,右转车辆常常难以穿越,为尽快通过交叉口,选择提前转弯.
(2) U2类中心为11.5 m,在成群非机动车释放完毕后,非机动车陆续驶出,成群现象有所减弱,该类右转机动车寻求可接受间隙实现转弯.
同理,受侧向非机动车干扰时右转车辆轨迹穿越位置分为2类U3和U4,参照如图 12所示,得到如下结论:
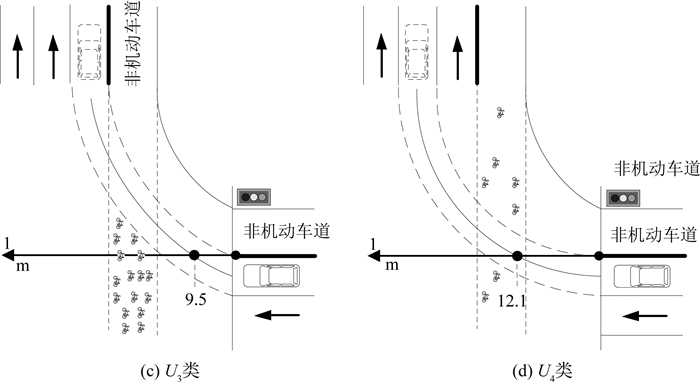
|
图 12 受侧向非机动车干扰时右转车辆2类轨迹分布 Fig. 12 Two right-turning maneuvers affected by side direction bicycles |
(1) U3类中心为9.5 m,侧向进口道绿灯初期释放的成群非机动车到达冲突区,右转机动车为尽快通过交叉口,常常压缩转弯路径,实现转弯,因此穿越位置更靠近原点.
(2) U4类中心为12.1 m,绿灯末期,非机动车陆续驶出,成群现象有所减弱,右转机动车寻求可接受间隙实现转弯.
通过聚类分析可知,有干扰条件下轨迹除受交叉口几何条件、车辆速度的影响,也与右转车辆与非机动车的冲突有关,其中冲突主要包括与同向非机动车的冲突和侧向非机动车的冲突2种,且四相位控制交叉口二者不会同时发生,机非冲突会使转弯车辆轨迹发生变化,因此机非冲突是影响右转轨迹的重要因素.
机非冲突数以机动车与非机动车的到达率为基础,结合冲突特性,是判别机非冲突严重性的重要指标.本文选择该指标将机非冲突对转弯轨迹的影响进行量化,以星明街-现代大道西进口为研究对象,分析同向非机动车干扰对右转轨迹的影响,将同相干扰的机非冲突数M划分为3组,如表 7所示,统计不同组之前轨迹差异,如图 13所示,由图可知同相干扰时机非冲突数越大,平均轨迹在相同横坐标下的纵坐标值越小.同理,分析侧向非机动车对平均轨迹的影响,得到相似结论.
| 表 7 基本信息表 Table 7 Basic information about the intersection |
|
图 13 不同机非冲突影响情况下轨迹分布示意图 Fig. 13 Trajectories of vehicles at different conflict number |
因此最终确定,将V、θ、l、R、N作为有干扰条件下右转车辆轨迹模型的影响因素.对有干扰条件下4个交叉口16个进口道的右转轨迹进行统计,以周期为单位,每处地点统计12个周期,分别计算每个周期的小时机非冲突数和平均轨迹,由于受干扰的右转车辆不一定同时受到同向和侧向非机动车的较大干扰,对小时机非冲突数小于10的干扰时期下的平均轨迹进行剔除,共得到168组轨迹数据,其中受同向非机动车干扰下的平均轨迹69组,受侧向非机动车干扰下的平均轨迹99组.
4.2 模型建立由4.1节分析可知,有干扰条件下右转轨迹除受交叉口几何条件、车辆速度的影响,也与机非冲突数有关,接下来将结合无干扰条件轨迹建模思想对有干扰条件右转车辆平均轨迹进行建模.
通过采集得到车辆转弯轨迹坐标以及速度等数据,结合图 13可知,轨迹纵坐标与横坐标的关系为二次函数或对数函数,且车辆在转弯过程中的速度虽与无干扰条件相比有所不同.但也呈现先减小后增大的变化趋势,因此仍然选择复合函数和二次函数对168组平均轨迹进行拟合,最终选择拟合结果更好的复合函数作为平均轨迹的基础函数,如公式(17)所示.
| $ y = a + b\ln x + c{v^2} + dv. $ | (17) |
分别选择受同向非机动车干扰与受侧向非机动车干扰的2组轨迹数据,以θ,l,N作为回归分析模型的自变量,平均轨迹模型参数a, b, c, d为回归模型的因变量,分别进行线性回归、二次多项式回归、其他复合函数回归,对比回归结果,选择最优函数.最终得到受同向非机动车干扰的右转车辆轨迹模型如下:
| $ y = a + b\ln x + c{v^2} + dv. $ | (18) |
| $ \begin{array}{l} a = 20.453 - 0.699RN - 5.131l + 2.24{R^2} + \\ \;\;\;\;\;\;1.314{l^2}. \end{array} $ | (19) |
| $ \begin{array}{l} b = 58.789 - 0.3472RN - 11.04l + \\ \;\;\;\;\;0.127{R^2} - 10.599{\theta ^2}. \end{array} $ | (20) |
| $ c = 0.0721 + 0.039R - 0.417lN + 0.023{R^2}. $ | (21) |
| $ \begin{array}{l} d = 153.9 - 1.623R - 208.2\theta - 1.325{R^2} + \\ \;\;\;\;\;\;59.98{\theta ^2} + 3.985R \times \theta . \end{array} $ | (22) |
受侧向非机动车干扰的右转车辆轨迹模型如下:
| $ y = a + b\ln x + c{v^2} + dv. $ | (23) |
| $ \begin{array}{l} a = 19.986 - 0.892RN - 6.141l + \\ \;\;\;\;\;\;2.27{R^2} + 1.213{l^3}. \end{array} $ | (24) |
| $ \begin{array}{l} b = 61.134 - 0.3997RN - 11.431l + \\ \;\;\;\;\;0.1354{R^2} - 11.58{\theta ^2}. \end{array} $ | (25) |
| $ c = 0.0923 + 0.086R - 0.412lN + 0.012{R^2}. $ | (26) |
| $ \begin{array}{l} d = 123.5 - 1.785R - 195.2\theta - 1.123{R^2} + \\ \;\;\;\;\;\;52.34{\theta ^2} + 2.546R\theta . \end{array} $ | (27) |
选择非机动车流量较大的星都街-苏惠路南进口作为有干扰条件轨迹模型的验证地点,该进口道右转车辆受到同向和侧向非机动车的干扰比较严重,调查时间为2016年9月,该交叉口为四相位控制,几何尺寸如下: θ=1.462 8 rad, l=1.75 m, R=19.22 m.
共统计34个信号周期,通过筛选,得到受同向非机动车干扰和受侧向非机动车干扰的平均轨迹各10条,利用模型代入参数计算平均轨迹,并与调查得到的轨迹数据进行对比,计算平均相对误差,结果如表 8所示,有干扰条件轨迹模型计算的轨迹与实际计算得到的平均轨迹的最大平均相对误差为7.31%,虽然与无干扰条件轨迹模型相比预测效果并不理想,然而,该模型可以反映右转车辆在受非机动车干扰时轨迹的集中情况,可以为对交叉口渠化、信号控制、右转机动车车与非机动车冲突分析等提供依据.
| 表 8 平均相对误差统计表 Table 8 Average relative error statistics |
以小时机非冲突数为依据对右转车辆有无机非干扰条件进行定量划分,在此基础上,对比分析了不同条件下右转车辆轨迹穿越位置分布.基于交叉口几何条件和车辆速度,建立了无干扰条件下信号交叉口右转机动车轨迹模型,运用实测数据对模型进行了参数标定和检验,并与其他模型进行对比,结果表明本文方法预测效果更好,平均相对误差为2.14%,满足精度要求.对有干扰条件轨迹穿越位置进行聚类,建立平均轨迹模型,并对轨迹模型进行验证,该模型可以反映右转车辆受非机动车干扰时轨迹分布情况,为右转机非冲突分析提供了直接依据.
| [1] |
STOVER V G. Issues relating to the geometric design of intersections[C]//Proceedings of the 8th International Conference in ACCESS Management. Baltimore. MD, USA: [s. n. ]. 2008. https://trid.trb.org/view/1247289
|
| [2] |
ALHAJYASEEN W K M, ASANO M, NAKAMURA H, et al. Stochastic approach for modeling the effects of intersection geometry on turning vehicle paths[J]. Transportation Research Part C:Emerging Technologies, 2013, 32: 179-192. DOI:10.1016/j.trc.2012.09.006 |
| [3] |
DECABOOTER P H., SOLBERG C E. Designated highway system truck operation study, "geometric considerations"[C]//Proceedings of the 67th Annual Meeting of the Transportation Research Board. Washington D C, USA: [s. n. ]. 1988. https://www.amazon.com/Designated-highway-system-truck-operation/dp/B000738YQM
|
| [4] |
REED M P. Intersection kinematics: a pilot study of driver turning behavior with application to pedestrian obscuration by A-pillars[R]. America, state of Michigan University of Michigan Transportation Research Institute, 2008. http://www.umtri.umich.edu/our-results/publications/intersection-kinematics-pilot-study-driver-turning-behavior-application
|
| [5] |
ASANO M, ALHAJYASEEN W K M, SUZUKI K, et al. Modeling variation in the trajectory of left-turning vehicles considering intersection Geometry[C]//Proceedings of the 90th Transportation Research Board Annual Meeting. Washington DC, USA: [s. n. ]. 2011.
|
| [6] |
关宏志, 陈艳艳, 刘小明. 基本路段机非混合交通流的解析模型[J]. 北京工业大学学报, 2001, 01: 12-15. GUAN Hong-zhi, CHEN Yan-yan, LIU Xiao-ming. An analysis model for mixed traffic flow on street[J]. Journal of Beijing Polytechnic University, 2001, 01. |
| [7] |
景春光, 曲大义, 梁春岩. 两相位交叉口机非冲突对机动车饱和流率的影响研究[J]. 公路交通科技, 2007, 8: 124-127. JING Chung-guang, QU Da-yi, LIANG Chun-yan. Research on effect of vehicle-bicycle conflict on vehicle saturation rate in two-phase intersection[J]. Journal of Highway & Transportation Research & Development, 2007, 8: 124-127. |
| [8] |
陈晓明. 混合交通条件下城市道路信号交叉口通行能力理论研究[D]. 北京交通大学, 2009. CHEN Xiao-ming. Theoretical research for capacity of signalized intersection on urban road network in mixed traffic condition[D]. Beijing: Beijing Jiaotong University, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1578646 |
| [9] |
王殿海, 梁春岩, 冯天军, 等. 混合交通下右转机动车信号配时方法[J]. 哈尔滨工业大学学报, 2009, 41(10): 251-254. WANG Dian-hai, LIANG Chun-yan, FENG Tian-jun, et al. Signal timing method of right-turn vehicles based on mixed traffic[J]. Journal of Harbin Institute of Technology, 2009, 41(10): 251-254. DOI:10.3321/j.issn:0367-6234.2009.10.056 |
| [10] |
江晟, 王殿海, 曲昭伟, 等. 交叉口机动车运动轨迹特征提取与标定[J]. 西南交通大学学报, 2012, 47(5): 784-789. JIANG Sheng, WANG Dian-hai, QU Zhao-wei, et al. Extraction and calibration of trajectory characteristics of vehicles at intersections[J]. Journal of Southwest Jiaotong University, 2012, 47(5): 784-789. |
| [11] |
胡鲜朝. 信号交叉右转机非冲突机理研究及应用[D]. 北京: 北京交通大学, 2011. HU Xian-chao. Research on the theory and application of conflict between right-turning vehicles and bicycles at signalized intersection[D]. Beijing: Beijing Jiaotong University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10004-1011102966.htm |
| [12] |
RÄSÄNEN M, KOIVISTO I, SUMMALA H. Car driver and bicyclist behavior at bicycle crossings under different Priority Regulations[J]. Journal of Safety Research, 1999, 30(1): 67-77. DOI:10.1016/S0022-4375(98)00062-0 |
| [13] |
WOLFERMANN A, ALHAJYASEEN W K M, NAKAMURA H. Modeling speed profiles of turning vehicles at signalized intersections[C]//3rd International Conference on Road Safety and Simulation. Indianapolis: Transportation Research Board TRB, 2011. https://trid.trb.org/view.aspx?id=1290448
|
| [14] |
ROUSSEEUW P J. Silhouettes:A graphical aid to the interpretation and validation of cluster analysis[J]. Journal of Computational & Applied Mathematics, 1987, 20(20): 53-65. |



 ,
曹宁博,
邓晓磊,
汪昆维
,
曹宁博,
邓晓磊,
汪昆维