2. 清华大学 水沙科学与水利水电工程国家重点实验室, 北京 100084
2. State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China
我国素来是水沙灾害十分严重的国家,如何治理水沙灾害是几十年来水利工作者和地理学家面临的一个十分重大且棘手的问题[1-2].黄河是中国最重要的河流,素以水沙灾害严重闻名.本文基于黄河泥沙数据讨论多频声学测沙技术的频率优选问题[2].
常用的悬移质泥沙浓度和粒径测量技术有传统采样测量技术、光学测量技术、声学测量技术[3-4].传统采样技术无法获得实时的,连续的剖面测量数据.基于光学的测量方法对于点的泥沙数据测量十分可靠,但是能够获得剖面数据.基于声学反向散射原理的悬移质泥沙测量技术具有实时无侵入,高时空分辨率,低成本和剖面测量等特点,近年来被广泛关注,并被认为是最有潜力的河流泥沙浓度与粒径实时数据获取手段[5].
声学测沙技术可以分为单频和多频声学测沙技术[6].单频声学测沙技术假设测量水体的悬沙粒径均值已知,且测量水体的悬沙粒径剖面分布为均匀分布,通过接收所得声学回波电压剖面即可反演获得悬沙浓度剖面.多频声学测沙技术同时使用多个频率的声波进行测量,假设测量水体悬沙粒径剖面的分布类型已知(如对数正态分布),通过将各个频率测量的数据联立从而估计出泥沙粒径均值,继而计算出泥沙浓度.较单频的声学测沙技术,多频声学测沙技术的假设更加符合实际泥沙状况,且可以同时测量得到泥沙粒径和浓度剖面,测量误差较小.
国外的声学测沙技术研究始于上世纪40年代[7].上世纪80年代起,声学测沙技术取得了较大的发展.Hay[7]通过一系列的单频测量实验证明了悬移质泥沙浓度声学测量方法的可行性,开启了对这项技术的系统性研究.1992年,Hay等[8]使用1,2.25,5 MHz这3个声波频率实现了多频测沙技术,利用能量比算法同时反演出了浓度和粒径剖面.1993年Crawford等[9]利用差值算法,1997年Jan Schat[10]使用最近临算法均实现了多频测沙技术对浓度和粒径剖面的同时测量.1996年至2002年,Thorne等[6, 11-12]通过对一系列的实验数据分析得出了对于非黏性沙声学测量的经典公式,如公式(1).2011年,Hurther等[13]使用多频声学测沙技术对河床边界层的泥沙输运过程进行研究.2012年,Moate等[14]研究了当悬浮泥沙具有不同矿物组成成分时多频声学测沙技术的性能.
相比国外,国内在声学测沙技术方面的研究比较迟滞.1996年中科院东海观测站张叔英等[15-16]研制出声学悬浮泥沙观测系统(Acoustic suspended sediments observing, system ASSM-Ⅱ)型,在长江口等地实际测量误差为20%~50%.之后,国内学者大多利用商用声学多普勒流速仪(Acoustic Doppler current proficer, ADCP)来进行悬移质泥沙浓度剖面测量.1999年,汪亚平等[17]利用300kHz ADCP在胶州湾等海域进行了走航式断面观测.2009年,基于虎门洪季大潮期间的水流泥沙观测资料, 尹小玲等[18]通过校正ADCP回波信号和拟合分析悬移质泥沙浓度,得到虎门深槽C站悬移质泥沙浓度的估测式.总体而言,现阶段中国对于声学测沙技术的研究大多应用单频测量技术,缺乏对于多频悬移质泥沙反演算法的理论探究和仿真实现,研究相对国外滞后.本文分析多频测沙原理,并基于中国河流数据进行仿真,探讨该技术应用于中国河流的可行性.计算得出不同河流状况下的优选测量频率,为国内声学测沙技术的研究和实际使用提供参考.
1 声学测沙原理声学测沙技术使用发射换能器发射声脉冲信号照射水体, 接收换能器记录悬移质泥沙散射的回波信号.接收信号中携带了悬移质泥沙的粒径和浓度等物理特征, 通过声学反演算法可以从中获取浓度和粒径等相关物理参数.
1.1 基本方程式(1)为Thorne等[6]提出的经典公式,直观地描述了悬移质泥沙浓度与声学信号回波强度的关系,已被国内外大量的实验室和野外实验所证实可以较准确的反演出悬移质泥沙浓度剖面[13, 19-20],本文假设该公式适用于所讨论的探测区域.
| $ {\rho _{\rm{B}}} = {\left( {\frac{{{V_{{\rm{rms}}}}\psi r}}{{{k_{\rm{t}}}{k_{\rm{s}}}}}} \right)^2}\exp \left( {4r\left( {{a_{\rm{w}}} + {a_{\rm{s}}}} \right)} \right). $ | (1) |
式中:ρB为悬浮泥沙浓度;Vrms为测量仪器接收等效电压幅值;ψ为计算泥沙散射时实际泥沙颗粒对理想球面偏离程度的修正因子;r为探测器距离散射粒子团的距离;kt为测量系统参数,与声波换能器灵敏度等参数有关;ks为测量环境参数,与泥沙密度,悬浮泥沙粒径分布等有关;as为粒子散射衰减系数;aw为水固有吸收衰减系数.其中[5],
| $ {k_{\rm{s}}} = \frac{{F\left( {{x_0}} \right)}}{{\sqrt {{a_0}} }}. $ | (2) |
| $ {a_0} = \int_0^\infty {an\left( a \right){\rm{d}}a} . $ | (3) |
| $ F\left( {{x_0}} \right) = {\left[ {\frac{{\int_0^\infty {an\left( a \right){\rm{d}}a} \int_0^\infty {{a^2}{{\left( {\frac{{{f_i}}}{{\sqrt {{\rho _0}} }}} \right)}^2}n\left( a \right){\rm{d}}a} }}{{\int_0^\infty {{a^3}n\left( a \right){\rm{d}}a} }}} \right]^{1/2}}. $ | (4) |
| $ \begin{array}{*{20}{c}} {\frac{{{f_i}}}{{\sqrt {{\rho _0}} }} = \frac{{{x^2}\left( {1 + 0.6\exp \left( { - {{\left( {\left( {x - 2.9} \right)/1.15} \right)}^2}} \right)} \right)}}{{42 + 25{x^2}}} \times }\\ {\left( {1 - 0.25\exp \left( { - {{\left( {\left( {x - 1.5} \right)/0.35} \right)}^2}} \right)} \right).} \end{array} $ | (5) |
| $ {a_{\rm{s}}} = \int_0^r {\xi {\rho _{\rm{B}}}{\rm{d}}r} . $ | (6) |
| $ \xi = \frac{{3\chi \left( {{x_0}} \right)}}{{4{a_0}}}. $ | (7) |
| $ \chi \left( {{x_0}} \right) = \frac{{\int_0^\infty {an\left( a \right){\rm{d}}a} \int_0^\infty {{a^2}\left( {{\chi _i}/{\rho _0}} \right)n\left( a \right){\rm{d}}a} }}{{\int_0^\infty {{a^3}n\left( a \right){\rm{d}}a} }}. $ | (8) |
| $ {\chi _i}/{\rho _0} = \frac{{0.09{x^4}}}{{1380 + 560{x^2} + 150{x^4}}}. $ | (9) |
| $ x = \frac{{2{\rm{ \mathsf{ π} }}f}}{c}a\left( {{x_0} = \frac{{2{\rm{ \mathsf{ π} }}f}}{c}{a_0}} \right). $ | (10) |
式中:F为泥沙粒子团平均反向散射函数,表示具有某种粒径分布的泥沙粒子团对于探测声波的总体反向散射能力, fi为粒子声波反向散射耦合函数.χ为粒子团平均散射衰减函数,表示具有某种粒径分布的泥沙粒子团对于探测声波的散射衰减能力, ξ为粒子声波衰减耦合函数.a为单个泥沙粒子的粒径,a0为泥沙粒子团的平均粒径,n(a)以a0为粒径均值的对数正态分布,ρ0为泥沙密度,c为水中声速.F和χ均为无量纲参数,与泥沙粒子团的粒径分布n(a),粒径均值a0和探测频率f有关.科学家们做了大量实验来对F,χ进行测量 ,本文采用的是Thorne等[5]提出的F和χ参数模型,该模型能较好的拟合目前发表的大部分实验结果[5, 19].
值得指出的是,as与测量距离和泥沙浓度有关.当as很小时,回波电压平方与悬沙浓度成正比.对于50 cm的测量距离,浓度大于5 kg/m3时,由于泥沙粒子造成的声学衰减as开始变得显著[8].根据公式(6),该衰减与浓度的积分项相关,求解方程变成隐性方程.并且此时声波在泥沙粒子间更可能发生多次反射,而基于声波单次反射提出的F与χ公式将产生很大误差.这些因素都会导致在泥沙浓度增高时,测量难度的增高.Thorne等[5]提出,在悬沙浓度大于40 kg/m3,由于声波在粒子间多次反射严重,基于方程(1)的声学测沙技术将不再适用.即使如此,声学测沙技术的浓度测量范围依然远大于光学测沙技术,具有很高的研究价值[22].在目标测量距离为50 cm时,对于泥沙浓度大于5 kg/m3的水流对于声学测量即为高含沙水流.黄河的泥沙浓度一般超过这个值,而汛期更是可超过100 kg/m3,在中国类似黄河的河流都可视为声学高含沙水流.
1.2 多频反演算法能量比算法是一种应用最广泛的多频反演算法,其求解过程是:使用2组测量频率i,j进行测量,文中带有下标i,j的各物理量均为使用频率i,j进行测量所得前文已解释的对应物理量.将量测数据代入方程(1),根据假设,有ρBi=ρBj,将2组方程作比联立,可求解得到浓度和粒径.如式(11).
| $ \frac{{{\rho _{{\rm{B}}i}}}}{{{\rho _{{\rm{B}}j}}}} = \frac{{{{\left( {{{\left( {\frac{{{V_{{\rm{rms}}}}\psi r}}{{{k_{\rm{t}}}{k_{\rm{s}}}}}} \right)}^2}\exp \left( {4r\left( {{a_{\rm{w}}} + {a_{\rm{s}}}} \right)} \right)} \right)}_i}}}{{{{\left( {{{\left( {\frac{{{V_{{\rm{rms}}}}\psi r}}{{{k_{\rm{t}}}{k_{\rm{s}}}}}} \right)}^2}\exp \left( {4r\left( {{a_{\rm{w}}} + {a_{\rm{s}}}} \right)} \right)} \right)}_j}}} = 1. $ | (11) |
进行移项,可以得到
| $ \begin{array}{l} \frac{{{V_j}{k_{tj}}}}{{{V_j}{k_{ti}}}}\exp \left( {2r\left( {{a_{{\rm{w}}i}} - {a_{{\rm{w}}j}}} \right)} \right) \cdot \exp \left( {2r\left( {{a_{{\rm{s}}i}} - {a_{{\rm{s}}j}}} \right)} \right) = \\ \;\;\;\;\;\frac{{{k_{{\rm{s}}i}}}}{{{k_{{\rm{s}}j}}}} = \frac{{{F_i}\left( {{x_0}} \right)}}{{{F_j}\left( {{x_0}} \right)}} = \frac{{{F_i}\left( {{a_0}} \right)}}{{{F_j}\left( {{a_0}} \right)}} = {F_{ij}}\left( {{a_0}} \right). \end{array} $ | (12) |
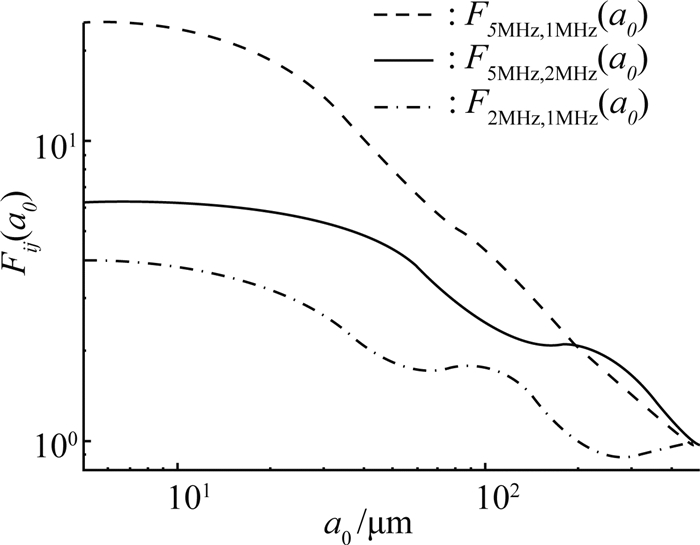
F(a0)可由公式(4)所得,假设悬浮泥沙粒径分布类型符合已知的某个典型分布,如对数正态分布,且其方差为与平均粒径相关的某典型值,如0.4a0[19, 23].则由公式(4)、(12)可以计算得到如图 1所示的关于悬沙平均粒径的函数.公式(12)中Fij(a0)称作能量比值函数,图 1中F51,F52,F21则为i, j分别取5,2,1 MHz中的2个频率时计算出的Fij(a0).若悬移质泥沙浓度较低,粒子散射衰减as可以忽略[5],等式(12)左边的值均为已知或可探测,则可以计算出每一组Fij(a0),根据图 1可反演出对应的平均半径a0.
|
图 1 不同频率比对应的能量比值函数随粒径变化图 Fig. 1 Energy ratio function versus particle size with different frequency ratio |
但在声学高含沙水流中,粒子散射衰减as往往不可忽略,根据式(6),某一个测量点的as的计算是关于声波换能器至该点的路径上的所有测量点的悬移质泥沙浓度和ξ乘积的积分.为了实现浓度计算,将测量区域分层,逐层计算as,a0和ρB这3个参数,逐层迭代算法简要步骤如下.
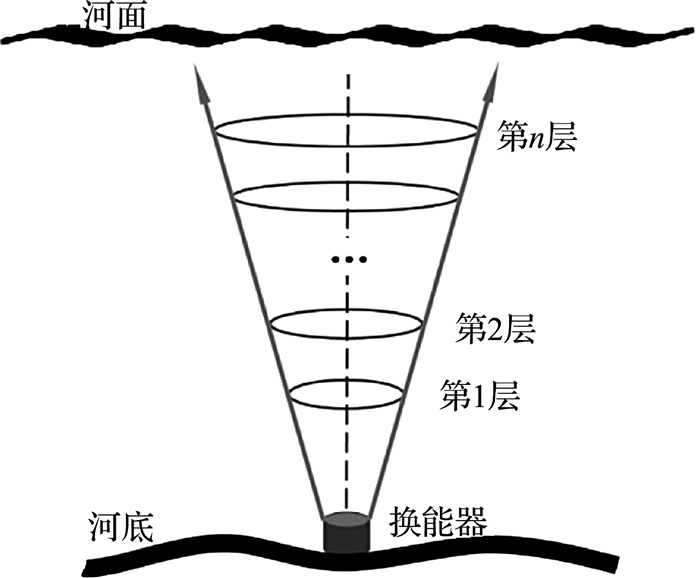
1) 如图 2所示,将测量水体分为n层(每层之间的空间距离对应空间分辨率).
|
图 2 测量区域分层示意图 Fig. 2 Diagram for layered measurement area |
2) 对于第1层,首先令粒子散射衰减初始值as10=0(1代表第1层,0代表初次迭代).使用上述能量比算法可以计算出时的该层的浓度迭代初始值ρB10,粒径初始值a010.将结果代入公式(6),可以求得粒子散射衰减计算值as11.
3) 将计算出的as11代入式(1)~(12),又可以计算出ρB11,a011.如此迭代,直到计算出的ρB,as,a0收敛,将其作为第1层的理想值.
4) 将第2层的粒子散射衰减初始值等于第1层(前1层)衰减的理想值,即as20=as1,重复步骤2, 3中的迭代过程,可计算的出第2层ρB,as,a0的理想值.
5) 对于第3层至第n层,重复步骤2、3、4, 可以计算得出每一层的理想值,进而得到剖面的浓度和粒径的计算理想值.
2 多频声学测沙仿真本节将基于河流悬移质泥沙浓度和粒径沿深度分布的典型剖面对多频声学测沙技术进行仿真和分析.悬沙浓度和粒径沿深度变化的剖面受波浪地形等不同因素影响,不同的河流情况下,悬沙浓度和粒径沿深度会有不同的分布.基于Thorne等[19]对不同波浪动力和泥沙粒径环境下的波浪状河床底部悬移质泥沙浓度和粒径的大量观测,以及文献的大量引用[13, 22],本节使用Rouse剖面仿真黄河靠近河床的泥沙浓度和粒径沿深度分布典型剖面.并且将Rouse剖面与均匀分布剖面的结果对比, 进行典型剖面敏感度分析.
2.1 仿真过程Rouse剖面描述悬沙浓度和粒径沿深度分布的公式如下:
| $ \overline {{\rho _{\rm{B}}}} \left( z \right) = \overline {{\rho _{{\rm{B}}r}}} \left( {\frac{z}{{{z_r}}}} \right) - p. $ | (13) |
| $ \bar a\left( z \right) = \overline {{a_r}} \left( {\frac{z}{{{z_r}}}} \right) - p. $ | (14) |
式中:z为距离河床高度,p为Rouse参数,p=ws/κu*,u*为摩阻流速,κ为冯卡曼常数,ws为粒子沉降速度,
在2.1.1,2.1.2两小节中,将使用2010年1月份头道拐水电站的实测数据来说明整个多频声学测沙仿真过程,包括回波电压计算仿真以及浓度粒径剖面反演仿真.仿真的目的在于找出某种泥沙条件下的优选测量频率区间.
仿真思想是,利用已知的典型浓度和粒径剖面正算出回波电压剖面,再根据回波电压剖面,通过能量比算法,反算出浓度和粒径剖面,将算出的剖面与原始的理想剖面对比,并进行频率和典型剖面敏感度分析.为了考察算法的抗噪功能,在算出的回波电压剖面中加入了20 dB高斯噪声,模拟实际测量环境的噪声影响.
2.1.1 回波电压计算根据《中国河流泥沙公报2010》和《河流悬移质泥沙测验规范GB/T50159-2015》等数据[24-26],对于2010年1月头道拐水电站,

|
图 3 头道拐水文站3个测量频率回波信号剖面 Fig. 3 Voltage profile of three measuring frequency, Toudaoguai |
|
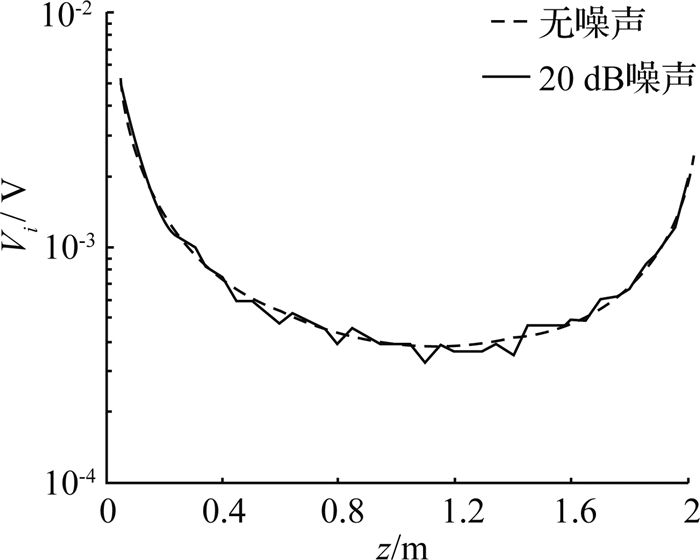
图 4 20 dB噪声下头道拐水文站1MHz回波信号剖面 Fig. 4 Voltage profile of 1MHz with 20 dB noise, Toudaoguai |
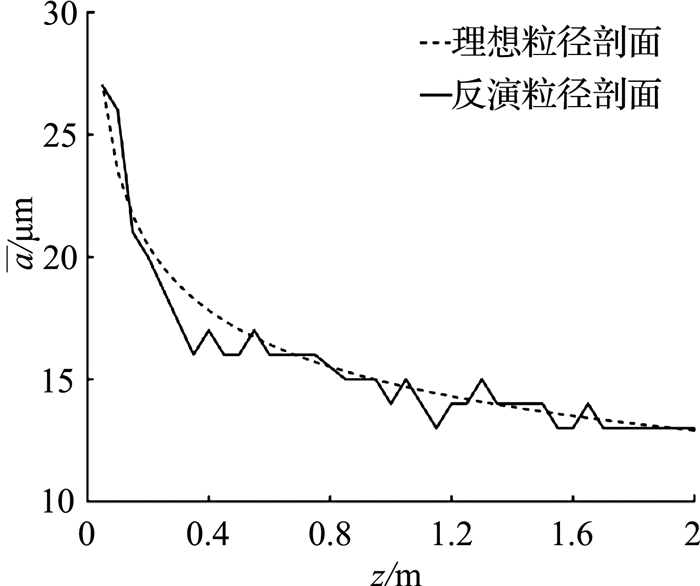
根据第2节中所介绍的能量比算法原理,可以反演计算出相应的浓度和粒径剖面,其中粒径剖面为1,2,4 MHz这3个频率共同反演得出,浓度剖面为基于粒径剖面利用2 MHz探测信号计算得出,如图 5、6实线所示.
|
图 5 理想粒径剖面与反演粒径剖面比较 Fig. 5 Comparison between ideal and calculated radius profile |

|
图 6 理想浓度剖面与反演浓度剖面比较 Fig. 6 Comparison between ideal and calculated concentration profile |
为了更直观地分析频率优选问题,将反演剖面与理想剖面对比,并对剖面平均的反演误差error进行量化,如公式(15),ρB0指理想的浓度剖面,ρB1反演所算出的浓度剖面.
| $ {\rm{error}} = \frac{{\left| {{\rho _{{\rm{B1}}}} - {\rho _{{\rm{B0}}}}} \right|}}{{{\rho _{{\rm{B0}}}}}}. $ | (15) |
根据式(15)可以计算出在20 dB的噪声情况下粒径剖面平均反演误差为3.1%,浓度剖面平均反演误差为7.1%.结果显示,在20 dB噪声的条件下,能量比反演算法对于2010年1月份头道拐水文站的泥沙数据可以实现比较精确的反演,具有可行性.
进行频率敏感度分析,将1,2,4 MHz对浓度的反演可以假设为中心频率f0为2 MHz的反演,于是对于在0.2到10 MHz间,以0.2 MHz为间隔的每个频率,都选取0.5f0,f0,1.5f0这3个频率进行浓度反演,计算出平均反演误差,将该误差作为反演中心频率为f0时的多频反演误差.
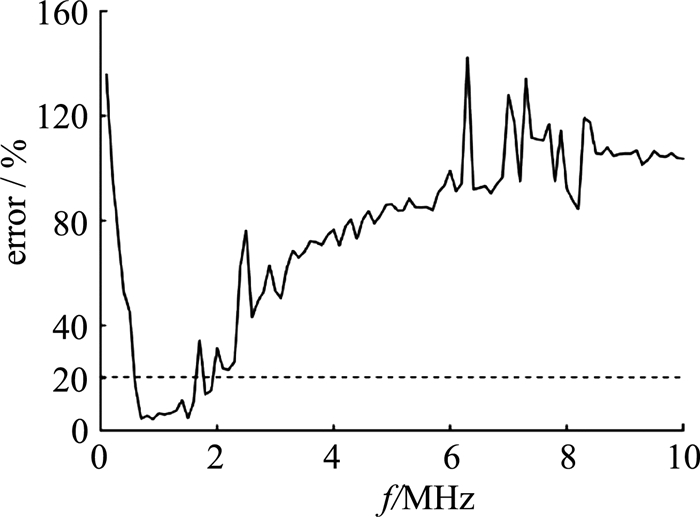
定义优选测量频率区间为,在20 dB的环境噪声中,满足20%的浓度剖面测量误差要求的频率区间.如图 7所示,对于头道拐水文站,优选频率区间为0.4~1.6 MHz.由图 7可知,不同测量频率的测量误差差异很大,对于头道拐水文站2010年1月泥沙数据,选择优选探测频率十分重要.若合理地选择测量频率,可以实现低误差测量.
|
图 7 Rouse分布时不同频率对应的浓度剖面反演误差 Fig. 7 Mean error for different measuring frequency in Rouse concentration profile |
在剖面平均悬沙浓度相同的情况下,不同的典型浓度剖面也会影响反演误差.同样基于2010年1月份头道拐水电站的泥沙数据,本小节将分析在剖面平均悬沙浓度与Rouse剖面的平均浓度相同的情况下,均匀分布的浓度剖面的反演误差与测量频率的关系.为了更好的对比,粒径分布依然使用Rouse剖面分布,结果如图 8所示.

|
图 8 均匀分布时不同频率对应的浓度剖面反演误差 Fig. 8 Mean error for different measuring frequency in homogeneous concentration suspension |
2个仿真的悬沙剖面平均浓度相同,对比图 7、8,可以得到以下几点结论.
1) 均匀分布的反演误差总体高于Rouse分布.这是因为Rouse浓度分布大部分剖面属于低浓度区间,在此区间内由于散射衰减很小,导致迭代计算时可以快速收敛,测量误差很低.
2) 2个仿真粒径分布相同,低误差频率区间也相近.这个现象反应了泥沙粒径与优选频率较强的关联性,将在第4节对此进行详细分析.
3) 通过典型剖面敏感度分析可得,分布剖面对于测量误差和优选频率的影响还是归因于泥沙浓度和粒径对测量误差和优选频率的影响.
3 声学测沙技术可行性分析 3.1 泥沙状况为了更好地研究声学高含沙水流中多频声学测沙技术的可行性和优选频率问题,本文选取了黄河作为代表,仿真分析其实测数据.如图 9所示中的浓度范围在本技术测量量程内,如图 10所示黄河的平均粒径主要在15 ~30 μm之间,而Hurther等[13, 19]的实验在泥沙粒径10 ~100 μm时均实现低误差测量,说明多频声学测沙对于黄河泥沙的粒径状况具有实用性.不过Thorne等[19]在文献中指出,对于测量泥沙浓度大于40 kg/m3的情况,由于声波多次反射,无法准确标定相关参数,将无法进行准确地声学泥沙测量.对于黄河的低浓度水流状况,该技术具有适用性.但是对于汛期出现的大于40 kg/m3的高浓度水流状况,多频声学测沙技术不再适用, 本文使用黄河平均泥沙浓度数据均未超过40 kg/m3.

|
图 9 黄河各水文站近60年平均含沙量 Fig. 9 Mean concentration in last 60 years of Yellow River |

|
图 10 黄河各水文站近60年平均中值粒径 Fig. 10 Mean radius in last 60 years of Yellow River |
黄河上、中、下游3个区段的水流携沙条件各不相同,对于声学测沙频率的要求也各不相同.本文选取了位于黄河上游的唐乃亥水文站,上游与中游交界处的头道拐水文站,中游的潼关水文站和龙门水文站,中游和下游交界处的花园口水文站和下游的利津水文站2010年之前近60年观测数据的泥沙浓度和粒径平均值,对于黄河各区段多频声学测沙方法的可行性及频率优选问题进行了分析.并基于2010年年内不同月份的泥沙数据,讨论了部分水文站年内不同月份的多频声学测沙技术的频率优选问题,以研究在汛期和非汛期优选测量频率的选取问题.
根据水利部颁发的《中国河流水沙公报2010》中黄河不同区段不同季节条件的悬移质泥沙浓度和中值粒径d50,基于住建部《河流悬移质泥沙测验规范GB/T50159-2015》, 可以计算出黄河不同区段不同季节条件的悬移质泥沙典型浓度和粒径剖面.假设悬移质泥沙粒径的时空分布符合对数正态分布,应用第2节中的分析方法,对于黄河不同区段,不同季节条件下的典型浓度和粒径剖面,在满足一定误差要求的条件下,可以得到与之对应的合适的测量频率区间.
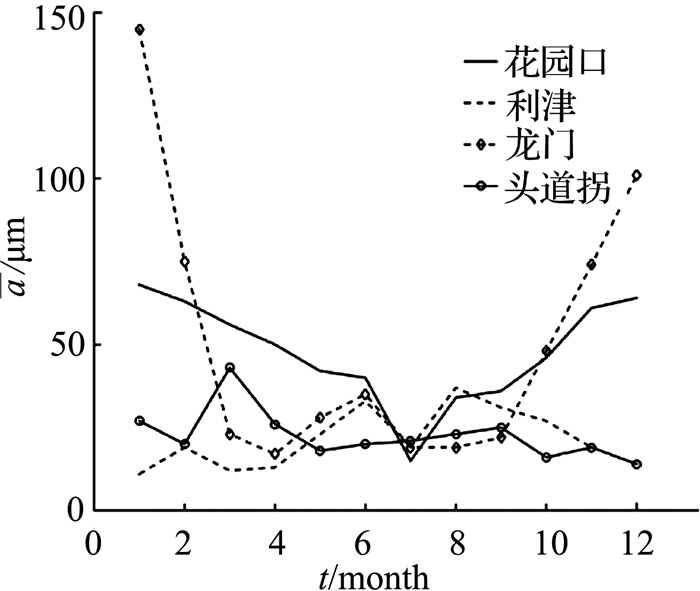
如图 9~12所示分别描述了黄河各站多年平均泥沙浓度和粒径变化以及2010年各月平均浓度及粒径变化, 其中ρBaver为多年平均含沙量,aaver为多年平均粒径,S1、S2、S3、S4、S5、S6分别表示唐乃亥,头道拐,潼关,龙门,花园口,利津水电站.由图 9、10可知,黄河不同区段的泥沙状况差距很大,若使用相同的测量频率对其测量,可能会引入较大的测量误差.由图 11、12可知,年内的泥沙含量于6、7、8、9这4个汛期月份达到高峰,其他月份较低.除了中游的龙门和花园口水文站,粒径总体上在年内的变化不大.由于年内泥沙浓度含量变化较大,若需要在汛期进行测量,需要考虑到高泥沙浓度对于高频段声波信号的衰减较大等问题,进行频率优选十分必要.

|
图 11 2010年黄河月平均泥沙浓度图 Fig. 11 Mean concentration per month of Yellow River |
|
图 12 2010年黄河月平均泥沙中值粒径图 Fig. 12 Mean Radius per month of Yellow River |
2.2小节中将测量误差小于20%的频率区间定义为优选频率区间,基于2.2节中的仿真分析方法,将黄河各水文站不同区段多年平均泥沙数据及2010年内不同月份的泥沙浓度ρB,粒径a0数据代入模型,进行仿真计算,验证多频声学技术在声学高含沙水流的中实现低误差测量的可行性,并计算出各个水文站的泥沙条件对应的优选频率fopti,结果如表 1、2所示.
| 表 1 20 dB噪声下黄河各站点年平均数据优选测量频率 Table 1 Optimum measuring frequency for Yellow river with 20 dB noise based on lasted 60 years' sediments data |
| 表 2 20 dB噪声下2010年各月黄河各站点优选测量频率 Table 2 Optimum measuring frequency for Yellow river with 20 dB noise based on sediments data in 2010 |
根据图 7可以得出,测量误差对于探测频率敏感性较大,合理地选取适合不同环境的探测频率,对于准确测量具有重要的意义.表 1和2的结果分别基于黄河的多年平均泥沙数据,和2010年内的各月份平均泥沙数据,对于研究不同区段,和年内各月份的声学测沙问题具有典型的代表性,在实际选取优选抗噪频率区间时,该结果具有参考意义.
4 误差分析及优选频率问题基于第3节分析,结合图 7的误差随频率变化图可得,优选测量频率一般为一个连续区间,对于泥沙粒径较大的测量环境,可能出现间隔不远的2个优选频率区间,而距离优选频率区间越远的频率,测量误差会越大.本节将基于误差分析,解释优选频率出现上述特征的原因,探讨优选频率的计算方法.
4.1 误差分析本小节主要任务是分析测量误差的影响因素和提出提高测量系统抗噪声能力的方法.在实际环境中测量时,由于系统噪声,环境噪声等原因,回波信号中会带有一定噪声.不同的探测信号会引入不同的噪声,但是因信号本身的受到测量环境的影响也不同,比如相比1 MHz的信号,5 MHz的信号的噪声更小,可是其衰减更大,回波信号更弱,信噪比不一定更好,于是如何量化噪声的影响是一个慎重的问题.综合考虑,本次仿真中以分贝的形式,在回波电压处加上噪声,这样可以统一噪声和环境衰减对于信号的影响.为了方便分析,将回波电压处加的噪声视为本次仿真中测量系统噪声的唯一噪声来源.在浓度和粒径反演时,此噪声会不断地累积,如果不对其进行一定的滤除,其会对于测量结果产生很大的影响.
通过仿真分析,对于最终浓度测量结果误差的来源主要有以下3个方面:
1) 因为实际测量时的各种噪声导致回波电压有误差(根本误差源).
2) 带有误差的回波电压会反演出带有误差的泥沙粒径,并计算出带有误差的浓度(初级误差).
3) 远端的粒子衰减as的计算需要用到近端的浓度,计算时使用逐层迭代的方法,又会导致误差会逐层累积(迭代误差).
4.2 声学低含沙水流频率优选问题4.1小节提到,最终测量误差的来源,主要包括3个方面的贡献,其中第2环节误差是初级误差,误差在此被第1次传递.若能从第2环节抑制初级误差的放大,对于提高系统的抗噪能力十分重要.本小节将从第2环节初级误差入手,讨论影响初级误差因素以及提高系统抗噪能力的方法.为此,假设探测泥沙剖面分布为均匀分布,并暂且先不考虑粒子散射衰减as的影响,依据1.2小节中的定义,此时的测量水流为声学低含沙水流.初级误差在通过式(12)反演粒径时由于电压端的噪声而首次引入,如果能使反演的粒径对于电压端的噪声不敏感,便可以提高系统抵抗初级误差的能力.
根据式(12),选取不同的测量频率比,设纵坐标为y,横坐标为x,如图 13所示,
| $ \Delta y = k \cdot \Delta x. $ | (16) |
式中:k为该处斜率,Δy为电压端噪声,Δx可以理解成该噪声在反演粒径时造成的初级误差,也是本节关注的误差.对于某一固定的Δy,如果能量比函数的斜率k越大时,其所传递造成的初级误差Δx越小.
基于上述分析,从图 13中可得以下结论:

|
图 13 不同测量频率的能量比值函数图 Fig. 13 Energy ratio function versus particle size for different frequency |
1) 图 13中所画的3个频率的能量比值函数图,当频率从低到高变化时,函数粒径较小侧移动,其斜率最大处所对应的粒径也由大到小变化.可解释大粒径适合低频率测量,而小粒径适合高频率测量的现象.
2) 对于某一固定粒径的环境,根据图 13,可以得出,频率很低或很高时,能量比值图在该粒径处的图像均是平的,斜率几乎为0.可解释图 7中,优选测量频率区间两侧,测量误差变大的现象.
3) 图 13中的频率比值函数拥有2个单调下降的大斜率区间,可解释表 2中某些情况下会出现间隔不远的两个优选测量频率区间的现象.
4) 实际测量时,可根据测量环境经验粒径范围,选择对应的在该粒径出的最大斜率的测量频率,可以最好地避免初级误差.
根据以上讨论,基于已发表文章[5],在声学低含沙水流中,如图 13所示,对于横坐标的某一个粒径,在该处最大斜率的能量比函数曲线对应的频率,为其克服初级误差的优选频率.
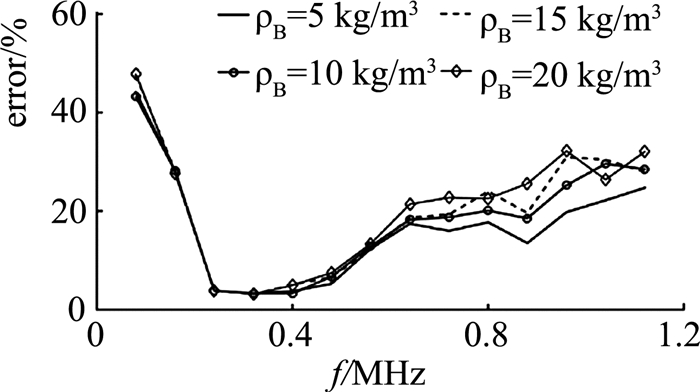
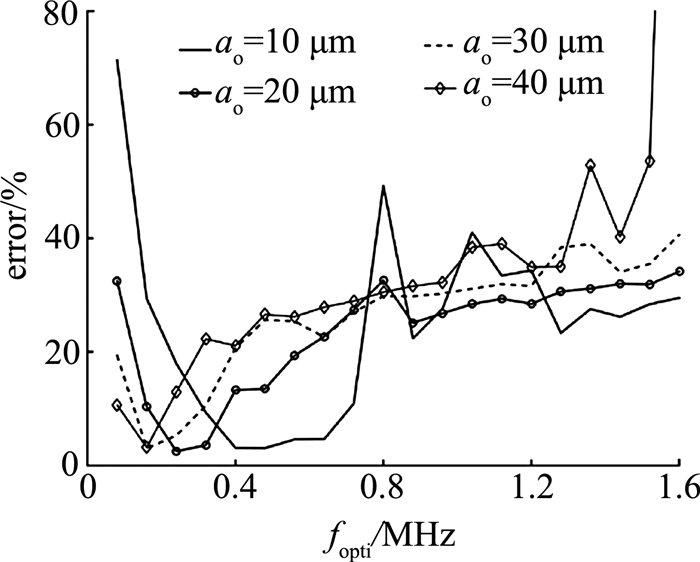
4.3 声学高含沙水流频率优选问题在声学高含沙水流中,受到粒子散射衰减as影响,频率优选问题会更加复杂.相对声学低含沙水流,声学高含沙水流的优选频率应该根据含沙浓度进行一定的修正,通过如图 14、15所示对于声学高含沙水流的频率优选问题进行分析.
|
图 14 当a0=20 μm时不同浓度的误差随频率变化图 Fig. 14 Error curve versus frequency in the condition of different concentration and same radius (20 μm) |
|
图 15 当ρB=10 kg/m3时不同粒径误差随频率变化图 Fig. 15 Error curve versus frequency in condition of different radius and same concentration (10 kilogram per cubic meter) |
图 14描绘了当粒径相同时,不同浓度对应的误差曲线,图 15描述了当浓度相同时,不同粒径对应的误差曲线.由图 14中可以看出1)浓度增加对于低频区段测量误差的影响低于高频区段.2)浓度越高,测量误差整体变大,但对优选频率区间影响不大.
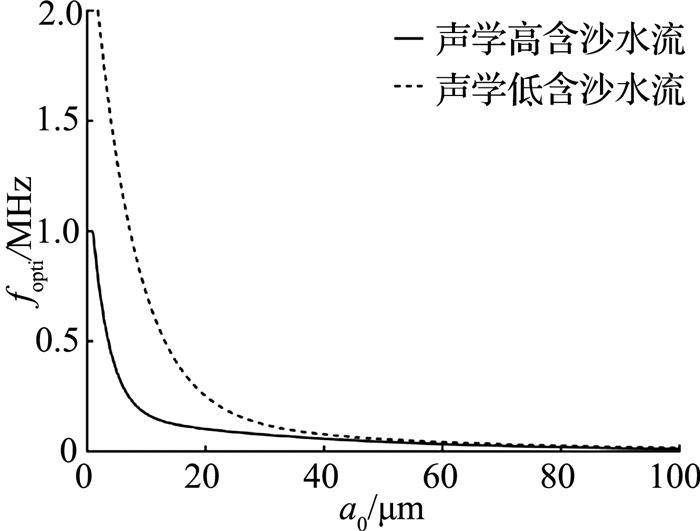
这是由于高浓度会增加粒子散射衰减,增大累积误差.根据仿真经验,高浓度会导致M,as,a0三者迭代时更加难以收敛,甚至造成反演算法发散.由图 15中可以看出,相同浓度,不同粒径的误差曲线差异很大,随着粒径的增大,优选探测频率降低,区间宽度变窄.由图 14,15可知,在高浓度下,误差随频率变化曲线主要受粒径影响,其变化趋势与低浓度下的变化趋势相近,但取值整体减小.基于2.2节中的仿真分析,取泥沙浓度为10 kg/m3,考虑as的影响,计算出声学高含沙水流中在泥沙粒径为1~100 μm时的优选测量频率,如图 16中实线所示.图 16中虚线表示根据4.2节的分析计算出的声学低含沙水流中对于泥沙粒径为1~100 μm时优选频率曲线.对比可知,浓度的增加会导致优选频率区间向低频区间移动,该结论符合前文的分析,也与Thorne等[5, 11]的实验结果一致.
|
图 16 声学高、低含沙水流中不同粒径的优选测量频率对比 Fig. 16 Comparison between high and low concentration sediment-laden flow for optimum measuring frequency versus different radius |
本文基于黄河典型剖面泥沙数据进行仿真,解决了声学高含沙水流中粒子散射衰减项as不能忽略的问题.分析了测量系统的误差来源,提出了声学测沙优选频率,计算得到在低泥沙浓度的情况下,不同测量环境的优选测量频率.为了研究高泥沙浓度情况下的频率优选问题,本文主要分析了悬沙浓度,粒径以及测量频率3个变量对于系统总测量误差的影响.在声学高含沙水流中,优选频率主要受所测量的泥沙粒径影响,其与粒径的关系曲线如图 16中实线所示.图 16中代表声学高、低含沙水流的实线、虚线趋势一致,但声学高含沙水流中优选频率数值整体相对较小.
结果表明,当针对所测量环境选择优选频率测量时,声学测沙技术对于本文所举环境具有一定可行性.本文所进行的工作对于声学悬移质泥沙测量方法应用于黄河及相似河流具有参考价值,文中关于优选频率的讨论对于提升多频声学悬移质泥沙测量方法的抗噪声能力具有一定意义.由于中国主要河流的汛期泥沙浓度远大于40 kg/m3,故对于提高声学测沙技术的浓度测量范围值得进一步研究.
| [1] |
王光谦. 中国泥沙研究述评[J]. 水科学进展, 1999, 10(3): 337-344. WANG Guang-qian. A review on the sediments research in China[J]. Advances Water Science, 1999, 10(3): 337-344. |
| [2] |
孙志林, 倪晓静, 许丹, 等. 河口泥沙数学模型的若干问题[J]. 浙江大学学报:工学版, 2015, 49(2): 232-237. SUN Zhi-lin, NI Xiao-jing, Xu Dan. Some problems on mathematical model of sediment transport in estuary[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(2): 232-237. |
| [3] |
HOLDAWAY G P, THORNE P D, DAVID F, et al. Comparison between ADCP and transmissometer measurements of suspended sediment concentration[J]. Continental Shelf Research, 1999, 19(3): 421-441. DOI:10.1016/S0278-4343(98)00097-1 |
| [4] |
RAI A K, KUMAR A. Continuous measurement of suspended sediment concentration:Technological advancement and future outlook[J]. Measurement, 2015, 76: 209-227. DOI:10.1016/j.measurement.2015.08.013 |
| [5] |
THORNE P D, HURTHER D. An overview on the use of backscattered sound for measuring suspended particle size and concentration profiles in non-cohesive inorganic sediment transport studies[J]. Continental Shelf Research, 2014, 73: 97-118. DOI:10.1016/j.csr.2013.10.017 |
| [6] |
THORNE P D, HANES D M. A review of acoustic measurement of small-scale sediment processes[J]. Continental Shelf Research, 2002, 22: 602-632. |
| [7] |
HAY A E. The remote acoustic detection of suspended sediment at long wavelengths[J]. Journal of Ceephysical Research, 1983, 88(C12): 7525-7545. DOI:10.1029/JC088iC12p07525 |
| [8] |
HAY A E, SHENG J Y. Vertical profiles of suspended sand concentration and size from multifrequency acoustic backscatter[J]. Journal of Ceephysical Research, 1992, 97(C10): 15661-15677. DOI:10.1029/92JC01240 |
| [9] |
CRAWFORD A M, HAY A E. Determining suspended sand size and concentration from multifrequency acoustic backscatter[J]. Journal of the Acoustical Society of America, 1993, 94(6): 3312-3324. DOI:10.1121/1.407237 |
| [10] |
SCHAT J. Multifrequency acoustic measurement of concentration and grain size of suspended sand in water[J]. Journal of the Acoustical Society of America, 1997, 101(1): 209-217. DOI:10.1121/1.418003 |
| [11] |
THORNE P D, HARDCASTLE P J. Acoustic measurements of suspended sediments in turbulent currents and comparison with in-situ samples[J]. Journal of the Acoustical Society of America, 1997, 101(5): 2603-2614. DOI:10.1121/1.418501 |
| [12] |
RICHARDS S D, HEATHERSHAW A D, THORNE P D. The effect of suspended particulate matter on sound attenuation in seawater[J]. Journal of the Acoustical Society of America, 1996, 100(3): 1447-1450. DOI:10.1121/1.415991 |
| [13] |
HURTHER D, THORNE P D. A multi-frequency acoustic concentration and velocity profiler (ACVP) for boundary layer measurements of fine-scale flow and sediment transport processes[J]. Coastal Engineering, 2011, 58: 594-605. DOI:10.1016/j.coastaleng.2011.01.006 |
| [14] |
MOATE B D, THORNE P D. Scattering from suspended sediments having different and mixed mineralogical compositions:comparison of laboratory measurements and theoretical predictions[J]. Journal of the Acoustical Society of America, 2013, 13(33): 20-34. |
| [15] |
凌鸿烈, 任来法, 刘宁华, 等. ASSM_Ⅱ型声学悬浮泥沙观测系统[J]. 声学技术, 1996, 15(2): 68-72. REN Lai-fa, LIN Hong-lei, LIU Ning-hua. ASSM-Ⅱ Acoustical suspended sediments sbserving system[J]. Technical Acoustics, 1996, 15(2): 68-72. |
| [16] |
张叔英, 李允武. 声学悬浮泥沙观测系统的研制和应用[J]. 海洋学报, 1998, 20(5): 114-119. ZHANG Shu-ying, LI Yu-wu. Development and application of acoustic suspended sediment observation system[J]. Acta Oceanologica Sinica, 1998, 20(5): 114-119. |
| [17] |
汪亚平, 高抒, 李坤业. 用ADCP进行走航式悬沙浓度测量的初步研究[J]. 海洋与湖沼, 1999, 30(6): 758-763. WANG Ya-ping, GAO Shu, LI Kun-ye. Preliminary research on the suspended sediment concentration measurement with ADCP[J]. Oceanologia et limnologia Sinica, 1999, 30(6): 758-763. |
| [18] |
尹小玲, 张红武, 任杰. 应用ADP对虎门洪季悬沙浓度的观测研究[J]. 环境科学与技术, 2009, 32(6): 1-5. YIN Xiao-lin, ZHANG Hong-wu, Ren Jie. Observationin flood season of humen suspended sediment concentration with ADP[J]. Environmental Sciences & Techndogy, 2009, 32(6): 1-5. |
| [19] |
THORNE P D, DAVIES F, BOLANOS R. Measurement and modelling of suspended sediment size profiles above sandy rippled beds under waves 21434040@zju. edu. cn[C]//Proceedings of Coastal Sediments. Miami: World Scientific Publishing Co Pte Ltd, 2011: 1620-1633. http://www.worldscientific.com/doi/abs/10.1142/9789814355537_0122
|
| [20] |
MOATE B D, THORNE P D. Interpreting acoustic backscatter from suspended sediments of different and mixed mineralogical composition[J]. Continental Shelf Research, 2012, 46(1): 67-82. |
| [21] |
SHEN J Y, HAY A E. An examination of the spherical scatterer approximation in aqueous suspensions of sand[J]. Journal of the Acoustical Society of America, 1987, 83(2): 598-600. |
| [22] |
THORNE P D, AGRWAL Y C, CACCHIONE D A. A comparison of near-bed acoustic backscatter and laser diffraction measurements of suspended sediments[J]. IEEE Journal of Oceanic Engineering, 2007, 321(1): 225-235. |
| [23] |
SOULSBY R L. Dynamics of marine sands:a manual for practical applications[M]. London, UK: Thomas Telford publications, 1997.
|
| [24] |
中华人民共和国水利部. 中国河流泥沙公报[M]. 北京: 中国水利水电出版社, 2010. The ministry of water resources of the people's republic of china. The bulletin of river and sediment in china[M]. Beijing: China Water & Power Press, 2010. |
| [25] |
GB/T 50159-2015. 河流悬移质泥沙测验规范[S]. 北京: 中国计划出版社, 2015. GB/T 50159-2015. Standard for measurement of suspended sediment[S]. Beijing: China Planning Press, 2015. http://www.doc88.com/p-031716563001.html |
| [26] |
孙维婷, 穆兴民, 赵广举. 黄河干流悬移质泥沙粒径构成变化分析[J]. 人民黄河, 2015, 37(5): 4-9. SUN Wei-ting, MU Xing-ming, ZHAO Guang-ju. The analysis on the sediments grain size composition of Yellow River mainstream[J]. Yellow River, 2015, 37(5): 4-9. |



