近年来,因传统化石能源消耗造成的环境问题日益突出,严重影响人们的健康和生活[1].开发和利用可再生能源已经成为解决能源与环境问题的重要途径[2].潮流能作为可再生能源的一种,具有储量大、能量密度高并且对环境的影响小等特点,具有广阔的开发前景[3].
根据装置特点,水轮机主要有水平轴水轮机,垂直轴水轮机以及振荡翼等[4].由于垂直轴水轮机具有结构简单,不受潮流流向的限制以及噪音小等特点[5],具有更好的应用前景.阻力型水轮机作为垂直轴水轮机的一种,具有良好的自启性[6],以阻力型Savonius风力机为设计原型的S式水轮机是最典型的阻力型水轮机.Nakajima等[7]研究S式水轮机水动力学特性,并分析水槽间距对S式水轮机影响.Khan等[8]进行多级转子S式水轮机水槽实验,结果表明双级转子S式水轮机性能最优.Hassan等[9]研究螺旋式阻力型水轮机的水动力特性,结果表明螺旋式阻力型水轮机具有更好的自启性,Kailash等[10]分析改进式S式水轮机性能,结果表明改进式S式水轮机具有更高功率系数, 水动力性能更优.Yaakob等[11]研究叶尖速比、挡板等参数对S式水轮机的影响.Hassanzadeh等[12]进行Benesh式阻力型水轮机模拟仿真,并与S式水轮机流场进行对比分析.在国内,S式水轮机的研究相对较少, 上海海洋大学王永鼎等[13]通过仿真与水槽实验相结合来分析不同叶片数的S式水轮机性能,结果表明两叶片S式水轮机性能最优.
但是,目前很少有研究者对S式水轮机功率系数较低的原因进行分析,同时也缺乏对重叠比的影响研究.因此,本文应用ANSYS软件对S式水轮机流场特性进行分析,研究叶尖速比与重叠比对S式水轮机的水动力学性能的影响.
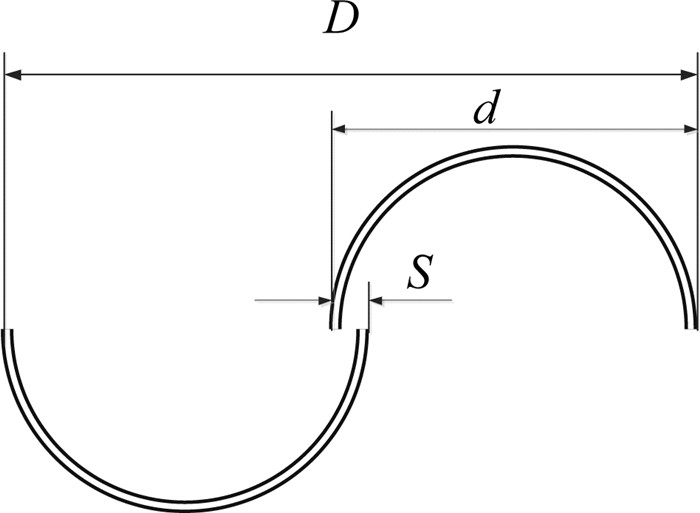
1 S式水轮机工作原理水轮机旋转过程中叶片将受到力及力矩的作用,由于S式水轮机两侧叶片的受力不均使水轮机旋转,将流体的动能转化为水轮机的机械能[14].S式水轮机主要由2个半圆柱形叶片组成,其结构如图 1所示(不考虑中心转轴等).
|
图 1 S式水轮机结构简图 Fig. 1 Structure diagram of Savonius water turbine |
图中D为水轮机直径,S为叶片间隙,d为叶片直径,重叠比e定义为
| $ e = \frac{S}{d}. $ | (1) |
在流体的作用下, 水轮机的2个叶片将受到平行于流速方向的阻力,由于2个叶片结构的不同, 凹凸叶片产生的阻力也不同,从而产生驱动水轮机旋转的力矩.其每个叶片所受阻力为
| $ {F_{\rm{d}}} = \frac{1}{2}\rho \left( {U \pm u} \right)A{C_{\rm{d}}}. $ | (2) |
式中:U为来流速度;ρ为水密度;u为叶片平均速度;A为扫流面积;Cd为阻力系数.
由式(2)可知左右两侧叶片所受阻力Fd1、Fd2分别为
| $ {F_{{\rm{d}}1}} = \frac{1}{2}\rho \left( {U-u} \right)A{C_{{\rm{d}}1}}. $ | (3) |
| $ {F_{{\rm{d}}2}} = \frac{1}{2}\rho \left( {U + u} \right)A{C_{{\rm{d}}2}}. $ | (4) |
则水轮机整体所受静推力F及平均功率P为
| $ F = {F_{{\rm{d}}1}}-{F_{{\rm{d}}2}}. $ | (5) |
| $ P = \frac{W}{T} = \frac{1}{T}\int\limits_0^{2{\rm{ \mathsf{ π} }}} F \frac{D}{2}{\rm{d}}\theta . $ | (6) |
式中:W为水轮机所做的功,T为时间周期,θ为旋转角度.水轮机力矩系数Cm及水轮机功率系数Cp定义为
| $ {C_{\rm{m}}} = \frac{M}{{\frac{1}{2}\rho {U^2}Ad}}. $ | (7) |
| $ {C_{\rm{p}}} = \frac{P}{{\frac{1}{2}\rho {U^3}A}} = \frac{{M\omega }}{{\frac{1}{2}\rho {U^3}A}} = \lambda {C_{\rm{m}}}. $ | (8) |
式中:M为水轮机所受力矩,ω为水轮机转速,λ为叶尖速比,其定义为
| $ \lambda = \frac{{\omega D}}{{2U}}. $ | (9) |
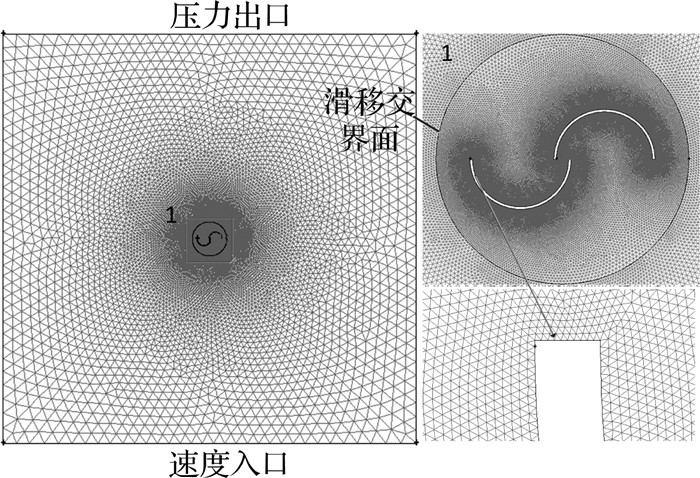
Savonius式水轮机结构简单,本文为减少计算量,将水轮机简化为二维模型.本文采用前处理软件Gambit进行网格划分.采用完全非结构化网格对整个区域进行网格划分,并对水轮机壁面添加边界层.利用滑移网格能够有效的避免水轮机的转动对网格质量造成的影响.同时,对叶片及交界面附近的网格进行加密,如图 2所示,图中网格模型约有203 000的网格单元.
|
图 2 S型水轮机网格模型 Fig. 2 Mesh model of Savonius water turbine |
本文湍流模型采用S-A模型,压力和速度耦合方式采用PISO算法,动量离散格式采用二阶迎风格式,时间离散采用一阶隐式格式,流场求解器采用基于压力的分离求解算法,残差的绝对收敛标准为10-5,分析水轮机的水动力学特性.
建立不同网格单元总数的网格模型,选取不同时间步长进行独立性验证.网格单元数量N1、单位周期时间步数N2及数值结果如表 1所示.由表 1可知,本文的数值结果与模型的网格疏密、时间步长无关.为了验证本文的数值模拟方法及软件参数设置的正确性,本文在与文献11相同的条件下(λ=0.8, e=0.2, U=1.5 m/s)进行比较分析验证.经验证,本文的结果Cm=0.280和Cp=0.224与文献11的结果Cm=0.271和Cp=0.216相差不大,因此本文的数值模拟方法设置合理.
| 表 1 网格密度和时间步长独立性验证 Table 1 Grid and time independence study |
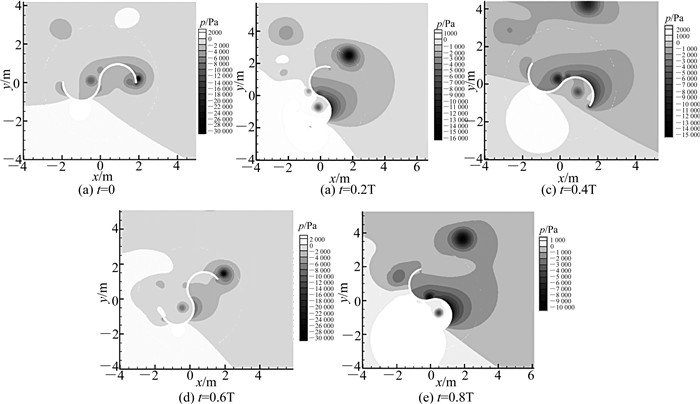
水轮机流场能够直观地反映水轮机的受力以及流场分布等.为了研究S式水轮机流场特性,本文采用软件ANSYS进行数值仿真.如图 3所示,图中t为时间,p为压力.水轮机在来流速度U=2 m/s,叶片角速度ω=1 rad/s,叶尖速比λ=1,重叠比e=0条件下不同时刻的流场压力云图.
|
图 3 水轮机不同时刻压力云图 Fig. 3 Pressure contours of Savonius water turbine at different time |
通过分析不同时刻水轮机压力云图可知,水轮机内部流场以及其周围区域非定常性,在不同时刻水轮机叶片周围的压力分布情况不同.在t=0、0.4T、0.6T时刻左侧叶片的压力值高于右侧叶片压力值,此时水流对水轮机产生一个负力矩,其与水轮距旋转方向相反,阻碍水轮机的旋转,这也是导致水轮机的功率系数低的主要原因.在t=0.2T、0.8T时刻,右侧叶片压力值高于左侧叶片压力值,此时水流对水轮机产生一个正力矩,维持水轮机的旋转.
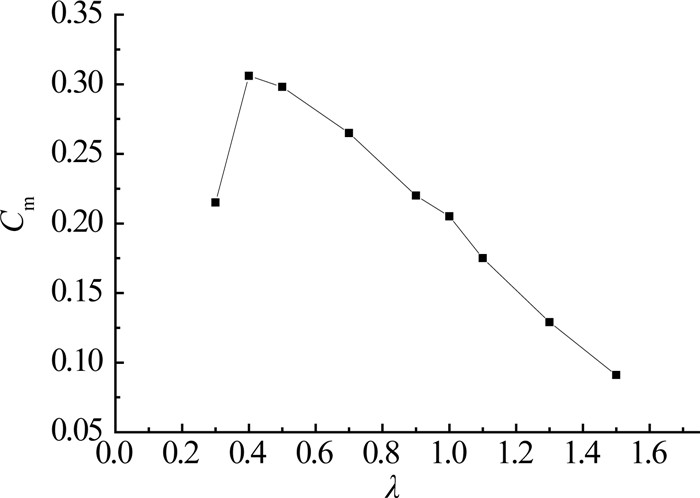
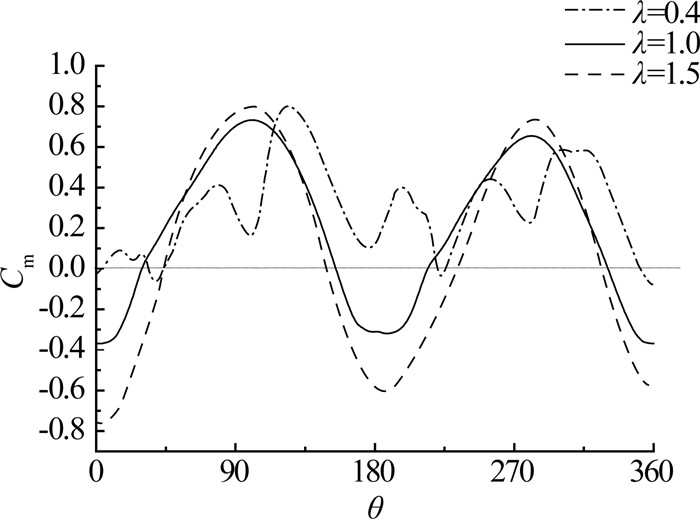
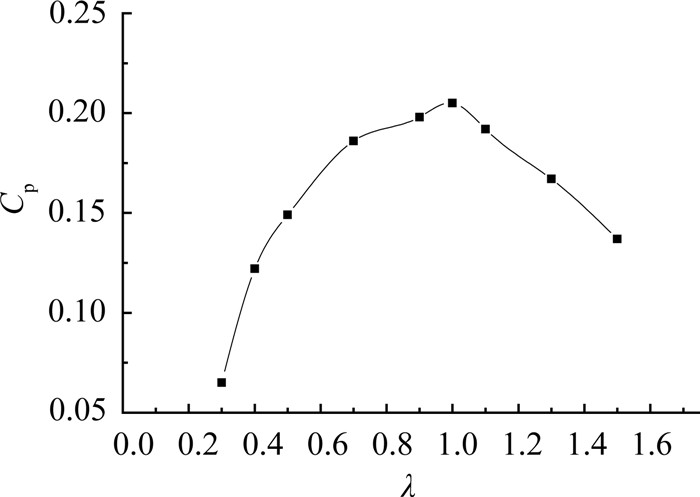
3.2 叶尖速比λ对S式水轮机的影响分析在水轮机水动力特性的研究中,功率系数、力矩系数与叶尖速比的关系是衡量水轮机性能优劣的主要标准.根据式(7)、(8)可知力矩系数与功率系数都与角速度ω、来流速度U以及叶尖速比λ相关.本文在叶尖速比λ=0.3~1.5时,分析功率系数以及力矩系数的变化情况.根据ANSYS模拟结果得到不同叶尖速比λ的力矩系数和功率系数,以及力矩系数随旋转角度变化趋势,其结果如图 4、5、6所示.
|
图 4 力矩系数与叶尖速比关系图 Fig. 4 Torque coefficient versus tip speed ratio |
|
图 5 不同叶尖速比下力矩系数变化曲线图 Fig. 5 Torque coefficient versus rotation angle with different tip speed ratio |
|
图 6 功率系数与叶尖速比关系图 Fig. 6 Power coefficient versus tip speed ratio |
从图 4中可看出,在较低叶尖速比的情况下力矩系数较大,随着叶尖速比增大,力矩系数逐渐减小.当λ=0.4时,水轮机的力矩系数达到最大值0.306.当λ>0.4时,力矩系数与叶尖速比呈负相关,其随着叶尖速比的增大而降低.因此,S式水轮机适合在低叶尖速比的情况下工作.
从图 5中可以看出,在不同叶尖速比下力矩系数随旋转角度变化的峰值基本上相等,造成三者力矩系数不同在于其负值区域,当λ=0.04时力矩系数基本上都为正数,而叶尖速比λ为0.10、0.15时力矩系数有较长时间为负值,这也是力矩系数随着叶尖速比增大而减小的原因.
从图 6中可看出,功率系数与叶尖速比近似成抛物线关系,存在一个最佳叶尖速比使水轮机的功率系数达到最大;当λ=1时,功率系数达到最大值0.205.综合力矩系数、功率系数随叶尖速比变化可知,S式水轮机适合在低叶尖速比条件下工作,在给定参数条件下当叶尖速比为1时,S式水轮机的性能最优.
3.3 重叠比e对S式水轮机的影响分析S式水轮机具有自启性好、结构简单等优点,但其工作效率较低.本文通过改变2个叶片之间的重叠比e来提高水轮机的功率系数.
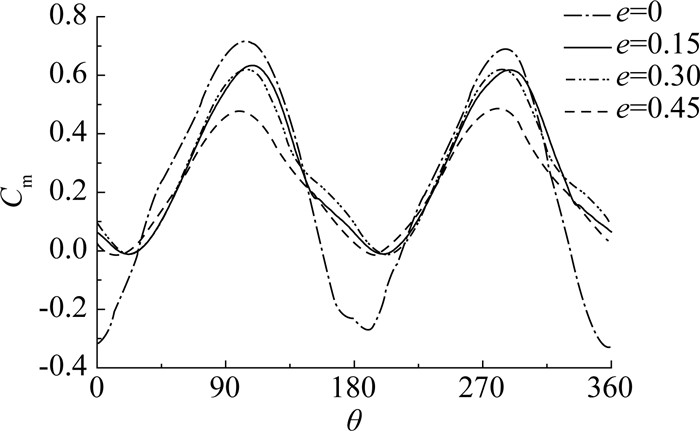
带有重叠比的S式水轮机的参数设置与S式水轮机基本相同.湍流模型采用S-A模型,来流速度U=2 m/s, 角速度ω=1 rad/s,叶片直径d=2 m.选取不同的叶片重叠比e进行数值仿真,并分析重叠比对水轮机的水动力及能量提取性能的影响.在不同的重叠比e下,力矩系数随旋转角度θ变化如图 7所示.
|
图 7 不同重叠比下力矩系数变化曲线图 Fig. 7 Torque coefficient versus the rotation angle with the different over lap ratio |
从图 7中可看出,力矩系数与旋转角度近似呈简谐变化趋势.力矩系数在旋转角度105°时达到最大值,旋转角度为190°时,力矩系数的值最小.此外,重叠比对力矩系数的影响主要在力矩出现负值阶段.没有重叠比的S式水轮机在旋转过程中力矩系数在较长的时间段内为负值,而带有重叠比的S式水轮机能够有效的减少甚至完全消除水轮机在运动过程中的负力矩现象.
在不同的重叠比e下,力矩系数、功率系数与重叠比e关系如表 2所示.由表 2可知,当e=0时,水轮机的力矩系数最小,当e=0.3时,力矩系数最大,达到0.294;当e=0.45时,水轮机的功率系数最低,当e=为0.15时,水轮机的功率系数最高,达到0.256.综合比较分析,重叠比能改善S式水轮机性能,在研究的参数范围内,当重叠比e=0.15时性能最优.
| 表 2 力矩系数、功率系数与重叠比e的关系表 Table 2 Power coefficient and torque coefficient versus the overlap ratio |
本文建立了S式水轮机二维网格模型,通过ANSYS软件对S式水轮机进行数值仿真分析,研究水动力及能量提取性能,并进一步分析叶尖速比与重叠比对S式水轮机水动力性能的影响,主要得到以下几个结论:
(1) S式水轮机具有自启性好、不受水流方向等影响优点,但是在旋转过程中出现负力矩情况,这是造成其功率系数较低的主要原因.
(2) S式水轮机适合在低叶尖速比情况下工作,并且力矩系数与叶尖速比近似成线性关系,存在一个最优叶尖速比使水轮机的功率系数达到最大;在给定参数条件下,S式水轮机在叶尖速比为1时水动力性能较好,并且功率系数达到最大值0.205.
(3) 带有重叠比的S式水轮机能够有效的减少甚至完全消除水轮机在运动过程中的负力矩的情况,从而改善S式水轮机水动力性能.在研究的参数范围内,在重叠比e=0.15附近时,S式水轮机综合性能最优.
| [1] |
王勇, 刘海宾, 谢玉东, 等. 双水翼耦合振荡捕获潮流能系统2维数值模拟[J]. 四川大学学报:工程科学版, 2016, 48(5): 173-179. WANG Yong, LIU Hai-bin, XIE Yu-dong, et al. Two-dimensional numerical simulation of Dual-oscillating hydrofoils in an energy extraction system[J]. Journal of Sichuan University:Engineering Science, 2016, 48(5): 173-179. |
| [2] |
张亮, 李新仲, 耿敬, 等. 潮流能研究现状2013[J]. 新能源进展, 2013, 1(1): 53-68. ZHANG Liang, LI Xin-zhong, GENG Jing, et al. Tidal current energy update 2013[J]. Advances in New and Renewable Energy, 2013, 1(1): 53-68. |
| [3] |
刘富铀, 赵世明, 张智慧, 等. 我国海洋能研究与开发现状分析[J]. 海洋技术, 2007, 26(3): 118-120. LIU Fu-you, ZHAO Shi-ming, ZHANG Zhi-hui, et al. Analysis on research and development of oceanic energy in China[J]. Ocean Technology, 2007, 26(3): 118-120. |
| [4] |
马鹏磊, 王勇, 刘海宾, 等. 振荡翼改进模型的水动力性能分析[J]. 华中科技大学学报:自然科学版, 2017, 45(3): 65-69. MA Peng-lei, WANG Yong, LIU Hai-bin, et al. Hydrodynamic performance analysis on modified model of oscillating airfoil[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2017, 45(3): 65-69. |
| [5] |
SWIRYDCZUK J, DOERFFER P, SZYMANIAK M. Unsteady flow through the gap of Savonius turbine rotor[J]. Centrum Informatyczne Trójmiejskiej Akademicki Sieci Komputerowej, 2011, 15(1): 59-70. |
| [6] |
SHELDAHL R E, FELTZ L V, BLACKWELL B F. Wind tunnel performance data for two-and three-bucket savonius rotors[J]. Journal of Energy, 1978, 2(3): 160-164. DOI:10.2514/3.47966 |
| [7] |
NAKAJIMA M, ⅡO S, IKEDA T. Performance of Savonius rotor for environmentally friendly hydraulic turbine[J]. Journal of Fluid Science & Technology, 2008, 3(3): 420-429. |
| [8] |
KHAN I, IQBAL T, HINCHEY M, et al. Performance of Savonius rotor as a water current turbine[J]. Journal of Ocean Technology, 2009, 4(2): 71-83. |
| [9] |
HASSAN MI, KHAN N. Performance of a quarter-pitch twisted Savonius Turbine[C]. //Utility Exhibition on Power & Energy Systems: Issue & Prospects for Asia. Pattaya City: IEEE, 2011: 1-4. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6497756
|
| [10] |
KAILASH G, ELDHO T I, PRABHU S V. Influence of the deflector plate on the performance of modified Savonius water turbine[J]. Applied Energy, 2011, 88(9): 3207-3217. DOI:10.1016/j.apenergy.2011.03.025 |
| [11] |
YAAKOB O B, ISMAIL M A, AHMED Y M. Parametric study for Savonius vertical axis marine current turbine using CFD simulation[C]. //Proceedings 7th International Conference on Renewable Energy Sources (RES'13). Kuala Lumpur: Asia-pacific Workshop on Marine Hydrodynamics, 2013: 200-205. http://www.researchgate.net/publication/262966784_Validation_Study_for_Savonius_Vertical_Axis_Marine_Current_Turbine_Using_CFD_Simulation
|
| [12] |
HASSANZ A R, YAAKOB O B, AHMED Y M, et al. Numerical simulation for unsteady flow over marine current turbine rotors[J]. Wind and Structures An International Journal, 2016, 23(4): 301-311. DOI:10.12989/was.2016.23.4.301 |
| [13] |
卢好阳. 一种小型垂直轴潮流能发电装置的设计与研究[D]. 上海: 上海海洋大学, 2016: 44-48. LU Hao-yang, The innovative design and simulation analysis of small tidal current generation device[D]. Shanghai: Shanghai Ocean University, 2016: 44-48. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D01094355 |
| [14] |
刘同平. 垂直轴阻力型风力机气动特性分析及优化设计[D]. 重庆: 重庆大学, 2011: 49. LIU Tong-ping, Analysis of aerodynamic characteristic and optimal design of resistance-type vertical axis wind turbine[D]. Chongqing: Chongqing University, 2011: 49. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D283186 |




