2. 南京工业大学 江苏省工业装备数字制造及控制技术重点实验室, 江苏 南京 210009;
3. 重庆大学 机械传动国家重点实验室, 重庆 400044
2. Jiangsu Key Laboratory of Digital Manufacturing for Industrial Equipment and Control Technology, Nanjing Tech University, Nanjing 210009, China;
3. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China
精密数控成形磨齿机通常用于精加工齿轮表面.在磨削齿面时,磨齿机的高速电主轴内部会产生大量热量,导致电主轴产生热变形.而由热变形导致的热误差占整个机床误差的比重很大.研究表明,由机床热变形引起的热误差占机床总误差的40%~70%[1-3].
为了减少热误差对机床加工精度的影响,国内外专家和学者提出许多改进的方法.主要有以下3类:热误差避免、热误差控制与热误差补偿.其中,热误差避免和热误差控制均需要改进电主轴的材料或结构.然而,热误差补偿往往被认为是一种局限性小和经济性好的降低热误差的方法[4].该方法的核心是如何在热误差和温度之间建立一个有效的模型[5],这将直接影响补偿的精度,进而影响机床的加工精度.
为了获得一个高精度和高鲁棒性的热误差模型,国内外学者研究了很多建模方法.有限元法[6-8]被广泛用来分析研究机床的温度场和热变形情况.Du等[9]运用ANSYS软件仿真得到在任意转速下的电主轴热误差模型为自然指数模型,并与实验结果进行对比.然而,由于电主轴具有复杂和密闭的结构,使得电主轴热误差受到内部众多复杂变量相互耦合的影响,故在建立数值模型过程中很难建立可靠的边界条件和准确的获得热传递特性的参数.Han等[10-12]利用回归分析法建立了具有较高精度的机床热误差模型.Li等[13-14]通过最小二乘法建立了具有较高预测能力的热误差模型.Tan等[15]将最小二乘原理和多元线性回归理论结合建立了具有很高的鲁棒性的综合热误差预测模型.Yan等[16-17]均采用灰色理论建立机床热误差模型,结果表明,经过优化变量的模型表现得更好,建模的精度有很大的提高.Abdulshahed等[18]采用自适应神经模糊推理系统与模糊C均值聚类法相结合建立热预测模型.Huang等[19]将GA和BP算法相结合建立了可以迅速解决全局最小搜索问题的高速主轴热误差模型.Yang等[20-21]采用模糊聚类分析方法对温度变量进行优化,并运用人工神经网络方法建立热误差模型.以上方法在机床热致误差的预测方面都取得了一些成功的应用,但是这些方法都存在一些局限性和不足之处:回归模型的设计比较耗时和繁琐;最小二乘法拟合精度不高;灰色理论模型对建模误差数据光滑性有严格要求;神经网络模型在容易产生过学习或欠学习问题的同时,对样本的要求也较高;模糊系统存在人工干预多、推理速度慢、精度较低等缺点,很难实现自适应学习的功能.
由于模糊神经网络模型具有处理非线性、模糊性等问题的优越性,且有效解决了模型欠学习、过学习等问题.因此,本文采用模糊神经网络模型建主轴热误差模型.首先,分析高速电主轴结构和传热机理,并对磨齿机电主轴系统的温度场和热变形进行了有限元仿真.然后,基于电主轴热误差实验数据,采用模糊神经网络和BP神经网络分别建立主轴热误差模型,通过对比2种模型的建模精度,建立具有较高精度和鲁棒性的电主轴的热误差预测模型,揭示电主轴系统温升与热误差之间的规律,进而提高了磨齿机的加工精度.
1 高速电主轴的结构和热特性分析高速电主轴是精密成形磨齿机中最重要的组件之一.高速电主轴的结构主要包括旋转轴、转子、定子、混合陶瓷球轴承、外壳结构以及冷却系统.其内置电机的功率损耗和轴承处的摩擦将会导致电主轴内部温度升高,进而使得电主轴产生热变形.
另一个影响高速电主轴热变形的重要因素是电主轴内部的热对流.电主轴内部的热对流包括:定子与冷却液间的对流换热、定子和转子间气隙的对流换热、转子端部与周围空气的对流换热、前后密封环气隙的对流换热、前端轴承与冷却液间的对流换热、主轴头部等运动表面与周围空气之间的对流换热、主轴外壳等静止表面与周围空气的自然对流换热.这些热对流的强度受到电主轴内部定子与转子和轴承温度,以及外部环境温度的影响.
本文利用有限元ANSYS Workbench软件对电主轴温度场和热变形进行分析.在对电主轴进行有限元分析时首先需要确定热源的实际热生成率和电主轴内部的热对流系数.为提高运算效率,可将电主轴系统的几何模型简化如图 1所示.

|
图 1 电主轴简化几何模型图 Fig. 1 Simplified geometric model of motorized spindle |
电主轴内置电机额定功率的损耗通常转化为定转子发热所产生的热量,根据近似公式计算功率损耗[22]:
| $ {P_{\rm{s}}} = {P_{\rm{e}}}\left( {1 - \eta } \right). $ | (1) |
式中:Ps为损耗功率,kW;Pe为额定功率,kW;η为电机效率.
取η=0.75,由于本文研究的电主轴的额定功率为25 kW,得电主轴的功率损耗约为6.25 kW.研究表明[23],电主轴在高速运转下,电机发热量的1/3是由电机转子产生,约为2 kW,其余2/3的热量由定子生产,约为4.2 kW.定转子生热率计算公式为
| $ q = {P_{\rm{m}}}/V. $ | (2) |
式中:Pm为电机内部的损耗功率,kW;V为体积,m3;q为生热率,W/m3.
转子和定子的生热率如表 1所示.其中,d为定子和转子的内径,D为定子和转子的外径,L为定子和转子的长度.
| 表 1 定转子尺寸参数和生热率 Table 1 Parameters and heat generation rate of the stator and rotor |
根据Palmgren方法[24],计算电主轴轴承的发热功率为
| $ {P_{\rm{b}}} = 1.047 \times {10^{ - 4}}Mn. $ | (3) |
式中:Pb为轴承的发热功率,kW;M为轴承摩擦力矩,N·m;n为轴承转速,r/min.
电主轴的前端、中部和后端均有一对角接触球轴承采用背靠背方式安装.其尺寸参数如表 2所示.轴承的发热功率和生热率如表 3所示.其中,B为轴承的宽度,β0为轴承的接触角,F为轴承预紧力,E为轴承的弹性模量,ρ为材料的密度,ν为泊松比.
| 表 2 轴承尺寸参数 Table 2 Parameters of bearing |
| 表 3 轴承生热率 Table 3 Heat generation rate of bearing |
根据努塞尔数准则,对流传热系数为
| $ h = \left( {Nu \cdot \lambda } \right)/L. $ | (4) |
式中:Nu为努塞尔数;L为特征尺寸,m;λ为流体导热系数,W/(m·℃).
根据磨齿机实际加工情况测得,环境温度为28.5 ℃,主轴转速为1 800 r/min.由经典传热理论,计算得出电主轴内部对流换热系数,如表 4所示.
| 表 4 电主轴对流换热系数 Table 4 Convective heat transfer coefficient of motorizedspindle |
利用有限元ANSYS Workbench分析软件,对简化后的电主轴三维模型进行划分网格.通过采用自动划分法、六面体网格划分法和patch conforming算法相结合,对电主轴三维模型不同部位采用不同的方法进行网格划分,模型被划分为112 778个单元,如图 2所示.设电主轴的旋转轴、轴承和定转子材料分别为45钢、GCr15和硅钢,其余部位材料为Q235.如表 5所示为电主轴系统中不同部位的材料特性.表中,c为材料的比热容,γ为材料的热膨胀系数.

|
图 2 电主轴有限元网格模型图 Fig. 2 Finite element mesh model of motorized spindle |
| 表 5 电主轴材料特性 Table 5 Material properties of motorized spindle |
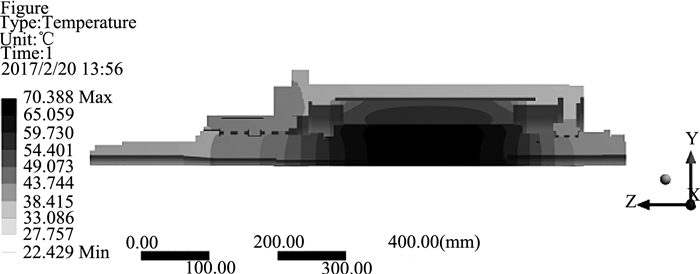
将第1节计算的边界条件和热载荷以及材料特性施加在电主轴有限元模型上,可以计算得出电主轴的稳态温度场,如图 3所示.最高温度点位于电主轴内置电机转子上,达到70.388 ℃,这是因为转子周围没有冷却装置,温度难以散发.后轴承处温度达到35.54 ℃,前端两轴承温度分别为30.56 ℃和33.11 ℃,这表明后轴承处温度要高于前端轴承处的温度.这是因为前端轴承处设有冷却套,对轴承起到降温冷却的作用.由图 3可知,轴承和电机定转子是电主轴的主要热源,这对电主轴热误差实验中的温度传感器的布置提供了指导.
|
图 3 电主轴的稳态温度场 Fig. 3 Steady state temperature field of motorized spindle |
将电主轴稳态温度场分析的结果作为热载荷施加在电主轴上,进而对电主轴进行热变形场分析,分析结果如图 4所示.从图 4(a)中可知,非均匀温度场引起电主轴系统产生严重的热变形,最大综合热变形发生在旋转轴的根部达到67.95 μm,旋转轴头部的综合热变形量达到55.53 μm.电主轴头部的径向、轴向热变形分别达到了37.53、18.37 μm,如图 4(b)、(c)所示.

|
图 4 电主轴在稳态温度场下的热变形场 Fig. 4 Thermal deformation field of motorized spindle in steady state temperature field |
根据有限元分析结果可知,电主轴系统中温度最高的部位在转子处,热变形最大的部位在旋转轴根部.由于砂轮是直接安装在旋转轴的头部,故由旋转轴头部产生的热变形将直接映射到砂轮上,这将会影响砂轮磨削时的运动轨迹,进而影响磨齿机的磨削精度.所以,对由热引起电主轴产生的变形进行预测分析有着极其重要的意义.
3 模糊神经网络模型的建立 3.1 Takagi-Sugeno模糊模型Takagi-Sugeno模糊系统是一种自适应能力很强的模糊系统,该模型既能够自动更新,又能不断修正模糊子集的隶属函数.Takagi-Sugeno模糊系统用“if-then”规则形式来定义,在规则Ri的情况下,模糊推理如下:
| $ \begin{array}{l} {R^i}:{\rm{If}}\;\;{x_1}\;{\rm{is}}\;A_1^i,{x_2}\;{\rm{is}}\;A_2^i, \cdots ,{x_k}\;{\rm{is}}\;A_k^i\\ {\rm{Then}}\;\;{y_i} = p_0^i + p_1^i{x_1} + \cdots + p_k^i{x_k}. \end{array} $ |
式中:Aji为模糊系统的模糊集;pji(j=1, 2, …, k)为模糊系统的参数;yi为根据模糊规则得到的输出,输入部分(即if部分)是模糊的,输出部分(即then部分)是确定的,该模糊推理表示输出为输入的线性组合.
假设对于输入量x=[x1, x2, …, xk],首先根据模糊规则计算各输入变量xj的隶属度:
| $ \begin{array}{l} {\mu _{A_j^i}} = \exp \left( { - {{\left( {{x_j} - g_j^i} \right)}^2}/b_j^i} \right).j = 1,2, \cdots ,k;\\ \;\;\;\;\;\;\;i = 1,2, \cdots ,\xi . \end{array} $ | (5) |
式中:gji,bji分别为隶属度函数的中心和宽度;k为输入参数;ξ为模糊子集数.
将各隶属度进行模糊计算,采用模糊算子为连乘算子:
| $ \begin{array}{l} {\omega ^i} = {\mu _{A_j^1}}\left( {{x_1}} \right) \times {\mu _{A_j^2}}\left( {{x_2}} \right) \times \cdots \times {\mu _{A_j^k}}\left( {{x_k}} \right).\\ \;\;\;\;\;\;\;i = 1,2, \cdots ,\xi \end{array} $ | (6) |
式中:ωi为输入参数隶属度连乘积.
根据模糊计算结果计算模糊模型的输出值为
| $ {y_i} = \sum\limits_{i = 1}^\xi {{\omega _i}\left( {p_0^i + p_1^i{x_1} + \cdots + p_k^i{x_k}} \right)} /\sum\limits_{i = 1}^\xi {{\omega _i}} . $ | (7) |
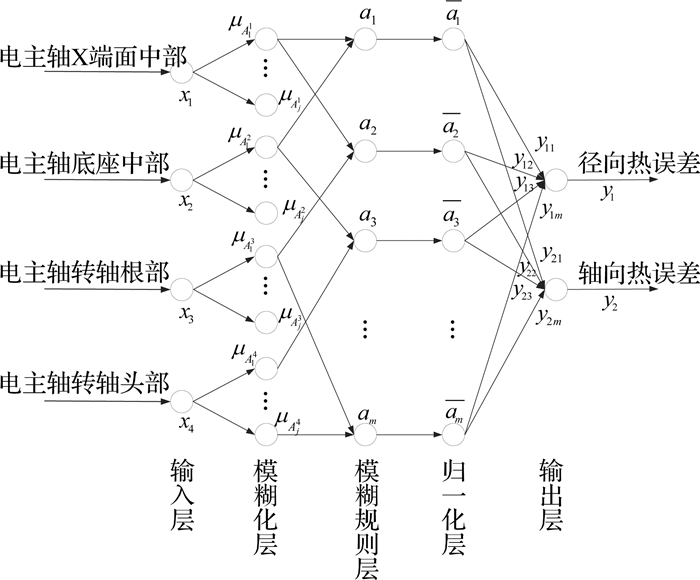
Takagi-Sugeno模糊神经网络分为输入层、模糊化层、模糊规则计算层、归一化层和输出层,如图 5所示.输入层与输入向量xi连接,节点数与输入向量的维数相同.模糊化层采用隶属度函数(5)对输入值进行模糊化得到模糊隶属度值μ.模糊规则计算层采用模糊连乘式(6)计算得到ω,并计算每条规则的适应度.归一化层的作用是对模糊规则的适应度进行归一化计算.输出层采用式(7)计算模糊神经网络的输出.
|
图 5 模糊神经网络简化结构图 Fig. 5 Simplified structure of Fuzzy Neural Network |
模糊神经网络的学习算法如下:
1) 误差计算
| $ e = \frac{1}{2}{\left( {{y_{\rm{d}}} - {y_{\rm{g}}}} \right)^2}. $ | (8) |
式中:yd为网络期望输出;yg为网络实际输出;e为期望输出和实际输出的误差.
2) 系数修正
| $ p_j^i\left( k \right) = p_j^i\left( {k - 1} \right) - \alpha \frac{{\partial e}}{{\partial p_j^i}}. $ | (9) |
| $ \frac{{\partial e}}{{\partial p_j^i}}=\left( {{y_{\rm{d}}} - {y_{\rm{g}}}} \right){\omega ^i}/\sum\limits_{i = 1}^m {{\omega ^i} \cdot {x_j}} . $ | (10) |
式中:α为网络学习率;xj为网络输入参数.
3) 参数修正
| $ g_j^i\left( k \right) = g_j^i\left( {k - 1} \right) - \alpha \frac{{\partial e}}{{\partial g_j^i}}. $ | (11) |
| $ b_j^i\left( k \right) = b_j^i\left( {k - 1} \right) - \alpha \frac{{\partial e}}{{\partial b_j^i}}. $ | (12) |
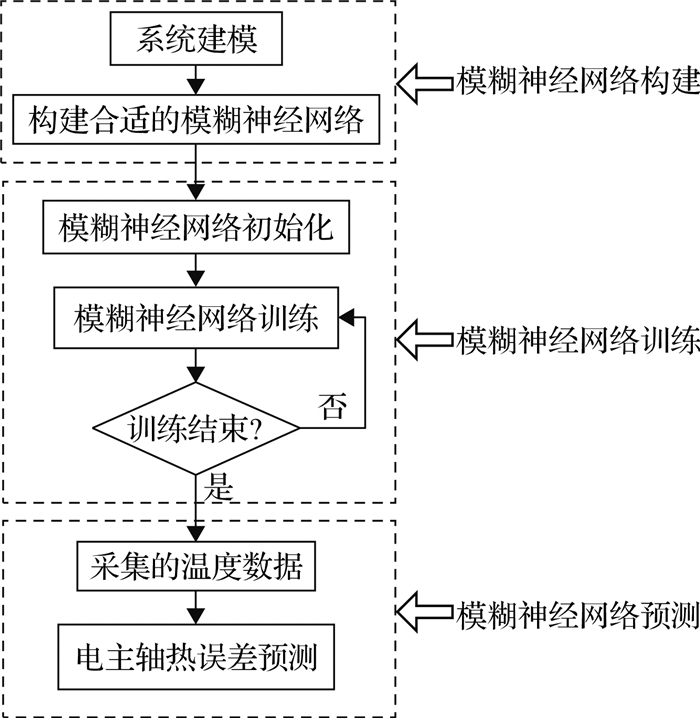
基于Takagi-Sugeno模糊神经网络的磨齿机电主轴热误差预测流程如图 6所示.其中,模糊神经网络根据训练样本的输入、输出维数确定网络的输入和输出节点数,由于输入数据维数为4,输出数据维数为2,所以确定网络的输入节点个数为4,输出节点个数为2.根据网络输入输出节点个数,确定隶属度函数的个数为12,因此构建的网络结构为4-12-2,随机初始化模糊隶属度函数中心g,宽度b和系数p0~p4.
|
图 6 基于模糊神经网络的电主轴热误差预测流程图 Fig. 6 Flow diagram of motorized spindle thermal error prediction based on Fuzzy Neural Network |
为了获得训练模糊神经网络的数据和了解实际加工中电主轴的热误差大小,对某公司生产的大型数控成形磨齿机SKMC-3000/20上的电主轴进行热误差测量实验.根据第1节对磨齿机高速电主轴的热源分析,可以判断电主轴的电机定子、转子和轴承处为主要热源,并结合2.1小节对电主轴有限元仿真的温度场结果以及实际加工时电主轴的热源位置,故选择电主轴X端面中部、电主轴底座中部、电主轴转轴根部和电主轴转轴头部这4个位置作为电主轴的温度的测量点,如图 7所示.

|
图 7 电主轴热误差测量实验 Fig. 7 Thermal error measurement experiment of motorized spindle |
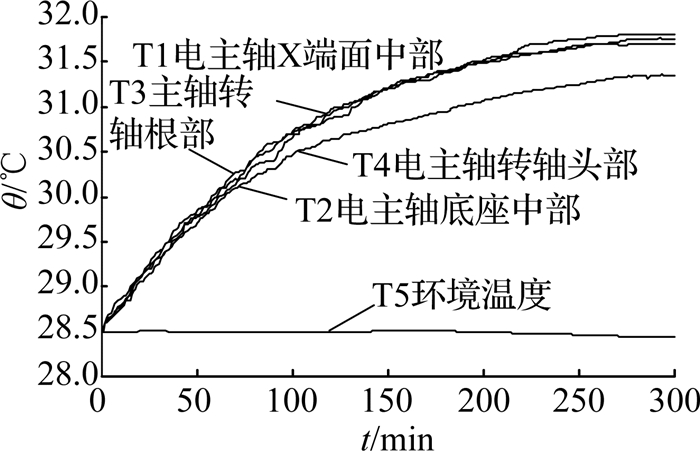
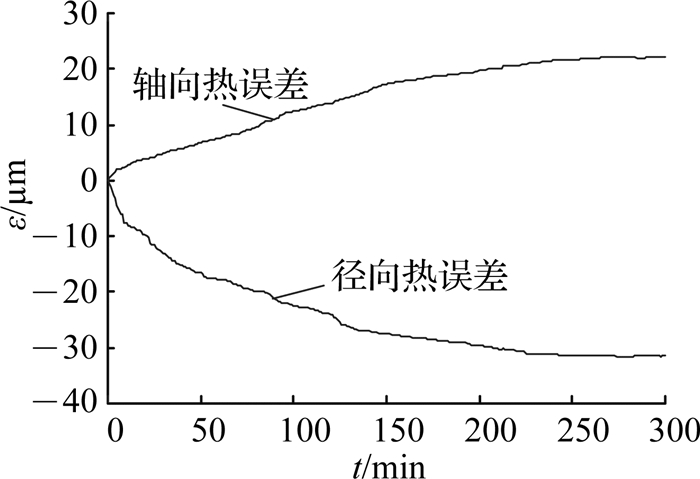
所有的温度传感器均采用热电阻Pt100传感器,采用LTS-25-02型激光位移传感器记录热位移情况.另外,为了尽可能多的获得磨齿机电主轴的温度变化和热误差数据,提高模型的预测精度,每分钟采集一次电主轴温度和位移数据,实验持续了5 h,直至电主轴达到热平衡状态,如图 8、9所示.其中,t为实验数据的采集时间,θ为测点的温度变化量,ε为主轴热误差的变化量.
|
图 8 电主轴温升图 Fig. 8 Temperature variation diagram of motorized spindle |
|
图 9 电主轴热误差变化曲线图 Fig. 9 Thermal error variation diagram of motorized spindle |
由图 8可知,电主轴工作240 min后基本达到热平衡状态.由于转轴头部靠近冷却系统,冷却液带走一部分热量,使得其头部的温度略低于根部,分别为31.3与31.7 ℃.与有限元理论分析结果(30.56与32.09 ℃)相比,理论与实际误差值均小于3%,与利用有限元分析得到的稳态温度场结果相符.其中,环境温度的变化在±0.2 ℃之内,相对于热源对电主轴的热误差的影响,环境温度在本文中对电主轴热误差的影响可以忽略不计.
由图 9可知,电主轴热误差会随着温度的升高而逐渐增加.运行270 min后,其径向与轴向热误差均达到最大值,分别为31.396 2、21.998 6 μm.与有限元分析结果(37.53、18.37 μm)相比,理论与实际误差值均小于20%,表明利用有限元分析得到的热位移场结果基本符合实际情况.
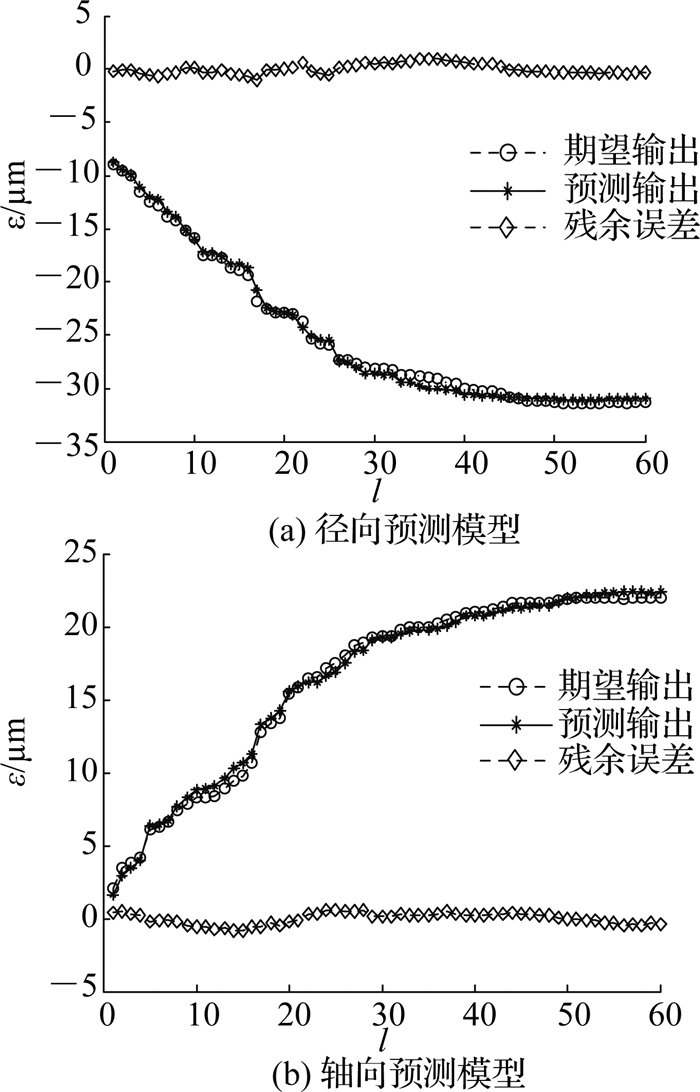
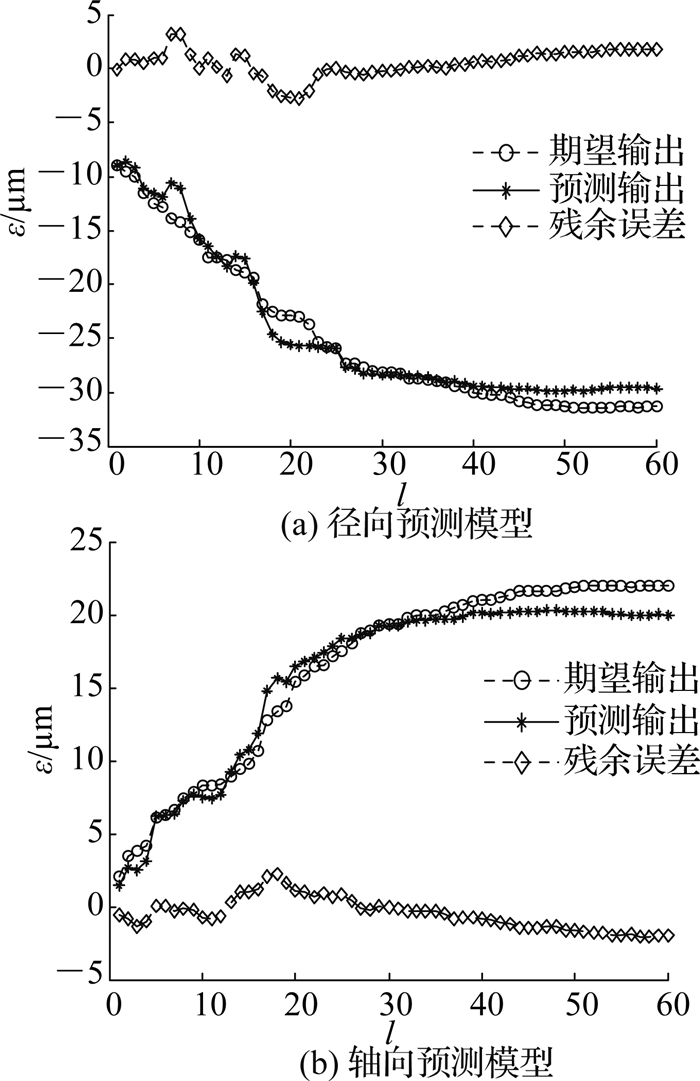
4.2 电主轴热误差预测为了训练模糊神经网络模型、建立电主轴热误差模型,将测量到的温度与热误差数据导入MATLAB软件.其中,随机选取240组数据作为原始数据,并利用剩余60组数据进行模型验证.经MATLAB软件拟合,运用模糊神经网络与BP神经网络预测模型的热误差拟合图像分别如图 10、11所示.其中,l为样本序号.结果表明,经过模糊神经网络建立的电主轴径向、轴向热误差模型的均方差分别为Efnn-x=0.225 3、Efnn-y=0.258 1;BP神经网络建立的径向、轴向热误差模型的均方差分别为Ebp-x=1.749 2、Ebp-y=1.584 4.
|
图 10 模糊神经网络预测模型 Fig. 10 Fuzzy neural network prediction model |
|
图 11 BP神经网络预测模型 Fig. 11 BP neural network prediction model |
综上所述,由模糊神经网络所建立的热误差预测模型的均方差均比BP神经网络的小且该模型的泛化性更好、预测精度更高.
4.3 电主轴热误差预测结果评价磨齿机电主轴热误差预测模型的主要精度指标如表 6所示,εmax为原始最大误差,Δεmax为最大残余误差,Δε为平均残余误差,τ表示建模精度.其中,模糊神经网络建立的径向、轴向热误差模型的最大残差分别为1.021 2、0.874 9 μm,建模精度分别为96.74%、96.02%;而BP神经网络建立的径向、轴向热误差模型的最大残差分别为3.210 7、2.248 9 μm,建模精度分别为89.77%、89.78%.表明模糊神经网络热误差模型的预测精度、稳定性和泛化能力均高于BP神经网络所建立的热误差模型,可以更准确的预测电主轴的热误差,进而提高磨齿机的加工精度.
| 表 6 预测模型的主要精度指标 Table 6 Main precision index of prediction model |
为了减小电主轴的热误差、进一步提升磨齿机加工精度,以某公司生产的大型数控成形磨齿机SKMC-3000/20上的电主轴为研究对象.得出以下结论:
(1) 分析了电主轴的内部结构、热源以及热误差产生的机理,表明内置电机的功率损耗和轴承摩擦发热是导致电主轴内部温度升高的主要因素.而电主轴内部的对流换热是影响电主轴热变形的另一个重要因素.这两部分因素最终将会影响磨齿机的加工精度.
(2) 利用ANSYS Workbench有限元软件分析了电主轴稳态温度场的分布以及相应的热变形情况,揭示了电主轴系统中温升最高的部位在电主轴系统的电机转子处,而热变形最大的部位在旋转轴根部.分析并比较有限元分析结果与磨齿机热误差实验发现,有限元仿真结果与实验结果基本相符.
(3) 在磨齿机热误差理论与实验研究基础上,采用Takagi-Sugeno型模糊神经网络方法预测磨齿机电主轴热误差.通过MATLAB软件训练模糊神经网络建立电主轴热误差预测模型,结果表明电主轴的径向热误差模型的建模精度从BP神经网络模型的89.77%提高到了模糊神经网络模型的96.74%.综合表明,采用模糊神经网络建立的热误差模型在预测精度上有了较高的改善,泛化能力和鲁棒性也得到了明显提高.
| [1] |
BRYAN J. International status of thermal error research[J]. CIRP Annals-Manufacturing Technology, 1990, 39(2): 645-656. DOI:10.1016/S0007-8506(07)63001-7 |
| [2] |
姚晓栋, 黄奕乔, 马晓波, 等. 基于时间序列算法的数控机床热误差建模及其实时补偿[J]. 上海交通大学学报, 2016, 50(5): 673-679. YAO Xiao-dong, HUANG Yi-qiao, MA Xiao-bo, et al. Thermal error modeling and real-time compensation of CNC machine tools based on time series method[J]. Journal of Shanghai Jiaotong University, 2016, 50(5): 673-679. |
| [3] |
拓占宇, 黄奕乔, 沈牧文, 等. 基于3次样条插值的数控机床几何与热复合定位误差建模[J]. 上海交通大学学报, 2016, 50(5): 668-672. TUO Zhan-yu, HUANG Yi-qiao, SHEN Mu-wen, et al. Modeling of geometric and thermal complex positioning error of CNC machine tools based on cubic spline interpolation[J]. Journal of Shanghai Jiaotong University, 2016, 50(5): 668-672. |
| [4] |
LI J W, ZHANG W J, YANG G S, et al. Thermal error modeling for complex physical systems:the-state-of-arts review[J]. The International Journal of Advanced Manufacturing Technology, 2009, 42(1): 168-179. |
| [5] |
CREIGHTON E, HONEGGER A, TULSIAN A, et al. Analysis of thermal errors in a high-speed micro-milling spindle[J]. International Journal of Machine Tools & Manufacture, 2010, 50(4): 386-393. |
| [6] |
MIAN N S, FLETCHER S, LONGSTAFF A P, et al. Efficient estimation by FEA of machine tool distortion due to environmental temperature perturbations[J]. Precision Engineering, 2013, 37(2): 372-379. DOI:10.1016/j.precisioneng.2012.10.006 |
| [7] |
ZHAOC, GUAN X. Thermal analysis and experimental study on the spindle of the high-speed machining Center[J]. Aasri Procedia, 2012, 1(4): 207-212. |
| [8] |
MA C, MEI X, YANG J, et al. Thermal characteristics analysis and experimental study on the high-speed spindle system[J]. The International Journal of Advanced Manufacturing Technology, 2015, 79(1): 469-489. |
| [9] |
DU Z C, YAO S Y, YANG J G. Thermal behavior analysis and thermal error compensation for motorized spindle of machine tools[J]. International Journal of Precision Engineering and Manufacturing, 2015, 16(7): 1571-1581. DOI:10.1007/s12541-015-0207-x |
| [10] |
HAN J, WANG L, WANG H, et al. A new thermal error modeling method for CNC machine tools[J]. The International Journal of Advanced Manufacturing Technology, 2012, 62(1): 205-212. |
| [11] |
王时龙, 杨勇, 周杰, 等. 大型数控滚齿机热误差补偿建模[J]. 中南大学学报:自然科学版, 2011, 42(10): 3066-3072. WANG Shi-long, YANG Yong, ZHOU Jie, et al. Modeling of thermal error compensation of large-scale numerical control gear hobbing machine[J]. Journal of Central South University:Science and Technology, 2011, 42(10): 3067-3072. |
| [12] |
李逢春, 王海同, 李铁民. 重型数控机床热误差建模及预测方法的研究[J]. 机械工程学报, 2016, 52(11): 154-160. LI Feng-chun, WANG Hai-tong, LI Tie-min. Research on thermal error modeling and prediction of heavy CNC machine tools[J]. Journal of Mechanical Engineering, 2016, 52(11): 154-160. |
| [13] |
LI Y, ZHAO W. Axial thermal error compensation method for the spindle of a precision horizontal machining center[C]//IEEE International Conference on Mechat-ronics and Automation. Chengdu: IEEE, 2012: 2319-2323.
|
| [14] |
YANG J, SHI H, FENG B, et al. Thermal error modeling and compensation for a high-speed motorized spindle[J]. The International Journal of Advanced Manufacturing Technology, 2015, 77(5): 1005-1017. |
| [15] |
TAN B, MAO X, LIU H, et al. A thermal error model for large machine tools that considers environmental thermal hysteresis effects[J]. International Journal of Machine Tools & Manufacture, 2014, 82-83(7): 11-20. |
| [16] |
YAN J Y, YANG JG. Application of synthetic grey correlation theory on thermal point optimization for machine tool thermal error compensation[J]. The International Journal of Advanced Manufacturing Technology, 2009, 43(11): 1124-1132. |
| [17] |
张毅, 杨建国. 基于灰色理论预处理的神经网络机床热误差建模[J]. 机械工程学报, 2011, 47(7): 134-139. ZHANG Yi, YANG Jian-guo. Modeling for machine tool thermal error based on grey model preprocessing neural network[J]. Journal of Mechanical Engineering, 2011, 47(7): 134-139. |
| [18] |
ABDULSHAHED A M, LONGSTAFF A P, FLETCHERS, et al. Thermal error modelling of machine tools based on ANFIS with fuzzy c-means clustering using a thermal imaging camera[J]. Applied Mathematical Modelling, 2015, 39(7): 1837-1852. DOI:10.1016/j.apm.2014.10.016 |
| [19] |
HUANG Y, ZHANG J, LI X, et al. Thermal error modeling by integrating GA and BP algorithms for the high-speed spindle[J]. The International Journal of Advanced Manufacturing Technology, 2014, 71(9): 1669-1675. |
| [20] |
YANG J, SHI H, FENG B, et al. Applying neural network based on fuzzy cluster pre-processing to thermal error modeling for coordinate boring machine[J]. Procedia Cirp, 2014, 17: 698-703. DOI:10.1016/j.procir.2014.01.080 |
| [21] |
马驰, 赵亮, 梅雪松, 等. 基于粒子群算法与BP网络的机床主轴热误差建模[J]. 上海交通大学学报, 2016, 50(5): 686-695. MA Chi, ZHAO Liang, MEI Xue-song, et al. Thermal error modeling of machine tool spindle based on particle swarm optimization and neural network[J]. Journal of Shanghai Jiaotong University, 2016, 50(5): 686-695. |
| [22] |
徐文龙. 高速铣削电主轴热特性分析及热误差补偿方法研究[D]. 广东: 广东工业大学, 2016. XU Wen-long. Thermal characteristics analysis and thermal error compensation method of high-speed milling motor spindle[D]. Guangdong: Guangdong University of technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-11845-1016156999.htm |
| [23] |
王志强. 基于ANSYS的高速电主轴温度场分析[D]. 兰州: 兰州理工大学, 2011. WANG Zhi-qiang. Temperature field analysis of motorized spindle based on ANSYS[D]. Lanzhou: Lanzhou University of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10731-1011134210.htm |
| [24] |
HARRIST A. Rolling Bearing Analysis[M]. 3th ed. Wiley: CRC Press, 1991, 540-560.
|



