当前大多公司依赖集成供应链保持竞争力[1].激烈的竞争环境已经促使很多公司利用新兴市场较低的生产成本,扩展他们的供应链到低成本地区,这也导致了更复杂的供应链系统[2].在一个复杂的动态的环境中, 尤其当供应链面对中断风险时, 管理供应链活动是一个极具挑战性的工作[3].供应中断是指意料之外的事件造成供应者无法按时供货, 导致供应链上的生产者无法生产、下游客户需求无法满足的状况[4].
供应、生产和配送是供应链的主要运作职能.要实现一个高效能的供应链,关键是集成这3个职能以一种协调的方式联合调度,集成决策在处理供应链中断风险中展示了它的有效性[5].
如今有较多的关于集成生产、配送的调度问题研究,集成供应部分的研究较少,供应通常被单独考虑[6].例如:Li等[7]研究了一个集成装配和多目的地空运配送的电子产品供应链网络,问题被拆成了2部分,空运安排是通过混合整数规划模型来构建和解决,装配调度问题通过2个启发式算法解决.Lei等[8]研究了一个集成生产、库存和配送路径的问题,提出了一个融合启发式路径算法的混合整数规划方法来协调生产、库存和配送.
集成生产和配送运作问题主要是确定性调度模型,而供应链风险管理主要聚焦于中断风险下供应者选择和订单数量分配,以期找到供应中断风险下合适的缓解和应急策略[9-10].Ruiz-Torres等[11]研究了一个由多个制造者和多个零部件供应者组成的两级供应链,建立了一个考虑中断-应急计划的供应者选择和订单分派混合整数规划模型,目标函数是总成本最小,并对供应者的供应柔性和供应稳定性进行了灵敏度分析,发现应急计划可以降低总供应成本. Sawik[12]研究了一个集成供应、生产、配送调度的供应链网络,建立了多周期、双目标混合整数规划模型,以总成本和服务水平归一化后的加权和为目标函数,对供应组合和订单分派进行决策,通过不同的运输方式的对比分析,发现对于所有运输方式,均有服务导向的供应组合比成本导向的供应组合更分散化的特点.
本文主要研究了制造业企业的供应、制造、配送的三级联合调度问题,建立了两阶段、双目标、多周期混合整数规划模型,将中断风险下的供应者选择、生产配送调度进行集成决策优化,并对中断情景下基于供应者供应柔性的应急计划进行了决策分析.
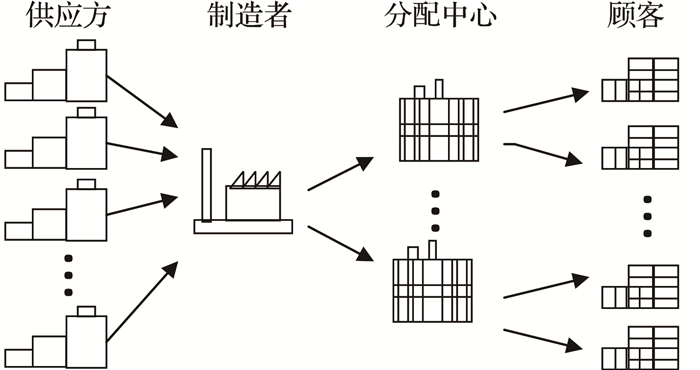
1 问题描述如图 1所示,一个四级供应链,由一个关键零部件的多个供应者,一个产品类型的制造者,多个配送中心,受各配送中心服务的多个顾客构成.基于多生产周期下制造者总供应链成本最低和总体服务水平最优,对供应者选择和订单分配以及生产配送调度进行集成决策研究,并且对可能的供应中断提供应急计划.
|
图 1 四级供应链模型 Fig. 1 Multi-echelon Supply chain model |
供应链模型的索引与集合如下:
制造者:p={1}.
供应者:i∈I={1, …, I}.
客户:j∈J={1, …, J}.
分配中心:k∈K={1, …, K}.
计划周期:t∈T={1, …, T}.
每个供应者都会面临供应中断风险,但是各自的中断风险概率不同.他们均具有一定的供应柔性,当其他供应者发生供应中断时,未中断的供应者可以额外提供一定数量的零件,但不能超出各自的制造能力,除此之外每个供应者的固定订购成本、单位订购成本、交付到制造者的时间也不相同.
每个供应者i∈I的特征参数:
oi:供应者i的单位采购成本.
ei:供应者i的固定采购成本.
σi:供应者i到生产者p的运输时间.
pi:供应者i发生中断的概率.
mi:供应者i的供应量.
mi, max供应者i的最大供应量.
fli:供应者i的柔性参数.
fci:当交付数量超过约定分配数量时,供应者i的额外单位费用.
制造者p每周期具有一定的产能限制,当一周期的产品制造全部完成时,即刻配送至配送中心.配送至不同的分配中心会有不同的运输时间.
制造者p的特征参数:
cp:生产者p每周期的生产量.
τk:生产者p到分配中心k的常量运输时间.
t+τk+1:在周期t装货的产品会在t+τk+1周期交付.
每个客户有不同的需求量、不同的产品交期,同时当产品拖延交货时会有拖延惩罚,当产品未能交货时会有未完成惩罚.
客户j∈J的特征参数:
bj:客户j的需求量.
B:所有客户的总需求量
dj:客户j的订单交付到分配中心k的最晚周期
gj:客户j订单的单位拖延惩罚成本
hj:客户j订单的未完成惩罚成本
所有的中断情景有S=2I种,s∈S={1, …, S}
中断情景s参数:
Ps:情境s概率
Is⊂I:未中断的供应者集合
des, i:情境s下,供应者i是否交付成功, 即判断供应者i交付与否,即它是否中断
Ps的计算公式为
| $ {P_s} = \prod\limits_{i \in {I_s}} {\left( {1 - {p_i}} \right)} \prod\limits_{i \in I\backslash {I_s}} {{p_i}} $ |
为了使研究更具针对性和可行性,对问题做如下假设:
●每个产品成品需要一个这样的关键零部件
●所有顾客的订单在规划周期的开始已知
●来自供应者的订单单独一次性交付
●每个顾客被划分到一个分配中心
●每个客户对应一个订单
●不考虑应急计划造成的拖延
●单个顾客订单能够被生产者在一个单独的计划周期内生产
●以到分配中心的交付期代替客户的交付期
●到分配中心的运输时间是常量,交付日由到分配中心的装货日决定
●不考虑单个顾客的运输时间和成本,运输路径也不是决策的一部分
●不考虑零件和产品的库存
●运输方式只有一种:周期生产完成后,即时运输,不考虑运输成本,只考虑运输时间
●当供应者发生供应中断时,该供应者的订单成本不予考虑
●以配送到分配中心的时间作为配送到供应者的时间.
2 数学模型混合整数规划模型的决策变量:
ui∈{0,1},供应者i是否被选择
vi∈[0, 1],供应者i的订单占总需求的初始分配比例.
ys, i=[0, 1],在情境s下,来自供应者i的订单占总需求的比例.
wjts∈{0, 1},生产安排变量,中断情境s,客户j的订单在周期t安排生产, 同时在周期t+1送到配送中心.即生产占用1个周期.
在中断情景s∈S, 所有客户需求∑j∈Jbj可以划分为3种满意水平:
●未拖延,
●拖延,
●未制造,
τkj这里指的是从制造者p到服务于客户j的分配中心K的运输时间.
各个相关成本如式(1)~(5):
固定订购成本为
| $ {\rm{FE}} = \prod\limits_{i \in I} {{e_i}{u_i}} . $ | (1) |
采购成本为
| $ {\rm{FO}} = \sum\limits_{s \in S} {{P_s}} \sum\limits_{i \in {I_s}} {B{o_i}{y_{s,i}}} ; $ | (2) |
拖延惩罚成本为
| $ {\rm{FG}} = \sum\limits_{s \in S} {{P_s}} \sum\limits_{j \in J} {{g_j}{b_j}\left( {\sum\limits_{t \in T} {w_{jt}^s} - \sum\limits_{t \in T:t \le {d_j} - {\tau _{{k_j}}}} {w_{jt}^s} } \right)} . $ | (3) |
未交付惩罚成本为
| $ {\rm{FH}} = \sum\limits_{s \in S} {{P_s}} \sum\limits_{j \in J} {{g_j}{b_j}\left( {1 - \sum\limits_{t \in T} {w_{jt}^s} } \right)} . $ | (4) |
应急额外订购成本为
| $ {\rm{PC}} = \sum\limits_{s \in S} {\sum\limits_{i \in {I_s}} {{f_{{c_i}}}B\left( {{y_{s,i}} - {v_i}} \right)} } . $ | (5) |
每个产品的期望成本是E1,期望的服务水平是E2,这里期望服务水平E2是通过用未拖延订单数量除以订单总数量的比值来表示.E1、E2归一化后的值分别是f1和f2,定义如下:
| $ {E_1} = \left( {{\rm{FE}} + {\rm{FO}} + {\rm{FG}} + {\rm{FH}} + {\rm{PC}}} \right)/B, $ | (6) |
| $ {E_2} = \sum\limits_{s \in S} {\sum\limits_{j \in J} {\sum\limits_{t \in T:t \le {d_j} - {\tau _{{k_j}}}} {{P_s}{b_j}w_{jt}^s/B} } } , $ | (7) |
| $ {f_1} = \frac{{{E_1} - {{\underline E }_1}}}{{{{\bar E}_1} - {{\underline E }_1}}}, $ | (8) |
式中:E1 E1分别是E1的最小值、最大值.
| $ {f_2} = \frac{{{{\bar E}_2} - {E_2}}}{{{{\bar E}_2} - {{\underline E }_2}}}. $ | (9) |
式中:E2 E2分别是E2的最小值、最大值.
问题的目标函数为
| $ R = \min \lambda {f_1} + \left( {1 - \lambda } \right){f_2};0 \le \lambda \le 1. $ | (10) |
参数λ用来设置不同的成本与服务偏好.
供应组合选择约束:
| $ \sum\limits_{i \in I} {{v_i}} = 1. $ | (11) |
| $ {v_i} \le {u_i};i \in I. $ | (12) |
| $ B{v_i}\left( {1 + {f_{{l_i}}}} \right) \le {u_i}{m_{i,\max }};i \in I. $ | (13) |
| $ B{y_{s,i}} \le B{v_i}\left( {1 + {f_{{l_i}}}} \right)d{e_{s,i}};i \in I,s \in S. $ | (14) |
| $ B{y_{s,i}} \ge B{v_i}d{e_{s,i}};i \in I,s \in S. $ | (15) |
| $ B\left( {{y_{s,i}} - {v_i}} \right)d{e_{s,i}};i \in I,s \in S. $ | (16) |
客户订单安排约束:
| $ \sum\limits_{t \in T} {w_{jt}^s} \le 1;j \in J,s \in S. $ | (17) |
| $ \sum\limits_{j \in J} {{b_j}w_{jt}^s} \le {C_p};t \in T,s \in S. $ | (18) |
供应生产协调约束:
| $ \sum\limits_{j \in J} {\sum\limits_{t' \in T:t' \le t} {{b_j}w_{jt}^s} } \le B\sum\limits_{i \in {I_s}:{\sigma _i} \le t - 1} {{v_i}} ;s \in S. $ | (19) |
非负和整数条件:
| $ {u_i} \in \left\{ {0,1} \right\};i \in I. $ | (20) |
| $ {v_i} \in \left[ {0,1} \right];i \in I. $ | (21) |
| $ w_{jt}^s \in \left\{ {0,1} \right\};j \in J,t \in T,s \in S. $ | (22) |
约束(11)~(16)定义了一个可行的供应组合.
约束(17)~(18)定义了每个中断情景下的规划周期内可行的顾客订单安排.
约束(19)定义了供应生产协调约束,确保每个中断情景s,到t周期为止,所有顾客订单的累积需求不大于到t-1周期为止的累积供应(来自非中断供应者i∈Is)
约束(20)~(22)确保了非负和整数条件.
最小化(10)满足约束:(6)~(9),(11)~(22)
E1、E1、E2、E2通过求解2个混合整数模型获得:
最小化E1, 受约束于(11)~(22)
最大化E2, 受约束于(11)~(22)
提出的模型是两阶段混合整数规划模型,在这个混合整数规划模型中, 第1阶段的决策是包含将来结果的不确定性,第2阶段的决策是在第1阶段将潜在的结果综合评估得出一种决策组合之后,再在此决策下考虑各种可能的中断情景.
第1阶段决策变量是ui和vi,在不知道任何特定情境结果的情况下获得的,目标函数是考虑所有中断可能的情况下最小化(10).
第2阶段是决策变量是ys, i,目标函数是在第1阶段决策基础上,针对各种可能的中断情景,进行再次决策优化,分别给出最优决策.
这个模型是一个综合的决策模型,把第1和第2阶段决策包含在一起,在不同阶段求解时带入变量不同.解决小规模的问题,可以通过此模型利用商业整数规划软件方便求解.本研究中使用了IBM ILOG CPLEX 12.6.3与微软EXCEL+VBA.
3 数值实验供应链由电子产品的多个零件供应商、单个成品(例如智能手机)的制造商、和一组服务于特定顾客的分配中心构成.每周期产品由制造商完成后立即运往配送中心.
在这个案例中制造者生产单周期能力限制为
| $ {c_p} = 4000. $ |
供应者信息如表 1所示,描述了9个供应者各供应能力、供应柔性、订货成本、中断概率、运送时间等输入参数的具体值.
| 表 1 供应者参数 Table 1 Suppliers parameter |
客户信息如表 2所示,描述了K1、K2、K3这3个配送中心所服务的15个不同客户的各个订单需求量、惩罚成本、交期等不同参数行为下的响应.
| 表 2 客户需求信息 Table 2 Customersdemand information |
未考虑应急计划得到的初始供应组合及相关参数如表 3所示,详细展示了不同λ的供应组合及供应组合的综合成本和服务水平的具体信息.
| 表 3 初始供应组合(未考虑应急计划) Table 3 Initial Supplyportfolio(without contingency) |
如图 2所示为不考虑应急计划时,不同λ下供应决策组合和对应组合下的期望成本和服务水平.可以看出随着λ值变大,即由服务偏好转向成本偏好,供应组合决策越来越集中于价格较低的供应者,但是受供应者的供应能力和供应周期限制,不得不选择部分服务水平高、供应周期短但价格较高的供应者.随着服务偏好转向成本偏好,期望供应成本和期望服务水平均呈现了下降趋势.

|
图 2 不同λ下的初始供应组合和期望表现 Fig. 2 Initial supply portfolio and their expected performance under different λ |
取λ=0.5,即对服务水平和成本有相同的偏好时,在第1阶段未考虑应急计划的集成决策基础上,对初始供应组合进行第2阶段的应急计划决策,使得当发生供应中断时,采取的应急计划决策是此情景下的最优决策,总共有S =2I=29=512种中断组合,每种组合都有每种中断情景的应急计划如表 4所示,S代表供应情景,s1是正常供应, s2是供应者9发生中断, s512是所有供应者均发生中断.
| 表 4 当λ=0.5时所有中断组合的应急计划表 Table 4 Contingency planning of all disruption scenarios under λ=0.5 |
如表 4所示为每种情景下的决策,表中δY为应急计划的服务水平,δN为非应急计划的服务水平,ηY为应急计划成本,ηN为非应急计划成本.通过对比非中断情景、中断应急、中断非应急3种情况的服务水平和成本,不难发现,在中断发生时,采取应急计划相比不采取应急计划在维持甚至降低供应成本的情况下可以显著提高制造者的服务水平.
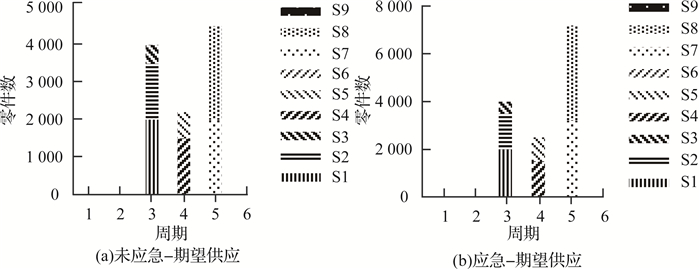
如图 3和4所示为取λ=0.5, 供应者S9发生供应中断时,对采取应急计划与不采取应急计划的供应、生产、配送进行了图视化直观对比.
|
图 3 λ=0.5供应者9发生供应中断时应急计划与非应急计划下的供应 Fig. 3 Supply scenarios of contingency and non-contingency under λ=0.5 and supplier 9 failed |
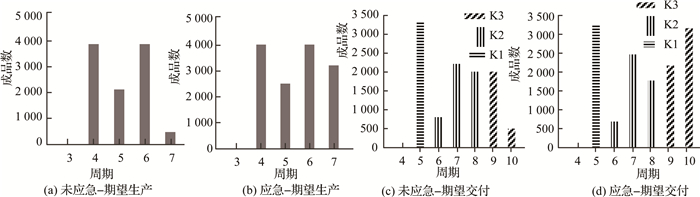
|
图 4 λ=0.5供应者9发生供应中断时应急计划与非应急计划下的生产、配送 Fig. 4 production and distribution scenarios of contingency and non-contingency under λ=0.5 and supplier 9 failed |
当S9发生供应中断时,S9的供应3 000会分配给S5、S7、S8,分别是300、1 200、1 500.结果, 不采取应急计划的服务水平62.77%,采取应急计划的服务水平86.86%,正常供应成本305 215元,采取应急计划成本306 628元.
4 结论本文研究了一个集成供应者的选择和生产分配调度的三级供应链,供应者存在供应柔性,当某一供应者供应失败时,可以额外提供一定量的订单需求.交付的运输方式选择了周期生产完成后即刻送到客户需求终端.
模型包含了供应-生产约束、生产-分配约束、供应-配送约束,协调供应、生产、配送调度.
通过商业数学规划软件CPLEX、Excel、VBA协调计算,得到基于真实问题的数值实验结果,发现:
(1) 当λ的值不同时,即成本与服务水平的不同偏好时,服务导向的偏好(λ≤0.3)倾向于选用更多的供应商和更稳定的供应商,而成本导向的偏好(λ≥0.7)倾向于选择更少的供应商、成本更低的供应商,但都服从了供应周期和供应者生产能力的限制.当λ=0,即只考虑服务水平时,期望服务水平达到100%,而此时期望成本也达到了最高.当λ=1,即只考虑成本时,期望成本最小,而期望服务水平只有不到50%.
(2) 当λ=0.5,即成本和服务水平偏好程度相同时,第2阶段决策,发现考虑供应者柔性的中断应急计划在不改变甚至减少供应链成本的情况下,提高了供应者服务水平.从而保证了中断发生时的期望成本和期望服务水平都不会受到损失.
尽管实验结果与参数设置有关,但结果显示的趋势是与参数无关的,生产者可以根据服务与成本的偏好不同采取不同的供应策略,与供应商协定供应柔性是一个很好的缓和供应中断风险的方式.
将来的研究,可以更多的基于大量企业供应链数据,建立相应数学模型,然后进行实验结果与实际结果的对比,再进行可行性研究.
| [1] |
HOULIHAN J B. International supply chain management[J]. International Journal of Physical Distribution & Materials Management, 1985, 15(1): 22-38. |
| [2] |
TANG S Y, GURNANI H, GUPTA D. Managing disruptions in decentralized supply chains with endogenous supply process reliability[J]. Production and Operations Management, 2014, 23(7): 1198-1211. DOI:10.1111/poms.2014.23.issue-7 |
| [3] |
CHOPRA S, SODHI M S. Reducing the risk of supply chain disruptions[J]. MIT Sloan Management Review, 2014, 55(3): 73. |
| [4] |
HOU J, ZENG A Z, ZHAO L. Coordination with a backup supplier through buy-back contract under supply disruption[J]. Transportation Research Part E:Logistics and Transportation Review, 2010, 46(6): 881-895. DOI:10.1016/j.tre.2010.03.004 |
| [5] |
GURNANI H, MEHROTRA A, RAY S. Supply chain disruptions:Theory and practice of managing risk[J]. Ssrn Electronic Journal, 2011, 1-19. |
| [6] |
ERENGÜÇ Ş, SIMPSON N C, VAKHARIA A J. Integrated production/distribution planning in supply chains:an invited review[J]. European Journal Of Operational Research, 1999, 115(2): 219-236. DOI:10.1016/S0377-2217(98)90299-5 |
| [7] |
LI K P, GANESAN V K, SIVAKUMAR A I. Synchronized scheduling of assembly and multi-destination air-transportation in a consumer electronics supply chain[J]. International Journal of Production Research, 2005, 43(13): 2671-2685. DOI:10.1080/00207540500066895 |
| [8] |
LEI L, LIU S, RUSZCZYNSKI A, et al. On the integrated production, inventory, and distribution routing problem[J]. ⅡE Transactions, 2006, 38(11): 955-970. |
| [9] |
MERZIFONLUOGLU Y. Risk averse supply portfolio selection with supply, demand and spot market volatility[J]. Omega, 2015, 57: 40-53. DOI:10.1016/j.omega.2015.03.006 |
| [10] |
RUIZ-TORRES A J, Mahmoodi F. The optimal number of suppliers considering the costs of individual supplier failures[J]. Omega, 2007, 35(1): 104-115. DOI:10.1016/j.omega.2005.04.005 |
| [11] |
RUIZ-TORRES A J, Mahmoodi F, Zeng A Z. Supplier selection model with contingency planning for supplier failures[J]. Computers & Industrial Engineering, 2013, 66(2): 374-382. |
| [12] |
SAWIK T. Integrated supply, production and distribution scheduling under disruption risks[J]. Omega, 2016, 62: 131-144. DOI:10.1016/j.omega.2015.09.005 |


