2. 浙江大学 浙江省海洋可再生能源电气装备与 系统技术研究重点实验室, 浙江 杭州 310027;
3. 国网冀北电力有限公司电力科学研究院, 北京 100026
2. Zhejiang Provincial Key Laboratory of Electrical Equipment and Systems on Marine Renewable Energy, Zhejiang University, Hangzhou 310027, China;
3. Electric Power Research Institute of State Grid Jibei Electric Power Limited Company, Beijing 100026, China
大区互联电网的出现和扩张,提高了系统发输电的经济性和可靠性,实现了资源的大范围优化配置.但是系统互联带来的区域低频振荡问题日益突出,严重危及了电力系统的安全稳定运行,甚至超越暂态稳定问题,成为系统安全稳定运行的主要障碍[1-2].2001年,华东电网与福建电网互联初期,发生了联络线功率低频振荡现象[3].2005年9月,蒙西电网发生了3次相对于华北主网的低频振荡[4].华北电网一直存在着蒙西-山东振荡模式,当华北电网出现大功率缺额时,蒙西-山东振荡模式呈负阻尼,从而诱发互联区域间的功率振荡,制约了省间功率的输送[5-6].因此,迫切需要对区域间低频振荡采取有效的抑制措施.
特征值灵敏度可以定量地给出某振荡模式随着系统参数变化的发展趋势,是小干扰稳定分析中的手段之一.现有文献中,特征值灵敏度大致可以分为解析法和数值微分两种方法.解析法是基于数学推导特征值与系统参数关系的显示表达式的严格数学方法,如文献[6, 7]中详细推导临界特征值对系统参数(元件参数、运行参数和传递函数等)的灵敏度解析表达式,问题最终转化为求解系统矩阵元素对相应参数的灵敏度计算过程.Luo等[8]提出基于连续的不变子空间方法,求解特征值灵敏度,避免了采用传统解析法求解灵敏度时需要求解维数庞大的左特征向量.当状态方程系数矩阵A中的元素对参数可严格解析时,这类方法可以通过公式推导,直接快速计算结果.该类方法的不足之处是当系数矩阵元素对参数的一阶导数不易直接求导[9]时,即两者存在复杂的隐式关系,如参数为系统运行参数(如节点注入功率、节点电压等)或者传递函数(如PSS传递函数等).
数值微分方法是基于灵敏度的数值微分定义,利用若干离散点进行相关导数的近似计算并最终得出结果.差商法又称为摄动法,是计算特征值灵敏度的常用方法之一.Chung等[10]在算例仿真中,利用摄动法计算特征值对运行参数的灵敏度作为分析依据,肯定了摄动法进行灵敏度计算的有效性.Dong等[9]的研究结论表明,差商法需要选择合适的摄动步长结果,较好地逼近解析法的计算效果.除了差商法,较常见的一阶数值微分方法还有插值法、正则化方法等[11-12].当针对实际大规模电力系统进行灵敏度分析计算时,系统中动态模型不准(负荷模型时变[13])等因素使得解析法的结果不适用;数值微分算法甚至可以不依赖系统模型,通过参数扰动前、后的数据轨迹直接计算结果,成为一种数据驱动计算方法[14].
本文系统地研究差商法、插值法和改进正则化法3种数值微分方法的方法原理,从步长选择和样本误差影响两个方面对比分析3种方法的特点,提出利用商业软件,基于数值微分方法的阻尼灵敏度自动计算流程.通过实际算例,对比研究3种方法在阻尼灵敏度的特点、验证方法的可行性及有效性.
1 灵敏度理论基础电力系统的数学模型可以由如下的代数微分方程表示:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\dot x}} = f\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},p} \right),\\ 0 = g\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}},p} \right). \end{array} \right\} $ | (1) |
式中:x ∈Rn表示状态变量;y ∈Rn表示代数变量;p∈R为某一系统参数;f和g分别为n维和m维的非线性向量值函数.
当开展电力系统小干扰稳定分析时,在稳态平衡点(x0,y0)附近,对式(1)所描述的动态系统进行线性化,可得
| $ \left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{\dot x}}}\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&\mathit{\boldsymbol{B}}\\ \mathit{\boldsymbol{C}}&\mathit{\boldsymbol{D}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{x}}}\\ {\Delta \mathit{\boldsymbol{y}}} \end{array}} \right]. $ | (2) |
进一步可得
| $ \Delta \mathit{\boldsymbol{\dot x}} = {\mathit{\boldsymbol{A}}_{{\rm{sys}}}}\Delta \mathit{\boldsymbol{x}}. $ | (3) |
式中:Asys=A -BD-1C.
Asys的特征值为电力系统稳定性提供了有效判据.在特征值分析中,任意的振荡模式λ=σ±jω,可以计算相应的阻尼比,刻画了电力系统受到扰动后的稳定性能:
| $ \xi = - \frac{\sigma }{{\sqrt {{\sigma ^2} + {\omega ^2}} }}. $ | (4) |
假设阻尼比随p变化的特性用ξ(p)来表示,引入阻尼灵敏度这一指标来考察系统在平衡点附近的阻尼比变化特性:
| $ \frac{{{\rm{d}}\xi \left( p \right)}}{{{\rm{d}}p}} = \frac{{{\rm{d}}\xi }}{{{\rm{d}}\lambda }}\frac{{{\rm{d}}\lambda }}{{{\rm{d}}p}}. $ | (5) |
式中:系统参数p包含元件参数、运行参数及传递函数等.由式(5)可知,精确的阻尼灵敏度必须通过求解特征值灵敏度得到,当后者无法简单获得解析表达式时,可以借助数值微分方法来进行求解.
2 基于数值微分的阻尼灵敏度计算数值微分法的原理是利用原始函数的一些离散点,构造特定函数来近似代替原始函数,然后将构造函数的导数作为原始函数的近似导数.
基于数值微分法的灵敏度计算过程大致如下:a)通过若干次摄动获得参数离散点序列;b)分别计算每个参数离散点对应运行状态的系统特征值及阻尼比;c)构造ξ(p)的近似函数g(p);d)将近似函数的导数g′(pi)作为原函数导数ξ′(pi)的近似值.
具体来说,将系统参数稳定运行点p=p0以摄动步长Δp分别向递增和递减方向进行摄动,记摄动点pi为
| $ {p_i} = {p_0} + i\Delta p;i = 0, \pm 1, \pm 2, \cdots . $ | (6) |
计算相应的阻尼比,将相应的真值函数值记为ξi.借鉴实测系统中的测量概念,将实际计算值
| $ \left| {{{\tilde \xi }_i} - {\xi _i}} \right| \le \delta . $ | (7) |
式中:δ为样本数据的测量误差.
根据近似函数g(p)和离散点个数的选取,研究3种常见数值微分方法在阻尼灵敏度计算中的应用,包括差商法、插值法及改进Tikhonov正则化法.
2.1 差商法在差商法中,通过2个离散点计算确定近似函数g(p).已知在当前系统参数p=p0处,阻尼比的初始值为
| $ \xi '\left( {{p_0}} \right) \approx \frac{{{{\tilde \xi }_1} - {{\tilde \xi }_0}}}{{\Delta p}}. $ | (8) |
利用差商法进行灵敏度的近似计算,存在如下两种误差.
1) 截断误差.当不考虑阻尼比测量误差时,基于Taylor展开,可以得到解析导数与差商法计算的近似导数之间的关系,如下:
| $ \xi '\left( {{p_0}} \right) = \frac{{{\xi _1} - {\xi _0}}}{{\Delta p}} + o\left( {\Delta p} \right). $ | (9) |
截断误差ο(Δp)与步长Δp成线性关系,Δp越大,误差越大.
2) 舍入误差.在通常情况下,系统阻尼比计算存在一定的舍入误差.当考虑如式(7)所示的测量误差时,利用差商法求一阶导数的误差可以表示为
| $ \left| {\frac{{{{\tilde \xi }_1} - {{\tilde \xi }_0}}}{{\Delta p}} - \xi '\left( {{p_0}} \right)} \right| \le o\left( {\Delta p + \frac{\delta }{{\Delta p}}} \right). $ | (10) |
差商法对测量误差非常敏感,当Δp较小时,误差随着Δp的减小而增大.后续的插值法存在由样本点测量误差造成的灵敏度舍入误差,故不再赘述,只分析不考虑测量误差的阻尼比计算值的截断误差.
2.2 插值法当选取插值函数作为近似函数时,相应的灵敏度计算是数值微分中常见的插值法.较常见的插值法有三点插值法和五点插值法,即分别需要3个及5个离散点用于计算.选取计算精度较高的五点插值法及相应的四次Lagrange插值多项式作为近似函数g(p).当Lagrange插值函数收敛于原函数时,插值函数的导数不一定收敛于原函数的导数,故引入具有数值稳定性更好的样条插值函数.讨论四次Lagrange插值和三次样条插值两种插值函数下的误差分析.
2.2.1 四次Lagrange插值选取g(p)为四次Lagrange插值多项式,已知5个参数摄动点pi(i=0, ±1, ±2)及阻尼比计算值为
| $ g\left( p \right) = \sum\nolimits_i {{{\tilde \xi }_i}{c_i}\left( p \right)} . $ | (11) |
插值基函数为
| $ {c_i}\left( p \right) = \prod\limits_{\begin{array}{*{20}{c}} {j = - 2}\\ {j \ne i} \end{array}}^2 {\frac{{p - {p_j}}}{{{p_i} - {p_j}}}} . $ | (12) |
对式(11)求导化简,可得在p=p0处近似的系统阻尼灵敏度:
| $ \begin{array}{l} \xi '\left( {{p_0}} \right) \approx g'\left( {{p_0}} \right)\left| {_{p = {p_0}}} \right. = \frac{1}{{12\Delta p}}\left[ {{{\tilde \xi }_{ - 2}} - 8{{\tilde \xi }_{ - 1}} + } \right.\\ \;\;\;\;\;\;\left. {8{{\tilde \xi }_1} - {{\tilde \xi }_2}} \right]. \end{array} $ | (13) |
由式(13)可见,利用四次Lagrange插值的一阶导数计算公式求解灵敏度,需要4个样本点.
基于插值余项定理可知,四次插值余项为
| $ R\left( p \right) = \xi \left( p \right) - g\left( p \right) = \frac{{{g^{\left( 5 \right)}}\left( \tau \right)}}{{5!}}\omega \left( p \right). $ | (14) |
式中:
对式(14)两端关于p求导,可得四次Lagrange插值型数值微分的截断误差:
| $ \begin{array}{l} R'\left( p \right) = \xi '\left( p \right) - g'\left( p \right) = \\ \frac{{{g^{\left( 5 \right)}}\left( \tau \right)}}{{5!}}\omega '\left( p \right) + \frac{{\omega \left( p \right)}}{{5!}}\frac{{\rm{d}}}{{{\rm{d}}p}}{g^{\left( 5 \right)}}\left[ {\tau \left( p \right)} \right]. \end{array} $ | (15) |
将p=p0代入式(15),可得阻尼灵敏度的计算截断误差:
| $ R'\left( {{p_0}} \right) = o\left( {\Delta {p^4}} \right). $ | (16) |
由此可见,四次Lagrange插值型的截断误差随步长Δp的减小而快速减小.
2.2.2 三次样条插值选取g(p)为三次样条插值函数,可以由5个离散点(同2.2.1节)确定.g(p)满足如下条件.
1)g(p)在各子区间(即相邻离散点之间)分别为如下的三次插值多项式函数:
| $ g\left( p \right) = \left\{ \begin{array}{l} \sum\limits_{j = 1}^4 {a_j^{\left( { - 2} \right)}{{\left( {p - {p_{ - 2}}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_{ - 2}},{p_{ - 1}}} \right);\\ \sum\limits_{j = 1}^4 {a_j^{\left( { - 1} \right)}{{\left( {p - {p_{ - 1}}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_{ - 1}},{p_0}} \right);\\ \sum\limits_{j = 1}^4 {a_j^{\left( 0 \right)}{{\left( {p - {p_0}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_0},{p_1}} \right);\\ \sum\limits_{j = 1}^4 {a_j^{\left( 1 \right)}{{\left( {p - {p_1}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_1},{p_2}} \right). \end{array} \right. $ | (17) |
式中:p∈[pi,pi+1)(i=-2, -1, 0, 1)为离散点定义的分段区间.
2)g(p)在每个离散点(首末端点除外)上的2阶导数连续,即
| $ \left. \begin{array}{l} g\left( {p_i^ + } \right) = g\left( {p_i^ - } \right);\\ g'\left( {p_i^ + } \right) = g'\left( {p_i^ - } \right);\\ g''\left( {p_i^ + } \right) = g''\left( {p_i^ - } \right),i = - 1,0,1. \end{array} \right\} $ | (18) |
式中:
| $ {p^ + } = p + \mathop {\lim }\limits_{\Delta p \to {0^ + }} \Delta p,{p^ - } = p + \mathop {\lim }\limits_{\Delta p \to {0^ - }} \Delta p, $ |
在实际计算中,引入非扭结边界条件,即两端点的三阶导数与邻近点的三阶导数相等[15].根据式(18)利用待定系数法可得,三次样条函数系数aj(i)由如下的线性方程组确定:
| $ \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}}, $ | (19) |
| $ \begin{array}{l} \mathit{\boldsymbol{x}} = \left[ {a_1^{\left( { - 2} \right)},a_2^{\left( { - 2} \right)},a_3^{\left( { - 2} \right)},a_4^{\left( { - 2} \right)},a_1^{\left( { - 1} \right)},a_2^{\left( { - 1} \right)},a_3^{\left( { - 1} \right)},} \right.\\ \;\;\;\;\;\;{\left. {a_4^{\left( { - 1} \right)},a_1^{\left( 0 \right)},a_2^{\left( 0 \right)},a_3^{\left( 0 \right)},a_4^{\left( 0 \right)},a_1^{\left( 1 \right)},a_2^{\left( 1 \right)},a_3^{\left( 1 \right)},a_4^{\left( 1 \right)}} \right]^{\rm{T}}}, \end{array} $ | (20) |
| $ \mathit{\boldsymbol{b}} = {\left[ {0,0,0,0,0,0,0,0,0,0,0,{{\tilde \xi }_{ - 2}},{{\tilde \xi }_{ - 1}},{{\tilde \xi }_0},{{\tilde \xi }_1},{{\tilde \xi }_2}} \right]^{\rm{T}}}. $ | (21) |
线性方程组系数矩阵A高度稀疏,具体表达式见附录A.通过该稀疏矩阵三角分解,可以快速求解x,进而确定近似函数g(p).对g(p)进行一阶求导,可得灵敏度为
| $ \xi '\left( {{p_0}} \right) \approx \xi '\left( p \right)\left| {_{p = {p_0}}} \right. = a_2^{\left( 0 \right)}. $ | (22) |
截断误差为
| $ \xi '\left( {{p_0}} \right) - g'\left( {{p_0}} \right) = o\left( {\Delta {p^3}} \right). $ | (23) |
从上述误差分析可以看出,四次Lagrange插值灵敏度计算方法的计算精度为四阶,比三次样条插值的计算精度高一阶;从数值稳定性角度考虑,三次样条插值的插值函数具有一致收敛性,克服了Lagrange插值方法可能存在的不收敛缺点[16].
2.3 改进Tikhonov正则化法根据2.1和2.2节的分析可知,差商法和插值法的计算精度不仅由摄动步长Δp决定,还受样本点测量误差的影响,如式(10)中,当Δp→0时,误差估计的上限会趋于无穷大,这说明上述两种方法均可能因样本点测量误差而导致数值不稳定.引入改进Tikhonov正则化法来求解阻尼灵敏度,构建并求解一个近似问题来逼近原问题的解,不存在上述数值稳定性问题[17].
2.3.1 基本原理改进Tikhonov正则化法背后的数学思想为选取的近似函数g(p)尽可能平滑地逼近原函数g(p),具体来说,g(p)在各样本点处的一阶导数变化最小,即g(p)在各样本点的二阶导范数最小.根据附录B,给定2n+1个参数pi (i=0, ±1, ±2, …, ±n)及阻尼计算值
1) 在各分段区间p-n < … <p0 < …pn内达到如下目标泛函最小:
| $ \begin{array}{l} J\left( g \right) = \frac{1}{{2n - 1}}\sum\nolimits_{i = - \left( {n - 1} \right)}^{n - 1} {{{\left( {{{\tilde \xi }_i} - g\left( {{p_i}} \right)} \right)}^2}} + \\ \;\;\;\;\;\alpha \left\{ {\int_{{p_{ - \left( {n - 1} \right)}}}^{{p_{n - 1}}} {{{\left( {g''\left( p \right)} \right)}^2}{\rm{d}}p} + } \right.\\ \;\;\;\;\;\left. {\frac{1}{2}\Delta p\left[ {{{\left( {g''\left( {{p_{ - n}}} \right)} \right)}^2} + {{\left( {g''\left( {{p_n}} \right)} \right)}^2}} \right]} \right\}. \end{array} $ | (24) |
2) 满足下面的性质a)~c):a)g(p)是二阶可导且连续的函数;b)两端点p-n和pn处误差为零,即
加权系数设为α=δ2,δ为测量误差.具体的基本原理的详细介绍参考附录B.
2.3.2 确定近似函数g(p)由附录B推导可知,满足上述条件的最优函数g*为由一系列条件确定的特殊三次样条函数.当仅考虑使用5个参数摄动点pi及相应阻尼比计算值
| $ {g_ * } = \left\{ \begin{array}{l} \sum\limits_{j = 1}^3 {a_j^{\left( { - 2} \right)}{{\left( {p - {p_{ - 2}}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_{ - 2}},{p_{ - 1}}} \right);\\ \sum\limits_{j = 1}^4 {a_j^{\left( { - 1} \right)}{{\left( {p - {p_{ - 1}}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_{ - 1}},{p_0}} \right);\\ \sum\limits_{j = 1}^4 {a_j^{\left( 0 \right)}{{\left( {p - {p_0}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_0},{p_1}} \right);\\ \sum\limits_{j = 1}^3 {a_j^{\left( 1 \right)}{{\left( {p - {p_1}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_1},{p_2}} \right). \end{array} \right. $ | (25) |
三次样条函数系数aj(i)由类似2.2.2节的待定系数法形成一个线性方程组,其中的系数矩阵高度稀疏,最后推导得到的系统阻尼灵敏度表达式如式(22),具体的推导过程可见附录B.
改进Tikhonov正则化方法根据带误差的测量数据重构函数,最优逼近函数是特殊的三次样条函数,受步长影响的性质与三次样条函数相似.
2.4 阻尼灵敏度计算常见的电力系统仿真计算软件如BPA、PSS/E、DIgSILENT等,都具有小干扰稳定分析功能,计算相关振荡模式的特征值和阻尼比.可以利用计算机语言如Python,结合商业软件的小干扰稳定计算与数值微分方法,实现阻尼灵敏度的自动计算.以改进Tikhonov正则化法为例,介绍具体的计算步骤如下.
1) 设定该系统参数的摄动步长Δp,根据数值微分方法的特点,确定参数样本点个数,如改进Tikhonov正则化法需要重新确定4个参数点pi=p0+iΔp(i=±1, ±2).
2) 针对该系统参数的不同取值pi,分别调用小干扰稳定商业软件进行计算,得到相应的带有测量误差的阻尼比
3) 求解特殊三次样条函数系数相关的线性方程组,计算p0处的阻尼灵敏度ξ′(p0)≈a2(0).
评估阻尼灵敏度计算方法的性能需要综合考虑计算量及计算误差.表 1总结了4种数值微分方法的技术特点.各方法的计算量主要由方法涉及的需要重新计算特征值样本点数决定:四次Lagrange插值方法、三次样条插值法和改进型正则化方法3种方法的计算量相同,差商法的计算量最少.各方法的计算误差主要由截断误差和测量误差两个方面决定:当选取相同的摄动步长时,四次Lagrange插值方法的截断误差最小,三次样条插值法和改进型正则化方法次之,差商法的截断误差最大;改进型正则化方法的灵敏度计算结果受测量误差的影响最小,差商法、四次Lagrange插值方法和三次样条插值法的灵敏度计算结果受测量误差的影响较大.综合计算量和计算误差可知,改进型正则化方法的计算性能优于其他数值微分方法.
| 表 1 数值微分方法的技术特点比较 Table 1 Comparison of numerical differentiation methods |
2014年冬季,在特高压南送5 800 MW,山东对外送电方式,华北电网存在2个阻尼较弱的区域间振荡模式,如表 2所示.山西-山东-内蒙振荡模式(简称模式1)的阻尼比为0.011 2,山东-内蒙振荡模式(简称模式2)的阻尼比为0.038 7,其中模式1不满足国网公司电力系统安全稳定计算规定中关于小干扰稳定性的运行要求(阻尼比大于0.03),成为制约华北电网动态稳定水平的关键模式.利用差商法、四次Lagrange插值、三次样条插值及改进型正则化方法4种数值微分方法,对于振荡模式1和模式2,分析阻尼比对振荡区域的机组有功出力灵敏度.该仿真软件选用PSD-BPA小干扰稳定程序进行小干扰稳定分析计算[18],阻尼比测量误差设为δ=10-6.
| 表 2 小干扰稳定性分析结果(λ=σ±jω) Table 2 Result of small signal stability analysis |
采用如下的标准差指标来验证各种数值微分方法中样本点摄动步长对灵敏度计算结果的影响:
| $ {\rm{SD}} = \sqrt {\frac{1}{{n - 1}}\sum\nolimits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} } . $ | (26) |
式中:xi为利用某种数值微分方法基于摄动步长为Δpi的特征值样本点求得的灵敏度;
为了衡量步长选取对各种数值微分方法的影响程度,以振荡模式1的阻尼比对机组“鲁邹县F”出力的灵敏度为例,表 3列出4种数值微分方法基于多种步长的样本序列的灵敏度计算结果.
| 表 3 振荡模式1阻尼比对“鲁邹县F”出力灵敏度 Table 3 Sensitivity of damping ratio of mode 1 to power generation of Luzouxian F |
由表 3可知,针对多种步长的样本序列进行灵敏度计算,采用差商法得到的计算结果标准差最大,即差商法的计算精度受步长的影响最大.四次Lagrange插值的计算结果与三次样条插值的计算结果基本一致.改进型正则化方法考虑了小干扰稳定计算时的舍入误差,并且受步长选取的影响较小,因此相应的标准差最小.
表 4列出4种数值微分方法基于多种步长的样本序列的山东-内蒙振荡阻尼比对“蒙乌新G1”机组出力灵敏度计算结果,与表 3的结论一致.
| 表 4 模式2阻尼比对“蒙乌新G1”出力灵敏度 Table 4 Sensitivity of damping ratio of mode 1 to power generation of Mengwuxin G1 |
利用数值微分方法,分别基于多种摄动步长对山西、山东、内蒙3个区域所有机组出力进行阻尼比灵敏度计算,然后计算相应的标准差以衡量该方法对所有机组灵敏度计算的整体适用性能.图 1展示了针对山西、山东、内蒙共535台机组,利用差商法、三次样条插值法及改进型正则化方法这3种数值微分方法,基于多种步长的测量样本组的计算结果标准差.图中,GenNo为机组编号,SD为机组灵敏度计算结果的标准差.由图 1可见,差商法计算的阻尼比对各机组灵敏度的标准差都较大,因此差商法受步长选取差异的影响最大;三次样条插值法和改进型正则化方法受步长差异的影响较小,灵敏度计算结果较精确.相较于三次样条插值法,由于改进型正则化方法考虑了样本点本身的计算误差,阻尼比对各机组的灵敏度计算误差整体都较小.
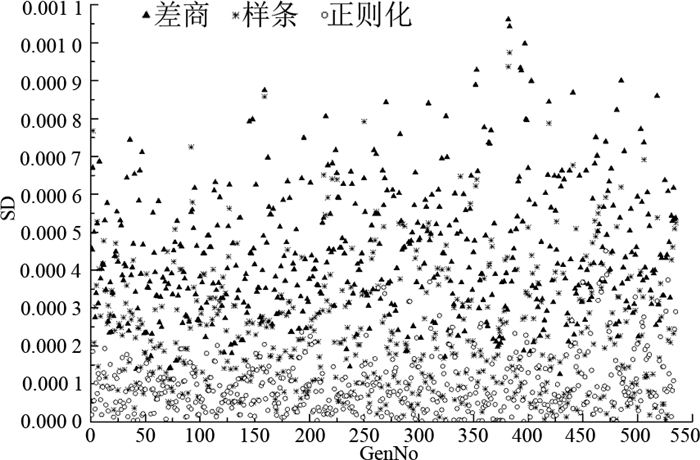
|
图 1 基于各数值微分方法的灵敏度计算标准差 Fig. 1 Standard deviation of sensitivity calculated by several numerical differentiation |
从步长鲁棒性和样本测量误差影响两个角度,对差商法、插值法和改进Tikhonov正则化法等多种数值微分计算方法进行比较分析.正则化方法进行灵敏度计算时受步长选取的影响较小,还考虑了小干扰稳定分析程序对大规模电力系统计算特征值时的舍入误差,计算结果的稳定性较好.结合商业软件的小干扰稳定分析程序与数值微分方法,代替了目前大规模电力系统低频振荡阻尼灵敏度的解析计算,创建了快速自动化的灵敏度计算工具.
附录A 三次样条函数利用三次样条函数求解阻尼灵敏度至少需要5个离散点.为了减少计算量,考虑用5个样本点
| $ g\left( p \right) = \left\{ \begin{array}{l} \sum\limits_{j = 1}^4 {a_j^{\left( { - 2} \right)}{{\left( {p - {p_{ - 2}}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_{ - 2}},{p_{ - 1}}} \right);\\ \sum\limits_{j = 1}^4 {a_j^{\left( { - 1} \right)}{{\left( {p - {p_{ - 1}}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_{ - 1}},{p_0}} \right);\\ \sum\limits_{j = 1}^4 {a_j^{\left( 0 \right)}{{\left( {p - {p_0}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_0},{p_1}} \right);\\ \sum\limits_{j = 1}^4 {a_j^{\left( 1 \right)}{{\left( {p - {p_1}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_1},{p_2}} \right). \end{array} \right. $ | (A1) |
式中:系数aj(i)为三次样条函数中分段函数的各次项待定系数,约束条件如下:
| $ g\left( {p_i^ + } \right) = g\left( {p_i^ - } \right),\;\;\;i = - 1,0,1; $ | (A2) |
| $ g'\left( {p_i^ + } \right) = g'\left( {p_i^ - } \right),\;\;\;i = - 1,0,1; $ | (A3) |
| $ g''\left( {p_i^ + } \right) = g''\left( {p_i^ - } \right),\;\;\;i = - 1,0,1; $ | (A4) |
| $ \left\{ \begin{array}{l} g\left( {{p_i}} \right) = {{\tilde \xi }_i},i = - 2, - 1,0,1;\\ g\left( {{{\bar p}_2}} \right) = {{\tilde \xi }_2}. \end{array} \right. $ | (A5) |
| $ {g^{\left( 3 \right)}}\left( {p_{ - 2}^ + } \right) = {g^{\left( 3 \right)}}\left( {{p_{ - 1}}} \right); $ | (A6) |
| $ {g^{\left( 3 \right)}}\left( {p_2^ - } \right) = {g^{\left( 3 \right)}}\left( {{p_1}} \right). $ | (A7) |
其中,g(3)(·)为g(p)的三阶导数.式(A2)~(A4)为三次样条函数条件,式(A5)表示5个离散点满足函数g(p),式(A6)和(A7)为实际计算中引入的非扭结边界条件.将pi=p0+iΔp以及上述条件代入式(A1),经过整理,可得三次样条函数系数由如下的线性方程组确定:
| $ \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}}, $ | (A8) |
| $ \begin{array}{l} \mathit{\boldsymbol{x}} = \left[ {a_1^{\left( { - 2} \right)},a_2^{\left( { - 2} \right)},a_3^{\left( { - 2} \right)},a_4^{\left( { - 2} \right)},a_1^{\left( { - 1} \right)},a_2^{\left( { - 1} \right)},a_3^{\left( { - 1} \right)},a_4^{\left( { - 1} \right)},} \right.\\ {\left. {a_1^{\left( 0 \right)},a_2^{\left( 0 \right)},a_3^{\left( 0 \right)},a_4^{\left( 0 \right)},a_1^{\left( 1 \right)},a_2^{\left( 1 \right)},a_3^{\left( 1 \right)},a_4^{\left( 1 \right)}} \right]^{\rm{T}}}, \end{array} $ | (A9) |
| $ \mathit{\boldsymbol{b}} = {\left[ {0,0,0,0,0,0,0,0,0,0,0,{{\tilde \xi }_{ - 2}},{{\tilde \xi }_{ - 1}},{{\tilde \xi }_0},{{\tilde \xi }_1},{{\tilde \xi }_2}} \right]^{\rm{T}}}, $ | (A10) |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{M}}&{ - {\mathit{\boldsymbol{I}}_4}}&{{{\bf{0}}_{4 \times 4}}}&{{{\bf{0}}_{4 \times 4}}}\\ {{{\bf{0}}_{3 \times 4}}}&\mathit{\boldsymbol{N}}&{ - {\mathit{\boldsymbol{I}}_3}}&{{{\bf{0}}_{3 \times 4}}}\\ {{{\bf{0}}_{4 \times 4}}}&{{{\bf{0}}_{4 \times 4}}}&\mathit{\boldsymbol{M}}&{ - {\mathit{\boldsymbol{I}}_4}}\\ {{\mathit{\boldsymbol{E}}_{11}}}&{{\mathit{\boldsymbol{E}}_{21}}}&{{\mathit{\boldsymbol{E}}_{31}}}&{{\mathit{\boldsymbol{E}}_{41}}} \end{array}} \right]. $ | (A11) |
式中:
| $ \mathit{\boldsymbol{M}} = {\left[ {\begin{array}{*{20}{c}} \begin{array}{l} 1\\ 0\\ 0\\ 0 \end{array}&\begin{array}{l} \Delta p\\ 1\\ 0\\ 0 \end{array}&\begin{array}{l} \Delta {p^2}\\ 2\Delta p\\ 1\\ 0 \end{array}&\begin{array}{l} \Delta {p^3}\\ 3\Delta {p^2}\\ 3\Delta p\\ 1 \end{array} \end{array}} \right]_{4 \times 4}}, $ |
| $ \mathit{\boldsymbol{N}} = {\left[ {\begin{array}{*{20}{c}} \begin{array}{l} 1\\ 0\\ 0 \end{array}&\begin{array}{l} \Delta p\\ 1\\ 0 \end{array}&\begin{array}{l} \Delta {p^2}\\ 2\Delta p\\ 1 \end{array}&\begin{array}{l} \Delta {p^3}\\ 3\Delta {p^2}\\ 3\Delta p \end{array} \end{array}} \right]_{3 \times 4}},\;\;\;{\mathit{\boldsymbol{I}}_n} = {\left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0& \ddots &0\\ 0&0&1 \end{array}} \right]_{n \times n}} $ |
其中,Eij表示5×4维矩阵,且矩阵中的第i行第j列元素为1,其余元素为0.
上述线性方程组系数矩阵A高度稀疏,通过稀疏矩阵三角分解可以快速求解x,进而确定了近似函数g(p).对函数g(p)求解一阶导数,系统阻尼比对系统参数的灵敏度为
| $ g'\left( {{p_0}} \right) \approx g'\left( p \right)\left| {_{p = {p_0}}} \right. = a_2^{\left( 0 \right)}. $ | (A12) |
Tikhonov正则化法背后的数学思想为选取的近似函数g(p)尽可能平滑地逼近原函数,具体来说,g(p)在各样本点处的一阶导数变化最小,即g(p)在各样本点的二阶导范数最小.不失一般性,给定2n+1个参数pi(i=0, ±1, ±2, …, ±n)及阻尼计算值
| $ \begin{array}{*{20}{c}} {\psi \left( p \right) = \xi \left( p \right) + {{\tilde \xi }_{ - n}} - \xi \left( {{p_{ - n}}} \right) + }\\ {\left[ {{{\tilde \xi }_n} - \xi \left( {{p_n}} \right) + \xi \left( {{p_{ - n}}} \right) - {{\tilde \xi }_{ - n}}} \right]p} \end{array} $ | (B1) |
代替原函数ξ(p),易知ψ(p-n)=
构造具有二阶可导且连续的函数g(p)来近似逼近原函数ξ(p),以实现在各分段区间p-n < … <p0 < … <pn内的如下目标泛函最小:
| $ \min \left\{ {\int_{{p_{ - n}}}^{{p_n}} {{{\left( {g''\left( p \right)} \right)}^2}{\rm{d}}p} } \right.. $ | (B2) |
考虑测量误差约束,g(p)须满足:
| $ \frac{1}{{2n - 1}}\sum\nolimits_{i = - \left( {n - 1} \right)}^{n - 1} {{{\left( {{{\tilde \xi }_i} - g\left( {{p_i}} \right)} \right)}^2}} \le {\delta ^2}. $ | (B3) |
引入加权系数α,目标泛函变为
| $ \begin{array}{*{20}{c}} {J\left( g \right) = \frac{1}{{2n - 1}}\sum\nolimits_{i = - \left( {n - 1} \right)}^{n - 1} {{{\left( {{{\tilde \xi }_i} - g\left( {{p_i}} \right)} \right)}^2}} + }\\ {\alpha \int_{{p_{ - n}}}^{{p_n}} {{{\left( {g''\left( p \right)} \right)}^2}{\rm{d}}p} .} \end{array} $ | (B4) |
重构函数g*(p)可由如下问题而得:
| $ {g_ * } = \arg \min J\left( g \right). $ | (B5) |
传统Tikhonov正则化方法要求重构函数在两端点p=p-n和p=pn的二阶导数为零[11];当真值函数ξ(p)不满足该条件时,g′*(p)在端点的逼近误差较大,且样本点数目较少时中间样本点的逼近效果较差.为了克服这个困难,采用文献[17]的改进Tikhonov正则化法,令构造函数g(p)在首、末两个区间[p-n,p-(n-1))和[pn-1,pn]为二次多项式函数,则目标泛函变成:
| $ \begin{array}{l} J\left( g \right) = \frac{1}{{2n - 1}}\sum\nolimits_{i = - \left( {n - 1} \right)}^{n - 1} {{{\left( {{{\tilde \xi }_i} - g\left( {{p_i}} \right)} \right)}^2}} + \\ \alpha \int_{{p_{ - \left( {n - 1} \right)}}}^{{p_{n - 1}}} {{{\left( {g''\left( p \right)} \right)}^2}{\rm{d}}p} + \\ \left. {\frac{1}{2}\Delta p\left[ {{{\left( {g''\left( {{p_{ - n}}} \right)} \right)}^2} + {{\left( {g''\left( {{p_n}} \right)} \right)}^2}} \right]} \right\}. \end{array} $ | (B6) |
简言之,数值微分的求解问题转化为寻找最优逼近函数g*(p),使得g′*(p)平滑逼近ξ′(p).
为了简化计算,改进Tikhonov正则化法的加权系数设置为α=δ2[19].可以推导优化问题(B6)的最优泛函g*为满足如下KKT条件的特殊三次样条函数[17].g*的一般形式如下:
| $ {g_ * }\left( p \right) = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {\sum\limits_{j = 1}^3 {a_j^{\left( i \right)}{{\left( {p - {p_i}} \right)}^{j - 1}}} ,p \in \left[ {{p_i},{p_{i + 1}}} \right),}\\ {i = - n,n;} \end{array}\\ \begin{array}{*{20}{c}} {\sum\limits_{j = 1}^4 {a_j^{\left( i \right)}{{\left( {p - {p_i}} \right)}^{j - 1}}} ,p \in \left[ {{p_i},{p_{i + 1}}} \right),}\\ {i = - \left( {n - 1} \right), \cdots ,n - 1.} \end{array} \end{array} \right. $ | (B7) |
在两端点处满足:
| $ {{\tilde \xi }_{ - n}} = \xi \left( {{p_{ - n}}} \right) = {g_ * }\left( {{p_{ - n}}} \right), $ | (B8) |
| $ {{\tilde \xi }_n} = \xi \left( {{p_n}} \right) = {g_ * }\left( {p_n^ - } \right). $ | (B9) |
样条函数的约束条件如下所示:
| $ {g_ * }\left( {p_i^ + } \right) = {g_ * }\left( {p_i^ - } \right),\;\;\;i = - \left( {n - 1} \right), \cdots ,n - 1; $ | (B10) |
| $ {{g'}_ * }\left( {p_i^ + } \right) = {{g'}_ * }\left( {p_i^ - } \right),\;\;\;i = - \left( {n - 1} \right), \cdots ,n - 1; $ | (B11) |
| $ {{g''}_ * }\left( {p_i^ + } \right) = {{g''}_ * }\left( {p_i^ - } \right),\;\;\;i = - \left( {n - 1} \right), \cdots ,n - 1. $ | (B12) |
KKT条件如下所示:
| $ \begin{array}{*{20}{c}} {\left[ {{g_ * }\left( {{p_{ - \left( {n - 1} \right)}}} \right) - {{\tilde \xi }_{ - \left( {n - 1} \right)}}} \right]\Delta p + }\\ {\alpha \left[ {g_ * ^3\left( {p_{ - \left( {n - 1} \right)}^ + } \right) - \frac{{{{g''}_ * }\left( {{p_{ - n}}} \right)}}{{\Delta p}}} \right] = 0;} \end{array} $ | (B13) |
| $ \begin{array}{*{20}{c}} {\left[ {{g_ * }\left( {{p_i}} \right) - {{\tilde \xi }_i}} \right]\Delta p + \alpha \left[ {g_ * ^3\left( {p_i^ + } \right) - g_ * ^3\left( {p_i^ - } \right)} \right] = 0,}\\ { - \left( {n - 2} \right) \le i \le n - 2;} \end{array} $ | (B14) |
| $ \begin{array}{l} \left[ {{g_ * }\left( {{p_{n - 1}}} \right) - {\xi _{n - 1}}} \right]\Delta p + \alpha \left[ { - g_ * ^{\left( 3 \right)}\left( {p_{n - 1}^ - } \right) - } \right.\\ \left. {\frac{{{{g''}_ * }\left( {p_n^ - } \right)}}{{\Delta p}}} \right] = 0. \end{array} $ | (B15) |
式中:g*(3)(·)为g*(p)的三阶导数.
2 确定近似函数由于g*是三次样条函数,利用改进Tikhonov正则化法求解阻尼灵敏度至少需要5个样本点.为了减少计算量,考虑用5个含测量误差的样本点
| $ {g_ * } = g\left( p \right) = \left\{ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^4 {a_j^{\left( { - 2} \right)}{{\left( {p - {p_{ - 2}}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_{ - 2}},{p_{ - 1}}} \right);}\\ {\sum\limits_{j = 1}^4 {a_j^{\left( { - 1} \right)}{{\left( {p - {p_{ - 1}}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_{ - 1}},{p_0}} \right);}\\ {\sum\limits_{j = 1}^4 {a_j^{\left( 0 \right)}{{\left( {p - {p_0}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_0},{p_1}} \right);}\\ {\sum\limits_{j = 1}^4 {a_j^{\left( 1 \right)}{{\left( {p - {p_1}} \right)}^{j - 1}}} ,\;\;\;p \in \left[ {{p_1},{p_2}} \right).} \end{array}} \right. $ | (B16) |
系数aj(i)为三次样条函数中分段函数的各次项待定系数,约束条件如下:
| $ g\left( {p_i^ + } \right) = g\left( {p_i^ - } \right),\;\;\;i = - 1,0,1; $ | (B17) |
| $ g'\left( {p_i^ + } \right) = g'\left( {p_i^ - } \right),\;\;\;i = - 1,0,1; $ | (B18) |
| $ g''\left( {p_i^ + } \right) = g''\left( {p_i^ - } \right),\;\;\;i = - 1,0,1; $ | (B19) |
| $ \begin{array}{l} \left[ {{g_ * }\left( {{p_{ - 1}}} \right) - {{\tilde \xi }_{ - 1}}} \right]\Delta p + \alpha \left[ {g_ * ^{\left( 3 \right)}\left( {p_{ - 1}^ + } \right) - } \right.\\ \left. {\frac{{{{g''}_ * }\left( {{p_{ - 2}}} \right)}}{{\Delta p}}} \right] = 0; \end{array} $ | (B20) |
| $ \left[ {{g_ * }\left( {{p_0}} \right) - {{\tilde \xi }_0}} \right]\Delta p + \alpha \left[ {g_ * ^{\left( 3 \right)}\left( {p_0^ + } \right) - g_ * ^{\left( 3 \right)}\left( {p_0^ - } \right)} \right] = 0; $ | (B21) |
| $ \left[ {{g_ * }\left( {{p_1}} \right) - {{\tilde \xi }_1}} \right]\Delta p + \alpha \left[ { - g_ * ^{\left( 3 \right)}\left( {p_1^ - } \right) - \frac{{{{g''}_ * }\left( {p_2^ - } \right)}}{{\Delta p}}} \right] = 0; $ | (B22) |
| $ g\left( {{p_{ - 2}}} \right) = {{\tilde \xi }_{ - 2}}; $ | (B23) |
| $ g\left( {p_2^ - } \right) = {{\tilde \xi }_2}. $ | (B24) |
式(B16)为式(B7)的具体展开式;式(B17)~(B19)为样条函数在给节点处的二阶导数连续条件,式(B20)~(B22)为上述KKT条件;式(B23)、(B24)为端点无误差条件.将pi=p0+iΔp以及上述条件代入式(B16),经过整理,可得三次样条函数系数由如下的线性方程组确定:
| $ \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}}, $ | (B25) |
| $ \begin{array}{l} \mathit{\boldsymbol{x}} = \left[ {a_1^{\left( { - 2} \right)},a_2^{\left( { - 2} \right)},a_3^{\left( { - 2} \right)},a_1^{\left( { - 1} \right)},a_2^{\left( { - 1} \right)},a_3^{\left( { - 1} \right)},a_4^{\left( { - 1} \right)},} \right.\\ {\left. {a_1^{\left( 0 \right)},a_2^{\left( 0 \right)},a_3^{\left( 0 \right)},a_4^{\left( 0 \right)},a_1^{\left( 1 \right)},a_2^{\left( 1 \right)},a_3^{\left( 1 \right)}} \right]^{\rm{T}}}. \end{array} $ | (B26) |
| $ \mathit{\boldsymbol{b}} = {\left[ {0,0,0,0,0,0,0,0,0,{{\tilde \xi }_{ - 2}},{{\tilde \xi }_{ - 1}},{{\tilde \xi }_0},{{\tilde \xi }_1},{{\tilde \xi }_2}} \right]^{\rm{T}}}. $ | (B27) |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{M}}&{ - {\mathit{\boldsymbol{I}}_3}}&{{{\bf{0}}_{3 \times 1}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 1}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&\mathit{\boldsymbol{M}}&\mathit{\boldsymbol{N}}&{ - {\mathit{\boldsymbol{I}}_3}}&{{{\bf{0}}_{3 \times 1}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 1}}}&\mathit{\boldsymbol{M}}&\mathit{\boldsymbol{N}}&{ - {\mathit{\boldsymbol{I}}_3}}\\ {{\mathit{\boldsymbol{E}}_1}}&{{{\bf{0}}_{1 \times 3}}}&0&{{{\bf{0}}_{1 \times 3}}}&0&{{{\bf{0}}_{1 \times 3}}}\\ {{\mathit{\boldsymbol{R}}_1}}&{{\mathit{\boldsymbol{E}}_2}}&{{\mathit{\boldsymbol{P}}_1}}&{{\mathit{\boldsymbol{E}}_3}}&{{\mathit{\boldsymbol{P}}_2}}&{{\mathit{\boldsymbol{R}}_2}}\\ {{{\bf{0}}_{1 \times 3}}}&{{{\bf{0}}_{1 \times 3}}}&0&{{{\bf{0}}_{1 \times 3}}}&0&\mathit{\boldsymbol{T}} \end{array}} \right]. $ | (B28) |
式中:
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} 1&{\Delta p}&{\Delta {p^2}}\\ 0&1&{2\Delta p}\\ 0&0&1 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} {\Delta {p^3}}\\ {3\Delta {p^2}}\\ {3\Delta p} \end{array}} \right],{\mathit{\boldsymbol{I}}_3} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{P}}_1} = {\left[ {\frac{{6{\delta ^2}}}{{\Delta p}}, - \frac{{6{\delta ^2}}}{{\Delta p}},0} \right]^{\rm{T}}},\;\;{\mathit{\boldsymbol{P}}_1} = {\left[ {0,\frac{{6{\delta ^2}}}{{\Delta p}}, - \frac{{6{\delta ^2}}}{{\Delta p}}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{R}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0&{ - \frac{{2{\delta ^2}}}{{\Delta {p^2}}}}\\ 0&0&0\\ 0&0&0 \end{array}} \right],\;\;\;\;{\mathit{\boldsymbol{R}}_2} = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 1&0&{ - \frac{{2{\delta ^2}}}{{\Delta {p^2}}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{E}}_1} = \left[ {1,0,0} \right],\;\;{\mathit{\boldsymbol{E}}_2} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&0&0\\ 0&0&0 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{E}}_3} = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ 1&0&0\\ 0&0&0 \end{array}} \right],\;\;\;\mathit{\boldsymbol{T = }}\left[ {1,\Delta p,\Delta {p^2}} \right]. $ |
上述线性方程组系数矩阵A高度稀疏,通过稀疏矩阵三角分解可以快速求解x,进而确定了最优函数g*(p).
对g*(p)求解一阶导数,系统阻尼比对系统参数的灵敏度为
| $ \xi '\left( {{p_0}} \right) \approx {{\xi '}_ * }\left( p \right)\left| {_{p = {p_0}}} \right. = a_2^{\left( 0 \right)}. $ | (29) |
改进Tikhonov正则化方法根据带误差的测量数据进行重构函数,充分考虑了样本测量误差,使其微分更好地拟逼近精确函数微分,减小了其对数值微分方法中步长选取的影响.从上述推导可知,最优逼近函数是特殊的三次样条函数,因此受步长影响的性质与三次样条函数相似.
| [1] |
杨慧敏, 易海琼, 文劲宇, 等. 一种实用的大电网低频振荡概率稳定性分析方[J]. 电工技术学报, 2010, 25(3): 124-129. YANG Hui-min, YI Hai-qiong, WEN Jin-yu, et al. A practical stability analysis method for large-scale power system based on low-frequency-oscillation probability[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 124-129. |
| [2] |
宋墩文, 杨学涛, 丁巧林, 等. 大规模互联电网低频振荡分析与控制方法综述[J]. 电网技术, 2011, 35(10): 22-28. SONG Dun-wen, YANG Xue-tao, DING Qiao-lin, et al. A survey on analysis on low frequency oscillation in large-scale interconnected power grid and its control measures[J]. Power System Technology, 2011, 35(10): 22-28. |
| [3] |
赵学强, 杨增辉. 华东-福建联网低频振荡问题分析[J]. 华东电力, 2006, 34(2): 21-24. ZHAO Xue-qiang, YANG Zeng-hui. Study on low frequency oscillation after the interconnection of eastchina and Fujian power grids[J]. East China Electric Power, 2006, 34(2): 21-24. |
| [4] |
李丹, 苏为民, 张晶, 等. "9.1"内蒙古西部电网振荡的仿真研究[J]. 电网技术, 2006, 30(6): 41-47. LI Dan, SU Wei-min, ZHANG Jing, et al. Simulation study on west inner mongolia power grid oscillations occurred on September 1st, 2005[J]. Power System Technology, 2006, 30(6): 41-47. |
| [5] |
齐军, 万江, 张红光, 等. 内蒙古电网小干扰安全稳定性分[J]. 内蒙古电力技术, 2007, 25(4): 18-21. QI Jun, WAN Jiang, ZHANG Hong-guang, et al. Safety and stability analysis of low interferences in inner mongolia power grid[J]. Inner Mongolia Electric Power, 2007, 25(4): 18-21. |
| [6] |
MA J, DONG Z Y, ZHANG P. Eigenvalue sensitivity analysis for dynamic power system[C]//2006 International Conference on Power System Technology. Chongqing:[s. n.], 2006:22-26. http://ieeexplore.ieee.org/document/4116349/
|
| [7] |
刘涛, 宋新立, 汤涌, 等. 特征值灵敏度方法及其在电力系统小干扰稳定分析中的应用[J]. 电网技术, 2010, 34(4): 82-87. LIU Tao, SONG Xin-li, TANG Yong, et al. Eigenvalue sensitivity and its application in power system small signal stability[J]. Power System Technology, 2010, 34(4): 82-87. |
| [8] |
LUO C, AJJARAPU V. A new method of eigenvalue sensitivity calculation using continuation of invariant subspaces[J]. IEEE Transactions on Power Systems, 2011, 26(1): 479-480. DOI:10.1109/TPWRS.2010.2052963 |
| [9] |
DONG Z Y, PANG C K, ZHANG P. Power system sensitivity analysis for probabilistic small signal stability assessment in a deregulated environment[J]. International Journal of Control, Automation and Systems, 2005, 3(2): 355-362. |
| [10] |
CHUNG C Y, DAI B. A generalized approach for computing most sensitive eigenvalues with respect to system parameter changes in large-scale power systems[J]. IEEE Transactions on Power Systems, 2016, 31(3): 2278-2288. DOI:10.1109/TPWRS.2015.2445792 |
| [11] |
王彦博. 数值微分及其应用[D]. 上海: 复旦大学, 2005. WANG Yan-bo. Numerical differentiation and its application[D]. Shanghai:Fudan University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10246-2005121218.htm |
| [12] |
张华. 一维数值微分问题的Matlab软件包[D]. 河北: 河北工业大学, 2007. ZHANG Hua. A Matlab package for one dimensional numerical differentiation[D]. Hebei:Hebei University of Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10080-2007189979.htm |
| [13] |
宋歌. 电力负荷实测建模及时变性研究[D]. 北京: 华北电力大学, 2015. SONG Ge. Research on measurement-based load modeling and time-variation[D]. Beijing:North China Electric Power University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10079-1015643720.htm |
| [14] |
PETRIE A, ZHAO X P. Estimating eigenvalues of dynamical systems from time series with applications to predicting cardiac alternans[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Science, 2012, 468(2147): 3649-3666. DOI:10.1098/rspa.2012.0098 |
| [15] |
朱立勋. 三次样条插值的收敛性及一类三次广义样条插值的误差估计[D]. 吉林: 吉林大学, 2006. ZHU Li-xun. The convergence of cubic spline interpolation and the error estimations of certain generalized cubic spline interpolation[D]. Jilin:Jilin University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10183-2006092444.htm |
| [16] |
耿爱成. Matlab在三次样条函数教学中的应用[J]. 价值工程, 2016(18): 181-182. GENG Ai-cheng. The application of Matlab in teaching of cubic spline interpolation function[J]. Value Engineering, 2016(18): 181-182. |
| [17] |
王希云, 黄建国, 陈宇, 等. 基于正则化方法的一个新型数值微分算法[J]. 高等学校计算数学学报, 2009, 31(3): 246-256. WANG Xi-yun, HUANG Jian-guo, CHEN Yu, et al. A new numerical differentiation algorithm with regularization[J]. Numerical Mathematics A Journal of Chinese Universities, 2009, 31(3): 246-256. |
| [18] |
中国电力科学研究院. PSD-BPA小干扰稳定程序用户手册4. 0版[Z]. 2007.
|
| [19] |
CHENG J, YAMAMOTO M. One new strategy for a priori choice of regularizing parameters in Tikhonov's regularization[J]. Inverse Problems, 2000, 16(4): 31-38. DOI:10.1088/0266-5611/16/4/101 |



