2. 国家海洋局第二海洋研究所, 浙江 杭州 310012;
3. 宁波大榭开发区交通局, 浙江 宁波 315812
2. Second Institute of Oceanography, SOA, Hangzhou 310012, China;
3. Transportation Bureau of Ningbo Daxie, Ningbo 315812, China
异重流(gravity current), 也称密度流(density current), 是指2种或2种以上比重相差不大的流体互相接触时, 因为密度差异而产生的流动[1].异重流现象在自然界和工程界十分常见.在水库中, 水流由于携带泥沙而形成的浑水异重流可以有效进行水库排沙[2-4];在湖泊中, 上游注入温度较低的河水, 由于温度差异产生的组分异重流(compositional gravity current)对湖泊水质及生态系统影响很大;在深海环境中, 流体由于挟沙形成的浊流对海底物质运移和地形变化有重要的影响[5].由于异重流的重要性, 水利工程、海洋工程、流体力学等学科的学者们对其进行了大量的研究.
异重流的发生具有很大的随机性和不可预测性[6], 现存的异重流现场观测资料较少.在过去的几十年中, 水槽实验[7-9]已成为研究异重流的重要手段之一.对于异重流在均匀水体环境中沿平坡或者斜坡的运动特性的研究, 目前已取得较为丰硕的成果[7, 10-13].然而在自然界真实的水体环境中, 由于温度、盐度差异导致的水体密度分层现象普遍存在[1-2, 14], 如:河口区域的咸淡水混合形成的分层、深海中不同深度处由于温度不同而形成的温跃层[15]等, 这种分层水体环境对异重流的发展、掺混和演变具有重要影响[16].He等[17]对开闸式(lock-exchange)异重流在线性分层环境中沿斜坡的运动进行了系统研究.结果表明, 异重流在分层水体和均匀水体中沿斜坡的运动有着本质差异, 由于在水体深度方向上存在密度差, 异重流会经历加速、减速和分离3个阶段, 基于经典的“热理论(thermal theory)”[13, 18], 通过考虑水体深度方向上的密度分层效应, 得出了异重流在减速阶段头部位置和头部速度的计算公式, 提出了用于预测异重流离开斜坡以及水平侵入环境水体时的分离深度的新公式.
除了环境水体的分层效应以外, 在自然环境或实际工程中, 异重流发展过程中也常遇到地形突起、构筑物等障碍物[19], 如:海风传播遇到山丘, 海底浊流前进时遇到地形变化等.Kubo[20]的实验结果表明, 随着障碍物高度的增加, 异重流中10%~30%的来流会被阻挡在障碍物的前端, 这种阻挡作用会使泥沙异重流中所携带的大部分泥沙颗粒形成堆积效应.Tokyay等[21]通过大涡模拟(LES)手段, 证实了2种不同来流方式(连续入流式和开闸式)产生的异重流都会随着障碍物高度的改变而产生较为显著的改变.Nasr-Azadani等[22]通过直接数值模拟(DNS)证实了障碍物的存在会影响颗粒异重流中的流场结构, 从而进一步影响泥沙沉降和湍流混合特性.前人研究表明, 异重流的运动速度、涡旋结构、与环境水体之间的掺混等特性也会极大地受到水体障碍物的影响[9, 23].分层水体环境中的异重流在发展过程中遇到地形突变的现象极为常见[5].可以预见的是, 分层水体和障碍物的协同作用效应, 势必会对异重流的水动力学特性造成显著的改变.到目前为止, 还没有学者针对这种协同效应对异重流运动特性的影响展开研究.
本研究对由盐度差形成的开闸式组分异重流沿斜坡运动的水动力学特性展开研究, 综合考虑分层水体和障碍物的影响.实验中通过高速摄像机记录异重流的发展过程, 获取形态结构、头部位置和头部速度, 利用激光粒子图像测速技术(PIV)得到异重流局部结构、速度场和涡度场等信息, 以揭示发展过程中相应水动力特性的时空变化.通过对实验结果的分析比较, 得出不同因素对异重流的作用机制.
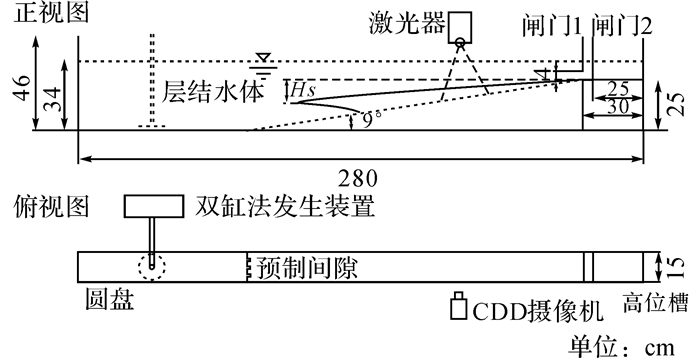
1 实验设置 1.1 实验装置及步骤实验水槽长280 cm、宽15 cm、高46 cm, 如图 1所示.水槽中的线性分层水体利用“双缸法(two-tank system)”[1, 15, 19]生成.实验中采用的装置已被证明可以获得非常稳定的线性分层水体[1, 15].在水槽斜坡右端的闸室使用2个闸门, 其中闸门1可以有效减小突然开启闸门2时所引起的水面波动[19].在整个实验过程中, 保持闸门1的开度hl=4 cm.在所有工况实验中, 水槽中分层水体的高度都保持在34 cm.当线性分层水体生成后, 在闸门2后方的闸室缓慢注入经高锰酸钾染色的高浓度盐水, 直至水深和闸门2左方分层水体的深度一致.快速升高闸门2, 产生的异重流沿斜坡逐渐向下发展, 实验中使用帧率为25帧/s的Nikon摄像机记录异重流发展的整个过程.在局部区域内, 使用PIV系统来记录异重流的流场形态.PIV系统由1台CCD(Charge-Coupled Device)高速相机和1台MGL-N-532激光器组成.CCD相机的最大帧率为200帧/s, 拍摄图片的分辨率为2 320×1 726.通过PIV Lab[24]来处理PIV系统所采集的图片, 并获取异重流运动的速度场、涡度场等信息.
|
图 1 实验水槽示意图 Fig. 1 Sketch of experimental tank |
已有研究[1, 17]表明, 当相对层结度S>1时, 异重流在线性分层水体中沿斜坡的运动可以分为加速、减速和分离阶段.对于有障碍物时的工况, 障碍物位于相应无障碍物工况下的异重流处于减速阶段区域内, 研究中暂不考虑障碍物处于其他位置的情况.本实验中, 控制障碍物的高度hob分别为3 cm和5 cm.障碍物形状为等边三棱柱, 宽15 cm, 放置在距斜坡顶端39 cm处.实验步骤与上文所述无障碍物存在的工况相同.
1.2 特征参数与实验工况异重流现象产生的原因为不同流体之间存在一定的密度差[4].由于在实验中很难连续测量随时间变化的有效重力加速度g′, 采取文献[16]中的做法, 即用初始有效重力加速度g′0来描述密度差异并构造其他特征参数, 定义为
| $ g{'_0} = g\frac{{{\rho _{{\rm{c0}}}}{\rm{-}}{\rho _{{\rm{h0}}}}}}{{{\rho _{{\rm{c0}}}}}}. $ | (1) |
式中:g为重力加速度;ρc0为闸室中初始异重流盐水密度, ρh0为斜坡顶端处环境水体的密度, ρc0-ρh0为闸室中盐水与斜坡顶端处环境水体的密度差.
采用浮力频率[16]描述环境水体分层情况:
| $ N = {\left( {-\frac{g}{{({\rho _{{\rm{c0}}}} + {\rho _{{\rm{h0}}}})/2}}\frac{{{\rm{d}}{\rho _{\rm{0}}}(z)}}{{{\rm{d}}z}}} \right)^{1/2}} \approx {\left( {\frac{{g{'_0}}}{D}} \right)^{1/2}}. $ | (2) |
式中:ρ0(z)表示水深为z处的水体密度, D为在初始状态下, 水槽中与闸室内盐水密度相同的某点到闸室底部水平延长线的垂直距离.
在分层水体实验中, 相对层结度S是描述异重流与环境水体之间相对分层情况的一个重要的无量纲参数[1, 25], 定义为
| $ S = \frac{{{\rho _{\rm{B}}}-{\rho _{{\rm{h0}}}}}}{{{\rho _{{\rm{c0}}}}-{\rho _{{\rm{h0}}}}}}. $ | (3) |
式中:ρB为水槽底部处环境水体的密度.
相对层结度S为包括异重流密度和环境水体密度在内的无量纲参数, 也是确定异重流水平是否侵入水体的重要参数.S>1表明当异重流运动到斜坡某处时, 会从斜坡上发生分离然后水平侵入到环境水体中[1, 17], 分离高度Hs为从分离点到闸室底部水平延长线的垂直距离.
采用整体雷诺数来描述异重流的运动状态[13]:
| $ Re = \frac{{{h_1}}}{\upsilon }\sqrt {g{'_0}{h_1}} . $ | (3) |
式中:hl为闸门1的开度, ν为水的运动黏滞系数.与文献[13]类似, 研究中忽略ν随水体密度的变化.实验中所有工况的雷诺数均大于1 000, 表明黏滞力的影响可以忽略[13, 17].
实验中保持初始异重流的盐度为19.2 g·L-1, 斜坡角度为9°.实验工况列表如表 1所示, 其中hob为障碍物的高度.每组实验重复2次, 首次实验用摄像机记录异重流运动的整个过程, 重复实验用PIV系统对部分区域进行记录, PIV的记录范围为斜坡上距斜坡顶端32~63 cm.
| 表 1 实验工况及相关参数 Table 1 Experimental cases and parameters |
如图 2(a)和(b)所示分别为在均匀水体和线性分层水体中异重流沿斜坡运动遇到高度为5 cm的障碍物时的发展过程, 其中Xf表示头部位置, 为斜坡顶端沿斜坡至异重流头部前锋的距离, Hs表示分离深度, 为斜坡顶端距异重流前锋的垂直距离.在均匀水体中, 异重流到达障碍物之前, 其形态结构与不存在障碍物时的工况基本一致;当异重流头部到达障碍物时, 会继续沿着障碍物的表面爬坡, 而在障碍物后方, 部分流体会被阻挡而滞留.随着异重流的爬升, 当到达最高点时, 由于惯性的作用, 异重流头部会继续上升, 随后表现出下潜行为.此时, 在障碍物的尖端附近会有一些小漩涡生成.在越过障碍物之后, 主体部分被阻挡回流, 而少部分盐水依然可以形成一个典型的异重流头部结构, 并且沿着斜坡继续下潜.被阻挡的部分盐水会沿着斜坡上下缓慢振动, 随后逐渐静止.

|
图 2 异重流遇到5 cm障碍物时的发展过程 Fig. 2 Evolution process of gravity currents encountering obstacle with height of 5 cm |
在线性分层水体中, 由于深度方向具有密度梯度, 异重流内部不同深度的水体都表现出水平入侵的趋势, 使得异重流的整体尺寸更大[1, 17].障碍物对异重流形态及发展的影响体现在头部接近和到达障碍物的时刻.在分层环境中, 异重流虽然也会表现出爬坡行为, 但是当越过障碍物后, 不能再次形成继续沿斜坡运动的异重流主体.此时, 由于在深度方向上存在密度梯度, 使得越过障碍物后的盐水在不同深度处均表现出较为缓慢的水平入侵趋势, 从而显著增大这部分水体的体积.
图 3展示了PIV系统所采集的异重流在均匀水体和分层水体中越过障碍物瞬间的形态结构.在越过障碍物后, 分层水体中异重流的漩涡结构和开尔文-亥姆霍兹不稳定性(Kelvin-Helmholtz instability)表现得更为明显.这是由于在非分层环境下, 异重流头部速度更大一些, 使得流体的不稳定性更强, 漩涡更加容易破碎形成湍流结构, 从而更加容易形成尺度较小的漩涡.

|
图 3 异重流越过5 cm高度障碍物时的结构 Fig. 3 Structures of gravity currents getting overobstacle with height of 5 cm |
文献[1]和[17]的实验结果表明, 在没有障碍物的情况下, 均匀水体中异重流沿斜坡运动的头部速度首先会经历一个较为短暂的加速过程, 而后略有减小;而在线性分层环境中, 异重流在经历加速阶段后, 头部速度会显著减小.分析利用Matlab摄像机获得的影像资料, 可以得到异重流随时间发展的头部位置Xf, 将头部位置对时间求导可得相应时刻的头部速度.如图 4所示为异重流在均匀水体和分层水体中不同工况下的头部速度变化图.将速度和时间分别利用以下方式无量纲化:
|
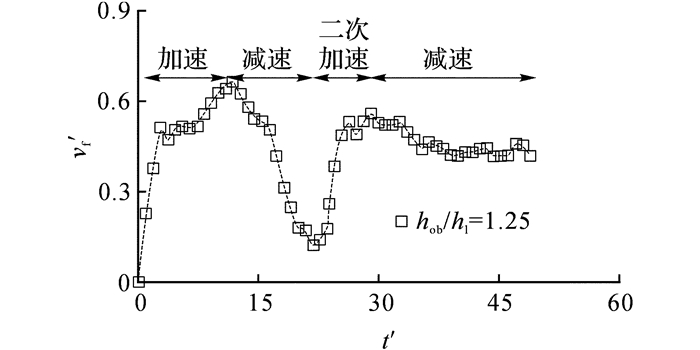
图 4 均匀水体中异重流遭遇障碍物时的典型四阶段运动过程 Fig. 4 Typical four-stage movement processes of gravity currents encountering obstacle in uniform water |
| $ v{'_f} = \frac{{{v_{\rm{f}}}}}{{\sqrt {g{'_0}{h_1}} }},t' = t\sqrt {\frac{{g{'_0}}}{{{h_1}}}} . $ | (5) |
式中:vf、t分别为实验中所记录的异重流头部速度和时间;v′f、t′则为无量纲化后的头部速度和时间.
从整体趋势来看, 当不存在障碍物(hob/hl=0)时, 均匀水体和分层水体中异重流的运动趋势和文献[1]的实验结果一致.当有障碍物时, 均匀水体和分层水体中4种工况下异重流的头部速度变化趋势都较为统一:在遇到障碍物之前, 异重流头部速度都会经历一个先加速而后明显减小的过程, 这个减小过程一直持续到异重流爬升到障碍物的最高处, 此后头部速度会再次经历一个短暂的“二次加速”过程.对于均匀水体中的异重流, 由于越过障碍物的部分盐水依然会形成一个较为典型的异重流头部, 在“二次加速”过程中, 可以达到的最大速度只比遇到障碍物前的最大速度约小10%;随后头部速度略有减小(如图 4所示, 速度波动是由头部位置处的三维结构和水体掺混交换引起的[26]).对于分层水体中的异重流, 由于密度分层的存在, 越过障碍物后的部分异重流在不同深度处均形成了水平入侵的趋势, 使得流体较为散乱, 二次加速过程中达到的最大速度比在均匀水体中至少小47%.
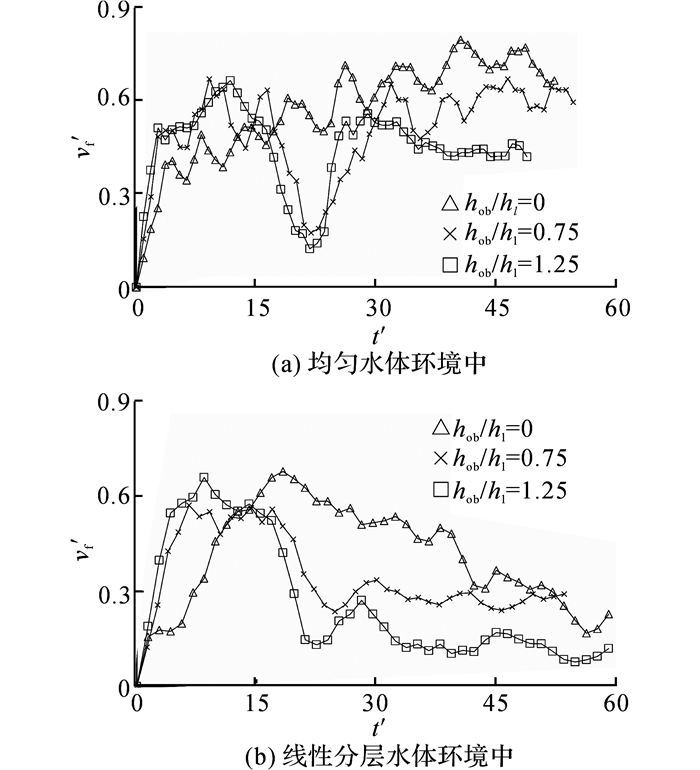
从图 5(b)线性分层水体环境中可以得出, 在hob/h1为0.75和1.25时, 二次加速开始前, 分层水体中异重流的头部速度从首次加速阶段达到的最大值到由于障碍物的阻挡作用而形成的最小值, 减小幅度分别为56%和76%.这一较为明显的数值差异表明, 在环境水体分层情况下, 异重流的运动速度受到障碍物的影响更大.越过障碍物后, 两者均会经历一个非常短暂的二次加速过程.与在均匀水体情况下类似, 障碍物越高, 二次加速结束后异重流的头部速度越小.在异重流发生水平分离前, 头部速度均会趋近于0.
|
图 5 不同环境中异重流在不同工况下的头部速度发展过程 Fig. 5 Developmental processes of front velocity under different working conditions of gravity currents in different environments |
异重流在线性分层环境中沿斜坡向下运动时, 由于周围环境水体密度不断增大, 异重流不断与周围水体发生卷吸掺混, 使得两者之间的密度差不断减小;当异重流的密度减小到与环境水体一致时, 会离开斜坡并水平入侵到周围水体中[16, 27].值得注意的是, 异重流离开斜坡水平入侵的分离深度在工程上具有重大意义, 可以决定异重流对周围环境的影响范围[25]:如果人工建筑物离水面的深度在分离深度之下, 就不会受到异重流的冲击和破坏.基于量纲分析的方法, Well等[27]提出了针对连续入流式异重流在线性分层环境中分离深度的预测公式, 并且利用水槽实验和观测数据验证了公式的有效性.He等[17]通过考虑周围环境水体的层结度、斜坡角度和入流流量等因素, 提出了新公式来预测开闸式异重流在线性分层环境中沿斜坡运动时的分离深度.Snow等[25]也对开闸式颗粒异重流的分离深度进行了研究.然而以上研究均没有考虑到斜坡上地形的变化, 而这样的地形突变已经被证明会显著影响异重流与周围环境水体之间的掺混交换[22], 从而进一步影响异重流的分离深度.本节通过测量对比有无障碍物情况下异重流的分离深度, 得出障碍物对异重流与环境水体的掺混交换和分离深度的定性影响, 为后续的研究提供参考数据.
如表 2所示为不同工况下异重流分离深度的数据.测量分离深度的具体方法如下:当异重流越过障碍物并且运动状态保持稳定后, 使用测量尺对分离深度Hs进行测量, 测量时的读数误差可以忽略.从整体来看, 当周围环境水体分层情况基本不变时, 随着障碍物高度的增加, 异重流分离深度逐渐减小:从没有障碍物的工况到遇到3 cm障碍物的工况, 分离深度减小了20%;从遇到3 cm障碍物的工况到遇到5 cm障碍物的工况, 分离深度仅减小了5.3%.这表明障碍物会明显减小异重流分离深度, 并且有无障碍物比障碍物高度变化对分离深度的影响更大.在没有障碍物的情况下, Hs与D较为接近, 表明因流体运动造成的异重流与环境水体之间的掺混并不明显, 异重流密度虽有降低, 但是变化不大.随着障碍物高度的增加, Hs与D之间的相对差异也逐渐增大.一方面, 这表明了障碍物会加剧异重流与环境水体之间的掺混交换, 使得异重流密度明显减小, 从而提前从斜坡分离.另一方面, 随着障碍物高度的增大, 障碍物对水体之间掺混交换的加剧效应也越来越突出.
| 表 2 不同工况下异重流的分离深度 Table 2 Separation depth under different working conditions |
在异重流越过障碍物时, 由于障碍物的阻水作用以及爬坡过程中的复杂结构, 使得利用传统方法难以对其进行精确测量.本实验利用高精度PIV系统对异重流越过障碍物的过程进行记录.
如图 6所示为异重流到达3 cm障碍物正上方时以及相应无障碍物工况下的流场图和涡度图, 图中右下角表示0.02 m/s的速度对应的速度矢量的长度.从图 6(a)、(b)可以看出, 当异重流头部爬升到障碍物最上方时, 三角形障碍物尖端附近的异重流出现了一小块明显的负涡度带.正是逆时针涡度的出现, 加剧了异重流与环境水体之间的掺混.在均匀水体环境中, 异重流具有较大的头部速度.当较大的头部速度受到障碍物的阻挡时, 障碍物的后方出现了更为强劲的回流现象, 使得均匀水体环境中的异重流在爬坡时身后有着更大的厚度, 同时上部的顺时针涡度更加明显.

|
图 6 异重流到达障碍物位置处的流场图和涡度图 Fig. 6 Velocity and vorticity fields of gravity currents arriving at obstacle's location |
如图 7所示为异重流越过3 cm障碍物正上方时以及相应无障碍物工况下的流场图和涡度图.当异重流整体越过障碍物后, 比较图 7(a)、(b)和(c)可以发现:在障碍物的上游区域内(L<37.3 cm, L为障碍物中点至闸室底部沿斜坡的距离), 异重流在有无障碍物情况下的涡度场比较一致, 即在均匀水体和分层水体中均存在着较为明显的正、负涡度层.此时, 由于在均匀水体中异重流有着更大的头部速度, 处于障碍物上方区域(0.7 cm<L<37.3 cm)的盐水爬升高度变大, 上层的正向涡度值也变大.在障碍物的下游区域(L>40.7 cm)时, 均匀水体中异重流由于速度变大, 头部上层的速度场和涡度场受到不规则掺混的影响更强, 表现更为散乱.在下层区域内, 速度场和涡度场主要由黏性作用决定, 速度矢量方向与斜坡方向大致平行, 同时负向涡度带再次出现.对比图 7(b)分层水体中的异重流速度场和涡度场可知, 由于在深度方向上环境水体存在密度梯度, 不同位置处异重流内部的盐水入侵环境水体, 使得涡度场未能再形成上、下两层的正负涡度带, 同时靠近斜坡处的速度矢量不再与斜坡平行.这表明在异重流越过障碍物后, 环境水体层结度越强, 对异重流头部形态结构的破坏越明显, 从而影响异重流进一步沿斜坡方向的传播运动.

|
图 7 异重流越过障碍物位置处的流场图和涡度图 Fig. 7 Velocity and vorticity fields of gravity currents after passing obstacle's location |
为进一步分析分层环境及障碍物对异重流涡度场的影响, 计算图 6和7中不同工况下异重流上层正向涡度值之和:图 6(a)为1 620 s-1, (b)为1 065.7 s-1, (c)为1 354.3 s-1;图 7(a)为2 717.1 s-1, (b)为1 779.2 s-1, (c)为2 009.5 s-1.不同工况下异重流到达和越过障碍物之后的涡度值均表现出了相同的变化规律:即在分层环境和障碍物同时存在的情况(a2)下, 上层正向涡度值最小;存在障碍物的情况下, 当工况从均匀水体转变为分层水体时, 正向涡度值减小了52%;在分层水体中, 当工况从无障碍物转变为有障碍物时, 正向涡度值减小了27%.这些数据表明:分层环境和障碍物均会抑制异重流正向涡度场的发展, 但分层环境对异重流涡度场的抑制作用更强;当两者共同存在时, 异重流的涡度最弱.
3 结论(1) 当障碍物与闸门的高度比在0.75~1.25时, 异重流头部到达障碍物后会沿着障碍物表面爬升, 但是部分流体会被阻挡而滞留.均匀水体中越障的部分盐水依然可以形成一个典型的异重流头部结构, 并沿斜坡继续下潜运动;在线性分层环境中, 由于沿深度方向上存在密度梯度, 异重流越过障碍物后, 内部不同深度处的水体表现出较为缓慢的水平入侵趋势, 不能再次形成继续沿斜坡运动的异重流.
(2) 在存在障碍物的情况下, 无论在分层还是均匀水体中, 异重流的头部速度变化均表现为“加速—减速—二次加速—减速”的过程.在均匀水体中异重流在二次加速的过程中可以达到的最大速度仅比遇到障碍物前略小约10%;但是在分层水体中, 异重流二次加速过程中可以达到的最大速度明显比在均匀水体中小至少47%.在均匀水体中, 当障碍物与初始闸门的高度比在0.75~1.25时, 二次加速结束前, 异重流速度无明显区别;在分层水体中, 闸门越高, 异重流运动速度越小.
(3) 异重流在越过障碍物的过程中会出现明显的负向漩涡, 加剧异重流与环境水体之间的掺混交换.在均匀水体中, 异重流越障后其涡度场表现出较为明显的正、负2层;在线性分层水体中, 异重流越障后的速度场和涡度场比在均匀水体中都更为散乱.分层水体和障碍物均会抑制异重流正向涡度场的发展, 但分层环境对异重流正向涡度场的抑制作用更强;当两者共同存在时, 异重流的正向涡度场最弱.
| [1] |
贺治国, 林挺, 赵亮, 等. 异重流在层结与非层结水体中沿斜坡运动的实验研究[J].
中国科学:技术科学, 2016, 46(6): 570–578.
HE Zhi-guo, LIN Ting, ZHAO Liang, et al. Experiments on gravity currents down a ramp in unstratified and linearly stratified salt water environments[J]. Scientia Sinica Technologica, 2016, 46(6): 570–578. |
| [2] |
张小峰, 姚志坚, 陆俊卿. 分层水库异重流试验[J].
武汉大学学报:工学版, 2011, 44(4): 409–413.
ZHANG Xiao-feng, YAO Zhi-jian, LU Jun-qing. Experiments of density currents in stratified reservoir[J]. Engineering Journal of Wuhan University, 2011, 44(4): 409–413. |
| [3] | ZHANG X, SHI R, LU J, et al. Effect of thermal stratification on interflow travel time in stratified reservoir[J]. Journal of Zhejiang University-SCIENCE A:Applied Physics and Engineering, 2015, 16(4): 265–278. |
| [4] | 张瑞瑾. 河流泥沙动力学[M]. 第二版. 北京: 中国水利水电出版社, 2008: 211. |
| [5] | MEIBURG E, RADHAKRISHNAN S, NASR-AZADANI M. Modeling gravity and turbidity currents:computational approaches and challenges[J]. Applied Mechanics Reviews, 2015, 67(4): 40802. DOI:10.1115/1.4031040 |
| [6] | TOKYAY T E, GARCÍA M H. Effect of initial excess density and discharge on constant flux gravity currents propagating on a slope[J]. Environmental Fluid Mechanics, 2014, 14(2): 409–429. DOI:10.1007/s10652-013-9317-0 |
| [7] | SIMPSON J E. Gravity currents in the laboratory, atmosphere, and ocean[J]. Annual Review of Fluid Mechanics, 1982, 14(1): 213–234. DOI:10.1146/annurev.fl.14.010182.001241 |
| [8] | MEIBURG E, KNELLER B. Turbidity currents and their deposits[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 135–156. DOI:10.1146/annurev-fluid-121108-145618 |
| [9] | HO H, LIN Y. Gravity currents over a rigid and emergent vegetated slope[J]. Advances in Water Resources, 2015, 76: 72–80. DOI:10.1016/j.advwatres.2014.12.005 |
| [10] | BENJAMIN T B. Gravity currents and related phenomena[J]. Journal of Fluid Mechanics, 1968, 31(2): 209–248. DOI:10.1017/S0022112068000133 |
| [11] |
范家骅. 异重流运动的实验研究[J].
水利学报, 1959, 5(5): 30–48.
FAN Jia-hua. Experimental studies on density currents[J]. Journal of Hydraulic Engineering, 1959, 5(5): 30–48. |
| [12] | 范家骅. 异重流与泥沙工程实验与设计[M]. 北京: 中国水利水电出版社, 2011: 13-15. |
| [13] | DAI A. Experiments on gravity currents propagating on different bottom slopes[J]. Journal of Fluid Mechanics, 2013, 731: 117–141. DOI:10.1017/jfm.2013.372 |
| [14] |
任实, 张小峰, 陆俊卿. 温度分层水库中间层流运动影响因素分析[J].
哈尔滨工程大学学报, 2015(5): 648–652.
REN Shi, ZHANG Xiao-feng, LU Jun-qing. Influencing factors of the inflow in temperature-stratified reservoirs[J]. Journal of Harbin Engineering University, 2015(5): 648–652. |
| [15] |
张巍, 赵亮, 贺治国, 等. 线性层结盐水中的羽流运动特性[J].
水科学进展, 2016, 27(4): 1–7.
ZHANG Wei, ZHAO Liang, HE Zhi-guo, et al. Characteristics of plumes in linearly stratified salt-water[J]. Advances in Water Science, 2016, 27(4): 1–7. |
| [16] | BAINES P G. Mixing in flows down gentle slopes into stratified environments[J]. Journal of Fluid Mechanics, 2001, 443: 237–270. |
| [17] | HE Z, ZHAO L, LIN T, et al. Hydrodynamics of gravity currents down a ramp in linearly stratified environments[J]. Journal of Hydraulic Engineering, 2017, 143(3): 4016085. DOI:10.1061/(ASCE)HY.1943-7900.0001242 |
| [18] | BEGHIN P, HOPFINGER E J, BRITTER R E. Gravitational convection from instantaneous sources on inclined boundaries[J]. Journal of Fluid Mechanics, 1981, 107: 407–422. DOI:10.1017/S0022112081001821 |
| [19] |
林挺. 层结水体中异重流沿坡运动的试验研究[D]. 杭州: 浙江大学, 2016.
LIN Ting. Experimental study on gravity currents down a ramp in linearly stratified environments[D]. Hangzhou:Zhejiang University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10335-1016182976.htm |
| [20] | KUBO Y. Experimental and numerical study of topographic effects on deposition from two-dimensional, particle-driven density currents[J]. Sedimentary Geology, 2004, 164(3-4): 311–326. DOI:10.1016/j.sedgeo.2003.11.002 |
| [21] | TOKYAY T, CONSTANTINESCU G. The effects of a submerged non-erodible triangular obstacle on bottom propagating gravity currents[J]. Physics of Fluids, 2015, 27(5): 56601. DOI:10.1063/1.4919384 |
| [22] | NASR-AZADANI M M, MEIBURG E, KNELLER B. Mixing dynamics of turbidity currents interacting with complex seafloor topography[J]. Environmental Fluid Mechanics, 2016: 1–23. |
| [23] | CONSTANTINESCU G. Les of lock-exchange compositional gravity currents:a brief review of some recent results[J]. Environmental Fluid Mechanics, 2014, 14(2): 295–317. DOI:10.1007/s10652-013-9289-0 |
| [24] | THIELICKE W, STAMHUIS E. Pivlab-towards user-friendly, affordable and accurate digital particle image velocimetry in Matlab[J]. Journal of Open Research Software, 2014, 2(1): e30. |
| [25] | SNOW K, SUTHERLAND B R. Particle-laden flow down a slope in uniform stratification[J]. Journal of Fluid Mechanics, 2014, 755: 251–273. DOI:10.1017/jfm.2014.413 |
| [26] | IEONG K K, MOK K M, YEH H. Fluctuation of the front propagation speed of developed gravity current[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(Suppl.): 351–355. |
| [27] | WELLS M, NADARAJAH P. The intrusion depth of density currents flowing into stratified water bodies[J]. Journal of Physical Oceanography, 2009, 39(8): 1935–1947. DOI:10.1175/2009JPO4022.1 |



