河流突发污染事故往往给饮用水安全造成极大的危害[1].当污染事故突发时, 各部门迫切需要了解污染事故对下游(特别是水厂取水口等)的影响, 掌握实时的污染物浓度及其变化趋势数据, 包括污染物浓度峰值、峰值到达时间及污染物浓度超标持续时间等信息[2], 为科学决策提供技术支持, 尽可能降低污染事故产生的负面影响.
预测污染物浓度的数学模型一般称为水质模型.较早的水质模型例子为1925年由Streeter和Phelps提出的S-P模型[3].随着计算机技术和环境科学的发展, 科学家们在此基础上陆续开发了QUAL模型、WASP模型等机理模型[4-5], 并利用模糊数学、人工神经网络、贝叶斯网络、灰色理论等方法建立了非机理模型[6-9].受各种条件的制约, 早期的研究不少是建立在历史数据建模的基础上, 河流状态的动态变化考虑得不尽充分.随着检测手段的进步, 突发污染事故后相关部门获得断面污染物实时浓度值的能力大为提升, 将这部分实时数据纳入水质预测过程可望提高模型预测精度.另一方面, 对于突发污染事故往往没有现成的水质模型可供利用, 要获取大量历史数据进行建模, 时间上也不允许.为此, 面对突发污染事故如何降低模型构建的复杂程度、进一步提高模型预测结果与动态数据的相互结合校正, 是近年来兴起的一个研究热点.
Zhang等[10]建立了基于SD-GIS的突发水污染事故水质时空模拟方法, 在一维水质模型的基础上运用动态系统方法并利用GIS提高可视化, 其研究在松花江污染事故中得到了验证.Hou等[11]结合蒙特卡洛方法和层次分析法提出了基于不确定分析的突发水污染事故实时预警模型.宋筱轩等[12]提出基于动态数据驱动的河流突发污染事故预警系统.这些模型和方法建立在一维水质模型的基础上, 降低了模型复杂度, 在突发污染事故中的适用性增强, 并将实测数据纳入预测过程, 提高了突发污染事故应急水平.但从模型建立和预测计算方法等方面来看, 上述研究中尚未重点考虑模型与观测误差等因素以及支流对污染物扩散影响.观测误差存在系统误差和人为误差, 前者可以离线校正, 但后者则存在不确定性, 需要进行实时校正.另一方面, 模型结构误差与河道状况息息相关, 有必要进行实时校正以减少误差.在观测误差无法避免且河道支流较多的情况下, 这将不利于污染物浓度预测结果的提升.
本文提出一种引入卡尔曼滤波方法对预测模型和测量值误差进行综合考虑的污染物浓度预测方法.卡尔曼滤波算法的基本原理是由测量值重构系统的状态向量, 因综合考虑了模型结构误差和测量误差, 利用实时观测值对模型预测值进行校正, 有助于提高模型预测精度[13].卡尔曼滤波理论在天气预报、洪水水文预报及流量水位预测中已有相关报道[13-15], 但应用于河流突发污染水质预测方面的研究尚较少.
在水质突发污染事件检测和预测过程中, 水质模型结构和参数会不可避免地存在误差, 水质监测值也会含有系统误差或人为误差影响结果的准确性, 这些不利因素往往不可忽视;需要选取合适的数据处理方法方可求出误差为最小的真实信号估计值.为此, 本文在一维水质模型的基础上尝试将卡尔曼滤波应用于河流突发污染事故水质预测.利用历史数据估计水质模型参数;利用水质模型建立状态空间方程;将观测数据纳入预测过程利用卡尔曼滤波校正预测结果, 降低模型结构误差和测量误差.同时, 考虑支流对污染物扩散的影响, 对所提出的模型进行支流校正.
1 污染物浓度校正算法 1.1 水质模型离散化污染物在水体中的扩散和分布由河流横向, 垂向和纵向长度决定, 对于较长河段, 河流横向和垂向长度相对于河流纵向长度可以忽略不计, 因此, 选用一维水质模型进行研究, 其方法可以推广到高维模型.一维污染物扩散方程[16]为
| $ \frac{{\partial p}}{{\partial t}} + u\frac{{\partial \rho }}{{\partial x}} = E\frac{{{\partial ^2}\rho }}{{\partial {x^2}}} - k\rho . $ | (1) |
式中:ρ为污染物浓度, 表示单位体积水体内含有的污染物质量;u为纵向水流流速;E为纵向弥散系数;x为河水流动距离;k为综合降解系数;t为时间.
应用有限差分法对时间和空间坐标离散化, 整理后可得
| $ \begin{array}{l} \rho _i^{t + 1} = \frac{{{E_i}\Delta t}}{{\Delta {x^2}}}\rho _{i + 1}^t + \left( {1 - \frac{{2{E_i}\Delta t}}{{\Delta {x^2}}} - {k_i}\Delta t - \frac{{{u_i}\Delta t}}{{\Delta x}}} \right)\rho _i^t + \\ \;\;\;\;\;\;\;\;\;\left( {\frac{{{E_i}\Delta t}}{{\Delta {x^2}}} + \frac{{{u_i}\Delta t}}{{\Delta x}}} \right)\rho _{i - 1}^t. \end{array} $ | (2) |
式中:i表示断面, Δx表示空间步长, Δt表示时间步长, Ei表示第i河段的纵向弥散系数, ki表示第i河段的污染物综合降解系数, ui表示第i河段的河流平均流速.
从式(2)可以看出, 第i河段下一时刻(t+1)污染物浓度跟相邻上、下河段当前时刻污染物浓度以及第i河段的纵向弥散系数、污染物综合降解系数和当前河段平均流速相关.只要知道初始河段的污染物浓度, 即可通过计算得到整条河流的污染物浓度时空变化规律.在式(2)的基础上计算各个断面的污染物浓度, 并假设起始断面污染物已混合均匀.简化起见, 假设目标河段的纵向弥散系数和流速总体稳定, 忽略局部死区等对污染物扩散的影响.
1.2 卡尔曼滤波算法 1.2.1 卡尔曼滤波模型运用卡尔曼滤波进行实时校正首先需要建立状态方程.本文选取n个断面的污染物浓度为状态向量, 即
| $ {\mathit{\boldsymbol{x}}_t} = {\left[ {{\rho _1},{\rho _2}, \cdots ,{\rho _n}} \right]^{\rm{T}}}. $ | (3) |
根据式(2)可得到系统状态方程为
| $ \left[ {\begin{array}{*{20}{c}} {\rho _1^{t + 1}}\\ {\rho _2^{t + 1}}\\ {\rho _3^{t + 1}}\\ \vdots \\ {\rho _n^{t + 1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} b&a&0& \cdots &0&0&0\\ d&b&a& \cdots &0&0&0\\ 0&d&b& \cdots &0&0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots \\ 0&0&0& \cdots &0&d&b \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\rho _1^t}\\ {\rho _2^t}\\ {\rho _3^t}\\ \vdots \\ {\rho _n^t} \end{array}} \right]. $ | (4) |
式中:
| $ a = \frac{{{E_i}\Delta t}}{{\Delta {x^2}}},b = 1 - \frac{{2{E_i}\Delta t}}{{\Delta {x^2}}} - {k_i}\Delta t - \frac{{{u_i}\Delta t}}{{\Delta x}}, $ |
| $ d = \frac{{{E_i}\Delta t}}{{\Delta {x^2}}} + \frac{{{u_i}\Delta t}}{{\Delta x}}. $ |
式(4)可记为
| $ {x_{t + 1}} = A{x_t}, $ |
加入系统噪声得到状态方程:
| $ {x_{t + 1}} = A{x_t} + {w_t}. $ | (5) |
取浓度观测值为观测向量, 并加入观测噪声, 则观测方程为
| $ {y_t} = H{x_t} + {v_t}. $ | (6) |
式中:yt为观测向量, H为观测矩阵, vt为观测噪声误差方差.
根据式(5)、(6)结合式(7)~(11)即可利用卡尔曼滤波实时校正模型误差和观测误差:
| $ x\left( {t + 1\left| t \right.} \right) = Ax\left( {t\left| t \right.} \right) + w\left( t \right), $ | (7) |
| $ P\left( {t + 1\left| t \right.} \right) = AP\left( {t\left| t \right.} \right)A' + V, $ | (8) |
| $ {K_g}\left( {t + 1} \right) = P\left( {t + 1\left| t \right.} \right)H'/\left[ {HP\left( {t + 1\left| t \right.} \right)H' + R} \right], $ | (9) |
| $ \begin{array}{l} x\left( {t + 1\left| {t + 1} \right.} \right) = x\left( {t + 1\left| t \right.} \right) + {K_g}\left( {t + 1} \right)\left[ {y\left( {t + 1} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {Hx\left( {t + 1\left| t \right.} \right)} \right], \end{array} $ | (10) |
| $ P\left( {t + 1\left| {t + 1} \right.} \right) = \left[ {1 - {K_g}\left( {t + 1} \right)H} \right]P\left( {t + 1\left| t \right.} \right). $ | (11) |
式中:x(t|t)为t时刻最优估计值, x(t+1|t)为t+1时刻模型直接预测值, P(t+1|t)为预测误差方差, P(t|t)为卡尔曼滤波误差方差, Kg(t+1)为卡尔曼增益, x(t+1|t+1)为t+1时刻最优估计值, y(t+1)为观测值, V为系统噪声误差方差, R为测量噪声误差方差.
1.2.2 实时预测流程如图 1所示为基于卡尔曼滤波的污染物浓度实时预测流程图.获取系统噪声和测量噪声是进行卡尔曼滤波的关键一步, 一般而言, 数学上比较常用的方法是Sage-Husa算法, 工程应用中则主要采用经验法来确定V和R.本文首先通过初步率定和经验知识分析得到系统噪声误差方差V和测量噪声误差方差R, 并利用历史数据校正模型参数.然后设置模型计算时间, 判断是否有观测值.若有, 则利用卡尔曼滤波算法, 通过观测值和当前时刻预测值校正下一时刻浓度预测值, 即一步预测校正;若没有, 则直接利用式(2)及过去的校正值预测未来各断面的污染物浓度值, 即多步预测.

|
图 1 基于卡尔曼滤波的污染物浓度实时预测流程图 Fig. 1 Flow chart of real-time prediction for pollutant concentration based on Kalman filter |
在模型结构确定的情况下, 模型参数的准确性很大程度上决定了模型的好坏.本文模型参数校正通过历史污染物浓度数据进行(若缺乏历史数据则通过经验给定模型参数值).对模型参数k、u、E建立优化函数:
| $ F = \min \sum\limits_{i = 1}^m {{{\left( {\rho _i^t - \rho _i^{t'}} \right)}^2}} . $ | (12) |
式中:m为用于参数校正的实测值个数, ρit为i断面处t时刻实测污染物浓度, ρit′为i断面处t时刻污染物浓度预测值.
在实际应用中由于水流流速u可根据实测信息获取, 在平均流速u已知的情况下式(12)是一个二变量无约束寻优问题.传统的网格寻优算法在步长选择过大时容易漏掉最优解, 而步长选择过小时计算时间过长.本文采用改进的网格寻优算法, 在一次寻优的基础上减少搜索步长进行二次寻优以求得最优解, 主要步骤如下.
1) 根据初步率定或经验法得到参数的上、下限, 初次搜索时选择较大的搜索步长;
2) 按一定规律对网格上所有点进行搜索比较, 始终保存并即时更新当前最优解, 搜索完毕后得到参数组合为粗略估计, 需进一步搜索;
3) 设定较小的搜索步长, 在步骤2)得到的结果附近选择小区间进行二次搜索得到最优参数组.
对于突发污染事故人们更关心的是下游的污染物扩散情况.在一步预测校正的基础上进行多步预测达到实时校正下游污染物浓度预测值的目的.此时将一步预测校正结果作为边界条件, 利用式(2)预测下游污染物浓度.
以往的水质模型往往忽略支流的作用, 这在一定程度上会影响预测精度.考虑支流对污染物扩散的影响, 校正方法如下.
1) 整理待测河流的主要支流, 根据支流位置对河道进行分段, 获得支流实时流量数据;
2) 根据质量守恒定律, 支流汇合前、后污染物质量应保持不变, 满足:
| $ {Q_1}{\rho _1} = \left( {{Q_1} + {Q_2}} \right){\rho _2}. $ | (13) |
式中:ρ1为支流汇合前污染物浓度, ρ2为汇合后污染物浓度, Q1为汇合前干流流量, Q2为支流流量.
在每个分段界面, 根据式(13)可以实时求出支流汇合后的污染物浓度, 并将其作为当前断面浓度继续计算, 直到得到所有断面浓度.
2 案例研究 2.1 实验设计设计基于风浪水槽的污染物模拟扩散实验.风浪水槽可用长为39.0 m, 高为1.6 m, 净宽为1.2 m, 最大水深1.0 m.共进行3组实验, 将其中2组作为历史数据用于参数校正, 另一组用于验证.
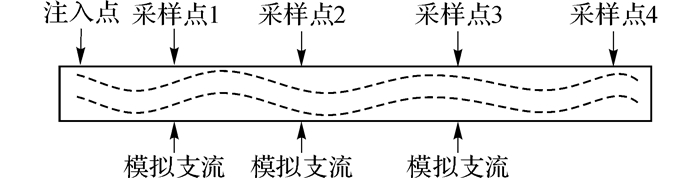
实验装置及实验方案如图 3所示, 实验主要内容和步骤如下.
|
图 3 实验装置、采样点布置及模拟支流示意图 Fig. 3 Schematic diagram of experimental device, sampling point distributions and simulation of tributaries |
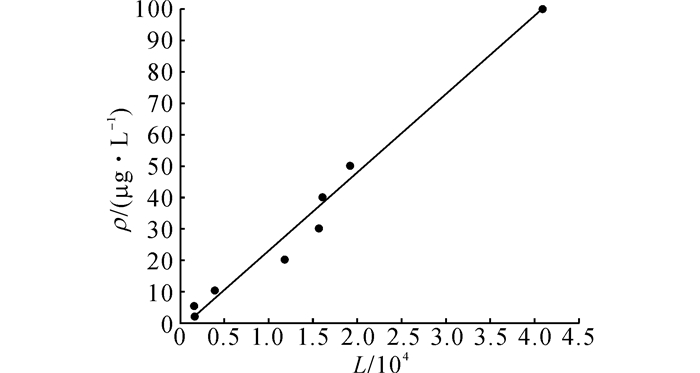
1) 选取罗丹明B作为模拟污染物.罗丹明B在水中稀释可以显现肉眼可见的红色, 可以直观地看到污染物扩散过程, 而且罗丹明B在溶液中有强烈的荧光, 可利用荧光仪直接测量.利用荧光仪得到的是光谱数据, 为得到浓度数据需首先进行标定实验, 得到浓度标准曲线, 标定结果如图 2所示, 荧光强度和污染物浓度满足方程:
|
图 2 罗丹明B荧光强度和浓度标准曲线 Fig. 2 Fluorescence intensity and concentration standard curve of Rhodamine B |
| $ y = 0.0025x - 2.3606. $ | (14) |
其中, 相关系数R2=0.981 5, 可见两者线性度较好, 可用于间接测量污染物浓度.
2) 采样点设置如图 3所示, 考虑污染物混合均匀需要一定距离, 在4.5 m处设置第1个采样点, 之后每隔10.5 m设一个采样点, 共4个采样点.
3) 配置一定浓度的溶液, 设置水深和水流流速, 在污染物注入点按(4)中的方法注入污染物, 下游采样点按等时间间隔采样.设置水流流速为0.1 m/s, 水深0.3 m, 并配置包含30 mg罗丹明B的溶液, 采样时间间隔为5 s.为模拟支流, 在采样点1、2、3按一定3.2 L/min的流量注入自来水.
4) 根据污染物持续注入时间有3种不同的污染物注入方式, 分别是连续注入、瞬时注入和间歇性注入.本文采用瞬时注入的方式注入污染物.
5) 样品处理与分析.利用荧光仪扫描每个水样的光谱数据, 并利用平行因子分析法计算各吸收峰上的荧光强度, 接着根据式(14)计算得到各样本污染物浓度.
2.2 结果分析 2.2.1 模型参数确定根据1.2.2节所述, 可认为实验流速等于设定值, 因此需要确定的参数为E和k.由于缺少历史数据, 首先利用前两组实验结果初步率定E和k, 并据此得到取值上下限, 然后利用改进的网格寻优算法得到最优参数组.纵向弥散系数E是跟河道相关的系数, 可通过实验法、经验法、图解法等[17]得到, 利用文献[17]所述的图解法得到.综合降解系数k是与试剂本身和试剂扩散载体相关的参数, 可通过实验法、类比法、经验法等[18]得到.利用实验数据, 通过式(15)进行估算.经过初步率定确定k初始取值为0.20 d-1, 取值下限0.05 d-1, 取值上限0.50 d-1;E初始取值0.1 m2/s, 取值下限0.05 m2/s, 取值上限0.5 m2/s.
| $ k = \frac{{\left( {\ln {\rho _{\rm{a}}} - \ln {\rho _{\rm{b}}}} \right)u}}{x}. $ | (15) |
式中:ρa和ρb分别为上、下断面的污染物浓度.
按照1.2.2所述方法进行寻优计算, 得到最优参数组合.寻优步长选择太大容易错过最优解, 太小时运行效率不高.本文根据经验法确定k和E的大步距为0.05, 二次寻优过程中k和E的小步距为0.01.
2.2.2 一步预测校正根据经验给定系统噪声误差方差矩阵V和测量噪声误差方差矩阵R, 均取为对角阵, 且对角线上所有元素为0.01, 并假定噪声符合高斯白噪声特性[14].
实时校正过程中关键参数取值如下:Δt为5 s, Δx为1.5 m, E为0.1 m2/s, u为0.1 m/s, k为0.12 d-1, V和R分别为对角元素为0.01的对角阵.
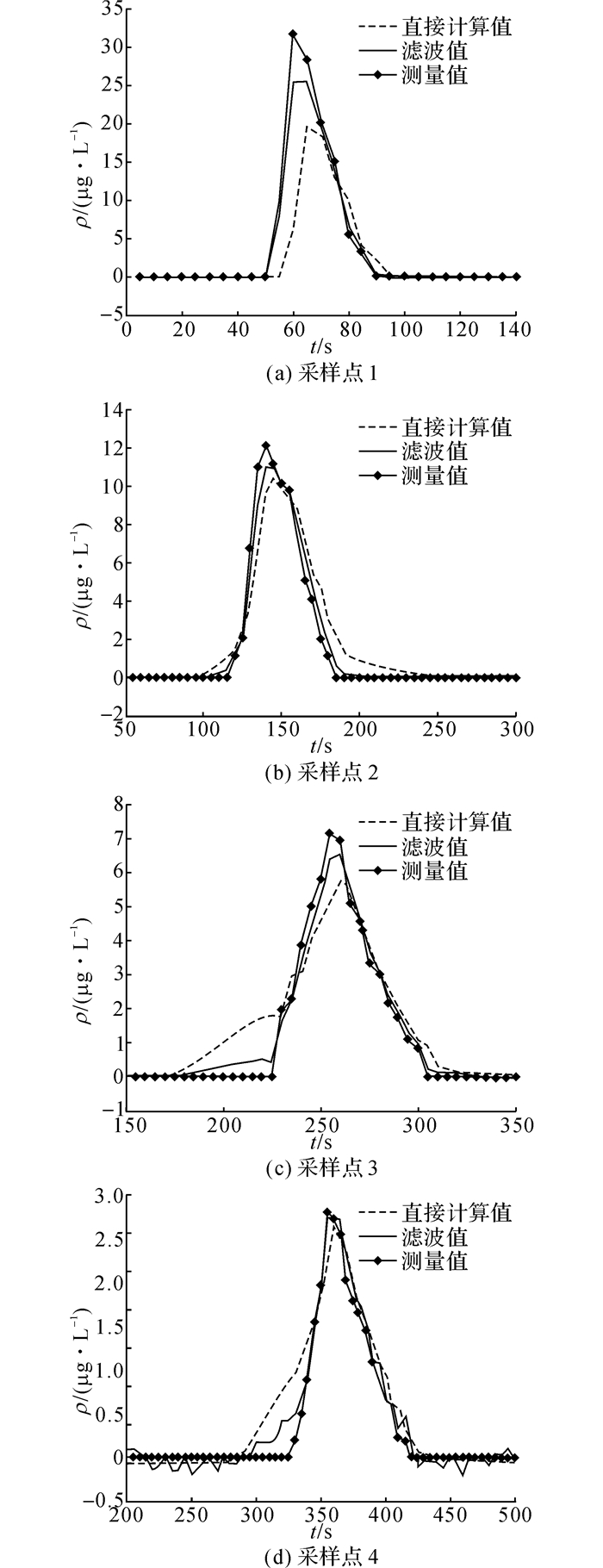
利用第3组实验结果进行验证.如图 4所示为第3组实验4个采样点污染物浓度测量值、直接计算值和滤波值的对比情况.本实验采样点位于支流汇合点下游所以一步预测不考虑支流校正.可以看出测量值、直接计算值和滤波值趋势总体吻合良好.
|
图 4 污染物浓度观测值、直接计算值和滤波值对比 Fig. 4 Pollutant concentration of observation, directly calculated value and filter value |
对于突发污染事故人们比较关心的是峰现(污染物峰值浓度出现时间)和峰值浓度, 因此选取这两者作为评价指标.4个采样点污染物浓度峰值和峰现时间如表 1、2所示.表中, ρo、ρbf、ρaf分别表示污染物浓度观测峰值、直接计算峰值和滤波峰值, δbf、δaf分别表示直接计算峰值和滤波峰值相对误差, to、tbf、taf、tebf、teaf分别表示实测峰现、直接计算峰现、滤波峰现、直接计算峰现误差和滤波峰现误差.从表 2可以看出, 峰现时间差别不大, 这主要是因为本实验中流速比较稳定.从图 4和表 1可以看出滤波峰值浓度相对误差较直接预测均有大幅下降, 证明卡尔曼滤波可以实时校正一步预测值.但采样点1两个预测值误差都较大, 这是由于采样点1距离投放点较近, 污染物可能还未充分扩散便通过该点, 而随着时间推移, 污染物均匀混合且实测数据逐渐增多, 预测效果也更加准确.
| 表 1 污染物观测、直接计算和滤波峰值浓度对比 Table 1 Comparison of observed, directly calculated and filtered peak pollutant concentration |
| 表 2 污染物观测、直接计算和滤波峰现时间对比 Table 2 Comparison of observed, directly calculated and filtered pollutant peak times |
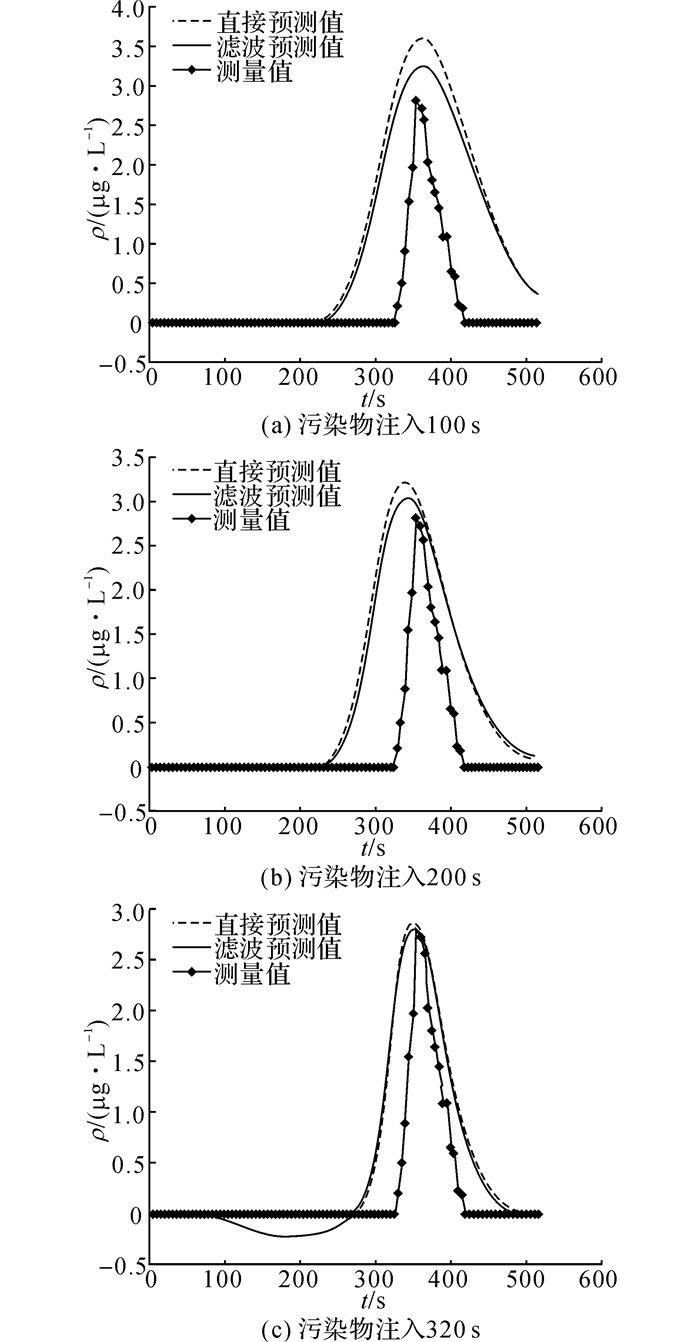
取采样点4为观察点.多步预测校正分别在污染物注入100 s、200 s和320 s时进行, 利用当前时刻及历史最优估计值预测下游污染物浓度趋势.如图 5所示为未考虑支流情况下的多步预测结果.可以看出, 由于流速稳定, 峰现时间差别不大.
|
图 5 不同时刻采样点4多步预测结果 Fig. 5 Multiple step predicted results at sample point Ⅳ at different times |
如表 3所示为不同时刻预测峰值浓度和峰现时间对比.表中, Tp表示预测时刻, ρdp、ρfp、δdp、δfp分别表示直接预测峰值浓度、滤波预测峰值浓度、直接预测相对误差和滤波预测相对误差.从图 5和表 3可以看出, 无论直接预测还是滤波预测, 时间越靠后预测相对误差都有大幅下降, 说明将观测数据纳入预测过程的必要性.此外同一时刻滤波预测相对误差均比直接预测相对误差小, 说明利用卡尔曼滤波进行多步预测校正可以提高预测精度.
| 表 3 不同时刻采样点4多步预测污染物峰值浓度对比 Table 3 Comparison of multistep predicted peak pollutant concentration at sampling point Ⅳ at differenttimes |
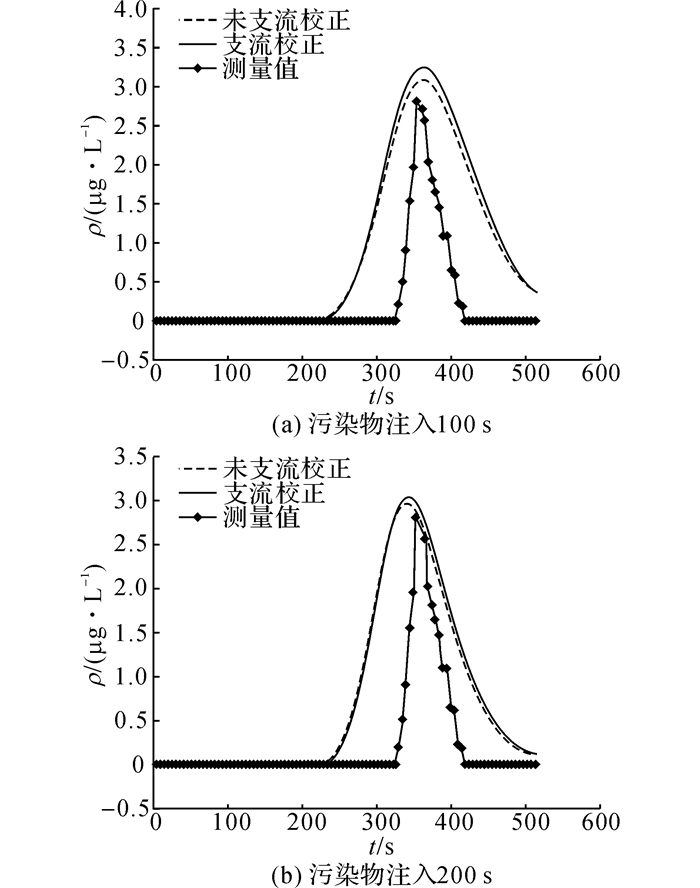
支流校正指在多步预测过程中在支流汇入点处根据干流流量、支流流量以及汇合点前的污染物浓度, 根据式(13)实时校正汇合后的污染物浓度.如图 6所示为不同时刻支流校正后的多步预测结果.320 s时所有采样点的观测值均是支流稀释后的值所以此时未进行支流校正.可以看出峰现时间差别不大.
|
图 6 不同时刻采样点4支流校正预测结果 Fig. 6 Predicted results at sample point Ⅳ after Tributary-calibration at different times |
如表 4所示为支流校正后的预测峰值浓度对比.表中, ρbt、ρat、δbt、δat分别为支流校正前、后采样点4预测峰值浓度及相对误差.从图 6和表 4可以看出, 支流校正后多步预测精度有显著提升.
| 表 4 不同时刻采样点4支流校正预测污染物峰值浓度对比 Table 4 Comparison of predicted peak pollutant concentration at sampling point Ⅳ at different times after tributary-calibration |
(1) 河流突发污染事故污染物浓度预测中, 由于水环境、污染事件本身等存在着很强的不确定性会影响预测结果.实验结果表明, 基于卡尔曼滤波算法的污染物实时预报模型综合考虑模型结构误差和测量误差, 通过反馈机制可以实时校正污染物一步和多步预测结果, 提高预测精度.
(2) 实际河道中存在很多支流, 在动态预测过程中考虑支流对污染物的稀释作用进行支流校正可以进一步使污染物预测浓度接近真实值, 提高结果的准确性可可靠性.
(3) 本研究工作对河流突发污染事故应急决策技术支持具借鉴意义.
系统噪声误差方差V和测量噪声误差方法R的确定是卡尔曼滤波的关键, 本文采用经验法获得, 后续工作中将采用数值方法;实际河道错综复杂, 后续研究需要进一步在实际河道中验证本文提出的方法理论.
| [1] |
周林岩. 我国饮用水安全保障问题研究[D]. 吉林: 吉林大学, 2011.
ZHOU Lin-yan. Research on legal system of drinking water safety in China[D]. Jilin:Jilin University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10183-1011095258.htm |
| [2] | HOU D B, SONG X X, ZHANG G X, et al. An early warning and control system for urban, drinking water quality protection:China's experience[J]. Environmental Science and Pollution Research, 2013, 20(7): 4496–4508. DOI:10.1007/s11356-012-1406-y |
| [3] | STREETER H W, PHELPS E B. A study of the pollution and natural purification of the Ohio River[R]. US Department of Health, Education, and Welfare, 1958. |
| [4] | CAMARA A S, RANDALL C W. The QUAL Ⅱ model[J]. Journal of Environmental Engineering, 1984, 110(5): 993–996. DOI:10.1061/(ASCE)0733-9372(1984)110:5(993) |
| [5] |
唐大元. WASP水质模型国内外应用研究进展[J].
安徽农业科学, 2011, 39(34): 21265–21267.
TANG Da-yuan. Research progress of the application of WASP water quality model in domestic and abroad[J]. Journal of Anhui Agricultural Science, 2011, 39(34): 21265–21267. DOI:10.3969/j.issn.0517-6611.2011.34.126 |
| [6] | LI R Z, SHIGEKI M. Fuzzy model for Two-Dimensional river water quality simulation under sudden pollutants discharged[J]. Journal of Hydrodynamics, 2007, 19(4): 434–441. DOI:10.1016/S1001-6058(07)60137-1 |
| [7] | ZHANG Q Q, XU Y P, XU X, et al. Application of Bayesian network in water quality risk analysis and pollution reduction decision making from small data[C]//2011 International Conference on Remote Sensing, Environment and Transportation Engineering (RSETE). Nanjing:IEEE, 2011:84-88. http://ieeexplore.ieee.org/document/5964222/ |
| [8] | NEELAKANTAN T R, PUNDARIKANTHAN N V. Neural network-based simulation-optimization model for reservoir operation[J]. Journal of Water Resources Planning and Management, 2000, 126(2): 57–64. DOI:10.1061/(ASCE)0733-9496(2000)126:2(57) |
| [9] |
李沫, 徐鸣, 冒莹. 主成分分析与灰色模型在水磨河污染成因分析及污染预测中的应用[J].
干旱环境监测, 2012, 26(4): 216–221.
LI Mo, XU Ming, MAO Ying. Application of principal components analysis and grey model to pollution origin analysis and forecast in Shuimo River[J]. Arid Environmental Monitoring, 2012, 26(4): 216–221. |
| [10] | ZHANG B, QIN Y, HUANG M X, et al. SD-GIS-based temporal-spatial simulation of water quality in sudden water pollution accidents[J]. Computers and Geosciences, 2011, 37(7): 874–882. DOI:10.1016/j.cageo.2011.03.013 |
| [11] | HOU D B, GE X F, HUANG P J, et al. A real-time, dynamic early-warning model based on uncertaintyanalysis and risk assessment for sudden water pollution accidents[J]. Environmental Science and Pollution Research, 2014, 21(14): 8878–8892. DOI:10.1007/s11356-014-2936-2 |
| [12] |
宋筱轩. 动态数据驱动的河流突发性水污染事故预警系统关键技术研究[D]. 杭州: 浙江大学, 2014.
SONG Xiao-xuan. Research on the key techniques of dynamic data driven early warning system for sudden river pollution accidents[D]. Zhejiang:Zhejiang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014227119.htm |
| [13] |
赖瑞勋, 方红卫, 徐兴亚, 等. 水沙实时预测数学模型研究[J].
水利学报, 2014(8): 930–937.
LAI Rui-xun, FANG Hong-wei, XU Xing-ya, et al. Dynamic numerical model for the prediction of water and sediment transport[J]. Journal of Hydraulic Engineering, 2014(8): 930–937. |
| [14] | WU X L, WANG C H, CHEN X, et al. Kalman filtering correction in real-time forecasting with hydrodynamic model[J]. Journal of Hydrodynamics, 2008, 20(3): 391–397. DOI:10.1016/S1001-6058(08)60072-4 |
| [15] |
高山红, 吴增茂, 谢红琴. Kalman滤波在气象数据同化中的发展与应用[J].
地球科学进展, 2000(5): 571–575.
GAO Shan-hong, WU Zeng-mao, XIE Hong-qing. The developments and application of Kalman filters in meteorological data assimilation[J]. Advance in Earth Sciences, 2000(5): 571–575. |
| [16] | RAUCH W, HENZE M, KONCSOS L, et al. River water quality modeling:Ⅰ. state of the art[J]. Water Science and Technology, 1998, 38(11): 237–244. |
| [17] |
宰松梅, 郭树龙, 王洪胜. 几种计算河流纵向弥散系数方法的比较[J].
人民黄河, 2008, 30(5): 20–21.
ZAI Song-hai, GUO Shu-long, WANG Hong-sheng. Comparison of several kinds of methods which calculating longitudinal dispersion coefficient[J]. Yellow River, 2008, 30(5): 20–21. |
| [18] | 中国环境规划院. 全国水环境容量核定技术指南[R]. 北京: 中国环境规划院, 2003. |



