2. 山地城镇建设与新技术教育部重点实验室, 重庆 400045;
3. 重庆科技学院 建筑工程学院, 重庆 401331
2. Key Laboratory of New Technique for Construction of Cities in Mountain Area, Chongqing 400045, China;
3. School of Civil Engineering and Architecture, Chongqing University of science & technology, Chongqing 401331, China
建筑结构允许发生一定程度的损伤和破坏以抵抗强震作用, 大量震害表明, 具有合理的损伤机制是结构实现预期抗震性能的关键[1].叶列平[2]基于结构系统的层次性原理, 给出了预期结构抗震性能, 进而提出了结构地震破坏机制和破坏过程的控制原理和可行方法;白久林等[3]综合考虑构件在不同侧力模式下的损伤概率和塑性铰出铰顺序, 提出了通过加强结构局部构件实现结构整体损伤机制的方法.罗文文[4]从预期损伤构件和预期非损伤构件2方面控制结构实现预期的损伤机制, 提出RC框架结构基于预设损伤的抗震设计方法和设计流程.陈佩圆[5]认为损伤机制是影响结构耗能能力的主要因素;董晓峰[6]利用Park-Ang双参数模型, 提出以结构梁柱损伤比作为量化损伤机制和评估层屈服风险的安全性指标.而针对损伤机制的合理性评价, 仅使用安全性指标会忽略结构的经济性以及可恢复性.马宏旺等[7]以结构顶点位移作为结构的性能指标, 并结合经济性对结构可修性进行评价;曲哲等[8]提出了“破坏-安全”的结构抗震理念, 同时考虑了结构的安全性和经济性;罗文文[4]采用简化的PEER-PBEE评价方法, 同时考虑安全性和经济性, 选择加权组合方法, 提出合理性指标.
上述研究虽然分析了结构损伤机制并提出了同时考虑安全和经济性的概念, 但具体计算方法还不成熟.简化的PEER-PBEE方法过于复杂, 且在简化过程中会引入误差, 较难用于工程实践.因此, 在建立综合评价不同损伤机制下结构的安全、经济、可恢复性的框架进而给出可用于实际工程的评价指标方面还需进一步完善.Bruneau等[9]提出考虑安全、经济、可恢复性的体系恢复力概念后, Bruneau等[10], Fujita等[11], 金书淼[12]已将可恢复指标应用到了供水系统等大型系统工程的综合评价中.本文将体系恢复力概念引入到给定烈度下单体结构地震可恢复指标计算中;对5种典型损伤机制的RC框架结构, 进行易损性分析和恢复力参数计算, 得到结构可恢复指标;给出可恢复指标对各主要恢复力参数的敏感性;基于参数的敏感性以及损伤状态与恢复函数的相关性, 提出修正的给定烈度区下结构可恢复指标计算方法.
1 基于可恢复指标的恢复力评价方法综合评价结构的损伤机制对基于性能的抗震设计具有重要基础性意义.Bruneau等[9]提出的体系恢复力概念较全面的体现了影响结构抗震性能的因素, 可以引入到综合评价单体结构的损伤机制中.
1.1 体系恢复力 1.1.1 恢复力曲线多学科地震研究所(MCEER)把体系(例如供水系统)在灾害下的性能用一个变量来表示, 即恢复力.而Bruneau等[9]进一步将体系在地震作用下的恢复力定义为, 社会单元为了减轻震害, 抑制震害的影响而采取应急响应措施以减轻社会单元的损失.因此, 提高体系恢复力能减少地震作用下生命和财产的损失.综合考虑体系在地震下的响应, Chang等[13]提出了体系恢复力曲线, 如图 1所示.图中, Q(t)为时间变量的体系功能函数, 代表体系在时的使用功能, t为时间,tRE为恢复时间, 100%表示体系没有发生损伤, 0%表示体系已完全损伤, 体系在tOE时遭遇地震作用引起Q(t)下降, tOE+tRE时Q(t)恢复至地震前水平.体系恢复力的计算如下:
| $ R = \int\limits_{{t_{OE}}}^{{t_{OE}} + {t_{RE}}} {Q\left( t \right){\rm{d}}t} . $ | (1) |
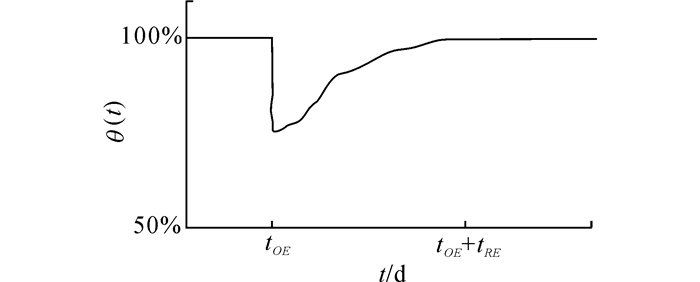
|
图 1 体系恢复力曲线 Fig. 1 Seismic resilience function of system |
定量评估体系在地震作用下的恢复力是保证体系可恢复性的基础.恢复力的定量计算根据鲁棒性、冗余性、智能性和快速性4个特性;而提高恢复力应从技术维度、组织维度、经济维度、社会维度4个方面着手.
鲁棒性:在地震作用下体系避免完全失效的能力.在恢复力曲线中体现为体系残余功能.
| $ {\rm{Robustness}}\left( \% \right) = Q\left( {{t_{OE}}} \right). $ | (2) |
快速性:体系在震后恢复其功能的速度快慢.体现为tOE至tOE+tRE时段功能函数的斜率.
| $ {\rm{Rapidity}}\left( t \right) = \frac{{{\rm{d}}Q\left( t \right)}}{{{\rm{d}}t}}. $ | (3) |
冗余性:体系在抗震设防的多道防线是体系冗余度.
智能性:通过识别体系在地震作用下的损伤状态以及体系的重要性, 选择相应的应急响应策略, 使恢复时间简短, 经济损失减少.
1.2 给定烈度区中单体结构恢复力单体结构恢复力主要涵盖技术和社会2个维度, 虽然体系恢复力已经建立完善的评估理论, 但定量评估还较少涉及单体结构.且该评价方法引入国内后, 需考虑在规范烈度区划分框架下进行结构恢复力评价.因此, 本文选取Bocchini等[14]给出的单位时间可恢复指标体现恢复力, 其表达式为
| $ r = \frac{{\int\limits_{{t_{OE}}}^{{t_{OE}} + {t_{RE}}} {Q\left( t \right){\rm{d}}t} }}{{{t_{RE}}}}. $ | (4) |
式中:功能函数Q(t)为反应体系的性能随时间变化的函数曲线, 其具体计算可参考Cimellaro等[15]提出功能函数Q(t)的定量计算公式:
| $ Q\left( t \right) = 1- {L_{{\rm{LD}}}}\left\{ {H\left( {t- {t_{OE}}} \right)- H\left[{t-\left( {t + {t_{RE}}} \right)} \right]} \right\}{f_{{\rm{REC}}}}. $ | (5) |
式中:H(t)为赫维赛德阶跃函数;fREC为恢复函数;LLD为结构在给定地震烈度区(LD)下结构的损失函数.
1.2.1 恢复时间tRE恢复时间是结构修复至原使用功能, 或所期望功能水平所需要的时间.恢复时间是不确定的随机变量, 它与结构所在地区和损伤程度有关, 体现了结构在恢复阶段应急响应策略的智能性.恢复时间的影响因素较为复杂且离散性较大, 本文采用李英民等[16]拟合的结构损伤指数(damage factor, DF)与修复时间率(repair time ratio, CRTR)的关系(如图 2所示), 其中结构损伤指数(DF)与结构损伤状态的关系参考Park模型[17]如表 1所示, 本文选取各损伤状态对应的损伤指数中值进行计算, 损伤指数中值如表 1所示.
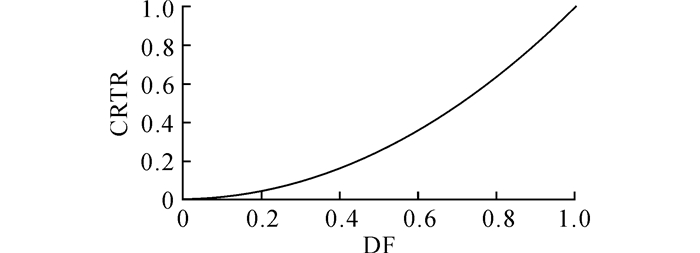
|
图 2 损伤指数与修复时间率关系函数 Fig. 2 Function of damage factor (DF) and repair time ratio (CRTR) |
| 表 1 各损伤状态对应的损伤指数(Park模型) Table 1 Damage factors (DF) associated with different damage states (Park model) |
LLD是在给定地震烈度区(LD)下结构的损失函数, 从图 1恢复力曲线可以看出结构在地震作用下的损伤程度, 体现结构的鲁棒性和冗余度.从结构安全性和经济性考虑, 结构在地震作用下的损伤越小越好.但是由于地震作用的随机性, 结构在地震作用下的损伤也是随机的.考虑所有影响结构损失的参数, 将结构在地震作用下的损失分为结构损失和因结构损失引起的直接因果损失.其中, 结构损失可以分为结构构件损失LS和非结构构件损失LNS+LNS, DC.损失函数LLD为
| $ {L_{{\rm{LD}}}} = {L_{\rm{S}}} + {L_{{\rm{NS}}}} + {L_{{\rm{NS}}, {\rm{DC}}}}. $ | (6) |
结构构件损失可表示为
| $ {L_{\rm{S}}} = \sum\limits_{j = 1}^k {\left\{ {\frac{{{C_{{\rm{S}}, j}}}}{{{I_{\rm{S}}}}} \cdot \prod\limits_{i = 1}^{{T_i}} {\frac{{\left( {1 + {\delta _i}} \right)}}{{1 + {r_i}}} \cdot \sum\nolimits_{I = 0}^n {\left[{f\left( I \right) \cdot {p_j}\left( I \right)} \right]} } } \right\}} . $ | (7) |
| $ {P_j} = \sum\limits_{I = 0}^n {f\left( I \right) \cdot {p_j}\left( I \right).} $ | (8) |
式中:j为结构损伤状态;Cs, j/IS为结构在j损伤状态下, 修复成本与修建成本的比值, 即结构损失比;δi为第i年贴现率;ri为第i年折旧率;Ti表示结构在第Ti年发生损伤;Pj为设计基准期内不同损伤机制的结构出现某一损伤状态j的概率, 是通过对各地震强度水平进行加权求和得到;I表示在给定地震烈度区(LD)下的某地面加速度强度区间的代表值;pj(I)为结构在地面加速度强度代表值为I时, 结构出现损伤状态j概率, 可以利用基于IDA的易损性分析得到结构处于各损伤状态的概率分布;n表示结构所在给定烈度区重现期为2 475年所对应的地面加速度强度水平;f(I)是在给定地震烈度区(LD)下至少发生一次某地面加速度强度地震事件的概率, 可利用地震危险性曲线的插值后相减得到, 地震危险性曲线如下[18]:
| $ {\lambda _{{\alpha _{\min }}}} = {k_0}{\left( {{\alpha _{\min }}} \right)^{-k}}. $ | (9) |
式中:αmax为地震影响系数最大值;λαmax为αmax对应的年平均超越概率;k0和k为常数.
非结构构件损失函数LNS可表示为
| $ {L_{{\rm{NS}}}} = \left\{ {\sum\limits_{K = 1}^{{N_{{\rm{ns}}}}} {{W_{K \cdot }}{L_{{\rm{NS, }}K}}\left( I \right)} } \right\}/{N_{{\rm{ns}}}}. $ | (10) |
式中:Nns为结构中非结构构件的数量;WK为权重系数, 是每一个非结构构件与所有非结构构件的重量比;LNS, K利用式(7)计算第K个非结构构件的损失.
直接因果损失函数LNS, DC可表示为
| $ {L_{{\rm{NS}}{\rm{.DC}}}} = {N_{{\rm{in}}}}/{N_{{\rm{tot}}}}. $ | (11) |
在同一地震下, 结构响应是随机函数, 造成的人员伤亡也是随机函数.Ntot为结构容纳的总人数;Nin为地震中受伤和遭受财产损失的人数.
1.2.3 恢复函数fREC恢复函数的主要影响因素是结构的损伤程度和恢复速度.恢复函数体现了结构应急响应的速率, 即恢复力体系的快速性, 反映出结构的重要性和决策者对结构的重视程度.根据结构的损伤程度和社会应急响应速度, 恢复函数有不同的形式[19].式(12)~(14)给出3种简化的恢复函数, 分别是线性函数型, 指数函数型和三角函数型.
| $ {f_{{\rm{REC}}}}\left( {t, {t_{RE}}} \right) = 1-{L_{LD}}\left( {1-\frac{{t-{t_{OE}}}}{{{t_{RE}}}}} \right). $ | (12) |
| $ {f_{{\rm{REC}}}}\left( {t, {t_{RE}}} \right) = 1- {L_{LD}}\exp \left[{-\left( {t-{t_{OE}}} \right)\frac{{\ln 200}}{{{t_{RE}}}})} \right]. $ | (13) |
| $ \begin{array}{l} {f_{{\rm{REC}}}}\left( {t, {t_{RE}}} \right) = \\ 1- {L_{LD}} \cdot 0.5\left\{ {1 + \cos \left[{\pi \left( {t-{t_{OE}}} \right)/{t_{RE}}} \right]} \right\}. \end{array} $ | (14) |
指数函数型适用于恢复资源和恢复储备充足, 结构损伤不严重, 社会反应非常快的情况;线性函数型适用于恢复资源和资源储备情况不明, 结构损伤程度和社会反应情况不确定的情况;三角函数型用于恢复资源和恢复储备不足, 结构损伤严重或者社会反应比较慢的情况.各恢复函数图形如图 3所示.目前较常采用的是选取其中一种恢复函数进行后续的可恢复指标计算及恢复力评价.
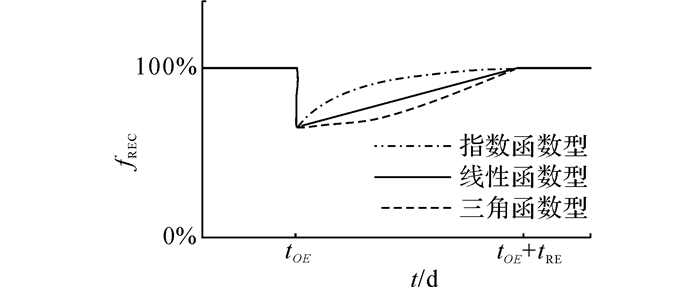
|
图 3 3种简化的恢复函数 Fig. 3 Three kinds of simplified recovery functions |
体现结构恢复力的可恢复指标计算方法主要有5个步骤:地震危险性分析、结构响应分析、地震易损性分析、损失分析和可恢复性分析, 分析流程如图 4所示.

|
图 4 可恢复指标计算方法流程图 Fig. 4 Flow chart of seismic resilience index caculation |
上述已将体系恢复力概念引入给定烈度区中单体结构可恢复指标计算, 本节根据基于预设损伤的抗震设计方法设计出不同损伤机制的RC框架结构, 通过易损性分析, 计算和对比各损伤机制对应的RC框架结构在给定烈度区中结构的恢复力.
2.1 RC框架结构设计首先以8度区(0.3g,g为重力加速度)为例, 设计了一个3×3的5层RC框架结构.场地类别为Ⅱ类, 计地震分组为第2组.平面结构如图 5(a)所示, 跨度均为6 m, 梁截面尺寸为300 mm×700 mm;结构立面图见图 5中(b), 首层层高3.3 m, 其余层高均3.0 m, 柱截面尺寸为500 mm×500 mm.楼面、屋面恒荷载标准值5.0 kN/m2, 活载标准值取2.0 kN/m2, 板厚取120 mm.混凝土强度C40, 纵筋采用HRB400, 箍筋采用HPB300.利用基于我国规范[20]的PKPM软件进行标准结构的配筋设计, 配筋结果如图 5(c)所示.因结构规则对称, 后续分析仅以图 5中B轴对应的一榀框架代替整体结构.
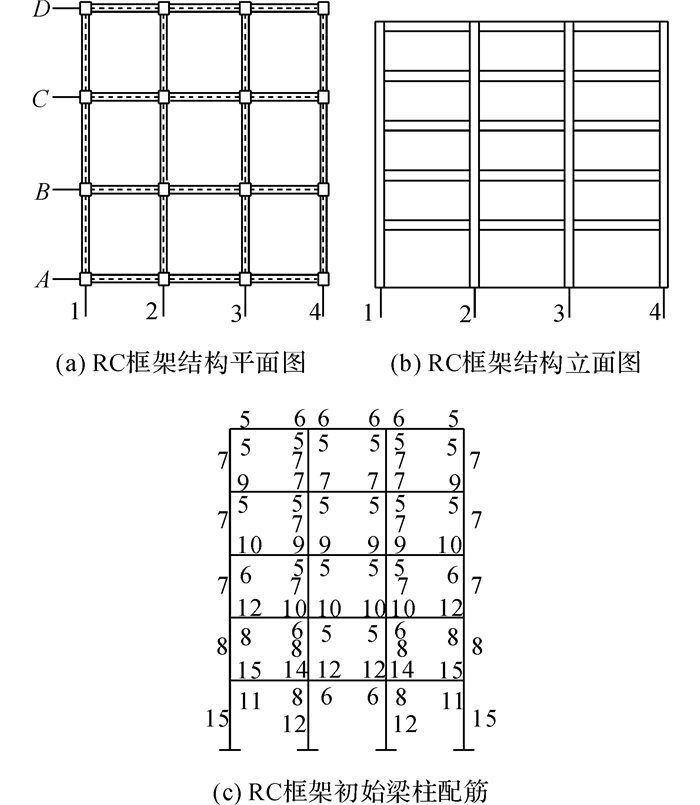
|
图 5 算例中RC框架标准结构布置图 Fig. 5 Layout of standardized RC frame structure in example |
按照我国规范设计的RC框架结构常见的5种损伤机制分别为:梁铰整体损伤机制, 梁铰局部损伤机制, 柱铰整体损伤机制, 柱铰局部损伤机制和层屈服机制[21].为实现预期损伤机制, 在约束截面的基础上, 预期损伤构件仍采用标准结构相应的配筋方案, 预期不损伤构件通过保证大震弹性且满足规范要求而进行重新配筋.为了计入现浇楼板的作用, 将梁考虑为T型截面, 并将板筋配置在翼缘里.通过调整结构配筋的方式, 设计出与5种损伤机制相对应的5个RC框架结构, 各损伤机制对应结构的梁柱配筋如图 6所示.

|
图 6 算例中基于不同损伤机制的RC框架结构配筋图 Fig. 6 Structure reinforcement design of RC frames associated with different failure modes in example |
根据8度0.3 g区、Ⅱ类场地、计地震分组等参数确定选波所用目标反应谱曲线.采用双频段选波方法选出20条地震波.由于结构可恢复指标计算需要在同一烈度区及场地类别下, 对各地震强度作用下结构的损伤进行加权求和.因此, 将地震加速度峰值(peak of ground motion acceleration, PGA)以50 cm/s2为间隔、500 cm/s2为上限, 分隔为10个地震动强度区间, 各区间的概率f(I)依次为0.185、0.293、0.178 5、0.089、0.048、0.035、0.028、0.016、0.010、0.006.所选20条地震波均按照所分隔地震加速度强度区间的代表值进行调幅.
2.3 结构易损性分析本文采用基于IDA的易损性分析方法, 以PGA作为地震强度指标, 对选出的20条地震波, 进行10次等步长调幅, 考虑现浇楼板影响, 计算得到IDA曲线.通过易损性分析, 得到各损伤机制对应结构在8度区(0.3g)的易损性曲线.各损伤机制对应的结构易损性曲线如图 7所示, 横坐标为PGA, 纵坐标P为超越极限概率.易损性分析中采用结构最大层间位移角(θmax)作为结构损伤状态的判别准则, 钢筋混凝土框架结构在各损伤状态对应的最大层间位移角范围取值与抗震规范一致[20、22].
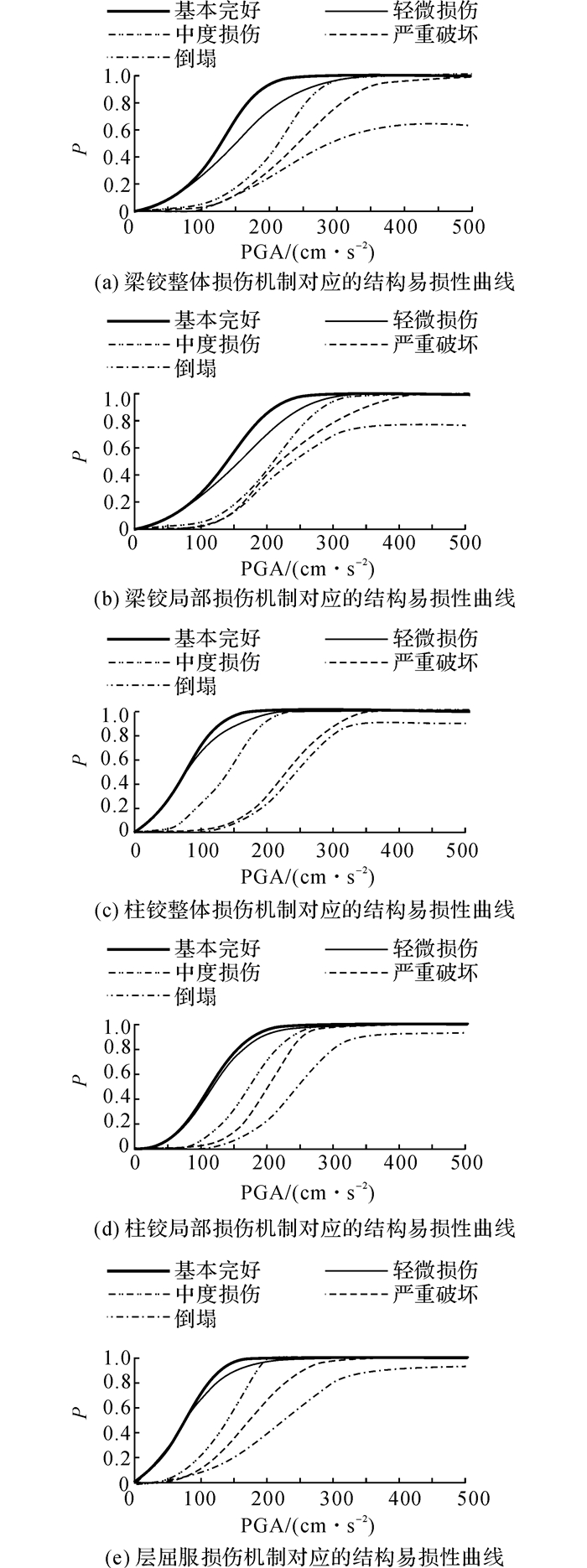
|
图 7 算例中基于不同损伤机制的RC框架结构易损性曲线 Fig. 7 Vulnerability curves of RC frames associated with different failure modes in numericalexample |
对各损伤机制的结构进行易损性分析后, 可以利用式(8)对各地震强度水平进行加权求和, 得到设计基准期内不同损伤机制的结构出现某一损伤状态的概率Pj, 所得概率值如表 2所示.
| 表 2 不同损伤机制的RC框架结构出现各损伤状态的概率 Table 2 Probability of Structural damage states of RC frames associated with different failure modes |
从表 2可以看出, 在轻微损伤状态和中度损伤状态下, 梁铰机制与柱铰机制的损伤概率绝对值相差较小.其主要原因是Pj的计算中考虑了各地震强度水平的贡献, 而中小震下结构进入塑性的程度并不深, 使得对各地震强度水平加权求和后得到的Pj差别不明显.在严重破坏状态及倒塌状态下, 梁铰机制与柱铰机制的损伤概率的相对比值达到了2倍及以上, 能体现较大差别.总体而言, 柱铰机制及层屈服机制更易发生较大的破坏.
2.4 不同损伤机制对应结构可恢复指标对比本文主要针对结构构件的损伤机制进行恢复力评价, 而非结构损失因建筑用途的不同而相差较大, 因此, 本文暂时忽略非结构构件及人员伤亡的影响.结构损失比是指工程结构某一破坏等级的修复单价与重置单价之比.房屋破坏损失比可根据结构类型、损伤状态, 在《地震现场工作第4部分:灾害直接损失评估》[23]给出的范围中选取适当的值, 一般选取中值.表 3给出钢筋混凝土框架结构在各损伤状态对应的损失比中值LRC.
| 表 3 RC框架结构不同损伤状态对应的结构损失比 Table 3 Structure loss ratios of RC frames associated with different damage states |
将各损伤状态的损失比和各损伤机制对应结构的损伤状态概率代入式(7)、(8)得到结构损失LS.根据国内情况, 取年平均贴现率为4.5%, 年平均折旧率为1%, 建筑结构设计寿命为50 a.选用式(13)所示指数型恢复函数作为功能函数模型, 代入式(4)和(5)计算各损伤机制的可恢复指标.可恢复指标计算结果如表 4所示.
| 表 4 算例中不同损伤机制RC框架结构的可恢复指标 Table 4 Seismic resilience indexes of RC frames associated with different failure modes in example |
通过对比可以发现:在同一地震烈度下, 梁铰损伤机制的可恢复指标高于柱铰和层屈服损伤机制, 而整体损伤机制的可恢复指标高于局部损伤机制.各损伤机制的恢复力从高到低依次为:梁铰整体、梁铰局部、柱铰整体、柱铰局部、层屈服.其中, 梁铰整体和梁铰局部与我国规范所提倡的“强柱弱梁”概念相符.虽然对比结果符合已有研究对各损伤机制优劣的定性判别, 但可恢复指标差异不太明显, 且恢复函数的选取存在一定的片面性.
3 可恢复指标敏感性分析上述分析得到了8度0.3g烈度区下基于指数恢复函数的各不同损伤机制对应的RC框架结构可恢复指标, 进而用可恢复指标对比结构恢复力.本节将给出可恢复指标对烈度水平、恢复时间模型以及恢复函数的敏感性, 为可恢复指标的修正提供参考.
3.1 烈度水平为对比各烈度区结构可恢复指标的差异, 本节按前述方法, 重新设计8度0.2g区的5种损伤机制对应的RC框架结构.并依此计算该烈度区下各地面加速度强度水平区间概率、损失函数等参数, 最终得到可恢复指标.各损伤机制对应结构在8度0.3g区和8度0.2g区下的可恢复指标如图 8所示.

|
图 8 不同烈度区各损伤机制可恢复指标 Fig. 8 Seismic resilience indexes of different failure modes in different intensity regions |
通过对比可以发现:随着地震烈度的变化, 各损伤机制的可恢复指标总体变化不大, 说明各烈度区的建筑按规范进行抗震设计后, 均能达到各烈度区对应的性能目标, 并不会使结构因烈度区改变而让抗震性能差异较大.
3.2 恢复时间本文所参考的恢复时间模型所基于的统计案例有限, 并不能考虑不同地区经济水平以及技术水平的差异, 因此不能够绝对的确定任何地区的恢复时间.本文将恢复时间模型在时域上进行压缩和伸展, 对比恢复时间放大0.5倍以及缩小0.5倍后, 8度0.3g区各损伤机制RC框架结构的可恢复指标的变化趋势, 如图 9所示.

|
图 9 不同恢复时间的各损伤机制可恢复指标 Fig. 9 Seismic resilience indexes of different failure modes with different resilience time |
对比可知, 3种恢复时间下的可恢复指标仅在柱铰整体机制下稍有变化, 这是由于可恢复指标r是恢复函数积分后在(tDE, tDE+tRE)区间的平均值, 故恢复时间的绝对值对可恢复指标的影响很小.
3.3 恢复函数选取从社会维度和组织维度考虑, 结构所在地区和重要程度有一定差异, 结构出现不同损伤状态后对资源储备的需求也不同, 组织震后应急响应策略不同.因此, 视具体情况不同, 恢复函数fREC的选取也不同.本文分别选取1.2节中3种恢复函数计算8度0.3 g区各损伤机制RC框架结构的可恢复指标, 并对比指标的变化趋势, 如图 10所示.
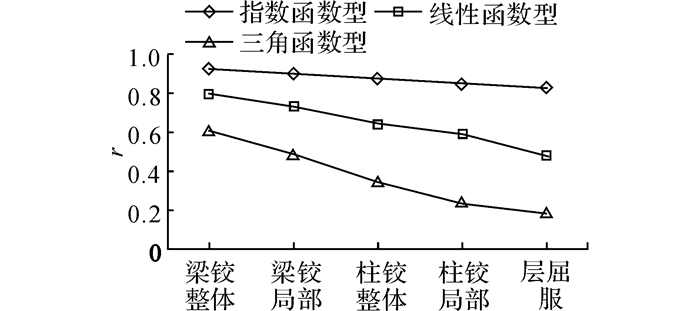
|
图 10 不同恢复函数的各损伤机制可恢复指标 Fig. 10 Seismic resilience indexes of different failure modes with different recovery functions |
通过对比图 10中各损伤机制对应RC框架结构选取不同恢复函数后的可恢复指标, 可以发现:可恢复指标对恢复函数的选取较为敏感, 其中指数型恢复函数的可恢复指标明显高于线性型和三角函数型.因此, 根据结构的损伤程度, 结构重要性以及震后的应急响应策略, 确定恢复储备和恢复资源, 进而选取合适的恢复函数, 对结构可恢复指标的准确性有较大影响.
4 修正的可恢复指标计算方法从上述计算结果可看出, 将恢复力评价方法直接引入给定烈度区结构损伤机制的对比评价后, 各损伤机制的可恢复指标有差异, 但差异大小对恢复函数的选取极其敏感.结构在各损伤状态均选取同一恢复函数并不符合实际情况, 且会忽略各损伤状态恢复函数对结构可恢复指标的贡献.Decò[24]对不同损伤状态的桥梁系统定义了不同的考虑修复延迟的恢复函数曲线.因此, 本文在保持原单体结构可恢复指标主要计算流程不变的前提下, 对可恢复指标中的功能函数Q(t)进行修正.修正的功能函数Q(t)表达式如下:
| $ \begin{array}{l} Q\left( t \right) = 1- \left\{ {H\left( {t- {t_{OE}}} \right)- H\left[{t-\left( {t + {t_{RE}}} \right)} \right]} \right\} \cdot \\ \;\;\;\;\;\;\;\;\;\;\sum\nolimits_{j = 0}^4 {\left[{{L_{{\rm{LD, }}j}} \cdot {f_{{\rm{REC}}, j}}} \right]} . \end{array} $ | (15) |
式中:j为结构损伤状态, j=0、j=1、j=2、j=3、j=4分别对应:基本完好、轻微破坏、中等破坏、严重破坏、倒塌;LLD, j为结构在烈度区LD中出现j损伤状态时的损失, 可参考式(7)、(8)进行计算;fREC, j为结构出现j损伤状态时对应的恢复函数.其他参数意义与式(5)一致.
通过对功能函数Q(t)进行修正后, 可以考虑结构不同损伤状态所对应的恢复函数对可恢复指标的贡献, 更符合实际, 减少了只选取单一恢复函数所引起可恢复指标的不确定性.本文基于Bocchini等[25]的六参数恢复函数模型和Decò等[24]的考虑修复响应延迟的结构损伤状态与恢复函数关系, 确定出各损伤状态的恢复函数, 如图 11所示.
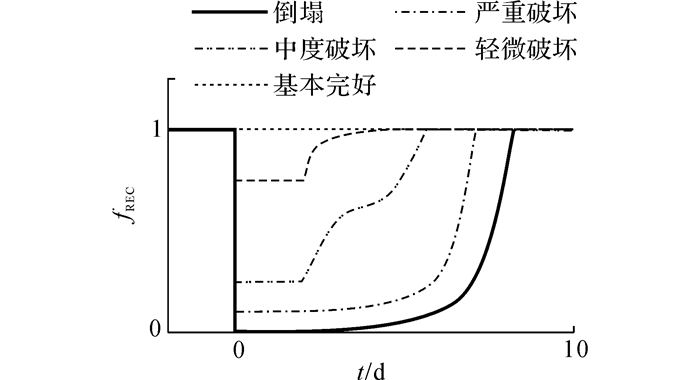
|
图 11 各损伤状态的恢复函数曲线 Fig. 11 Recovery functions of different damage states |
对恢复力评价方法进行修正后, 重新得到8度0.3 g区RC框架结构各损伤机制的可恢复指标, 如图 12所示.从图 12可看出, 与原方法选取单一的指数恢复函数所得计算结果相比, 修正后的各损伤机制可恢复指标相对关系没有变化, 但指标数值更稳定, 区分度更明显, 可比性更强, 也更符合已有研究对各损伤机制优劣的定性判别.因此, 本文所提出的修正的可恢复性指标能体现结构的安全性、经济性以及可恢复性, 能够对结构损伤机制的恢复力进行评价, 为设计者选取合理损伤机制提供较好的参考.
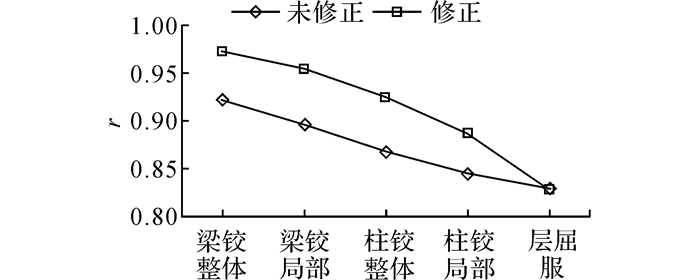
|
图 12 修正后的各损伤机制可恢复指标 Fig. 12 Seismic resilience indexes of different failure modes with modified method |
本文基于体系恢复力概念(resilience of system), 提出了修正的可恢复指标, 用于对比评价给定烈度区下单体结构各损伤机制的恢复力(即安全性、经济性、可恢复性), 得出结论如下:
(1) 体系恢复力概念可综合体现安全性、经济性和可恢复性.将其引入单体结构, 能够较全面的对RC框架结构各损伤机制抗震性能进行全寿命的综合对比评价.
(2) 不同RC框架结构损伤机制的鲁棒性、快速性、智能性和冗余性有较大区别, 进而使得结构的损失函数、恢复函数以及可恢复指标有差异.
(3) 可恢复指标稳定性较好, 各烈度区RC框架结构的可恢复指标并不会因烈度的改变而有较大差异, 即基于同一设防目标的RC结构的抗震性能不会因烈度区的改变而产生较大变化.
(4) 修正的结构可恢复指标能更好的区分各损伤机制的恢复力, 并且符合已有研究对各损伤机制优劣的定性判别, 能为结构损伤机制的评价以及结构抗震概念设计提供参考.
(5) 已有研究中的结构损伤机制评价方法较难应用到工程实践中, 而本文所给出的方法较为简便实用.本文仅以简单案例进行了分析, 而在结构设计参数、建筑用途、恢复函数等方面的细节考虑上还可进一步研究.因此, 在实际工程中, 对特定地区中某特定的重要结构进行恢复力评价时, 还需利用更详细资料对可恢复指标的计算进一步完善.
| [1] |
叶列平, 曲哲, 马千里, 等. 从汶川地震框架结构震害谈"强柱弱梁"屈服机制的实现[J]. 建筑结构, 2008, 38(11): 52-59. YE Lie-ping, QU Zhe, MA Qian-li, et al. Study on ensuring the strong column-weak beam mechanism for RC frames based on the damage analysis in the Wenchuan earthquake[J]. Journal of Architectural Structure, 2008, 38(11): 52-59. |
| [2] |
叶列平. 基于系统概念的建筑结构地震破坏机制和破坏过程的控制[J]. 工程抗震与加固改造, 2009, 31(5): 1-7. YE Lie-ping. Failure mechanism and its control of building structures under earthquakes based on system concept[J]. Earthquake Resistant Engineering and Retrofitting, 2009, 31(5): 1-7. |
| [3] |
白久林, 欧进萍. 基于IDA方法的钢筋混凝土结构失效模式优化[J]. 工程力学, 2011, 28(S2): 198-203. BAI Jiu-lin, OU Jin-ping. Optimization of failure modes for reinforced concrete buildings based on IDA mothod[J]. Journal of Engineering Mechanics, 2011, 28(S2): 198-203. |
| [4] |
罗文文. RC框架结构基于损伤控制的抗震设计方法研究[D]. 重庆: 重庆大学, 2015. LUO Wen-wen. Study on seismic damage control-based design methodology for RC frames[D]. Chongqing:Chongqing University, 2015. https://link.springer.com/article/10.1007/s00158-003-0299-2 |
| [5] |
陈佩圆. 基于耗能特性的RC框架结构破坏模式合理性评价[D]. 重庆: 重庆大学, 2012. CHEN Pei-yuan. Rationality review on failure mode of RC frame structures based on energy dissipation characteristics[D]. Chongqing:Chongqing University, 2012. http://ir.canterbury.ac.nz/bitstream/handle/10092/9234/12649144_Morris_ReviewUncertaintiesInRCPerformanceChchEqs_NZSEE_2014.pdf;sequence=1 |
| [6] |
董晓峰. 地震作用下框架结构的破坏模式研究[D]. 重庆: 重庆大学, 2012. DONG Xiao-feng. Study on the failure mode of frame structure under earthquake action[D].Chongqing:Chongqing University, 2012. |
| [7] |
马宏旺, 吕西林, 陈晓宝. 建筑结构"中震可修"性能指标确定方法[J]. 工程抗震与加固改造, 2005, 27(5): 26-32. MA Hong-wang, LV Xi-lin, CHEN Xiao-bao. A new method to determine the performance index of "repairable under moderate earthquake" for buildings[J]. Earthquake Resistant Engineering and Retrofitting, 2005, 27(5): 26-32. |
| [8] |
曲哲, 叶列平. "破坏-安全"结构抗震理念及其应用[J]. 震灾防御技术, 2009, 4(3): 241-255. QU Zhe, YE Lie-ping. "Fail-safe" concept in seismic design and its applications[J]. Technology For Earthquake Disaster Prevention, 2009, 4(3): 241-255. DOI:10.11899/zzfy20090301 |
| [9] |
BRUNEAU M, CHANG S, EGUCHI R, et al. A framework to quantitatively assess and enhance the seismic resilience of communities[J]. EERI Spectra Journal, 2003, 19(4): 733-752. DOI:10.1193/1.1623497 |
| [10] |
BRUNEAU M, REIHORN A. Exploring the concept of seismic resilience for acute care facilities[J]. Earthquake Spectra, 2007, 23(1): 41-62. DOI:10.1193/1.2431396 |
| [11] |
FUJITA YUSHI, INC TECHNOVA. Learning from the fukushima nuclear power plant accident-a resilience point of view[C]//Southeast Asian Network of Ergonomics Societies Conference(SEANES). Langkawi:IEEE, 2012:1-5. http://ieeexplore.ieee.org/articleDetails.jsp?arnumber=6299591
|
| [12] |
金书淼. 城市供水系统地震灾害风险及恢复力研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. JIN Shu-miao. Research on earthquake disaster risk and resilience of urban water supply system[D].Harbin:Harbin Institute of Technology, 2013. http://www.sciencedirect.com/science/article/pii/B9780128021699000021 |
| [13] |
CHANG S E, SHINOZUKA M. Measuring Improvements in the disaster resilience of communities[J]. EERI Spectra Journal, 2004, 20(3): 739-755. DOI:10.1193/1.1775796 |
| [14] |
FRAMGOPOL D M, BOCCHINI Paolo. Resilience as optimization criterion for the rehabilitation of bridges belonging to a transportation network subject to earthquake[C]//2011 Structure Congress. LasVegas NV:ASCE, 2011:2044-2055. http://searchworks.stanford.edu/view/9377354
|
| [15] |
CIMELLARO GP, REINHORN AM, BRUNEAU M. Seismic resilience of a hospital system[J]. Structure and Infrastructure Engineering, 2010, 6(1/2): 127-144. |
| [16] |
LI Ying-min, LUO Wen-wen. Study on evaluation indices and methods of seismic reparability for RC buildings[C]//Proceedings of 15th World Conference of Earthquake Engineering. Lisbon:IAEE, 2012:no.5375. https://link.springer.com/article/10.1007/s10518-015-9824-0
|
| [17] |
PARK Y J, ANG AH S. Damage-limiting aseismic design of buildings[J]. Earthquake Spectra, 1987, 3(1): 1-26. DOI:10.1193/1.1585416 |
| [18] |
CORNELL C A, JALAYER F, HAMBURGER R.O, et al. Probabilistic Basis for 2000 SAC Federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526-533. DOI:10.1061/(ASCE)0733-9445(2002)128:4(526) |
| [19] |
CIMELLARO G P, REINHORN A M, BRUNEAU M. Multidimensional fragility of structures:formulation and evaluation[R]. Technical Report MCEER-06-0002. Buffalo (NY):University at Buffalo, 2006. http://www.academia.edu/3045507/Multi-Dimensional_Fragility_of_Structures_Formulation_and_Evaluation
|
| [20] |
GB 50011-2010. 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010. GB 50011-2010.Code for seismic design of buildings[S]. Beijing:China Architecture & Building Press, 2010. |
| [21] |
JALAYER F, FRANCHIN P, PINTO P E. A scalar damage measure for seismic reliability analysis of RC frames[J]. Earthquake Engineering & Structural Dynamics, 2007, 36(13): 2059-2079. |
| [22] |
羡丽娜, 何政. 不同CMR的RC框架结构地震损失分析[J]. 工程力学, 2014, 31(12): 155-163. XIAN Li-na, HE Zheng. Earthquake loss analysis of frame structures with different collapse margin ratio[J]. Journal of Engineering Mechanics, 2014, 31(12): 155-163. |
| [23] |
GB/T 18208. 4-2005. 地震现场工作第4部分: 灾害直接损失评估[S]. 北京: 地震出版社, 2005. GB/T 18208.4-2005. Post-earthquake field works-Part 4:Assessment of direct loss[S]. Beijing:Seismological Press, 2005. |
| [24] |
DECÒ A, BOCCHINI P, FRANGOPOL DM. A probabilistic approach for the prediction of seismic resilience of bridges[J]. Earthquake Engineering & Structural Dynamics, 2013, 42(10): 1469-87. |
| [25] |
BOCCHINI P, DECÒ A, FRANGOPOL DM. Probabilistic functionality recovery model for resilience analysis[C]//Bridge Maintenance, Safety, Management, Resilience and Sustainability, Biondini F, Frangopol DM (eds). Taylor and Francis:CRC Press, 2012:1920-1927. http://www.crcnetbase.com/doi/pdfplus/10.1201/b12352-283
|


