整体稳定是空间结构设计中的关键问题之一.为跟踪结构受载全过程平衡路径, Riks[1]提出弧长控制法, Crisfield等[2]对该方法进行修正.基于弧长加载策略, 罗永峰等[3~6]提出了改进弧长法, 解决预定荷载水平的求解、平衡路径跟踪及分枝点和极值点的确定问题.现阶段, 弧长法已成为数值计算最稳定、计算效率最高的结构后屈曲路径跟踪方法.
目前, 单点荷载-位移曲线是最常用的结构稳定分析平衡曲线, 但该曲线仅能反映单点的变形路径, 且特征点的选取缺乏理论依据, 主观性较大.现代空间结构形态新异、体系复杂, 单点荷载-位移曲线的劣势越来越明显[7-8].由于空间结构的稳定与整体刚度直接相关, 结构受载过程中的整体刚度变化是空间结构失稳发展过程的直接体现, 故研究空间结构受载全过程中整体刚度的变化, 并用于分析结构的整体稳定性, 可以克服单点荷载-位移曲线的劣势.
为研究结构整体刚度, Bergan等[9]提出当前刚度参数, 但该参数为无量纲参数, 仅适用于判断结构的刚化、软化, 且结构的当前刚度参数值-荷载因子曲线可能存在第2类间断点, 与实际不符.罗永峰[3]将当前刚度参数的正负作为弧长增量正负的判定依据, 研究了结构受载全过程性态, 但并未提出适用于描述整体刚度的参数.沈士钊等[10]基于拟壳法提出了网壳结构的整体等效刚度, 但该参数并不随结构受载过程变化.袁行飞等[11]通过弹性刚度、几何刚度、切线刚度矩阵的最小特征值对结构失稳过程中的性态进行研究, 但加载过程中刚度矩阵特征值的求解较为复杂.张沛等[12]利用切线刚度矩阵最小特征值用来度量张拉整体结构的刚度, 适用范围存在一定的局限性.相阳等[13-14]提出了结构整体刚度参数, 将该参数用于构造空间结构推覆分析中等效单自由度体系的本构模型, 但并未应用于静力稳定分析.在稳定性判定方面, 目前一般以结构切线刚度矩阵的主元首次出现奇异为准则, 此方法对于极值型失稳的结构, 可行性较差, 难以在通用有限元软件中应用.
本文在现有成果的基础上, 提出结构特征刚度和静力加载全过程特征曲线的概念, 验证了特征刚度为零可作为极值型屈曲结构稳定性临界状态的判定依据.选取一个K6型网壳和一个会议中心屋盖网壳进行算例验证, 将特征曲线与荷载-位移曲线进行对比, 以说明特征刚度法及特征曲线的正确性和适用性.
1 特征刚度基本理论 1.1 特征刚度在结构静力稳定分析中, 第i荷载步内的增量平衡方程为
| $ {\mathit{\boldsymbol{K}}_{{\rm{T}}i}}\Delta {\mathit{\boldsymbol{U}}_i} = \Delta {\mathit{\boldsymbol{P}}_i}. $ | (1) |
式中: KTi、ΔUi和ΔPi分别为第i荷载步切线刚度矩阵、位移增量和荷载增量.
由于外荷载为保守力系, 荷载增量可表示为
| $ \Delta {\mathit{\boldsymbol{P}}_i} = \Delta {\chi _i}\mathit{\boldsymbol{\varphi }}. $ | (2) |
式中:Δχi为第i荷载步荷载因子增量, φ为外荷载空间分布模式向量.
式(1)两端左乘ΔUiT, 得到方程如下:
| $ \Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_{{\rm{T}}i}}\Delta {\mathit{\boldsymbol{U}}_i} = \Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}\Delta {\mathit{\boldsymbol{P}}_i}. $ | (3) |
对式(3)左边项进行变换, 可得
| $ \frac{{\Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_{{\rm{T}}i}}\Delta {\mathit{\boldsymbol{U}}_i}}}{{\Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}\Delta {\mathit{\boldsymbol{U}}_i}}} = \Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}\Delta {\mathit{\boldsymbol{U}}_i} = \Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}\Delta {\mathit{\boldsymbol{P}}_i}. $ | (4) |
令
| $ k_i^ * = \frac{{\Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_{{\rm{T}}i}}\Delta {\mathit{\boldsymbol{U}}_i}}}{{\Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}\Delta {\mathit{\boldsymbol{U}}_i}}}. $ | (5) |
| $ \Delta u_i^ * = \Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}\Delta {\mathit{\boldsymbol{U}}_i}. $ | (6) |
| $ \Delta p_i^ * = \Delta \mathit{\boldsymbol{U}}_i^{\rm{T}}\Delta {\mathit{\boldsymbol{P}}_i}. $ | (7) |
定义ki*为结构第i荷载步特征刚度, 则式(4)可表示为
| $ k_i^ * \Delta u_i^ * = \Delta p_i^ * ,\;\;\;\;\;k_i^ * = \Delta p_i^ * /\Delta u_i^ * . $ | (8) |
式中:Δui*和Δpi*分别为第i荷载步特征位移增量和荷载增量功.
由式(5)可知, 特征刚度ki*具有与刚度相同的量纲, 其物理意义为当结构产生单位特征位移增量时, 外荷载增量所做的功.在2个相邻荷载步(第i、i-1荷载步)内, 当ki*>ki-1*时, 结构较前一荷载步刚化;当ki*<ki-1*时, 结构较前一荷载步软化.
式(5)说明, 结构特征刚度不依赖特定点的位移或特定的位移模态, 其值反映了结构整体抵抗变形的能力, 即结构的整体刚度.当结构整体失稳时, 荷载增量功Δp*=0, 特征刚度k*=0, 故结构特征刚度为零可作为一种结构静力稳定性临界状态的判定依据.
1.2 特征刚度和刚度矩阵的关系 1.2.1 结构切线刚度矩阵的谱分解在结构非线性分析中, 一般采用增量形式的平衡方程, 结合切线刚度矩阵进行迭代计算.结构切线刚度矩阵由弹性刚度矩阵、初位移刚度矩阵及初应力刚度矩阵组成.在外荷载作用下, 切线刚度矩阵随结构位形的改变而变化.
设λn和
| $ {\mathit{\boldsymbol{K}}_{\rm{T}}}\mathit{\boldsymbol{\phi}_n} = {\lambda _{\rm{n}}}\mathit{\boldsymbol{\phi}_n};n = 1,2, \cdots ,N. $ | (9) |
将特征值λn(n=1, 2, …, N)进行排序, 即λ1≤λ2≤…≤λN, 特征值对角阵和对应的特征向量矩阵可表示为
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = \left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&{}&{}&{}\\ {}&{{\lambda _2}}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{\lambda _N}} \end{array}} \right]. $ | (10) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\phi}_1}}&{\mathit{\boldsymbol{\phi}_2}}& \cdots &{\mathit{\boldsymbol{\phi}_N}} \end{array}} \right]. $ | (11) |
切线刚度矩阵可表示为
| $ {\mathit{\boldsymbol{K}}_{\rm{T}}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}. $ | (12) |
| $ \mathit{\boldsymbol{K}}_{\rm{T}}^{\rm{T}}{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}} \right)^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}} = {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}} \right)^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}. $ | (13) |
由于矩阵KT和矩阵KTT具有相同的特征值, 若设λn和ψn分别为矩阵KTT的特征值和右特征向量, 则有
| $ \mathit{\boldsymbol{K}}_{\rm{T}}^{\rm{T}}{\mathit{\boldsymbol{\psi }}_n} = {\lambda _n}{\mathit{\boldsymbol{\psi }}_n};n = 1,2, \cdots ,N. $ | (14) |
两端转置可得
| $ \mathit{\boldsymbol{\psi }}_n^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{T}}} = {\lambda _n}\mathit{\boldsymbol{\psi }}_n^{\rm{T}};n = 1,2, \cdots ,N. $ | (15) |
故ψnT即为矩阵KT的左特征向量, 对应的特征向量矩阵为ΨT, 且
| $ \mathit{\boldsymbol{K}}_{\rm{T}}^{\rm{T}} = \mathit{\boldsymbol{ \boldsymbol{\varPsi} \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{ - 1}}. $ | (16) |
由式(13)、(16)可得
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}} \right)^{\rm{T}}} = {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}} \right)^{ - 1}}. $ | (17) |
对左、右特征向量进行单位化, 根据矩阵左右特征向量的正交性, 则
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\psi }}_m^{\rm{T}}\mathit{\boldsymbol{\phi} _n} = 1,m = n,\;\;\;\;m,n = 1,2, \cdots ,N;\\ \mathit{\boldsymbol{\psi }}_m^{\rm{T}}\mathit{\boldsymbol{\phi}_n} = 0,m \ne n,\;\;\;\;m,n = 1,2, \cdots ,N. \end{array} \right\} $ | (18) |
结合式(12)、(18), 展开切线刚度矩阵为
| $ {\mathit{\boldsymbol{K}}_{\rm{T}}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{T}}} = \sum\limits_{n = 1}^N {{\lambda _n}\mathit{\boldsymbol{\phi}_n}\mathit{\boldsymbol{\psi }}_n^{\rm{T}}} . $ | (19) |
式(19)即为切线刚度矩阵KT的谱分解形式.同理, 切线柔度矩阵KT-1的谱分解形式为
| $ \begin{array}{l} \mathit{\boldsymbol{K}}_{\rm{T}}^{ - 1} = {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}} \right)^{ - 1}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{n = 1}^N {\frac{1}{{{\lambda _n}}}\mathit{\boldsymbol{\phi} _n}\mathit{\boldsymbol{\psi }}_{\rm{n}}^{\rm{T}}} . \end{array} $ | (20) |
在切线刚度矩阵KT的N维特征空间中, 荷载增量向量ΔP可按式(21)转化为N维特征向量的线性叠加, 即ΔP的特征空间分解形式, 且映射关系唯一
| $ \Delta \mathit{\boldsymbol{P}} = {q_1}\mathit{\boldsymbol{\phi} _1} + {q_2}\mathit{\boldsymbol{\phi} _2} + \cdots + {q_{\rm{N}}}\mathit{\boldsymbol{\phi} _N} = \sum\limits_{n = 1}^N {{q_n}\mathit{\boldsymbol{\phi} _n}} . $ | (21) |
式中:qn为第n阶特征向量的广义坐标.
根据KT-1的谱分解和ΔP的特征空间分解, 结合矩阵左右特征向量的正交性, 结构位移增量ΔU可表示为
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{U}} = \mathit{\boldsymbol{K}}_{\rm{T}}^{ - 1}\Delta \mathit{\boldsymbol{P}} = \left( {\sum\limits_{n = 1}^N {\frac{1}{{{\lambda _n}}}\mathit{\boldsymbol{\phi} _n}\mathit{\boldsymbol{\psi }}_{\rm{n}}^{\rm{T}}} } \right)\left( {\sum\limits_{m = 1}^N {{q_m}\mathit{\boldsymbol{\phi} _m}} } \right) = \\ \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^N {\frac{{{q_m}}}{{{\lambda _n}}}\mathit{\boldsymbol{\phi} _n}\mathit{\boldsymbol{\psi }}_{\rm{n}}^{\rm{T}}\mathit{\boldsymbol{\phi} _m}} } = \sum\limits_{n = 1}^N {\frac{{{q_m}}}{{{\lambda _n}}}\mathit{\boldsymbol{\phi} _n}} = \sum\limits_{n = 1}^N {{\alpha _n}\mathit{\boldsymbol{\phi} _n}} . \end{array} $ | (22) |
式中:αn为第n阶特征向量的权系数.
式(22)即为结构位移增量ΔU在N维特征空间中的特征空间分解, 其权系数αn为切线刚度矩阵特征值的函数.结构在静力加载过程中, 其屈曲模态不断改变, 接近极限平衡状态时, 切线刚度矩阵某一特征值λn趋于0, 其权系数αn理论上趋于无穷大, 位移增量向量与该阶屈曲模态n共线, 对应的屈曲模态n即为该状态下的结构主模态.若荷载变化对结构屈曲模态无显著影响, 则该主模态一般为第1阶, 即n=1;若荷载变化对结构屈曲模态有显著影响, 则该主模态可能是高阶模态, 即n≥2.
1.2.3 特征刚度与特征值的关系设结构位移增量为ΔU, 对其进行无量纲化和单位化, 可得
| $ \Delta \mathit{\boldsymbol{\bar U}} = \frac{{\Delta \mathit{\boldsymbol{U}}}}{{\sqrt {\Delta {\mathit{\boldsymbol{U}}^{\rm{T}}}\Delta \mathit{\boldsymbol{U}}} }}. $ | (23) |
则结构切线刚度矩阵关于单位位移增量的二次型可表示为
| $ f = \Delta {{\mathit{\boldsymbol{\bar U}}}^{\rm{T}}}{\mathit{\boldsymbol{K}}_{\rm{T}}}\Delta \mathit{\boldsymbol{\bar U}}. $ | (24) |
结合二次型表达式并引入拉格朗日乘子λ, 可构造新的泛函
| $ \mathit{\Theta }\left( {f,\lambda } \right) = \Delta {{\mathit{\boldsymbol{\bar U}}}^{\rm{T}}}{\mathit{\boldsymbol{K}}_{\rm{T}}}\Delta \mathit{\boldsymbol{\bar U}} - \lambda \left( {\Delta {{\mathit{\boldsymbol{\bar U}}}^{\rm{T}}}\Delta \mathit{\boldsymbol{\bar U}} - 1} \right). $ | (25) |
由泛函的驻值条件δΘ=0可得
| $ {\mathit{\boldsymbol{K}}_{\rm{T}}}\Delta \mathit{\boldsymbol{\bar U}} = \lambda \Delta \mathit{\boldsymbol{\bar U}}. $ | (26) |
| $ \lambda = \Delta {{\mathit{\boldsymbol{\bar U}}}^{\rm{T}}}{\mathit{\boldsymbol{K}}_{\rm{T}}}\Delta \mathit{\boldsymbol{\bar U}} = \frac{{\Delta {{\mathit{\boldsymbol{\bar U}}}^{\rm{T}}}{\mathit{\boldsymbol{K}}_{\rm{T}}}\Delta \mathit{\boldsymbol{\bar U}}}}{{\Delta {\mathit{\boldsymbol{U}}^{\rm{T}}}\Delta \mathit{\boldsymbol{U}}}} = {k^ * }. $ | (27) |
由式(26)、(27)可知, 当泛函Θ(f, λ)取极值时, 拉格朗日乘子λ即为切线刚度矩阵KT的特征值, 单位位移增量ΔU即为其特征向量.故当单位位移增量ΔU与主模态
设ui*、pi*和χi分别为第i荷载步的特征位移、荷载增量功和荷载因子, 则
| $ u_i^ * = \sum\limits_{j = 1}^i {\Delta u_j^ * } ,\;\;\;p_i^ * = \sum\limits_{j = 1}^i {\Delta p_j^ * } ,\;\;\;\chi _i^ * = \sum\limits_{j = 1}^i {\Delta \chi _j^ * } . $ | (28) |
本文以结构特征位移u*为横坐标, 分别以增量累积的荷载功p*、结构特征刚度k*和结构荷载因子χ为纵坐标, 绘制加载全过程荷载增量功-特征位移曲线、特征刚度-位移曲线和荷载-特征位移曲线, 并将其定义为结构静力加载全过程特征曲线.根据特征刚度的定义, p*关于u*的导函数即为k*;特征刚度变化曲线关于u*的积分, 即该曲线与横轴所围面积的代数和, 在数值上等于对应的p*.
根据结构受载性态特征, 其特征曲线的极值点, 即结构特征刚度为零的点, 可以分为2类, 定义为第1类极值点和第2类极值点, 分别对应结构荷载-位移曲线中snap-through和snap-back现象.第1个第1类极值点对应的结构状态为极限平衡状态, 对应的荷载因子为结构的临界荷载因子.
2.1 第1类极值点如图 1所示为结构snap-through型特征节点荷载-位移曲线, 引入特征刚度后, 可得到结构静力加载全过程特征曲线, 如图 2所示, 2条曲线加载阶段划分和特征点状态相互对应.OA段内, u*增加, p*增加, k*减小, 结构整体刚度减小;AB段内, u*增加, p*减小, k*先减后增, 结构整体刚度先减后增;BC段内, u*增加, p*增加, k*增加, 结构整体刚度增加.
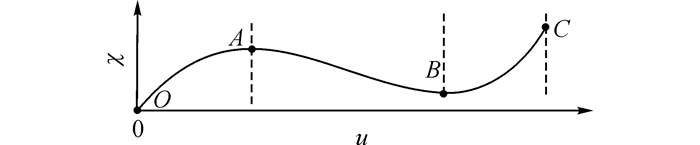
|
图 1 结构snap-through型特征节点荷载-位移曲线 Fig. 1 Nodal load-displacement curve for snap-through |

|
图 2 结构静力加载全过程特征曲线 Fig. 2 Whole characteristic curve under static load |
当结构平衡状态处于A点或B点时, 特征刚度k*=0, p*和χ均取极值, 结构处于极值临界平衡状态, 此特征曲线极值点定义为第1类极值点.当结构状态处于第1类极值点时, 结构切线刚度矩阵奇异, 荷载因子增量Δχ=0, 特征刚度k*=0.结构平衡路径各阶段参数正负值判断如表 1所示.
| 表 1 结构平衡路径各阶段参数正负值判断 Table 1 Parameter value in different stages of equilibrium path |
如图 3和4所示分别为结构snap-back型特征节点的荷载-位移曲线和结构静力加载全过程特征曲线.OA段内, u*增加, p*增加, k*减小, 结构整体刚度减小;AB段内, u*增加, p*减小, k*先减后增, 结构整体刚度先减后增;BC段内, u*增加, p*增加, k*先增后减, 结构整体刚度先增后减;CD段内, u*增加, p*减小, k*减小, 结构整体刚度减小.
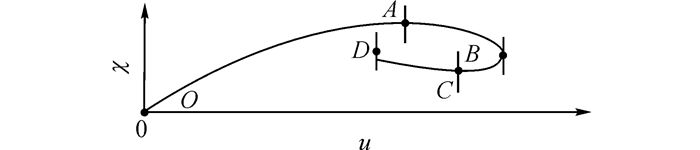
|
图 3 结构snap-back型特征节点荷载-位移曲线 Fig. 3 Nodal load-displacement curve for snap-back |

|
图 4 结构静力加载全过程特征曲线 Fig. 4 Whole characteristic curve under static load |
当结构平衡状态处于A点或C点时, 特征刚度k*=0, p*和χ均取极值, 结构处于极值临界平衡状态此极值点为第1类极值点;当结构平衡状态处于B点时, 特征刚度k*=0, p*取极值, χ不取极值, 此特征曲线极值点定义为第2类极值点, 结构平衡曲线出现回折.由于结构的回折现象属于局部回折, 或由局部回折导致的整体回折, 故不同特征节点对应的回折时刻可能不同.第2类极值点的出现表明结构局部产生了明显的回折现象, 在结构的N维特征空间中, ΔU与ΔP垂直, 故特征刚度k*=0.结构平衡路径各阶段参数正负值判断如表 2所示.
| 表 2 结构平衡路径各阶段参数正负值判断 Table 2 Parameter value in different stages of equilibriumpath |
本节分别对一个K6型球面网壳和某会议中心屋盖网壳进行整体稳定计算, 通过特征刚度对结构稳定性进行判定, 并利用特征曲线对结构整体刚度变化进行分析, 以说明该曲线相对于单点荷载-位移曲线的优势.
3.1 K6型网壳 3.1.1 结构模型结构跨度60 m, 矢高20 m, 矢跨比1/3.径向分为8环, 第5环及以内除主肋斜杆外, 杆件截面均采用114×3 mm;其余杆件均采用121×3 mm.构件材料为Q235钢材, 采用理想弹塑性模型, 弹性阶段弹性模量为2.06×105 MPa, 屈服强度为235 MPa.结构恒载为0.5 kN/m2, 活载为0.5 kN/m2, 支座为固定铰支座.网壳模型特征节点位置如图 5所示.
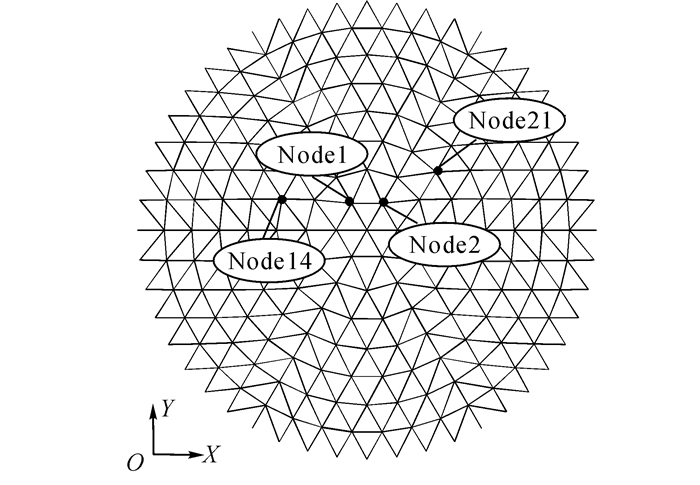
|
图 5 K6型网壳模型特征节点位置 Fig. 5 Key-points location of K6 shell modal |
按照文献[15]要求引入缺陷, 采用弧长法对上述结构进行加载全过程平衡路径跟踪及结构整体稳定性分析.仅考虑几何非线性时, 该结构极限荷载因子为4.853;考虑双重非线性时, 该结构极限荷载因子为3.922.
3.1.3 特征曲线及整体刚度分析本节根据特征曲线的绘制方法和数值分析结果, 分别绘制仅考虑几何非线性和考虑双非线性的特征曲线, 对结构整体刚度进行分析, 并与单点荷载-位移曲线进行比较.
1) 几何非线性分析特征曲线
根据稳定分析结果, 选取节点1、2和14作为结构特征点, 绘制荷载-位移曲线, 如图 6所示.结构静力加载特征曲线如图 7所示, 其中(a)、(b)中的截断曲线表示对原始曲线AJ段的细部描述.
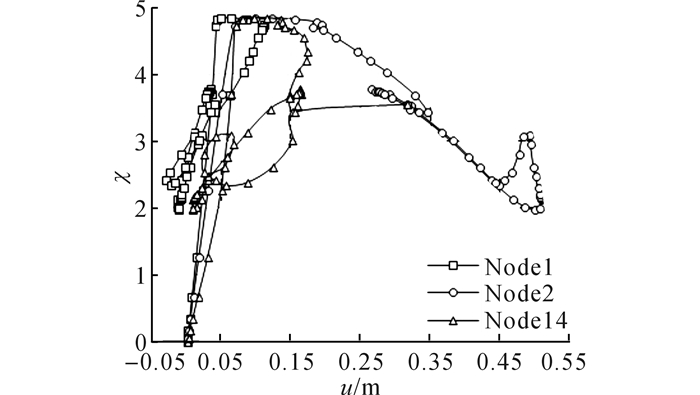
|
图 6 K6型网壳几何非线性分析特征点Z向荷载-位移曲线 Fig. 6 Z-direction nodal load-displacement curves for K6reticulated shell in geometrical non-linearity analysis |

|
图 7 K6型网壳几何非线性分析特征曲线 Fig. 7 Characterisitc curves for K6 reticulated shell in geometrical non-linearity analysis |
由图 6可知, 仅考虑几何非线性时, 各特征点荷载-位移曲线差异较大, 单点荷载-位移曲线存在较多折返、往复, 其仅能获得极限承载力以及该点运动路径等信息, 难以获得结构整体刚度变化特征.
由图 7可知, 由于特征位移单调递增的性质, 结构特征曲线无折返、无往复.特征曲线第1个极值点出现在A点, 对应的χA达极值, 故第1个极值点为第1类极值点, 结构处于极值临界平衡状态, 临界荷载因子为4.853, 与整体稳定计算结果相等.
静力加载初期, k*较大, p*增长较慢, 结构整体刚度较大;临近极限荷载时, k*迅速减小, 结构整体刚度减小, 结构处于临界失稳状态;在后屈曲路径中, k*处于较低水平, 由于结构失稳和回折出现, 其存在较多零点, 结构整体刚度变化较复杂.根据特征曲线斜率的变化, 即相邻荷载步特征刚度的变化, 可以判断结构整体刚度的变化, 如(b)曲线AB段内, 结构的整体刚度先减后增.由于(c)曲线中B点对应的荷载因子曲线处于下降状态, 故B点为第2类极值点.结构受载全过程中各极值点类别及整体刚度变化情况见表 3.
| 表 3 极值点类别及结构整体刚度变化 Table 3 Extreme points categories and overall structural stiffness variation |
2) 双非线性分析特征曲线
根据稳定分析结果, 选取节点1、2和21作为结构特征点, 绘制荷载-位移曲线, 如图 8所示.由图 8可知, 考虑双非线性时, 各特征点荷载-位移曲线差异较大, 单点荷载-位移曲线也存在折返、往复, 依然难以表明结构整体刚度变化.

|
图 8 K6型网壳双非线性分析Z向特征点荷载-位移曲线 Fig. 8 Z-direction nodal load-displacement curves for K6 reticulated shell in double non-linearity analysis |
考虑双非线性的特征曲线如图 9所示, 其中(a)、(b)中的截断曲线表示对原始曲线AD段的细部描述.由图 9可知, 结构特征曲线第1个极值点出现在A点, 对应的χA达极值, 故第1个极值点为第1类极值点, 结构处于极值临界平衡状态, 临界荷载因子为3.922, 与整体稳定计算结果相等.

|
图 9 K6型网壳双非线性分析特征曲线 Fig. 9 Characterisitc curves for K6 reticulated shell in double non-linearity analysis |
静力加载初期, k*较大, 结构整体刚度较大;临近极限荷载时, k*迅速减小, 结构整体刚度减小, 结构处于临界失稳状态;在后屈曲路径中, 由于不同杆件的先后屈服, k*上下波动, 其值处于较低水平, 结构的整体刚度较小.考虑双非线性时, 静力加载过程中特征曲线仅有1个极值点, 即A点.结构受载各阶段整体刚度变化情况如表 4所示.
| 表 4 结构受载各阶段整体刚度变化 Table 4 Overall structural stiffness variation in different stages under static load |
会议中心采用肋环形球面网壳结构, 直径为37.3 m, 矢高29.35 m, 杆件采用矩形管截面, 节点形式为铸钢型节点.构件材料为Q345钢材, 采用理想弹塑性模型, 弹性阶段弹性模量为2.06×105 MPa, 屈服强度为345 MPa.结构恒载为0.9 kN/m2, 活载为0.6 kN/m2, 支座为固定铰支座.网壳模型节点编号如图 10所示.

|
图 10 某会议中心结构示意图及特征节点位置 Fig. 10 Conference center structural modal and key-points location |
按照文献[15]要求引入缺陷, 采用弧长法对上述结构进行加载全过程平衡路径跟踪及结构整体稳定性分析.
仅考虑几何非线性时, 结构极限荷载因子为14.664;当结构达到极值临界平衡状态时, 结构无构件屈服, 故可不进行双非线性稳定验算.
3.2.3 特征曲线及整体刚度分析根据稳定分析结果, 选取节点10、155和202为结构特征点, 绘制荷载-位移曲线, 如图 11所示.由图 11可知, 各特征点荷载-位移曲线差异较大, 单点荷载-位移曲线存在折返、往复, 难以获得结构整体刚度变化.

|
图 11 会议中心结构几何非线性分析特征点荷载-位移曲线 Fig. 11 Nodal load-displacement curves for conference center in geometrical non-linearity analysis |
结构静力加载特征曲线如图 12所示, 其中(a)、(b)中的截断曲线表示对原始曲线AD段的细部描述.由图 12可知, 特征曲线第1个极值点出现在B点, 对应的χB达极值, 故第1个极值点为第1类极值点, 此时, 结构处于极值临界平衡状态, 由图 12(c)可知, 该结构的临界荷载因子为14.664, 故其计算结果与整体稳定计算结果相等.
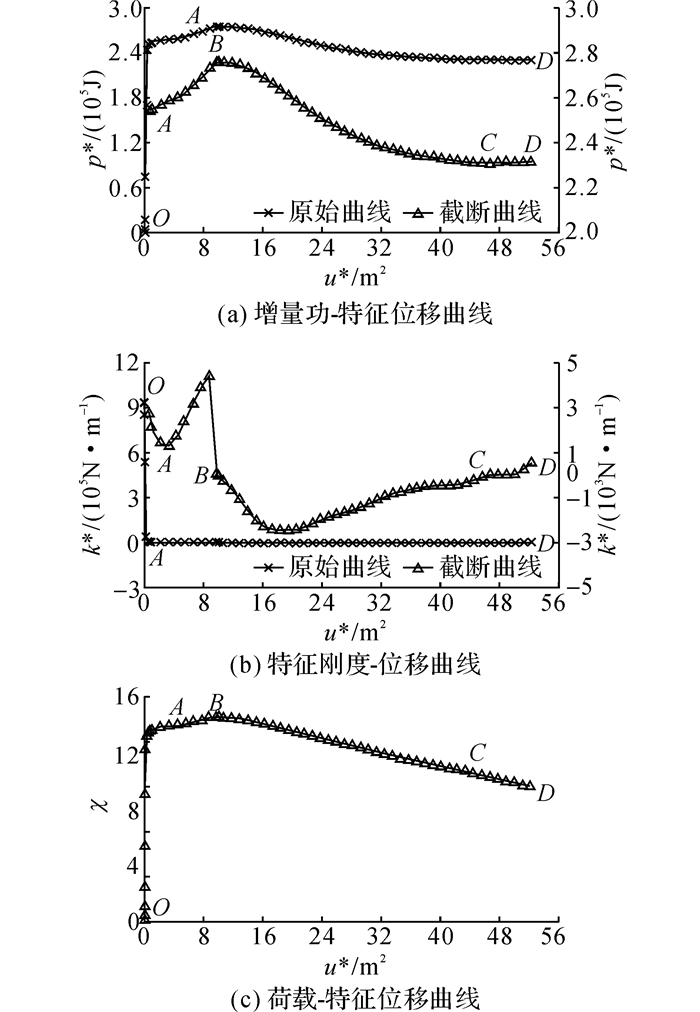
|
图 12 会议中心结构几何非线性分析特征曲线 Fig. 12 Characterisitc curve for conference center ingeometrical non-linearity analysis |
该特征曲线共2个极值点, 其中B点为第1类极值点, 结构受载至B点附近发生失稳;C点为第2类极值点, 结构受载至C点附近发生回折现象.结构受载全过程中各极值点类别及整体刚度变化情况如表 5所示.
| 表 5 全过程极值点类别及结构整体刚度变化 Table 5 Extreme point categories and overall structural stiffness variation in full-range analysis |
本文提出结构特征刚度的概念, 并用其对结构静力稳定性进行分析判定, 通过绘制结构静力加载全过程特征曲线, 对结构在受载过程中的性态和整体刚度的变化进行分析, 通过算例分析比较, 得到以下结论:
(1) 采用本文方法计算得到的结构失稳临界荷载与基于单点荷载-位移曲线所得结果相同, 证明利用结构特征刚度分析和评定结构静力稳定性正确、有效.
(2) 本文方法克服了传统结构静力稳定性分析中特征节点难以确定、单点荷载-位移曲线难以反映结构整体刚度变化等缺点.
(3) 研究结果表明, 特征刚度参数可作为极值型屈曲结构稳定性临界状态的判定参数, 且特征刚度参数能直观反映结构整体刚度的变化特征.
(4) 特征刚度与特征曲线对于结构静力稳定分析具有普适性, 易于程序化.
| [1] | RIKS E. An increment approach to the solution of snapping and buckling problems[J]. International Journal of Solids and Structures, 1979, 15(5): 529–551. |
| [2] | CRISFIELD M A. An arc-length method including line searches and accelerations[J]. International Journal for Numerical Methods in Engineering, 1983, 19(9): 1269–1289. DOI:10.1002/(ISSN)1097-0207 |
| [3] |
罗永峰. 网壳结构弹塑性稳定及承载全过程研究[D]. 上海: 同济大学, 1991.
LUO Yong-feng. Elastro-plastic stability and load bearing capability for lattice domes[D]. Shanghai:Tongji University, 1991. |
| [4] |
罗永峰, 滕锦光, 沈永兴, 等. 结构非线性分析中求解预定荷载水平的改进弧长法[J].
计算力学学报, 1997, 14(4): 88–93.
LUO Yong-feng, TENG Jin-guang, SHEN Yong-xing, et al. An improved arc-length method for searching pre-defined load levels in nonlinear analysis of structures[J]. Chinese Journal of Computational Mechanics, 1997, 14(4): 88–93. |
| [5] |
罗永峰, 滕锦光, 沈祖炎. 确定结构分支点及跟踪平衡路径的改进弧长法[J].
同济大学学报:自然科学版, 1997, 25(5): 502–507.
LUO Yong-feng, TENG Jin-guang, SHEN Zu-yan. Improved arc-length method for detecting bifurcation points and tracing buckling equilibrium path of structures[J]. Journal of Tongji University:Natural Science, 1997, 25(5): 502–507. |
| [6] |
李元齐, 沈祖炎. 稳定分析中极值点失稳与分枝点失稳的跟踪策略及程序实现[J].
土木工程学报, 1998, 31(3): 65–71.
LI Yuan-qi, SHEN Zu-yan. A study on tracing techniques for equilibrium paths of limit point types and bifurcation point types in nonlinear stability analysis[J]. China Civil Engineering Journal, 1998, 31(3): 65–71. |
| [7] |
田伟, 董石麟, 干钢. 网壳结构考虑杆件失稳过程的整体稳定分析[J].
建筑结构学报, 2014, 35(6): 115–122.
TIAN Wei, DONG Shi-lin, GAN Gang. Stability analysis method for lattice shells accounting for buckling of members[J]. Journal of Building Structures, 2014, 35(6): 115–122. |
| [8] |
张建军, 刘琼祥, 刘臣, 等. 深圳大运中心体育场钢屋盖整体稳定性能研究[J].
建筑结构学报, 2011, 32(5): 56–62.
ZHANG Jian-jun, LIU Qiong-xiang, LIU Chen, et al. Research on overall stability of the Shenzhen Universidad Sports Centre[J]. Journal of Building Structures, 2011, 32(5): 56–62. |
| [9] | BERGAN P G, HORRIAMOE G. Solution techniques for non-linear finite element problems[J]. International Journal for Numerical Methods in Engineering, 1978, 12(11): 1677–1696. DOI:10.1002/(ISSN)1097-0207 |
| [10] | 沈士钊, 陈昕. 网壳结构稳定性[M]. 北京: 科学出版社, 1999: 126. |
| [11] |
袁行飞, 周练, 李阿龙. 基于求解运动路径的几何非线性力法的结构屈曲分析[J].
土木工程学报, 2013, 46(6): 82–89.
YUAN Xing-fei, ZHOU Lian, LI A-long. Buckling analysis of structures based on geometrically nonlinear force method by solving kinematic path (GNFM-KP)[J]. China Civil Engineering Journal, 2013, 46(6): 82–89. |
| [12] |
张沛, 冯健. 张拉整体结构的稳定性判定及刚度分析[J].
土木工程学报, 2013, 46(10): 48–57.
ZHANG Pei, FENG Jian. Stability criterion and stiffness analysis of tensegrity structures[J]. China Civil Engineering Journal, 2013, 46(10): 48–57. |
| [13] |
相阳, 罗永峰, 郭小农, 等. 空间结构弹塑性地震反应分析的简化模型与方法[J].
东南大学学报:自然科学版, 2015, 45(4): 750–755.
XIANG Yang, LUO Yong-feng, GUO Xiao-nong, et al. Simplified model and procedure for elasto-plastic seismic response analysis of spatial structure[J]. Journal of Southeast University:Natural Science, 2015, 45(4): 750–755. |
| [14] |
相阳, 罗永峰, 郭小农, 等. 基于整体刚度参数的空间结构模态推覆分析[J].
同济大学学报:自然科学版, 2015, 43(12): 1771–1776.
XIANG Yang, LUO Yong-feng, GUO Xiao-nong, et al. Modal pushover analysis of spatial structures based on the overall structural stiffness parameter[J]. Journal of Tongji University:Natural Science, 2015, 43(12): 1771–1776. |
| [15] | JGJ 7-2010. 空间网格结构技术规程[S]. 北京: 中国建筑工业出版社, 2011: 3. |
| [26] | JGJ 7-2010. Technical specification for space frame structures[S]. Beijing:China Architecture Industry Press. 2011:3. http://www.worldstdindex.com/soft4/3193093.htm |



