2. 中设设计集团股份有限公司 城市轨道与地下空间设计所, 江苏 南京 210014
2. China Design Group Co. Ltd. Urban rail and underground space design institule, Nanjiang 210014, China
张拉整体结构是一类由连续的受拉单元与离散的受压单元组成的、特殊的索杆体系.在无外界约束的情况下, 张拉整体结构内部可形成自平衡的预应力(自应力), 结构的初始刚度由自应力提供.在无应力的状态下, 张拉整体结构将变为可动的体系, 无法稳定存在.这一特点使得张拉整体结构的形态对外界刺激较为敏感, 而实际应用中几何形状却往往需要满足较高的精度要求.例如, 索穹顶结构需要保持一定的设计形状以保证覆盖的膜面不发生褶皱;张拉整体结构的天线反射器必须保持一定的曲率以保证反射效率[1].为始终保证精度要求, 当结构在制造误差、温度变形、不可预测的外界荷载等因素的作用下发生的形状偏差超出允许量级时, 可以通过调整节点坐标来修正结构形状.这个形态调整的过程通常通过改变结构构件长度来实现[2-3].
针对张拉整体结构的形状控制问题, You[4]提出基于结构矩阵分析理论的预应力结构线性位移控制方法, 并通过试验验证了该方法的正确性.沈黎元等[5]针对2类预应力索网结构展开了类似的研究工作.许贤等[6]研究了索网结构的位移控制, 对线性结果和非线性结果进行了对比.Smith[7]结合随机搜索算法和动力松弛法提出了张拉整体结构的静态智能控制框架, 同时尝试采用神经网络提高动力松弛法对结构反应的预测值与实际测量值之间的差异[8].
本文针对张拉整体结构, 建立线性模型和基于线性规划的位移优化控制模型, 以三棱柱张拉整体单元为例, 研究了荷载工况、控制目标、作动器布置等因素对优化控制效果的影响, 并通过一个物理模型实验初步验证了所提出方法的正确性.
1 张拉整体结构位移控制的线性模型张拉整体结构位移控制的线性模型基于以下3点基本假定:1)节点为理想铰接节点, 压杆为理想二力杆, 拉索只能承受单向拉伸;2)构件内的应变为小应变, 材料处于线弹性变形范围;3)结构变形为小变形.严格意义上来讲, 张拉整体结构属于几何非线性特征比较明显的结构, 尤其是在成型过程及大幅度的形态调整过程中表现出较强的几何非线性[9], 但是在结构成型之后, 在设计荷载与一定的调控范围内, 结构的响应仍可认为是线性的, 这一点同时得到了理论[10-11]与试验[12-13]的佐证.
1.1 平衡状态方程考虑一个由nc根构件组成、具有nr个自由度的张拉整体结构, 结构的独立自应力模态数和独立机构位移模态数分别记为s和m.在节点荷载向量Fl作用下, 结构处于平衡状态, 其平衡方程为
| $ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{F}}_{\rm{t}}} = {\mathit{\boldsymbol{F}}_{\rm{l}}}. $ | (1) |
式中:A(nr×nc)为平衡矩阵, 其行数和列数分别为结构的总自由度数和单元数;Ft(nc×1)为构件内力向量.平衡矩阵与材料的本构关系无关, 仅与结构的几何拓扑关系有关.
对于处于线性小变形范围内的结构体系, 结构的位移协调方程为
| $ \mathit{\boldsymbol{Bd}} = \mathit{\boldsymbol{e}}. $ | (2) |
式中:协调矩阵B= AT, d为节点位移向量(nr×1), e为单元变形向量.
假设构件材料是线弹性的, 则本构方程为
| $ \mathit{\boldsymbol{e}} = {\mathit{\boldsymbol{e}}^0} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{F}}_{\rm{t}}}. $ | (3) |
式中:e0为单元初始长度, Γ为柔度矩阵.
利用平衡矩阵奇异值分解, 得到机构位移模态Um和自应力模态Vs, 节点位移可表示为特解和通解之和:
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{d'}} + {\mathit{\boldsymbol{U}}_{\rm{m}}}\mathit{\boldsymbol{\beta }}. $ | (4) |
式中: β为机构位移模态的组合系数向量, d′为公式(2)的特解, 通过奇异值分解可以表示为
| $ \mathit{\boldsymbol{d'}} = {\mathit{\boldsymbol{U}}_r}{\mathit{\boldsymbol{S}}^{ - 1}}\mathit{\boldsymbol{V}}_r^{\rm{T}}\mathit{\boldsymbol{e}}. $ | (5) |
式中:r表示平衡矩阵A的秩, 矩阵S为对角矩阵且对角线上的元素为A的奇异值, Ur、Vr分别为左、右奇异向量前r列构成的矩阵.
根据虚功原理, 可得
| $ \mathit{\boldsymbol{F}}_{\rm{l}}^{\rm{T}}\mathit{\boldsymbol{d}} = \mathit{\boldsymbol{F}}_{\rm{t}}^{\rm{T}}\delta \mathit{\boldsymbol{e}}. $ | (6) |
式中δe为无穷小变形.
假设结构发生无限小位移φUm, φ为比例系数.节点外荷载为Fl +φG, G为几何力矩阵, 是由于结构发生无限小机构位移产生的节点附加荷载.结构仍满足虚功原理:
| $ {\left( {{\mathit{\boldsymbol{F}}_1} + \varphi \mathit{\boldsymbol{G}}} \right)^{\rm{T}}}\mathit{\boldsymbol{d}} = \mathit{\boldsymbol{F}}_{\rm{t}}^{\rm{T}}\delta \mathit{\boldsymbol{e}}. $ | (7) |
比较式(6)、(7), 可得
| $ {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{d}} = 0. $ | (8) |
代入式(4), 可得
| $ {\mathit{\boldsymbol{G}}^{\rm{T}}}\left( {\mathit{\boldsymbol{d'}} + {\mathit{\boldsymbol{U}}_{\rm{m}}}\mathit{\boldsymbol{\beta }}} \right) = 0. $ | (9) |
由式(9)求得机构位移组合系数向量β, 再代入式(4)可求得节点位移向量d.
1.2 构件内力和节点位移表达定义 δj为第j根构件的调整长度.在本文前述的假定下, δj为一小量.定义结构的内力敏感度系数和位移敏感度系数, 分别推导结构内力增量和位移增量与构件伸长量的关系.
1.2.1 构件内力和调整长度关系定义αij为结构的内力敏感度系数, 表示第j根构件发生单位长度的增量, 即当δj=1时, 第i根构件产生的轴力增量.故第i根构件调整后的轴力为
| $ F_{{N_i}}^N = F_{{N_i}}^0 + \sum\limits_{j = 1}^n {{\alpha _{ij}}{\delta _j}} . $ | (10) |
式中:FNi0和FNiN分别为构件调整前后的内力.
内力敏感度系数αij的推导如下.
设结构调整之前的初始预应力为Ft0, 结构经过形态调整之后的内力向量为
| $ {\mathit{\boldsymbol{F}}_{\rm{t}}} = \mathit{\boldsymbol{F}}_{\rm{t}}^0 + \mathit{\boldsymbol{F}}_{\rm{t}}^{\rm{s}}. $ | (11) |
式中:Fts为内力增量, 可表示为
| $ \mathit{\boldsymbol{F}}_{\rm{t}}^{\rm{s}} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{e}}_{\rm{s}}}. $ | (12) |
式中: es为构件伸长量;H为构件改变单位长度时引起的内力变化, H=-S(STΓS)-1ST.
根据构件内力是否为控制内力, 式(12)可进一步表示为
| $ {\left[ {{\mathit{\boldsymbol{F}}_{{t_c}}},{\mathit{\boldsymbol{F}}_{{t_u}}}} \right]^{\rm{T}}} = {\left[ {{\mathit{\boldsymbol{H}}_{\rm{c}}},{\mathit{\boldsymbol{H}}_{\rm{u}}}} \right]^{\rm{T}}}{\mathit{\boldsymbol{e}}_{\rm{s}}}. $ | (13) |
式中:Ftc和Ftu分别为对应于控制内力和非控制内力的构件内力, Hc和Hu分别表示对应的H.
根据构件类型, Hc可分割成对应p(0<p ≤ nc)个主动构件的满秩子矩阵Hv和对应其余构件的子矩阵Hn, es可相应分割成ev和en, 则Ftc可表示为
| $ {\mathit{\boldsymbol{F}}_{{t_c}}} = \left[ {{\mathit{\boldsymbol{H}}_{\rm{v}}},{\mathit{\boldsymbol{H}}_{\rm{n}}}} \right]{\left[ {{\mathit{\boldsymbol{e}}_{\rm{v}}},{\mathit{\boldsymbol{e}}_{\rm{n}}}} \right]^{\rm{T}}} = {\mathit{\boldsymbol{H}}_{\rm{v}}}{\mathit{\boldsymbol{e}}_{\rm{v}}} + {\mathit{\boldsymbol{H}}_{\rm{n}}}{\mathit{\boldsymbol{e}}_{\rm{n}}}. $ | (14) |
当主动构件的伸长量ev为单位1时, 所求控制内力Ftc就是内力敏感度系数αij的矩阵.
1.2.2 节点位移和调整长度关系定义Cij为结构的位移敏感度系数, 表示第j根构件发生单位长度的增量, 即当δj=1时, 第i个节点产生的位移增量.故第i个节点调整后的位移可以表示为
| $ u_i^N = u_i^0 + \sum\limits_{j = 1}^n {{C_{ij}}{\delta _j}} . $ | (15) |
式中:ui0和uiN分别为节点调整前后的位移.
位移敏感度系数Cij的推导如下.
由式(2)、(3)可得
| $ \mathit{\boldsymbol{Bd}} = \mathit{\boldsymbol{e}}_{\rm{s}}^0 + \mathit{\boldsymbol{ \boldsymbol{\varGamma} F}}_{\rm{t}}^{\rm{s}} = \left[ {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} H}}} \right]{\mathit{\boldsymbol{e}}_{\rm{s}}}. $ | (16) |
式中:es0为结构调整前的构件伸长, I表示单位矩阵.
求解式(16), 可得
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{e}}_{\rm{s}}}. $ | (17) |
式中:E=B-1[I+ΓH].
根据节点位移是否为控制位移, 式(17)可进一步表示为
| $ \mathit{\boldsymbol{d}} = {\left[ {{\mathit{\boldsymbol{d}}_{\rm{c}}},{\mathit{\boldsymbol{d}}_{\rm{u}}}} \right]^{\rm{T}}} = {\left[ {{\mathit{\boldsymbol{E}}_{\rm{c}}},{\mathit{\boldsymbol{E}}_{\rm{u}}}} \right]^{\rm{T}}}{\mathit{\boldsymbol{e}}_{\rm{s}}}. $ | (18) |
式中: dc和du分别为对应于控制位移和非控制位移的节点位移, Ec和Eu分别为对应的E.
根据构件类型, Ec可分割成对应p个主动构件的满秩子矩阵Ev和对应其余构件的子矩阵En, es可相应分割成ev和en, 则dc可表示为
| $ {\mathit{\boldsymbol{d}}_{\rm{c}}} = {\mathit{\boldsymbol{E}}_{\rm{v}}}{\mathit{\boldsymbol{e}}_{\rm{v}}} + {\mathit{\boldsymbol{E}}_{\rm{n}}}{\mathit{\boldsymbol{e}}_{\rm{n}}}. $ | (19) |
当主动构件的伸长量ev为单位1时, 所求控制位移dc就是位移敏感度系数Cij的矩阵.
1.3 工作状态系数为准确度量结构工作状态, 定义第j根构件在外力作用下的工作状态系数为
| $ {k_j} = \left\{ \begin{array}{l} {F_{{N_j}}}/F_{{N_j}}^t,{F_{{N_j}}} \ge 0;\;\;\;j = 1,2 \cdots ,{n_c};\\ {F_{{N_j}}}/F_{{N_j}}^c,{F_{{N_j}}} < 0.\;\;\;j = 1,2 \cdots ,{n_c}. \end{array} \right. $ | (20) |
式中:FNjt、FNjc、FNj分别为第j根构件的受拉许用轴力、受压许用轴力和在外力作用下的内力.值得注意的是受压许用轴力应为压杆强度许用轴力与压杆屈曲临界荷载(欧拉荷载)的较小值.
2 基于线性规划的张拉整体结构位移优化控制模型 2.1 线性规划方法数学规划问题可以描述为在一定约束条件下, 求解某一目标函数的最大值或最小值, 所给的变量可以是连续的, 也可以是离散的.数学规划包括3个要素, 即设计变量、目标函数和约束条件, 其求解的优化问题通常可以表示为
| $ \left. \begin{array}{l} 求\;\;\;x\\ 使\;\;\;f\left( x \right) \to \min \\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;\;\;\;\;\;{g_j}\left( x \right) \le 0\;;j = 1, \cdots ,m. \end{array} \right\}. $ | (21) |
当目标函数和约束条件是线性函数时, 研究问题是线性规划问题.
2.2 张拉整体结构位移优化控制模型 2.2.1 设计变量在结构构件中布置作动器, 以作动器变形量作为设计变量.通过调节作动器, 可以改变构件长度, 实现结构的形态调整.
2.2.2 优化目标设结构中有q个节点自由度要求控制位移.以结构最大节点位移分量最小为优化目标.选择位移函数f(u1, …, uq)=max (|u1|, …, |uq|), 引入变量α(α≥0), 使得
| $ - {\alpha _j} \le {u_j} \le {\alpha _j}. $ | (22) |
对整个结构α= max (α1, …, αq), 位移函数f(u1, …, uq)达到最小转化为求α达到最小.
2.2.3 约束条件选择结构工作状态系数、作动器参数为约束条件.结构内力需满足0≤kj≤1.设作动器的最大调节量为δj、许用轴向力为
以结构最大节点位移分量最小为优化目标、结构工作状态系数和作动器参数为约束条件的情况为例, 结构的位移优化控制模型可表示为
| $ \left. \begin{array}{l} 求\;\;\;{\delta _j}\left( {j = 1,2, \cdots ,p} \right)\\ 使\;\;\;\alpha \to \min \\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;\;\;\;\;\;\alpha \ge 0\\ - {\alpha _i} \le {u_i} \le {\alpha _i}\left( {i = 1,2, \cdots ,q} \right)\\ - {{\bar \delta }_j} \le {\delta _j} \le {{\bar \delta }_j}\left( {j = 1,2, \cdots ,{p_c}} \right)\\ - {{\bar F}_{{F_j}}} \le {F_{{N_j}}} \le {{\bar F}_{{N_j}}}\left( {j = 1,2,p} \right)\\ 0 \le {k_j} \le 1\left( {j = 1,2, \cdots ,{n_C}} \right) \end{array} \right\}. $ | (23) |
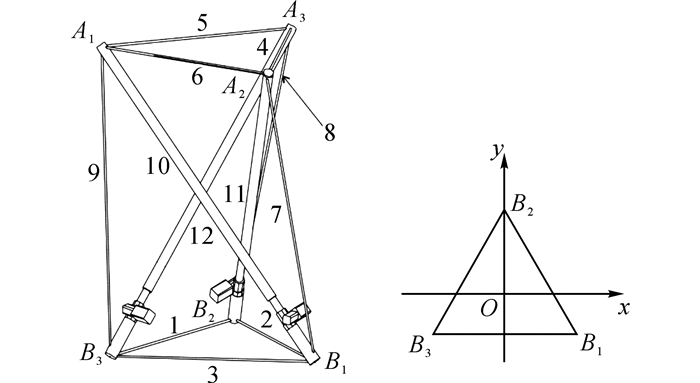
选取如图 1所示的三棱柱张拉整体单元, 以底面三角形的中心为原点建立右手坐标系, Z轴方向垂直向上指向顶面三角形的中心.建立结构位移优化控制的线性规划模型, 进行不同工况、不同控制指标、不同作动器数量及布置情况下的位移优化控制分析.
|
图 1 三棱柱张拉整体单元 Fig. 1 Tri-prism tensegrity unit |
记构件B1B2、B2B3和B3B1为第1组构件底索, 构件A1A2、A2A3和A3A1为第2组构件顶索, 构件A1B3、A2B1和A3B2为第3组构件斜索, 构件A1B1、A2B2和A3B3为第4组构件压杆, 如图 1进行编号.
模型参数如下:底索和顶索的长度为1 039.3 mm, 斜索的长度为1 531.8 mm, 压杆的长度为1 895.7 mm.压杆采用Q235圆钢管, 截面取Φ60×3, 材料弹性模量为206 GPa, 许用应力为210 MPa;索采用钢绞线, 截面取Φ6, 弹性模量为185 GPa, 许用应力为1 850 MPa;作动器刚度ka =100 kN/mm, 容许轴力为200 kN, 最大调整量为±300 mm;结构4组构件对应的初始预应力向量为[413.72, 413.72, 1 056.16, -1 307.07]T(单位N).对于布置作动器的构件, 考虑到作动器刚度影响, 按下式计算构件整体刚度:
| $ K = \frac{{{k_{\rm{a}}}{k_{\rm{b}}}}}{{{k_{\rm{a}}} + {k_{\rm{b}}}}}. $ | (24) |
式中:K为构件整体刚度, kb为构件除作动器以外部分的刚度.
3.1 不同工况下的位移优化控制在结构第4组构件上布置作动器作为主动构件, 以顶面3个顶点A1、A2和A3的z向位移最小为优化控制目标, 考虑3种不同工况下的位移优化控制:
工况一:1个节点承受竖向力8 kN.
工况二:2个节点承受竖向力8 kN.
工况三:3个节点承受竖向力8 kN.
3种工况下的作动器调节量和控制前后的关键节点位移见表 1, 控制前后的构件工作状态系数见表 2, 其中uz表示节点z向位移, kj为杆件工作状态系数.
| 表 1 不同工况下的位移优化控制结果 Table 1 Optimal displacement control results with different load cases |
| 表 2 不同工况下的构件工作状态系数 Table 2 Index of working states of elements with different load cases |
由表 1可知, 经优化控制3种工况下目标节点的z向位移均降低了一个数量级, 且工况三的控制效果最好, 这可能是由于该工况下结构具有很好的对称性.由表 2可知, 构件的工作状态系数虽然都有所上升, 但是均处于允许的范围内.另外, 上述工况中, 单个作动器的最大调节量为10.23 mm, 出现在工况二中.而从3个作动器的总调节量来看, 工况一至三呈递增规律, 即单点受力时作动器总调节量最小, 三点受力时作动器总调节量最大, 两点受力时作动器总调节量居中.
3.2 不同控制指标下的位移优化控制同样在结构第4组构件(构件10、11、12)上布置作动器, 在顶面3个顶点A1、A2和A3上各施加8 kN竖向力, 考虑以下2种控制指标下的位移优化控制:
情况一:控制3个顶点的x、y方向位移.
情况二:控制3个顶点的z方向位移.
2种情况下作动器调节量和控制前后的关键节点位移见表 3, 控制前后的构件工作状态系数见表 4, 其中作动器调节量按照作动器布置位置10、11、12依次从上到下表示, u为节点位移(依次表示x、y、z向位移).
| 表 3 不同控制指标下的位移优化控制结果 Table 3 Optimal displacement control results with different control objectives |
| 表 4 不同控制指标下的构件工作状态系数 Table 4 Index of working states of elements with different control objectives |
由表 3可知, 在当前条件下, 系统对竖向位移的控制效果要明显优于对水平位移的控制效果, 同时竖向位移和水平位移表现出较强的相关性.由表 4可知, 构件的工作状态系数均处于允许的范围内.情况一的作动器的总调节量为38.70 mm,大于情况二的作动器总调节量27.00 mm, 说明水平位移控制所需要消耗的作动能量大于竖向位移控制所需要消耗的作动能量.上述特性是由三棱柱张拉整体结构本身的结构特性以及当前的作动器布置决定的.
3.3 不同作动器数量及布置情况下的位移优化控制在顶面3个顶点A1、A2和A3上施加8 kN竖向力, 以顶面3个顶点A1、A2和A3的z向位移最小为优化目标, 考虑4种不同作动器数量及布置情况下的位移优化控制:
情况一:在斜索中布置作动器, 即在构件7、8、9中布置.
情况二:在顶索中布置作动器, 即在构件4、5、6中布置.
情况三:在斜索和顶索中布置作动器, 即在构件4、5、6、7、8、9中布置.
情况四:在压杆中布置作动器, 即在构件10、11、12中布置.
4种情况下作动器调节量和控制前后的关键节点位移见表 5, 其中作动器调节量根据上述情况中作动器布置位置顺序依次按从上到下、从左到右的顺序表示;控制前后的构件工作状态系数见表 6.
| 表 5 不同作动器数量及布置情况下的位移优化控制结果 Table 5 Optimal displacement control results with different number and arrangement of actuators |
| 表 6 不同作动器数量及布置情况下的构件工作状态系数 Table 6 Index of working states of elements with different number and arrangement of actuators |
由表 5可得, 仅在斜索中布置作动器时, 位移从-17.35 mm调整到-10.89 mm, 调节效果较差, 不建议采纳;仅在顶索中布置作动器时, 位移从-17.48 mm调整到-1.50 mm, 调节效果尚可;同时在斜索和顶索中布置作动器时, 位移从-17.06 mm调整到-0.41 mm, 调节效果优于情况一和情况二;仅在压杆中布置作动器时, 位移从-18.13 mm调整到-0.45 mm, 调整效果与情况三相当.从作动器总调节量来讲, 在压杆中布置有作动器时总的调节量为27 mm, 总调节量最小.由表 6可知, 构件的工作状态系数均处于允许的范围内.可见, 综合考虑控制效果和作动器总调节量, 在压杆中布置作动器是比较合理的方案.
4 张拉整体结构模型试验本文设计了一个具有主动单元的张拉整体结构模型, 主动单元长度可以调控, 通过位移优化控制试验来验证理论方法的正确性.
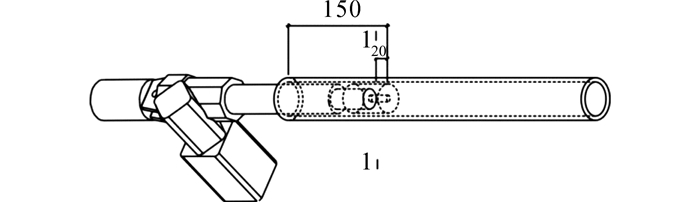
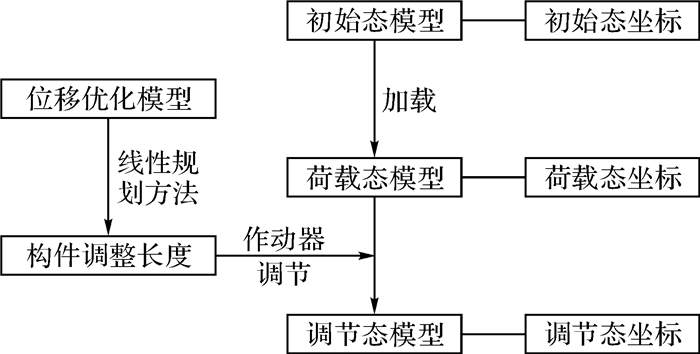
模型高度1.5 m, 俯视投影覆盖半径0.6 m, 底部为竖向支承, 实物如图 2所示.拉索选用6 mm高强钢丝绳, 底索、顶索长度为1 000 mm, 斜索长度为1 450 mm;压杆选用Φ60×3的不锈钢空心圆管, 长度均为1 550 mm;作动器型号选用lim-tec LAP25, 其所能承受的最大荷载为2 000 N, 调节范围±50 mm.考虑到控制效率、制作条件等因素, 在3根压杆上布置作动器作为结构的主动单元, 作动器与压杆的连接如图 3所示.调试后发现, 构件A1B1的作动器存在故障, 故在试验中将其视为非主动单元.试验流程如图 4所示.

|
图 2 具有主动压杆单元的试验模型 Fig. 2 Experimental model with active struts |
|
图 3 作动器和压杆连接关系 Fig. 3 Connection between actuator and strut |
|
图 4 张拉整体模型试验流程图 Fig. 4 Flow chart of experiment of tensegrity model |
实测得到的节点z向位移敏感度系数如表 7所示.
| 表 7 主动单元对节点的 z 向位移敏感系数Cij Table 7 Sensitivity coefficients of nodal displacements in z direction to active members |
在节点A1、A2、A3上分别施加3、0.8、6 kN竖直向下荷载.初始态、荷载态下的节点z向坐标和由于荷载作用产生的节点z向位移如表 8所示, 其中z0为初始态节点z向坐标, z′为荷载态节点z向坐标.
| 表 8 实际测量的节点 z 向位移 Table 8 Nodal displacements in z direction under given load |
第1种情况:要求控制A2节点的z向位移使其最小.运用线性规划方法得到, 将A2B2伸长3.65 mm, 即可达到控制目标.通过电脑串口调试窗口向作动器发出指令, 调节主动单元长度, 测量调节态结构的z向坐标, 实际位移调节量与调节后的位移值及理论位移调节量与调节后的位移值如表 9所示, 其中u′为位移调节量.
| 表 9 第1种情况的控制效果 Table 9 Control result of first case |
第2种情况:要求控制A2和A3节点的z向位移最小.运用线性规划方法得到, 将A2B2伸长0.69 mm, 将A3B3伸长2.53 mm, 即可达到控制目标.实际位移调节量与调节后的位移值及理论位移调节量与调节后的位移值见表 10.
| 表 10 第2种情况的控制效果 Table 10 Control result of second case |
第3种情况:要求控制节点A1、A2和A3的z向位移最小.运用线性规划方法得到, 将A2B2伸长0.79 mm, 将A3B3伸长2.44 mm, 即可达到控制目标.实际位移调节量与调节后的位移值及理论位移调节量与调节后的位移值见表 11.
| 表 11 第3种情况的控制效果 Table 11 Control result of third case |
上述试验结果中理论值与实际值的最大误差为1 mm, 误差主要来源于以下2个方面:
1) 索松弛产生的误差.在调控过程中, 索的当前应变未知, 可能出现索松弛的情况, 从而影响结构的线性和控制精度.
2) 测量误差.试验中采用全站仪进行位移测量, 全站仪的精度为1 mm, 导致一定的测量误差.
5 结论本文建立了基于线性规划的张拉整体结构位移优化控制模型, 选取三棱柱张拉整体单元模型为例进行计算分析, 得到如下结论.
(1) 在给定条件下, 结构竖向位移控制均可达到较好效果, 但对结构水平位移的控制效果相对较差, 这是由张拉整体单元本身的结构特性以及特定的作动器布置方式决定的.
(2) 同时在斜索和顶索中布置作动器时, 控制效果优于单独在斜索或顶索中布置作动器;单独在压杆中布置作动器的控制效果最优、作动器总调节量较小, 是综合最优的作动器布置方案.
需要强调的是, 虽然本文方法建立在张拉整体结构处于线性响应范围的假定之上, 但对于非线性较强的张拉整体结构位移控制问题同样具有借鉴意义, 例如可将非线性过程分段线性化或在线性控制算法的基础上引入一个迭代过程来实现非线性的位移控制.此外, 本文的定位是对位移可控张拉整体结构的概念性验证, 故选用了一个最基本的三棱柱张拉整体结构作为算例及模型试验的原型, 算例的规模都不算大, 同时目前研究位移控制是一个拟静态的过程, 一定程度上类似于对一个控制过程的方案设计, 算法的实时性要求并不高, 故文中未对算法的计算效率加以研究与讨论.若是要进行实时的动态控制, 则对算法的效率要求极高, 当结构的规模较大时, 线性规划方法恐无法满足实时优化控制计算的要求, 需要引入启发式、机器学习等技术加速优化控制的决策过程.上述问题将是笔者后续研究的重点方向之一.
| [1] | TIBERT A G. Deployment tensegrity structure for space applications[D]. Stockholm, Sweden:Royal Institute of Technology, 2002. https://www.mendeley.com/research-papers/deployable-tensegrity-structures-space-applications/ |
| [2] | EDBERG D L. Control of flexible structures by applied thermal gradients[J]. AIAA Journal, 1987, 25(6): 877–883. DOI:10.2514/3.9715 |
| [3] | FEST E, SHEA K, DOMER B, et al. Adjustable tensegrity structures[J]. Journal of Structural Engineering, 2003, 129(4): 515–526. DOI:10.1061/(ASCE)0733-9445(2003)129:4(515) |
| [4] | ZHONG You. Displacement control of prestresssed structures[J]. Computer Methods in Applied Mechanics and Engineering, 1997, 144(1): 51–59. |
| [5] |
沈黎元, 李国强, 罗永峰. 预应力索结构位移控制[J].
同济大学学报:自然科学版, 2006, 34(3): 291–295.
SHEN Li-yuan, LI Guo-qiang, LUO Yong-feng. Displacement control of prestressed cable structures[J]. Journal of Tongji University:Natural Science, 2006, 34(3): 291–295. |
| [6] | XU X, LUO Y. Non-linear displacement control of prestressed cable structures[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2009, 223(7): 1001–1007. DOI:10.1243/09544100JAERO455 |
| [7] | SHEA K, FEST E, SMITH I F C. Developing intelligent tensegrity structures with stochastic search[J]. Advanced Engineering Informatics, 2002, 16(1): 21–40. DOI:10.1016/S1474-0346(02)00003-4 |
| [8] | DOMER B, FEST E, LALIT V, et al. Combining dynamic relaxation method with artificial neural networks to enhance simulation of tensegrity structures[J]. Journal of Structural Engineering, 2003, 129(5): 672–681. DOI:10.1061/(ASCE)0733-9445(2003)129:5(672) |
| [9] |
许贤. 张拉整体结构的形态理论与控制方法研究[D]. 杭州: 浙江大学, 2009.
XU Xian. Tensegrity structure form-finding buckling of compression bar genetie algorithms shape control optimal control[D]. Hangzhou:Zhejiang University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10335-2009096457.htm |
| [10] |
肖新. 张力结构形状调整优化分析[D]. 杭州: 浙江大学, 2008.
XIAO Xin. Shape optimization analysis of tensegrity structure[D]. Hangzhou:Zhejiang University, 2008. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=zdzc200908031&dbname=CJFD&dbcode=CJFQ |
| [11] |
肖南, 黄玉香, 董石麟, 等. 张力结构位移限制下的形状调整强度优化分析[J].
浙江大学学报:工学版, 2010, 44(1): 166–173.
XIAO Nan, HUANG Yu-xiang, DONG Shi-lin, et al. Strength optimization analysis of tensegrity structure by shape adjustments under restricted displacements[J]. Journal of Zhejiang University:Engineering Science, 2010, 44(1): 166–173. |
| [12] |
符刚. 张拉整体结构的分析理论及其模型试验研究[D]. 杭州: 浙江大学, 2003.
FU Gang. Analytical theory and test stucy of tensegrity structures[D]. Hangzhou:Zhejiang University, 2003. http://cdmd.cnki.com.cn/Article/CDMD-10335-2003041719.htm |
| [13] |
张民锐, 邓华, 刘宏创, 等. 月牙形索桁罩棚结构的静力性能模型试验[J].
浙江大学学报:工学版, 2013, 47(2): 367–377.
ZHANG Min-rui, DENG Hua, LIU Hong-chuang, et al. Model experiment on the static behaviors of a crescent-shaped cable-truss canopy structure[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(2): 367–377. |



