2. 石家庄信息工程职业学院 计算机应用系, 河北 石家庄 050000;
3. 国家无线电监测中心成都监测站, 四川 成都 611139
2. Department of Computer Application, Shijiazhuang Information Engineering Vocational College, Shijiazhuang 050000, China;
3. Chengdu Monitoring Station of State Radio Monitoring Center, Chengdu 611139, China
随机共振(stochastic resonance, SR)理论是由Benzi等[1]首次提出, 使用“共振”描述仅用以强调信号、噪声和非线性系统之间达到某种最佳匹配.信号利用噪声能量, 使得系统输出显著加强, 出现最大输出信噪比.该方法是近年来随着非线性动力学和统计物理理论的突飞猛进而出现的一种用于微弱特征信号检测的新方法, 广泛应用于多个领域, 并取得了一定的研究成果[2-6].
随着对随机共振系统的深入研究, 级联随机共振系统逐渐引起了学者的关注.Yang等[6]通过调整参数, 将级联随机共振系统低通滤波的作用发挥到极致.林敏等[7]认为在级联双稳系统中, 分别给两级加入不同的驱动周期信号, 若时间尺度与势阱内跃迁速率、势阱间波动匹配时产生频率吸收现象, 则随机共振效果增强, 但林敏等[7]未提及如何选择参数, 选取的参数为经验值.在此理论基础上, 曲媛等[8]进一步探讨了加强级联双稳系统随机共振效应的条件, 给出所添加驱动周期信号的幅值和频率须满足的条件, 但该方法需要已知待测信号的相关特征信息, 不适于实际工程中的应用.赖志慧等[9]研究级联双稳系统能够获得更好随机共振输出效果的参数调节规律.通过调节变尺度系数、阻尼比、级数等参数, 证实了级联系统能够实现优于单级随机共振系统的输出.但上述文献均未考虑系统参数对级联随机共振输出性能的影响.实现随机共振现象的核心是系统参数的合理匹配, 因此系统参数的适当调节, 对加强级联随机共振的输出效果有一定的影响.热依扎等[10]提出基于级联随机共振与粒子群算法的方法, 采用自适应寻优算法对级联系统的形状参数进行优化.该算法的复杂度高, 一旦出现早熟性收敛, 则得到的输出效果不理想.
现有研究大多源于随机共振的绝热近似理论[11], 以Kramers逃逸率[12]为基础, 针对两级双稳系统作为研究对象展开讨论.范剑等[13]以随机共振系统非线性动力学行为为切入点, 基于吸引子曲线分析系统中各个参数对发生随机共振的影响.针对级联双稳随机共振系统加强的问题少有报道, 级联系统较单一双稳系统输出时域波形更能够体现信号的特征, 且频域输出峰值高, 可以获取较大的信噪比, 具有较高的理论研究和实际应用价值.
本文提出三级级联调参随机共振加强系统, 考虑系统参数对随机共振输出性能的影响及系统的级间联系, 目的是逐级加强系统的输出效果, 更好地实现微弱信号的检测.为了便于实际工程的应用, 进一步分析了级联大参数随机共振系统.结果表明, 该方法简单可行, 根据实际待测信号, 通过改变阻尼系数[14]和系统形状参数, 可以实现大参数信号的检测;调整参数能够加强级联随机共振系统的输出效果, 提高系统输出信噪比.将提出的级联调参随机共振加强系统应用于无线电微弱信号的高信噪比接收, 为后续无线电信号的解调工作打下基础.
1 基于吸引子曲线随机共振调参理论采用一阶非线性Duffing方程描述双稳随机共振系统:
| $k\dot x = ax - b{x^3} + A{\rm{sin}}(2{\rm{ \mathsf{ π} }}{f_0}t) + n\left( t \right).$ | (1) |
式中:k为阻尼系数;a、b为非线性双稳系统的形状参数, 且均大于零;Asin (2πf0t)为激励信号;n(t)是噪声强度为D的高斯白噪声, 均值E[n(t)]=0, E[n(t)n(t-τ)]=2Dσ(τ).
由系统吸引子曲线方程可知, 系统跃迁阈值σyq、q系统跃迁宽度lkd和吸引子曲线斜率KA决定了吸引子曲线的形态, 表达式如下:
| ${\sigma _{{\rm{yq}}}} = \sqrt {\frac{{4{a^3}}}{{27b}}} ,{K_{\rm{A}}} = 2a,{l_{{\rm{kd}}}} = 2\sqrt {\frac{a}{b}} .$ | (2) |
郝研等[15-16]证实随机共振系统检测小参数信号的有效性, 只讨论在信号频率f0和噪声强度D为大参数的条件下, k的调整对输出性能的影响.
令式(1) 中t=λτ, x(t)=z(τ), 则随机共振系统方程变形为
| $\dot x\left( t \right) = \frac{{{\rm{d}}x\left( t \right)}}{{{\rm{d}}t}} = \frac{{{\rm{d}}z\left( \tau \right)}}{{{\rm{d}}t}} = \frac{{{\rm{d}}z\left( \tau \right)}}{{{\rm{d}}\tau }}\frac{{{\rm{d}}\tau }}{{{\rm{d}}t}} = \frac{1}{\lambda }\frac{{{\rm{d}}z\left( \tau \right)}}{{{\rm{d}}\tau }} = \frac{1}{\lambda }\dot z\left( \tau \right).$ | (3) |
将式(1) 中的含t的项由τ作替换, 可得
| $\begin{array}{l} k'\frac{{{\rm{d}}z\left( \tau \right)}}{{{\rm{d}}\tau }} = \\ \quad az\left( \tau \right) - bz{\left( \tau \right)^3} + A{\rm{sin}}(2{\rm{ \mathsf{ π} }}\lambda {f_0}\tau ) + n\left( {\lambda \tau } \right). \end{array}$ | (4) |
式中:k′=k/λ.
通过式(1)~(4) 的推导, 可得阻尼系数依据待测信号频率变化的调整规则, 即当输入信号频率为λf0高频信号时, 若要获得与输入信号频率f0相同的输出特性时, 则应将阻尼系数变为原来的1/λ倍, 其余参数不变.
为了使结论更加充分完备, 基于吸引子曲线理论, 从Kramers逃逸速率公式推导分析调整阻尼系数的规律.
基于吸引子曲线, 由噪声引起的动点跃迁速率解析式为
| ${r_k} = {(2{\rm{ \mathsf{ π} }}k)^{ - 1}}\sqrt {U''({x_{\rm{s}}})} \sqrt {\left| {U''({x_{\rm{u}}})} \right|} {\rm{exp}}\left( { - \frac{{\Delta u}}{D}} \right).$ | (5) |
式中:
由此可得式(1) 的Kramers逃逸速率表达式:
| ${r_k} = \frac{a}{{\sqrt 2 {\rm{ \mathsf{ π} }}k}}{\rm{exp}}\left( { - \frac{{{a^2}}}{{4bD}}} \right).$ | (6) |
当系统发生随机共振时, 须满足:
| ${r_k} = 2{f_0}.$ | (7) |
若激励信号为λf0, 要发生随机共振, 由式(6)、(7) 可知, 须满足:
| $\frac{a}{{\sqrt 2 {\rm{ \mathsf{ π} }}k}}{\rm{exp}}\left( { - \frac{{{a^2}}}{{4bD}}} \right) = 2\lambda {f_0}.$ | (8) |
由式(8) 可知, 当待测信号频率为λf0时, 若要发生相同幅值的随机共振, 则只需阻尼系数变为原来的1/λ倍, 其余参数不变.与上述调整阻尼系数的结论一致.
取一组参数为基准进行研究, 其中A=0.3, D=2.5, a=1, b=1, 采样点数N=5 000, f0分别为10和100 Hz, fs=100f0.对式(1) 进行四阶Runge-Kutta数值计算, 得到随机共振系统输出在频谱频率f=f0处的谱峰值Am和频谱中最大的幅值Amax随k的变化规律, 如图 1(a)、(b)所示.保持图 1(a)的其他参数不变, 增大噪声强度D=6, 如图 1(c)所示.

|
图 1 阻尼系数的变化关系图 Fig. 1 Relation diagram of damping coefficient changed |
由图 1(a)、(b)对比可知, 系统输出频谱在f0处最大幅值(即发生最优随机共振时)相应的阻尼系数随着待测信号频率的增大而逐渐减小, 分别在0.015和0.001 5附近, 与阻尼调整的规律一致.当信号频率为大参数时, 待测信号频率与最优阻尼系数的量化关系如表 1所示.表中, k0为信号频率为f0时系统产生最优共振时相应的阻尼系数, 0<f0<1.对比图 1(a)、(c)可知, 伴随噪声强度的增大, 当系统发生最优随机共振时, 最优阻尼系数变大.
| 表 1 阻尼系数与信号频率关系图 Table 1 Relation of damping coefficient and frequency ofsignal |
针对信号频率f0为大参数的情况, 利用上述调节阻尼系数的方法可以实现随机共振, 最优阻尼系数与待测信号频率的量化关系如表 1所示.针对D为大参数的情况, 由于k表征了介质对布朗粒子的阻碍作用[17], 当噪声过大时, 为了防止出现“过随机共振”现象, 可以适当增大阻尼系数, 将系统发生最优随机共振时所需的噪声强度增加, 以降低噪声对系统的影响力.针对f0和D均为大参数的情况, 需要统筹调整阻尼系数, 实现随机共振.
1.2 跃迁阈值对系统输出性能的影响由式(2) 可知, 调整系统形状参数对跃迁阈值和跃迁宽度均产生作用.固定跃迁宽度, 通过调整跃迁阈值, 研究跃迁阈值对系统输出性能的影响.
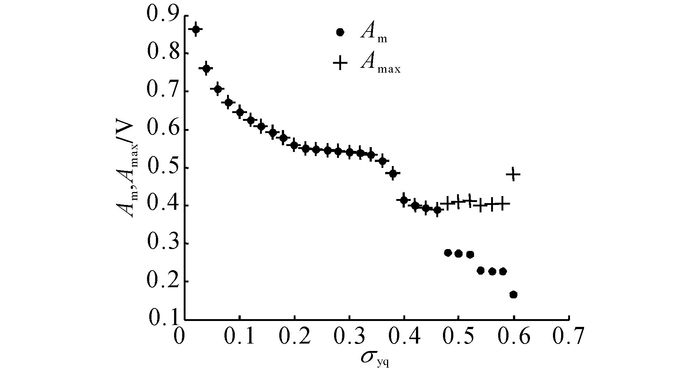
保持图 1(a)的参数不变, 其中阻尼系数为0.014(依据图 1(a)选取), 跃迁宽度为2, 跃迁阈值选取为[0.02, 0.6], 调整步长为0.02.构建随机共振系统, 检测微弱信号, 得到在不同跃迁阈值下、输出频谱频率f=f0处的谱峰值Am和频谱中最大的幅值, 如图 2所示.
|
图 2 跃迁阈值对系统输出性能关系图 Fig. 2 Relation diagram of transition threshold to output performance of system |
由图 2可知, 固定跃迁宽度, 随着跃迁阈值的增大, 与待测信号同频处的输出幅值逐渐减小, 较优的跃迁阈值为[0.2, 0.36], 与信号幅值不能相差过大.当跃迁阈值过大时, 系统未能发生随机共振;当跃迁阈值过小时, 信号中的强噪声部分起到主要作用, 此时系统将发生随机跃迁.只有当跃迁阈值在适当的范围内取值时, 系统可以发生与信号同频的稳定跃迁.当a非常小时, 将导致系统输出释放的现象, 影响信号检测的准确度.若要加强系统输出的性能, 则应适当地降低跃迁阈值, 且跃迁阈值须满足与待测信号幅值相差不能太大, a不能取值过小的条件;否则系统不能发生稳定随机共振, 影响检测效果.
1.3 跃迁宽度对系统输出性能的影响固定跃迁阈值, 研究跃迁宽度的调整对随机共振系统输出性能的影响.
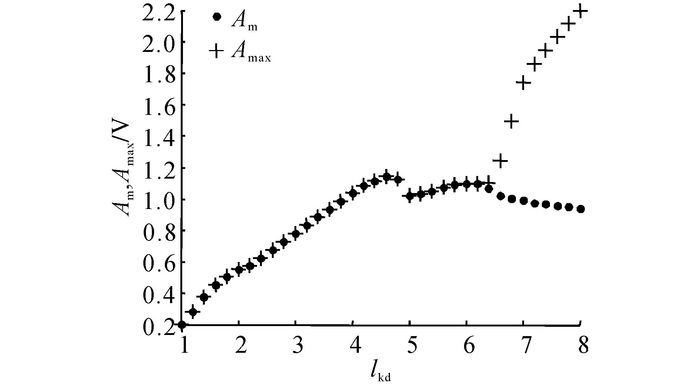
保持图 1(a)的参数不变, 其中跃迁阈值为0.3(依据图 2选取), 跃迁宽度取值为[1, 8], 调整步长为0.2, 构建随机共振系统检测微弱信号, 可得在不同跃迁宽度下f=f0处的谱峰值和频谱中最大的幅值, 如图 3所示.
|
图 3 跃迁宽度与系统输出性能的关系图 Fig. 3 Relation diagram of transition width to output performance of system |
跃迁宽度表征了系统产生跃迁的程度, 由图 3可知, 在固定跃迁阈值的基础上, 随着跃迁宽度在适当的区间内增大, 系统输出逐渐增大, 发生的随机共振现象更加明显.当跃迁宽度超出这一区间时, 即使噪声将部分能量转移给信号, 也未能使系统产生较大宽度的跃迁.通过适当地增大跃迁宽度, 能够使较小的输入信号获得较大的输出, 达到增强系统输出性能的目的.
2 加强级联随机共振系统的调参 2.1 三级级联随机共振加强系统级联双稳随机共振系统是将若干个双稳随机共振系统串联相接, 系统结构如图 4所示.

|
图 4 级联随机共振示意图 Fig. 4 Schematic diagram of cascade stochastic resonance |
级联双稳随机共振系统的方程可以表示为
| $\left. \begin{array}{l} {k_1}{{\dot x}_1} = {a_1}{x_1} - {b_1}x_1^3 + {s_{\rm{n}}}\left( t \right),\\ {k_2}{{\dot x}_2} = {a_2}{x_2} - {b_2}x_2^3 + {x_1}\left( t \right),\\ \quad \quad \quad \quad \quad \vdots \\ {k_n}{{\dot x}_n} = {a_n}{x_n} - {b_n}x_n^3 + {x_{n - 1}}\left( t \right). \end{array} \right\}$ | (9) |
式中:sn(t)=Asin (2πf0t)+n(t)为系统的输入含噪信号, xn(t)(n=1, 2, …)为当前级输出同时又是下一级输入, kn、an和bn分别为第n级随机共振系统参数.
单级随机共振系统将噪声部分能量转移给信号, 增强输出信号的能量;级联随机共振能够持续多次将能量转移, 最终的效果优于单级随机共振的输出性能.分析1节可知, 系统的输出性能可以通过调整跃迁阈值和跃迁宽度两个方面加强, 并且调整阻尼系数能够实现大参数信号的检测.
提出三级级联随机共振加强系统, 分别为每一级系统分配主控参数, 第1级(SR1) 主控参数为阻尼系数, 针对不同量级的信号和噪声, 调节阻尼系数, 保证系统产生跃迁;第2级(SR2) 主控参数为跃迁宽度, 增大系统稳定点的距离, 利于系统发生较大的跃迁;第3级(SR3) 主控参数为跃迁阈值, 易于系统发生较优的随机共振.通过调节每一级系统的主控参数, 逐层增强微弱信号的传输;同时为下一级系统更优地输出服务, 最终加强级联系统输出性能.其他参数为次控参数, 次控参数的取值可以根据实测信号而定.
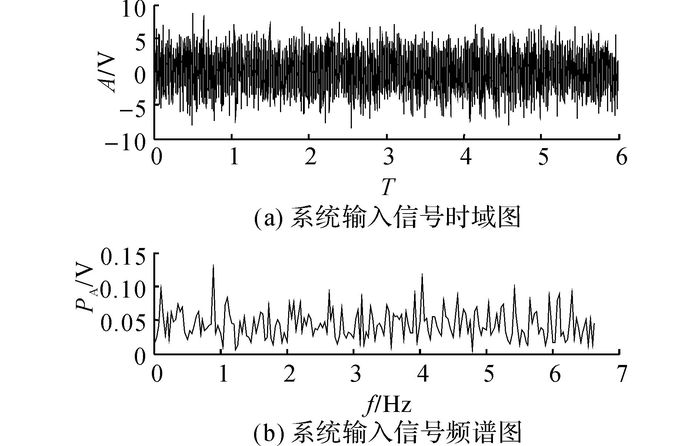
2.2 仿真分析 2.2.1 小参数信号检测取一组参数研究, 其中A=0.3, f0=0.005 Hz, D=0.4, 采样频率为800f0, N=4 800, 系统输入信号的时频域图如图 5所示.图中,T为周期个数,A为幅值,PA为频谱幅值.由图 5可以看出, 待测信号完全淹没在强噪声背景中, 时域频域均不能识别出来.
|
图 5 系统输入信号时频域图 Fig. 5 Time and frequency domain diagram of input signal |
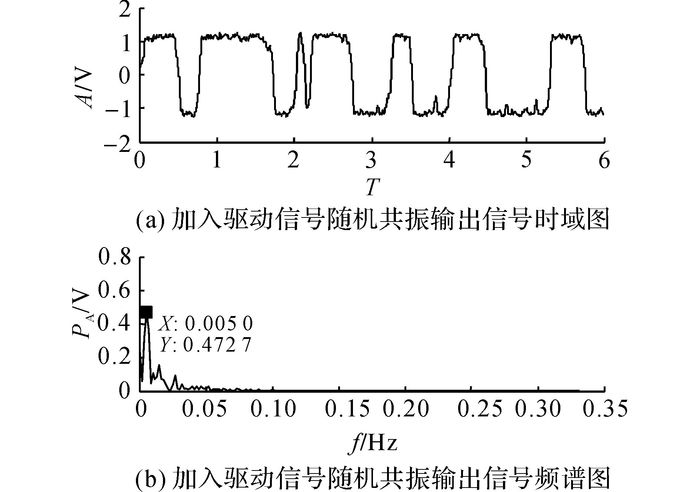
首先采用加入驱动周期信号的方法, 加强随机共振系统的输出性能.因检测信号和噪声信息同文献[8], 其余系统参数的选取与文献[8]一致, 得到级联系统输出信号时频域图, 如图 6所示.
|
图 6 加入驱动周期信号法系统输出信号时频域图 Fig. 6 Time and frequency domain diagram of output signal by adding drive period signalmethod |
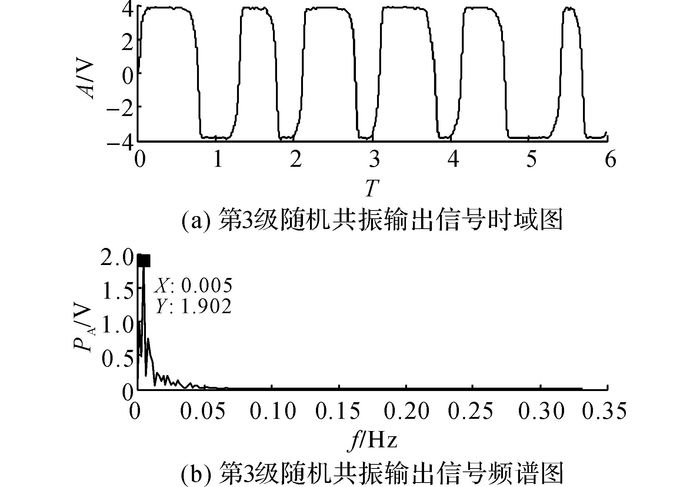
按照提出的三级级联加强系统的调参理论, 选取参数如下:k1=28, a1=1, b1=1;k2=28, a2=0.5, b2=0.125(跃迁宽度为4);k3=28, a3=0.26, b3=0.065(跃迁阈值为0.2).系统输出信号的时频域图如图 7所示.
|
图 7 三级级联加强系统输出信号时频域图 Fig. 7 Time and frequency domain diagram of output signal based on three stage cascade system |
对比图 6、7可知, 采用加入驱动周期信号法和本文提出的级联加强系统均可以实现信号检测, 且提高了输出性能和信号信噪比, 但所提加强系统的输出性能明显优于加入驱动周期信号法.
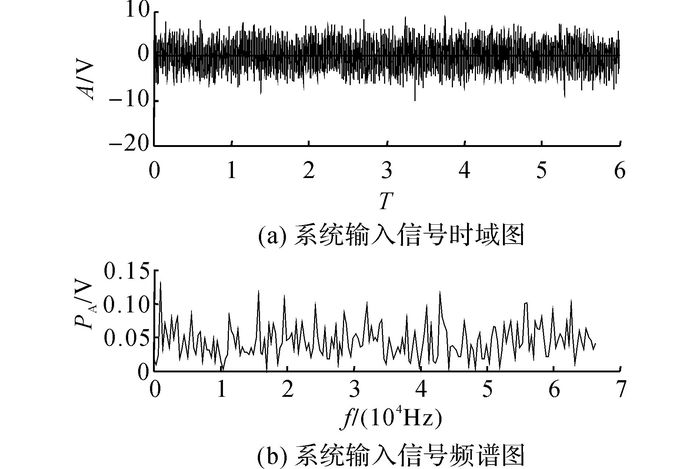
2.2.2 大参数信号检测针对大参数信号的检测, 保持2.2.1节的参数不变, 其中f0=40 Hz, D=2.5, 信号时频域图如图 8所示.可知, 待测微弱信号完全被噪声淹没.
|
图 8 系统输入信号时频域图 Fig. 8 Time and frequency domain diagram of input signal |
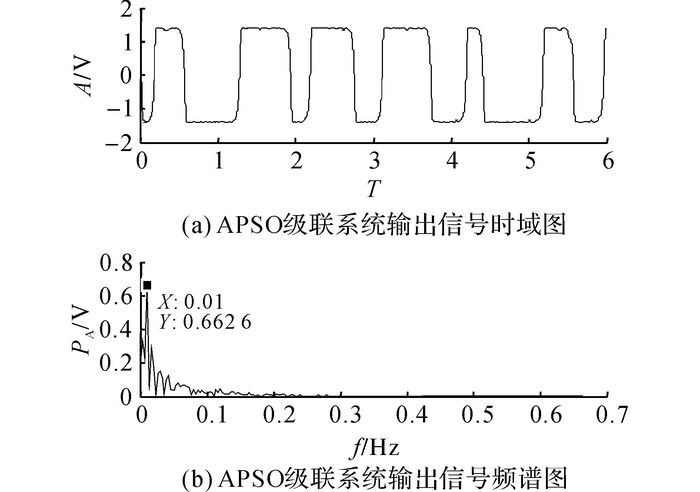
首先采用热依扎等[10]的算法对信号进行检测.其中阻尼系数为1, a和b的寻优范围均为[0.1, 10], 信噪比为适应度函数, 选取的尺度变换系数R=4 000, 相应的二次采样频率为fsr=fs/R=8 Hz.经过APSO级联随机共振系统输出信号的时频域如图 9所示.可知, 在f=0.01 Hz处出现信号的谱峰, 经频率反变换后与待测信号频率一致.
|
图 9 APSO级联随机共振系统输出时频域图 Fig. 9 Time and frequency domain diagram of output signal based on APSO-cascade stochastic resonance |
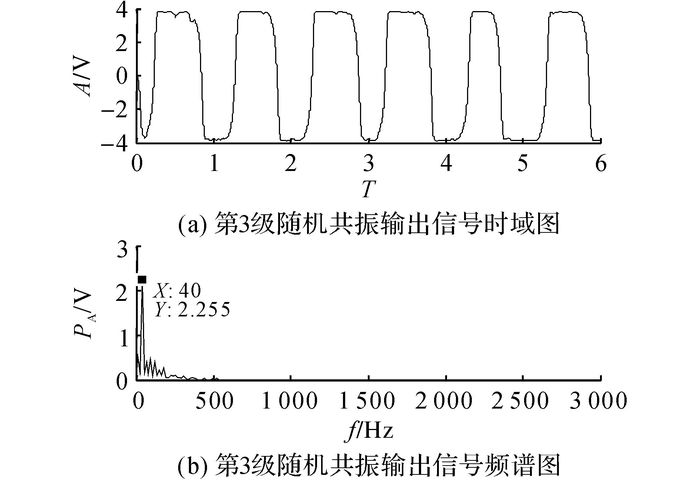
根据提出的三级级联加强系统的理论可知, 待测信号为大参数, 噪声强度略有增大.根据1.1节的调阻尼法, 设置k1=k2=k3=0.003 5, 其余参数选取与检测小参数信号时相同, 系统输出信号的时频域图如图 10所示.
|
图 10 三级加强系统输出信号时频域图 Fig. 10 Time and frequency domain diagram of output signal based on three stage cascade system |
对比图 9、10可知, 利用两种级联随机共振加强调参方法均可以实现大参数信号的检测, 且输出性能和信号信噪比都有所提高, 但所提方法在加强系统输出性能的幅度和检测效率上明显优于基于APSO自适应寻优的调参方法.
2.2.3 采样率对三级随机共振加强系统的影响SR1旨在保证系统发生随机共振, 是整个级联加强系统最基础、最重要的一级, 故该级对检测结果的稳定性提出较高的要求.在实际的信号检测中, 采样频率对系统的检测结果有很大的影响.分析不同采样频率下SR1输出的稳定性.
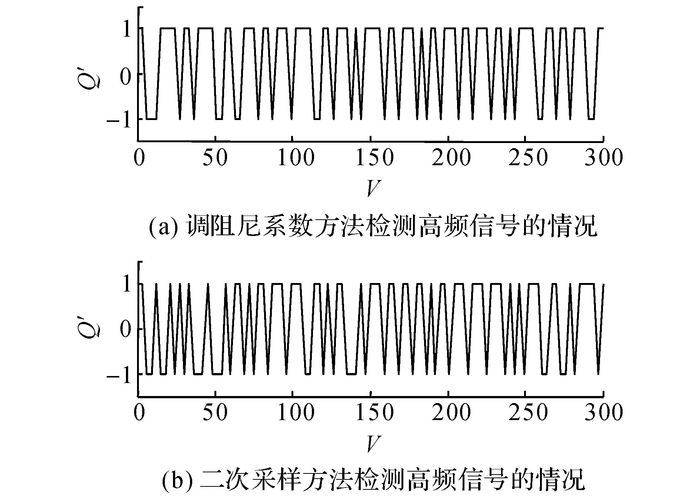
保持图 10中的SR1系统参数不变, 令采样频率与信号频率的比值V=fs/f0, 设定V的取值为[3, 300], 调整步长为3, 可得在不同采样频率(或V)所对应的相同参数条件下, f=f0处的输出谱峰值Am.为了更好地反映待测信号在输出频谱图上的可辨识度, 定义辨识度Q=Am/A′m, 其中A′m为除去Am后剩余谱值中最大的谱值, Q越大, 信号辨识度越高.为了体现变阻尼系数法的稳定性, 在相同的检测参数和条件下, 利用二次采样对大频率信号进行检测.规定当Q≥1.05时, 代表信号可辨识, 用1表示;反之用-1表示, 代表信号不可辨识.2种方法的检测结果如图 11所示.图中,Q′为量化后的辨识度.
|
图 11 辨识度区间随频率比值的变化图 Fig. 11 Effect of degree of identification with frequency ratio |
从图 11可以看出, 当V较小, 尤其为[3, 66]时, 利用二次采样法检测信号的可辨识度起伏波动, 调整阻尼系数法比较稳定, 没有随着采样频率减小而出现频繁的波动.
采用变阻尼系数随机共振调参方法对大频率微弱信号进行检测时, 检测稳定性较好, 采样频率的选择不会对检测结果产生较大的影响, 这对实际工程中微弱信号的检测有很大的意义.
3 实际应用 3.1 三级级联随机共振加强系统的调参策略结合实际应用, 总结出三级级联随机共振加强系统输出性能的调参策略如下.
1) 针对实际待测信号的特点, 预估待测微弱信号频率和噪声强度.
2) 调整主控参数阻尼系数k1, 加强SR1输出性能:利用1.1节的阻尼调整策略, 确定k1的取值;根据1.2节选取跃迁阈值范围, 依据取值间隔, 在阻尼系数范围内依次取值, 固定该阻尼系数, 在跃迁阈值范围内顺序取一个跃迁阈值, 由式(2) 可得a和b.最终选取最优的阻尼系数和形状参数构建SR1.
3) 调整主控参数跃迁宽度, 加强SR2输出性能:保持跃迁阈值与SR1相同, 根据式(2) 调整a2、b2, 适当增大SR2的跃迁宽度, 有利于较小输入信号发生较大的跃迁, 提高系统输出的信噪比, k2=k1.
4) 调整主控参数跃迁阈值, 加强SR3输出性能:保持跃迁宽度与SR2一致, 根据式(2) 调整a3、b3, 适当地减小SR3的跃迁阈值, 有利于系统发生更优的随机共振效果, 阻尼系数保持k3=k1.
5) 经过调参步骤2)~4), 环环相扣, 逐层增强微弱待测信号的传输, 最终实现加强级联随机共振系统输出性能的目的.
3.2 无线电微弱信号检测实例强噪声背景下无线电微弱信号的检测是无线电管理中一个重要的研究课题.现有文献主要是通过单级随机共振检测无线电信号[18-20], 但有时单级系统输出信号的信噪比无法满足后续解调或者解码处理的要求, 导致信息误码率较高, 而级联系统的输出性能明显优于单级系统, 因此采用级联加强系统检测无线电信号.
通用软件无线电外设(universal software radio peripheral, USRP)可以方便地实现对信号的接收与发射, 且内部自带数字上下变频、A/D及D/A转换.现由USRP B200接收到一无线电信号, 经过内部的模拟混频、数字下变频等预处理, 转换为基带信号.如图 12所示为采集的含噪无线电信号的时频域图.由图 12可知, 待测信号特别微弱, 完全淹没在噪声中, 无法辨别待测信号的特征.

|
图 12 系统输入含噪无线电信号时频域图 Fig. 12 Time and frequency domain diagram of radio signal with noise |
根据3.1节提出的加强调参策略可知, 预估信号频率f0=100 Hz.由于待测信号相对于噪声非常小, 现将采集到的信号全部当作白噪声, 估计D=3;因待测信号为大参数信号, 利用1.1节的阻尼调整策略, 确定阻尼系数选取为[0.000 8, 0.002], 依次间隔0.000 2取值;由预估信号的幅值设置跃迁阈值[0.08, 0.6], 据此构建一系列随机共振系统.对式(1) 进行四阶Runge-Kutta数值计算, 获得最优阻尼系数k1=0.001 3, a1=1.04, b1=1.04, 在该参数条件下, SR1输出时、频域如图 13所示.

|
图 13 SR1输出时频域图 Fig. 13 Time and frequency domain diagram of output signal in SR1 |
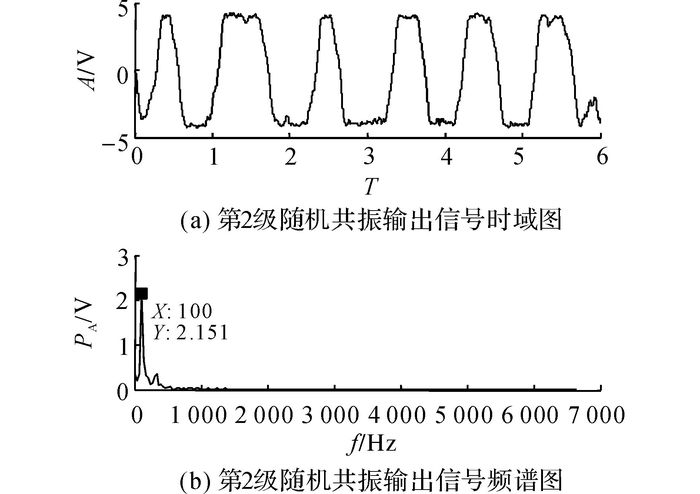
从图 13可知, 系统发生显著的跃迁, 在100 Hz处有谱峰值, 为了加强系统的输出性能, 提高系统的输出信噪比, 按照提出的调参方法继续调整SR2和SR3系统参数.选取系统形状参数a2=1/3, b2=1/27, lkd2=6;a3=0.108, b3=0.012, σyz3=0.12;k2=k3=0.001 3.SR2和SR3输出信号的时、频域图分别如图 14、15所示.
|
图 14 SR2输出时频域图 Fig. 14 Time and frequency domain diagram of output signal in SR2 |

|
图 15 SR3输出时频域图 Fig. 15 Time and frequency domain diagram of output signal in SR3 |
噪声的部分能量连续转化为信号的能量, 因此图 14、15上信号的跃迁宽度均略大于设置值.对比图 14、15可以看出, 无论是时域还是频域, SR3的输出性能均优于SR2, 信号增益增大, 信噪比提高.
通过在实际无线电信号中的应用, 证实了提出的加强级联随机共振输出性能调参策略的可行性.利用该方法可以提高信号信噪比, 满足解调解码对信噪比的要求, 降低误码率.根据实际需求调整系统参数, 可以操控系统的输出, 且无需复杂计算, 简单有效.
4 结语本文以随机共振系统非线性动力学行为为切入点, 考虑系统参数(阻尼系数、系统形状参数)对产生的随机共振现象的影响, 提出三级级联随机共振加强系统.通过调节每一级系统的主控参数, 层层递进, 逐层加强随机共振系统的输出效果, 更好地实现微弱信号基于级联随机共振系统的检测.研究表明, 利用分级调整系统参数(阻尼系数、跃迁宽度、跃迁阈值), 三级级联随机共振系统比单级和二级级联系统具有更优的输出特性;本文提出的调节策略方便、可行, 参数设置简单, 无需复杂计算.如何将三级级联随机共振系统加强调参方法应用于多频微弱信号的检测是下一步的研究方向.
| [1] | BENZI R, SUTERA A, VULPIANI A. The mechanism of stochastic resonance[J]. Journal of Physics A:Mathematical and General, 1981, 14(11): 453–457. DOI:10.1088/0305-4470/14/11/006 |
| [2] | YI Q, YI T, YE H, et al. Adaptive bistable stochastic resonance and its application in mechanical fault feature extraction[J]. Journal of Sound and Vibration, 2014, 333(26): 7386–7400. DOI:10.1016/j.jsv.2014.08.039 |
| [3] |
侯成郭, 罗柏文, 李地. 线性调频信号的级联随机共振数字化接收[J].
电子与信息学报, 2015, 37(12): 2866–2871.
HOU Cheng-guo, LUO Bo-wen, LI Di. Cascaded stochastic resonance for digitized receiving of linear frequency modulation signal[J]. Journal of Electronics and Information Technology, 2015, 37(12): 2866–2871. |
| [4] |
焦尚彬, 杨蓉, 张青, 等. 稳定噪声驱动的非对称双稳随机共振现象[J].
物理学报, 2015, 64(2): 020502-1–9.
JIAO Shang-bin, YANG Rong, ZHANG Qing, et al. Stochastic resonance of asymmetric bistable system with αstable noise[J]. Acta Physica Sinica, 2015, 64(2): 020502-1–9. |
| [5] |
崔伟成, 李伟, 孟凡磊, 等. 基于果蝇优化算法的自适应随机共振轴承故障信号检测方法[J].
振动与冲击, 2016, 35(10): 96–100.
CUI Wei-cheng, LI Wei, MENG Fan-lei, et al. Adaptive stochastic resonance method for bearing fault detection based on fruit fly optimization algorithm[J]. Journal of Vibration and Shock, 2016, 35(10): 96–100. |
| [6] | YANG B Y, WANG L L, RAN S H, et al. Weak signal detection based on adaptive cascaded bistable stochastic resonance system[C]//13th CIRP Conference on Computer Aided Tolerancing. Hangzhou:Procedia Cirp, 2015(27):292-297. http://www.sciencedirect.com/science/article/pii/S2212827115003431 |
| [7] |
林敏, 方利民. 双稳系统演化的时间尺度与随机共振的加强[J].
物理学报, 2009, 58(04): 2136–2140.
LIN Min, FANG Li-min. Time scales of the evolution in bistable system and the reinforcement of stochastic resonance[J]. Acta Physica Sinica, 2009, 58(04): 2136–2140. DOI:10.3321/j.issn:1000-3290.2009.04.003 |
| [8] |
曲媛, 王辅忠, 孙静静. 级联双稳系统随机共振的加强[J].
中国科学:物理学力学天文学, 2011, 41(10): 1190–1197.
QU Yuan, WANG Fu-zhong, SUN Jing-jing. Reinforcement of stochastic resonance in cascaded bistable system[J]. Scientia Sinica Physica, Mechanica and Astronomica, 2011, 41(10): 1190–1197. |
| [9] |
赖志慧, 冷永刚, 范胜波. 级联双稳Duffing系统的随机共振研究[J].
物理学报, 2013, 62(7): 070503-1–9.
LAI Zhi-hui, LENG Yong-gang, FAN Sheng-bo. Stochastic resonance of cascaded bistable duffing system[J]. Acta Physica Sinica, 2013, 62(7): 070503-1–9. |
| [10] |
热依扎.海然, 山拜.达拉拜, 岳石炼. 基于级联随机共振与APSO算法相结合的信号检测方法[J].
激光杂志, 2014, 35(4): 11–14.
RIZA H R, HAIBAI D L B, YUE Shi-lian. Signal detection method based on cascaded stochastic resonance combining with APSO algorithm[J]. Laser Journal, 2014, 35(4): 11–14. |
| [11] | MCNAMARA B, WIESENFIELD K, ROY R. Observation of stochastic resonance in a ring laser[J]. Physical Review Letters, 1988, 60(6): 2626–2629. |
| [12] | GAMMAITONI L, JUNG P, HÄNGGI P. Stochastic resonance[J]. Reviews of Modern Physics, 1998, 70(1): 223–287. DOI:10.1103/RevModPhys.70.223 |
| [13] |
范剑, 赵文礼, 张明路, 等. 随机共振动力学机理及其微弱信号检测方法的研究[J].
物理学报, 2014, 63(11): 110506-1–11.
FAN Jian, ZHAO Wen-li, ZHANG Ming-lu, et al. Nonlinear dynamics of stochastic resonance and its application in the method of weak signal detection[J]. Acta Physica Sinica, 2014, 63(11): 110506-1–11. |
| [14] |
郝静, 杜太行, 江春冬, 等. 调参随机共振在超高频微弱信号检测中的应用[J].
计算机应用, 2016, 36(9): 2374–2380.
HAO Jing, DU Tai-hang, JIANG Chun-dong, et al. Application of parameter-tuning stochastic resonance for detecting the weak signal with ultrahigh frequency[J]. Journal of Computer Applications, 2016, 36(9): 2374–2380. DOI:10.11772/j.issn.1001-9081.2016.09.2374 |
| [15] |
郝研, 王太勇, 万剑, 等. 基于级联双稳随机共振和多重分形的机械故障诊断方法研究[J].
振动与冲击, 2012, 31(8): 181–185.
HAO Yan, WANG Tai-yong, WAN Jian, et al. Mechanical fault diagnosis based on cascaded bistable stochastic resonance and multi-fractal[J]. Journal of Vibration and Shock, 2012, 31(8): 181–185. |
| [16] |
张广丽, 吕希路, 康艳梅. α稳定噪声环境下过阻尼系统中的参数诱导随机共振现象[J].
物理学报, 2012, 61(4): 040501-1–8.
ZHANG Guang-li, LV Xi-lu, KANG Yan-mei. Parameter-induced stochastic resonance in overdamped system with αstable noise[J]. Acta Physica Sinica, 2012, 61(4): 040501-1–8. |
| [17] |
冷永刚, 赖志慧. 基于Kramers逃逸速率的Duffing振子广义调参随机共振研究[J].
物理学报, 2014, 63(2): 020502-1–9.
LENG Yong-gang, LAI Zhi-hui. Generalized parameter adjusted stochastic resonance of Duffing oscillator based on Kramers rate[J]. Acta Physica Sinica, 2014, 63(2): 020502-1–9. |
| [18] | WANG J, REN X, ZHANG S, et al. Adaptive bistable stochastic resonance aided spectrum sensing[J]. IEEE Transactions on Wireless Communications, 2014, 13(7): 4014–4024. DOI:10.1109/TWC.2014.2317779 |
| [19] | LI Q, LI Z. A novel sequential spectrum sensing method in cognitive radio using suprathreshold stochastic resonance[J]. IEEE Transactions on Vehicular Technology, 2014, 63(4): 1717–1725. DOI:10.1109/TVT.2013.2287616 |
| [20] | LIN Y, HE C, JIANG L, et al. Cooperative spectrum sensing based on stochastic resonance in cognitive radio[J]. Science China Information Sciences, 2014, 57(2): 1–10. |



