2. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
比例边界有限单元法(scaled boundary finite element method, SBFEM)由Wolf等[1-2]提出, 是一种半解析的数值方法, 自提出以来, 已成功运用于诸多工程问题的数值分析中, 如钟红等[3-4]模拟了含裂缝结构的裂纹扩展问题;杜建国[5]分析地震荷载下地基与结构相互作用的问题;Liu等[6]将该方法应用于电磁问题研究;通过与FEM耦合, Yang等[7-8]大大提高了SBFEM的计算效率, 很好地模拟了结构裂纹扩展过程.目前, SBFEM无法求解非线性问题, 这使得该方法的应用受到限制.材料非线性特性是诸多数值分析无法回避的技术难题, 在岩土工程问题中尤为显著.
近年来, 基于SBFEM提出的多边形比例边界有限单元继承了多边形单元的优势, 已被证明精度和收敛性都高于多边形有限元[9-12]的数值算法[13].与传统单元相比:该单元边数任意, 能够灵活地处理更复杂的几何图形的网格剖分问题;可以快速建立跨尺度网格模型.
在许多复杂工程结构的数值分析中, 传统有限单元处理比较困难, 典型代表如挤压边墙结构.单个挤压边墙的尺寸较小, 整体结构形状复杂.采用传统有限单元处理较繁琐, 大多模拟中均不考虑该结构;研究结果表明, 挤压边墙对面板应力变形有改善作用, 在高坝中的影响有待进一步研究[14-15].若采用多边形比例边界有限单元模拟, 则可以方便、高效地处理该问题.
本文按照三角形单元积分法则, 提出在每个线单元覆盖的三角形域内引入3个内部高斯点, 利用半解析的弹性解来构造用于非线性分析的单元形函数, 解决了比例边界有限元用于材料非线性数值分析的限制问题, 拓宽了当前比例边界有限元方法的应用范围;采用多核并行算法, 将该单元集成到大型岩土工程有限元软件GEODYNA平台, 使得PSBFEM可以用于大型工程结构的非线性数值分析中.
1 多边形比例边界有限元法原理 1.1 多边形比例边界有限元对于任意求解域, 都可用n条边的任意多边形将问题域离散(n>2);每个多边形只需满足比例边界有限元的比例中心要求(从边界上的任意点都能看见比例中心), 就可将该多边形看作一个SBFEM子域, 对每一子域分别求解后, 可得整个问题的数值结果.
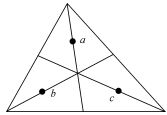
该方法应用广泛, 文献资料丰富, 仅介绍一些关键方程的作用[1-2].如图 1所示为SBFEM计算的多边形单元, 比例中心定义在多边形几何中心;多边形的边界采用一维线单元离散;引入局部坐标系ξ、s, 径向坐标ξ在比例中心O处取0, 在边界处取1;环形坐标取值为-1≤s≤1.线单元i上任意点的坐标可以根据边界的节点坐标求得, 如下所示:

|
图 1 比例边界有限元多边形单元 Fig. 1 Polygon representation of scaled boundary finite element method |
| $ {\mathit{\boldsymbol{x}}_{\rm{b}}}\left( s \right) = \mathit{\boldsymbol{N}}\left( s \right){\mathit{\boldsymbol{x}}_{\rm{b}}}, $ | (1) |
| $ {\mathit{\boldsymbol{y}}_{\rm{b}}}\left( s \right) = \mathit{\boldsymbol{N}}\left( s \right){\mathit{\boldsymbol{y}}_{\rm{b}}}, $ | (2) |
| $ \mathit{\boldsymbol{N}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {{N_1}\left( s \right),}&{{N_2}\left( s \right),}&{ \cdots ,}&{{N_m}\left( s \right)} \end{array}} \right]. $ | (3) |
式中:N(s)为含m个节点的线单元形函数, 可以取任意阶;由于每个单元只在边界离散, 形函数阶数的增加不会使网格剖分复杂化;可以方便地根据实际需要, 增加形函数阶数.采用标准的一维GLL形函数.在得到边界线单元的几何坐标后, 求解域内任一点坐标可以通过引入的径向坐标ξ求得.
| $ \mathit{\boldsymbol{x}}\left( s \right) = \mathit{\boldsymbol{\xi N}}\left( s \right){\mathit{\boldsymbol{x}}_{\rm{b}}}, $ | (4) |
| $ \mathit{\boldsymbol{y}}\left( s \right) = \mathit{\boldsymbol{\xi N}}\left( s \right){\mathit{\boldsymbol{y}}_{\rm{b}}}. $ | (5) |
对于每一边界线单元与比例中心连线构成的扇形区域, 任一点的位移场可以用SBFEM坐标表示为
| $ \mathit{\boldsymbol{u}}\left( {\xi ,s} \right) = {\mathit{\boldsymbol{N}}_u}\left( s \right)\mathit{\boldsymbol{u}}\left( \xi \right). $ | (6) |
式中:u(ξ)为比例中心与边界节点连线的径向位移函数, Nu(s)为边界线单元插值形函数. u(ξ)可以通过求解比例边界有限元方程得到:
| $ \begin{array}{l} {\mathit{\boldsymbol{E}}_0}{\xi ^2}u\left( \xi \right){,_{\xi \xi }} + \left( {{\mathit{\boldsymbol{E}}_0} - {\mathit{\boldsymbol{E}}_1} + \mathit{\boldsymbol{E}}_1^{\rm{T}}} \right)\xi \mathit{\boldsymbol{u}}\left( \xi \right){,_\xi } - {\mathit{\boldsymbol{E}}_2}\mathit{\boldsymbol{u}}\left( \xi \right) + \\ \;\;\;\;\mathit{\boldsymbol{F}}\left( \xi \right) = 0. \end{array} $ | (7) |
式(7) 为关于ξ的二阶非齐次偏微分方程.式中:Ei(i=0, 1, 2) 为只与材料属性和几何形状有关的系数矩阵.引入变量X(ξ), 可将方程转换为一阶齐次微分方程.
| $ {\mathit{\boldsymbol{E}}_0} = \int\limits_{ - 1}^{ + 1} {\mathit{\boldsymbol{B}}_1^{\rm{T}}\left( s \right)\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{B}}_1}\left( s \right)\left| {\mathit{\boldsymbol{J}}\left( s \right)} \right|{\rm{d}}s} , $ | (8a) |
| $ {\mathit{\boldsymbol{E}}_1} = \int\limits_{ - 1}^{ + 1} {\mathit{\boldsymbol{B}}_2^{\rm{T}}\left( s \right)\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{B}}_1}\left( s \right)\left| {\mathit{\boldsymbol{J}}\left( s \right)} \right|{\rm{d}}s} , $ | (8b) |
| $ {\mathit{\boldsymbol{E}}_2} = \int\limits_{ - 1}^{ + 1} {\mathit{\boldsymbol{B}}_2^{\rm{T}}\left( s \right)\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{B}}_2}\left( s \right)\left| {\mathit{\boldsymbol{J}}\left( s \right)} \right|{\rm{d}}s} . $ | (8c) |
式中:D为本构矩阵; |J(s)|为雅各比矩阵行列式;B1(s)和B2(s)为应变位移转换矩阵, 具体表达式见文献[2].
| $ \mathit{\boldsymbol{X}}\left( \xi \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}\left( \xi \right)}\\ {\mathit{\boldsymbol{q}}\left( \xi \right)} \end{array}} \right], $ | (9) |
| $ \xi \mathit{\boldsymbol{X}}\left( \xi \right){,_\xi } = - \mathit{\boldsymbol{ZX}}\left( \xi \right). $ | (10) |
式中:Z为Hamilton矩阵:
| $ \mathit{\boldsymbol{Z = }}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{E}}_0^{ - 1}\mathit{\boldsymbol{E}}_1^{\rm{T}}}&{ - \mathit{\boldsymbol{E}}_0^{ - 1}}\\ {{\mathit{\boldsymbol{E}}_1}\mathit{\boldsymbol{E}}_0^{ - 1}\mathit{\boldsymbol{E}}_1^{\rm{T}} - {\mathit{\boldsymbol{E}}_2}}&{ - {\mathit{\boldsymbol{E}}_1}\mathit{\boldsymbol{E}}_0^{ - 1}} \end{array}} \right]; $ | (11) |
q(ξ)为与u(ξ)相对应的内部节点力向量.
通过对Hamilton矩阵Z进行特征值分解, 对于每一多边形单元都可得到下式关系:
| $ \mathit{\boldsymbol{Z}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_u}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_q}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_u}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_q}} \end{array}} \right]{\mathit{\boldsymbol{S}}_n}. $ | (12) |
式中:Sn是由Z矩阵负特征值组成的对角矩阵, ψu和ψq分别为位移和应力模态对应的转换矩阵.可以求得与有限元相对应的等价形函数Φ(ξ, s), 表达式如下:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\xi ,s} \right) = {\mathit{\boldsymbol{N}}_u}\left( s \right){\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_u}{\xi ^{ - {\mathit{\boldsymbol{S}}_n}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_u^{ - 1}. $ | (13) |
在比例边界有限元方法中, Wolf[2]给出应变场表达式(14a), 代入位移场u(ξ), 可以求得应变位移转换矩阵B(ξ, s), 如下:
| $ \mathit{\boldsymbol{\varepsilon }}\left( {\xi ,s} \right) = {\mathit{\boldsymbol{B}}_1}\left( s \right)\mathit{\boldsymbol{u}}\left( \xi \right){,_\xi } + {\xi ^{ - 1}}{\mathit{\boldsymbol{B}}_2}\left( s \right)\mathit{\boldsymbol{u}}\left( \xi \right), $ | (14a) |
| $ \mathit{\boldsymbol{B}}\left( {\xi ,s} \right) = \left[ {{\mathit{\boldsymbol{B}}_1}\left( s \right){\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_u}\left[ { - {\mathit{\boldsymbol{S}}_n}} \right] + {\mathit{\boldsymbol{B}}_2}\left( s \right){\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_u}} \right]{\xi ^{ - {\mathit{\boldsymbol{S}}_n} - \mathit{\boldsymbol{I}}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_u^{ - 1}. $ | (14b) |
在求出节点位移后, 单元内部的位移场可以通过形函数插值求得.与有限元类似, 通过虚功原理, 可得
| $ \begin{array}{l} \int\limits_\mathit{\Omega } {{\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{\varepsilon }}^{\rm{T}}}\Delta \mathit{\boldsymbol{\sigma }}\left( {\xi ,s} \right){\rm{d}}\mathit{\Omega }} = \int\limits_\mathit{\Gamma } {\delta {\mathit{\boldsymbol{u}}^{\rm{T}}}{f_{\rm{t}}}{\rm{d}}\mathit{\Gamma }} + \int\limits_\mathit{\Gamma } {\delta {\mathit{\boldsymbol{u}}^{\rm{T}}}{f_{\rm{b}}}{\rm{d}}\mathit{\Gamma }} - \\ \;\;\;\;\int\limits_\mathit{\Omega } {{\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{\varepsilon }}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}\left( {\xi ,s} \right){\rm{d}}\mathit{\Omega }} . \end{array} $ | (15) |
式中:Δσ(ξ, s)为应力增量, ft和fb分别为边界切应力和体积力密度, δε(ξ, s)为虚位移场δu(ξ, s)对应的虚应变场.
式(15) 可以简写为
| $ {\mathit{\boldsymbol{K}}_{{\rm{ep}}}}\Delta {\mathit{\boldsymbol{u}}_{\rm{b}}} = {\mathit{\boldsymbol{R}}_{{\rm{ext}}}} - {\mathit{\boldsymbol{R}}_{{\rm{int}}}}. $ | (16) |
在求出单刚后, 通过自由度组装, 可得整个计算域的弹塑性刚度矩阵, 进一步可以列出计算域的平衡方程:
| $ \left( {\sum\limits_{i = 1}^{{n_{{\rm{Pol}}}}} {{\mathit{\boldsymbol{K}}_{{\rm{ep}}}}} } \right)\Delta {\mathit{\boldsymbol{U}}_{\rm{b}}} = \sum\limits_{i = 1}^{{n_{{\rm{Pol}}}}} {\left( {{\mathit{\boldsymbol{R}}_{{\rm{ext}}}} - {\mathit{\boldsymbol{R}}_{{\rm{int}}}}} \right)} . $ | (17) |
式中:ΔUb为整个计算域边界的节点位移增量.从上述推导可以看出, 求解刚度阵的核心是求出弹塑性本构矩阵Dep和应变位移转换矩阵B.
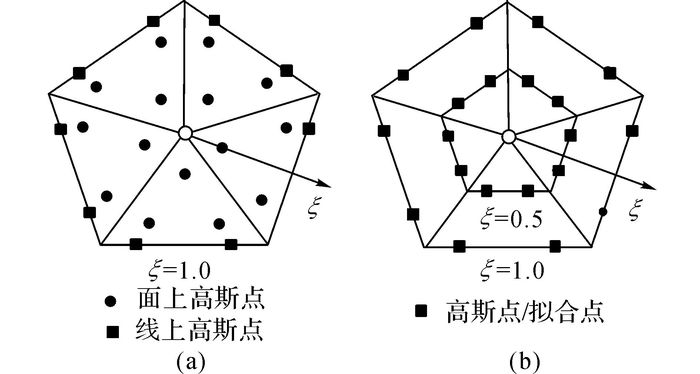
1.3.1 弹塑性本构矩阵如图 2所示, 在求解非线性问题时, Ooi等[16]采用最小二乘法拟合弹塑性本构矩阵Dep, 用笛卡尔坐标表示如下:
|
图 2 非线性PSBFEM高斯积分点 Fig. 2 Location of Gauss points to capture nonlinearity of PSBFEM |
| $ \begin{array}{l} {\mathit{\boldsymbol{D}}_{{\rm{ep}}}}\left( {x,y} \right) = {\mathit{\boldsymbol{D}}_0} + {\mathit{\boldsymbol{D}}_1}x + {\mathit{\boldsymbol{D}}_2}y + {\mathit{\boldsymbol{D}}_3}{x^2} + {\mathit{\boldsymbol{D}}_4}xy + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{D}}_5}{y^2} + \cdots . \end{array} $ | (18) |
系数矩阵Di(i=1, 2, 3…)通过最小二乘法曲线拟合技术求解, 可以通过边界上的高斯点实现.若要提高拟合精度, 则需增加额外拟合点, 可以根据需要沿径向插入对应的拟合点, 如图 2(b)所示, 详见文献[16].利用该方法求解了Dep和系数矩阵Ei(i=0, 1, 2), 将PSBFEM应用拓展到非线性领域.为了获得满意的精度, 该方法须将单元划分较小, 采用最小二乘法拟合会消耗较大的计算时间, 不宜在大规模数值分析中推广.
如图 2(a)所示, 在每一线单元覆盖的三角形域内引入3个高斯点, 每个高斯点的坐标可以通过三角形单元积分法则来确定, 如图 3所示.对于任意的三角形单元, 写成三角形坐标积分的表达式:
| $ \iint\limits_{{\mathit{\Omega }_e}} {f\left( {x,y} \right){\text{d}}x{\text{d}}y} = {A_e}\sum\limits_{i = 1}^m {{W_i}f\left( {L_1^i,L_2^i,L_3^i} \right) + E} . $ | (19) |
式中:(L1i, L2i, L3i)为第i个积分点的三角形坐标, Ae为三角形e的面积, m为每个三角形内的积分点个数, Wi和E分别为权重和积分残差.对于本文的3个高斯积分点, 如表 1所示.高斯点的位置分布及具体的积分表达式为
| $ \begin{gathered} \iint\limits_{{\mathit{\Omega }_e}} {f\left( {\xi ,s} \right){\text{d}}\xi {\text{d}}s} = \frac{1}{6}\left[ {f\left( {\frac{2}{3},\frac{1}{6},\frac{1}{6}} \right) + f\left( {\frac{1}{6},\frac{1}{6},\frac{2}{3}} \right) + } \right. \hfill \\ \;\;\;\;\;\left. {\left( {\frac{1}{6},\frac{2}{3},\frac{1}{6}} \right)} \right] + E. \hfill \\ \end{gathered} $ | (20) |
| 表 1 三角形单元积分点选择 Table 1 Integration points in triangular element |
实现非线性的主要思想如下:对于任意n边形, 线上高斯点数为2n, 面上高斯点数为3n.首先通过线上高斯积分点求解SBFEM的系数矩阵Ei(i=0, 1, 2);形成Z矩阵;按式(12) 进一步求解特征值和特征向量, 可以解出应变位移转换矩阵的表达式(14).Dep通过调用有限元程序的本构模块获得;单元刚度矩阵通过每个单元内部的面高斯点积分求解如下:
| $ {\mathit{\boldsymbol{K}}_{{\rm{ep}}}} = \sum\limits_{i = 1}^{3n} {{\mathit{\boldsymbol{B}}^i}\left( {\xi ,s} \right)\mathit{\boldsymbol{D}}_{{\rm{ep}}}^i{\mathit{\boldsymbol{B}}^i}\left( {\xi ,s} \right){A_i}} . $ | (21) |
按自由度组装获得计算域的总体刚度矩阵.
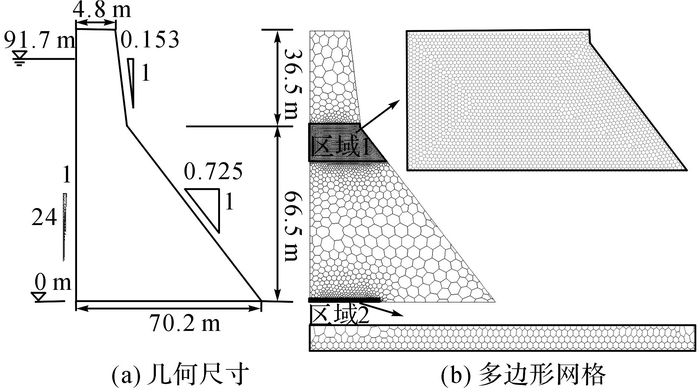
2 程序验证-Koyna大坝 2.1 计算模型Koyna大坝为典型非溢流坝型, 在1967年的强震中多处发生损伤破坏[17], 一直以来被研究者作为经典算例验证, 取得了丰硕的成果[18-22].该坝几何尺寸及多边形网格如图 3所示, 坝体总长850 m, 高103 m, 最高蓄水位为91.7 m.为了更精细地模拟损伤扩展, 在区域1和区域2位置进行局部加密.如图 4(b)所示, 计算模型共包括3 815个多边形单元和7 823个节点, 自由度数共为15 486.
|
图 3 Koyna大坝几何尺寸及多边形网格 Fig. 3 Geometry and polygon mesh of Koyna Dam |
|
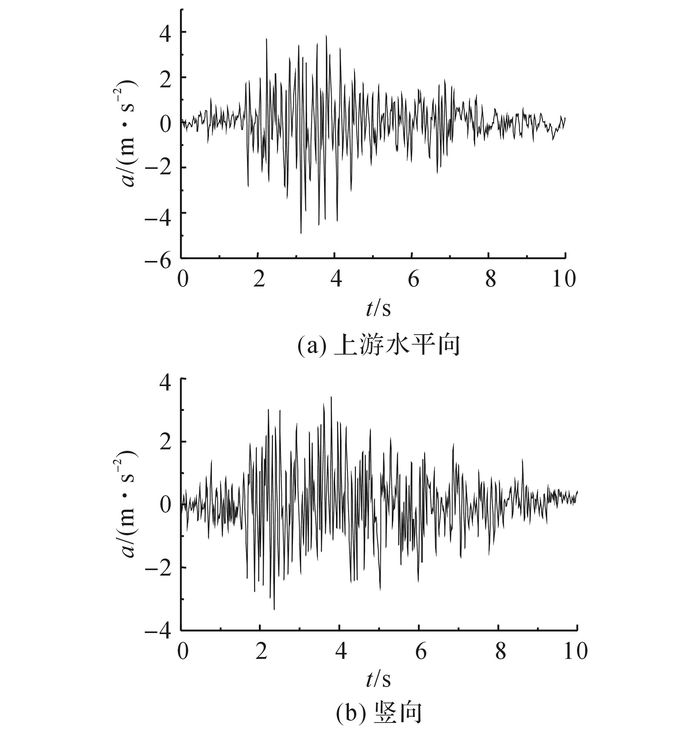
图 4 Koyna大坝实测加速度时程 Fig. 4 Koyna acceleration records |
根据Wang等[22]的研究成果可知, 计算参数如下:密度ρ=2.63 g/cm3, 弹性模量E=31 GPa, 泊松比ν=0.2, 混凝土抗拉强度取2.9 MPa, 断裂能取250 N·m.
坝体主要受自重及上游水压力的作用;底部采用刚性边界, 地震中, 动水压力采用附加质量法[23]施加.地震动输入采用实测地震波[17], 其中水平向最大加速度为4.9 m/s2, 竖向加速度峰值为3.4m/s2, 如图 4所示.图中,a为加速度.计算中, 时间间隔Δt=0.005 s.阻尼采用瑞利阻尼计算, 在混凝土材料动力计算中, 本文假定阻尼为5%[24].
由于混凝土抗拉强度远低于抗压强度, 只开展Koyna大坝的拉损伤分析.
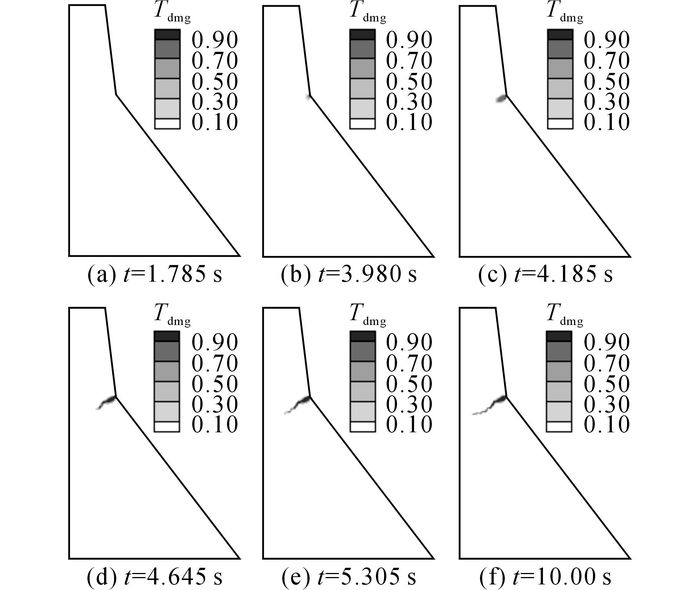
2.3 结果分析 2.3.1 损伤累积发展演化图 5给出损伤累积发展过程中的6个重要时刻.图中, Tdmg为拉损伤因子, 取值为0、1, 0表示完好无损, 1表示完全损坏.
|
图 5 Koyna大坝拉损伤累积发展演化 Fig. 5 Evolution of cumulative tensile damage in Koyna dam |
由于刚性边界约束的作用, 当t=1.785 s时, 上游坝底处开始出现损伤;当t=3.980 s时, 下游面开始损伤;正应力的作用导致坝块上半部晃动, 从而在4.185 s时, 上游面开始损伤.下游面损伤呈曲线式向下发展, 如图 6(d)、(e)所示;靠近上游面时, 损伤带开始转成水平向发展, 当t=10 s时, 整个损伤区域如图 6(f)所示.

|
图 6 NPSBFE计算的Koyna大坝整体损伤分布 Fig. 6 Distribution of global damage with polygons mesh in Koyna dam |
图 6给出大坝震后的整体损伤分布情况.可以看出, 损伤区域分布比较集中, 和Wang等[22]的研究成果吻合较好.
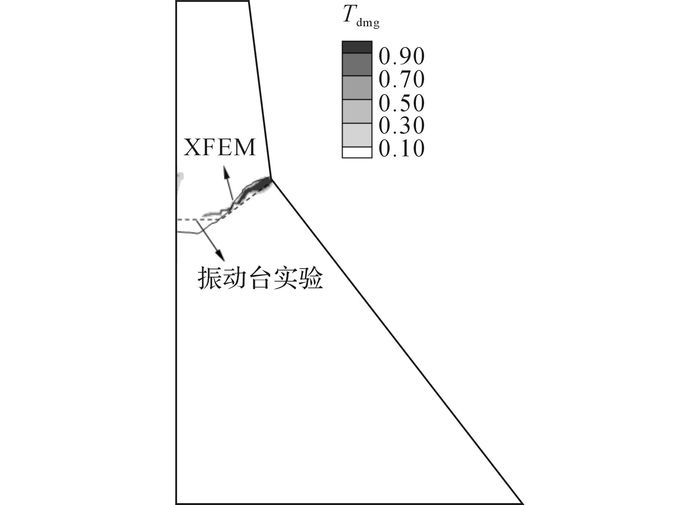
当Tdmg超过0.8时, 混凝土将开裂[19].连接损伤因子超过0.8的单元, 这些单元组成的区域可以看作是一条连通的裂纹.如图 7所示, 本文计算所得的损伤区域与XFEM[21]及振动台实验[18]所得的裂纹位置十分接近, 表明将本文实现的NPSBFE用于工程结构非线性动力响应的可靠性.
|
图 7 与XFEM及振动台实验结果对比图 Fig. 7 Contrast diagram between simulation results and shaking table test results |
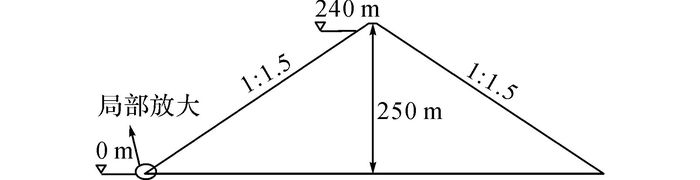
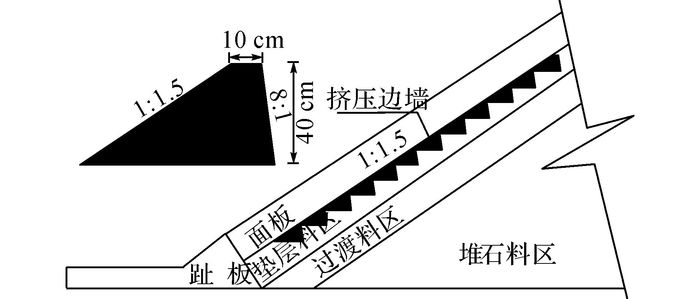
面板堆石坝计算模型坝高250 m, 如图 8所示, 上、下游坝坡均为1:1.5;面板顶部厚0.3 m, 底部厚1.2 m.主体结构分区如图 9所示, 包含面板、趾板、垫层料区、挤压边墙、过渡料区和主堆石料区, 并在面板与挤压边墙、挤压边墙与垫层料及垫层料与趾板之间设置接触面单元, 在面板与趾板之间设置缝单元.
|
图 8 二维混凝土面板坝模型 Fig. 8 Plane model of two-dimensional concrete-faced rockfill dam |
|
图 9 典型挤压边墙与坝体结构布置示意图 Fig. 9 Typical extrusion sidewall and partitioning of dam body materials |
单个挤压边墙的典型断面一般为梯形, 如图 9所示.在计算中, 挤压边墙断面高40 cm, 顶部宽为10 cm, 上游面坡度为1:1.5, 下游面坡度为8:1.
3.1 多边形过渡采用多边形比例边界有限单元进行疏密网格的衔接.采用该方法能够快速地处理任意形状计算模型任意位置的网格细分问题.主要步骤如下.
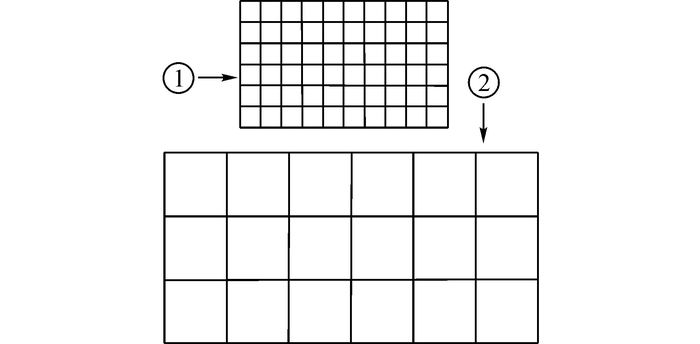
1) 如图 10所示, 第1部分为需要精细模拟的细密网格, 第2部分为较稀疏的网格.根据需要, 在同一模型中将两部分网格划分完毕, 为下一步工作作准备.
|
图 10 典型粗细网格示意图 Fig. 10 Representative mesh of coarse and fine |
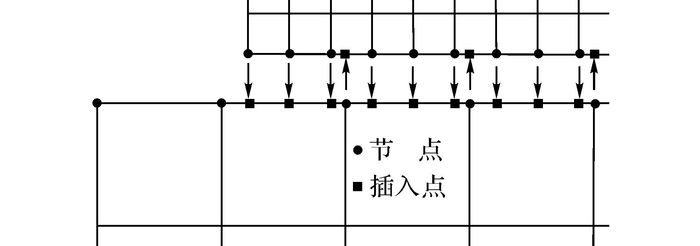
2) 在疏密网格衔接处, 在疏网格边界上插入与细网格边界节点对应的插入点, 细网格边界上插入与疏网格边界节点对应的插入点, 如图 11所示.
|
图 11 插入节点 Fig. 11 Inserting nodes |
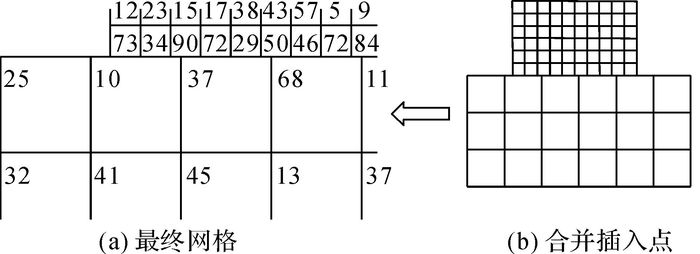
3) 在交界边上生成、合并插入点编号;至此, 疏密网格过渡处理完毕, 最终的计算网格见图 12(a).
|
图 12 合并插入节点 Fig. 12 Merge and compress inserting nodes |
上述疏密网格衔接技术简便、高效, 且已实现程序化操作, 可以大量减少前处理工作, 为数值仿真方案优选、精细数值模拟等提供技术支撑.
3.2 计算方案为了验证本文实现单元用于工程结构非线性分析的可靠性.将本文实现单元计算结果与有限元较密网格计算结果进行对比分析, 设置计算方案如下.
1) PSBFEM较疏网格计算.
2) 有限元较密网格计算.
3.2.1 PSBFEM疏网格计算采用五边形比例边界有限单元对挤压边墙进行模拟, 并用多边形单元过渡;疏密网格在同一模型中剖分完成后, 通过多边形过渡技术处理, 方便、快速地建立了一致的多尺度计算模型.局部网格如图 13所示, 过渡后共包含12 202个单元, 12 851个节点.计算中, 接触面和缝单元采用无厚度的Goodman单元, 其余单元均采用提出的非线性多边形比例边界有限单元.

|
图 13 PSBFEM局部放大网格图 Fig. 13 Partial detail mesh of PSBFEM |
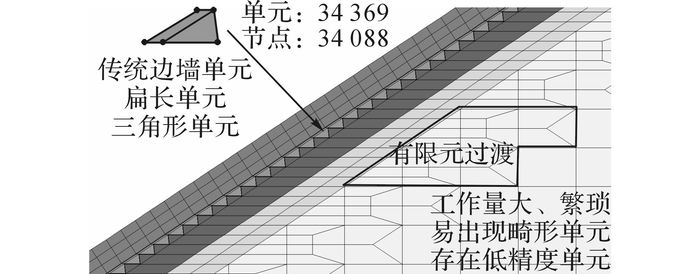
目前, 解决堆石体和面板之间的疏密过渡问题, 多采用将面板附近的堆石体(垫层、过渡层)进行逐渐加密过渡的方法[24], 这增加了大量的前处理工作量, 且过渡区网格质量不高, 影响计算精度.这种处理对平面问题尚可操作, 对于三维结构, 则相当困难.为了更准确地得到该问题的数值解, 采用较密的有限元网格, 过渡处理后的局部有限元网格见图 14;共包含34 369个单元, 34 088个节点.在计算中, 接触面和缝单元采用无厚度的Goodman单元, 其余单元均采用传统有限元等参单元.
|
图 14 FEM局部放大网格图 Fig. 14 Partial detail mesh of FEM |
静力分析模拟了坝体的施工填筑和蓄水过程;其中坝体分78层填筑完成, 面板为一次填筑完成, 水位分30级蓄至240 m高程.面板、趾板及挤压边墙采用线弹性模型, 参数如表 2所示.垫层、过渡和堆石体采用广义塑性模型模拟, 参数如表 3所示[25];接触面采用理想弹塑性接触面模型, 参数如表 4所示[26].
| 表 2 线弹性材料参数 Table 2 Parameters of concrete linear model |
采用广义塑性模型进行动力分析, 主堆石料计算参数如表 3所示, 参数的物理意义详见文献[24, 25].过渡料与垫层料均取堆石料参数.面板所受的动水压力采用附加质量法模拟[23].
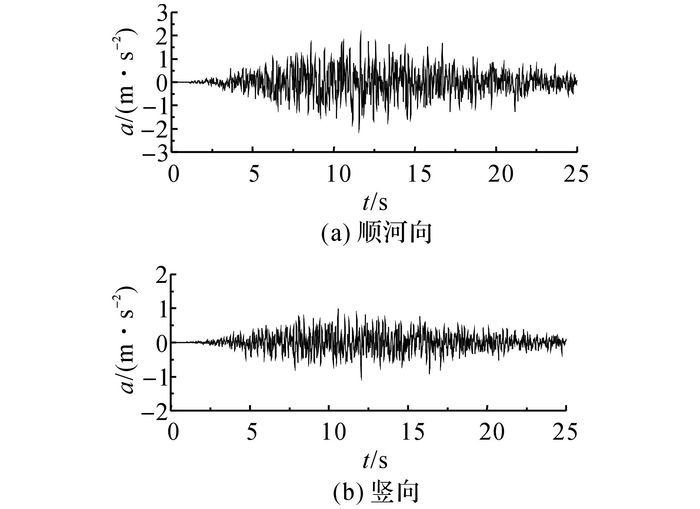
地震动输入采用《水工建筑物抗震设计规范》(DL-5073-2000) 规范谱人工地震波, 顺河向地震峰值加速度为2 m/s2, 竖向加速度为1 m/s2.地震波加速度时程如图 16所示.计算中, 地震波时长为25.00 s, 时间步长Δt=0.01 s.
|
图 16 地震波加速度时程曲线 Fig. 16 Input ground motion acceleration time history |
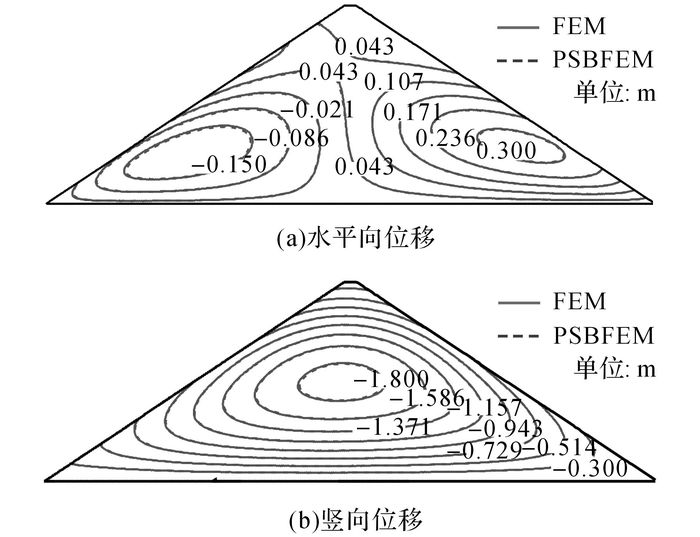
图 17给出满蓄期坝体位移对比的情况.可以看出, 本文实现的多边形比例边界有限单元疏网格与传统有限元较密网格的计算结果基本保持一致, 仅水平位移在局部有较小差别.
|
图 17 满蓄期坝体位移 Fig. 17 Displacement of dam after impoundment |
如图 18所示为满蓄期面板应力变形的计算结果.PSBFEM结果与FEM吻合较好, 其中最大挠度为0.406 m, 发生在高程100 m附近;顺坡向应力包络线仅在高程50 m附近的应力有较小差别.

|
图 18 满蓄期面板应力变形 Fig. 18 Deflection and stress along slope direction of face slabs after impoundment |
表 5给出满蓄时坝体和面板变形和应力的最值.可以看出:本文方法与有限元的计算结果相差甚小, 说明本文的PSBFEM精度可以得到保证.
| 表 5 静力计算满蓄期结果对比 Table 5 Comparison of displacement of dam after impoundment |
如图 19所示为地震过程中的面板顺坡向应力包络线.图中,σmin、σmax分别为最小和最大顺坡向应力.应力随高程的分布规律完全一致, 数值基本保持一致;其中最小顺坡向应力在高程50和200 m附近有较小差别, 最大顺坡向应力在高程50 m附近有微小差别.

|
图 19 地震动作用下面板顺坡向应力 Fig. 19 Stress along slope direction during earthquake |
表 6列出了2种方法动力计算中面板应力的最值情况.最小顺坡向应力相差2.51%, 最大顺坡向应力仅相差0.58%, 相差很小, 对于实际工程而言, 可以满足相应的精度, 说明PSBFEM在动力计算中能够保证满意的精度.
| 表 6 动力计算的面板应力对比 Table 6 Comparison of stress along slope direction duringearthquake |
在相同网格数量下, 由于SBFEM本身的特点, 计算时间较FEM慢, 但前者可以结合灵活的多边形单元, 便捷、快速地实现疏密过渡.为了更全面地显示采用NPSBFE过渡的优点, 表 7给出2种方法的计算时间.可以看出, 采用过渡后, 可以使网格数量减少64.5%, 大幅地降低网格数量.从计算时间上看, 由于网格数减少, 静力计算时间可以减少44.4%, 动力计算时间相应减少16.3%, 可以在一定程度上提高计算效率.若与FEM联合使用, 则只有疏密衔接处的多边形采用SBFEM, 其余单元采用FEM, 进一步提升了计算效率.
| 表 7 FEM和PSBFEM计算时间对比 Table 7 Comparison of computational times with FEM and PSBFEM |
考虑挤压边墙的面板堆石坝静、动力数值分析计算结果表明:NPSBFE疏网格计算的坝体位移和面板应力变形与有限元较密网格计算结果基本一致, 吻合度较好.用多边形比例边界有限元可以非常灵活地处理复杂的材料分区, 减少建模难度和单元数量, 提高计算效率.
4 结语本文在多边形比例边界有限元的基础上, 根据三角形单元积分法则, 提出在每个线单元覆盖的三角形域内引入3个内部高斯积分点.利用半解析的弹性解来构造用于非线性分析的单元形函数, 解决了比例边界有限元弹塑性数值分析的限制难点, 实现了非线性多边形比例边界有限单元(NPSBFE).
采用六边形为主的多边形单元, 对经典算例Koyna大坝进行塑性损伤动力响应分析, 并与振动台实验及XFEM模拟结果进行比较.坝体损伤扩展过程及损伤区域分布均与文献[20~22]及实验结果吻合较好, 验证了提出的NPSBFE用于非线性动力分析的可靠性.另外, 采用该单元模拟考虑挤压边墙的面板堆石坝弹塑性地震动响应模拟.用五边形单元模拟挤压边墙结构, 避免出现扁长单元或较低精度的三角形单元, 利用多边形单元进行疏密网格过渡, 大幅简化前处理工作量.NPSBFE模拟结果与FEM较密网格所得的结果吻合良好, 表明用多边形比例边界有限元可以非常灵活地处理复杂的材料分区, 减少建模难度和单元数量.在材料分区优化和尺度急剧变化区域跨尺度处理研究等方面具有突出的优势, 数值模拟的适用性更广.
本文的主旨在于验证NPSBFE在大坝结构的非线性动力响应数值计算中的可靠性与正确性, 进而将NPSBFEM推广到其他工程结构非线性数值分析.在实际应用中, 可以与有限元技术耦合.根据需要, 仅在局部复杂区域或尺度急剧变化的跨尺度衔接处使用本文提出的NPSBFE, 则计算效率大幅提高.本文工作将为大型复杂结构静动力精细分析、跨尺度/多尺度数值模拟、仿真方案优选、损伤破坏分析等提供了有力的技术支撑.
| [1] | WOLF J P, SONG C. Finite-element modelling of unbounded media[M]. Chichester: Wiley, 1996: 65-102. |
| [2] | WOLF J P. The scaled boundary finite element method[M]. West Sussex: Wiley, 2003: 48-87. |
| [3] |
钟红, 暴艳利, 林皋. 基于多边形比例边界有限元的重力坝裂缝扩展过程模拟[J].
水利学报, 2014, 45(supple.1): 30–37.
ZHONG Hong, BAO Yan-li, LIN Gao. Modelling of crack propagation of gravity dams based on scaled boundary polygons[J]. Journal of Hydraulic Engineering, 2014, 45(supple.1): 30–37. |
| [4] |
施明光, 徐艳杰, 钟红, 等. 基于多边形比例边界有限元的复合材料裂纹扩展模拟[J].
工程力学, 2014(7): 1–7.
SHI Ming-guang, XU Yan-jie, ZHONG Hong, et al. Modelling of crack propagation for composite materials based on polygon scaled boundary finite elements[J]. Engineering Mechanics, 2014(7): 1–7. DOI:10.6052/j.issn.1000-4750.2013.01.0027 |
| [5] |
杜建国. 基于SBFEM的大坝-库水-地基动力相互作用分析[D]. 大连: 大连理工大学, 2007.
DU Jian-guo. The dynamic interaction analysis of dam-reservoir-foundation based on SBFEM[D]. Dalian:Dalian University of Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10141-2007122873.htm |
| [6] | LIU Jun, LIN Gao. A scaled boundary finite element method applied to electrostatic problems[J]. Engineering Analysis with Boundary Elements, 2012, 36(12): 1721–1732. DOI:10.1016/j.enganabound.2012.06.010 |
| [7] | YANG Z J, WANG X F, YIN D S, et al. A non-matching finite element-scaled boundary finite element coupled method for linear elastic crack propagation modeling[J]. Computers and Structures, 2015, 153(2015): 126–136. |
| [8] | HUANG Y J, YANG Z J, LIU G H, et al. An efficient FE-SBFE coupled method for mesoscale cohesive fracture modeling of concrete[J]. Computational Mechanics, 2016, 58(4): 1–21. |
| [9] |
王兆清, 鹿晓阳. 基于平均值插值求解势问题的宏单元法[J].
数值计算与计算机应用, 2007, 28(3): 179–187.
WANG Zhao-qing, LU Xiao-yang. Macro-element approach based on mean value interpolation for solving potential problems[J]. Journal on Numerical Methods and Computer Applications, 2007, 28(3): 179–187. |
| [10] |
宋晓光, 刘沈如, 张景涛. 应用于弹性问题的重心坐标有限元法[J].
固体力学学报, 2010, 31(3): 310–318.
SONG Xiao-guang, LIU Shen-ru, ZHANG Jing-tao. Barycentric coordinates finite element method and the application in elasticity[J]. Chinese Journal of Solid Mechanics, 2010, 31(3): 310–318. |
| [11] | MOUSAVI S E, XIAO H, SUKUMAR N. Generalized Gaussian quadrature rules on arbitrary polygons[J]. International Journal for Numerical Methods in Engineering, 2010, 82(1): 99–113. |
| [12] |
丁胜勇, 邵国建. Wachspress型多边形有限元法积分方案[J].
东南大学学报:自然科学版, 2013, 43(1): 216–220.
DING Sheng-yong, SHAO Guo-jian. Integration scheme of Wachspress interpolation polygonal finite element method[J]. Journal of Southeast University:Natural Science Edition, 2013, 43(1): 216–220. |
| [13] | NATARAJAN S, OOI E T, CHIONG I, et al. Convergence and accuracy of displacement based finite element formulations over arbitrary polygons:Laplace interpolants, strain smoothing and scaled boundary polygon formulation[J]. Finite Elements in Analysis and Design, 2014, 85(4): 101–122. |
| [14] |
罗先启, 吴晓铭, 童富果, 等. 基于挤压边墙技术水布垭面板堆石坝应力-应变研究[J].
岩石力学与工程学报, 2005, 24(13): 2342–2349.
LUO Xian-qi, WU Xiao-ming, TONG Fu-guo, et al. Research on the stress-strain of shuibuya concrete face rockfill dam based on the concrete crushing-type side wall technology[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(13): 2342–2349. DOI:10.3321/j.issn:1000-6915.2005.13.024 |
| [15] |
童富果, 田斌, 孙大伟. 挤压边墙对高面板坝应力-变形影响分析[C]//中国水力发电工程学会水文泥沙专业委员会2007年学术年会暨高面板技术研讨会. 昆明: [s. n. ], 2007.
TONG Fu-guo, TIAN Bin, SUN Da-wei. The stress and deformation of high concrete face rockfill dam for impact analysis of extrusion sidewall[C]//Journal of Hydrologic and Sediment Professional Committee of China Hydropower Engineering Institute. Academic Conference and High Panel Technology Seminar Papers Album in 2007. Kunming:[s.n.], 2007. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-IGST200712001019.htm |
| [16] | OOI E T, SONG C, TIN-LOI F. A scaled boundary polygon formulation for elasto-plastic analyses[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 268(2014): 905–937. |
| [17] | CHOPRA A K, CHAKRABARTI P. The Koyna earthquake and the damage to Koyna dam[J]. Bulletin of the Seismological Society of America, 1973, 63(2): 381–397. |
| [18] | HALL J F. The dynamic and earthquake behaviour of concrete dams:review of experimental behaviour and observational evidence[J]. Soil Dynamics and Earthquake Engineering, 1988, 7(2): 58–121. DOI:10.1016/S0267-7261(88)80001-0 |
| [19] | LEE J, FENVES G L. A plastic-damage concrete model for earthquake analysis of dams[J]. Earthquake Engineering and Structural Dynamics, 1998, 27(9): 937–956. DOI:10.1002/(ISSN)1096-9845 |
| [20] | CALAYIR Y, KARATON M. A continuum damage concrete model for earthquake analysis of concrete gravity dam-reservoir systems[J]. Soil Dynamics and Earthquake Engineering, 2005, 25(11): 857–869. DOI:10.1016/j.soildyn.2005.05.003 |
| [21] | ZHANG S, WANG G, YU X. Seismic cracking analysis of concrete gravity dams with initial cracks using the extended finite element method[J]. Engineering Structures, 2013, 56(6): 528–543. |
| [22] | WANG C, ZHANG S, SUN B, et al. Methodology for estimating probability of dynamical system's failure for concrete gravity dam[J]. Journal of Central South University, 2014, 21(2014): 775–789. |
| [23] | XU H, ZOU D, KONG X, et al. Study on the effects of hydrodynamic pressure on the dynamic stresses in slabs of high CFRD based on the scaled boundary finite-element method[J]. Soil Dynamics and Earthquake Engineering, 2016, 88(2016): 223–236. |
| [24] | XU B, ZOU D, KONG X, et al. Dynamic damageevaluation on the slabs of the concrete faced rockfill dam with the plastic-damage model[J]. Computers and Geotechnics, 2015, 65(65): 258–265. |
| [25] | ZOU D, XU B, KONG X, et al. Numerical simulation of the seismic response of the Zipingpu concrete face rockfill dam during the Wenchuan earthquake based on a generalized plasticity model[J]. Computers and Geotechnics, 2013, 49(2013): 111–122. |
| [26] |
刘京茂, 孔宪京, 邹德高. 接触面模型对面板与垫层间接触变形及面板应力的影响[J].
岩土工程学报, 2015, 37(4): 700–710.
LIU Jing-mao, KONG Xian-jing, ZOU De-gao. Interface behavior between slab and cushion layer and its effects on slab stress of concrete faced rock-fill dam[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(4): 700–710. DOI:10.11779/CJGE201504016 |