潮流能作为一种清洁可再生能源, 具有蕴藏量大、分布广、周期性强和能量密度大等优点, 全球可供开发量达到500~1 000 TW·h/年[1], 仅中国沿海潮流能平均功率达到1.4×107 kW[2], 具有很大的开发利用价值.相对于垂直轴潮流能机组, 水平轴螺旋桨式潮流发电系统具有良好的能量捕获效率[3-4], 已经成为国内外的热门研究对象.
由于潮流能发电机组处于水下环境, 本文采用单级耦合增速器来缩小体积, 优化流场特性.考虑常规发电机中励磁所需集电环和电刷装置的高故障率, 采用永磁同步发电机(permanent magnet synchronous generator, PMSG), 避免了绕组损耗, 效率高, 结构简单, 体积小[5].针对百十千瓦级功率控制, 采用二极管整流-斩波-逆变结构, 开展发电机转速与并网控制.
潮流发电系统在水下环境的工作状态十分复杂, 本身是一个非线性、强干扰系统[6-7];另外, 水下环境的相关信号参数的精确测量是十分困难的.为了确保发电系统的长期安全、稳定、高效运行, 对功率和并网控制提出了很高的要求.
本文以浙江大学潮流发电系统为研究对象, 建立从叶轮到发电机的数学模型.针对叶轮处流速精确测量的困难性, 提出基于流速预测的PMSG转速控制来实现低流速下的最大功率捕获.考虑直接桨距角控制中存在的非线性、计算量庞大的问题, 采用基于功率反馈的变桨距控制, 实现超流速下的功率稳定控制, 确保整个系统长期安全稳定运行.采用直流母线电压控制与有功无功电流解耦来实现并网运行控制研究.
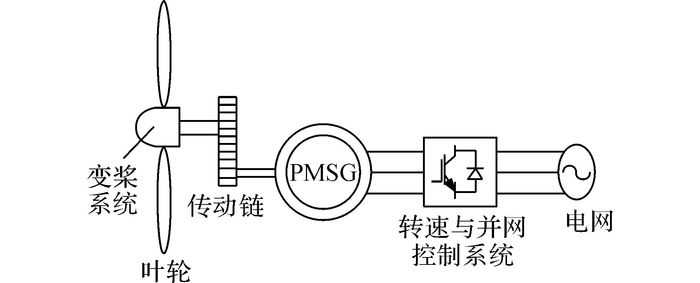
1 数学模型 1.1 系统描述如图 1所示为潮流发电系统方案配置图, 能量从潮流能转换至电网电能, 主要流经叶轮、传动链、永磁同步发电机、电力电子系统(转速控制系统、并网控制系统)、电网.功率的控制主要由变桨系统和发电机转速控制系统完成, 电能并网由并网控制系统完成.
|
图 1 潮流发电系统方案配置图 Fig. 1 Structure of tidal current energy conversion system |
叶轮的转矩为
| $ T = T\left( {\beta ,v,{\omega _{\rm{r}}}} \right). $ | (1) |
式中:β为桨距角, v为潮流流速, ωr为叶轮旋转角速度.
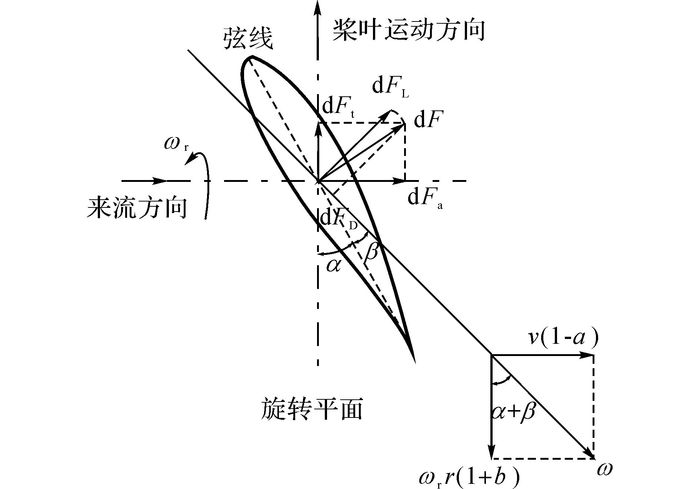
根据叶素理论(BET), 可得叶片微元(叶素)受力如图 2所示[8].图中, dF为叶素所受合力, dFL为叶素升力, dFD为叶素阻力, dFt为旋转方向叶素切向力, dFa为叶素轴向力(推力), ω为水流相对于叶素的速度, α为叶素攻角, r为叶素到轮毂中心的距离.
|
图 2 叶素受力分析 Fig. 2 Blade element force analysis |
考虑漩涡运动, 根据涡流理论引入轴向流动干扰因子a、切向流动干扰因子b, 可得第i个叶素上攻角为
| $ \alpha \left( i \right) = \arctan \left[ {\frac{{1 - a}}{{1 + b}} \cdot \frac{1}{{{\lambda _{\rm{r}}}\left( i \right)}}} \right] - \beta \left( i \right), $ | (2) |
| $ \omega \left( i \right) = v\sqrt {{{\left( {1 - a} \right)}^2} + \lambda _{\rm{r}}^2\left( i \right){{\left( {1 + b} \right)}^2}} . $ | (3) |
式中:第i个叶素的叶尖速比λr(i)=r(i)·ωr/v, r(i)为第i个叶素到轮毂中心的距离.
第i个叶素旋转方向上的切向力为
| $ \begin{array}{l} {\rm{d}}{F_{\rm{t}}}\left( i \right) = \frac{1}{2}\rho c\left( i \right){\omega ^2}\left( i \right){C_{\rm{L}}}\left( \alpha \right)\sin \left[ {\beta \left( i \right) + \alpha \left( i \right)} \right] \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\left[ {1 - \frac{{{C_{\rm{D}}}\left( \alpha \right)}}{{{C_{\rm{L}}}\left( \alpha \right)}}\cot \left( {\beta \left( i \right) + \alpha \left( i \right)} \right)} \right]{\rm{d}}r. \end{array} $ | (4) |
式中:ρ为潮流密度, CL(α)为升力系数, CD(α)为阻力系数.对于一个给定的叶片, CL(α)和CD(α)与α的关系是固定的[9].
第i个叶素的转矩为
| $ {\rm{d}}T\left( i \right) = r\left( i \right){\rm{d}}{F_{\rm{t}}}\left( i \right). $ | (5) |
叶轮的总转矩为
| $ T = N\int {r\left( i \right){\rm{d}}{F_{\rm{t}}}\left( i \right)} . $ | (6) |
式中:N为叶片数.
1.3 传动链模型传动链是刚性的, 主要组成部分是单级耦合增速器, 低速轴运动方程为
| $ {J_{\rm{r}}}\frac{{{\rm{d}}{\omega _{\rm{r}}}}}{{{\rm{d}}t}} = T - {T_{{\rm{ls}}}} - {K_{\rm{r}}}{\omega _{\rm{r}}}. $ | (7) |
式中:Jr为低速轴转动惯量, Tls为低速轴转矩, Kr为低速轴摩擦阻尼系数.
高速轴运动方程为
| $ {J_{\rm{g}}}\frac{{{\rm{d}}{\mathit{\Omega }_{\rm{g}}}}}{{{\rm{d}}t}} = {T_{{\rm{hs}}}} - {T_{{\rm{em}}}} - {K_{\rm{g}}}{\mathit{\Omega }_{\rm{g}}}. $ | (8) |
式中:Jg为发电机转子转动惯量, Ωg为发电机转子转速, Ths为高速轴转矩, Tem为发电机电磁转矩, Kg为发电机转子轴摩擦阻尼系数.
单级传动比n为
| $ n = \frac{{{T_{{\rm{ls}}}}}}{{{T_{{\rm{hs}}}}}} = \frac{{{\mathit{\Omega }_{\rm{g}}}}}{{{\omega _{\rm{r}}}}}. $ | (9) |
假设定子绕组正弦分布, 电磁对称, 忽略铁损且磁路未饱和, 将PMSG模型简化, 并通过Park变换实现(a, b, c)到(d, q)坐标系的转化, 当PMSG并网发电时, 模型为
| $ \left. \begin{array}{l} {u_d} = - R{i_d} - {L_d}\frac{{{\rm{d}}{i_d}}}{{{\rm{d}}t}} + {L_q}{p_{\rm{m}}}{\mathit{\Omega }_{\rm{g}}}{i_q},\\ {u_q} = - R{i_q} - {L_q}\frac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}} - \left( {{L_d}{i_d} + {\psi _{\rm{m}}}} \right){p_{\rm{m}}}{\mathit{\Omega }_{\rm{g}}}. \end{array} \right\} $ | (10) |
式中:ud、uq分别为d轴和q轴的定子电压分量;R为定子电阻;Ld、Lq分别为d轴和q轴的电感;id、iq分别为d轴和q轴的定子电流分量;pm为极对数;ψm为转子磁链, 表示转子磁钢在定子上的耦合磁链.
发电机电磁转矩方程为
| $ {T_{{\rm{em}}}} = {p_{\rm{m}}}\left[ {\left( {{L_d} - {L_q}} \right){i_d}{i_q} + {\psi _{\rm{m}}}{i_q}} \right]. $ | (11) |
潮流发电系统的功率控制主要分为以下2个阶段.1) 当流速低于额定流速时, 开展最大能量捕获.该阶段保持桨距角为最佳捕获效率, 主要进行发电机的转速控制, 改变叶尖速比.2) 当流速高于额定流速时, 限定功率输出, 维持功率在额定值附近.该阶段主要进行变桨距控制, 改变桨距角, 从而改变能量捕获效率.
2.1 潮流流速预测在整个潮流发电系统运行过程中, 流速信号对于控制系统都是一个至关重要的输入量.潮流发电机组置于水下环境, 传统测量流速方法一般只能测出前方一定距离的流场流速, 叶轮处流速的精确测量是十分困难的.潮流具有很强的周期性和稳定性, 结合实际试验所用超声多普勒流速流向仪, 提出叶轮处潮流流速预测方法.
流速流向仪与潮流发电机组的相对安装关系如图 3所示, 所采用的流速流向仪为单点式测量.为了降低潮流中湍流作用对流速测量的干扰, 采用在流速流向仪采样频率次数时间内, 对流速进行平均化处理, 如下:

|
图 3 流速流向仪安转位置示意图 Fig. 3 Layout schematic of acoustic Doppler velocimeter |
| $ {v_{\rm{d}}}\left( t \right) = \frac{1}{f}\sum\limits_{j = 1}^f {{v_{{\rm{d}}j}}} . $ | (12) |
式中:vd(t)为某时刻t平均化后的探测流速, f为时刻t-1到时刻t这1 s内的流速采集数量, vdj为流速流向仪实时探测的流速.
定义在T0时间段内的平均流速为
| $ {{\bar v}_{\rm{d}}}\left( t \right) = \frac{1}{{{T_0}}}\sum\limits_{k = 1}^{{T_0}} {{v_{\rm{d}}}\left( {t - {T_0} + k} \right)} . $ | (13) |
式中:t≥T0;vd(t)为T0时间段内的平均流速;vd(t-T0+k)为式(12) 中的平均化后的流速;T0由流速流向仪与发电机组的相对位置与当前潮流流速决定, T0=L0/vd(t)并向下取整, 其中L0为流速流向仪与发电系统轮毂中心的距离.
根据Δvd(t)=vd(t)-vd(t-T0), 预测潮流流速的变化趋势.叶轮轮毂中心处的实时流速可以根据下式得到:
| $ v\left( t \right) = {v_{\rm{d}}}\left( t \right) - \Delta {{\bar v}_{\rm{d}}}\left( t \right). $ | (14) |
式中:t≥2T.
2.2 PMSG转速控制对于一个翼型给定的桨叶, 捕能系数曲线随着桨距角而变化, 可以通过叶素动量理论计算获得.当潮流流速低于额定流速时, 保持叶片角度为能量捕获效率最高的最佳桨距角.
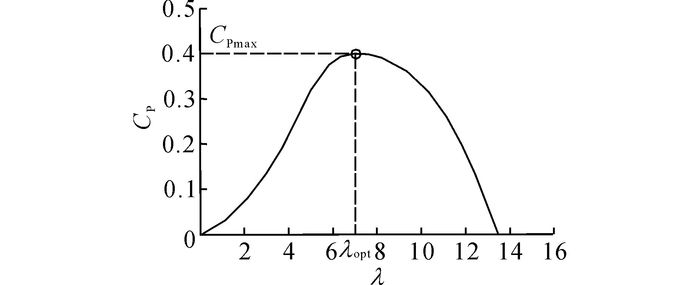
如图 4所示为最佳桨距角时的CP-λ曲线.图中, CP为捕能系数, λ为桨叶的叶尖速比.由图 4可知, 当λ=λopt时, CP达到最大值CPmax,
|
图 4 最佳桨距角的捕能特性曲线 Fig. 4 Curve of power characteristic at best pitch angle |
| $ \lambda = \frac{{{\omega _{\rm{r}}}{r_{\rm{b}}}}}{v}. $ | (15) |
式中:rb为叶轮的旋转半径.
由式(9)、(15) 可得
| $ {\mathit{\Omega }_{{\rm{g}} - {\rm{opt}}}} = n\frac{{{\lambda _{{\rm{opt}}}}}}{{{r_{\rm{b}}}}}v. $ | (16) |
通过所述的流速预测方法获得流速信号输入, 控制发电机转速跟随Ωg-opt, 可以实现最大能量捕获控制.
联立式(7)~(9), 可得
| $ \left( {\frac{{{J_{\rm{r}}}}}{{{n^2}}} + {J_{\rm{g}}}} \right)\frac{{{\rm{d}}{\mathit{\Omega }_{\rm{g}}}}}{{{\rm{d}}t}} = - \left( {\frac{{{K_{\rm{r}}}}}{{{n^2}}} + {K_{\rm{g}}}} \right){\mathit{\Omega }_{\rm{g}}} + \frac{1}{n}T - {T_{{\rm{em}}}}. $ | (17) |
由式(17) 可知, 该力矩平衡方程中, Ωg为被控对象;发电机电磁转矩Tem为控制量, 通过DC-DC斩波器来改变发电机d、q轴电压、电流来控制;T为叶轮输入力矩, 可以视为外部输入扰动, 精准的叶轮模型可以使控制量计算更加精确.
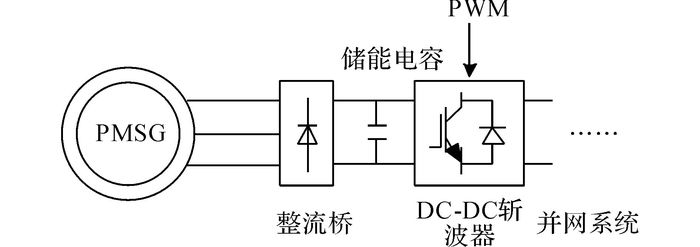
如图 5所示为PMSG的转速控制系统结构图.直流电流和发电机在(d, q)坐标系中电压电流会随着DC-DC斩波器状态的改变而改变[10], 本质是改变发电机终端的等效电阻.PMSG转速控制策略如图 6所示.
|
图 5 PMSG的转速控制系统结构图 Fig. 5 Structure of PMSG speed control system |
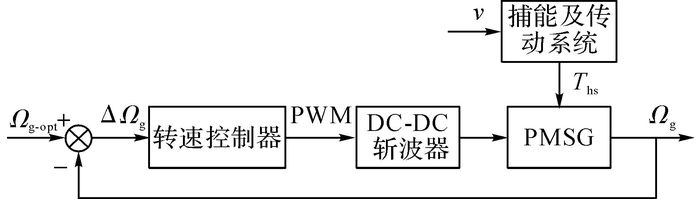
|
图 6 PMSG转速控制策略 Fig. 6 Control strategy of PMSG speed control system |
当潮流流速高于额定值时, 功率会超出额定值, 此时无论对机械系统还是电气系统, 都产生很大的负荷.为了系统的安全, 需要限定发电系统的功率输出.一般采用控制桨距角来限制叶轮的能量捕获效率.额定流速以下的最佳桨距角一般约为0°, 当高于额定流速时, 桨距角随着流速的增大而增大.不同桨距角的CP-λ曲线可以根据叶片翼型, 通过叶素动量理论计算.根据测量变换所得的ωr、v以及CP-λ曲线来反推目标桨距角.反推计算中出现的非线性和数据量庞大等问题会使直接桨距角控制的控制程序十分繁琐, 占用非常多的系统资源.一般采用直接功率反馈控制, 实现超流速下的功率稳定控制, 控制策略如图 7所示.图中, P0为额定功率, P为发电机输出功率, β*为桨距角控制目标值.
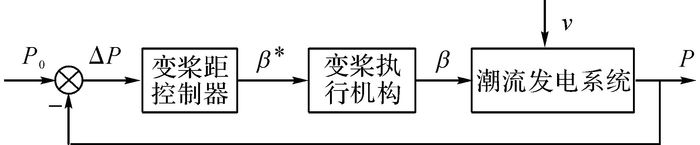
|
图 7 变桨距控制原理框图 Fig. 7 Block diagram of pitch control |
并网系统测量电网侧的电压、电流、频率和相位等相关参数, 使输出电能与电网侧匹配, 确保输出电能的质量符合标准.如图 8所示为潮流发电并网系统结构图.当潮流发电系统的叶轮转速达到一定值, 经过整流控制后直流母线端电压到达目标值时, DSP主控单元发送并网信号, 完成潮流发电系统并网功能.当潮流发电系统端或者电网侧发生故障, 达不到并网要求时, 主控单元发送脱网信号, 实现与电网的分离.当潮流流速过大, 过功率导致超出控制范围时, DSP主控单元控制IGBT, 调节卸荷负载的并入, 优化系统控制, 并起到保护作用.
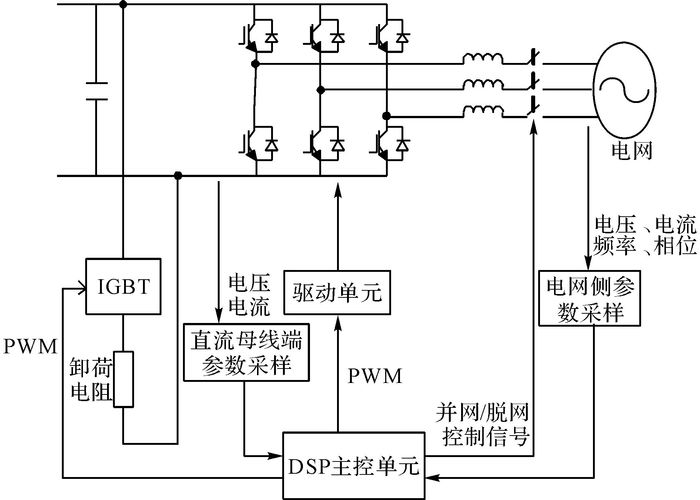
|
图 8 潮流发电并网系统结构图 Fig. 8 Structure of grid-connected system for tidal current energy conversion system |
如图 9所示为并网系统的控制原理图, 网侧有功功率和无功功率通过内部电流环igq、igd进行解耦控制[11].图中, VDC*为直流母线端电压参考值, 为结合DC-DC斩波器控制的目标值;VDC为直流母线端电压测量值;igd*为无功电流参考值, 采用PI控制器获得有功电流参考值igq*, 一般取常值igd*=0;Pmq和Pmd为电流控制器输出的脉宽调制因子;igA、igB、igC为并网系统输出到电网的三相电流;θ为电压相位角;通过Park变换可得igq、igd,

|
图 9 并网系统控制原理图 Fig. 9 Control schematic of grid-connected system |
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{i_{{\rm{g}}q}}}\\ {{i_{{\rm{g}}d}}} \end{array}} \right] = \\ \frac{2}{3}\left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\cos \left( {\theta - \frac{2}{3}{\rm{\pi }}} \right)}&{\cos \left( {\theta + \frac{2}{3}{\rm{\pi }}} \right)}\\ {\sin \theta }&{\sin \left( {\theta - \frac{2}{3}{\rm{\pi }}} \right)}&{\sin \left( {\theta + \frac{2}{3}{\rm{\pi }}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_{{\rm{g}}A}}}\\ {{i_{{\rm{g}}B}}}\\ {{i_{{\rm{g}}C}}} \end{array}} \right]. \end{array} $ | (18) |
采用额定流速为2 m/s, 额定功率为60 kW的一组叶片, 设计最佳桨距角为0°, 叶轮最佳叶尖速比为7, 置于浙江大学潮流发电机组上, 选定舟山海域开展海试试验研究.如图 10所示为浙江大学海上潮流发电系统.
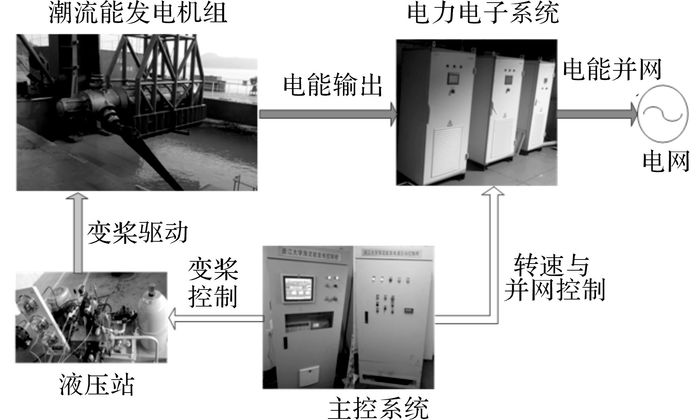
|
图 10 浙江大学海上潮流发电系统 Fig. 10 Tidal current energy conversion system of Zhejiang University |
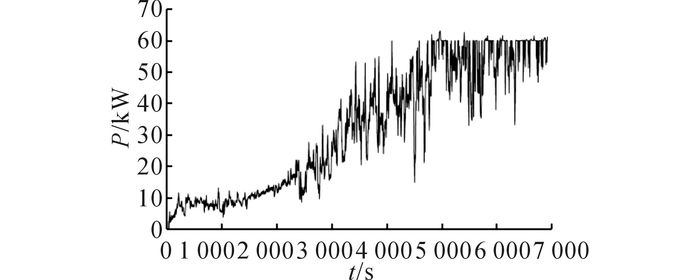
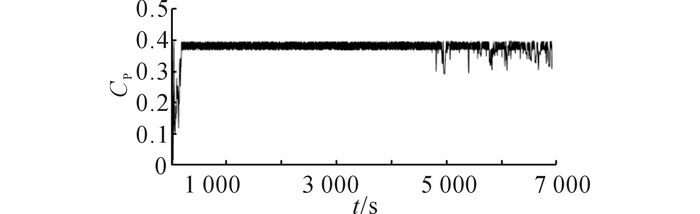
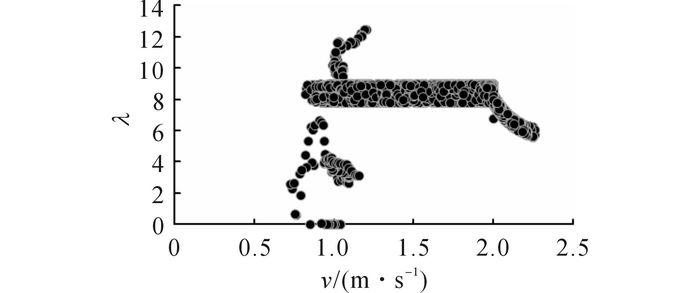
选取浙江大学海上潮流发电系统运行周期内的一组数据进行分析.如图 11所示为该运行时间段内的潮流流速曲线.根据测量点测量流速, 采用潮流流速预测方法, 获得叶轮轮毂处的流速, 为控制系统提供更精确的信号输入值.如图 12所示为发电机输出功率曲线.可知, 潮流发电机组的启动流速约为0.8 m/s, 当流速超过额定流速时, 变桨距控制能够将输出功率限定在额定功率附近.由图 13可知, 在低于额定流速的情况下, 叶轮能量捕获系数能够维持在0.37以上.如图 14所示为不同流速下的叶尖速比曲线, 经试验装置转速传感器测得发电机转速以及测量流速所预测的轮毂处流速数据.由式(9)、(15) 可得流速与叶尖速比的关系曲线.根据图 14可知, 在低于额定流速的情况下, 叶轮能够维持叶尖速比约为8;当流速高于额定流速时, 叶轮叶尖速比开始下降, 远离最佳叶尖速比.

|
图 11 潮流流速曲线 Fig. 11 Curves of tidal current velocity |
|
图 12 发电机输出功率曲线 Fig. 12 Output power curve of PMSG |
|
图 13 能量捕获系数曲线 Fig. 13 Curve of CP |
|
图 14 不同流速下的叶尖速比 Fig. 14 Tip speed ratio for different tidal current speeds |
结合图 11~14可知, 在低于额定流速期间, 基于流速预测的PMSG转速控制能够较好地实现最大功率捕获;在高于额定流速期间, 基于功率反馈的变桨距控制能够有效地维持功率在额定值附近, 稳定功率输出, 避免超负荷运行状态.根据图 12~14可知, 当潮流流速到达启动流速的启动阶段时, 发电机功率P、CP、λ与最佳值相差较远, 这是因为在启动阶段的转速较低, 导致λ偏离λopt较大.在进一步的工作中, 可以结合机组特性, 在流速到达启动流速前, 进行预变桨控制处理, 减小启动力矩, 使机组更早启动, 并缩短转速上升期, 从而缩小启动阶段的误差.
如图 15所示为并网系统电网侧电压u的变化情况, 为并网装置网侧实测曲线.可知, 并网三相电压曲线的抖动较小, 呈现良好的正弦波特性.如图 16、17所示分别为并网系统有功功率Pg和无功功率Qg的变化情况.可知, 并网系统能够有效地将电能馈入电网.结合图 15~17可知, 并网系统具有良好的并网控制特性和较高的输出电能质量.

|
图 15 并网系统电网侧电压曲线 Fig. 15 Voltage curves of grid-connected system in grid side |

|
图 16 并网系统有功功率曲线 Fig. 16 Active power curve of grid-connected system |

|
图 17 并网系统无功功率曲线 Fig. 17 Reactive power curve of grid-connected system |
(1) 以可变桨叶轮-单级增速-永磁同步发电机为机械传动结构的力矩传递数学模型, 考虑了漩涡运动与转轴阻尼, 具有一定的准确性.
(2) 基于流速预测的PMSG转速控制能够有效地实现低于额定流速下的最大功率捕获.
(3) 在超额定流速下, 基于功率反馈的变桨距控制能够较好地限定功率输出, 保护系统安全.
(4) 采用直流母线电压控制与有功无功电流解耦相结合的并网系统具有良好的并网控制特性和较高的输出电能质量.
(5) 考虑试验装置的加工精度问题, 控制过程中的一些参数不确定性, 工作环境与系统自身复杂性导致的负载扰动、参数摄动等非线性动态, 使系统运行过程中的叶尖速比、捕能系数与设计理想值存在误差.后期将针对系统的状态观测与自适应控制进行深入的研究.
| [1] | CHARLIER R H. A "sleeper" awakes:tidal current power[J]. Renewable and Sustainable Energy Reviews, 2003, 7(6): 515–529. DOI:10.1016/S1364-0321(03)00079-0 |
| [2] |
王传崑, 施伟勇. 中国海洋能资源的储量及其评价[C]//中国可再生能源学会海洋能专业委员会第一届学术讨论会文集. 杭州: 国家海洋技术中心, 2008: 169-179.
WANG Chuan-kun, SHI Wei-yong. Evaluation of China ocean energy reserves[C]//Proceedings of the First Conference of China Marine Renewable Energy Society. Hangzhou:National Ocean Technology Center Press, 2008:169-179. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-KZSH200803001020.htm |
| [3] |
刘宏伟. 水平轴海流能发电机械关键技术研究[D]. 杭州: 浙江大学, 2009.
LIU Hong-wei. Study on the key technologies of horizontal axis marine current turbine's mechanics[D]. Hangzhou:Zhejiang University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10335-2010055991.htm |
| [4] |
马舜. 水平轴潮流能转换系统能量转换率及功率控制研究[D]. 杭州: 浙江大学, 2011.
MA Shun. Study on energy conversion efficiency and power control of horizontal axis tidal current energy conversion systems[D]. Hangzhou:Zhejiang University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10335-1012321290.htm |
| [5] |
张新燕, 王维庆. 大型直驱永磁风力发电机及其并网运行研究[J].
太阳能学报, 2008, 29(04): 412–416.
ZHANG Xin-yan, WANG Wei-qing. Study on direct-driven permanent wind turbine generator and on-grid operation[J]. Acta Energiae Solaris Sinica, 2008, 29(04): 412–416. DOI:10.3321/j.issn:0254-0096.2008.04.007 |
| [6] | MYERS L, BAHAJ A S. Simulated electrical power potential harnessed by marine current turbine arrays in the Alderney Race[J]. Renewable Energy, 2005, 30(11): 1713–1731. DOI:10.1016/j.renene.2005.02.008 |
| [7] | GU Y J, YIN X X, LIU H W, et al. Fuzzy terminal sliding mode control for extracting maximum marine current energy[J]. Energy, 2015, 90: 258–265. DOI:10.1016/j.energy.2015.06.068 |
| [8] | BURTON T, JENKINS N, SHARPE D, et al. Wind energy handbook[M]. New York: Wiley, 2011: 60-65. |
| [9] | MUNTEANU I, CUTULULIS N A, BRATCU A I, et al. Optimal control of wind energy systems[M]. London: Springer, 2008: 37-42. |
| [10] |
石茂顺, 李伟, 林勇刚, 等. 海流能发电系统的负载控制仿真研究[J].
太阳能学报, 2014, 35(01): 119–124.
SHI Mao-shun, LI Wei, LIN Yong-gang, et al. Study on the simulation of the load control for the marine current energy power system[J]. Acta Energiae Solaris Sinica, 2014, 35(01): 119–124. DOI:10.3969/j.issn.0254-0096.2014.01.020 |
| [11] | POLLER M A. Doubly-fed induction machine models for stability assessment of wind farms[C]//Proceedings of 2003 IEEE Power Tech Conference. Bologna:IEEE, 2003. https://core.ac.uk/display/21568721 |



