2. 南通锻压设备股份有限公司, 江苏 南通 226578
2. Nantong Metalforming Equipment Limited Company, Nantong 226578, China
对于液压机的压力控制而言, 目前工业界普遍采用的方案是利用比例溢流阀调节主缸内的压力[1-2]:对于压力控制要求不高的场合, 只需对比例溢流阀进行开环控制;对于压力控制要求相对较高的场合, 通常需要对比例溢流阀进行闭环控制.此外, 有一些场合采用比例方向阀来调节液压机的压制力, 这种方式往往需要对主缸内的压力进行闭环控制.在PID控制器的基础上引入某种非线性调节机制对其参数进行在线调节是一种比较合理的策略, 例如广泛应用于液压机压力控制场合的模糊PID控制器[3-4]等.近年来, 随着非线性控制理论的蓬勃发展, 各种非线性控制策略被应用于电液系统的压力控制:例如反馈线性化[5]、鲁棒控制[6]和自适应控制[7]等.
对于液压机的运动控制而言, 需要解决以下2个关键问题:1) 外负载的建模及补偿, 这里的外负载主要包括工件变形产生的变形力以及摩擦力等;2) 运动控制策略的选择以克服电液系统的强非线性特性以及参数不确定性.对于外负载的建模及补偿问题, 国内外学者进行了广泛而深入的研究, 例如锻压变形力的理论计算法[8]、锻压变形力的线性建模法[9]、锻压变形力的模糊建模法[10]、锻压变形力的神经网络建模法[11]、锻压变形力的支持向量机(SVM)建模法[12]等;此外, 基于扰动观测器[13-14]的外负载补偿法是一种被证明了的比较有效的手段.对于液压机电液系统的运动控制策略选择问题, 国内外研究中涉及到的控制方法主要有传统的PID控制[15]、模糊PID控制[16]以及鲁棒控制[17]、自适应控制[18]、自适应鲁棒控制[19]等非线性控制策略.
本文主要针对液压机在慢速加压阶段的压力、运动控制策略展开研究, 提出非线性级联控制器来解决液压机慢速加压阶段的位移、压力复合控制问题.提出非线性级联控制器的压力控制环,采用扰动观测器对油液体积弹性模量、伺服比例阀流量增益、液压缸泄漏系数等参数的不确定性所产生的集中扰动进行在线估计及补偿, 以克服系统参数不确定性对压力控制带来的显著影响, 利用无源性定理证明了压力控制环的稳定性.考虑到系统参数不确定性以及各种外负载对滑块位移控制带来的不利影响, 提出非线性级联控制器的位移控制环基于滑模控制而设计.在慢速加压阶段, 液压机先进行位移控制;当滑块位移满足切换条件之后, 液压机由位移控制模式自动切换到压力控制模式.实验结果表明, 本文提出的非线性级联控制器能够使得液压机在慢速加压阶段实现高精度、平稳的位移控制和高精度、平稳的压力控制, 并且实现这两种控制模式之间的平稳切换.
1 工作原理介绍及数学建模 1.1 工作原理介绍研究的液压机在慢速加压阶段的原理如图 1所示.来自液压源的高压油通过伺服比例阀进入主缸, 驱动滑块带着上模慢速下行, 通过控制伺服比例阀的开口可以控制滑块下行的速度;回程缸内的液压油通过支撑阀(溢流阀)回到油箱, 支撑阀的作用是提供一定的背压, 保证滑块不会在重力的作用下自动下滑.当上模接触到工件以后, 控制模式由位移控制切换到压力控制:通过伺服比例阀控制主缸的加压过程, 保证产品的加工质量.
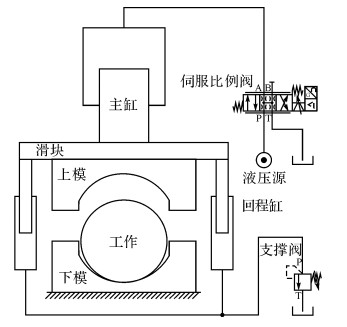
|
图 1 液压机在慢速加压阶段的原理图 Fig. 1 Schematic of hydraulic press during slow compression stage |
根据牛顿第二定律可知, 滑块在慢速下行过程中的动力学方程可以表示为
| $ m{{\ddot x}_{\rm{L}}} = {p_1}{A_1} - {p_2}{A_2} + G - {F_{\rm{f}}} - {F_{\rm{d}}}. $ | (1) |
式中:m为滑块的等效质量, xL为滑块的位移, p1为主缸内的压力, A1为主缸的作用面积, p2为回程缸内的压力, A2为回程缸的作用面积, G为滑块的等效重力, Ff为滑块受到的摩擦力, Fd为滑块受到的工件变形力.
滑块在慢速下行过程中, 上模尚未接触工件, 因此Fd可以认为是0;滑块受到的摩擦力Ff通常可以表示为
| $ {F_{\rm{f}}} = {F_{\rm{c}}}\tanh \left( {{\sigma _1}{{\dot x}_{\rm{L}}}} \right) + {\sigma _2}{{\dot x}_{\rm{L}}}. $ | (2) |
式中:Fc为库仑摩擦力, tanh(·)为双曲正切函数, σ1为一正值, σ2为黏性摩擦系数.
在通常情况下, 滑块在慢速下行过程中回程缸内的压力可以近似为一恒定值.忽略回程缸的压力动态, 仅考虑主缸的压力动态.根据压力容腔的压力公式可知, 主缸的压力动态可以表示为
| $ {p_1} = \frac{{{\beta _{\rm{e}}}}}{{{V_1}}}\left( {{q_V} - {C_{\rm{m}}}{p_1} - {A_1}{{\dot x}_{\rm{L}}}} \right). $ | (3) |
式中:βe为油液体积弹性模量;V1为主缸的控制容积,V1=Vp1+A1xL,其中Vp1为主缸的死容积;qV为通过伺服比例阀进入主缸的流量;Cm为主缸的泄漏系数.
根据节流小孔的流量公式可知, qV可用下式表示:
| $ \left. \begin{array}{l} {q_V} = {k_{\rm{q}}}{x_{\rm{v}}}\sqrt {{p_{\rm{s}}} - {p_{\rm{l}}}} ,{x_{\rm{v}}} \ge 0;\\ {q_V} = {k_{\rm{q}}}{x_{\rm{v}}}\sqrt {{p_{\rm{l}}} - {p_{\rm{r}}}} ,{x_{\rm{v}}} < 0. \end{array} \right\} $ | (4) |
式中:kq为伺服比例阀的流量增益, xv为伺服比例阀的阀芯位移, ps为液压源的供油压力, pr为油箱的回油压力.
一般而言, 液压机在慢速加压阶段所期望的系统频响远小于伺服比例阀的固有频率.伺服比例阀的阀芯动态可以简单地近似为
| $ {x_{\rm{v}}} = {k_{\rm{v}}}u. $ | (5) |
式中:kv为伺服比例阀的阀芯位移增益, u为伺服比例阀的输入电压.
定义状态变量X=[x1, x2, x3]T=[xL,
| $ \left. \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = \frac{1}{m}\left[ {{A_1}{x_3} - {A_2}{p_2} + G - {F_{\rm{c}}}\tanh \left( {{\sigma _1}{x_2}} \right) - } \right.\\ \;\;\;\;\;\;\;\left. {{\sigma _2}{x_2} - {F_{\rm{d}}}} \right],\\ {{\dot x}_3} = h\left( {{x_1}} \right){\beta _{\rm{e}}}\left[ {{k_{\rm{q}}}g\left( {{x_3}} \right)u - {C_{\rm{m}}}{x_3} - {A_1}{x_2}} \right]. \end{array} \right\} $ | (6) |
式中:
| $ \left. \begin{array}{l} h\left( {{x_1}} \right) = \frac{1}{{{V_{{\rm{pl}}}} + {A_1}{x_1}}};\\ g\left( {{x_3}} \right) = {k_{\rm{v}}}\sqrt {{p_{\rm{s}}} - {x_3}} ,u \ge 0;\\ g\left( {{x_3}} \right) = {k_{\rm{v}}}\sqrt {{x_3} - {p_{\rm{r}}}} ,u < 0. \end{array} \right\} $ | (7) |
对于式(6) 所示的液压机在慢速加压阶段的控制模型, 控制器设计的目的归纳如下.1) 在位移控制阶段, 给定有界的期望位移x1d、期望速度
采用非线性级联控制器来实现上述目的.该非线性级联控制器采用滑模控制设计位移控制环, 以滑块的期望位移x1d、期望速度
给定有界的期望压力x3d及期望压力微分
| $ \left. \begin{array}{l} {{\dot z}_3} = {{\dot x}_3} - {{\dot x}_{3{\rm{d}}}} = h\left( {{x_1}} \right)g\left( {{x_3}} \right){\beta _{{\rm{e}}0}}{k_{{\rm{q}}0}}u + f\left( X \right) + d - {{\dot x}_{3{\rm{d}}}},\\ f\left( X \right) = - h\left( {{x_1}} \right){\beta _{{\rm{e}}0}}{C_{{\rm{m}}0}}{x_3} - h\left( {{x_1}} \right){\beta _{{\rm{e}}0}}{A_1}{x_2}. \end{array} \right\} $ | (8) |
式中:βe0为油液体积弹性模量的估计值, kq0为伺服比例阀流量增益的估计值, Cm0为主缸泄漏系数的估计值, d为由油液体积弹性模量、伺服比例阀流量增益、主缸泄漏系数的参数不确定性所产生的集中扰动.
定义
| $ \left. \begin{array}{l} d = {d_0} + h\left( {{x_1}} \right)g\left( {{x_3}} \right){{\tilde K}_{{\rm{eq}}}}u,\\ {d_0} = - h\left( {{x_1}} \right)\left[ {{{\tilde \beta }_{\rm{e}}}{C_{{\rm{m}}0}}{x_3} + {\beta _{{\rm{e}}0}}{{\tilde C}_{\rm{m}}}{x_3} + {\beta _{\rm{e}}}{{\tilde C}_{\rm{m}}}{x_3} + {{\tilde \beta }_{\rm{e}}}{A_1}{x_2}} \right],\\ {{\tilde K}_{{\rm{eq}}}} = {{\tilde \beta }_{\rm{e}}}{k_{{\rm{q}}0}} + {{\tilde \beta }_{{\rm{e}}0}}{{\tilde k}_{\rm{q}}} + {{\tilde \beta }_{\rm{e}}}{{\tilde k}_{\rm{q}}}. \end{array} \right\} $ | (9) |
设计如下扰动观测器:
| $ \left. \begin{array}{l} \hat d = {k_{\rm{p}}}\left( {{x_3} - {{\hat x}_3}} \right) + {k_{\rm{i}}}\int {\left( {{x_3} - {{\hat x}_3}} \right){\rm{d}}t} ,\\ {{\dot {\hat x}}_3} = h\left( {{x_1}} \right)g\left( {{x_3}} \right){\beta _{{\rm{e}}0}}{k_{{\rm{q}}0}}u + f\left( X \right) + \hat d. \end{array} \right\} $ | (10) |
式中:kp和ki为两个正值,
定义
| $ \tilde d = \frac{{{s^2}}}{{{s^2} + {k_{\rm{p}}}s + {k_{\rm{i}}}}} = G\left( s \right)d. $ | (11) |
式中:s为拉普拉斯算子, G(s)为d到
由式(11) 可知, d到
由式(11) 可得, d到
| $ \hat d = d - \tilde d = \frac{{{k_{\rm{p}}}s + {k_{\rm{i}}}}}{{{s^2} + {k_{\rm{p}}}s + {k_{\rm{i}}}}}d = H\left( s \right)d. $ | (12) |
定理1 对于式(8) 所示的压力跟踪误差动态, 采用式(10) 所示的扰动观测器以及式(13) 所示的控制律, 可以保证系统是稳定的.
| $ \left. \begin{array}{l} u = \frac{{{{\dot x}_{3{\rm{d}}}} - f\left( \mathit{\boldsymbol{X}} \right) - \hat d}}{{h\left( {{x_1}} \right)g\left( {{x_3}} \right){\beta _{{\rm{e0}}}}{k_{{\rm{q}}0}}}} + \frac{v}{{h\left( {{x_1}} \right)g\left( {{x_3}} \right){\beta _{{\rm{e0}}}}{k_{{\rm{q}}0}}}},\\ v = - {c_3}{z_3} - {c_4}\left| {f\left( \mathit{\boldsymbol{X}} \right)} \right|{\mathop{\rm sgn}} \left( {{z_3}} \right). \end{array} \right\} $ | (13) |
式中:c3为任意正值;c4为一正值, 且须满足c4≥|1-H(s)
为了证明定理1, 将式(13) 分别代入式(8)、(9), 可得
| $ {{\dot z}_3} = v - \hat d + d. $ | (14) |
| $ \left. \begin{array}{l} d = \xi - \delta f\left( X \right) - \delta \hat d + \delta v,\\ \xi = \frac{{{{\tilde K}_{{\rm{eq}}}}}}{{{\beta _{{\rm{e0}}}}{k_{{\rm{q}}0}}}}{{\dot x}_{3{\rm{d}}}} + {d_0},\delta = \frac{{{{\tilde K}_{{\rm{eq}}}}}}{{{\beta _{{\rm{e0}}}}{k_{{\rm{q}}0}}}}. \end{array} \right\} $ | (15) |
通过选取合适的βe0及kq0, 可以保证式(15) 中的δ为正值.此外, 由之前的分析可知, d0和
将式(12) 代入式(15), 可得
| $ \hat d = \frac{{H\left( s \right)}}{{1 + \delta H\left( s \right)}}\left[ {\xi - \delta f\left( \mathit{\boldsymbol{X}} \right) + \delta v} \right]. $ | (16) |
将式(15) 代入式(14), 结合式(16), 可得
| $ \begin{array}{l} s{z_3} = v - \hat d + d = \\ \;\;\;\;\left( {1 + \delta } \right)v - \left( {1 + \delta } \right)\hat d + \xi - \delta f\left( \mathit{\boldsymbol{X}} \right) = \\ \;\;\;\;\frac{{1 + \delta }}{{1 + \delta H\left( s \right)}}v + \frac{{1 - H\left( s \right)}}{{1 + \delta H\left( s \right)}}\left[ {\xi - \delta f\left( \mathit{\boldsymbol{X}} \right)} \right]. \end{array} $ | (17) |
定义
| $ s{z_3} = \frac{1}{{1 + \delta H\left( s \right)}}\left[ {\left( {1 + \delta } \right)v + \tilde \xi - {f_2}\left( \mathit{\boldsymbol{X}} \right)} \right]. $ | (18) |
系统(18) 可以用图 2所示的方块图来表示.

|
图 2 系统(18) 的方块图表示 Fig. 2 Block diagram of system shown in (18) |
根据无源性定理[21]可得如下结论.如果图 2中的前向通道传递函数H1(s)=1/[1+δH(s)](1/s)是正实的, 并且反馈通道是严格输入无源的, 那么该反馈系统是有限增益L2稳定的.
根据式(19), 容易证明Re[H1(jw)]的分母大于0;Re[H1(jw)]的分子等于δkpw4>0;因此, Re[H1(jw)]>0.根据正实传递函数的定义[21]可知, H1(s)是正实的.
| $ \begin{array}{l} {H_1}\left( {{\rm{j}}w} \right) = \frac{1}{{1 + \delta H\left( {{\rm{j}}w} \right)}}\frac{1}{{{\rm{j}}w}} = \\ \;\;\;\;\;\frac{{\left( { - {w^2} + {k_{\rm{i}}}} \right) + {\rm{j}}w{k_{\rm{p}}}}}{{ - \left( {1 + \delta } \right){k_{\rm{p}}}{w^2} + {\rm{j}}w\left[ { - {w^2} + \left( {1 + \delta } \right){k_{\rm{i}}}} \right]}}. \end{array} $ | (19) |
由f2(X)的定义, 可知
| $ \left| {{f_2}\left( \mathit{\boldsymbol{X}} \right)} \right| \le {\left| {\left[ {1 - H\left( s \right)} \right]\delta } \right|_\infty }\left| {f\left( \mathit{\boldsymbol{X}} \right)} \right|. $ | (20) |
定义反馈通道的输出y如下:
| $ y = \left( {1 + \delta } \right)\left[ {{c_3}{z_3} + {c_4}\left| {f\left( \mathit{\boldsymbol{X}} \right)} \right|{\mathop{\rm sgn}} \left( {{z_3}} \right)} \right] + {f_2}\left( \mathit{\boldsymbol{X}} \right). $ | (21) |
结合式(20)、(13) 中c4须满足的条件, 可得
| $ \begin{array}{l} {z_3}y = \left( {1 + \delta } \right)\left[ {{c_3}z_3^2 + {c_4}\left| {f\left( \mathit{\boldsymbol{X}} \right)\left\| {\left( {{z_3}} \right)} \right.} \right|} \right] + \\ \;\;\;\;\;\;\;\;{f_2}\left( \mathit{\boldsymbol{X}} \right){z_3} \ge {c_3}z_3^2 + {c_4}\left| {f\left( \mathit{\boldsymbol{X}} \right)\left\| {\left( {{z_3}} \right)} \right.} \right| - \\ \;\;\;\;\;\;\;\;{\left| {\left[ {1 - H\left( s \right)} \right]\delta } \right|_\infty }\left| {f\left( \mathit{\boldsymbol{X}} \right)\left\| {{z_3}} \right.} \right| \ge {c_3}z_3^2. \end{array} $ | (22) |
从式(22) 可知, 反馈通道是严格输入无源[21]的.之前已经证明, 前馈通道H1(s)是正实的;根据无源性定理[21]可知, 图 2所示的系统(18) 是有限增益L2稳定的, 从而证明了定理1的正确性.
2.2 位移控制环的设计给定的滑块期望位移x1d、期望速度
| $ \left. \begin{array}{l} S = {{\dot z}_1} + {c_1}{z_1} = {x_2} - {x_{2{\rm{eq}}}},\\ {x_{2{\rm{eq}}}} = {{\dot x}_{1{\rm{d}}}} - {c_1}{z_1}. \end{array} \right\} $ | (23) |
式中:c1为任意正值.从式(23) 可知, 使z1收敛等效于使S收敛.接下去的工作是使S以确定的瞬态特性收敛.S关于时间的导数如下:
| $ \left. \begin{array}{l} \dot S = {{\dot x}_2} - {{\dot x}_{2{\rm{eq}}}} = \frac{1}{m}\left[ {{A_1}{x_3} - {A_2}{P_2} + G - } \right.\\ \;\;\;\;\;\;\;\left. {{F_{\rm{c}}}\tanh \left( {{\sigma _1}{x_2}} \right) - {\sigma _2}{x_2}{F_{\rm{d}}}} \right] - {{\dot x}_{2{\rm{eq}}}},\\ {{\dot x}_{2{\rm{eq}}}} = {{\ddot x}_{1{\rm{d}}}} - {c_1}{{\dot z}_1}. \end{array} \right\} $ | (24) |
定义θ=[θ1, θ2, θ3, θ4, θ5, θ6]T=[A1/m, A2/m, G/m, Fc/m, σ2/m, Fd/m]T, 对于实际的液压机驱动系统而言, θ必须满足如下条件:
| $ {\theta _i} \in {\mathit{{\Omega }}_{{\theta _i}}} = \left\{ {{\theta _i}:{\theta _{i\min }} \le {\theta _i} \le {\theta _{i\max }}} \right\};i = 1 \sim 6. $ | (25) |
式中:θimin、θimax分别为θi的最小、最大值.
定义
| $ \left. \begin{array}{l} {\alpha _2} = {\alpha _{2{\rm{a}}}} + {\alpha _{2{\rm{s}}}},\\ {\alpha _{2{\rm{a}}}} = \frac{1}{{{{\hat \theta }_1}}}\left[ {{{\hat \theta }_2}{P_2} - {{\hat \theta }_3} + {{\hat \theta }_4}\tanh \left( {{\sigma _1}{x_2}} \right) + {{\hat \theta }_5}{x_2} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {{{\hat \theta }_6} + {{\dot x}_{2{\rm{eq}}}}} \right],\\ {\alpha _{2{\rm{s}}}} = - \frac{1}{{{\theta _{1\min }}}}\left( {\frac{{{B_2}}}{{{\varepsilon _2}}} + {c_2}} \right)S. \end{array} \right\} $ | (26) |
式中:ε2为一个任意小的正值, c2为任意正值.
控制律(26) 中B2的定义如下:
| $ \left. \begin{array}{l} {B_2} = \left| {\mathit{\boldsymbol{\tilde \theta }}_{\max }^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_2}} \right|,\\ {{\mathit{\boldsymbol{\tilde \theta }}}_{\max }} = {\left[ {{\theta _{1\max }} - {\theta _{1\min }}, \cdots ,{\theta _{6\max }} - {\theta _{6\min }}} \right]^{\rm{T}}},\\ {\mathit{\boldsymbol{\varphi }}_2} = {\left[ {{\alpha _{2{\rm{a}}}}, - {P_2},1, - \tanh \left( {{\sigma _1}{x_2}} \right), - {x_2}, - 1} \right]^{\rm{T}}}. \end{array} \right\} $ | (27) |
定义一个半正定的Lyapunov函数V2=S2/2, 将式(26) 代入式(24), 可得[19]
| $ \begin{array}{l} {{\dot V}_2} = S\dot S = - \frac{{{\theta _1}}}{{{\theta _{1\min }}}}{c_2}{S^2} - \frac{{{\theta _1}}}{{{\theta _{1\min }}}}\frac{{{B_2}}}{{{\varepsilon _2}}}{S^2} + {{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}{\mathit{\boldsymbol{\varphi }}_2}S \le \\ \;\;\;\;\;\;\; - {c_2}{S^2} + \frac{{{\varepsilon _2}{B_2}}}{4}. \end{array} $ | (28) |
根据不等式比较定理[22], 可知
| $ \begin{array}{l} {\left| {S\left( t \right)} \right|^2} \le \\ \;\;\;{\left| {S\left( 0 \right)} \right|^2}\exp \left( { - 2{c_2}t} \right) + \frac{{{\varepsilon _2}{B_2}}}{{4{c_2}}}\left[ {1 - \exp \left( { - 2{c_2}t} \right)} \right]. \end{array} $ | (29) |
式中:S(t)、S(0) 分别为t时刻和0时刻滑模面的值.式(29) 意味着滑模面S将渐进收敛到一个比
从之前的设计可知, 压力控制环相当于位移控制环的内环:位移控制的实现依赖于压力控制环的正常工作;如果仅作压力控制, 则不需要位移控制环.对于液压机而言, 在慢速加压阶段, 液压机先进行位移控制;当上模接触工件以后, 需要按照一定的加载规律对工件进行加压, 液压机由位移控制模式切换到压力控制模式.针对该问题, 提出如下切换规则:
| $ \left. \begin{array}{l} {x_{3{\rm{d}}}} = {\alpha _2},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_1} \le {x_{{\rm{up}}}};\\ {x_{3{\rm{d}}}} = \frac{{{x_{3{\rm{e}}}} + {x_{3{\rm{s}}}}}}{2} + \frac{{{x_{3{\rm{e}}}} - {x_{3{\rm{s}}}}}}{2}\sin \left[ {{\rm{\pi lim}}\left( {\frac{{t - {t_{\rm{s}}}}}{{{t_{\rm{e}}} - {t_{\rm{s}}}}}} \right) - {\rm{\pi }}/2} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_1} > {x_{{\rm{up}}}}. \end{array} \right\} $ | (30) |
| $ \left. \begin{array}{l} {x_{3{\rm{d}}}} = {\alpha _2},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_1} \le {x_{{\rm{up}}}};\\ {x_{3{\rm{d}}}} = {x_{3{\rm{s}}}} + \left( {{x_{3{\rm{e}}}} - {x_{3{\rm{s}}}}} \right)\lim \left( {\frac{{t - {t_{\rm{s}}}}}{{{t_{\rm{e}}} - {t_{\rm{s}}}}}} \right),{x_1} > {x_{{\rm{up}}}}. \end{array} \right\} $ | (31) |
式中:xup为液压机位移/压力控制的切换点, 该值通常是已知的;x3e为主缸的最终加压压力;x3s为位移控制切换到压力控制时主缸内的压力;ts为位移控制切换到压力控制的时刻;te为加压结束的时刻.
切换规则(30) 意味着从位移控制切换到压力控制后, 主缸内的压力按照正弦规律逐渐加载;切换规则(31) 意味着主缸内的压力在压力控制阶段按照斜坡规律逐渐加载.式(30)、(31) 中, 函数lim(·)的定义如下:
| $ \left. \begin{array}{l} \lim \left( \cdot \right) = 1, \cdot > 1;\\ \lim \left( \cdot \right) = 0, \cdot < 0;\\ \lim \left( \cdot \right) = \cdot ,其他. \end{array} \right\} $ | (32) |
从式(13) 可知, 对于参数c4, 理论上应该先计算它的下界, 即计算|1-H(s)
对于式(26) 中的鲁棒控制律α2s, 如果令参数c2s满足式(33) 所示的条件, 则可用α2s=-c2sS来代替式(26) 中的鲁棒控制律.
| $ {c_{2{\rm{s}}}} \ge \frac{1}{{{\theta _{1\min }}}}\left( {\frac{{{B_2}}}{{{\varepsilon _2}}} + {c_2}} \right). $ | (33) |
类似地, 对于参数c2s, 理论上应先计算它的下界, 即计算(1/θ1min)(B2/ε2+c2), 然后确定c2s;但是这增加了控制器实施的难度.与上述关于c4的取值类似, 本文不再计算c2s的下界, 直接选择一个较大的、不会使系统产生不稳定的参数.该方式不仅方便、实用, 而且可以大大地减少控制器的计算量.
3 实验研究 3.1 实验设置为了验证所提控制策略的有效性, 搭建图 3~5所示的液压机慢速加压实验平台.滑块被驱动缸带着在机械框架内作往复运动, 模拟液压机的压制动作及回程动作;滑块的模拟加载通过加载缸来实现;集成阀组控制整个实验平台的动作, 主要由伺服比例阀(Rexroth, 4WRREH6VB40L, ±100%控制信号下的频响为80 Hz)、比例溢流阀(Rexroth, DBE6-2X/200Y)等组成;伺服比例阀负责驱动缸无杆腔的控制;比例溢流阀负责在慢速下行过程中控制加载缸无杆腔的压力, 给驱动缸进行模拟加载;溢流阀负责在滑块慢速下行过程中提供一定的背压, 同时为驱动缸有杆腔提供安全保护;电磁球阀为驱动缸有杆腔的进油控制阀, 用于滑块回程;减压阀-单向阀的组合用于在回程过程中给加载缸无杆腔补充一股低压油;泵源负责给实验平台提供一个21×106 Pa的恒压油源;滑块的位移由磁栅尺进行检测;泵源压力、驱动缸无杆腔、有杆腔压力由压力传感器进行检测.实验平台的测控系统基于Simulink Real-Time实时控制系统搭建:上位机负责编写控制程序并进行编译, 编译完成后的代码通过以太网下载到下位机中执行;下位机装有NI公司的PCI-6251数据采集卡, 负责采集实验平台的信号, 根据上位机编译产生的控制程序生成相应的控制信号控制伺服比例阀、比例溢流阀及电磁球阀的动作, 从而实现实验平台的实时控制.在实验过程中, 下位机程序执行的周期设为1 ms.
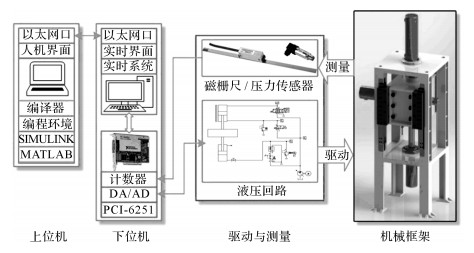
|
图 3 液压机实验平台结构框架 Fig. 3 Frame structure of experiment platform forhydraulic press |

|
图 4 液压机实验平台照片 Fig. 4 Picture of experiment platform for hydraulic press |
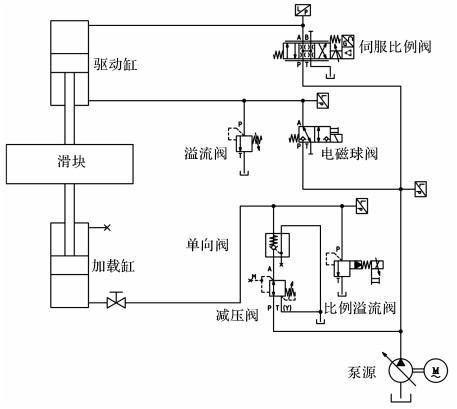
|
图 5 液压机实验平台液压原理图 Fig. 5 Hydraulic diagram of experiment platform for hydraulic press |
对比图 1所示的液压机在慢速加压阶段的原理图以及图 5所示的实验平台液压原理图, 可知:本文所采用的实验平台完全能够模拟液压机在慢速加压过程中的各个动作;驱动缸有杆腔的压力在慢速下行过程中基本不变, 因此驱动缸的内泄漏和外泄漏只与驱动缸无杆腔的压力相关, 用式(6) 来描述实验平台是合理的.综上所述, 用图 3~5所示的实验平台来验证所提非线性级联控制器的控制性能是合理的.
在实验中, 与实验平台有关的参数如表 1所示.提出的非线性级联控制器(实验研究中简称NCC-DOB)的控制参数如表 2所示.为了对比分析所提NCC-DOB的优越性, 引入不带扰动观测器的非线性级联控制器(实验研究中简称NCC)以及式(34) 所示的传统PID控制器作为比较对象;除了kp=ki=0外, 其余NCC的控制参数与NCC-DOB一致.
| 表 1 液压机实验平台的参数 Table 1 Parameters of experiment platform for hydraulicpress |
| 表 2 实验中NCC-DOB的参数 Table 2 Parameters of NCC-DOB in experiment |
| $ \left. \begin{array}{l} {u_1}\left( {{\rm{PID}}} \right) = 800\left( {{x_{1{\rm{d}}}} - {x_1}} \right) + 10\int {\left( {{x_{1{\rm{d}}}} - {x_1}} \right){\rm{d}}t} ,\\ {u_2}\left( {{\rm{PID}}} \right) = 2 \times {10^7}\left( {{x_{3{\rm{d}}}} - {x_3}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{10^{ - 8}}\int {\left( {{x_{3{\rm{d}}}} - {x_3}} \right){\rm{d}}t} . \end{array} \right\} $ | (34) |
式中:u1(PID)和u2(PID)分别表示伺服比例阀在位移控制阶段及压力控制阶段的控制律.
3.2 压力控制研究首先开展压力控制研究, 验证所提NCC-DOB的压力控制环的性能.在实验中, 为了模拟液压机接触工件以后的工况, 比例溢流阀的控制信号按以下函数给出:upr=10 000×x1(V)(即滑块往下运动1 mm, 则比例溢流阀给出10 V的控制信号).期望的压力为2个不同频率的正弦信号, 分别为x3d=1.1×107+7×106×sin ((π/2.5)t-π/2) 及x3d=1.1×107+7×106×sin (πt-π/2).
PID、NCC及NCC-DOB在上述2个不同频率正弦指令下的压力跟踪误差epr如图 6所示.可知, NCC-DOB的压力跟踪误差明显小于PID和NCC的压力跟踪误差, 这主要是因为式(10) 所示的扰动观测器能够有效估计并补偿油液体积弹性模量、伺服比例阀流量增益、液压缸泄漏系数等参数不确定性所产生的集中扰动d;此外, PID的性能在2次实验中都略逊于NCC.NCC-DOB对于集中扰动d的估计曲线
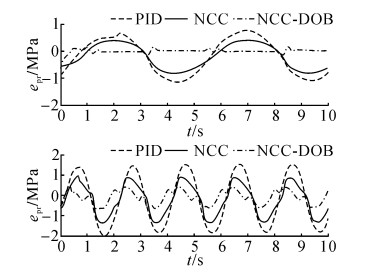
|
图 6 不同频率正弦指令下的压力跟踪误差 Fig. 6 Pressure tracking errors under different frequency sine instructions |
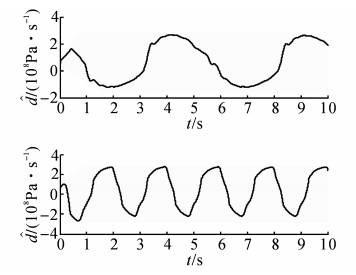
|
图 7
NCC-DOB在不同频率正弦指令下的 |
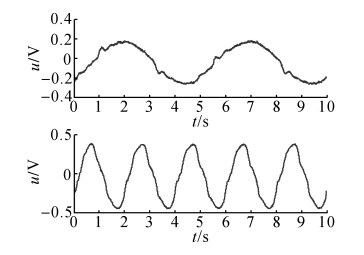
|
图 8 NCC-DOB在不同频率正弦指令下的控制律 Fig. 8 Control laws of NCC-DOB under differentfrequency sine instructions |
为了定量分析上述3个控制器的压力控制性能, 提出式(35) 所示的评价指标L2(z3):该指标代表T1~T2时间段内压力跟踪误差的均方根值(root mean square value of pressure tracking error, RMSPE).上述3个控制器在0~10 s内的RMSPE如表 3所示, 可知:在0.2 Hz正弦指令下, NCC-DOB的RMSPE比PID减少了88.19%, 比NCC减少了83.84%;在0.5 Hz正弦指令下, NCC-DOB的RMSPE比PID减少了71.57%, 比NCC减少了57.37%.
| 表 3 压力控制实验中不同控制器的RMSPE Table 3 RMSPEs of different controllers in pressure controlexperiment |
| $ {L_2}\left( {{z_3}} \right) = \sqrt {\left[ {1/\left( {{T_2} - {T_1}} \right)} \right]\int_{{T_1}}^{{T_2}} {{{\left| {{z_3}\left( t \right)} \right|}^2}{\rm{d}}t} } . $ | (35) |
在验证了压力控制性能之后, 重点研究NCC-DOB的位移控制性能.与滑块的慢速下行类似, 滑块的运动只受非线性摩擦力的影响, 不考虑工件变形力, 即比例溢流阀的信号始终保持为upr=0 V.滑块的期望位移信号有2种:1) 正弦信号, 即x1d=0.05+0.05×sin((π/10)t-π/2)(m);2) 斜坡信号, 即x1d=0.01t(m).
PID、NCC及NCC-DOB在上述正弦、斜坡位移指令下的位移跟踪误差epos如图 9所示.可知, 不管是正弦指令还是斜坡指令, NCC-DOB的位移控制精度都高于NCC;进一步地, NCC的位移控制精度高于PID.NCC-DOB在正弦、斜坡指令下的
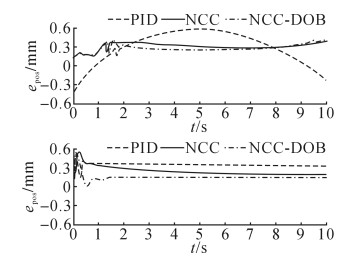
|
图 9 位移控制实验中不同控制器的位移跟踪误差 Fig. 9 Position tracking errors of different controllers in position control experiment |
|
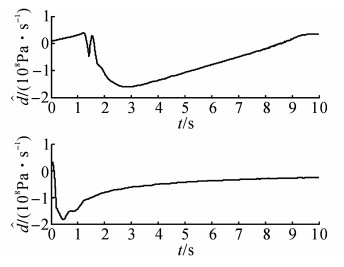
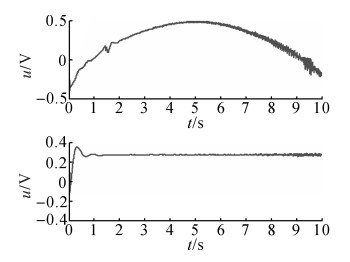
图 10
NCC-DOB在位移控制实验中的 |
|
图 11 NCC-DOB在位移控制实验的控制律 Fig. 11 Control laws of NCC-DOB in position controlexperiment |
为了定量分析上述3个控制器的位移控制性能, 提出式(36) 所示的评价指标L2(z1):该指标代表T1~T2时间段内位移跟踪误差的均方根值(root mean square value of displacement tracking error, RMSDE).上述3个控制器在0~10 s内的RMSDE如表 4所示.可知, 在正弦位移指令下, NCC-DOB的RMSDE比PID减少了28.32%, 比NCC减少了8.67%;在斜坡位移指令下, NCC-DOB的RMSDE比PID减少了55.06%, 比NCC减少了37.77%.
| 表 4 位移控制实验中不同控制器的RMSDE Table 4 RMSDEs of different controllers in position control experiment |
| $ {L_2}\left( {{z_1}} \right) = \sqrt {\left[ {1/\left( {{T_2} - {T_1}} \right)} \right]\int_{{T_1}}^{{T_2}} {{{\left| {{z_1}\left( t \right)} \right|}^2}{\rm{d}}t} } . $ | (36) |
在上述压力控制和位移控制研究的基础上, 研究NCC-DOB的位移/压力复合控制性能.比例溢流阀的控制信号按下式给出(即滑块在0.05 m的地方接触工件).
| $ \left. \begin{array}{l} {u_{{\rm{pr}}}} = 0,{x_1} < 0.05;\\ {u_{{\rm{pr}}}} = 10\;000\left( {{x_1} - 0.05} \right),{x_1} \ge 0.05. \end{array} \right\} $ | (37) |
滑块在位移控制阶段的期望位移与3.3节一致, 分为正弦指令与斜坡指令两种.类似地, 滑块在压力控制阶段的期望压力分为式(30) 所示的正弦指令以及式(31) 所示的斜坡指令两种.在整个复合控制过程中, 若位移控制阶段的期望位移为正弦类型, 则压力控制阶段的期望压力为正弦类型;类似地, 若位移控制阶段的期望位移为斜坡类型, 则压力控制阶段的期望压力为斜坡类型.
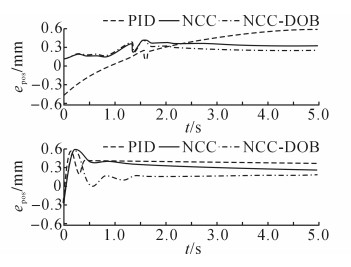
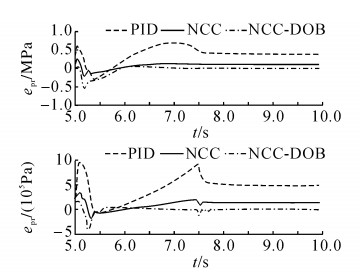
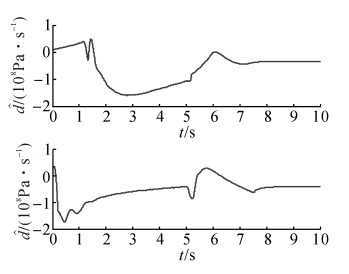
PID、NCC及NCC-DOB在位移控制阶段的位移跟踪误差如图 12所示, 相应的RMSDE如表 5所示;上述3个控制器在压力控制阶段的压力跟踪误差如图 13所示, 相应的RMSPE如表 6所示.分析图 12及表 5可知:在位移控制阶段, 不管是正弦指令还是斜坡指令, NCC-DOB的位移控制精度都高于NCC和PID;在正弦指令下, NCC-DOB的RMSDE比PID减少了34.98%, 比NCC减少了16.00%;在斜坡指令下, NCC-DOB的RMSDE比PID减少了49.58%, 比NCC减少了42.16%.分析图 13及表 6可知:在压力控制阶段, 不管是正弦指令还是斜坡指令, NCC-DOB的控制效果都优于NCC, NCC进一步优于PID;在正弦指令(5~10 s)下, NCC-DOB的RMSPE比PID减少了74.94%, 比NCC减少了6.09%;在斜坡指令(5~10 s)下, NCC-DOB的RMSPE比PID减少了87.43%, 比NCC减少了46.67%.进一步分析表 6中上述3个控制器在6~10 s内的RMSPE, 结合图 13, 可知:提出的NCC-DOB在压力控制稳定之后基本实现了无差控制, PID和NCC则始终存在控制偏差;在正弦指令(6~10 s)下, NCC-DOB的RMSPE比PID减少了95.08%, 比NCC减少了78.60%;在斜坡指令(6~10 s)下, NCC-DOB的RMSPE比PID减少了95.88%, 比NCC减少了83.95%.在本次实验中, NCC-DOB在不同类型指令下的
|
图 12 复合控制实验中不同控制器的位移跟踪误差 Fig. 12 Position tracking errors of different controllers in hybrid control experiment |
|
图 13 复合控制实验中不同控制器的压力跟踪误差 Fig. 13 Pressure tracking errors of different controllers in hybrid control experiment |
|
图 14
NCC-DOB在复合控制实验中的 |
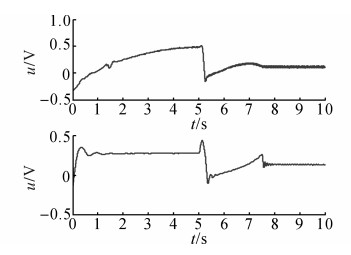
|
图 15 NCC-DOB在复合控制实验中的控制律 Fig. 15 Control laws of NCC-DOB in hybrid controlexperiment |
| 表 5 复合控制实验中不同控制器的RMSDE Table 5 RMSDEs of different controllers in hybrid control experiment |
| 表 6 复合控制实验中不同控制器的RMSPE Table 6 RMSPEs of different controllers in hybrid controlexperiment |
针对液压机在慢速加压阶段的位移、压力复合控制问题, 本文提出非线性级联控制器.该非线性级联控制器的压力控制环采用扰动观测器对油液体积弹性模量、伺服比例阀流量增益、液压缸泄漏系数等参数的不确定性所产生的集中扰动进行在线估计及补偿, 以克服系统参数不确定性对压力控制带来的显著影响, 利用无源性定理证明了压力控制环的稳定性;考虑到系统参数不确定性以及各种外负载对滑块位移控制带来的不利影响, 该非线性级联控制器的位移控制环基于滑模控制而设计;位移控制和压力控制的切换取决于当前位移.实验结果表明:利用提出的非线性级联控制器能够使得液压机在慢速加压阶段实现高精度、平稳的位移控制及高精度、平稳的压力控制, 可以实现这两种控制模式之间的平稳切换;在慢速加压的位移控制阶段(位移/压力复合控制实验), 采用提出的非线性级联控制器可以比传统的PID控制器减少34.98%(正弦指令)/49.58%(斜坡指令)的位移跟踪误差, 比没有扰动观测器的非线性级联控制器减少16.00%(正弦指令)/42.16%(斜坡指令)的位移跟踪误差;在慢速加压的压力控制阶段(位移/压力复合控制实验), 采用提出的非线性级联控制器可以比传统的PID控制器减少95.08%(正弦指令)/95.88%(斜坡指令)的压力控制误差, 比没有扰动观测器的非线性级联控制器减少78.60%(正弦指令)/83.95%(斜坡指令)的压力控制误差.
| [1] |
李贵闪, 翟华. 电液比例控制技术在液压机中的应用[J].
锻压装备与制造技术, 2005, 40(6): 28–30.
LI Gui-shan, ZHAI Hua. Application of electro-hydro proportional control in hydraulic press[J]. China Metal Forming Equipment and Manufacturing Technology, 2005, 40(6): 28–30. |
| [2] |
李贵闪, 翟华. 液压机液压系统比例压力控制方法探讨[J].
机床与液压, 2011, 39(16): 67–68.
LI Gui-shan, ZHAI Hua. Discussion on methods of proportional pressure control in hydraulic system of hydraulic press[J]. Machine Tool and Hydraulics, 2011, 39(16): 67–68. DOI:10.3969/j.issn.1001-3881.2011.16.024 |
| [3] | TRUONG D Q, AHN K K. Force control for press machines using an online smart tuning fuzzy PID based on a robust extended Kalman filter[J]. Expert Systems with Applications, 2011, 38(5): 5879–5894. DOI:10.1016/j.eswa.2010.11.035 |
| [4] | ZHANG Q, WEI J H, FANG J H, et al. High performance pressure control for the hydraulic press based on the soft relief fuzzy PID controller[C]//ASME/BATH 2015 Symposium on Fluid Power and Motion Control. Chicago:ASME, 2015. |
| [5] | AYALEW B, JABLOKOW K W. Partial feedback linearising force-tracking control:implementation and testing in electrohydraulic actuation[J]. IET Control Theory and Applications, 2007, 1(3): 689–698. DOI:10.1049/iet-cta:20060186 |
| [6] | SANADA K. A method of designing a robust force controller of a water-hydraulic servo system[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ:Journal of Systems and Control Engineering, 2002, 216(2): 135–141. |
| [7] | ZHU W H, PIEDBOEUF J C. Adaptive output force tracking control of hydraulic cylinders with applications to robot manipulators[J]. Journal of Dynamic Systems, Measurement and Control, 2005, 127(2): 206–217. DOI:10.1115/1.1898237 |
| [8] | 林治平. 锻压变形力的工程计算[M]. 北京: 机械工业出版社, 1986. |
| [9] | LEI J, LU X J, LI Y B, et al. Approximate-model based estimation method for dynamic response of forging processes[J]. Chinese Journal of Mechanical Engineering (English Edition), 2015, 28(3): 565–572. DOI:10.3901/CJME.2015.0114.015 |
| [10] | LU X J, LI H X, DUAN J A, et al. Integrated design and control under uncertainty:a fuzzy modeling approach[J]. Industrial and Engineering Chemistry Research, 2010, 49(3): 1312–1324. DOI:10.1021/ie901457j |
| [11] | LU X J, LI Y B, HUANG M H. Operation-region-decomposition-based singular value decomposition/neural network modeling method for complex hydraulic press machines[J]. Industrial and Engineering Chemistry Research, 2013, 52(48): 17221–17228. DOI:10.1021/ie402189y |
| [12] | LU X J, FAN B, HUANG M H. A novel LS-SVM modeling method for a hydraulic press forging process with multiple localized solutions[J]. IEEE Transactions onIndustrial Informatics, 2015, 11(3): 663–670. DOI:10.1109/TII.2015.2422614 |
| [13] | ZHANG Q, WEI J H, FANG J H, et al. Nonlinear motion control of the hydraulic press based on an extended piecewise disturbance observer[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ:Journal of Systems and Control Engineering, 2016, 230(8): 830–850. DOI:10.1177/0959651816655040 |
| [14] | CHEN W H. Disturbance observer based control for nonlinear systems[J]. IEEE/ASME Transactions on Mechatronics, 2004, 9(4): 706–710. DOI:10.1109/TMECH.2004.839034 |
| [15] | YAO J, LI B, KONG X D, et al. Displacement and dual-pressure compound control for fast forginghydraulic system[J]. Journal of Mechanical Science and Technology, 2016, 30(1): 353–363. DOI:10.1007/s12206-015-1240-5 |
| [16] | ZHENG J M, ZHAO S D, WEI S G. Application of self-tuning fuzzy PID controller for a SRM direct drive volume control hydraulic press[J]. Control Engineering Practice, 2009, 17(12): 1398–1404. DOI:10.1016/j.conengprac.2009.07.001 |
| [17] | FANG Y, YANG J, CHAI X D. Hybrid control of hydraulic press machine based on robust control[J]. Chinese Journal of Mechanical Engineering (English Edition), 2008, 21(2): 72–76. DOI:10.3901/CJME.2008.02.072 |
| [18] | KADDISSI C, KENNE J P, SAAD M. Indirect adaptive control of an electrohydraulic servo system based on nonlinear backstepping[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(6): 1171–1177. DOI:10.1109/TMECH.2010.2092785 |
| [19] | ZHANG Q, FANG J H, WEI J H, et al. Adaptive robust motion control of a fast forging hydraulic press considering the nonlinear uncertain accumulator model[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ:Journal of Systems and Control Engineering, 2016, 230(6): 483–497. DOI:10.1177/0959651816628994 |
| [20] | KIM W, SHIN D, WON D, et al. Disturbance-observer-based position tracking controller in the presence of biased sinusoidal disturbance for electrohydraulic actuators[J]. IEEE Transactions on Control Systems Technology, 2013, 21(6): 2290–2298. DOI:10.1109/TCST.2013.2237909 |
| [21] | 哈里尔. 非线性系统[M]. 朱义胜, 董辉, 李作洲, 等, 译. 3版. 北京: 电子工业出版社, 2011. |
| [22] | YAO B, BU F P, REEDY J, et al. Adaptive robust motion control of single-rod hydraulic actuators:theory and experiments[J]. IEEE/ASME Transactions on Mechatronics, 2000, 5(1): 79–91. DOI:10.1109/3516.828592 |



