RV减速器作为工业机器人专用的一种精密减速器, 具有定位精度高、运转灵活、长时工作稳定的特点.RV减速器作为一种传递扭矩的二级精密减速器, 定位精度高、运转灵活意味着RV减速器主轴承必须具有低摩擦力矩的特性.
国内外学者对滚动轴承摩擦力矩作过许多研究.Palmgren[1]通过对各式轴承的实验, 获得摩擦力矩的经验公式.Snare[2]通过拟静力学, 对轴承的各个摩擦力矩作了详细的研究.Todd等[3]对不同沟曲率系数下球轴承摩擦力矩的特性进行分析研究.Houpert[4-6]在基于沟道控制理论的基础上, 通过纯滚动线的位置求解轴承的差动滑动摩擦力矩与自旋摩擦力矩, 给出计算公式以及拟合公式, 研究油膜润滑引起的摩擦力矩、弹性滞后摩擦力矩等对球、滚子轴承的影响, 并进行实验验证.Harris等[7]建立在只受轴向力的情况下, 固体润滑与流体润滑摩擦力和摩擦力矩对轴承影响的力学模型并进行求解分析, 同时作了实验对比, 证实了沟道控制理论在求解轴承载荷中的局限性.Gonçalves等[8]通过SKF的计算公式, 计算在不同稠化剂含量下, 采用聚合物脂润滑的推力球轴承的摩擦力矩变化特性, 并通过实验进行验证.在国内方面, Deng[9]在轴承动力学的基础上, 给出基于能量守恒的角接触球轴承摩擦力矩计算模型, 考虑不同保持架兜孔形状、保持架间隙、沟曲率半径系数随着转速升高对摩擦力矩的影响, 对计算结果进行分析与实验验证.陈剑等[10]基于热弹性流体动力润滑理论, 将滚动体打滑与油膜剪切效应考虑在内, 建立超高速电主轴轴承摩擦力矩的计算分析模型, 但未进行实验验证.陶润等[11]通过最小二乘法的方式, 对摩擦力矩与转速的关系进行拟合, 得到摩擦力矩与转速和径向力之间的经验公式, 并通过试验对比证明拟合公式的精度.姜绍娜等[12-13]在Houpert的研究基础上, 运用沟道控制理论中计算姿态角的方法代替了Houpert考虑姿态角的方法, 对弹性滞后摩擦力矩、差动滑动摩擦力矩、自旋摩擦力矩等进行计算和实验验证, 分析摩擦力矩随内、外沟曲率变化的趋势, 但没有摆脱沟道控制理论的束缚, 也没有对趋势出现的原因进行理论解释.
实际上, 沟道控制理论仅仅是油润滑球轴承在特定工况下一种非常有限的状态, 虽然在很大程度上简化了轴承力学模型的推导与求解, 但不能准确反映轴承在低速以及从低速到高速的变化过程中的姿态角[7, 14].对于同一转速, 根据所采用的外沟道或内沟道控制理论的不同, 求得的姿态角具有较大的差距.作为耦合参数之一, 姿态角的选取影响轴承整个拟静力学方程的求解结果.为了能够准确地研究在低速工作条件下RV减速器的摩擦力矩特性, 采用合适的理论求解准确的姿态角是很有必要的.
基于上述问题, 本文在拟静力学的基础上, 采用丁长安等[14]提出的基于达朗贝尔原理计算滚动体姿态角的方法, 摆脱沟道控制理论的限制, 重新给出计算轴承球和滚道接触椭圆内纯滚动线位置的方法, 修正了Houpert提出的计算公式.根据RV减速器低速重载的工况, 对型号为H76/182的RV减速器主轴承的弹性滞后摩擦力矩、差动滑动摩擦力矩、自旋摩擦力矩进行理论分析计算.详细分析摩擦力矩的不同组成部分随内、外沟曲率变化的规律, 并给出可能的解释.对提出的摩擦力矩计算方法进行实验验证, 并与SKF经验计算公式[15]和Houpert的计算公式进行比较.
1 纯滚动线位置关系的研究通过Houpert等[4, 12]的研究表明, 轴承球与滚道接触所产生的赫兹接触椭圆中存在2个纯滚动点, 并且过滚动点连线的纯滚动线与球自转轴线、轴承的转动线交于一点.
纯滚动线与Hertz接触椭圆的应力分布如图 1所示.分析图 1可知, 将滚道与球接触处变形的曲线近似等效为抛物线, 在抛物线最低点的曲率半径为赫兹接触半径Ra, 由此可以推知抛物线的公式为

|
图 1 纯滚动线与Hertz接触椭圆应力分布 Fig. 1 Pure rolling line and stress distribution of Hertz contact ellipse |
| $ Z \approx \frac{{{X^2}}}{{2{R_{\rm{a}}}}}. $ | (1) |
式中:Ra=2rD/(2r+D), 其中D为轴承球的直径, r为沟曲率半径.
由式(1) 推知Z1、Z2的高度, 第j球处的内、外圈纯滚动线与球和滚道接触点的切线的夹角可以通过下式计算:
| $ \tan\gamma _{{\rm{i}},{\rm{o}}}^j = \frac{{Z_{{\rm{i}},{\rm{o}}}^{1j} - Z_{{\rm{i}},{\rm{o}}}^{2j}}}{{a_{{\rm{i}},{\rm{o}}}^{1j} - a_{{\rm{i}},{\rm{o}}}^{2j}}}. $ | (2) |
式中:a为接触椭圆的长半轴值, a1、a2为纯滚动线所在接触椭圆的长半轴上的位置, 下标i、o分别表示内、外圈, 上标j表示第j球.
球和滚道接触区的纯滚动线几何位置关系如图 2所示.对图 2进行几何关系分析可知, 在ΔAOB中, 有

|
图 2 纯滚动线几何位置关系 Fig. 2 Geometric position relationship of pure rolling line |
| $ \cos\left( {\alpha _{\rm{i}}^j + \frac{{\rm{\pi }}}{2} - {\beta _j}} \right) = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2OA \cdot OB}}. $ | (3) |
式中:α为轴承的接触角, OA=D/2, OB=dm/(2sin βj), 其中dm为轴承的公称直径, 其中A点为轴承自转轴线OA与过滚动点的纯滚动连线AB的交点.
根据式(3) 可以推得AB的表达式, 同时, 在ΔAFB中, 有
| $ \sin \left( {{\beta _j} - \gamma _{\rm{i}}^j} \right) = \frac{{R_{\rm{i}}^j}}{{AB}}. $ | (4) |
式中:Ri为内滚道和轴承球接触处到轴承中心的距离.对于第j球处的内外圈, 有
| $ R_{{\rm{i}},{\rm{o}}}^j = \frac{{{d_{\rm{m}}}}}{2} \mp \frac{{D\cos \alpha _{{\rm{i}},{\rm{o}}}^j}}{2}. $ | (5) |
整理式(3)、(4) 可得, 内圈纯滚动线与赫兹接触切线的夹角γi为
| $ \gamma _{\rm{i}}^j = - \arcsin \left( {\frac{{2R_{\rm{i}}^j\sin {\beta _j}}}{{\sqrt {{D^2}{{\sin }^2}{\beta _j} + d_{\rm{m}}^2 - 2D \cdot {d_{\rm{m}}} \cdot \sin {\beta _j} \cdot \sin \left( {{\beta _j} - \alpha _{\rm{i}}^j} \right)} }}} \right) + {\beta _j}. $ | (6) |
同理, 通过类似的几何推导可以推知, 对于外圈有
| $ \gamma _{\rm{o}}^j = \arcsin \left( {\frac{{2R_{\rm{o}}^j\sin {\beta _j}}}{{\sqrt {{D^2}{{\sin }^2}{\beta _j} + d_{\rm{m}}^2 - 2D \cdot {d_{\rm{m}}} \cdot \sin {\beta _j} \cdot \sin \left( {\alpha _{\rm{o}}^j - {\beta _j}} \right)} }}} \right) - {\beta _j}. $ | (7) |
式中:αi、αo为内、外接触角, 较准确的β的计算由文献[14]根据达朗贝尔原理而摆脱沟道控制理论的限制, 通过拟静力学模型计算.如图 3所示为角接触球轴承的滚动体受载示意图.图 3中, ωsij、ωsoj为角位置j处的滚动体与内、外圈之间自旋角速度;ωbj为角位置j处滚动体的自转角速度;ωm为轴承的第j个球的轨道速度, 是接触角的函数, 并非常数;ω′bj为角位置j处滚动体的瞬时旋转角速度, 有ω′bj=ωbj+ωm(矢量和);Msij、Msoj为角位置j处内、外套圈与滚动体之间产生的自旋摩擦力矩.

|
图 3 滚动体受载示意图 Fig. 3 Sketch of single rolling load |
根据图 3, 以滚动体为同一参照系, 假设内圈旋转, 则有Msij和ωsij方向相同并作正功.同理, 由于外圈静止, 则有Msoj和ωsoj方向相反并作负功.整个平衡力系对于瞬时转动轴线, 有
| $ {M_{\rm{f}}} - M_{{\rm{si}}}^j\sin \left( {{\alpha _{\rm{i}}} - {\theta _j}} \right) + M_{{\rm{so}}}^j\sin \left( {{\theta _j} - {\alpha _{\rm{o}}}} \right) = 0. $ | (8) |
式中:θj为角位置j处, X轴的负方向与ω′bj间的夹角;Mf为平衡力系中, 除自旋力矩外其他力对瞬时转轴的力矩;Ms为平衡力系中的自旋摩擦力矩.
将式(8) 乘以ω′bj, 可得
| $ \omega _{\rm{b}}^{'j}{M_{\rm{f}}} - \omega _{\rm{b}}^{'j}\left[ {M_{{\rm{si}}}^j\sin \left( {{\alpha _{\rm{i}}} - {\theta _j}} \right) - M_{{\rm{so}}}^j\sin \left( {{\theta _j} - {\alpha _{\rm{o}}}} \right)} \right] = 0. $ | (9) |
根据达朗贝尔原理可知, 当惯性力作用于物体上, 任何时刻该物体都处于力的平衡状态.假设Pf为除自旋力矩外其他各个力对滚动体作的功, 则对于图 3, 有下式成立:
| $ {P_{\rm{f}}} = M_{{\rm{si}}}^j\omega _{{\rm{si}}}^j - M_{{\rm{so}}}^j\omega _{{\rm{so}}}^j = 0. $ | (10) |
将Pf=ω′bjMf代入式(9), 则根据式(9)、(10) 可得
| $ \begin{array}{l} M_{{\rm{so}}}^j\omega _{{\rm{so}}}^j - M_{{\rm{si}}}^j\omega _{{\rm{si}}}^j - \omega _{\rm{b}}^{'j}\left[ {M_{{\rm{si}}}^j\sin \left( {{\alpha _i} - {\theta _j}} \right) - } \right.\\ \;\;\;\;\left. {M_{{\rm{so}}}^j\sin \left( {{\theta _j} - {\alpha _{\rm{o}}}} \right)} \right] = 0. \end{array} $ | (11) |
式中:
| $ \begin{array}{l} {\theta _j} = \arctan \left( {\frac{{{\omega _{\rm{b}}}\sin \beta }}{{{\omega _{\rm{b}}}\cos \beta - {\omega _{\rm{m}}}}}} \right),{{\omega '}_{{{\rm{b}}_j}}} = \sqrt {\omega _{\rm{b}}^2 + \omega _{\rm{m}}^2 + 2{\omega _{\rm{b}}}{\omega _{\rm{m}}}\cos \beta } \\ \left( {标量计算} \right). \end{array} $ |
根据Harris对滚动体的运动学分析, 忽略陀螺力矩产生的枢轴运动, 可以得到ωbj、ωm、ωsij及ωsoj的角速度计算公式[7].将这4个角速度公式与式(9)、(10) 代入式(11), 整理可得球的姿态角计算公式为
| $ \tan \beta = \frac{{\eta \left( {\zeta + 1} \right)\sin {\alpha _{\rm{i}}} + 2\sin {\alpha _{\rm{o}}}}}{{\eta \left( {\zeta + 1} \right)\cos {\alpha _{\rm{i}}} + 2\left( {\cos {\alpha _{\rm{o}}} + \xi } \right) + A}}. $ | (12) |
式中:
| $ \begin{array}{l} \xi = \frac{D}{{{d_{\rm{m}}}}},\eta = \frac{{{Q_{\rm{i}}}{a_{\rm{i}}}{E_{\rm{i}}}}}{{{Q_{\rm{o}}}{a_{\rm{o}}}{E_{\rm{o}}}}},\zeta = \frac{{1 + \xi \cos {\alpha _{\rm{o}}}}}{{1 - \xi \cos {\alpha _{\rm{i}}}}},\\ A = \xi \eta \left[ {\cos \left( {{\alpha _{\rm{i}}} - {\alpha _{\rm{o}}}} \right) - \zeta } \right]. \end{array} $ |
其中, Εi, o为内外圈第二类椭圆积分, Qi, o为内外圈轴承球作用在滚道上的法向载荷.
在求得姿态角的准确计算方式后, 可以将所得姿态角与传统的沟道控制理论求得的数值在型号为H76/182的RV减速器主轴承的工作工况下(外加轴向力为13 720 N, 径向力为3 000 N, 工作转速为40 r/min)进行对比, H76/182轴承的主要结构参数如表 1所示.表中, D为轴承球径, di、do分别为轴承内、外沟底圆直径, ri、ro为轴承沟曲率半径, Z为球数.不同理论下的姿态角结算结果如表 2所示.表中, α为受载后的静态接触角, βp为利用式(12) 求得的接触角, β1、β2分别为采用内、外沟道控制理论所求得的姿态角, 计算公式可以参见文献[7].
| 表 1 H76/182主轴承的主要结构参数 Table 1 Important structural parameters of H76/182 mainbearing |
| 表 2 不同理论下的姿态角计算结果 Table 2 Results calculated by different theoretical methods |
在低速情况下, 由于离心力的影响很小, 内外接触角近似相等, 轴承的姿态角应约等于受载后的静态接触角.按照沟道控制理论所求得的姿态角远大于该数值.通过表 2的对比可知, 无论是外沟道或是内沟道控制理论所得的姿态角β1、β2, 均与实际接触角相差过大;βp与α近似相等, 符合低速条件下轴承接触角与姿态角近似相等的推论.
验证式(12) 在轴承低速运转情况下的求解有效性之后, 将式(12) 代入式(6)、(7), 并将式(2)、(6)、(7) 组合得到关于两个未知数a1、a2的一个位置关系方程(内圈和外圈):
| $ \begin{array}{l} \arctan \left( {\frac{{Z_{{\rm{i}},{\rm{o}}}^{1j} - Z_{{\rm{i}},{\rm{o}}}^{2j}}}{{a_{{\rm{i}},{\rm{o}}}^{1j} - 1ja_{{\rm{i}},{\rm{o}}}^{2j}}}} \right) \pm \\ \;\;\;\;\arctan \left( {\frac{{2R_{{\rm{i}},{\rm{o}}}^j\sin {\beta _j}}}{{\sqrt {{D^2}{{\sin }^2}{\beta _j} + d_{\rm{m}}^2 - 2D{d_{\rm{m}}}\sin {\beta _j} \cdot S} }}} \right) - \\ \;\;\;\;{\beta _j} = 0. \end{array} $ | (13) |
式中:对于内圈, 有S=sin (βj-αij);对于外圈, 有S=sin (αoj-βj).
2 基于纯滚动线位置的摩擦力矩的计算在接触椭圆上, 由于纯滚动线的存在, 表面的摩擦切应力在忽略陀螺运动的影响后, 分布可以简化如图 1所示.摩擦切应力通过下式计算:
| $ \tau = \pm \mu \sigma . $ | (1) |
式中:μ为局部接触摩擦系数; σ为接触区内的法向应力,
| $ \sigma = \frac{{3Q}}{{2{\rm{\pi }}ab}}{\left[ {1 - {{\left( {\frac{x}{a}} \right)}^2} - {{\left( {\frac{y}{b}} \right)}^2}} \right]^{\frac{1}{2}}}, $ |
其中Q为球和滚道之间的接触法向力.
在接触椭圆的摩擦切应力积分区域内, 单位积分的摩擦切向力可以表示为
| $ {\rm{d}}{F_{\rm{s}}} = \left\{ {\int_{ - b\sqrt {1 - {x^2}/{a^2}} }^{b\sqrt {1 - {x^2}/{a^2}} } {\tau {\rm{d}}y} } \right\}{\rm{d}}x. $ | (2) |
令χ=x/a, 将式(2) 整理可得
| $ {\rm{d}}{F_{\rm{s}}} = \pm \mu \frac{{3Q}}{4}\left( {1 - {{\rm{\chi }}^2}} \right){\rm{d\chi }}{\rm{.}} $ | (3) |
可以推出整个椭圆积分域内的摩擦切向力为
| $ {F_{\rm{s}}} = \mu \frac{{3Q}}{4}\left( {\int\limits_{ - 1}^1 {\left( {1 - {{\rm{\chi }}^2}} \right){\rm{d\chi }}} - 2\int\limits_{{{\rm{\chi }}_2}}^{{{\rm{\chi }}_1}} {\left( {1 - {{\rm{\chi }}^2}} \right){\rm{d\chi }}} } \right). $ | (4) |
通常认为Fs相较μQ来说, 是极小量[6], 因此可以将式(4) 化简成一个只含χ1、χ2的方程.
将化简后的式(4) 与1章得到的关于滚动线位置的方程(13) 联立成含有两个未知数χ1、χ2的二元方程组.求解得到每个球内外圈的χ1、χ2, 并代入到后续的摩擦力矩计算中.若方程组在椭圆区域内只求得一条纯滚动线的位置χ1, 则令χ2=-1;若只求得χ2, 则令χ1=1;同时, 若χ1、χ2求出的正负与规定相反, 则将各自的值赋给对方作调换.
轴承的自旋摩擦力矩是由摩擦切向力对接触椭圆的中心所产生的力矩, 差动滑动摩擦力矩是由于在球和滚道接触处, 除纯滚动线位置外两物体各个点的线速度皆不相同而产生的微观滑动.根据上述定义可知,
| $ M_{{{\rm{S}}_{{\rm{i}},{\rm{o}}}}}^j = \int\limits_{ - a_{{\rm{i}},{\rm{o}}}^j}^{a_{{\rm{i}},{\rm{o}}}^j} {{\rm{d}}{F_{\rm{s}}} \cdot x} , $ | (5) |
| $ M_{{{\rm{D}}_{{\rm{i}},{\rm{o}}}}}^j = \int\limits_{ - a_{{\rm{i}},{\rm{o}}}^j}^{a_{{\rm{i}},{\rm{o}}}^j} {{\rm{d}}{F_{\rm{s}}} \cdot z} . $ | (6) |
式中:Mjsi, o为第j球处的内圈、外圈自旋摩擦力矩, MjDi, o为第j球处的内、外圈差动滑动摩擦力矩.将式(5)、(6) 进行进一步推导, 可得
| $ \begin{array}{l} M_{{{\rm{S}}_{{\rm{i}},{\rm{o}}}}}^j = \mu \frac{{3Q_{i,o}^j}}{4}\left[ {\int\limits_{ - 1}^{{\rm{\chi }}_{2{\rm{i}},{\rm{o}}}^j} {a{\rm{\chi }}\left( {1 - {{\rm{\chi }}^2}} \right){\rm{d\chi }}} - } \right.\\ \left. {\;\;\;\;\;\;\;\int\limits_{{\rm{\chi }}_{2{\rm{i}},{\rm{o}}}^j}^{{\rm{\chi }}_{1{\rm{i}},{\rm{o}}}^j} {a{\rm{\chi }}\left( {1 - {{\rm{\chi }}^2}} \right){\rm{d\chi }}} + \int\limits_{{\rm{\chi }}_{1{\rm{i}},{\rm{o}}}^j}^1 {a{\rm{\chi }}\left( {1 - {{\rm{\chi }}^2}} \right){\rm{d\chi }}} } \right], \end{array} $ | (7) |
| $ \begin{array}{l} M_{{{\rm{D}}_{{\rm{i}},{\rm{o}}}}}^j = \mu \frac{{3Q_{i,o}^ja}}{{8{R_{\rm{a}}}}}\left[ {\int\limits_{ - 1}^{{\rm{\chi }}_{2{\rm{i}},{\rm{o}}}^j} {{{\rm{\chi }}^2}\left( {1 - {{\rm{\chi }}^2}} \right){\rm{d\chi }}} - } \right.\\ \left. {\;\;\;\;\;\;\;\int\limits_{{\rm{\chi }}_{2{\rm{i}},{\rm{o}}}^j}^{{\rm{\chi }}_{1{\rm{i}},{\rm{o}}}^j} {{{\rm{\chi }}^2}\left( {1 - {{\rm{\chi }}^2}} \right){\rm{d\chi }}} + \int\limits_{{\rm{\chi }}_{1{\rm{i}},{\rm{o}}}^j}^1 {{{\rm{\chi }}^2}\left( {1 - {{\rm{\chi }}^2}} \right){\rm{d\chi }}} } \right]. \end{array} $ | (8) |
轴承在保持相同的载荷下, 加载和卸载所产生的弹性形变不一致, 证明在该过程中有能量损失, 即摩擦功耗.关于弹性滞后摩擦力矩的计算方法, 国内外多有不同, 但通常认为这种摩擦力矩相比较其他摩擦力矩而言较小, 只有在球作用在滚道上的法向载荷足够大、轴承转速较高时, 弹性滞后摩擦阻力才会比较明显[7].弹性摩擦力矩的产生机理与推导不是本文重点, 根据文献[16], 采用下式计算:
| $ M_{{{\rm{E}}_{{\rm{i}},{\rm{o}}}}}^j = \frac{{3{\lambda _{\rm{h}}}b_{i,o}^jQ_{i,o}^j}}{{16R_{{a_{{\rm{i}},{\rm{o}}}}}^j}}R_{{\rm{i}},{\rm{o}}}^j. $ | (9) |
式中:b为接触椭圆的短半轴的长度, 可以通过轴承的拟静力学模型计算得到;λh为弹性滞后损失能量系数, 金属取0.008~0.01, 此处取0.008.
在轴承的运行过程中, 由于保持架的兜孔形状与球并非完全吻合, 球和保持架的兜孔之间会产生相应的摩擦.本文根据金津将幸等[17]的研究结果, 采用下式计算该摩擦力矩:
| $ \begin{array}{l} {M_{\rm{c}}} = \frac{{{m_{\rm{c}}}g{\mu _{\rm{c}}}{d_{\rm{m}}}}}{4}\left( {1 - \frac{D}{{{d_{\rm{m}}}}}{{\cos }^2}\alpha } \right) \times \\ \;\;\;\;\;\;\;\;\;\sin \left( {\alpha + \arctan \left( {\frac{{2D\sin \alpha }}{{{d_{\rm{m}}} - D\cos \alpha }}} \right)} \right). \end{array} $ | (10) |
式中:mc为保持架的质量;g为重力涤速度;μc为球和保持架兜孔间的摩擦系数, 对于钢和胶木之间的摩擦, 取0.2.
当计算得到各个摩擦力矩后, 须将各个组成部分的摩擦力矩等效为作用在轴承的旋转中心上的摩擦力矩.其中, 利用式(9) 计算得到的摩擦力矩在文献[6]中已作等效处理.差动滑动摩擦力矩的等效分解可见图 4.

|
图 4 摩擦力矩等效分解 Fig. 4 Friction torque equivalent decomposition |
由图 4可知, 差动滑动摩擦力矩MD需要分解成等效力FD与力臂GH.将分解后的力乘以等效力臂, 即该力的作用点到轴承转动中心的距离, 可得整个轴承绕转动中心的摩擦力矩.由式(5)、(6) 可以看出, 差动滑动摩擦力矩的作用轴线位于球上, 等效力臂可以取Ri, o.
由于自旋摩擦力矩的旋转轴与滑动区的关系复杂, 不能简单地用轴承的几何关系对自旋摩擦力矩作等效处理, 可以通过能量守恒的方法来确定自旋摩擦力矩的全局等效值[6].轴承的总自旋摩擦消耗Ps等于各个球上单独的自旋摩擦能量消耗之和, 对于内圈旋转的轴承, 有
| $ \begin{array}{l} {P_{\rm{s}}} = \left| {\sum\limits_{j = 1}^Z {M_{{{\rm{s}}_{\rm{i}}}}^j \cdot \left( {{\omega _{\rm{i}}} - {\omega _{\rm{m}}}} \right)\sin \alpha _{\rm{i}}^j} } \right| + \\ \;\;\;\;\;\;\;\left| {\sum\limits_{j = 1}^Z {M_{{{\rm{s}}_{\rm{o}}}}^j \cdot {\omega _{\rm{m}}}\sin \alpha _{\rm{o}}^j} } \right|. \end{array} $ | (11) |
将式(11) 左、右两边同除ωi, 可以得到轴承自旋摩擦的总等效力矩Mstotal为
| $ \begin{array}{l} M_{\rm{s}}^{{\rm{total}}} = \left| {\sum\limits_{j = 1}^Z {M_{{{\rm{s}}_{\rm{i}}}}^j \cdot \left( {1 - \frac{{{\omega _{\rm{m}}}}}{{{\omega _{\rm{i}}}}}} \right)\sin \alpha _{\rm{i}}^j} } \right| + \\ \;\;\;\;\;\;\;\;\;\;\;\left| {\sum\limits_{j = 1}^Z {M_{{{\rm{s}}_{\rm{o}}}}^j \cdot \frac{{{\omega _{\rm{m}}}}}{{{\omega _{\rm{i}}}}}\sin \alpha _{\rm{i}}^j} } \right|. \end{array} $ | (12) |
轴承的公转角速度ωm与滚道旋转速度(对于内圈旋转为ωi)之比[7]为
| $ \frac{{{\omega _{\rm{m}}}}}{{{\omega _{\rm{i}}}}} = \frac{1}{{1 + \frac{{\left( {1 + \xi \cos {\alpha _{\rm{o}}}} \right)\left( {\cos {\alpha _{\rm{i}}} + \tan \beta \sin {\alpha _{\rm{i}}}} \right)}}{{\left( {1 + \xi \cos {\alpha _{\rm{i}}}} \right)\left( {\cos {\alpha _{\rm{o}}} + \tan \beta \sin {\alpha _{\rm{o}}}} \right)}}}}. $ | (13) |
式中:ξ=D/dm, 姿态角β采用式(12) 来计算.将式(13) 代入式(12), 可以求得Mstotal.
将各个等效摩擦力矩相加, 可得总的摩擦力矩T的计算公式为
| $ \begin{array}{l} T = \frac{{\left| {\sum\limits_{j = 1}^Z {M_{{{\rm{D}}_{\rm{i}}}}^j \cdot {R_{\rm{o}}}} } \right| + \left| {\sum\limits_{j = 1}^Z {M_{{{\rm{D}}_{\rm{o}}}}^j \cdot {R_{\rm{i}}}} } \right|}}{D} + \\ \;\;\;\;\;\;\;\left| {\sum\limits_{j = 1}^Z {M_{{{\rm{E}}_{\rm{i}}}}^j} } \right| + \left| {\sum\limits_{j = 1}^Z {M_{{{\rm{E}}_{\rm{o}}}}^j} } \right| + \left| {{M_{\rm{c}}}} \right| + M_{\rm{s}}^{{\rm{total}}}. \end{array} $ | (14) |
摩擦力矩的计算需要滑动摩擦系数μ.根据采用的润滑油的油品特性、轴承转速以及轴承的其他使用条件, 结合轴承的基本结构参数, 可以采用文献[15]从理论上计算滑动摩擦系数μ为
| $ \mu = {\phi _{{\rm{bl}}}}{\mu _{{\rm{bl}}}} + \left( {1 - {\phi _{{\rm{bl}}}}} \right){\mu _{{\rm{EHL}}}}. $ | (15) |
式中:Φbl为滑动摩擦系数的权重系数;μbl为根据润滑剂中添加剂情况而变化的系数, 一般约为0.15;μEHL为全油膜条件下的摩擦系数, 根据润滑油的油品特性而变化.以上各系数均可从文献[15]中找出计算方式.
3 算例分析根据式(14), 对型号为H76/182的RV减速器主轴承的摩擦力矩特性进行计算分析.该主轴承在工作工况外加轴向力为13 720 N, 径向力为3 000 N, 规定最高工作转速为40 r/min的情况下, 以拟静力学模型为基础, 计算得到总摩擦力矩、差动滑动摩擦力矩、接触载荷、自旋摩擦力矩及弹性滞后摩擦力矩随内、外沟曲率系数变化的规律, 如图 5~11所示.图中,fi、fo分别为内、外沟道曲率系数.

|
图 5 总摩擦力矩随内、外沟曲率变化的三维图 Fig. 5 Three dimensional diagram of change of total friction torque with curvature of inner and outer groove |

|
图 11 弹性滞后摩擦力矩随沟曲率变化的三维图 Fig. 11 Three dimensional diagram of change of elastic rolling resistance moment with curvature of inner and outer groove |
根据轴承设计约束以及RV减速器的疲劳寿命要求[18-20], 确定沟曲率为0.51~0.555, 选定间隔为0.005.H76/182轴承的主要结构参数如表 1所示.
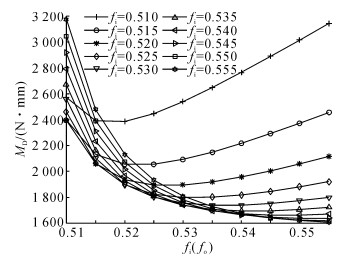
总摩擦力矩随内、外沟曲率变化的三维、二维图如图 5、6所示.可以看出, 在本文的沟曲率选定范围内, 且内、外沟曲率相同的情况下, 总摩擦力矩随着内、外沟曲率的增大而减小;当内、外沟曲率不同时, 选定内沟道或外沟道曲率系数不变, 总摩擦力矩随着另一沟曲率系数的增大呈现先减小、后增大的趋势, 即内、外沟曲率的差值越大, 总摩擦力矩越大.从图 5、6看出, 摩擦力矩的最小值可以出现在内、外沟曲率系数相差约0.01的范围内.

|
图 6 总摩擦力矩随内、外沟曲率变化二维图 Fig. 6 Two dimensional diagram of change of total friction torque with curvature of inner and outer groove |
如图 7、8所示为差动滑动摩擦力矩随内、外沟曲率的变化三维、二维图, 图 9展示了接触载荷随内、外沟曲率的变化三维图.由图 7、8可知, 差动滑动摩擦力矩随着沟曲率变化的趋势与总摩擦力矩类似, 在出现拐点之后, 摩擦力矩随着沟曲率的增大而增大.可能的原因是虽然沟曲率的增大使得轴承球与滚道间的密合度减小, 但是由图 9可知, 轴承接触载荷随着沟曲率的增大而增大, 同时, 内、外沟曲率差值越大, 整个轴承的摩擦切应力对于接触椭圆内的积分会增大, 从而导致差动滑动摩擦力的增加.

|
图 7 差动滑动摩擦力矩随内、外沟曲率的变化三维图 Fig. 7 Three dimensional diagram of change of sliding friction moment due to curvature effects with curvature of inner and outer groove |
|
图 8 轴承差动滑动摩擦力矩随内、外沟曲率的变化二维图 Fig. 8 Two dimensional diagram of change of sliding friction moment due to curvature effects with curvature of inner and outer groove |

|
图 9 接触载荷随内、外沟曲率的变化三维图 Fig. 9 Three dimensional diagram of change of contact load with curvature of inner and outer groove |
自旋摩擦力矩随内、外沟曲率变化的三维图可以参见图 10.自旋摩擦力矩随着内、外沟曲率的增大而减小, 这是由于虽然沟曲率的增大导致球和滚道的接触载荷增大, 但同时导致球与滚道的接触角减小, 邓四二等[16]指出, 自旋摩擦力矩随着接触角的增大而增大, 可知接触角的减小会显著减小自旋摩擦力矩.
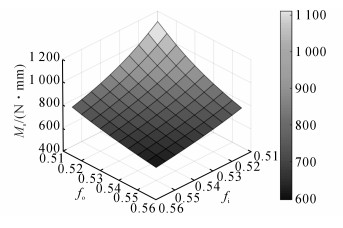
|
图 10 自旋摩擦力矩随内、外沟曲率的变化三维图 Fig. 10 Three dimensional diagram of change of friction moment due to pivoting effects with curvature of inner and outer groove |
弹性滞后摩擦力矩随沟曲率的变化三维图如图 11所示, 弹性滞后摩擦力矩随着内、外沟曲率的增大而增大.这是由于弹性滞后摩擦力矩是轴承球与滚道在加载和卸载过程中的一个损失量, 与轴承球和滚道的材料与所受载荷关系最密切.前面指出, 内、外沟曲率增大会导致轴承接触载荷的增大, 因而在轴承材料不变的情况下, 弹性滞后摩擦力矩随着内、外沟曲率的增大而增大.
4 摩擦力矩试验采用M9940机器人轴承摩擦力矩测量仪, 对同一批生产的共8套型号为H76/182的RV减速器主轴承进行摩擦力矩的测量.轴向加载量程为0~1 000 N.该测量仪采用传递测量法的原理, 将被测轴承内圈安装于空气主轴上, 空气主轴与力矩传感器相连, 力矩传感器同驱动电机相连, 被测轴承外圈通过与附件过盈配合防止旋转, 并通过气缸向轴承施加轴向载荷.当驱动电机带动被测轴承内圈旋转时, 由于轴承存在着阻碍转动的摩擦力矩M, 该摩擦力矩M经空气轴传递到力矩传感器上, 产生的阻碍力矩为M0, 经力矩传感器测量M0.由于空气主轴自身产生的摩擦力矩极小, 可以忽略不计, 并且若轴承的摩擦力矩M为唯一的阻碍力矩, 则力矩传感器的阻碍力矩M0即为M.力矩传感器将测到的轴系摩擦力矩转换为电信号, 经过放大滤波后, 送入计算机进行数据处理.M9940摩擦力矩试验机的结构示意图如图 12所示.

|
图 12 M9940摩擦力矩试验机结构示意图 Fig. 12 Schematic diagram of M9940 friction torque tester |
试验轴承的主要组成部分为内外套圈、球和保持架, 未装密封圈.在测量前, 被测轴承经过汽油洗涤以去油污与杂质, 并对每套被测轴承采用N15机械油进行稀油润滑.实验前, 将测试环境温度控制为10~15 ℃, 并保证实验环境的清洁, 确认被测轴承未被磁化.在实验过程中, 确保被测轴承远离电场、磁场的干扰.轴承附件(工装夹具)的质量mf约为3.5 kg, 重力作用为轴承提供微量的轴向预紧, 本文在通过拟静力学采用式(14) 计算总摩擦力矩时, 实际输入轴向载荷为Fa+mfg.其中, Fa为气缸的轴向加载.测量的受载条件为600~1 000 N的轴向加载, 加载间隔为100 N, 测量转速恒定为40 r/min(RV减速器规定的最高工作转速).
试验前, 先对装置作空载调零处理, 并将正、反转误差调至5%的误差范围内.为了保证测得的动态摩擦力矩数据的稳定性与准确性, 设置程序为电机启动后5 s开始记录测量数据, 设置试验采集的时间为正转、反转各15 s(即轴承两个方向各转10圈).通过实验得到的测量平均力矩Mmean计算方式为Mmean=(Mleft+Mright)/2.其中Mleft与Mright分别为正转或反转测得的摩擦力矩.SKF摩擦力矩的计算方法可以参考文献[15], Luc Houpert的摩擦力矩计算公式可以参考文献[5].如表 3所示为利用不同理论计算得到的摩擦力矩与实验数据的对比.表中, Fa为轴向加载,TSKF、TLuc、Tt分别为利用SKF计算公式、Houpert计算公式和本文计算公式得到的摩擦力矩,eSKF、eLuc、et分别为前三者与Mmean的误差的绝对值.
| 表 3 采用不同方法计算的摩擦力矩与实验数据对比 Table 3 Friction torques calculated by different methods are compared with experimental data |
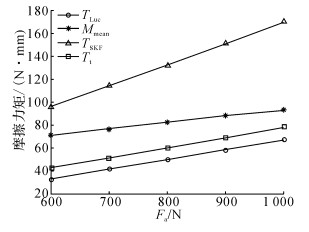
不同理论的计算结果与实验得到的摩擦力矩对比可见图 13.由表 3和图 13可知, SKF、Houpert和本文的理论计算公式与实际测得的摩擦力矩均有一定的误差.利用SKF计算公式得到的摩擦力矩大于实验值, 摩擦力矩的误差随着轴向加载的增大而增大;本文计算所得的摩擦力矩小于实验值, 摩擦力矩的误差随着轴向加载的增大而减小;利用Houpert的计算公式得到的摩擦力矩结果比本文计算结果更小, 变化趋势类似, 然而误差更大.
|
图 13 理论与实验摩擦力矩对比 Fig. 13 Theoretical and experimental comparison of friction torque |
本文的理论计算没有考虑润滑黏性引起的摩擦力矩、保持架和套圈引导面之间的摩擦力矩和密封圈引起的摩擦力矩, 由于实验所测轴承未加密封圈, 则本文的计算值和实验值之间存在的理论误差为润滑黏性导致的摩擦力矩、保持架和套圈引导面之间的摩擦力矩, 本文的计算值应小于实验值.同时, 当轴向载荷增大时, 会导致轴承球与滚道之间的接触载荷增大, 由式(1) 可知, 接触区切应力与接触载荷成正比关系, 会直接导致Ms、MD和ME的增大.接触载荷的增大对润滑剂黏性和引导面与保持架之间产生的摩擦力矩不会产生显著影响, 润滑剂黏性导致的摩擦力矩主要与转速和润滑剂的特性有关, 保持架和套圈引导面的摩擦力矩主要与保持架本身的结构参数、引导方式及保持架和引导面的速度差有关, 两者受轴承外加载荷的影响较小[7].测试用的轴承采用尼龙材料的保持架, 对滚动体及滚道的影响较小.在恒定的转速下, 随着轴向载荷的增加, Ms、MD和ME在总摩擦力矩中的占比会逐渐增大, 成为摩擦力矩的主要组成部分.本文的理论计算公式更加贴合该情况下的实际摩擦力矩, 并且计算误差会随着轴向加载的增大而减小.
SKF计算公式为经验拟合公式, 对非SKF轴承型号的H76/182的RV减速器主轴承计算误差相对较大.Houpert的计算公式由于简单地运用了初始接触角, 代替了球的姿态角进行纯滚动线位置的分析, 未能正确求解球和滚道载荷接触区的摩擦切应力的分布情况, 造成了低速工况下摩擦力矩占比较大的两种因素Ms和MD求解不够精确, 因而导致误差大于本文的计算结果.
5 结语在RV减速器主轴承的低速重载工况下, 当内、外沟曲率相同, 取值为0.51~0.555时, 轴承总摩擦力矩随着沟曲率系数的增大而增大.当内、外沟曲率不同时, 总摩擦力矩、差动滑动摩擦力矩随着内、外沟曲率系数差值的增大而增大, 非传统轴承设计中简单地认为摩擦力矩会随着密合度的减小而减小, 这是由于差动滑动摩擦力矩所占的比重最大, 决定了总摩擦力矩的变化特性.自旋摩擦力矩、弹性滞后摩擦力矩随着内、外沟曲率系数的增大而减小, 并且前者占比逐渐降低, 后者逐渐增多.与SKF计算公式及摩擦力矩测量仪的实验结果对比表明, 在RV减速器的额定工作转速与轴向加载的情况下, 本文得到的计算公式与SKF计算公式和Houpert的计算公式相比, 对RV减速器主轴承有更高的精度, 能够反映RV减速器主轴承的摩擦力矩变化情况.
综上所述, 若只考虑设计低摩擦力矩的RV减速器主轴承, 不考虑轴承的其他性能要求, 则不应让内、外沟曲率系数的差值过大.差值在0.01左右, 可以获得最低的总摩擦力矩, 在此基础上, 选择较大的沟曲率系数有利于降低轴承的摩擦力矩.
本文理论工作存在的缺陷是没能将润滑黏性引起的摩擦力矩、保持架和套圈引导面之间的摩擦力矩考虑在内.因为RV减速器主轴承的主要工作工况为低速重载, 根据4章的分析可知, 润滑黏性引起的摩擦力矩、保持架和套圈引导面之间的摩擦力矩在主轴承的低速工况下所占比重较小, 忽略这些摩擦力矩不会对RV减速器主轴承的摩擦力矩特性分析产生大的影响.
| [1] |
PALMGREN A. Ball and roller bearing engineering[M]. Philadelphia: SKF Industries Inc, 1959.
|
| [2] |
SNARE B. Rolling resistance in loaded ball bearings[J]. BallBearing Journal, 1968, 155: 12-21. |
| [3] |
TODD M J, STEVENS K T. Frictional torque of angular contact ball bearings with different conformities[R]. Risley:Technical Report ESA-CR(P)-1221, 1978. https://www.researchgate.net/publication/294705872_Frictional_torque_of_angula_contact_ball_bearings_with_different_conformities
|
| [4] |
HOUPERT L. Numerical and analytical calculations in ball bearings[J]. European Space Agency, 1999, 438: 283-290. |
| [5] |
HOUPERT L. Ball bearing and tapered roller bearing torque:analytical, numerical and experimental results[J]. Tribology Transactions, 2002, 45(3): 345-353. DOI:10.1080/10402000208982559 |
| [6] |
HOUPERT L. Rolling bearing torque[M]. Boston: Springer, 2013.
|
| [7] |
HARRIS T A, KOTZALAS M N. Essential concepts of bearing technology[M]. New York: Taylor & Francis, 2006.
|
| [8] |
GONCALVES D, PINHO S, GRA A B, et al. Friction torque in thrust ball bearings lubricated with polymer greases of different thickener content[J]. Tribology International, 2016, 96: 87-96. DOI:10.1016/j.triboint.2015.12.017 |
| [9] |
DENG S. Frictional torque characteristic of angular contact ball bearings[J]. Journal of Mechanical Engineering, 2011, 47(05): 114-120. DOI:10.3901/JME.2011.05.114 |
| [10] |
陈剑, 李松生, 陈斌, 等. 超高转速电主轴轴承内部摩擦力矩分析[J]. 润滑与密封, 2012, 37(9): 61-65. CHEN Jian, LI Song-sheng, CHEN Bin, et al. Analysis on friction torque in ultra high-speed electric spindle bearing[J]. Lubrication Engineering, 2012, 37(9): 61-65. |
| [11] |
陶润, 侯之超. 受径向力滚动轴承摩擦力矩的测试和函数拟合[J]. 清华大学学报:自然科学版, 2014, 54(6): 744-749. TAO Run, HOU Zhi-chao. Measurement and curve fitting of the friction torque of rolling bearings subjected to radial loads[J]. Journal of Tsinghua University:Science and Technology, 2014, 54(6): 744-749. |
| [12] |
姜绍娜, 陈晓阳, 顾家铭, 等. 低速灵敏球轴承摩擦力矩分析[J]. 中国机械工程, 2010, 21(5): 510-514. JIANG Shao-na, CHEN Xiao-yang, GU Jia-ming, et al. Analysis of friction torque of sensitive ball bearing under low speed[J]. China Mechanical Engineering, 2010, 21(5): 510-514. |
| [13] |
姜绍娜, 陈晓阳, 顾家铭, 等. 陀螺框架轴承摩擦力矩分析[J]. 机械工程学报, 2016, 52(7): 60-68. JIANG Shao-na, CHEN Xiao-yang, GU Jia-ming, et al. Analysis of friction moment of gyroscope frame bearing[J]. Journal of Mechanical Engineering, 2016, 52(7): 60-68. |
| [14] |
丁长安, 周章福, 朱均, 等. 滚道控制理论与滚动体姿态角的确定[J]. 机械工程学报, 2001, 37(2): 58-65. DING Chang-an, ZHOU Zhang-fu, ZHU Jun, et al. Raceway control assumption and the determination of rolling element attitude angle[J]. Journal of Mechanical Engineering, 2001, 37(2): 58-65. |
| [15] |
SKF(中国)有限公司. SKF轴承综合型录[G]. 上海: 上海科学技术文献出版社, 2008.
|
| [16] |
邓四二, 贾群义. 滚动轴承设计原理[M]. 北京: 中国标准出版社, 2014.
|
| [17] |
金津将幸, 太田浩之. ポリマ潤滑剤を封入した玉軸受の回転トルク:回転トルクの計算式(機械要素, 潤滑, 工作, 生産管理など)[J]. 日本機械学會論文集:C編, 2005, 71(701): 272-279. MASAYUKI K, HIROYUKI O. Running torque of ball bearings with polymer lubricant[J]. Transactions of the Japan Society of Mechanical Engineers:Series C, 2005, 71(701): 272-279. |
| [18] |
GUPTA S, TIWARI R, NAIR S B. Multi-objective design optimisation of rolling bearings using genetic algorithms[J]. Mechanism and Machine Theory, 2007, 42(10): 1418-1443. DOI:10.1016/j.mechmachtheory.2006.10.002 |
| [19] |
SAVSANI V. Multi-objective design optimization of rolling element bearings using abc, aia and pso technique[J]. International Journal of Energy Optimization and Engineering, 2013, 2(3): 102-125. DOI:10.4018/IJEOE |
| [20] |
陈锦江. 轴承数字化设计及其在高速陶瓷球轴承结构设计中的应用[D]. 天津: 天津大学, 2004. CHEN Jin-jiang. Digital design of bearings and its application of high-speed ceramic ball bearings in the structural parameter design[D]. Tianjin:Tianjin University, 2004. |



