2. 江西财经职业学院, 江西 九江 332000;
3. 浙江大学 浙江省服务机器人重点实验室, 浙江 杭州 310027;
4. 上饶职业技术学院, 江西 上饶 334109;
5. 审计署驻上海特派员办事处, 上海 200051
2. Jiangxi Vocational College of Finance and Economics, Jiujiang 332000, China;
3. Zhejiang Provincial Key Laboratory of Service Robot, Zhejiang University, Hangzhou 310027, China;
4. Shangrao Vocational and Technical College, Shangrao 334109, China;
5. Shanghai Agency of National Audit Office, Shanghai 200051, China
由于Internet的快速发展, 人类日常生活中产生的数据量正以指数形式增长.这些数据被人们通过网络进行无障碍交流、交换信息和协同工作[1].在我们的社会中, 存在相当一部分特殊人群, 他们由于身体上的残疾与缺陷, 导致无法正常使用互联网.截至2010年, 中国共有8 502万残疾人[2], 全世界残疾人口数超过10亿人[3], 可见, 特殊人群迫切需要网站提供信息无障碍服务, 保障信息平等、无障碍的获取.
为了更好地了解网站的无障碍程度, 对网站进行无障碍评测是非常重要的.为了降低成本, 采用抽样算法选取具有代表性的网页进行无障碍合规性检测.常用的抽样算法有随机抽样[4-5]和基于聚类的抽样算法[6].本文提出基于节点拓扑特性的间隔抽样算法.该算法中, 节点的拓扑排序至关重要.早些年, 由Page等[7]提出的PageRank算法模拟在网页链接图上的随机游走过程, 该方法利用拓扑图性质帮助网页节点排序, 实现不同网页的权重排名计算.之后, Taher等[8-9]对该算法进行了一系列的深入和研究.肖俐平等[10]提出基于拓扑势的节点重要性评价算法, 利用节点受自身和近邻节点共同影响所具有的势值进行排序, 局部拓扑效果较好.Xu等[11]主要将节点拓扑性质中的结构洞特性反映到节点的重要性上, 利用拓扑中节点位置的中心性分层次来确定节点具有结构洞特性的程度, 从而实现节点重要性排序, 全局拓扑效果较好.以上描述不同角度对节点重要性的排序.由于上述算法选取的拓扑特性过于局部化或全局化, 不能很好地表征节点在网络中的重要性和它们间的相似关系.
基于以上研究, 本文选取的节点拓扑特性既能反映节点拓扑性质中的局部特性, 又能反映全局特性, 能够很好地反映节点间的相似性.实验表明, 本文的抽样算法具有更小的抽样误差, 且抽取样本的分布性更好.
1 基于KNN-Graph算法构建邻接拓扑结构拓扑图技术, 即根据节点的相关性映射产生对应的拓扑图结构, 利用该结构可以分析节点之间的数据信息特性和关联性.拓扑结构在大数据云计算中的经典运用, 即为聚类分析[12].该聚类方法主要利用构图的方式, 将数据节点的相关性通过拓扑图形式来体现.最常见的构图算法是KNN邻近构图算法(K nearest neighbor graph, KNN-Graph), 它通过节点之间的近邻性, 找出任意节点与它最近的k个邻居节点链接成局部拓扑图.KNN-Graph算法在系统上较容易实现, 在样本分类、回归和构图中使用广泛[13-15].KNN-Graph算法受3个因素的影响:训练集、距离(相似度计算)、k.目前, 节点间相似性度量方法有很多[16-17].本文采用欧式距离, 衡量网页节点间的相似度.取k个离该节点欧式距离最小的网页作为它在拓扑图中的邻接点, 构成有向或无向拓扑图.在有向拓扑图中, 有向箭头从该节点分别指向k个最邻近节点.两个节点欧式距离越近, 说明相似度越高.具体模型如下.
设网络拓扑为G(V, E, W), 其中V为节点向量, E为边向量, W为边的权值向量.eij和wij分别为节点vi和vj连接的边和对应的权值, 相邻节点间边的默认权值wij=1.n为节点个数.网页节点vi的第q个检测点表示为vi(q).每个网页节点共有m个检测点, 检测点即为节点的特征属性, 也可以作为网页节点的维数.两个网页节点的欧式距离dij为
| $ {d_{ij}} = \sqrt {\sum\limits_{q = 1}^m {{{\left[ {{v_i}\left( q \right) - {v_j}\left( q \right)} \right]}^2}} } . $ | (1) |
每个网页样本都可以用它最接近的k个邻接点属性来回归, 该样本可以近似表示周围k个邻接点.在无向图中, 该节点和周围相邻k个节点间产生相互影响的作用力是相同的.在有向图中, 该节点对周围k个相邻节点产生的作用力超过周围单个相邻节点对该节点产生的作用力.因此, 将该节点作为起点, 分别指向k个最邻近节点.
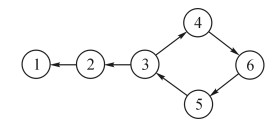
如图 1所示的有向图中, 设k=3, 离节点1最近的3个邻居是2、3和4, 节点4最近的3个邻居是1、5和6.

|
图 1 有向邻接拓扑图(k=3) Fig. 1 Directed adjacency topological graph (k=3) |
在网络拓扑中, 每个节点扮演着不同的角色, 不同角色的节点通过它们的拓扑性质来表征.如何准确地对节点重要性进行排序是后期抽样的基础.排序结果既反映节点在全网的重要性, 又能显示拓扑图密集子团, 子团里的节点应具有很高的相似度, 因此相似度高的节点会排列在一起.通过间隔采样, 选出相似节点中有代表性的样本点作为抽取的样本, 替代周围节点.采用以下常用的拓扑属性衡量节点局部和全局的重要性.
定义1 入度(Indegree)和出度(Outdegree).
对于有向图, 节点的入度是指进入该节点边的条数.入度反映其他节点到达该节点的概率.节点的入度越大, 说明节点越处于局部中心位置.该定义依据PageRank思想, 即节点的入度越大, 指向该节点的相邻节点会把越多的Score传递给该节点, 使得该节点的Score越高.该指标可以表示节点在局部拓扑图中的重要性.节点的出度指从该节点出发边的条数.它反映该节点到达其他节点的概率, 出度越大, 说明和该节点相似的邻接点越多, 越有可能成为该区域的核心节点.如图 1所示, 节点4的入度是1, 出度是3.当利用KNN-Graph算法构建有向图时, 由于k为每个节点邻接点的个数, 即每个节点的出度相同.将入度和出度结合起来, 作为一个属性运用于有向图中.设xi是节点vi的入度, yi是节点vi的出度.入度和出度的关系模式设为Ci, 如下所示:
| $ {C_i} = \left[ {1 - \exp \left( { - {x_i}} \right)} \right]\left( {1 - \exp \left( { - \ln {y_i}} \right)} \right);0 \le {C_i} \le 1. $ | (2) |
可知, Ci与入度和出度成正比关系.
定义2 马尔可夫稳定状态(Steady-state of Markov chain).
马尔可夫稳态性[18]有2个基本特征:一是“收敛性”, 马尔可夫过程逐渐趋于稳定状态, 与初始节点概率无关;二是“无后效性”, 即节点将来的状态概率, 只取决于该节点现在所处的状态, 与之前的时间状态无关.
设vi为当前节点, vj为相邻节点, vi的出度为d(i), 从vi开始随机游走, 到下一个节点vj的转移概率为Pij, 如下所示:
| $ {P_{ij}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\frac{1}{{d\left( i \right)}},}\\ {0,} \end{array}}&{\begin{array}{*{20}{c}} {节点\;{v_i}\;和\;{v_j}\;相邻;}\\ {节点\;{v_i}\;和\;{v_j}\;不相邻.} \end{array}} \end{array}} \right. $ | (3) |
每个节点经过多次跳转, 达到一个稳定状态.节点稳态概率越大, 说明节点在全局拓扑中的权重越高.设节点的转移概率矩阵为P, 节点处于稳定状态时的概率矩阵为π.设概率矩阵π中的元素为π(vi), 它表示节点vi经过多次变换后处于稳定状态的概率, 如下所示:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\pi }} = \mathit{\boldsymbol{\pi P}},\mathit{\boldsymbol{\pi }}\left( {{v_i}} \right) \in \mathit{\boldsymbol{\pi }},{P_{ij}} \in \mathit{\boldsymbol{P}};\\ \mathit{\boldsymbol{\pi }}\left( {{v_i}} \right) > 0,\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\pi }}\left( {{v_i}} \right) = 1.} \end{array} \right\} $ | (4) |
根据马尔科夫定理得出节点的转移概率矩阵P和节点处于稳态分布时的概率矩阵π, 根据π中元素的大小得出每个网页在该属性的值.
定义3 双连通性(Bi_connectivity).
节点的双连通性[19]指的是若有向图中两个节点之间既存在有向路径为e(vi, vj), 又存在有向路径为e(vj, vi), 则节点vi和节点vj可以相互到达, 它们互称双连通节点.一个节点的双连通节点个数越多, 说明该节点的连通性越强.双连通性越弱的节点越处于网络拓扑的信息传播边缘地位.双连通性越强的节点, 在有向图中越处于信息传播中心位置.从网页链接的角度考虑, 网页节点的连通能力越强, 说明用户可以从多个途径进入该网页, 它的可达性越强.从相似性来看, 说明与该节点的相似性高的节点个数越多, 该节点越具有普遍性.如图 2所示, 对于节点4, 它的双连通节点为3、6、5;对于节点1和2, 它没有双连通节点.从树形结构来看, 节点1和2是叶子节点, 处于边缘部位, 3、4、5、6处于主干部位.如果仅评价节点的双连通性可知, 3、4、5、6是等价的.
|
图 2 拓扑图示例样式 Fig. 2 Topology graph sample style |
定义4 介数(Betweenness).
拓扑图的介数特性[20]分为节点介数和边介数两种.节点介数定义为拓扑中经过该节点最短路径数目占所有节点最短路径总数的比例.边介数定义为网络中所有最短路径中经过该边的路径的数目占所有节点最短路径总数的比例.本文采用节点介数.节点介数越大, 说明经过该节点的路径越多, 该节点在拓扑图中越重要.设节点vi的介数为B(vi), 即
| $ B\left( {{v_i}} \right) = \sum\limits_{{v_s} \ne {v_i} \ne {v_t} \in V} {\frac{{{\delta _{{v_s}{v_t}}}\left( {{v_i}} \right)}}{{{\delta _{{v_s}{v_t}}}}}} . $ | (5) |
式中:δvsvt(vi)为vs到vt经过节点vi的最短路径个数, δvsvt为vs到vt所有最短路径个数.直观上来说, 介数反映节点作为桥梁的重要程度, 它是一个重要的全局几何量.
定义5 离心率(Eccentricity).
按图论定义可知, 离心率[21]是取节点到其他所有节点最短距离中的最大值作为该节点的离心率.离心率能够表征节点离拓扑重心的相对位置, 从拓扑结构的全局特征来评估节点重要性.节点离心率越小, 则离拓扑图的重心位置越近, 该节点越重要.离心率为
| $ E\left( {{v_i}} \right) = \max d\left( {{v_i},{v_j}} \right);{v_j} \in V. $ | (6) |
式中:E(vi)为节点vi的离心率, dij为节点vi到vj的最短距离.
定义6 集聚系数(Clustering_coefficient).
群簇反映相邻节点的聚集程度, 节点聚集程度越大, 说明它们通过网络进行传输和交互更容易.在图论中, 有一个指标可以衡量这种属性, 即集聚系数[22].有局部集聚系数, 也有全局集聚系数.对于节点vi, 它的邻居节点之间存在的边数与可能存在的最大边数的比值定义为节点vi的局部集聚系数.网络的全局集聚系数是对所有节点的集聚系数求平均值.该节点的集聚系数越高, 表征该节点处于密集子团的可能性越高, 越具有代表性.采用局部集聚系数作为节点拓扑特性的表征.设vi节点的集聚系数为CL(vi), 如下所示:
| $ {\rm{CL}}\left( {{v_i}} \right) = \frac{{2\left| {{e_{rk}}} \right|}}{{{a_i}\left( {{a_i} - 1} \right)}}. $ | (7) |
式中:|erk|为节点vi的相邻节点vr和vk间的链接边数, ai为节点vi的入度和出度之和.
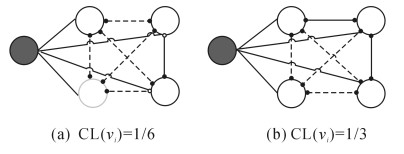
如图 3(a)、(b)所示为灰色节点vi和相邻4个节点的关系图.其中, 实线表示两个节点相连, 虚线表示两个节点不相连.
|
图 3 局部拓扑图节点集聚系数 Fig. 3 Local topological graph node clustering coefficient |
如何将节点的多个拓扑特性进行拟合, 从而得出每个节点在网络拓扑中的重要性.常用的多属性评估方法有简单线性加权法(simple weight adding), 它利用预定的各个属性权重, 对各个属性进行归一化处理.通过线性加权求出总方案的融合值, 根据融合值的大小进行排序选择最佳方案.理想点法[23](technique for order preference by similarity to ideal solution)借助样本点和正负理想样本点的距离的关系, 定义每个样本在多属性下的优先顺序.该方法需要定义一个测度, 衡量方案离理想方案和负理想方案的距离, 并且事先要准确挑选理想样本点和负理想样本点.由于样本数量庞大, 样本随机, 如何准确找出理想方案点和负理想方案点非常重要.本文提出一种最容易理解和计算的综合指标排序法.将网络节点的每一个拓扑属性看作一个方案, 得出对应的单属性在整个网络的分数, 然后进行归一化处理.对比同一节点的不同属性时, 要将各个属性值归一化到[0,1]内.设R为所有网页节点的多属性归一化后的分数矩阵, 如下:
| $ R = \left[ {\begin{array}{*{20}{c}} {{R_1}\left( 1 \right)}&{{R_1}\left( 2 \right)}& \cdots &{{R_1}\left( m \right)}\\ {{R_2}\left( 1 \right)}&{{R_2}\left( 2 \right)}& \cdots &{{R_2}\left( m \right)}\\ {{R_3}\left( 1 \right)}&{{R_3}\left( 2 \right)}& \cdots &{{R_3}\left( m \right)}\\ \vdots & \vdots &{}& \vdots \\ {{R_t}\left( 1 \right)}&{{R_t}\left( 2 \right)}& \cdots &{{R_t}\left( m \right)} \end{array}} \right]. $ | (8) |
式中:Rt(m)为第t个网页在第m个属性的归一化值, 即检测点的分数.
计算一个节点的各个属性分数的调和均值, 它作为该网页的总分, 并储存在MR(t)中.MR(t)代表该网页的权重, 如下所示:
| $ {\rm{MR}}\left( t \right) = {\left[ {\frac{{\sum\limits_{m = 1}^m {R_t^{ - 1}\left( m \right)} }}{m}} \right]^{ - 1}}. $ | (9) |
网页总分越高, 表明权重越高.根据总分从大到小对节点进行排序, 可以得到网页排序后的索引向量idx, 如下所示:
| $ {\bf{idx}} = {\left[ {{\rm{i}}{{\rm{d}}_1},{\rm{i}}{{\rm{d}}_2},{\rm{i}}{{\rm{d}}_3}, \cdots ,{\rm{i}}{{\rm{d}}_t}} \right]^{\rm{T}}}. $ | (10) |
式中:idt表示排在第t个位置的网页id号.根据网页索引向量找到对应的样本矩阵, 以便后期进行间隔抽样.
3 间隔抽样上述过程能够建立节点间的相似关系, 将具有相似性高的网页排列在一起.若不采用间隔抽样, 直接抽取排在前面的节点, 则可以得到具备结构洞性质的节点[11], 即许多子图都要通过具有结构洞性质的节点连接起来.若没有这些点, 则整个拓扑图变成一些小的子图.它们称为拓扑图的支点, 这些点往往是分布在全局的点, 但只占少部分.大部分节点都是通过结构洞链接的子团节点, 每个子团中节点的重要性与它链接的结构洞节点的重要性相关.越是核心的节点, 它周围的节点重要性越高.例如, 在网站中重要的网页都是点击率极高的网页.这样的网页是很多网页链接的桥梁, 它会把点击率影响到周围链接的网页中.总之, 从节点排序中可以从不同角度看到节点的性质分布, 获取感兴趣的节点.本文提出利用间隔抽样算法, 提升抽取节点的全局覆盖性.
节点的拓扑性质体现它在图中的重要程度, 因此通过提出的多个拓扑性质来对节点进行排序.可以把具有相同拓扑特性的节点排列在一起, 从而可以在排序后的网页中进行间隔抽样, 增大抽取样本的多样性.设抽取样本索引号矩阵为sa, 样本总数为n, 抽取的样本数目为sn, 抽取样本的间隔长度为x, 它们的关系如下所示:
| $ \left. {\begin{array}{*{20}{c}} {x = \left\lfloor {\frac{{n - 1}}{{{s_n}}}} \right\rfloor ,}\\ {{\mathit{\boldsymbol{s}}_{\rm{a}}} = \left[ {1,x + 1,2x + 1,3x + 1, \cdots ,{s_{\rm{n}}}x + 1} \right].} \end{array}} \right\} $ | (11) |
按照一定的间隔长度进行抽样, 以便从不同区域的相似节点中抽取样本点, 使抽样效果更具有区域分布性, 避免同一个区域的相似样本抽取多次.
若考虑从单个属性排序结果进行间隔抽样, 则会造成一定的误差.例如, 入度和出度、集聚系数是从节点局部特征出发考虑的拓扑性质, 不包含全局位置信息, 这样会造成不同位置具有相同的入度和出度的节点排列到一起, 局部子团节点也排列在一起, 从而使得间隔抽样不能具有较好的全局覆盖性, 抽样均值与总体样本均值相比, 误差较大;若单从全局特征属性进行排序, 如离心率和介数等, 从全局位置考虑节点重要性的拓扑特性, 则局部子团节点的相关性会被丢弃, 导致排序中局部子团无法集聚, 间隔抽样误差较大.本文对节点的排序是结合拓扑图节点的局部和全局特性进行综合评估, 对间隔抽样具有较好的适应性.
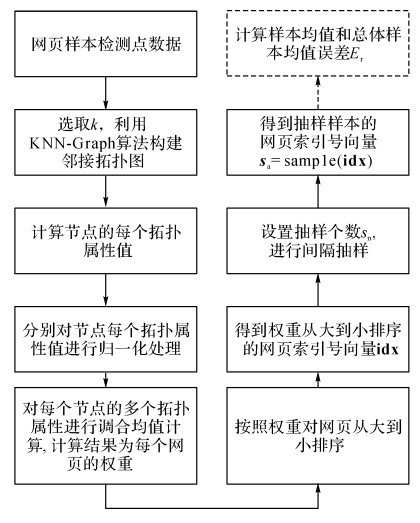
具体的抽样过程如图 4所示.首先, 利用样本间的特征数据转换为邻接相似拓扑图.之后, 对节点的每个拓扑属性进行归一化, 利用调和均值计算节点多属性的综合排序权重.最后, 采用间隔抽样算法进行分布抽样.
|
图 4 基于节点拓扑特性的抽样模型 Fig. 4 Sampling model based on node topological characteristics |
实验平台建立在浙江省服务机器人重点实验室——无障碍网站检测平台.无障碍网站检测平台是从多个检测点进行测试, 评估网页是否符合国家无障碍标准, 以便符合残疾人的使用要求.实验中所用的网站数据分为各个网页检测点信息及检测点实际达标数据.前者作为网页的特征向量, 用于计算网页间相似度构图;后者代表网页评测结果, 用于衡量利用不同抽样算法所得的评估结果与真实评估结果的误差.
如表 1所示为各地区残联网站的样本总数.每个地区的样本为一个样本数据集.如表 2所示为浙江省无障碍网站的部分检测数据.选择前3个检测点数据和对应检测点的3个达标数据, 分别计算总体样本通过率的均值和抽样算法抽取样本的通过率均值.
| 表 1 各地区残联网站数目 Table 1 Number of disabled person federation website |
| 表 2 浙江省残联网站部分检测数据 Table 2 Part detection data of Zhejiang disabled person federation website |
设每个网页第i个检测点通过率为passrate(i), n为计算通过率的网页样本数量, avg(passrate(i))为网页中第i个检测点通过率的均值, 即
| $ \left. \begin{array}{l} {\rm{passrate}}\left( i \right) = \frac{{{\rm{checkpoint}}\left( i \right)}}{{{\rm{check}}\left( i \right)}},\\ {\rm{avg}}\left( {{\rm{passrate}}\left( i \right)} \right) = \sum\limits_{i = 1}^n {{\rm{passrate}}\left( i \right)} /n. \end{array} \right\} $ | (12) |
式中:check(i)为网页样本集满足无障碍的第i个标准数据, checkpoint(i)为实际对网页进行检测的第i个达标数据.首先, 提取无障碍检测平台对各地区残联网监控的6个检测点数据check(i).利用KNN-Graph构图算法对9个地区、6个检测点数据分别构建邻接拓扑图, 根据不同网站的网页数量设定k.邻接拓扑图中节点的7个拓扑属性如下所示:s1→马尔可夫稳定状态概率, s2→入度和出度关系, s3→双连通, s4→介数, s5→集聚系数, s6→离心率, s7→入度.
其中, s1、s4、s5、s6用于无向图, s2、s3、s7用于有向图.可得每个节点各个属性归一化后的数据值.利用调合均值, 可得所有网页在本网站中的权重, 从大到小进行排序.之后, 按照每个网站的网页数量和抽取样本数量的对应关系进行分布抽样.如表 3所示为本文算法和其他4种算法对浙江省残联网站中的5 714个样本进行抽样检测时, 抽取10个样本的单次样例.如表 4所示, At为总样本均值,Ao为本文抽样算法均值.以浙江省为例, 对本文方法的评估结果与真实结果进行对比.
| 表 3 浙江省残联网站抽取10个样本的单次样例 Table 3 Zhejiang disabled person federation website with extracting 10 samples one time |
| 表 4 浙江省残联网站通过率均值对比 Table 4 Zhejiang disabled person federation website passing rate average comparison |
为了论证本文的抽样算法具有更好的抽样效果.将本文算法与其他抽样算法进行对比分析.随机抽样算法常作为对比算法, 用于比较抽样算法[24-26]的效果.随机抽样算法保证抽样数据集中的每个部分都有同等被抽中的概率, 是一种完全依照机会均等原则进行的抽样调查, 因此该算法的适用范围广泛.将本文算法与PageRank[7]算法、基于KMeans的抽样算法及Top算法进行比较.将本文节点排序算法换成PageRank节点排序算法, 在PageRank排序的基础上采用间隔抽样.KMeans算法是聚类分析中常用的划分方法.本文通过KMeans算法将原始数据划分为k个聚类, 聚类个数与抽样个数一致, 从每个聚类抽取一个样本作为该类的样本点.Top算法基于本文节点排序, 取前n个样本.在本文实验中, 同时对9个地区残联网站进行多种抽样算法测试, 并分别抽取50次, 每次对应抽取1~50个样本进行误差分析.由于随机算法抽取的样本不稳定, 单次随机抽取时样本误差较大或较小.为此, 实验要求每次随机抽取50次样本, 并利用这50次样本的平均误差代表随机算法的误差, 以便减少单次实验结果的特殊性.
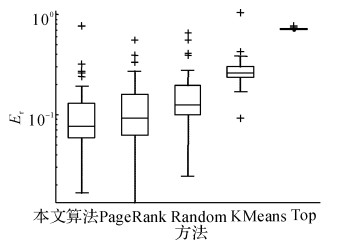
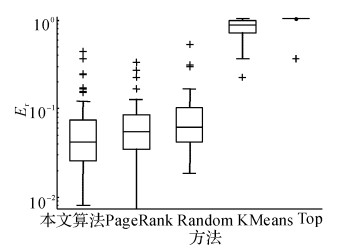
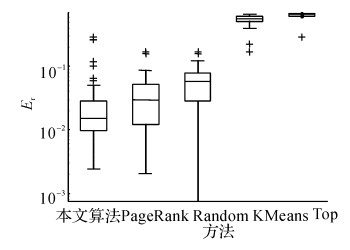
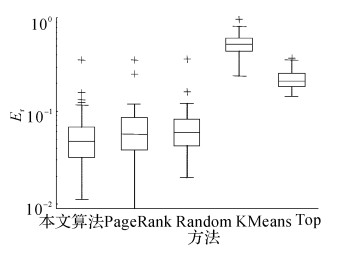
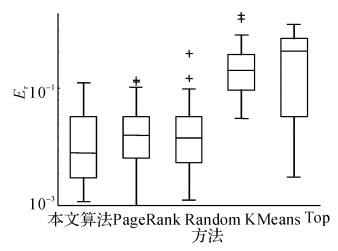
如图 5~13所示为各个省份的误差示意图.如图 14所示为不同省份按1%的总样本进行抽样的误差对比图.平均误差数据如表 5所示.从实验结果可知, 本文算法的抽样效果最好, 误差分布最稳定.例如表 5中广东省PageRank算法的平均抽样误差虽然最小, 但对照广东省误差示意图可知, 本文算法的抽样误差更稳定, PageRank算法的误差波动较大, 因此PageRank算法不理想.Top算法效果最差, 说明本文采用的间隔抽样算法在不同节点排序上, 效果是显著的.随机算法的抽样误差较稳定, 但整体误差较大, 不合适.KMeans算法误差较大, 由于原始数据样本分布不均匀, 一些过大的异常值会带来很大影响, 造成聚类时存在一定的误差.综上所述, 本文算法的总体效果最好.
| 表 5 算法平均误差比较 Table 5 Comparison of mean error between differentalgorithms |
|
图 5 浙江省残联网站数据误差比较(k=23, sn=1~50) Fig. 5 Zhejiang disable person federation website data error comparison |
|
图 6 广东省残联网站数据误差比较(k=283, sn=1~50) Fig. 6 Guangdong disable person federation website data error comparison |
|
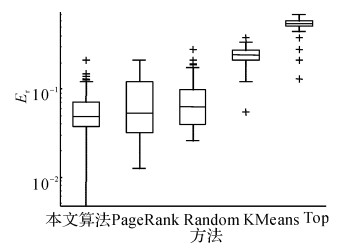
图 7 江西省残联网站数据误差比较(k=251, sn=1~50) Fig. 7 Jiangxi disable person federation website data error comparison |
|
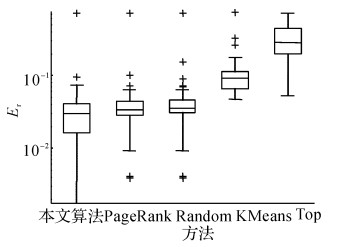
图 8 重庆残联网站数据误差比较(k=29, sn=1~50) Fig. 8 Chongqing disable person federation website data error comparison |
|
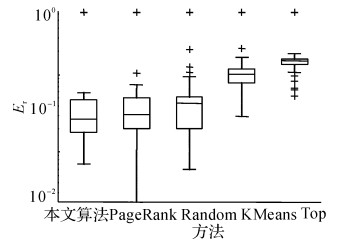
图 9 江苏省残联网站数据误差比较(k=235, sn=1~50) Fig. 9 Jiangsu disable person federation website data error comparison |
|
图 10 宁夏残联网站数据误差比较(k=295, sn=1~50) Fig. 10 Ningxia disable person federation website data error comparison |
|
图 11 贵州残联网站数据误差比较(k=267, sn=1~50) Fig. 11 Guizhou disable person federation website data error comparison |
|
图 12 新疆残联网站数据误差比较(k=219, sn=1~50) Fig. 12 Xinjiang disable person federation website data error comparison |

|
图 13 湖北残联网站数据误差比较(k=291, sn=1~50) Fig. 13 Hubei disable person federation website data error comparison |
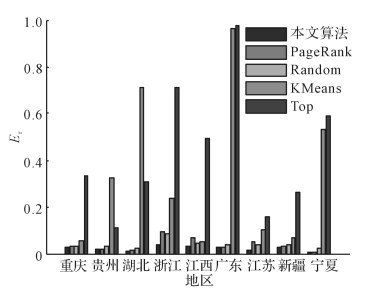
|
图 14 抽取样本的误差比较 Fig. 14 Extracting sample for error comparison |
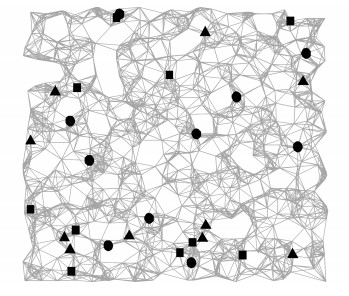
为了更好地比较本文算法与PageRank算法及随机算法抽样效果的分布性, 采用二维可视化平面图的方式, 分别生成300、1 000、3 000个二维数据, 可视化效果如图 15~17所示.圆形点是本文抽取的样本点, 方形点是随机抽样算法抽取的样本点, 三角形是PageRank算法抽取的样本点.本文将二维数据映射到可视化的拓扑图中.可以看出, 在图 15~17中, 本文算法在各个区域基本上都进行了样本抽取, 覆盖面更广, 每个区域基本上都有样本点被抽取, 抽取的样本点分布均衡.其他两种算法的覆盖性较差, 一些区域的样本没有被抽取, 一些区域的相似样本被抽取多次, 抽取样本的代表性较差.3种算法在二维样本数据的抽样误差如表 6所示.可知, 无论是从抽样误差还是分布性上来看, 本文算法的抽样效果均最优.

|
图 15 300个二维数据样本 Fig. 15 300 two-dimension data samples |
|
图 16 1 000个二维数据样本 Fig. 16 1 000 two-dimension data samples |

|
图 17 3 000个二维数据样本 Fig. 17 17 3 000 two-dimension data samples |
| 表 6 二维数据抽样误差 Table 6 Two-dimensional data sample error |
无障碍网站的抽样算法研究是一项重要的研究课题.基于现有的抽样算法存在样本误差大和抽取的样本分布不均衡等问题, 本文提出基于节点拓扑特性的间隔抽样算法.从拓扑结构入手, 将节点间的相似性以拓扑结构的形式展现出来.利用节点的拓扑属性得出节点的权重, 按照权重大小进行排序, 将相似的节点集聚起来, 并按照一定的间隔长度进行采样, 使采集的样本更具有分布性和多样性.对各地区残联网站进行抽样检测, 与4种典型算法进行对比分析.通过真实数据的实验结果验证可知, 本文的抽样方法是可行的.该方法不仅适用于无障碍网站, 而且适用于其他多维特征的网站数据.接下来的研究任务是确定k与样本总数据量间的关系, 检测维度更高的样本数据.用多维可视化的形式显示实验数据, 使实验更具有充分性和论证性.
| [1] |
刘智慧, 张泉灵. 大数据技术研究综述[J].
浙江大学学报:工学版, 2014, 48(6): 957–972.
LIU Zhi-hui, ZHANG Quan-ling. Reseach overview of big data technology[J]. Journal of Zhejiang University:Engineering Science, 2014, 48(6): 957–972. |
| [2] | 中国残疾人联合会关于使用2010年末全国残疾人总数及各类、不同残疾等级人数的通知[R/OL]. [2012-06-26]. http://www.cdpf.org.cn/ggtz/201203/t20120312_410693.shtml. |
| [3] | WHO, 世界银行世界残疾问题报告[R/OL]. [2011-06-09]. http://www.docin.com/p-297463652.html. |
| [4] |
刘学慧, 王东博, 曲波, 等. 随机抽样方法在医学教学中的应用及计算机实现[J].
中国医科大学学报, 2013, 42(5): 460–462.
LU Xue-hui, WANG Dong-bo, QU Bo, et al. Application of random sampling method in medical teaching and comuter implementation[J]. Journal of China Medical University, 2013, 42(5): 460–462. |
| [5] | WEST P W. Sample random sampling of individualitems in the absence of a sampling frame that lists the individuals[J]. New Zealand Journal of ForestryScience, 2016, 46(15): 1–7. |
| [6] | HUANG Z. Extensions to the Kmeans algorithm for clustering large data sets with categorical values[J]. Data Mining and Knowledge Discovery, 1998, 2(3): 283–304. DOI:10.1023/A:1009769707641 |
| [7] | PAGE L, BRIN S, MOTWANI R, et al. Technical report, Stanford Digital Library Technologies Project. The PageRank citation ranking:bringing order to the web[R/OL].[2001-10-13]. http://dbpubs.stanford.edu/pub/1999-66. |
| [8] | TAHER H H. Topic-sensitive PageRank[C]//Proceedings of the 11th International Conference on World Wide Web. Honolulu:IEEE, 2002:517-526. https://en.wikipedia.org/wiki/Topic-Sensitive_PageRank |
| [9] | TAHER H H. Technical report, Stanford University. Efficient computation of PageRank[R/OL].[2000-02-25]. http://dbpubs.stanford.edu:8090/pub/1999-31. |
| [10] |
肖俐平, 孟晖, 李德毅. 基于拓扑势的网络节点重要性排序及评价方法[J].
武汉大学学报:信息科学版, 2008, 33(4): 380–383.
XIAO Li-ping, MENG Hui, LI De-yi. Approach to node ranking in a network based on topology potential[J]. Geomatics and Information Science of Wuhan Uni-versity, 2008, 33(4): 380–383. |
| [11] | XU H, ZHANG J P, YANG J. Measurement of nodes importance for structural-holes-oriented[C]//Proceedings of Pioneering Computer Scientists, Engineers and Educators(ICYCSEE). Harbin:Springer, 2016:458-469. |
| [12] | ULRIKE V L. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4): 395–416. DOI:10.1007/s11222-007-9033-z |
| [13] | ZHANG S C, ZONG M, SUN K, et al. Efficient KNN algorithm based on graph sparse reconstruction[C]//Proceedings of Advanced Data Mining and Applications(ADMA). Guilin:[s. n.], 2014:356-369. https://link.springer.com/chapter/10.1007/978-3-319-14717-8_28 |
| [14] | MASAJIRO I. Pruned bi-directed K-nearest neighbor graph for proximity search[C]//Proceedings of Similarity Search and Applications (SISAP). Tokyo:Springer, 2016:20-33. https://link.springer.com/chapter/10.1007/978-3-319-46759-7_2 |
| [15] | UGUR D, FAMOUSH B, CYRUS S, et al. Towards K-nearest neighbor search in time dependent spatial network databases[C]//Proceedings of Databases in Networked Information Systems(DNIS). Aizu-Wakamatsu:Springer, 2010:296-310. https://link.springer.com/chapter/10.1007/978-3-642-12038-1_20 |
| [16] | MAX K, JORGEN Z. A. Similarity measure in Bayesian classification based on characteristic attributes of objects[C]//Proceedings of Information Fusion. Heidelberg:IEEE, 2016, 5:1-8. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7527927 |
| [17] | ALFIRNA R L, ADHISTYA E P, NOOR A S. Cosine similarity to determine similarity measure:Study case in online essay assessment[C]//Proceedings of International Conference on Cyber and it Service management. Djakarta:IEEE, 2016. https://www.deepdyve.com/lp/institute-of-electrical-and-electronics-engineers/cosine-similarity-to-determine-similarity-measure-study-case-in-online-71FSFnrJ3R |
| [18] | GOBEL F, JAGERS A A. Random walks on graphs[J]. Stochastic Processes and Their Applications, 1974, 2(4): 311–336. DOI:10.1016/0304-4149(74)90001-5 |
| [19] | SEAN G, TINA E R, LAN D. Guided learning for role discovery (GLRD):framework, algorithms, and applications[C]//Proceedings of Knowledge Discovery and Data Mining. Chicago:ACM, 2013:113-121. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.385.6512 |
| [20] | WATTS D J, STROGATZ S H. Collective dynamics of "small-world" networks[J]. Nature, 1998, 393: 440–442. DOI:10.1038/30918 |
| [21] | MURIEL G, RICARDO A, JOSE C Q, et al. Encyclopedia of astrobiology[M]. Berlin: Springer, 2011: 28-29. |
| [22] | FREEMAN L C. A set of measures of centrality based upon betweenness[J]. Sociometry, 1977, 40(1): 35–41. DOI:10.2307/3033543 |
| [23] |
于会, 刘尊, 李勇. 基于多属性决策的复杂网络节点重要性综合评价方法[J].
物理学报, 2013, 62(2): 41–49.
YU Hui, LIU Zun, LI Yong. Key nodes in complex networks identified by multi-attribute decision-making method[J]. Acta Physica Sinica, 2013, 62(2): 41–49. |
| [24] | HENZINGER M R, HEYDON A, MITZENMACHER M, et al. On near-uniform URL sampling[J]. Computer Networks, 2000, 33(1): 295–308. |
| [25] | ZHANG M N, WANG C, BU J J, et al. A sampling method based on URL clustering for fast Web accessibility evaluation[J]. Frontiers of Information Technology and Electronic Engineering, 2015, 16(6): 449–456. |
| [26] |
周宇. 基于抽样和模板的网站无障碍检测方法[D]. 杭州: 浙江大学, 2014.
ZHOU Yu. Web accessibility evaluation approaches based on sampling and template detection[D]. Hangzhou:Zhejiang University, 2014. |



